Automatic Atrial Fibrillation Arrhythmia Detection Using Univariate and Multivariate Data
Abstract
:1. Introduction
2. Clinical Experience
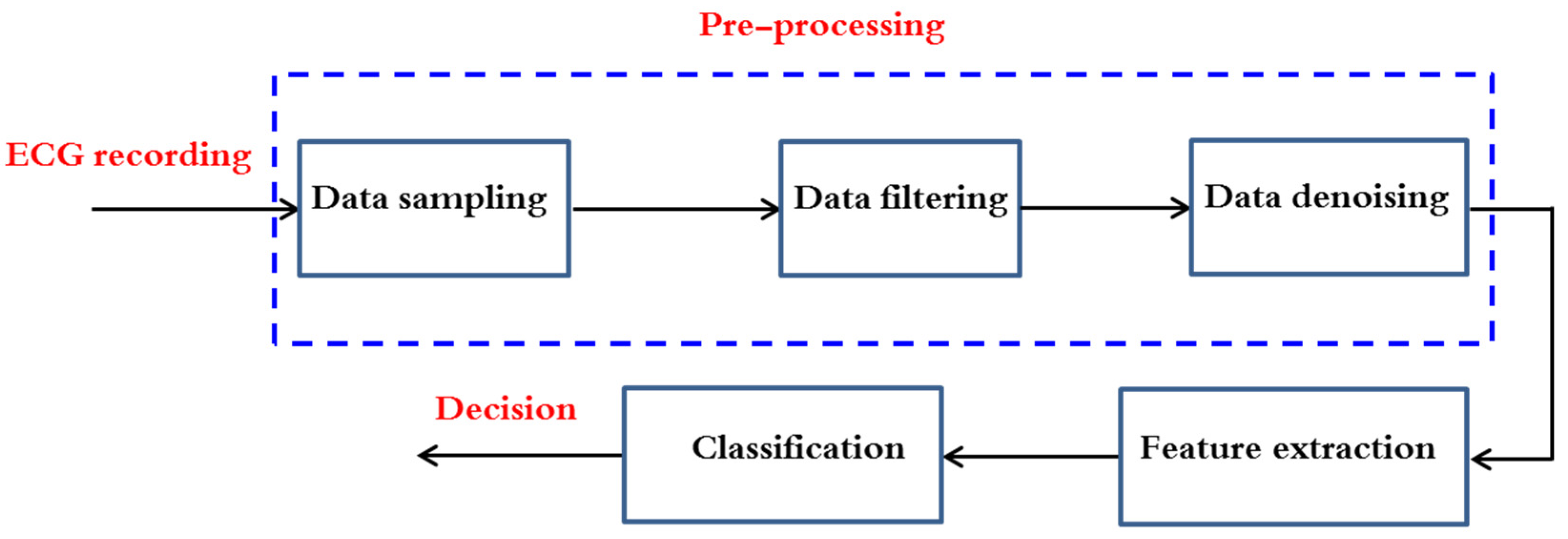
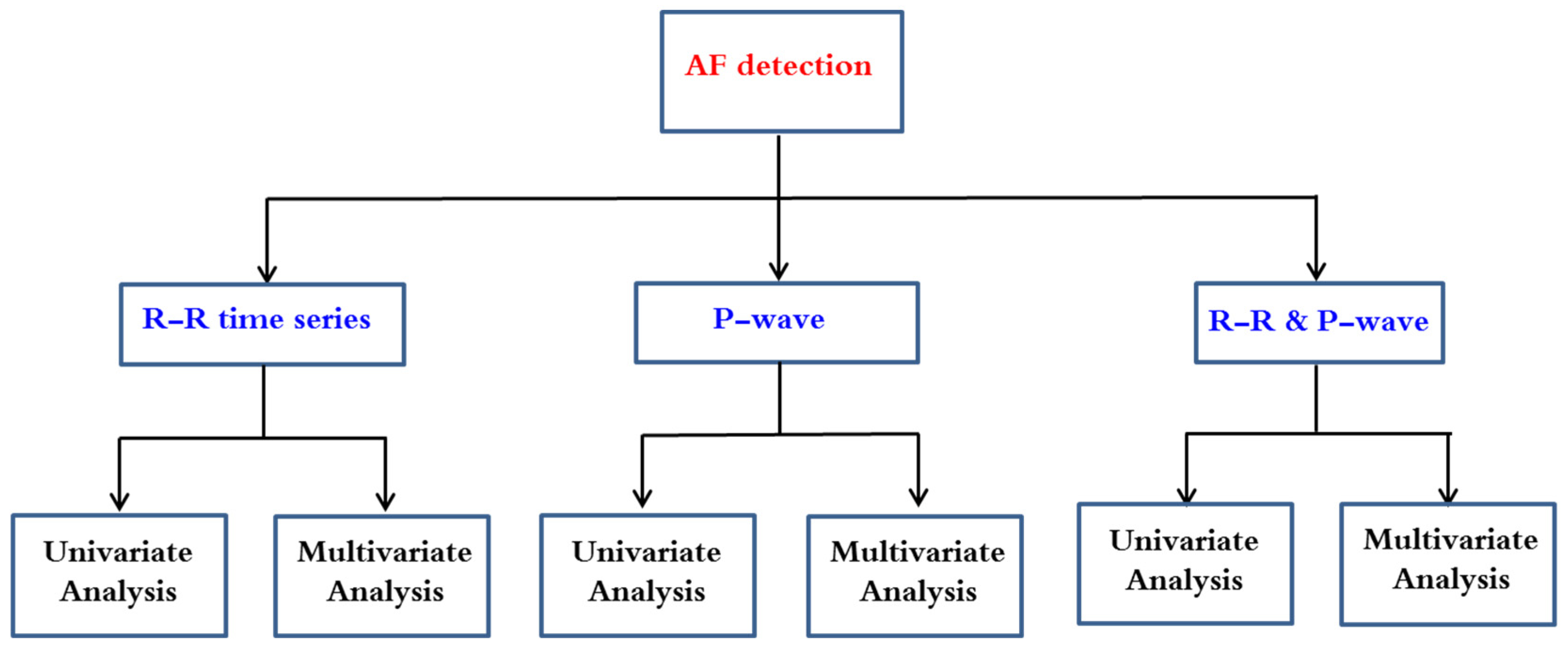
3. AF Arrhythmia Detection Methods
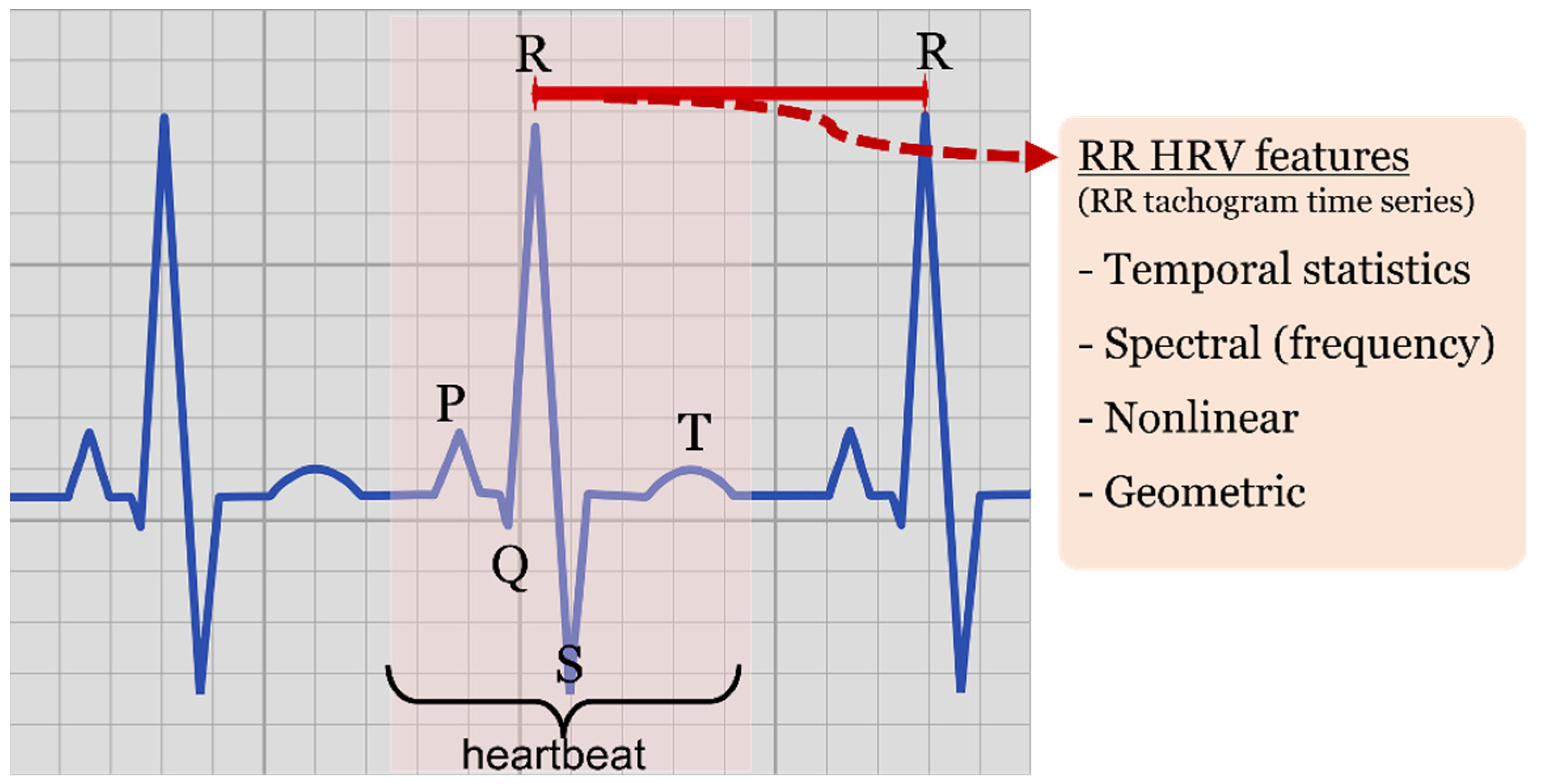
- Statistical features of temporal nature, such as minimum RR intervals (minRR), maximum RR interval (maxRR), mean RR (<RR>), RR standard deviation (SDRR), root mean square of successive ΔRR differences (RMSSD) and standard deviation of successive differences (SDSD) working as derivative approximations, pNN20 and pNN50 ratios characterizing the amount of heartbeat intervals greater than a given value (20 or 50 milliseconds, respectively) with respect to all the intervals within the processed window.
- Nonlinear features, such as those derived by the elliptic geometry of the recurrence plot depicting RRi-RRi+1 consecutive interval relationship (known as Poincaré recurrence plot or Lorenz plot depending on the research discipline).
- Spectral (frequency) features of the tachogram, characterizing power spectral densities, and different spectral band ratios obtained by spectral analysis methods such as Fourier transform approximations, Lomb-Scargle estimates or wavelet transforms, among others.
- Geometric features, derived by histogram shape analysis, such as triangular indexes and interpolation.
3.1. Application of Univariate Data Analysis on RR Time Series
3.2. Application of Multivariate Data Analysis on RR Time Series
3.3. Summary of RR-Based Automated AF Detection Research Studies
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Vilahur, G.; Badimon, J.J.; Bugiardini, R.; Badimon, L. Perspectives: The burden of cardiovascular risk factors and coronary heart disease in Europe and worldwide. Eur. Heart J. Suppl. 2014, 16, A7–A11. [Google Scholar] [CrossRef] [Green Version]
- World Health Organization. Cardiovascular Diseases, 2021. Available online: https://www.who.int/en/news-room/fact-sheets/detail/cardiovascular-diseases-(cvds) (accessed on 25 May 2022).
- Naccarelli, G.V.; Varker, H.; Lin, J.; Schulman, K.L. Increasing prevalence of atrial fibrillation and flutter in the United States. Am. J. Cardiol. 2009, 104, 1534–1539. [Google Scholar] [CrossRef] [PubMed]
- Stewart, S.; Murphy, N.; Walker, A.; McGuire, A.; McMurray, J.J.V. Cost of an emerging epidemic: An economic analysis of atrial fibrillation in the UK. Heart 2004, 90, 286–292. [Google Scholar] [CrossRef] [Green Version]
- Jabaudon, D.; Sztajzel, J.; Sievert, K.; Landis, T.; Sztajzel, R. Usefulness of ambulatory 7-day ECG monitoring for the detection of atrial fibrillation and flutter after acute stroke and transient ischemic attack. Stroke 2004, 35, 1647–1651. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Heeringa, J.; van der Kuip, D.A.; Hofman, A.; Kors, J.A.; van Herpen, G.; Stricker, B.H.C.; Stijnen, T.; Lip, G.Y.H.; Witteman, J.C.M. Prevalence, incidence and lifetime risk of atrial fibrillation: The Rotterdam study. Eur. Heart J. 2006, 27, 949–953. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, L.S.C.; Wang, C.C.; Xia, Y.L.; Wu, G.; Wang, F.; Xu, C.Q.; Wang, P.Y.; Li, X.C.; Wang, D.; Xiong, X.; et al. Assessment of association of rs2200733 on chromosome 4q25 with atrial fibrillation and ischemic stroke in a Chinese Han population. Hum. Genet. 2009, 126, 843–849. [Google Scholar]
- Go, A.S.; Hylek, E.M.; Phillips, K.A.; Chang, Y.C.; Henault, L.E.; Selby, J.V.; Singer, D.E. Prevalence of diagnosed atrial fibrillation in adults—National implications for rhythm management and stroke prevention: The AnTicoagulation and Risk Factors in Atrial Fibrillation (ATRIA) study. J. Am. Med. Assoc. 2001, 285, 2370–2375. [Google Scholar] [CrossRef] [PubMed]
- Stewart, S.; Hart, C.L.; Hole, D.J.; McMurray, J.J.V. Population prevalence, incidence, and predictors of atrial fibrillation in the Renfrew/Paisley study. Heart 2001, 86, 516–521. [Google Scholar] [CrossRef]
- Feinberg, W.M. Prevalence, Age Distribution, and Gender of Patients with Atrial Fibrillation. Arch. Intern. Med. 1995, 155, 469. [Google Scholar] [CrossRef]
- Murphy, N.F.; Simpson, C.R.; Jhund, P.S.; Stewart, S.; Kirkpatrick, M.; Chalmers, J.; MacIntyre, K.; McMurray, J.J.V. A national survey of the prevalence, incidence, primary care burden and treatment of atrial fibrillation in Scotland. Heart 2007, 93, 606–612. [Google Scholar] [CrossRef]
- Tsang, T.S.; Petty, G.W.; Barnes, M.E.; O’Fallon, W.M.; Bailey, K.R.; Wiebers, D.O.; Sicks, J.D.; Christianson, T.J.; Seward, J.B.; Gersh, B.J. The prevalence of atrial fibrillation in incident stroke cases and matched population controls in Rochester, Minnesota: Changes over three decades. J. Am. Coll. Cardiol. 2003, 42, 93–100. [Google Scholar] [CrossRef] [Green Version]
- Kornej, J.; Börschel, C.S.; Benjamin, E.J.; Schnabel, R.B. Epidemiology of Atrial Fibrillation in the 21st Century. Circ. Res. 2020, 127, 4–20. [Google Scholar] [CrossRef] [PubMed]
- Poli, S.; Barbaro, V.; Bartolini, P.; Calcagnini, G.; Censi, F. Prediction of atrial fibrillation from surface ECG: Review of methods and algorithms. Ann. Dell’istituto Super. Di Sanità 2003, 39, 195–203. [Google Scholar]
- Larburu, N.; Lopetegi, T.; Romero, I. Comparative Study of Algorithms for Atrial Fibrillation Detection. Comput. Cardiol. 2011, 38, 265–268. [Google Scholar]
- Committee to Develop Guidelines for the Management of Patients with Atrial Fibrillation. A Report of the American College of Cardiology/ American Heart Association Task Force on Practice Guidelines and the European Society of Cardiology Committee for Practice Guidelines and Policy Conferences. Circulation 2001, 104, 2118–2150. [Google Scholar] [CrossRef] [Green Version]
- Kirchhof, P.; Benussi, S.; Kotecha, D.; Ahlsson, A.; Atar, D.; Casadei, B.; Castella, M.; Diener, H.C.; Heidbuchel, H.; Hendriks, J.; et al. 2016 ESC Guidelines for the management of atrial fibrillation developed in collaboration with EACTS. Eur. Heart J. 2016, 37, 2893–2962. [Google Scholar] [CrossRef] [Green Version]
- Babaeizadeh, S.; Gregg, R.E.; Helfenbein, E.D.; Lindauer, J.M.; Zhou, S.H. Improvements in atrial fibrillation detection for real-time monitoring. J. Electrocardiol. 2009, 42, 522–526. [Google Scholar] [CrossRef]
- Carvalho, P.; Henriques, J.; Couceiro, R.; Harris, M.; Antunes, M.; Habetha, J. Model-based atrial fibrillation detection. In ECG Signal Processing, Classification and Interpretation; Gacek, A., Pedrycz, W., Eds.; Springer: London, UK, 2012; pp. 99–133. [Google Scholar]
- Ramos, G.; Alfaras, M.; Gamboa, H. Real-Time Approach to HRV Analysis. In Proceedings of the 11th International Joint Conference on Biomedical Engineering Systems and Technologies, Funchal, Portugal, 19–21 January 2018; pp. 208–215. [Google Scholar]
- Oster, J.; Clifford, G.D. Impact of the presence of noise on RR interval-based atrial fibrillation detection. J. Electrocardiol. 2015, 48, 947–951. [Google Scholar] [CrossRef]
- Kikillus, N.; Hammer, G.; Lentz, N.; Stockwald, F.; Bolz, A. Three Different Algorithms for Identifying Patients Suffering from Atrial Fibrillation during Atrial Fibrillation Free Phases of the ECG. Comput. Cardiol. 2007, 34, 801–804. [Google Scholar]
- Kikillus, N.; Hammer, G.; Wieland, S.; Bolz, A. Algorithm for identifying patients with paroxysmal atrial fibrillation without appearance on the ECG. In Proceedings of the 29th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Lyon, France, 23–26 August 2007; Volume 1–16, pp. 275–278. [Google Scholar]
- Langley, P.; Dewhurst, M.; Di Marco, L.Y.; Adams, P.; Dewhurst, F.; Mwita, J.C.; Walker, R.; Murray, A. Accuracy of algorithms for detection of atrial fibrillation from short duration beat interval recordings. Med. Eng. Phys. 2012, 34, 1441–1447. [Google Scholar] [CrossRef]
- Lake, D.E.; Moorman, J.R. Accurate estimation of entropy in very short physiological time series: The problem of atrial fibrillation detection in implanted ventricular devices. Am. J. Physiol. Heart Circ. Physiol. 2011, 300, H319–H325. [Google Scholar] [CrossRef] [PubMed]
- Hargittai, S. Is it Possible to Detect Atrial Fibrillation by Simply using RR Intervals? Comput. Cardiol. 2014, 41, 897–900. [Google Scholar]
- Lian, J.; Wang, L.; Muessig, D. A Simple Method to Detect Atrial Fibrillation Using RR Intervals. Am. J. Cardiol. 2011, 107, 1494–1497. [Google Scholar] [CrossRef] [PubMed]
- Ghodrati, A.; Murray, B.; Marinello, S. RR Interval Analysis for Detection of Atrial Fibrillation in ECG Monitors. In Proceedings of the 30th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Vancouver, BC, Canada, 20–25 August 2008; Volume 30, pp. 601–604. [Google Scholar]
- Ghodrati, A.; Marinello, S. Statistical Analysis of RR Interval Irregularities for Detection of Atrial Fibrillation. Comput. Cardiol. 2008, 35, 1057–1060. [Google Scholar]
- Kay, S.M. Fundamentals of Statistical Signal Processing: Detection Theory; Prentice Hall: Upper Saddle River, NJ, USA, 1998. [Google Scholar]
- Petrėnas, A.; Maroza, V.; Sörnmo, L. Low-complexity detection of atrial fibrillation in continuous long-term monitoring. Comput. Biol. Med. 2015, 65, 184–191. [Google Scholar] [CrossRef]
- Hong-wei, L.; Ying, S.; Min, L.; Pi-ding, L.; Zheng, Z. A probability density function method for detecting atrial fibrillation using R–R intervals. Med. Eng. Phys. 2009, 31, 116–123. [Google Scholar] [CrossRef]
- Takens, F. Detecting Strange Attractors in Turbulence; Springer: Berlin, Germany, 1981; pp. 366–381. [Google Scholar]
- Cerutti, S.; Mainardi, L.T.; Porta, A.; Bianchi, A.M. Analysis of the Dynamics of RR Interval Series for the Detection of Atrial Fibrillation Episodes. Comput. Cardiol. 1997, 24, 77–80. [Google Scholar]
- Tateno, K.; Glass, L. A Method for Detection of Atrial Fibrillation Using RR Intervals. Comput. Cardiol. 2000, 27, 391–394. [Google Scholar]
- Tateno, K.; Glass, L. Automatic detection of atrial fibrillation using the coefficient of variation and density histograms of RR and ΔRR intervals. Med. Biol. Eng. Comput. 2001, 39, 664–671. [Google Scholar] [CrossRef]
- Petrucci, E.; Balian, V.; Filippini, G.; Mainardi, L.T. Atrial Fibrillation Detection Algorithms for Very Long Term ECG Monitoring. Comput. Cardiol. 2005, 32, 623–626. [Google Scholar]
- Ruan, X.; Liu, C.; Wang, X.; Li, P. Automatic Detection of Atrial Fibrillation Using RR Interval Signal. In Proceedings of the 4th International Conference on Biomedical Engineering and Informatics (BMEI), Shanghai, China, 15–17 October 2011; Volume 4, pp. 644–647. [Google Scholar]
- Zhou, X.; Ding, H.; Ung, B.; Pickwell-MacPherson, E.; Zhang, Y. Automatic online detection of atrial fibrillation based on symbolic dynamics and Shannon entropy. BioMed. Eng. OnLine 2014, 13, 18. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhou, X.; Ding, H.; Wu, W.; Zhang, Y. A Real-Time Atrial Fibrillation Detection Algorithm Based on the Instantaneous State of Heart Rate. PLoS ONE 2015, 10, 0136544. [Google Scholar]
- Dash, S.; Chon, K.; Lu, S.; Raeder, E. Automatic real time detection of atrial fibrillation. Ann. Biomed. Eng. 2009, 37, 1701–1709. [Google Scholar] [CrossRef]
- Winkler, S.; Axmann, C.; Schannor, B.; Kim, S.; Leuthold, T.; Scherf, M.; Downes, R.; Nettlau, H.; Koehler, F. Diagnostic accuracy of a new detection algorithm for atrial fibrillation in cardiac telemonitoring with portable electrocardiogram devices. J. Electrocardiol. 2011, 44, 460–464. [Google Scholar] [CrossRef]
- Logan, B.; Healey, J. Robust Detection of Atrial Fibrillation for a Long Term Telemonitoring System. Comput. Cardiol. 2005, 32, 619–622. [Google Scholar]
- Moody, G.; Mark, R. A new method for detecting atrial fibrillation using RR intervals. Comput. Cardiol. 1983, 10, 227–230. [Google Scholar]
- Huang, C.; Ye, S.; Chen, H.; Li, D.; He, F.; Tu, Y. A Novel Method for Detection of the Transition between Atrial Fibrillation and Sinus Rhythm. IEEE Trans. Biomed. Eng. 2011, 58, 1113–1119. [Google Scholar] [CrossRef] [PubMed]
- Young, B.; Brodnick, D.; Spaulding, R. A Comparative Study of a Hidden Markov Model Detector for Atrial Fibrillation. In Proceedings of the IEEE Signal Processing Society Workshop, Boston, MA, USA, 25 August 1999; pp. 468–476. [Google Scholar]
- McManus, D.D.; Lee, J.; Maitas, O.; Esa, N.; Pidikiti, R.; Carlucci, A.; Harrington, J.; Mick, E.; Chon, K.H. A novel application for the detection of an irregular pulse using an iPhone 4S in patients with atrial fibrillation. Heart Rhythm 2013, 10, 315–319. [Google Scholar] [CrossRef] [Green Version]
- Lee, J.; McManus, D.; Chon, K. Atrial Fibrillation Detection using Time-Varying Coherence Function and Shannon Entropy. In Proceedings of the 2011 Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Boston, MA, USA, 30 August–3 September 2011; Volume 33, pp. 4685–4688. [Google Scholar]
- Lee, J.; Reyes, B.; McManus, D.; Mathias, O.; Chon, K. Atrial fibrillation detection using an Iphone 4S. IEEE Trans. Biomed. Eng. 2013, 60, 203–206. [Google Scholar] [CrossRef]
- Duverney, D.; Gaspoz, J.M.; Pichot, V.; Roche, F.; Brion, R.; Antoniadis, A.; Barthélémy, J.C. High Accuracy of Automatic Detection of Atrial Fibrillation Using Wavelet Transform of Heart Rate Intervals. J. Pacing Clin. Electrophysiol. 2002, 25, 457–462. [Google Scholar] [CrossRef]
- Hindricks, G.; Taborsky, M.; Wohlgemuth, P.; Rieger, G.; Beckers, F.; Albers, B. Atrial Fibrillation Detection by a Subcutaneous Monitoring Device. Comput. Cardiol. 2008, 35, 413–416. [Google Scholar]
- Brignole, M.; Bellardine-Black, C.L.; Thomsen, P.E.B.; Sutton, R.; Moya, A.; Stadler, R.W.; Cao, J.; Messier, M.; Huikuri, H.V. Improved Arrhythmia Detection in Implantable Loop Recorders. J. Cardiovasc. Electrophysiol. 2008, 19, 928–934. [Google Scholar] [CrossRef] [PubMed]
- Colloca, R.; Johnson, A.E.W.; Mainardi, L.; Clifford, G.D. A Support Vector Machine Approach for Reliable Detection of Atrial Fibrillation Events. Comput. Cardiol. 2013, 40, 1047–1050. [Google Scholar]
- Sarkar, S.; Ritscher, D.; Mehra, R. A detector for a chronic implantable atrial tachyarrhythmia monitor. IEEE Trans. Biomed. Eng. 2008, 55, 1219–1224. [Google Scholar] [CrossRef]
- Linker, D.T. Long-Term Monitoring for Detection of Atrial Fibrillation. U.S. Patent 7,630,756, 8 December 2009. [Google Scholar]
- Mohebbi, M.; Ghassemian, H. Detection of Atrial Fibrillation Episodes Using SVM. In Proceedings of the 30th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Vancouver, BC, Canada, 20–25 August 2008; Volume 30, pp. 177–180. [Google Scholar]
- Asl, B.M.; Setarehdan, S.K.; Mohebbi, M. Support vector machine-based arrhythmia classification using reduced features of heart rate variability signal. Artif. Intell. Med. 2008, 44, 51–64. [Google Scholar] [CrossRef] [PubMed]
- Mohebbi, M.; Ghassemian, H. Prediction of paroxysmal atrial fibrillation based on non-linear analysis and spectrum and bispectrum features of the heart rate variability signal. Comput. Methods Programs Biomed. 2012, 105, 40–49. [Google Scholar] [CrossRef]
- Kim, D.; Seo, Y.; Youn, C.H. Detection of Atrial Fibrillation Episodes Using Multiple Heart Rate Variability Features in Different Time Periods. In Proceedings of the 30th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Vancouver, BC, Canada, 20–25 August 2008; Volume 30, pp. 5482–5485. [Google Scholar]
- Artis, S.G.; Mark, R.G.; Moody, G.B. Detection of Atrial Fibrillation Using Artificial Neural Networks. Comput. Cardiol. 1991, 173–176. [Google Scholar] [CrossRef]
- Carrara, M.; Carozzi, L.; Moss, T.J.; de Pasquale, M.; Cerutti, S.; Ferrario, M.; Lake, D.E.; Moorman, J.R. Heart rate dynamics distinguish among atrial fibrillation, normal sinus rhythm and sinus rhythm with frequent ectopy. Physiol. Meas. 2015, 36, 1873–1888. [Google Scholar] [CrossRef]
- Yaghouby, F.; Ayatollahi, A.; Bahramali, R.; Yaghouby, M. Robust genetic programming-based detection of atrial fibrillation using RR intervals. Expert Syst. 2012, 29, 183–199. [Google Scholar] [CrossRef]
- Brameier, M.; Banzhaf, W. Linear Genetic Programming; Springer: New York, NY, USA, 2007. [Google Scholar]
- Oltean, M.; Grossan, C. Evolving evolutionary algorithms using multi expression programming. In Advances in Artificial Life; Banzhaf, W., Ziegler, J., Christaller, T., Dittrich, P., Kim, J.T., Eds.; Springer: Berlin/Heidelberg, Germany, 2003; Volume 2801, pp. 651–658. [Google Scholar]
- Pudil, P.; Novovicova, J.; Kittler, J. Floating search methods in feature selection. Pattern Recognit. Lett. 1994, 15, 1119–1125. [Google Scholar] [CrossRef]
- Park, J.; Lee, S.; Jeon, M. Atrial fibrillation detection by heart rate variability in Poincare plot. BioMed. Eng. OnLine 2009, 8, 38. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Acharya, U.R.; Sankaranarayanan, M.; Nayak, J.; Xiang, C.; Tamura, T. Automatic identification of cardiac health using modeling techniques: A comparative study. Inf. Sci. 2008, 178, 4571–4582. [Google Scholar] [CrossRef]
- Tsipouras, M.G.; Fotiadis, D.I. Automatic arrhythmia detection based on time and time—Frequency analysis of heart rate variability. Comput. Methods Programs Biomed. 2004, 74, 95–108. [Google Scholar] [CrossRef]
- Shouldice, R.B.; Heneghan, C.; de Chazal, P. Automated Detection of Paroxysmal Atrial Fibrillation from Inter-Heartbeat Intervals. In Proceedings of the 29th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Lyon, France, 23–26 August 2007; Volume 27, pp. 686–689. [Google Scholar]
- Faust, O.; Shenfield, A.; Kareem, M.; San, T.R.; Fujita, H.; Acharya, U.R. Automated detection of atrial fibrillation using long short-term memory network with RR interval signals. Comput. Biol. Med. 2018, 102, 327–335. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mendez, M.M.; Hsu, M.C.; Yuan, J.T.; Lynn, K.S. A Heart Rate Variability-Based Paroxysmal Atrial Fibrillation Prediction System. Appl. Sci. 2022, 12, 2387. [Google Scholar] [CrossRef]
- Ramesh, J.; Solatidehkordi, Z.; Aburukba, R.; Sagahyroon, A. Atrial Fibrillation Classification with Smart Wearables Using Short-Term Heart Rate Variability and Deep Convolutional Neural Networks. Sensors 2021, 21, 7233. [Google Scholar] [CrossRef]
- Pons, J.F.; Haddi, Z.; Deharo, J.C.; Charaï, A.; Bouchakour, R.; Ouladsine, O.; Delliaux, S. Heart rhythm characterization through induced physiological variables. Sci. Rep. 2017, 7, 5059. [Google Scholar] [CrossRef]
- Haddi, Z.; Ananou, B.; Trardi, T.; Pons, J.-F.; Delliaux, S.; Deharo, J.-C.; Ouladsine, M. Advanced Machine Learning Coupled with Heart-Inter-beat derivatives for Cardiac Arrhythmia Detection. In Proceedings of the American Control Conference (ACC), Denver, CO, USA, 1–3 July 2020; pp. 5433–5438. [Google Scholar] [CrossRef]
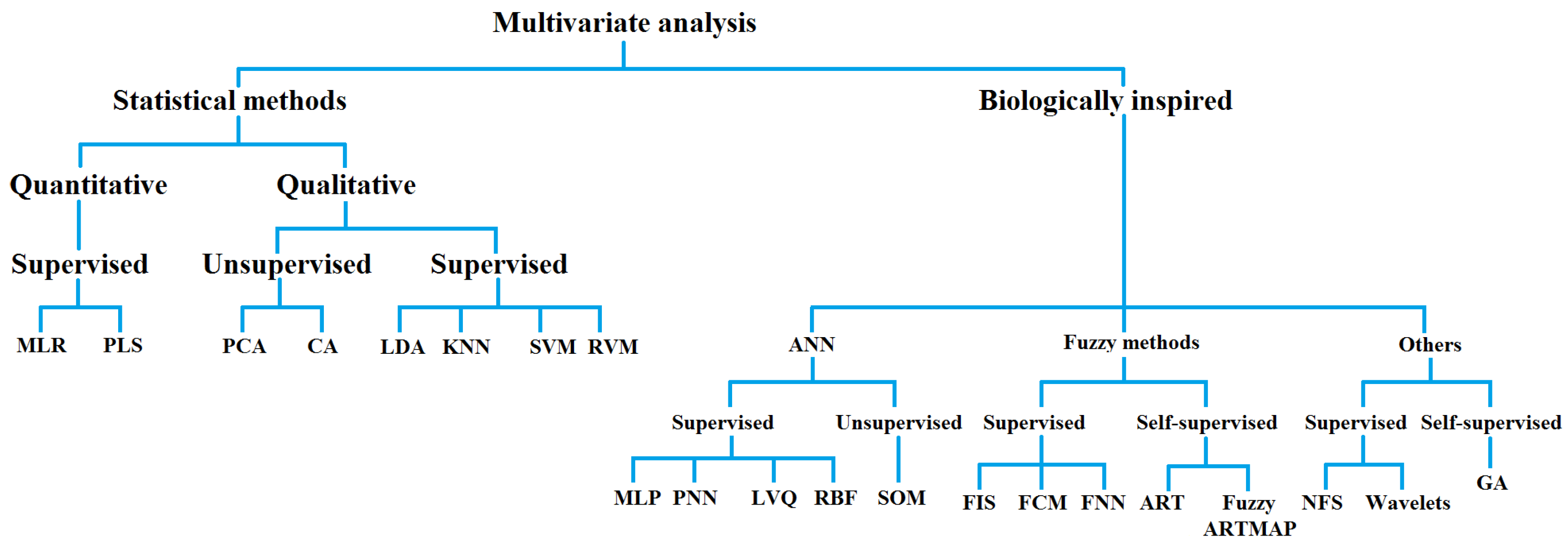
| Statistical Methods of Multivariate Analysis | Biologically Inspired Methods of Multivariate Analysis |
|---|---|
| MLR: Multiple linear regression | ANN: Artificial neural networks |
| PLS: Partial least square | MLP: Multi-layer perceptron |
| PCA: Principal component analysis | PNN: Probabilistic neural network |
| CA: Cluster analysis | LVQ: Learning vector quantization |
| LDA: Linear discriminant analysis | RBF: Radial basis function |
| KNN: K-nearest neighbors | SOM: Self-organizing map |
| SVM: Support vector machine | FIS: Fuzzy inference system |
| RVM: Relevance vector machine | FCM: Fuzzy c-means |
| FNN: Fuzzy neural network | |
| ART: Adaptive resonance theory | |
| NFS: Neuro fuzzy system | |
| GA: Genetic algorithm |
| Year [Ref] | Main Features | Techniques and Algorithms Used | Datasets | Best % PERFORMANCE | Limitations and Remarks |
|---|---|---|---|---|---|
| 2000 [35] | 100-RR and ΔRR density histogram similarity | Standard vs. Kolmogorov–Smirnov methods (dens. hist. template matching) | AFDB, MITDB | Se = 93.2 Sp = 96.7 (AFDB test) | Low Sp for short AF episodes |
| 2001 [36] | RR and ΔRR studied by density histograms and coefficient of variation CV test | Statistics and Kolmogorov–Smirnov test | AFDB, MITDB | Se = 94.4 Sp = 97.2 | Higher performance for Kolmogorov–Smirnov on ΔRR |
| 2002 [50] | Spectral and nonlinear features of high HRV | Discrete wavelet transform DWT and fractal analysis applied to Power Spectral Density | Local or proprietary | Se = 99.2, Sp = N/A (ChAF); Se = 96.1 Sp = 92.6 (ParAF) | Class separation of Chronic (ChAF) and Paroxysmal (ParAF); Local DB limitation on reproducibility |
| 2005 [43] | RR, smoothed normalized RR and RR variance | Basic statistics and initial AF detection followed by majority vote approach (600 beat) | AFDB | Se = 96 Sp = 89 | Application to 10 s RR segments |
| 2005 [37] | Modal behavior (statistics) and base width or height (geometrical) features of week-long histograms of RR and ΔRR distribution plots | Basic statistics | AFDB | Se = 92 Pr = 78 | Only applicable to AF episodes > 2 min. Best performance for ΔRR dist. widths |
| 2007 [22,23] | SDSD with Poincaré plot eye diagram analysis (I), 45 min spectral integrals (II), RR difference histograms and pNN200 (III) | Statistics, 3500 interval representation of Poincaré plots and FFT | AFDB, NSRDB | Se = 91.5 Sp = 96.9 (test I); Se = 93.3 Sp = 92.8 (test II); Se = 94.1 Sp = 93.4 (test III) | Tests performed on 3500-interval time series and 60 bpm time normalization applied |
| 2008 [28,29] | Normalized absolute deviation of RR, normalized absolute difference of successive RR and probability density function comparisons | Basic statistics, Gaussian vs. Laplacian probability density function estimation, Neyman–Pearson test | MITDB, AFDB, Draeger AF (proprietary) | Se = 92 Pr = 73 (MITDB); Se = 89 Pr = 87 (AFDB); Se = 87 Pr= 94 (Draeger) | Class separation of Chronic (ChAF) and Paroxysmal (ParAF); Normalized absolute differences and Laplacian PDF yielding the best results; Proprietary DB limiting reproducibility |
| 2008 [51,52] | Subcutaneous R-wave and 2-min HRV RR Lorenz (Poincaré) geometric features | Representation of RR Lorenz plots | Local | Se = 90.6 (AF > 2 min) Se = 98.1 (AF > 4 min) Pr = 55.1 (mean) | In vivo study with low Pr; Performance limited in AF < 2 min episodes |
| 2009 [41] | RR RMSSD, Turning point ratio, Entropy | Basic statistics | MITDB, AFDB | Se = 90.2 Sp = 91.2 (MITDB); Se = 94.4 Sp = 95.1 (AFDB) | Techniques applied to 128-RR segments with 50% AF ratios |
| 2009 [32] | RR Takens phase space, kn slope of probability density function of nonlinear attractor distance | Basic statistics and Takens embedding for m-dimensional phase space computation | AFDB | Se = 97.8 Sp = 99.0 | Results achieved for time series as short as 40RRs |
| 2011 [45] | 100-ΔRR distance difference curve (dRDDC) with AF event classification (onset, stop, none) | Basic statistics and Kolmogorov–Smirnov test | AFDB, NSRDB | Se = 96.1 Sp = 98.1 (AFDB) | Observed limitations in short AF episodes (4–62 beats) |
| 2011 [25] | Sample entropy, quadratic sample entropy (QSE, ad hoc) and RR variability for template matching | Basic statistics, logistic regression, Wald-χ2 statistic and developed COSEn algorithm | MITDB (training), UVa Virginia Holter (local) | Se = 91 Sp = 98 Pr = 63 | |
| 2011 [27] | Geometrical nonlinear features of RR vs. dRR difference maps (with different resolutions) | Representation of recurrence plots | MITDB, NSRDB, AFDB, NSR2DB | Se = 95.9 Sp = 95.4 (combined DBs) | Suitable for short 32-beat AF episodes; Different window size resolutions studied (32/64/128) |
| 2011 [48] | Time-varying coherence using ARMA and Shannon Entropy | Time-varying transfer functions | AFDB, NSRDB | Se = 97.41 Sp = 97.54 Ac = 97.49 | Applied to adjacent 128-RR sets |
| 2011 [31] | RR 3-point median and specific decision thresholds (Se = Sp) | Bigeminal suppression, signal fusion | AFDB, NSRDB | Se = 97.1 Sp = 98.3 | Technique applied to 8-RR windows |
| 2011 [38] | Vector angular index (VAI), vector length index (VLI), SD1 and SD2 geometric features of 1-min RR recurrence plots | Statistics (with Mann–Whitney test) and ellipse fitting for recurrence plot | AFTermDB | Se = 98.3 Sp = 100 (SD1 and VAI) | No generalization insight despite high performance (additional clinical samples tests) |
| 2011 [42] | AF index derived from histogram geometric features (width/height ratio, peak) and premature beat presence | Basic statistics | MITDB (index setup), Local (testing) | Se = 92.9 Sp = 90.9 | Method applied to 120 s RR series; Limitation on generalization claims due to closed DB |
| 2012 [24] | RR Coefficient of variation (CV), mean successive difference and COSEn | Basic statistics | 2 Local DBs (2130 10-s ECG samples) | Se > 94 Sp ≈ 93 | RR time interval only approach |
| 2013 [47,49] | RR RMSSD, Shannon entropy, SampEn, RMSSD/<RR> (64RR sets) | Cubic spline (interpolation) and decision logic | AFDB, NSRDB | Se = 97.26 Sp = 95.91 (combined) | Method developed for iPhone 4S use. |
| 2014 [26] | Modified Lorenz dRR, RR RMSSD, Shannon entropy, turning point ratio and SampEn | Statistical methods and representation of dRR recurrence plots | MITDB, AFDB, Long-Term AF | Se = 95.79 Sp = 95.26 (MITDB for dRR) | High performances achieved across different single features |
| 2014 [39] | Three-pass: Median + low-pass filters, symbolic dynamics and Shannon entropy | Low/high scale reference sequence generation and statistics on successive differences | Long-Term AF, AFDB (testing) | Se = 96.89 Sp = 98.25 (AFDB) | False negative detection foreseen for short AF episodes |
| 2015 [40] | Symbolic dynamics and Shannon entropy with adapted thresholds | Long-Term AF (training), AFDB, MITDB, NSRDB | Se = 97.37 Sp = 98.44 (AFDB) | Adapted thresholds and test generalization to other DBs |
| Year [Ref] | Main Features | Techniques and Algorithms Used | Datasets | Best % Performance | Limitations and Remarks |
|---|---|---|---|---|---|
| 2004 [68] | RR Temporal STD, RMSSD, SDSD, Δ%5, Δ%10, Δ%50 (ANN) and spectral t-f features (FFBPNN) | ANN and Feed-Forward Back-propagation (FFBPNN) applied respectively to RR and time-frequency analysis obtained by Short-time FT and t-f distributions | MITDB (AF aggregated) | Se = 87.5 Sp= 89.5 (time) Se = 90 Sp = 93 (time-frequency) | 32-RR intervals used |
| 2007 [29] | Trimmed <RR>, sqrt(spread), NormSqSum(50 ms) | Linear discriminant classifier (LDC) | MITDB, AFDB, NSRDB, NSR2DB | Ac = 92 Ac = 94 Ac = 100 Ac = 100 | Tested on 100-RR interbeat blocks, subject to performance loss due to other arrhythmia |
| 2008 [67] | Spectral FFT features and RR autoregressive (AR), moving average (MA) and Autoregressive moving average (ARMA) model features | FFT for spectral analysis and Multi-layer perceptron (MLP) networks | Kasturba Medical college (proprietary) | Correct classification rate of AF = 66.67 (ARMA features) | Not AF-centered. Ambitious study covering different arrhythmia classes, with small local datasets |
| 2008 [57] | Combination of 15 RR HRV features obtained from 32-RR sequences and reduced to 6 | Generalized Discriminant Analysis (GDA) and SVM with radial basis for 6 class detection | MITDB | Ac = 98.53 (AF) | Scope is broader than AF only; one-against-one vs. one-against-all |
| 2008 [59] | 4-period RR HRV features | Logistic regression | AFDB | Success rate = 95.5 | RR filtering and day/evening discrimination criteria applied |
| 2008 [56] | Combination of 5 RR time, 1 frequency and 3 nonlinear features | Principal component vs. Linear discriminant (PCA vs. LDA) applied before SVM | MITDB | Se = 99.07 Sp = 100 Pr = 100 | AF episode target; Radial-basis optimized |
| 2009 [66] | Poincaré plot features | K-means | ParAFDB AFTermDB | Se = 91.4 Sp = 92.9 | |
| 2012 [58] | Combination of 14 RR HRV features: 4 spectral, 6 cross-spectral and 4 nonlinear | SVM | AFDB | Se = 96.30 Sp = 93.10 | |
| 2012 [62] | Combination of 5 RR temporal (Mean, STD, RMSSD and pNN50) and 2 geometrical (Triangular index and interpolation) features | Linear genetic program. vs. Multi-expression program. vs. weighted Least Squares regression. Improved forward floating selection (IFFS) of features | MITDB | Se = 99.11 Sp = 98.91 | Best performance obtained for LGP |
| 2013 [53] | Combination of 10 specific features: COSEn, SampEn, RR-RR origin counts, compensatory pause feature, AF evidence, irregularity RR sparsity, median of absolute RR deviations, median heart rate, <RR> and minRR | SVM with radial basis function kernel | AFDB (training), NSRDB, MITDB | Se = 96.35 Sp = 98.81 (test) | 5-fold CV with window lengths WL = 12–300 s |
| 2015 [61] | Nonlinear and statistic RR features: COSEn, local dynamics scores, detrended fluctuation, <RR> and standard deviations | Advanced statistics, Logistic Regression, Knn and Random forests (RF) | Local 24 h Holter (2722 samples) | Pr = 97 | 10-min RR segments used, 10-fold CV approach and best performance for RF |
| 2018 [70] | 100-RR intervals with no feature extraction (simplistic approach) | RNNs with Long Short-Term Memory (LSTM) | AFDB database with a (20/3) patient training/test distribution | Se = 98.32 Sp = 98.67 (10-fold CV) | Computationally demanding training. Small dataset and splitting approach limitations |
| 2021 [72] | 13 RR HRV temporal features | CNNs | MITDB, AFDB, NSRDB | Se = 94.50 Sp = 96.00 (5-fold CV) Se = 77.80 Sp = 88.54 (field data) | Generalization focus via photoplethysmography field data |
| 2022 [71] | 400-RR point HRV Poincaré plots | Recurrence plot representation and CNN applied to Poincaré images | ParAFDB, NSRDB + AFDB (testing) | Se = 804 Pr = 890 | Very promising research line exploiting CNN image analysis capabilities |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Haddi, Z.; Ananou, B.; Alfaras, M.; Ouladsine, M.; Deharo, J.-C.; Avellana, N.; Delliaux, S. Automatic Atrial Fibrillation Arrhythmia Detection Using Univariate and Multivariate Data. Algorithms 2022, 15, 231. https://doi.org/10.3390/a15070231
Haddi Z, Ananou B, Alfaras M, Ouladsine M, Deharo J-C, Avellana N, Delliaux S. Automatic Atrial Fibrillation Arrhythmia Detection Using Univariate and Multivariate Data. Algorithms. 2022; 15(7):231. https://doi.org/10.3390/a15070231
Chicago/Turabian StyleHaddi, Zouhair, Bouchra Ananou, Miquel Alfaras, Mustapha Ouladsine, Jean-Claude Deharo, Narcís Avellana, and Stéphane Delliaux. 2022. "Automatic Atrial Fibrillation Arrhythmia Detection Using Univariate and Multivariate Data" Algorithms 15, no. 7: 231. https://doi.org/10.3390/a15070231
APA StyleHaddi, Z., Ananou, B., Alfaras, M., Ouladsine, M., Deharo, J.-C., Avellana, N., & Delliaux, S. (2022). Automatic Atrial Fibrillation Arrhythmia Detection Using Univariate and Multivariate Data. Algorithms, 15(7), 231. https://doi.org/10.3390/a15070231







