Network Modeling of Murine Lymphatic System
Abstract
:1. Introduction
2. Anatomy and Physiology of Murine Lymphatic System
| Property | Characteristic Value/Range | Commentaty/Source |
|---|---|---|
| Lymph nodes: | ||
| Number | 22 28–36 | (BALB/cAnNCr) [24] (DD/NIH) [23] |
| Diameter | 1–2.3 mm 1–17.3 mm | (C57Bl/6J, Nude, CB-17 SCID) [31,32] (DD/NIH) [23] |
| Thoracic duct: | ||
| Radius | 300 μm | [28] |
| Flow | 417–1250 μL/h | (10 mL/day for immobilized mice, 30 mL/day after movements) [28] |
| Velocity | 410–1228 μm/s | [28] |
| Vessels afferent to popliteal nodes: | ||
| Radius | 20–40 μm | [28,30] |
| Flow | 0.3–3.4 μL/h | (mean flow = 0.3 μL/h [30]) [28,29,30] |
| Velocity | 37–186 μm/s | (mean velocity = 53 ± 16 μm/s [30]) [28,29,30] |
| Collecting lymphatics in hind limbs: | ||
| Velocity | 50–100 μm/s | [31] |
| Collecting lymphatics in ears: | ||
| Velocity | 0–400 μm/s | [30] |
| Collecting lymphatics in the tail: | ||
| Velocity | 4.2 μm/s | [29] |
- number of inlet vertices ;
- vessel radii range 40–300 μm;
- vessel length = 7–60 mm;
- pressure at the sink nodes Pa;
- lymph viscosity = 1.81 mPa·s;
- lymph inflow mL/day.
3. Oriented Graph Model of Murine LS
3.1. Computing the Direction of Lymph Flows
- The Hagen–Poiseuille equationlinks the flow through the edge with the drop of pressure from the tail i to the head j vertices () by the conductances that depend on lymph viscosity and the radii and the lengths of the edges;
- The balance of flow through the vertices due to mass conservation:where is a set of vertices adjacent to i.
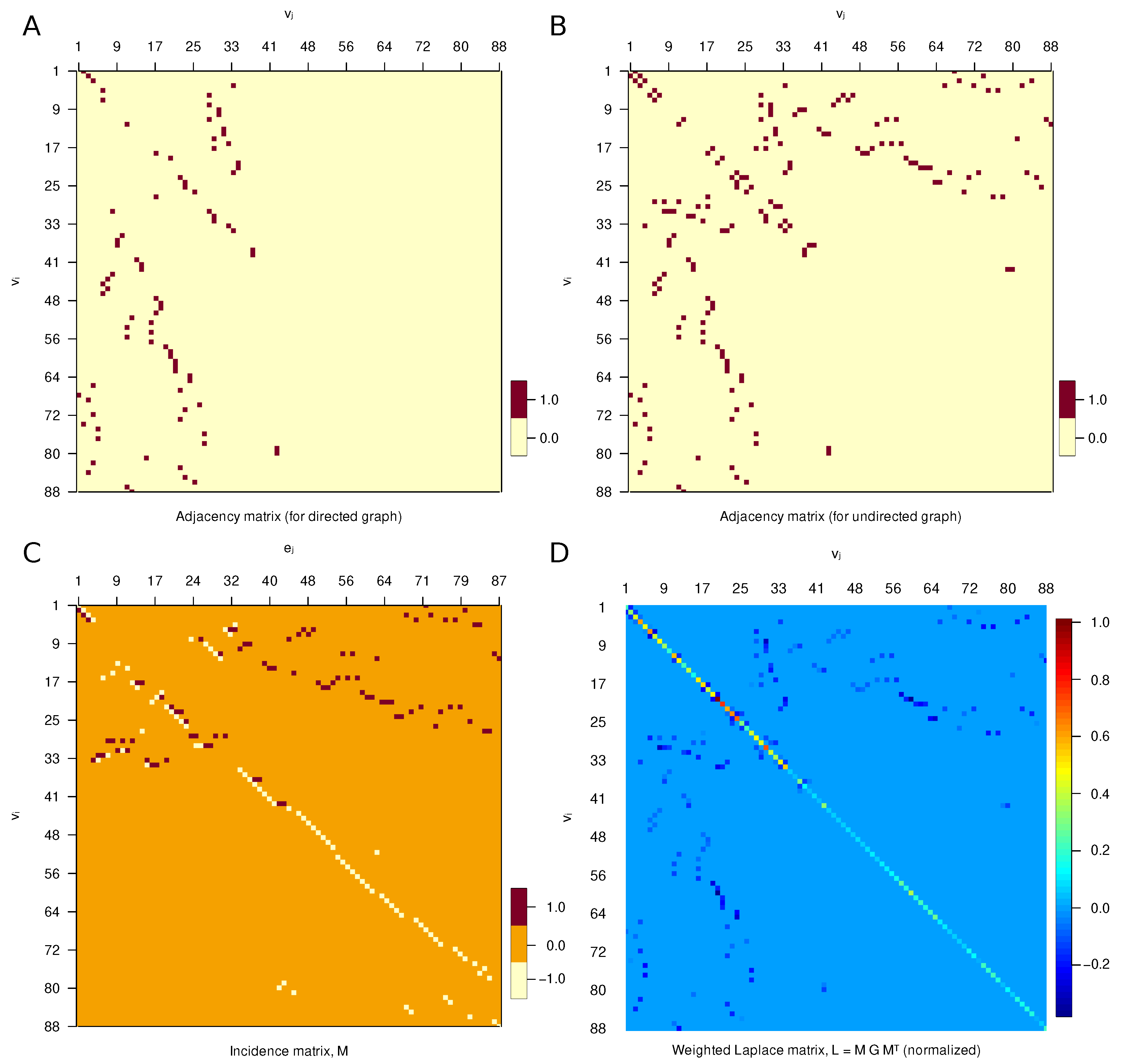
3.2. Matrix Representation
4. Quantitative Characterization of Lymph Flows through the LS
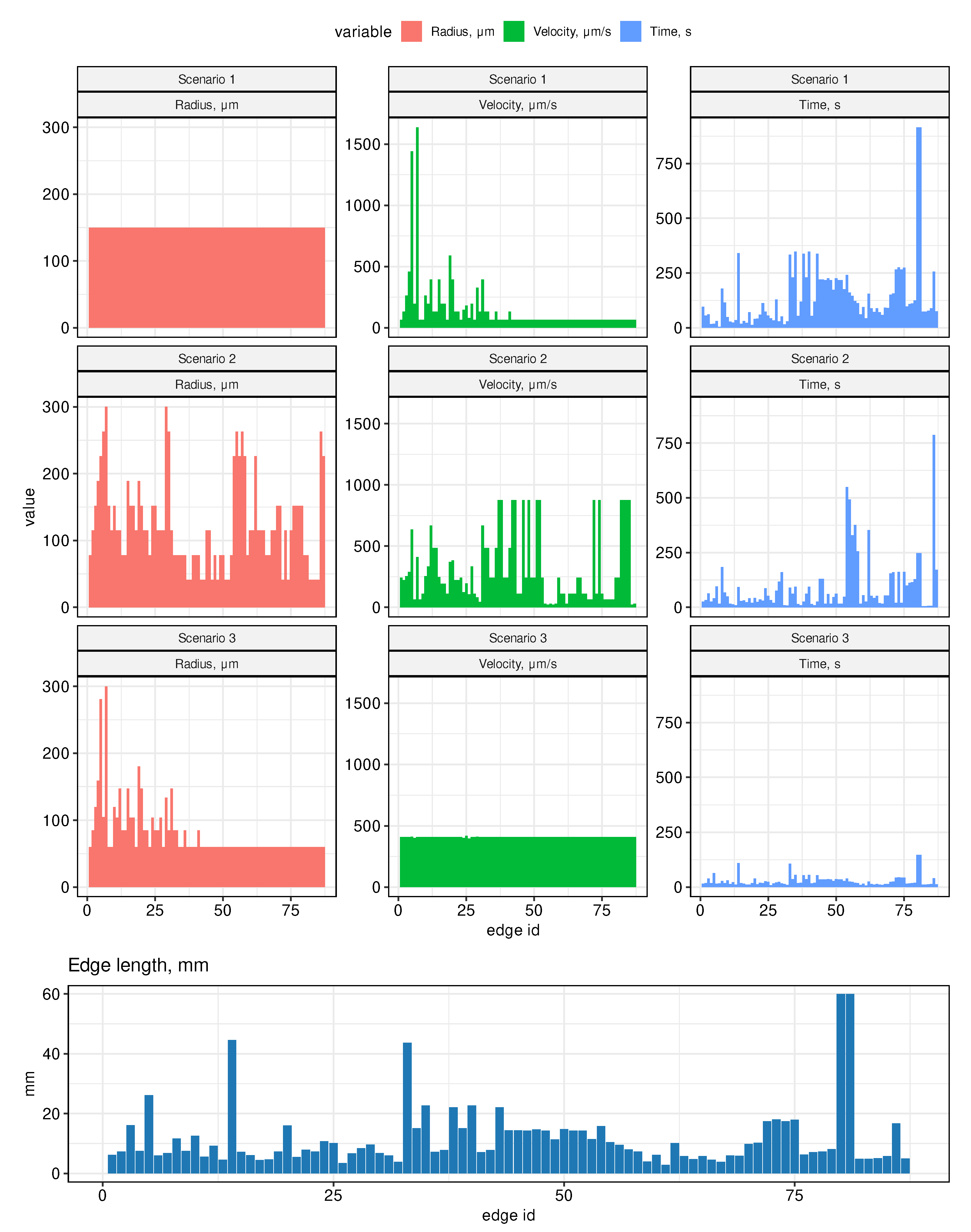
- Scenario 1. All radii in the graph are assumed to be the same, equal to 150 μm (half of the radius on the thoracic duct).
- Scenario 2. Edge radii decrease linearly with distance from the outlet vertices (jugular veins) to the inlet vertices. On the thoracic duct, the radius is assumed to be 300 μm, on the most distant edges (from the hindlimbs) it is assumed to be 41 μm. Therefore, on other edges from the inlet vertices, the value of the radius is equal to 41 μm and increases linearly when approaching the vein. On the subgraph collecting lymph into the right jugular vein, the radii are set symmetrically, equal to the radii in the left subgraph.
- Scenario 3. Edge radii are distributed so that the cross-sectional area of incoming and outgoing vessels for each vertex of the graph is preserved. On all inlet edges, the radii are assumed to be the same and are estimated so that the radius on the thoracic duct would be equal to 300 μm.
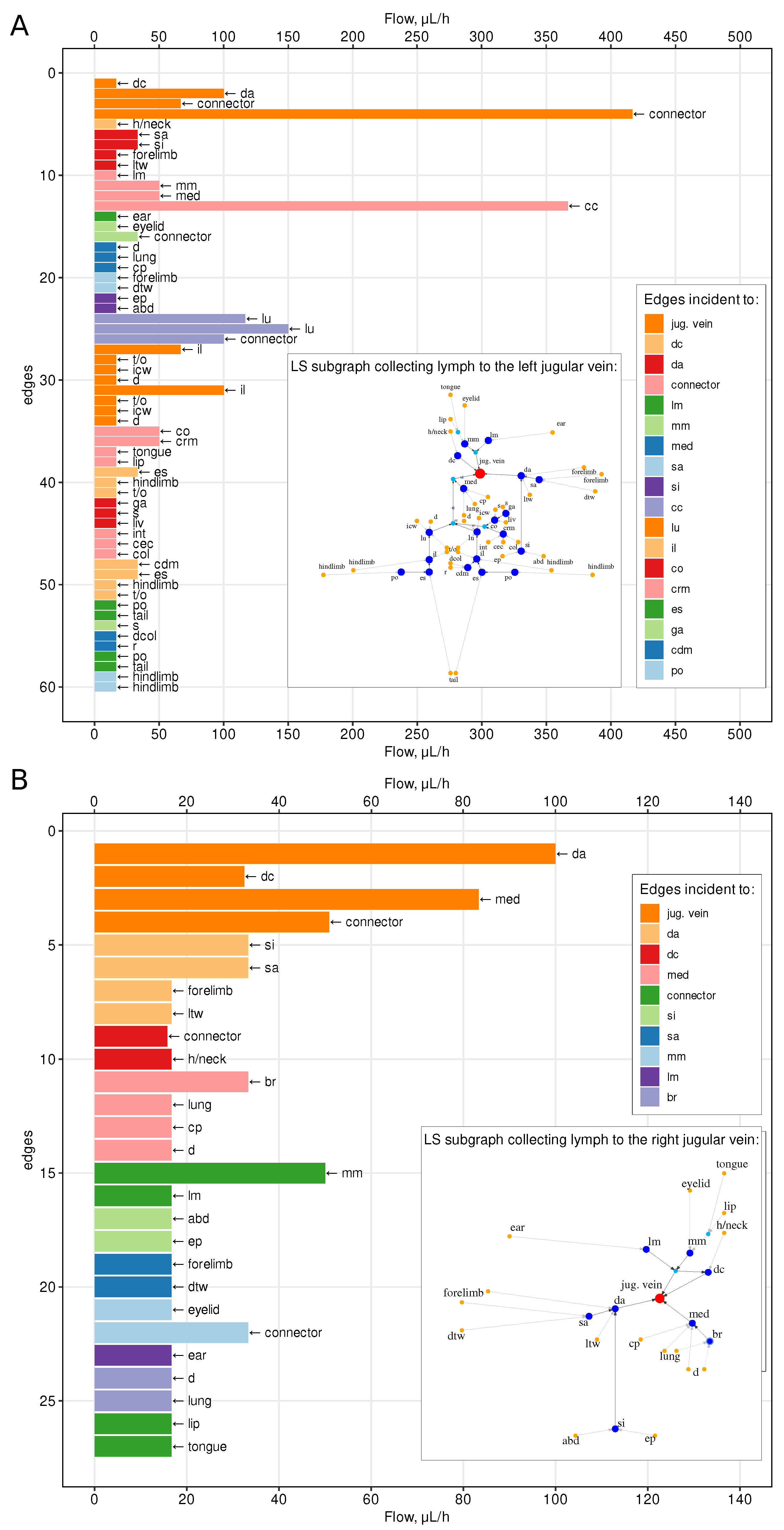
4.1. Lymph Transfer Rates between Lymph Nodes
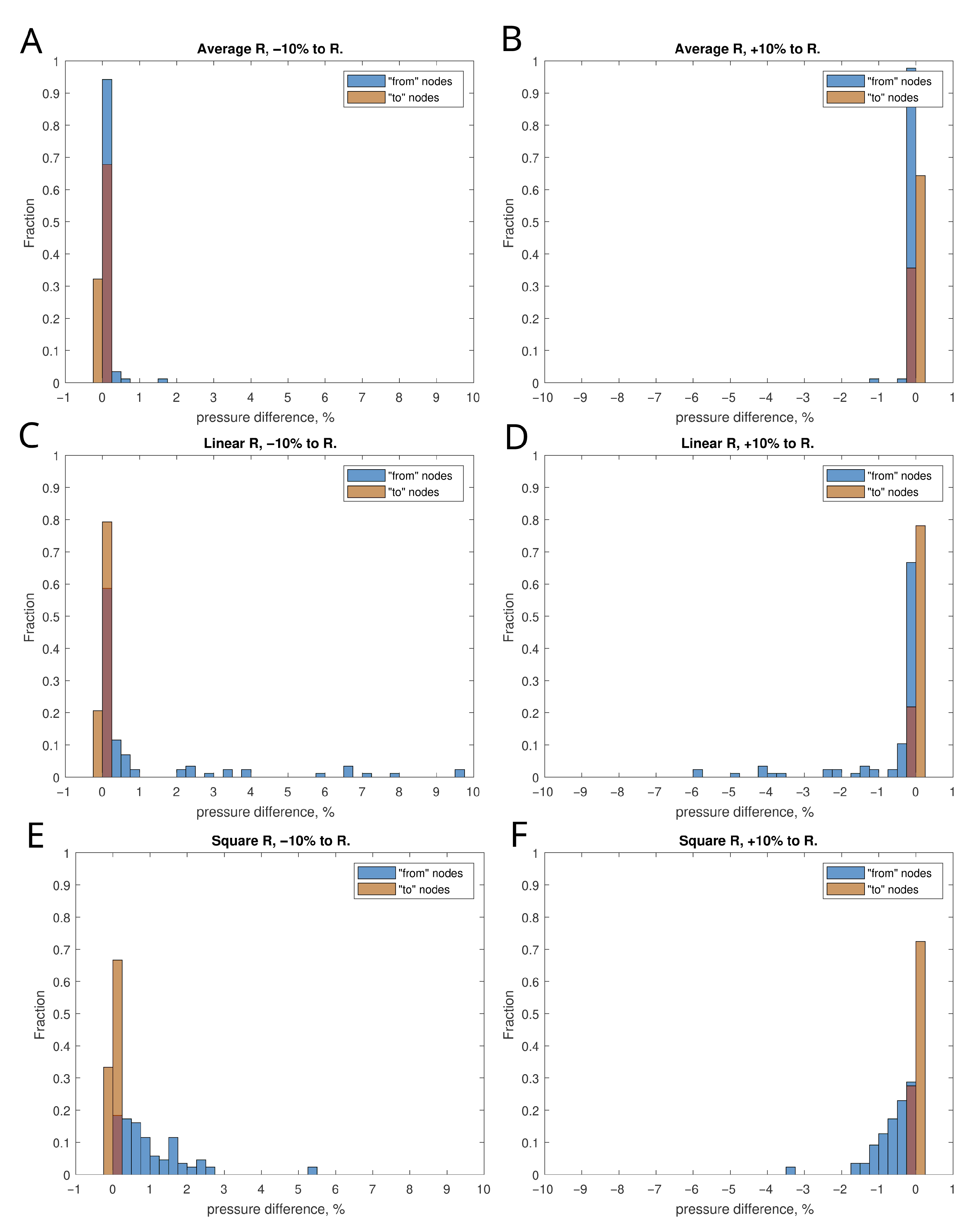
4.2. Sensitivity to Variations in Vessels Diameter
5. Topological Properties of the LS Graph
- The number of input nodes , i.e., the number of nodes with degree 1 and out-degree 0;
- Maximum degree of graph , i.e., the maximum degree of its vertices;
- Girth of the graph g, which is the length of the shortest cycle in the simple graph;
- Diameter, i.e., the longest geodesic distance (in other terms, maximum eccentricity of any vertex)where is the geodesic distance (shortest oriented path connecting vertices u and v), is the eccentricity of vertex v;
- Radius of the graph (minimum eccentricity of any vertex),
- Average path length (mean geodesic distance)
- The energy and the spectral radius of the graph are defined as follows,where stand for the eigenvalues of the adjacency matrix A of the graph;
- Edge density of the graph, i.e., the number of edges divided by the number of all possible edges,
- The clustering coefficient C (transitivity) measures the probability that two neighbors of a vertex are connected. It can be computed as function of adjacency matrix A:
- Number of separators , i.e., the vertices removal of which disconnects the graph;
- Topological diversity of the vertices as a function of the Shannon entropy associated with flow rates through the incident edges,where k is the number of ’s incident edges and is the proportion of the flow between the adjacent and to the total flow through the edges involving . The flow diversity is defined similar to the definition of network diversity in [33].
6. Conclusions
- Considering the biomechanics of lymphatic pumping through a chain of lymphangions and lymph nodes;
- Coupling the LS model with the cardiovascular system;
- Integration with multi-physics models of the immune system.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| LS | Lymphatic system |
| LN | Lymph node |
References
- Ivanov, P. The New Field of Network Physiology: Building the Human Physiolome. Front. Netw. Physiol. 2021, 1, 711778. [Google Scholar] [CrossRef]
- Hao, S.; Koon-Kiu, Y.; Liang, D.; Chenxi, Q.; Hongbo, C.; Jiyang, Y. Network Approaches for Dissecting the Immune System. iScience 2020, 23, 101354. [Google Scholar] [CrossRef]
- Randolph, G.; Ivanov, S.; Zinselmeyer, B.; Scallan, J. The Lymphatic System: Integral Roles in Immunity. Annu. Rev. Immunol. 2017, 35, 31–52. [Google Scholar] [CrossRef] [Green Version]
- O’Melia, M.; Lund, A.; Thomas, S. The Biophysics of Lymphatic Transport: Engineering Tools and Immunological Consequences. iScience 2019, 22, 28–43. [Google Scholar] [CrossRef] [Green Version]
- Moore, J.E., Jr.; Bertram, C.D. Lymphatic System Flows. Annu. Rev. Fluid Mech. 2018, 50, 459–482. [Google Scholar] [CrossRef] [PubMed]
- Singhal, D.; Börner, K.; Chaikof, E.; Detmar, M.; Hollmén, M.; Iliff, J.; Itkin, M.; Makinen, T.; Oliver, G.; Padera, T.; et al. Mapping the lymphatic system across body scales and expertise domains: A report from the 2021 National Heart, Lung, and Blood Institute workshop at the Boston Lymphatic Symposium. Front. Physiol. 2023, 14, 1099403. [Google Scholar] [CrossRef] [PubMed]
- Ernst, P.; Carvunis, A. Of mice, men and immunity: A case for evolutionary systems biology. Nat. Immunol. 2018, 19, 421–425. [Google Scholar] [CrossRef] [PubMed]
- Tao, L.; Reese, T. Making Mouse Models That Reflect Human Immune Responses. Trends Immunol. 2017, 38, 181–193. [Google Scholar] [CrossRef] [Green Version]
- Graham, A. Naturalizing mouse models for immunology. Nat. Immunol. 2021, 22, 111–117. [Google Scholar] [CrossRef]
- Margaris, K.; Black, R. Modelling the lymphatic system: Challenges and opportunities. J. R. Soc. Interface 2012, 9, 601–612. [Google Scholar] [CrossRef] [Green Version]
- Roose, T.; Swartz, M. Multiscale modeling of lymphatic drainage from tissues using homogenization theory. J. Biomech. 2012, 45, 107–115. [Google Scholar] [CrossRef]
- Bertram, C.; Macaskill, C.; Davis, M.; Moore, J.J. Contraction of collecting lymphatics: Organization of pressure-dependent rate for multiple lymphangions. Biomech. Model. Mechanobiol. 2018, 17, 1513–1532. [Google Scholar] [CrossRef] [PubMed]
- Morris, C.; Zawieja, D.; Moore, J.J. A multiscale sliding filament model of lymphatic muscle pumping. Biomech. Model. Mechanobiol. 2021, 20, 2179–2202. [Google Scholar] [CrossRef] [PubMed]
- Jamalian, S.; Davis, M.; Zawieja, D.; Moore, J.J. Network Scale Modeling of Lymph Transport and Its Effective Pumping Parameters. PLoS ONE 2016, 11, e0148384. [Google Scholar] [CrossRef] [Green Version]
- Reddy, N.; Krouskop, T.; Newell, P. A computer model of the lymphatic system. Comput. Biol. Med. 1977, 7, 181–197. [Google Scholar] [CrossRef]
- Farooqi, Z.; Mohler, R. Distribution models of recirculating lymphocytes. IEEE Trans. Biomed. Eng. 1989, 36, 355–362. [Google Scholar] [CrossRef]
- Mozokhina, A.; Mukhin, S. Pressure Gradient Influence on Global Lymph Flow. In Trends in Biomathematics: Modeling, Optimization and Computational Problems; Springer International Publishing: Berlin/Heidelberg, Germany, 2018; pp. 325–334. [Google Scholar]
- Savinkov, R.; Grebennikov, D.; Puchkova, D.; Chereshnev, V.; Sazonov, I.; Bocharov, G. Graph Theory for Modeling and Analysis of the Human Lymphatic System. Mathematics 2020, 8, 2236. [Google Scholar] [CrossRef]
- Mozokhina, A.; Savinkov, R. Mathematical Modelling of the Structure and Function of the Lymphatic System. Mathematics 2020, 8, 1467. [Google Scholar] [CrossRef]
- Hsu, M.; Itkin, M. Lymphatic Anatomy. Tech. Vasc. Interv. Radiol. 2016, 19, 247–254. [Google Scholar] [CrossRef] [PubMed]
- Hur, S.; Kim, J.; Ratnam, L.; Itkin, M. Lymphatic Intervention, the Frontline of Modern Lymphatic Medicine: Part I. History, Anatomy, Physiology, and Diagnostic Imaging of the Lymphatic System. Korean J. Radiol. 2023, 24, 95–108. [Google Scholar] [CrossRef]
- Deepa Maheshvare, M.; Raha, S.; Pal, D. A Graph-Based Framework for Multiscale Modeling of Physiological Transport. Front. Netw. Physiol. 2022, 1, 802881. [Google Scholar] [CrossRef] [PubMed]
- Yoshitsugu, K.; Makoto, S.; Yann-Ching, H.; Norio, K. The Lymph System in Mice. Jpn. J. Vet. Res. 1964, 12, 69–78. [Google Scholar] [CrossRef]
- Van den Broeck, W.; Derore, A.; Simoens, P. Anatomy and nomenclature of murine lymph nodes: Descriptive study and nomenclatory standardization in BALB/cAnNCrl mice. J. Immunol. Methods 2006, 312, 12–19. [Google Scholar] [CrossRef] [PubMed]
- Diestel, R. Graph Theory, 5th ed.; Springer: Berlin/Heidelberg, Germany, 2017; Volume 13, p. 428. [Google Scholar] [CrossRef]
- Nielsen, J.M.; Kristiansen, S.B.; Ringgaard, S.; Nielsen, T.T.; Flyvbjerg, A.; Redington, A.N.; Bøtker, H.E. Left ventricular volume measurement in mice by conductance catheter: Evaluation and optimization of calibration. Am. J. Physiol.-Heart Circ. Physiol. 2007, 293, H534–H540. [Google Scholar] [CrossRef] [Green Version]
- Xie, C.; Wei, W.; Zhang, T.; Dirsch, O.; Dahmen, U. Monitoring of Systemic and Hepatic Hemodynamic Parameters in Mice. J. Vis. Exp. 2014, 92, 51955. [Google Scholar] [CrossRef] [Green Version]
- Lindena, J.; Küpper, W.; Trautschold †, I. Catalytic Enzyme Activity Concentration in Thoracic Duct, Liver, and Intestinal Lymph of the Dog, the Rabbit, the Rat and the Mouse. Approach to a Quantitative Diagnostic Enzymology, II. Communication. Clin. Chem. Lab. Med. 1986, 24, 19–34. [Google Scholar] [CrossRef] [Green Version]
- Bouta, E.M.; Wood, R.W.; Brown, E.B.; Rahimi, H.; Ritchlin, C.T.; Schwarz, E.M. In vivo quantification of lymph viscosity and pressure in lymphatic vessels and draining lymph nodes of arthritic joints in mice: Lymph viscosity and pressure in arthritic joints. J. Physiol. 2014, 592, 1213–1223. [Google Scholar] [CrossRef]
- Blatter, C.; Meijer, E.F.J.; Nam, A.S.; Jones, D.; Bouma, B.E.; Padera, T.P.; Vakoc, B.J. In vivo label-free measurement of lymph flow velocity and volumetric flow rates using Doppler optical coherence tomography. Sci. Rep. 2016, 6, 29035. [Google Scholar] [CrossRef] [PubMed]
- Takeda, K.; Mori, S.; Kodama, T. Study of fluid dynamics reveals direct communications between lymphatic vessels and venous blood vessels at lymph nodes of mice. J. Immunol. Methods 2017, 445, 1–9. [Google Scholar] [CrossRef]
- Economopoulos, V.; Noad, J.C.; Krishnamoorthy, S.; Rutt, B.K.; Foster, P.J. Comparing the MRI Appearance of the Lymph Nodes and Spleen in Wild-Type and Immuno-Deficient Mouse Strains. PLoS ONE 2011, 6, e27508. [Google Scholar] [CrossRef]
- Eagle, N.; Macy, M.; Claxton, R. Network diversity and economic development. Science 2010, 328, 1029–1031. [Google Scholar] [CrossRef] [PubMed]
- Wen, Y.; Xu, H.; Wan, W.; Shang, W.; Jin, R.; Zhou, F.; Mei, H.; Wang, J.; Xiao, G.; Chen, H.; et al. Visualizing lymphocytic choriomeningitis virus infection in cells and living mice. iScience 2022, 25, 105090. [Google Scholar] [CrossRef] [PubMed]
- Agollah, G.; Wu, G.; Sevick-Muraca, E.; Kwon, S. In vivo lymphatic imaging of a human inflammatory breast cancer model. J. Cancer 2014, 5, 774–783. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ferdous, J.; Fricke, G.; Moses, M. Modeling Immune Search Through the Lymphatic Network. In Proceedings of the International Conference on Swarm Intelligence, Malaga, Spain, 2–4 November 2022; pp. 332–340. [Google Scholar] [CrossRef]
- Thomas, S.; Rohner, N.; Edwards, E. Implications of Lymphatic Transport to Lymph Nodes in Immunity and Immunotherapy. Annu. Rev. Biomed. Eng. 2016, 18, 207–233. [Google Scholar] [CrossRef] [Green Version]
- Maisel, K.; Stella, S.; Potin, L.; Swartz, M. Exploiting lymphatic vessels for immunomodulation: Rationale, opportunities, and challenges. Adv. Drug. Deliv. Rev. 2017, 114, 43–59. [Google Scholar] [CrossRef] [PubMed]

| Property | Whole Graph, g | Left Subgraph, | Right Subgraph, |
|---|---|---|---|
| Number of inlet vertices | 52 | 36 | 16 |
| Maximum degree | 5 | 5 | 5 |
| Girth | 3 | 0 | 3 |
| Diameter, oriented (simple) | 7 (11) | 7 (11) | 4 (7) |
| Radius | 4 | 6 | 4 |
| Average path length, dir. (undir.) | 2.5 (5.3) | 2.7 (5.5) | 1.9 (3.9) |
| Energy | 95.1 | 65.6 | 29.5 |
| Spectral radius | 2.93 | 2.9 | 2.93 |
| Edge density | 0.0114 | 0.0164 | 0.0385 |
| Clustering coefficient | 0.019 | 0 | 0.059 |
| Number of separators | 36 (in total) | 25 | 11 |
| Robustness | 0.917 | 0.863 | 0.825 |
| Average topological flow diversity, | |||
| - scenario 1: - scenario 2: - scenario 3: | 0.8252 0.8242 0.8242 | 0.8028 0.8028 0.8028 | 0.9039 0.9015 0.9023 |
| Number of LNs | 27 | 19 | 8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Grebennikov, D.; Savinkov, R.; Zelenova, E.; Lobov, G.; Bocharov, G. Network Modeling of Murine Lymphatic System. Algorithms 2023, 16, 168. https://doi.org/10.3390/a16030168
Grebennikov D, Savinkov R, Zelenova E, Lobov G, Bocharov G. Network Modeling of Murine Lymphatic System. Algorithms. 2023; 16(3):168. https://doi.org/10.3390/a16030168
Chicago/Turabian StyleGrebennikov, Dmitry, Rostislav Savinkov, Ekaterina Zelenova, Gennady Lobov, and Gennady Bocharov. 2023. "Network Modeling of Murine Lymphatic System" Algorithms 16, no. 3: 168. https://doi.org/10.3390/a16030168
APA StyleGrebennikov, D., Savinkov, R., Zelenova, E., Lobov, G., & Bocharov, G. (2023). Network Modeling of Murine Lymphatic System. Algorithms, 16(3), 168. https://doi.org/10.3390/a16030168







