Enhancing the Distributed Acoustic Sensors’ (DAS) Performance by the Simple Noise Reduction Algorithms Sequential Application

Abstract

Moving differential and dynamic window moving averaging are simple and well-known signal processing algorithms. However, the most common methods of obtaining sufficient signal-to-noise ratios in distributed acoustic sensing use expensive and precise equipment such as laser sources, photoreceivers, etc., and neural network postprocessing, which results in an unacceptable price of an acoustic monitoring system for potential customers. This paper presents the distributed fiber-optic acoustic sensors data processing and noise suppression techniques applied both to raw data (spatial and temporal amplitude distributions) and to spectra obtained after the Fourier transform. The performance of algorithms’ individual parts in processing distributed acoustic sensor’s data obtained in laboratory conditions for an optical fiber subjected to various dynamic impact events is studied. A comparative analysis of these parts’ efficiency was carried out, and for each type of impact event, the most beneficial combinations were identified. The feasibility of existing noise reduction techniques performance improvement is proposed and tested. Presented algorithms are undemanding for computation resources and provide the signal-to-noise ratio enhancement of up to 13.1 dB. Thus, they can be useful in areas requiring the distributed acoustic monitoring systems’ cost reduction as maintaining acceptable performance while allowing the use of cheaper hardware.

1. Introduction

Fiber-optic distributed acoustic sensors (DAS) based on optical time-domain reflectometry (OTDR) technology were proposed more than 40 years ago [1]. Their development is directly related to approximately simultaneous creation of low loss optical fiber [2] and an OTDR itself as their manufacturing quality control method [3]. Since then, this area has grown very rapidly. Utilizing the Rayleigh backscattering of light propagating in an optical fiber, coherent optical reflectometry—CO-OTDR [4], phase-sensitive optical reflectometry—φ-OTDR [5,6,7,8,9], and optical frequency domain reflectometry—OFDR [10,11,12,13,14] have been proposed. In contrast to them, Brillouin and Raman reflectometry [15,16,17,18,19,20,21] use various types of inelastic scattering. Many of these technologies are adapted to perceive both static and dynamic external impacts on optical fiber, such as sound and other mechanical vibrations, temperature variations, and mechanical stress. 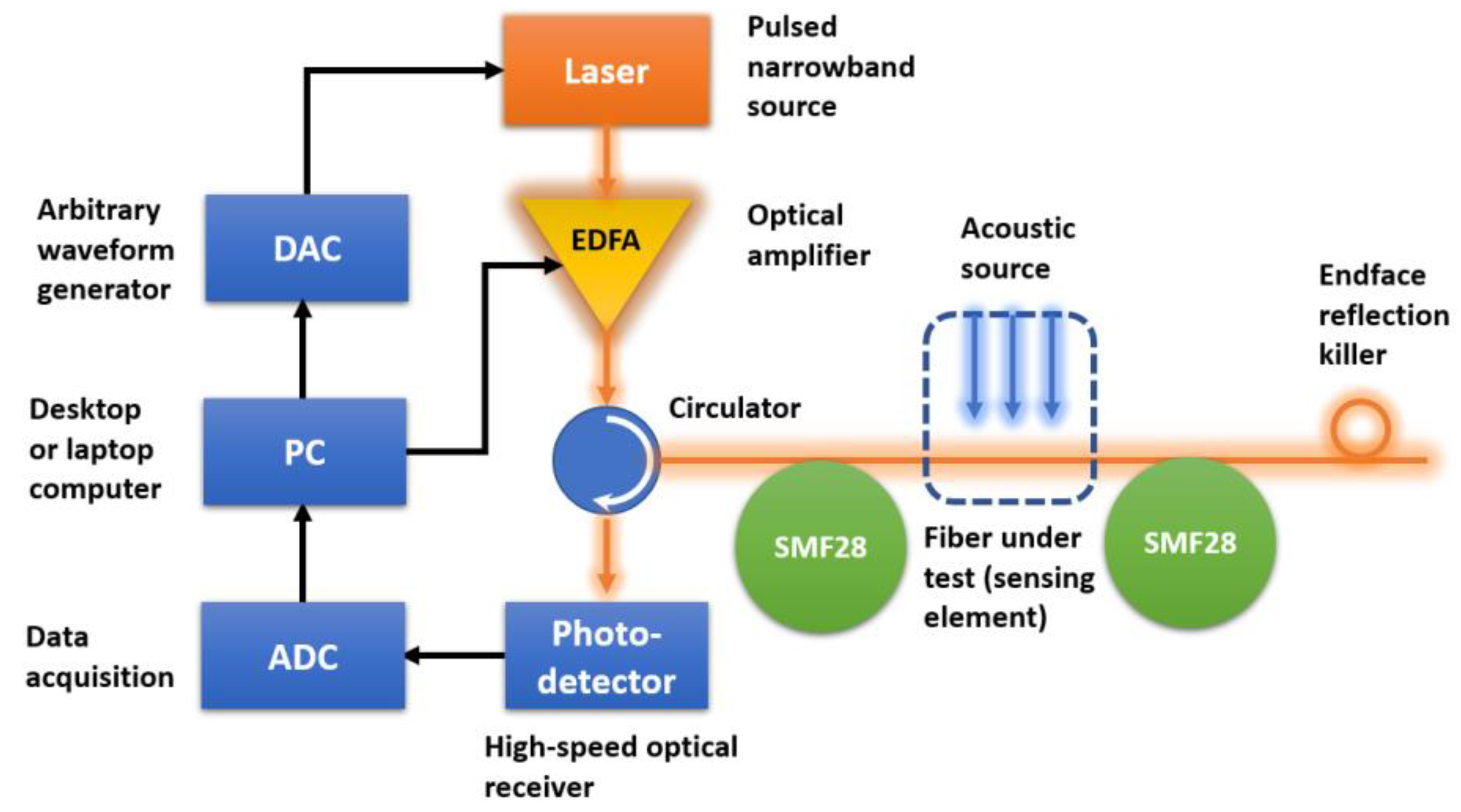Over the last few decades, acoustic monitoring has gained great popularity in many industries such as oil and gas production [22], processing [23], transportation [24], geophysics and mineral deposits exploration [25], protection of territories [26], and structural integrity monitoring of vital engineering constructions [27,28,29]. At the moment, such monitoring is usually performed by fiber optic DASs (due to their intrinsic advantages) using phase-sensitive technology (φ-DAS) implemented with the use of high-coherence light sources and direct or hybrid backscattering detection, since conventional OTDR is not sensitive to dynamic deformations, has a higher noise level, and requires additional time for the obtained data averaging. Moreover, its event response time is generally worse. At the same time, the necessity to use a highly coherent radiation source, a high-speed optical modulator [30], a photodetector, and ADC, as well as several optical amplifiers in DAS makes them rather expensive. Therefore, such systems are widespread only in top-financed areas of science and technology. However, state-of-the-art studies are more and more often dedicated to fiber optic acoustic sensors applications on behalf of less funded industries; for example, agriculture [31] and ecology [32,33]. It is reported that meteorology and biology [34,35] possess the need for a distributed acoustic sensor with sensitivity to acoustic events with certain frequencies. Thus, a sensor capable of satisfying such requests must have the most optimal price-performance ratio. This can be achieved by cost reduction, which can result from excluding some expensive setup elements and by bringing algorithms to the forefront instead of hardware where possible.

The state-of-the-art concept of processing distributed fiber-optic sensor signals mainly provides for automatic events classification occurring at a certain distance from the point where radiation is injected into the sensor. For this, specially created databases, correlation algorithms, neural networks, empirical mode decomposition, and variational mode decomposition are used [36,37,38,39]. In fact, the main idea of these studies is to decompose the signal not into the frequency spectrum using FFT, but into some modes that describe one or another physical process. In the pioneering work of [38], the variational mode decomposition technique for threat classification in phase-OTDR-based DAS systems was studied for the first time. To perform the high-precise processing, the Wavelet filtering technique was used before the decomposition, for the denoising of the raw data, and then high-pass filtering was applied. Another stage of denoising was the application of the autocorrelation function. The correlation peaks were interpreted as events, and only after that, the variational mode decomposition technique was applied to classify different impacts on the sensor. The mentioned study [38] showed that the raw signal of a distributed fiber optic sensor is quite difficult to use for decomposition or for machine learning, so it still requires pre-processing: for example, by Wavelet and Curvelet filtering or/and correlation algorithms [39,40,41,42]. Primary processing of raw data should be implemented on simple mathematical operations, since the volume of processed data is quite high, and the algorithms themselves are implemented with the use of programmable microcontrollers. Basically, these are simple algorithms, which are various types of integral or differential averaging of a discrete signal in a scanning window [43,44,45]. The number of simple mathematical operations at each individual moment when the scanning window is at a certain point in the trace rarely exceeds the number of discrete counts in this window. That is why it was decided to use just such methods for pre-processing data received from a distributed acoustic sensor.

Thus, the key task of this study is to test, evaluate, and improve the effectiveness of simple signal processing algorithms acting jointly or separately. Backscattered light traces, obtained using distributed fiber optic acoustic sensor subject to vibration impact and based on phase-sensitive time domain reflectometry, are considered as an input for the techniques under research. As it was mentioned above, it is vital to use simple algorithms here since the volume of data acquired with such instruments is generally quite large. The algorithms taken into account are expected to give a significant increase in the signal-to-noise ratio and, consequently, better distinguish signal and noise. This will allow the use of less expensive components, broader-band lasers, for instance, in the design of such tools. Various simple digital data processing methods, such as moving differential and dynamic window averaging, have already found their way into various fields of science and technology, proving their effectiveness. Distributed acoustic sensor’s data processing involves several stages and at each of them, supplementary changes can be made to the algorithm. Individual parameters of data processing methods may be subject to variation. The objective of this work is to determine the optimal signal processing stages at which one or another method can be involved in the calculation process, as well as to determine the basic parameters for their use. Similar results were obtained for various optical fiber samples and instrument configurations (on the order of 10s). The demonstration of the results is carried out on data that provides the most convenient visualization.

2. Approach

Such a sensor can be, for example, a system similar to φ-DAS, but using a pulsed, highly coherent current-controlled light source, eliminating the need to use an optical modulator and its control system, as well as only one optical amplifier and direct signal detection by a photodetector and ADC (Figure 1) without phase information extraction.

Nevertheless, when the length of the system approaches the coherence length of the light source used, the signal-to-noise ratio (SNR) decreases significantly, and thus the problem of distinguishing the useful signal from noise becomes quite relevant. At the moment, artificial intelligence technologies, such as neural networks, have become widespread in the field of DAS noise reduction [46]. However, they usually require a lot of computing resources and training data. This can negatively affect the final cost of the system.

2.1. Averaging and Moving Differential

The authors of [47] present a relatively simple algorithm having an acceptable efficiency under the research conditions. The algorithm operation was tested by processing data obtained with the DAS system using two different sources of radiation and two different sources of acoustic events: a shaker located at a distance of 3500 m from the sensitive element input facet and a piezoelectric transducer located at a distance of 1800 m, at frequencies exposure to 350, 500, 1200, 3700, and 5600 Hz. The sensitive element of the sensor consisted of 4 km of SMF-28 telecommunications optical fiber (Figure 2).

As a rule, any DAS technology works as follows: a light pulse is injected into the fiber optic sensing element through an optical circulator or coupler. As it propagates along the fiber, a part of its energy is scattered in all directions every moment on intrinsic refractive index inhomogeneities of subwavelength scale. Sometimes the inhomogeneities in the fiber could be specially induced (like fiber Bragg gratings, FBGs). A part of the scattered radiation guided by the optical fiber core begins to propagate in the direction opposite to the probing. The optical circulator or splitter at the input end of the fiber transmits this signal to the photodetector. The arrival time of backscattered signal from a specific point in the optical fiber unveils the information about the distance to this point, and its intensity, can, for example, give evidence of an acoustic impact presence or absence. This is possible due to the fact that acoustic waves are able to exert the pressure to an optical fiber and thus modulate its core refractive index and the positions of the inhomogeneities causing Rayleigh backscattering (and, therefore, its intensity in this location), with the frequency they have themselves. Thus, DAS raw data is a sequence of φ-OTDR traces recorded continuously for some time, that is, the dependences of the backscattering intensity on time. They can be arranged in the form of a matrix, the rows of which contain the backscattering intensity distribution along the length of the fiber, and the columns, respectively, the backscattering intensity distribution at a specific point of the fiber over time.

The data acquired by the sensor from [47] had exactly the same form. An $N\times M$ $\left\{s_{nm}\right\}$ matrix consisted of M = 8000 rows, corresponding to the distribution along the fiber (trace) and N = 932 columns, corresponding to the time distribution (932 traces sequentially obtained by the sensor). The noise suppression algorithm consisted of two parts. First, each element was averaged over the 20 nearest elements of the row—in the spatial domain:

$${\tilde{s}}_{nm}=\left[{\displaystyle \sum _a^b{s}_{nk}}\right]\left[w^{-1}\right]$$

(1)

where w = 21 and k increases from a = m − 0.5(w − 1) to b = m + 0.5(w − 1).

This allows one to reduce noise outside the spatial spectrum and make the resulting traces smoother. However, it reduces the spatial resolution in proportion to the number of neighboring elements selected to average the given one. In the second part, the moving differential algorithm [48] was applied to the time domain-matrix columns. This also made it possible to reduce the noise background and to obtain, after performing fast Fourier transform (FFT) over the matrix columns, frequency spectra with pronounced peaks at the frequencies of the vibrations applied to the sensor (Figure 3).

Since the bandwidth of the self-injection locked laser was considerably higher than that of the commercial one used, the bandwidth of the acoustic event recorded with it has consequently broader spectrum in contrast to that of the event recorded using commercial laser under the same conditions.

The presented algorithm, together with the modification of the equipment, made it possible to cut the DAS systems’ cost, since it became possible to use a telecommunication semiconductor laser with distributed feedback in them. This laser had the bandwidth of 1 MHz. The hardware modification consisted in creating a mode of its operation with the external resonator frequency self-injection locking. This reduced the bandwidth to 6 kHz. The traces obtained using such a laser source and their array processing with the presented technique allowed one to use the system as a DAS with the quality of the results practically the same as that provided by the use of a commercial fiber laser with a bandwidth of 100 Hz as a laser source. The role of the acquired data quality criterion was performed by SNR. The difference in SNR estimated from data obtained using a commercial fiber laser and a modified semiconductor laser with additional processing of the results was about 0.4 dB. In the entire frequency range of the applied acoustic impacts, the SNR was at least 8 dB. As the main advantage of this algorithm, one can note efficiency with general simplicity. As a disadvantage, there is a decrease in spatial resolution, which is very important parameter for distributed sensing [49,50,51,52,53].

2.2. Dynamic Spectrum Averaging

Researchers from [54], presented an algorithm for OFDR data processing. It is an averaging with a variable length (dynamic) window. The algorithm includes the following steps:

• A choice of scanning window with the length of w’, which allows fitting the most significant event on an OFDR trace consisting of N samples into it (Figure 4a);
• The process of spatial domain scanning using this window. During the scanning process, for all points from w’/2 to N − w’/2, the standard deviation σ of the signal values P at the points included in this window is calculated;
• Normalization of the obtained σ values to 1 (σ = σ_norm);
• A filtered trace (Figure 4b) calculation according to

$$i-\frac{w_j}{2}\ge 0; i-\frac{w_j}{2}<N\to P_{d(j)}=\frac{1}{w_j}{\displaystyle \sum _{i-\frac{w_j}{2}}^{i+\frac{w_j}{2}}{P}_i, w_j=w’(1-{\sigma }_{norm})}$$

(2)

Describing the proposed method in simple terms, it can be said that the algorithm focuses on sharp and significant changes in the spectrum. The higher the peak found when moving along a discretely given spectrum, the fewer samples on both sides of it will be used for averaging. The more abruptly the event gains its maximum intensity, the less it will be blurred. In order to minimize dynamic distortions of the original signal, in this study, the dependence of the window size on the standard deviation is assumed to be linear. Further work is expected to study the influence of the nature of this dependence on the output signal.

As an advantage of the algorithm, the simplicity and low computing resources requirements are also worth noting, and, in addition, the potential ability to work with any data. The main disadvantage here seems to be the possible loss of a low-intensity signal. Since an OFDR-trace is actually an FFT spectrum of backscattered data, and therefore has a similar nature to DAS spectra, it was decided to test this algorithm to improve the quality of distributed acoustic sensor data.

3. Results

As a part of the DAS optimization problem, it was decided to study the described algorithms operation in parts, in whole and together with various types of events recorded by the proposed design sensor (Figure 1). The sensing element consisted of 1 km of SMF-28 optical fiber. Four types of data were used for processing: 1 distributed event with a 2 kHz frequency, 1 distributed event with a 6.5 kHz frequency, 1 pointwise event with a 3 kHz frequency and harmonics at frequencies of 6 and 9 kHz, and one pointwise event with a 10 kHz frequency (Figure 5). Each data set contained both general background noise and signals that stood out against it and were not related to the useful one and did not depend on it (vertical bands corresponding to a certain frequency and recorded throughout the sensitive element, Figure 5). The frequency range taken into consideration was spaced between 0 and 11 kHz.

The study of the noise reduction technique’s effectiveness was carried out with those heat maps cross-sections (points of the optical fiber), in which the event had the highest amplitude, and in the case of a distributed event, with a frequency spectrum previously averaged over several points of the optical fiber. For each type of data, the algorithms of averaging over 20 neighboring elements in the spatial domain (SA—spatial averaging) and the moving differential (MD) in the time domain were first applied separately, and then together (filtering—F). After that, each of the four obtained results (NF—no filtering, SA, MD, and F) was subjected to the FFT, normalized to 1, and presented as input to the averaging algorithm with a dynamic window in the spectral domain (FDDA—frequency domain dynamic averaging).

For data with a distributed event at a frequency of 2 kHz, the combination of SA and FDDA algorithms demonstrated the most significant increase in SNR by 1.6 dB (Figure 6c). Moreover, it was the SA algorithm that made it possible to eliminate noise peaks in the signal (Figure 6b). Presumably, this is due to the fact that they have a rather unstable amplitude in the spatial domain. The negative effects of the SA, MD algorithms, and their combination (F) resulting in an unsufficient increase or decrease of SNR are described in Section 4.

However, it can be seen, that the FDDA algorithm, in its turn, not only exhibits edge effects—the noise level in the spectrum gradually increases from the edges to the middle but also places it above the zero level, whereas the spectrum does not contain components with an amplitude of less than a certain value, but greater than zero. These effects are explained by the fact that at the scanning dynamic window position i = 0, the first window element position in the array of discrete samples is equal to −w/2, and at i = N, the last window element falls to the position of N + w/2. It is easy to determine that these positions do not exist in the array of discrete samples, so they were initially replaced by zeros. The larger the window on the array boundaries, the more impact zero-padded areas introduce. All this leads to the fact that the resulting data is allocated on a kind of “pedestal”. Since the frequencies forming this pedestal are not physically present in the spectrum, they can be determined as noise and can be eliminated. The FDDA noise elimination algorithm modification can be represented as follows: first, a one-dimensional array M of input data with dimensions [0, (3N−1)] is created. It is filled according to

$$M_i=P_{i-N\times floor(L(M)/N)}$$

(3)

where floor(x) returns an integer part of x, L(x)—returns x length.

Thus, the values of the array M will correspond to the following original signal values P:

$$\begin{array}{l}{M}_i=P_i, i\in [0,(N-1)];\\ M_i=P_{i-N}, i\in [(N-1),(2N-1)];\\ M_i=P_{i-2N}, i\in [(2N-1),(3N-1)].\end{array}$$

(4)

Next, the resulting array M is processed according to Equation (2), and its values are replaced with the new ones. The received data is used to form a new M’ array of [0, (N−1)] size:

M’_i = M_i+N

(5)

After that, the sample m representing the minimum value is found in the array M’, by iterative enumeration. M’ values are overwritten as follows:

M’_i = M’_I−m

(6)

Then the values of M’_i are normalized to 1. Thus, the elimination of the noise pedestal in the processed spectrum is achieved. The FDDA modification made it possible to reach an increase in SNR in the studied case by 9.7 dB (Figure 7a). Therefore, for an distributed event with a 2 kHz frequency, the SNR turned out to be 20.6 dB after processing. In the initial data, it was equal to 10.9 dB. The results of distributed 6.5 kHz frequency event processing were practically the same (Figure 7b)—the considered combination of algorithms provided an increase in SNR by 13.1 dB.

For a frequency spectrum of a 3 kHz pointwise event with harmonics, the SNR was 14.7 dB before the processing. The best way to suppress noise in this case was provided by the FDDA algorithm. The increase in SNR was 6.6 dB (Figure 7c).

The original frequency spectrum in the case of a pointwise 10 kHz impact had an SNR of about 13.4 dB. Its greatest increase during noise suppression techniques tests was provided by the combination of MD and FDDA algorithms—5.2 dB (Figure 7d). This is probably due to the fact that the MD algorithm with the smallest possible window of 2 points played a role of a high-pass filter, significantly reducing the signal amplitude, and, accordingly, the noise in the frequency range below 10 kHz.

4. Discussion

The results of experimental data processing demonstrate that under various conditions, the best noise suppression is achieved using different algorithms, individually or in combination. The low efficiency of certain algorithms in some situations is inevitably associated with the peculiarities of their work. For example, the MD algorithm, which acts here as a high-pass filter, is prone to the manifestation of window effects: with a large window length, the spectrum takes the form of a values sequence which are tending to 0 or to the maximum with a certain constant period, so both noise and signal are reduced or increased in this process. In the case of the minimum length of the MD window, the maximum gain falls on the frequency region around 10 kHz. Since the region above 11 kHz was not taken into consideration, a significant increase in the noise level did not affect the SNR. However, in the case of the 3 kHz event frequency, this effect began to provide a significant contribution, affecting not only the SNR but also distorting the intensity values in the useful signal. This resulted in the harmonics with frequencies of 9 and 3 kHz getting an amplitude greater than that of the fundamental tone (Figure 8d).

Describing the case of 10 kHz event, it should be noted that the SA algorithm processing had a negative impact here, since it led to the rise of spurious peaks associated with noise that were almost imperceptible in the original spectrum (Figure 8a).

The FDDA algorithm, which proved to be quite effective in all the cases studied, nevertheless, has at least one drawback. If the useful signal components are located close enough in the frequency domain, the noise components between them will be reduced less compared to the area near the single-frequency event. The modified algorithm significantly reduces the effect, but does not eliminate the problem entirely (Figure 9b). This is due to the peculiarities of this algorithm operation and, in particular, the mechanism for the selection of window size, as the latter depends on the presence of the significant signal level increases nearby. In the case of the 3 kHz event, this manifested itself in the form of a spectrum noise component convex shape, which slightly decreased the SNR relative to the expected value (Figure 9c).

As already noted, the presented methods have both advantages and disadvantages. In general, when using both algorithms, part of the useful signal may be missed. It can be either a high-frequency signal or a signal of any frequency, but with a relatively low amplitude. To eliminate this shortcoming in the future, it is advisable to use the methods of machine learning and artificial intelligence [55,56,57], which can be used in combination with the described approaches. In particular, artificial intelligence can automatically select the integration and differentiation steps of a discrete signal when processing by the MA-MD method. This will improve the filtering quality and reduce the computation time since the interactive calculations will be replaced by a fairly fast neural network algorithm. Another option that improves the processing quality can be the use of artificial intelligence to control the influence of the results obtained by each of the methods on the final physical quantities. We have already successfully demonstrated such an approach for a distributed fiber-optic sensor based on stimulated Brillouin scattering [21]. In this work, the neural network in the learning process determines the effect of each of the Brillouin frequency shift extraction methods on achieving the most accurate result for each Brillouin gain spectrum with certain parameters. The increase in accuracy in this work was 10% (in comparison with the value obtained by averaging the results provided by all used methods). We are convinced that in the future it is necessary to apply this approach to data obtained using a distributed fiber optic sensor based on Rayleigh scattering. Lastly, the MD method can be applied in the frequency domain, just like FDDA, and the neural network will determine their contribution to the detection accuracy of the required frequency with maximum SNR. While using software methods to improve signal quality, one should not forget about the possibilities of hardware modification of the optoelectronic system [58,59,60,61,62,63] and sensor fiber or cable [57,64,65,66,67,68,69]. We believe that these works will be the priority of our scientific group in the future.

5. Conclusions

To conclude, it should be noted that this work solved one of the DAS software optimization problems. This was done by studying the operation of noise reduction algorithms that do not impose the significant requirements for the computing devices performance in various scenarios of impact on the sensor. The algorithms or their combinations demonstrating the highest efficiency were identified for each type of event, modifications were proposed to increase their performance. A summary of the comparison results is given in

Table 1. Results of the considered noise reduction algorithms comparison.

Event Frequency, kHz	Event Type	Most Efficient Technique	SNR Increase, dB
10	Pointwise	MD+FDDA	5.2
3	Pointwise with harmonics	FDDA	6.6
2	Distributed	SA+FDDA	9.7
6.5	Distributed	SA+FDDA	13.1

.

The first column in Table 1 corresponds to the frequency at which the fiber sensor was affected. This information is provided only to associate the results presented in the table with the figures above. As shown by numerous experiments, the efficiency of the filtering algorithms does not depend on frequency within the linear part of the sensor frequency response. Our studies have also shown that it is expedient to use the FDDA method after using the other considered algorithms. From Figure 4, for example, it can be seen that the first peak in the spectrum after processing turned out to have a significant spreading at its base. Thus, the limitation of this method is the lack of capacity to detect several neighboring frequencies. Another flaw, already mentioned above, is the disappearance of low-intensity oscillations from the useful signal under some conditions. In other cases, the FDDA method gives a noticeable increase in the signal-to-noise ratio, both when used alone or in combination with other algorithms.

We believe that the search for the most efficient data processing algorithms, along with the use of cost-consuming narrow-band laser solutions reported recently, can meet the demand for the use of DAS in an ever-expanding range of fields of science and technology.

The results obtained in this work can be applied to a wide range of problems. First, the presence of an inexpensive laser in the monitoring system will make it available not only for geological exploration, monitoring of pipelines, and mines, but also for new applications such as urban traffic monitoring and security systems [70,71,72,73]. New areas will open up where DAS technology can be applied. In addition to studies already carried out using a distributed acoustic sensor on the behavior of the red weevil in palm trees [74], acoustic observations of cicadas and bees seem to be the most obvious future work [75,76]. Perhaps this will provide key data to address issues related to declining bee populations around the world.

Secondly, the use of the proposed simple filters in combination or separately allows obtaining data with increased SNR when studying new materials and mechanical designs. A huge number of works are devoted to non-destructive testing, which indicates the importance of this area [77,78,79,80,81]. In a number of engineering tasks, it is required to obtain data on all spectral components: on the fundamental tone and additional harmonics [82]. In such cases, the MA and MD filters will give the desired SNR gain and allow the full spectrum to be saved for analysis. In tasks where it is required to obtain information about the fundamental tone of the acoustic vibration and to suppress the remaining harmonics along with noise, it is advisable to apply the FDDA filter after using the MA and MD algorithms. Such challenges may arise during the operation of vortex flowmeters or during the use of acoustic sensors for diagnosing new devices and products [83,84,85].

Another important and dynamically developing area, where the technology of distributed fiber-optic sensors can be applied in the very near future, is a smart home, smart city, smart production, and the Internet of Things [86,87,88]. With the spread of such systems, the issues of energy saving and increasing the lifetime of individual elements become more and more relevant. The DAS system in combination with the MA-MD and FDDA filters can be used to train and operate the scheduling algorithm based on learning automation for Internet of Things (SALA-IoT) [89]. We believe that this will speed up training, and at the operational stage, it could simplify the sensor’s design.