Physics-Informed Deep Learning for Traffic State Estimation: A Survey and the Outlook
Abstract
:1. Introduction
1.1. Scope of This Survey
1.2. Contributions
- propose a computational graph that visualizes both physics and data components in PIDL;
- establish a generic way of designing each module of the PIDL computational graphs for both predication and uncertainty quantification;
- benchmark the performance of various PIDL models using the same real-world dataset and identify the advantage of PIDL in the “small data” regime.
2. Preliminaries and Related Work
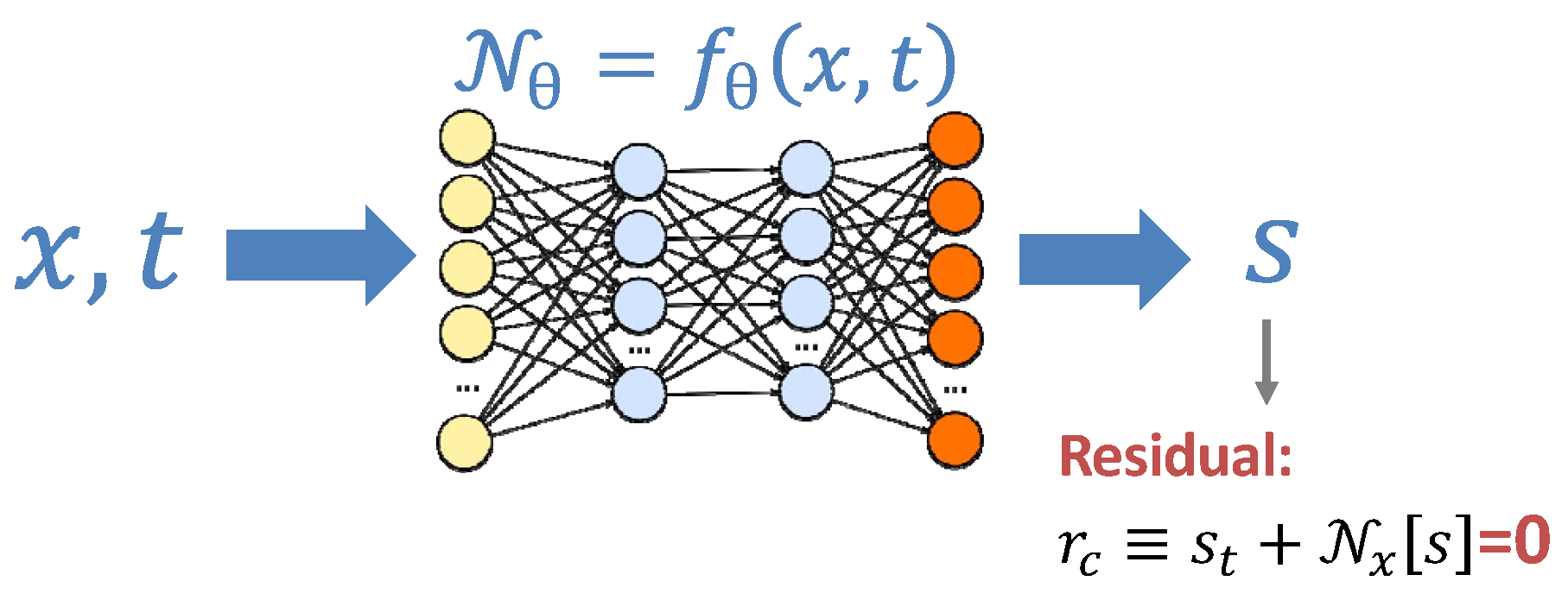
2.1. PIDL
2.2. Traffic State Estimation
- These three traffic quantities are connected via a universal formula:Knowing two of these quantities automatically derives the other. Thus, in this paper, we will primarily focus on , and q can be derived using Equation (4).
- , where is the capacity of a road, is the jam density (i.e., the bumper-to-bumper traffic scenario), and is the maximum speed (and usually represented by a speed limit). How to calibrate these parameters is shown in Table 1.
2.2.1. Physics-Based Models
2.2.2. Data-Driven Approach
2.2.3. PIDL
2.3. Two Classes of Problems
3. PIDL for Deterministic TSE
3.1. PIDL for Traffic State Estimation (PIDL-TSE)
3.2. Hybrid Computational Graph (HCG)
3.3. Training Paradigms
3.3.1. Sequential Training
3.3.2. Joint Training
Challenges
ML Surrogate
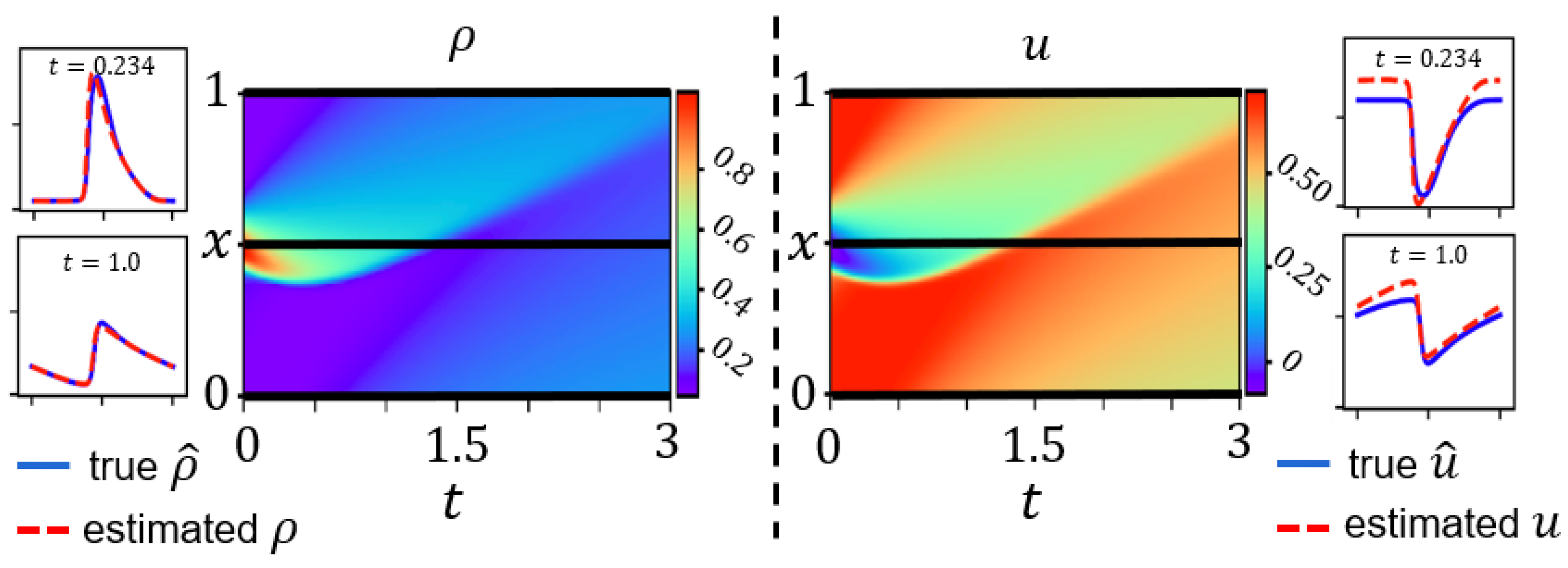
3.4. Numerical Data Validation for Three-Parameter-Based LWR
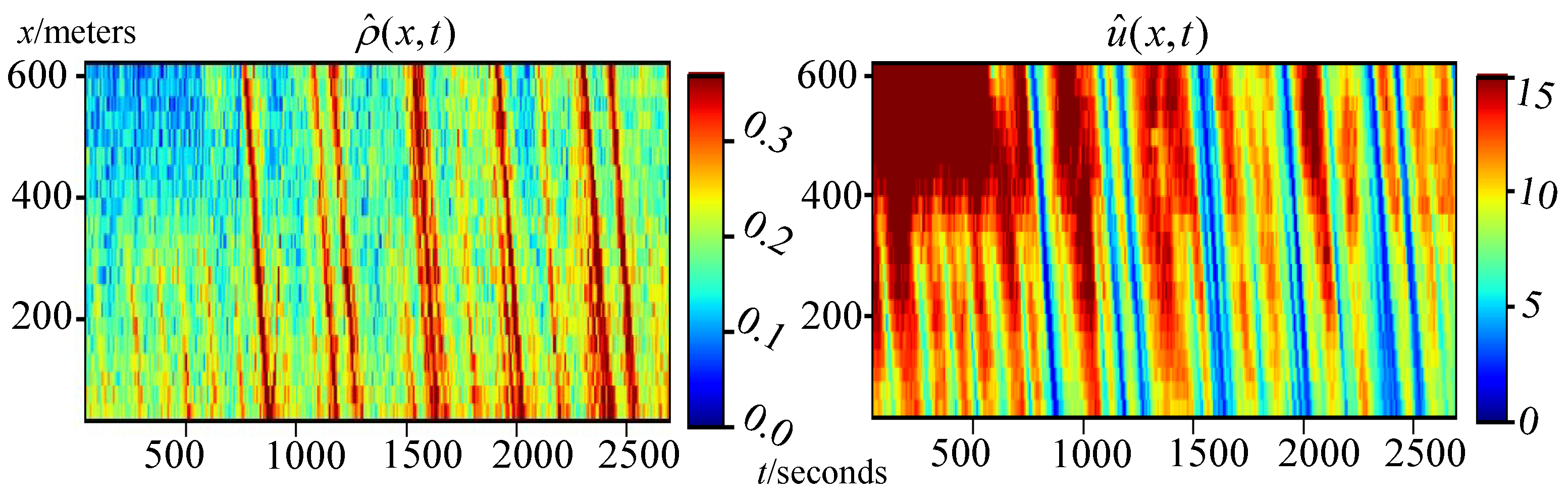
3.5. Real-World Data Validation
4. PIDL for UQ
- Aleatoric uncertainty (or data uncertainty): an endogenous property of data and thus irreducible, coming from measurement noise, incomplete data, or a mismatch between training and test data.
- Epistemic uncertainty (or knowledge uncertainty, systematic uncertainty, model discrepancy): a property of a model arising from inadequate knowledge of the traffic states. For example, traffic normally constitutes multi-class vehicles (e.g., passenger cars, motorcycles, and commercial vehicles). A single model can lead to insufficiency in capturing diversely manifested behaviors.
4.1. PIDL-UQ for TSE
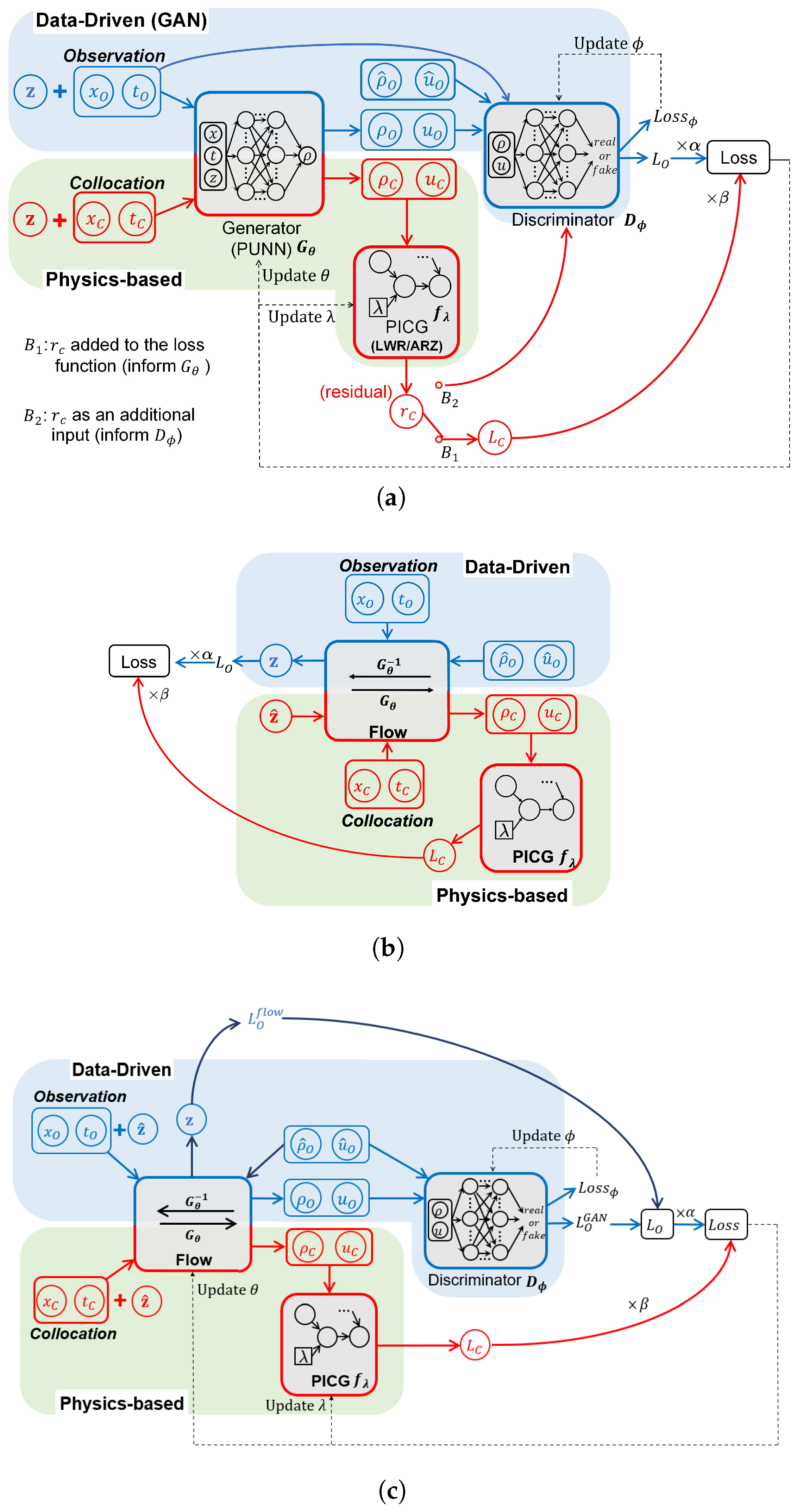
4.1.1. Physics-Informed Generative Adversarial Network (PhysGAN)
4.1.2. Physics-Informed Normalizing Flow (PhysFlow)
4.1.3. Physics-Informed Flow-Based GAN (PhysFlowGAN)
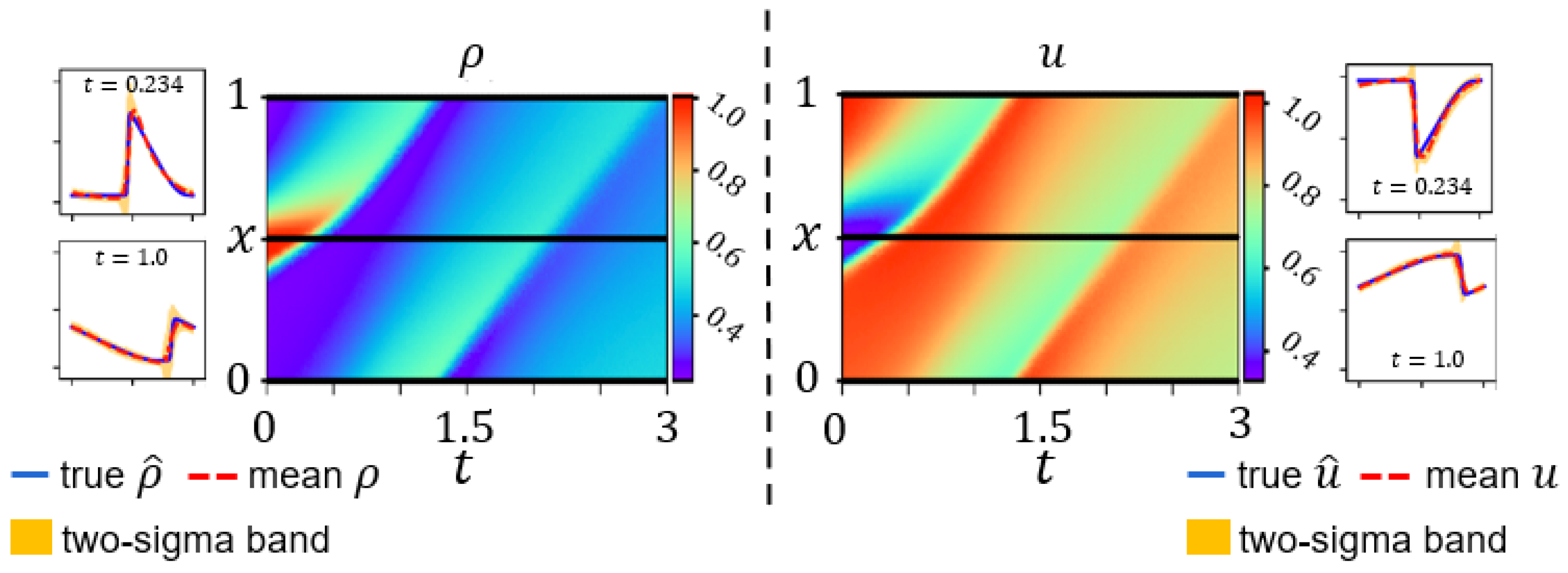
4.2. Numerical Data Validation for Greenshields-Based ARZ
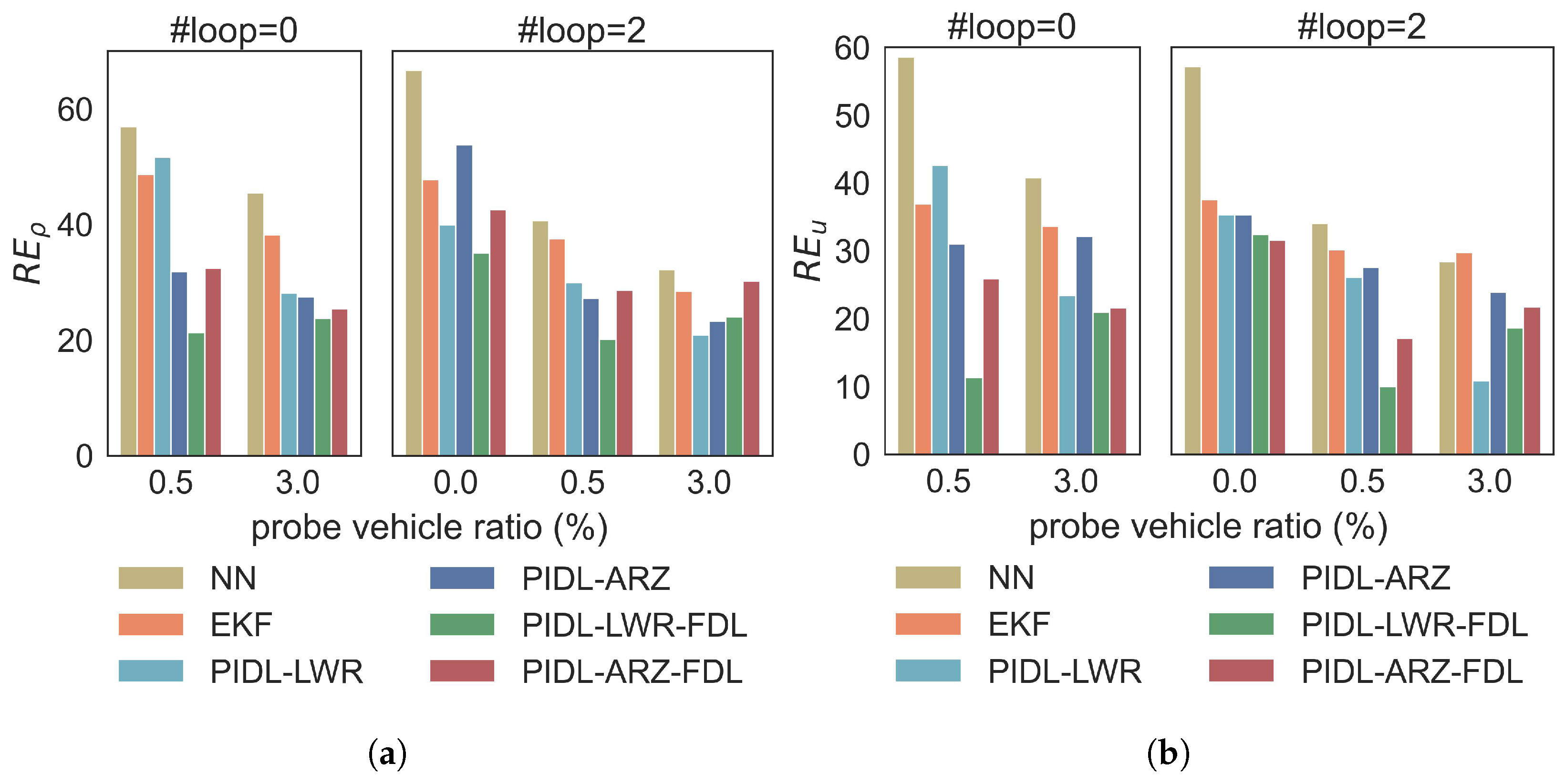
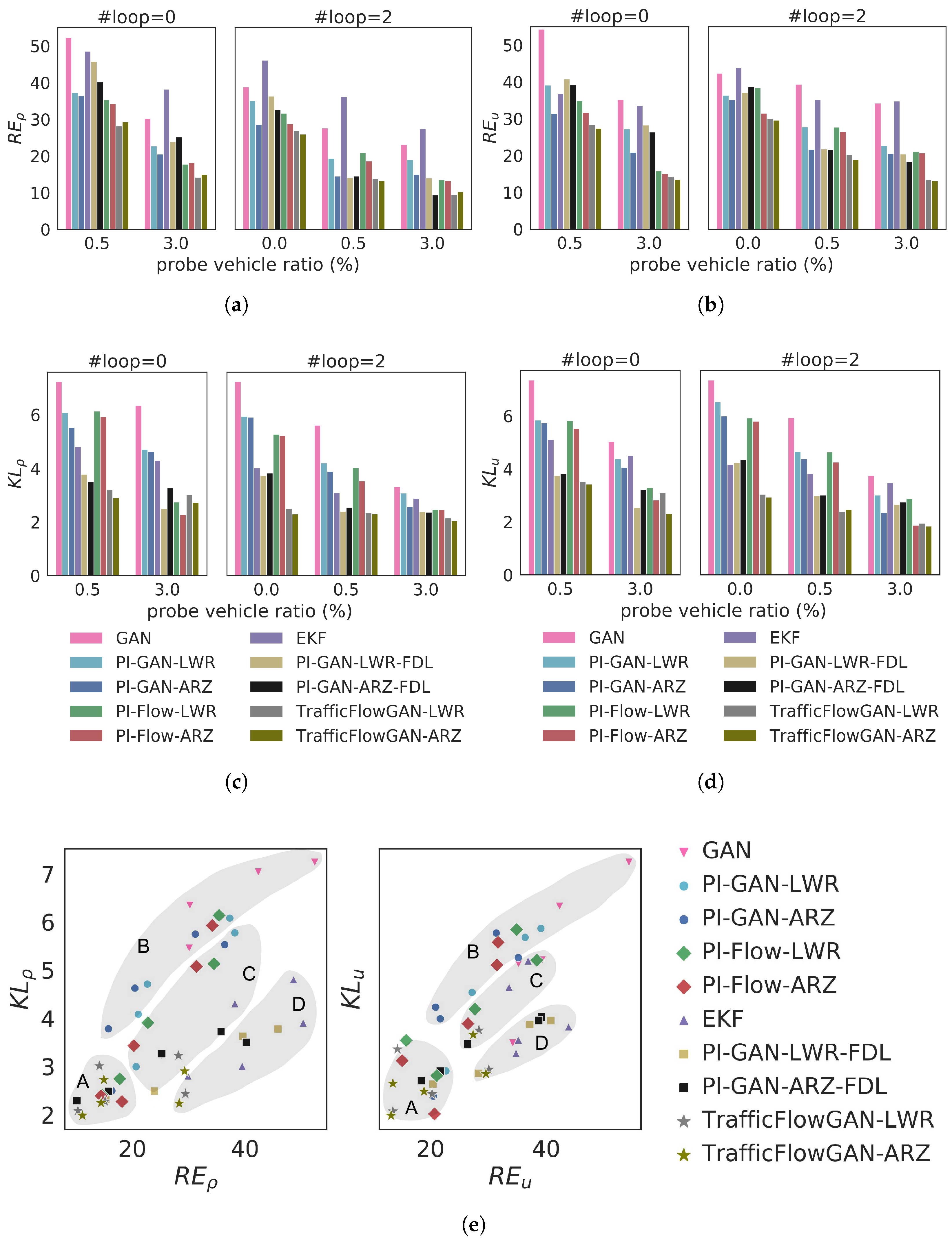
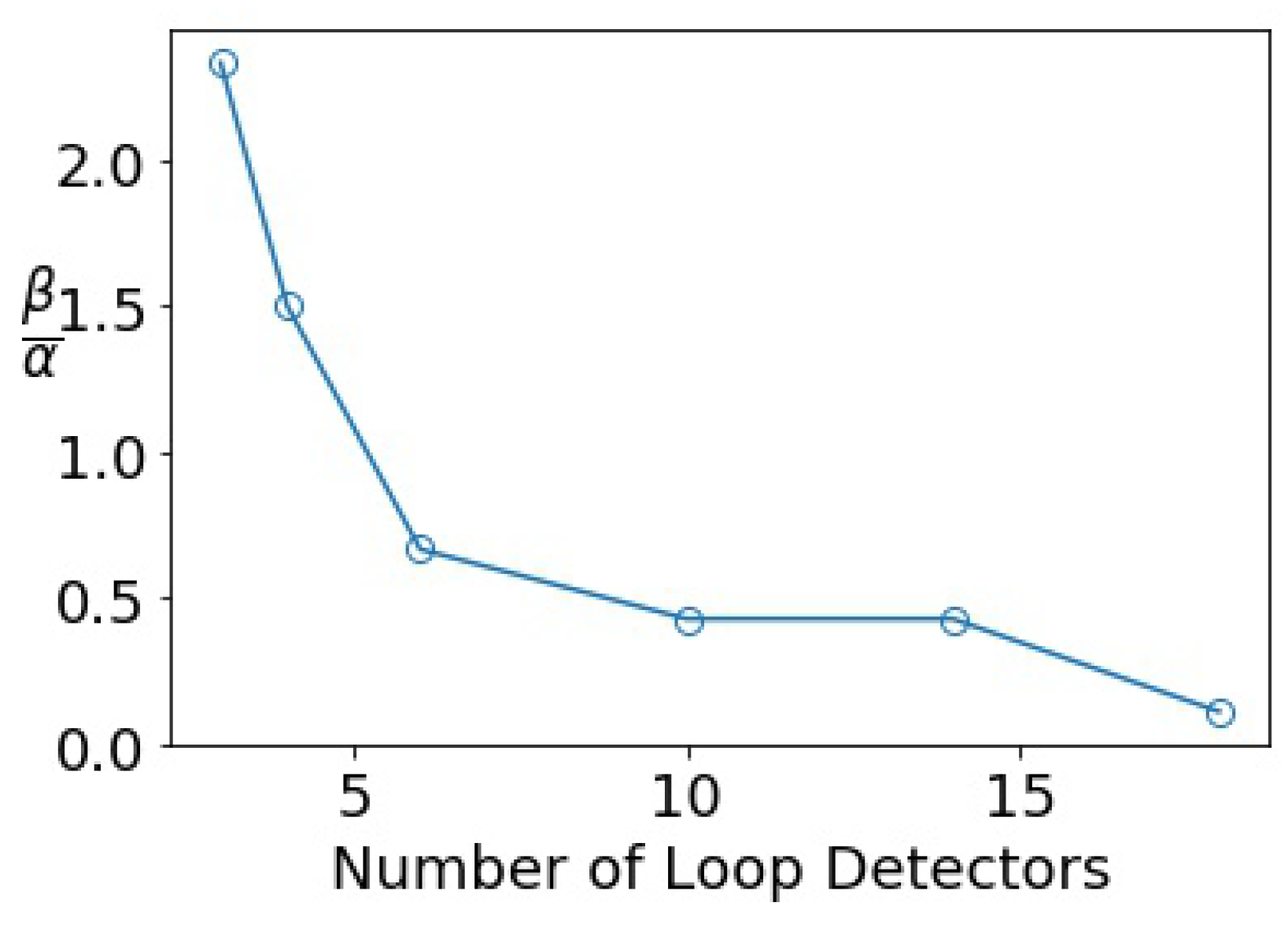
4.3. Real-World Data Validation
- Region A (optimal RE and KL): Most points in this region belong to the TrafficFlowGAN model type (stars), which shows that the combination of PI-GAN and PI-Flow helps to achieve the best performance in terms of both RE and KL.
- Region B (low RE and high KL): Most points in this region belong to GAN (inverted triangles) and PI-GAN (dots), which is a sign that the GAN-based models are prone to mode-collapse.
- Region C (balanced RE and KL): Most points in this region belong to the PI-Flow model type, indicating that explicit estimation of the data likelihood helps to balance RE and KL.
- Region D (high RE and low KL): Most points in this region belong to the EKF (triangles) and PI-GAN-FDL (squares), showing that these two types of model can better capture the uncertainty than the mean.
5. Conclusions and Future Work
5.1. Conclusions
5.2. Outlook
5.2.1. Physics Representation
5.2.2. Learning Discontinuity in Patterns
5.2.3. Transfer and Meta-Learning
5.2.4. IoT Data for Urban Traffic Management
5.2.5. TSE on Networks
- How do we leverage various observation data to fully exploit the strengths of PIDL?
- What types of sensors and sensing data would enrich the application domains of PIDL and better leverage its benefits?
- Would there exist a universal architecture of hybrid computational graphs across domains?
- What are robust evaluation methods and metrics for PIDL models against baselines?
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1. Experimental Details for TSE and System Identification Using Loop Detectors
Appendix A.1.1. Experimental Configurations
| Algorithm A1: PIDL training for deterministic TSE. |
1 Initialization: 2 Initialized PUNN parameters ; Initialized physics parameters ; Adam iterations ; Weights of loss functions , , and . 3 Input: The observation data ; collocation points ; boundary collocation points , e.g.,
|
Appendix A.1.2. Additional Experimental Results Using Numerical Data for Three-Parameter-Based LWR
| m | (%) | (%) | (%) | (%) | (%) | (%) |
|---|---|---|---|---|---|---|
| 3 | 75.50 | 54.15 | 124.52 | >1000 | >1000 | 99.95 |
| 4 | 10.04 | 59.07 | 72.63 | 381.31 | 14.60 | 6.72 |
| 5 | 3.186 | 2.75 | 4.03 | 6.97 | 0.29 | 3.00 |
| 6 | 1.125 | 0.69 | 2.49 | 2.26 | 0.49 | 7.56 |
| 8 | 0.7619 | 1.03 | 2.43 | 3.60 | 0.30 | 7.85 |
Appendix A.1.3. Additional Experimental Results Using Real-World Data
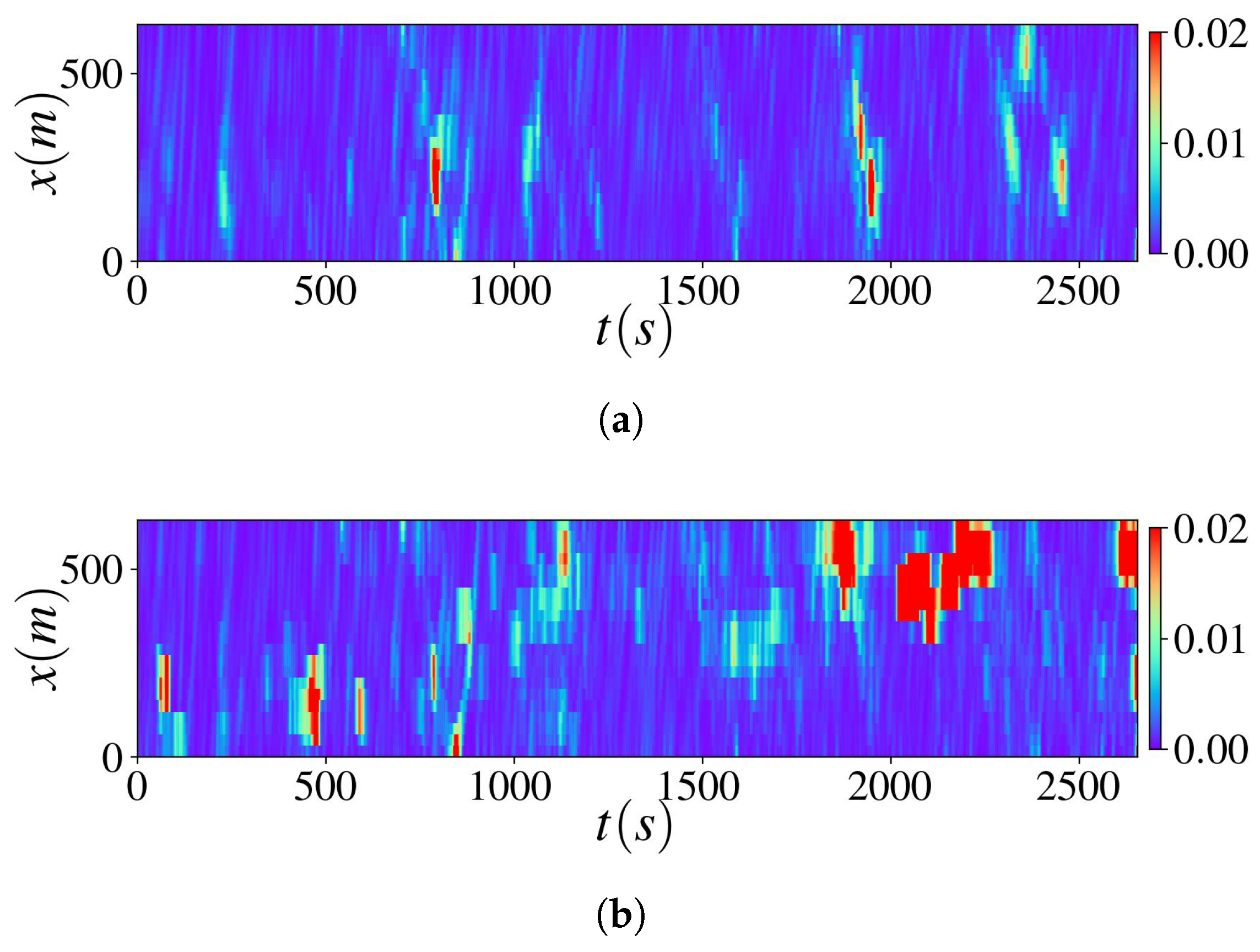
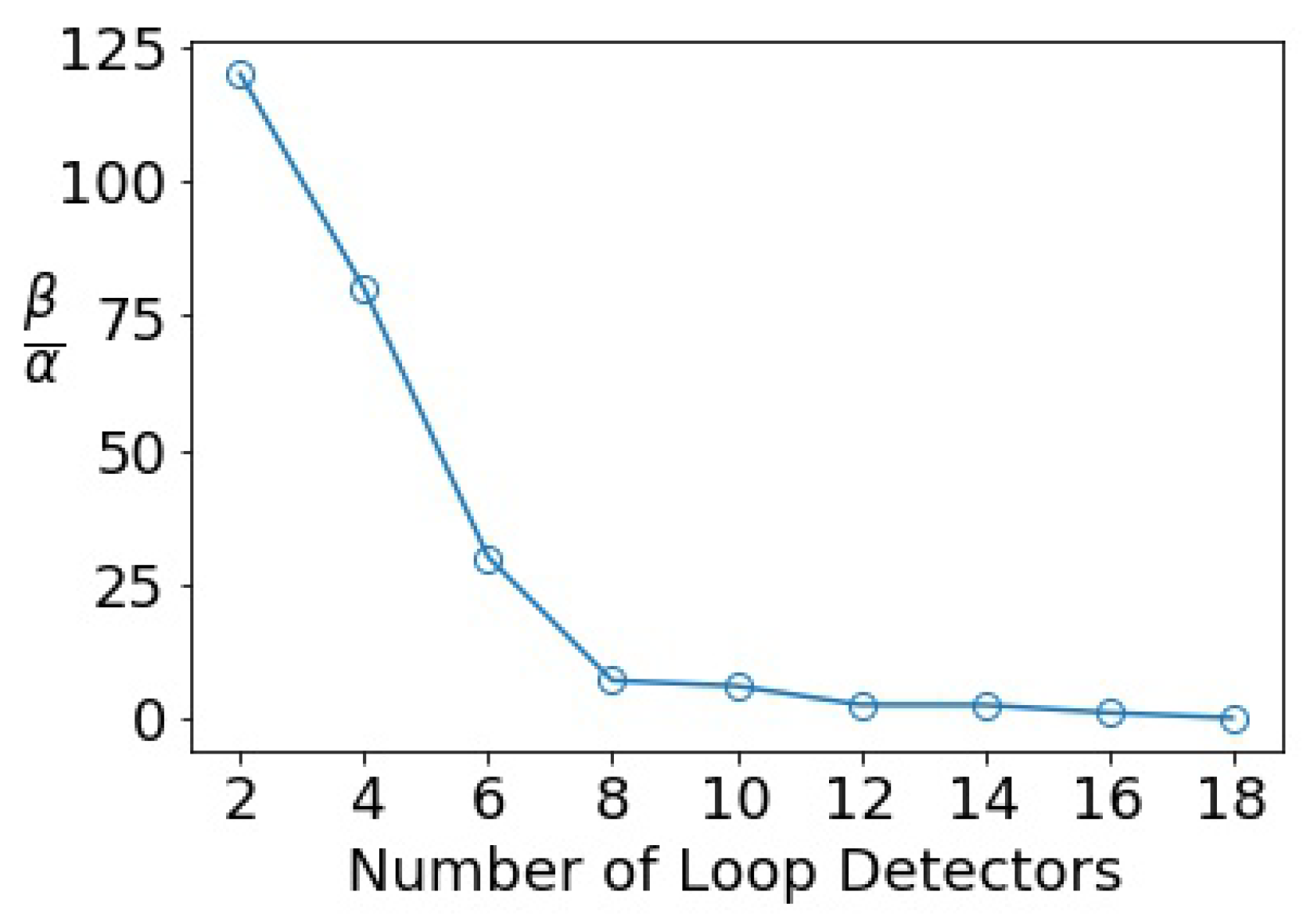
Appendix A.1.4. Sensitivity Analysis on Collocation Points
| (%) | (%) | (%) | (%) | (%) | (%) | |
|---|---|---|---|---|---|---|
| 0.0001 | 81.2 | 62.66 | 21.15 | 297.77 | 25.91 | 171.37 |
| 0.001 | 10.2 | 64.52 | 89.69 | 504.23 | 17.77 | 7.16 |
| 0.01 | 3.6 | 20.55 | 11.10 | 47.36 | 3.32 | 2.59 |
| 0.1 | 3.2 | 7.69 | 5.74 | 15.78 | 0.45 | 3.41 |
| 0.5 | 3.0 | 1.88 | 4.23 | 5.87 | 0.60 | 3.37 |
Appendix A.1.5. Computational Effort and Model Accuracy
| Model | Model Type | Computation Time | Prediction Error | ||
|---|---|---|---|---|---|
| Training (s) | Test (s) | ||||
| EKF | Physics-based | − | 1.5 | 39.5 | 35.2 |
| NN | Data-driven | 248 | 0.03 | 42.8 | 39.8 |
| PIDL | Hybrid | 647 | 0.04 | 31.5 | 30.5 |
| PIDL-FDL | Hybrid | 769 | 0.04 | 21.2 | 11.6 |
Appendix A.2. Experimental Details for UQ-TSE and System Identification Using Loop Detectors
Appendix A.2.1. Experimental Configurations
| Algorithm A2: PIDL-UQ training for stochastic TSE. |
1 Initialization: 2 Initialized physics parameters ; Initialized networks parameters , ; Training iterations ; Batch size m; Learning rate ; Weights of loss functions , , and . 3 Input: The observation data ; collocation points ; boundary collocation points , e.g.,
|
Appendix A.2.2. Additional Experimental Results Using Numerical Data Validation for Greenshields-Based ARZ
| m | (%) | (%) | (%) | (%) | ||
|---|---|---|---|---|---|---|
| 3 | 42.6 | 32.5 | 1.325 | 0.985 | 11.5 | 15.6 |
| 4 | 30.2 | 20.9 | 0.965 | 0.835 | 6.5 | 4.5 |
| 6 | 20.6 | 11.8 | 0.753 | 0.638 | 2.9 | 2.2 |
| 8 | 18.5 | 6.3 | 0.663 | 0.621 | 2.3 | 1.9 |
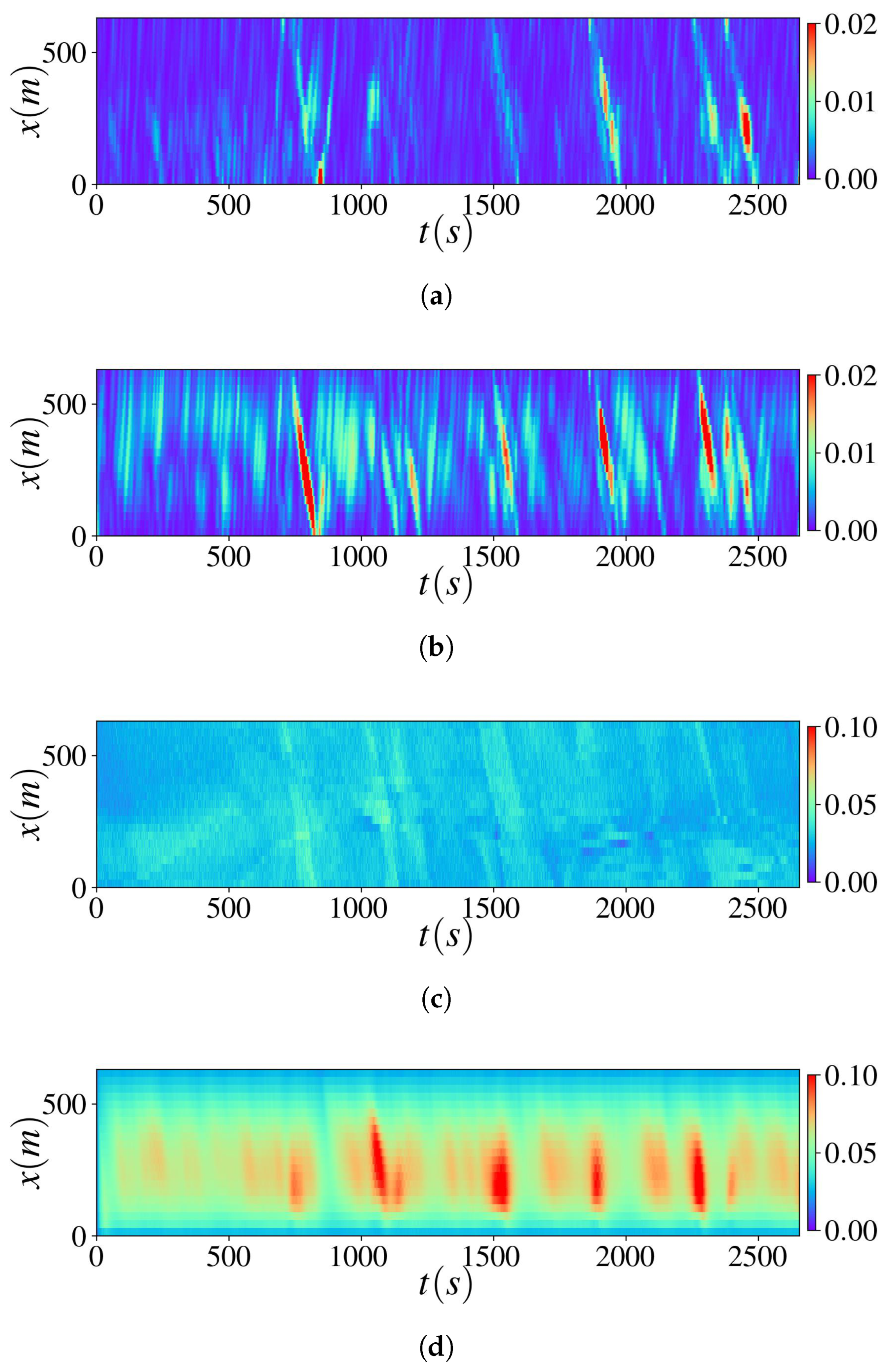
Appendix A.2.3. Additional Experimental Results Using Real-World Data
Appendix A.2.4. Computational Time and Model Accuracy
| Model | Model Type | Computation Time | Prediction Error | ||||
|---|---|---|---|---|---|---|---|
| Training (s) | Test (s) | ||||||
| EKF | Physics-based | − | 1.5 | 39.5 | 35.2 | 3.00 | 3.32 |
| GAN | Data-driven | 3235 | 0.03 | 30.1 | 39.3 | 5.45 | 5.12 |
| PI-GAN | Hybrid | 3326 | 0.03 | 21.1 | 27.8 | 4.08 | 4.02 |
| PI-GAN-FDL | Hybrid | 3453 | 0.03 | 15.4 | 21.7 | 2.33 | 2.57 |
| PI-Flow | Hybrid | 2548 | 0.02 | 22.8 | 27.7 | 3.90 | 4.00 |
| TrafficFlowGAN | Hybrid | 4323 | 0.02 | 15.2 | 20.3 | 2.27 | 2.07 |
Appendix A.3. Performance Metrics
- Relative Error (RE) measures the relative difference between the predicted and ground-truth traffic states. For the deterministic TSE, RE is calculated by:
- Squared Error (SE) measures the squared difference between the predicted and ground-truth traffic states at location x and time t. For the deterministic TSE, SE is calculated by:
- Mean Squared Error (MSE) calculates the average SE over all locations and times, which is depicted as follows:where N is the total number of data.
- Kullback–Leibler divergence (KL) measures the difference between two distributions and , which is depicted as follows:
References
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]
- Karpatne, A.; Atluri, G.; Faghmous, J.H.; Steinbach, M.; Banerjee, A.; Ganguly, A.; Shekhar, S.; Samatova, N.; Kumar, V. Theory-guided data science: A new paradigm for scientific discovery from data. IEEE Trans. Knowl. Data Eng. 2017, 29, 2318–2331. [Google Scholar] [CrossRef]
- Yu, T.; Canales-Rodríguez, E.J.; Pizzolato, M.; Piredda, G.F.; Hilbert, T.; Fischi-Gomez, E.; Weigel, M.; Barakovic, M.; Cuadra, M.B.; Granziera, C.; et al. Model-informed machine learning for multi-component T2 relaxometry. Med. Image Anal. 2021, 69, 101940. [Google Scholar] [CrossRef] [PubMed]
- Karniadakis, G.E.; Kevrekidis, I.G.; Lu, L.; Perdikaris, P.; Wang, S.; Yang, L. Physics-informed machine learning. Nat. Rev. Phys. 2021, 3, 422–440. [Google Scholar] [CrossRef]
- Cuomo, S.; Di Cola, V.S.; Giampaolo, F.; Rozza, G.; Raissi, M.; Piccialli, F. Scientific Machine Learning through Physics-Informed Neural Networks: Where we are and What’s next. arXiv 2022, arXiv:2201.05624. [Google Scholar] [CrossRef]
- Di, X.; Shi, R. A survey on autonomous vehicle control in the era of mixed-autonomy: From physics-based to AI-guided driving policy learning. Transp. Res. Part Emerg. Technol. 2021, 125, 103008. [Google Scholar] [CrossRef]
- Huang, K.; Di, X.; Du, Q.; Chen, X. Stabilizing Traffic via Autonomous Vehicles: A Continuum Mean Field Game Approach. In Proceedings of the the 22nd IEEE International Conference on Intelligent Transportation Systems (ITSC), Auckland, New Zealand, 27–30 October 2019. [Google Scholar]
- Huang, K.; Di, X.; Du, Q.; Chen, X. Scalable traffic stability analysis in mixed-autonomy using continuum models. Transp. Res. Part Emerg. Technol. 2020, 111, 616–630. [Google Scholar] [CrossRef]
- Mo, Z.; Shi, R.; Di, X. A physics-informed deep learning paradigm for car-following models. Transp. Res. Part Emerg. Technol. 2021, 130, 103240. [Google Scholar] [CrossRef]
- Mo, Z.; Di, X. Uncertainty Quantification of Car-following Behaviors: Physics-Informed Generative Adversarial Networks. In Proceedings of the 28th ACM SIGKDD in conjunction with the 11th International Workshop on Urban Computing (UrbComp2022), Washington, DC, USA, 15 August 2022. [Google Scholar]
- Wang, Y.; Papageorgiou, M. Real-time freeway traffic state estimation based on extended Kalman filter: A general approach. Transp. Res. Part Methodol. 2005, 39, 141–167. [Google Scholar] [CrossRef]
- Seo, T.; Bayen, A.M.; Kusakabe, T.; Asakura, Y. Traffic state estimation on highway: A comprehensive survey. Annu. Rev. Control 2017, 43, 128–151. [Google Scholar] [CrossRef] [Green Version]
- Alber, M.; Tepole, A.B.; Cannon, W.R.; De, S.; Dura-Bernal, S.; Garikipati, K.; Karniadakis, G.; Lytton, W.W.; Perdikaris, P.; Petzold, L.; et al. Integrating machine learning and multiscale modeling—Perspectives, challenges, and opportunities in the biological, biomedical, and behavioral sciences. NPJ Digit. Med. 2019, 2, 115. [Google Scholar] [CrossRef] [Green Version]
- Krishnapriyan, A.; Gholami, A.; Zhe, S.; Kirby, R.; Mahoney, M.W. Characterizing possible failure modes in physics-informed neural networks. Adv. Neural Inf. Process. Syst. 2021, 34, 26548–26560. [Google Scholar]
- Di, X.; Liu, H.; Davis, G. Hybrid Extended Kalman Filtering Approach for Traffic Density Estimation Along Signalized Arterials: Use of Global Positioning System Data. Transp. Res. Rec. 2010, 2188.1, 165–173. [Google Scholar] [CrossRef] [Green Version]
- Davis, G.A.; Kang, J.G. Estimating destination-specific traffic densities on urban freeways for advanced traffic management. Transp. Res. Rec. 1994, 1457, 143–148. [Google Scholar]
- Kang, J.G. Estimation of Destination-Specific Traffic Densities and Identification of Parameters on Urban Freeways Using Markov Models of Traffic Flow. Ph.D. Thesis, University of Minnesota, Minneapolis, MN, USA, 1995. [Google Scholar]
- Jabari, S.E.; Liu, H.X. A stochastic model of traffic flow: Theoretical foundations. Transp. Res. Part Methodol. 2012, 46, 156–174. [Google Scholar] [CrossRef]
- Seo, T.; Kusakabe, T.; Asakura, Y. Traffic state estimation with the advanced probe vehicles using data assimilation. In Proceedings of the 2015 IEEE 18th International Conference on Intelligent Transportation Systems, Gran Canaria, Spain, 15–18 September 2015; IEEE: Piscataway Township, NJ, USA, 2015; pp. 824–830. [Google Scholar]
- Cremer, M.; Papageorgiou, M. Parameter identification for a traffic flow model. Automatica 1981, 17, 837–843. [Google Scholar] [CrossRef]
- Fan, S.; Seibold, B. Data-fitted first-order traffic models and their second-order generalizations: Comparison by trajectory and sensor data. Transp. Res. Rec. 2013, 2391, 32–43. [Google Scholar] [CrossRef]
- Kurzhanskiy, A.A.; Varaiya, P. Active traffic management on road networks: A macroscopic approach. Philos. Trans. R. Soc. Math. Phys. Eng. Sci. 2010, 368, 4607–4626. [Google Scholar] [CrossRef]
- Fan, S.; Herty, M.; Seibold, B. Comparative model accuracy of a data-fitted generalized Aw-Rascle-Zhang model. arXiv 2013, arXiv:1310.8219. [Google Scholar] [CrossRef]
- Ngoduy, D. Kernel smoothing method applicable to the dynamic calibration of traffic flow models. Comput. Civ. Infrastruct. Eng. 2011, 26, 420–432. [Google Scholar] [CrossRef]
- Huang, J.; Agarwal, S. Physics informed deep learning for traffic state estimation. In Proceedings of the IEEE 23rd International Conference on Intelligent Transportation Systems (ITSC), Rhodes, Greece, 20–23 September 2020; pp. 3487–3492. [Google Scholar]
- Barreau, M.; Aguiar, M.; Liu, J.; Johansson, K.H. Physics-informed Learning for Identification and State Reconstruction of Traffic Density. In Proceedings of the 60th IEEE Conference on Decision and Control (CDC), Austin, TA, USA, 13–15 December 2021; pp. 2653–2658. [Google Scholar]
- Shi, R.; Mo, Z.; Huang, K.; Di, X.; Du, Q. Physics-informed deep learning for traffic state estimation. arXiv 2021, arXiv:2101.06580. [Google Scholar]
- Shi, R.; Mo, Z.; Di, X. Physics informed deep learning for traffic state estimation: A hybrid paradigm informed by second-order traffic models. In Proceedings of the AAAI Conference on Artificial Intelligence, virtually, 2–9 February 2021; Volume 35, pp. 540–547. [Google Scholar]
- Brunton, S.L.; Proctor, J.L.; Kutz, J.N. Discovering governing equations from data by sparse identification of nonlinear dynamical systems. Proc. Natl. Acad. Sci. USA 2016, 113, 3932–3937. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.; Barreau, M.; Čičić, M.; Johansson, K.H. Learning-based traffic state reconstruction using probe vehicles. IFAC-PapersOnLine 2021, 54, 87–92. [Google Scholar] [CrossRef]
- Shi, R.; Mo, Z.; Huang, K.; Di, X.; Du, Q. A physics-informed deep learning paradigm for traffic state and fundamental diagram estimation. IEEE Trans. Intell. Transp. Syst. 2022, 23, 11688–11698. [Google Scholar] [CrossRef]
- Chen, X.; Lei, M.; Saunier, N.; Sun, L. Low-rank autoregressive tensor completion for spatiotemporal traffic data imputation. IEEE Trans. Intell. Transp. Syst. 2021, 23, 12301–12310. [Google Scholar] [CrossRef]
- Chen, X.; Yang, J.; Sun, L. A nonconvex low-rank tensor completion model for spatiotemporal traffic data imputation. Transp. Res. Part Emerg. Technol. 2020, 117, 102673. [Google Scholar] [CrossRef]
- SAS. The Connected Vehicle: Big Data, Big Opportunities. 2015. Available online: https://www.sas.com/content/dam/SAS/en_us/doc/whitepaper1/connected-vehicle-107832.pdf (accessed on 30 April 2022).
- Chopra, K.; Gupta, K.; Lambora, A. Future Internet: The Internet of Things-A Literature Review. In Proceedings of the 2019 International Conference on Machine Learning, Big Data, Cloud and Parallel Computing (COMITCon), Faridabad, India, 14–16 February 2019; pp. 135–139. [Google Scholar]
- Chettri, L.; Bera, R. A Comprehensive Survey on Internet of Things (IoT) Toward 5G Wireless Systems. IEEE Internet Things J. 2020, 7, 16–32. [Google Scholar] [CrossRef]
- Abboud, K.; Omar, H.A.; Zhuang, W. Interworking of DSRC and Cellular Network Technologies for V2X Communications: A Survey. IEEE Trans. Veh. Technol. 2016, 65, 9457–9470. [Google Scholar] [CrossRef]
- Meinrenken, C.J.; Shou, Z.; Di, X. Using GPS-data to determine optimum electric vehicle ranges: A Michigan case study. Transp. Res. Part Transp. Environ. 2020, 78, 102203. [Google Scholar] [CrossRef]
- Elbers, J.; Zou, J. A Flexible X-haul Network for 5G and Beyond. In Proceedings of the 2019 24th OptoElectronics and Communications Conference (OECC) and 2019 International Conference on Photonics in Switching and Computing (PSC), Fukuoka, Japan, 7–11 July 2019; pp. 1–3. [Google Scholar]
- Porambage, P.; Okwuibe, J.; Liyanage, M.; Ylianttila, M.; Taleb, T. Survey on Multi-Access Edge Computing for Internet of Things Realization. IEEE Commun. Surv. Tutor. 2018, 20, 2961–2991. [Google Scholar] [CrossRef] [Green Version]
- Greenshields, B.D.; Bibbins, J.R.; Channing, W.S.; Miller, H.H. A study of traffic capacity. In Highway Research Board Proceedings; National Research Council (USA), Highway Research Board: Washington, DC, USA, 1935; Volume 1935. [Google Scholar]
- Lighthill, M.J.; Whitham, G.B. On kinematic waves II. A theory of traffic flow on long crowded roads. Proc. R. Soc. Lond. Ser. Math. Phys. Sci. 1955, 229, 317–345. [Google Scholar]
- Richards, P.I. Shock waves on the highway. Oper. Res. 1956, 4, 42–51. [Google Scholar] [CrossRef]
- Payne, H.J. Model of freeway traffic and control. In Mathematical Model of Public System; Simulation Councils, Inc.: La Jilla, CA, USA, 1971; pp. 51–61. [Google Scholar]
- Whitham, G.B. Linear and Nonlinear Waves; John Wiley & Sons: New York, NY, USA, 1974; Volume 42. [Google Scholar]
- Aw, A.; Klar, A.; Rascle, M.; Materne, T. Derivation of continuum traffic flow models from microscopic follow-the-leader models. SIAM J. Appl. Math. 2002, 63, 259–278. [Google Scholar] [CrossRef]
- Zhang, H.M. A non-equilibrium traffic model devoid of gas-like behavior. Transp. Res. Part Methodol. 2002, 36, 275–290. [Google Scholar] [CrossRef]
- Turner, D.S. 75 Years of the Fundamental Diagram for Traffic Flow Theory. In Proceedings of the Greenshields Symposium, Woods Hole, MA, USA, 8–10 July 2008. [Google Scholar]
- Wang, Y.; Papageorgiou, M.; Messmer, A. Real-time freeway traffic state estimation based on extended Kalman filter: Adaptive capabilities and real data testing. Transp. Res. Part Policy Pract. 2008, 42, 1340–1358. [Google Scholar] [CrossRef]
- Wang, Y.; Papageorgiou, M.; Messmer, A.; Coppola, P.; Tzimitsi, A.; Nuzzolo, A. An adaptive freeway traffic state estimator. Automatica 2009, 45, 10–24. [Google Scholar] [CrossRef] [Green Version]
- Mihaylova, L.; Boel, R.; Hegiy, A. An unscented Kalman filter for freeway traffic estimation. In Proceedings of the 11th IFAC Symposium on Control in Transportation Systems, Delft, The Netherlands, 29–31 August 2006. [Google Scholar]
- Blandin, S.; Couque, A.; Bayen, A.; Work, D. On sequential data assimilation for scalar macroscopic traffic flow models. Phys. Nonlinear Phenom. 2012, 241, 1421–1440. [Google Scholar] [CrossRef]
- Mihaylova, L.; Boel, R. A particle filter for freeway traffic estimation. In Proceedings of the 43rd IEEE Conference on Decision and Control (CDC), Nassau, Bahamas, 14–17 December 2004; pp. 2106–2111. [Google Scholar]
- Hinton, G.E.; Osindero, S.; Teh, Y.W. A fast learning algorithm for deep belief nets. Neural Comput. 2006, 18, 1527–1554. [Google Scholar] [CrossRef] [PubMed]
- Zhong, M.; Lingras, P.; Sharma, S. Estimation of missing traffic counts using factor, genetic, neural, and regression techniques. Transp. Res. Part Emerg. Technol. 2004, 12, 139–166. [Google Scholar] [CrossRef]
- Ni, D.; Leonard, J.D. Markov chain Monte Carlo multiple imputation using Bayesian networks for incomplete intelligent transportation systems data. Transp. Res. Rec. 2005, 1935, 57–67. [Google Scholar] [CrossRef]
- Tak, S.; Woo, S.; Yeo, H. Data-driven imputation method for traffic data in sectional units of road links. IEEE Trans. Intell. Transp. Syst. 2016, 17, 1762–1771. [Google Scholar] [CrossRef]
- Li, L.; Li, Y.; Li, Z. Efficient missing data imputing for traffic flow by considering temporal and spatial dependence. Transp. Res. Part Emerg. Technol. 2013, 34, 108–120. [Google Scholar] [CrossRef]
- Tan, H.; Wu, Y.; Cheng, B.; Wang, W.; Ran, B. Robust missing traffic flow imputation considering nonnegativity and road capacity. Math. Probl. Eng. 2014. [Google Scholar] [CrossRef] [Green Version]
- Ma, X.; Tao, Z.; Wang, Y.; Yu, H.; Wang, Y. Long short-term memory neural network for traffic speed prediction using remote microwave sensor data. Transp. Res. Part Emerg. Technol. 2015, 54, 187–197. [Google Scholar] [CrossRef]
- Polson, N.G.; Sokolov, V.O. Deep learning for short-term traffic flow prediction. Transp. Res. Part Emerg. Technol. 2017, 79, 1–17. [Google Scholar] [CrossRef] [Green Version]
- Tang, J.; Zhang, X.; Yin, W.; Zou, Y.; Wang, Y. Missing data imputation for traffic flow based on combination of fuzzy neural network and rough set theory. J. Intell. Transp. Syst. 2020, 25, 439–454. [Google Scholar] [CrossRef]
- Raissi, M. Deep hidden physics models: Deep learning of nonlinear partial differential equations. J. Mach. Learn. Res. 2018, 19, 932–955. [Google Scholar]
- Raissi, M.; Karniadakis, G.E. Hidden physics models: Machine learning of nonlinear partial differential equations. J. Comput. Phys. 2018, 357, 125–141. [Google Scholar] [CrossRef] [Green Version]
- Yang, Y.; Perdikaris, P. Adversarial uncertainty quantification in physics-informed neural networks. J. Comput. Phys. 2019, 394, 136–152. [Google Scholar] [CrossRef] [Green Version]
- Raissi, M.; Wang, Z.; Triantafyllou, M.S.; Karniadakis, G.E. Deep learning of vortex-induced vibrations. J. Fluid Mech. 2019, 861, 119–137. [Google Scholar] [CrossRef] [Green Version]
- Fang, Z.; Zhan, J. Physics-Informed Neural Network Framework For Partial Differential Equations on 3D Surfaces: Time Independent Problems. IEEE Access 2020. [Google Scholar]
- Raissi, M.; Yazdani, A.; Karniadakis, G.E. Hidden fluid mechanics: Learning velocity and pressure fields from flow visualizations. Science 2020, 367, 1026–1030. [Google Scholar] [CrossRef] [PubMed]
- Rai, R.; Sahu, C.K. Driven by data or derived through physics? a review of hybrid physics guided machine learning techniques with cyber-physical system (cps) focus. IEEE Access 2020, 8, 71050–71073. [Google Scholar] [CrossRef]
- Wang, K.; Sun, W.; Du, Q. A non-cooperative meta-modeling game for automated third-party calibrating, validating and falsifying constitutive laws with parallelized adversarial attacks. Comput. Methods Appl. Mech. Eng. 2021, 373, 113514. [Google Scholar] [CrossRef]
- Deng, W.; Lei, H.; Zhou, X. Traffic state estimation and uncertainty quantification based on heterogeneous data sources: A three detector approach. Transp. Res. Part Methodol. 2013, 57, 132–157. [Google Scholar] [CrossRef]
- Jagtap, A.D.; Kawaguchi, K.; Karniadakis, G.E. Adaptive activation functions accelerate convergence in deep and physics-informed neural networks. J. Comput. Phys. 2020, 404, 109136. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Zhou, Z.; Ying, S. DeLISA: Deep learning based iteration scheme approximation for solving PDEs. J. Comput. Phys. 2022, 451, 110884. [Google Scholar] [CrossRef]
- Wang, S.; Yu, X.; Perdikaris, P. When and why PINNs fail to train: A neural tangent kernel perspective. J. Comput. Phys. 2022, 449, 110768. [Google Scholar] [CrossRef]
- Zhang, G.; Yu, Z.; Jin, D.; Li, Y. Physics-infused Machine Learning for Crowd Simulation. In Proceedings of the 28th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, Washington, DC, USA, 14–18 August 2022; pp. 2439–2449. [Google Scholar]
- Boyd, S.; Parikh, N.; Chu, E.; Peleato, B.; Eckstein, J. Distributed optimization and statistical learning via the alternating direction method of multipliers. Found. Trends® Mach. Learn. 2011, 3, 1–122. [Google Scholar]
- Wang, J.; Yu, F.; Chen, X.; Zhao, L. ADMM for efficient deep learning with global convergence. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD), Anchorage, AK, USA, 4–8 August 2019; pp. 111–119. [Google Scholar]
- Barreau, M.; Liu, J.; Johanssoni, K.H. Learning-based State Reconstruction for a Scalar Hyperbolic PDE under noisy Lagrangian Sensing. In Proceedings of the 3rd Conference on Learning for Dynamics and Control (L4DC), Virtual Event, Switzerland, 7–8 June 2021; pp. 34–46. [Google Scholar]
- Smith, R.C. Uncertainty Quantification: Theory, Implementation, and Applications; SIAM: Philadelphia, PA, USA, 2013; Volume 12. [Google Scholar]
- Abdar, M.; Pourpanah, F.; Hussain, S.; Rezazadegan, D.; Liu, L.; Ghavamzadeh, M.; Fieguth, P.; Cao, X.; Khosravi, A.; Acharya, U.R.; et al. A review of uncertainty quantification in deep learning: Techniques, applications and challenges. Inf. Fusion 2021, 76, 243–297. [Google Scholar] [CrossRef]
- Bertsimas, D.; Brown, D.B.; Caramanis, C. Theory and applications of robust optimization. SIAM Rev. 2011, 53, 464–501. [Google Scholar] [CrossRef]
- Giles, M.B. Multilevel monte carlo path simulation. Oper. Res. 2008, 56, 607–617. [Google Scholar] [CrossRef] [Green Version]
- Sun, Q.; Du, Q.; Ming, J. Asymptotically Compatible Schemes for Stochastic Homogenization. SIAM J. Numer. Anal. 2018, 56, 1942–1960. [Google Scholar] [CrossRef]
- Efendiev, Y.; Hou, T.; Luo, W. Preconditioning Markov chain Monte Carlo simulations using coarse-scale models. SIAM J. Sci. Comput. 2006, 28, 776–803. [Google Scholar] [CrossRef] [Green Version]
- Brunton, S.L.; Brunton, B.W.; Proctor, J.L.; Kutz, J.N. Koopman invariant subspaces and finite linear representations of nonlinear dynamical systems for control. PLoS ONE 2016, 11, e0150171. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dietrich, F.; Thiem, T.N.; Kevrekidis, I.G. On the Koopman Operator of Algorithms. SIAM J. Appl. Dyn. Syst. 2020, 19, 860–885. [Google Scholar] [CrossRef] [Green Version]
- Goodfellow, I. Nips 2016 tutorial: Generative adversarial networks. arXiv 2016, arXiv:1701.00160. [Google Scholar]
- Dinh, L.; Sohl-Dickstein, J.; Bengio, S. Density estimation using real nvp. arXiv 2016, arXiv:1605.08803. [Google Scholar]
- Kingma, D.P.; Welling, M. Auto-encoding variational bayes. arXiv 2013, arXiv:1312.6114. [Google Scholar]
- Yang, L.; Zhang, D.; Karniadakis, G.E. Physics-informed generative adversarial networks for stochastic differential equations. SIAM J. Sci. Comput. 2020, 42, A292–A317. [Google Scholar] [CrossRef] [Green Version]
- Daw, A.; Maruf, M.; Karpatne, A. PID-GAN: A GAN Framework based on a Physics-informed Discriminator for Uncertainty Quantification with Physics. In Proceedings of the 27th ACM SIGKDD Conference on Knowledge Discovery & Data Mining, Singapore, 14–18 August 2021; pp. 237–247. [Google Scholar]
- Siddani, B.; Balachandar, S.; Moore, W.C.; Yang, Y.; Fang, R. Machine learning for physics-informed generation of dispersed multiphase flow using generative adversarial networks. Theor. Comput. Fluid Dyn. 2021, 35, 807–830. [Google Scholar] [CrossRef]
- Bilionis, I.; Zabaras, N. Multi-output local Gaussian process regression: Applications to uncertainty quantification. J. Comput. Phys. 2012, 231, 5718–5746. [Google Scholar] [CrossRef]
- Bajaj, C.; McLennan, L.; Andeen, T.; Roy, A. Robust learning of physics informed neural networks. arXiv 2021, arXiv:2110.13330. [Google Scholar]
- Zhang, D.; Lu, L.; Guo, L.; Karniadakis, G.E. Quantifying total uncertainty in physics-informed neural networks for solving forward and inverse stochastic problems. J. Comput. Phys. 2019, 397, 108850. [Google Scholar] [CrossRef] [Green Version]
- Yang, L.; Treichler, S.; Kurth, T.; Fischer, K.; Barajas-Solano, D.; Romero, J.; Churavy, V.; Tartakovsky, A.; Houston, M.; Prabhat, M.; et al. Highly-scalable, physics-informed GANs for learning solutions of stochastic PDEs. In Proceedings of the 2019 IEEE/ACM Third Workshop on Deep Learning on Supercomputers (DLS), Denver, CO, USA, 17 November 2019; IEEE: Piscataway Township, NJ, USA, 2019; pp. 1–11. [Google Scholar]
- Mo, Z.; Fu, Y.; Di, X. Quantifying Uncertainty In Traffic State Estimation Using Generative Adversarial Networks. In Proceedings of the 2022 IEEE 25th International Conference on Intelligent Transportation Systems (ITSC), Macau, China, 8–12 October 2022; IEEE: Piscataway Township, NJ, USA, 2022; pp. 2769–2774. [Google Scholar]
- Mo, Z.; Fu, Y.; Xu, D.; Di, X. TrafficFlowGAN: Physics-informed Flow based Generative Adversarial Network for Uncertainty Quantification. In Proceedings of the Joint European Conference on Machine Learning and Knowledge Discovery in Database; Springer: Berlin/Heidelberg, Germany, 2022. [Google Scholar]
- Guo, L.; Wu, H.; Zhou, T. Normalizing field flows: Solving forward and inverse stochastic differential equations using physics-informed flow models. J. Comput. Phys. 2022, 461, 111202. [Google Scholar] [CrossRef]
- Treiber, M.; Hennecke, A.; Helbing, D. Congested traffic states in empirical observations and microscopic simulations. Phys. Rev. 2000, 62, 1805. [Google Scholar] [CrossRef] [Green Version]
- Kesting, A.; Treiber, M.; Schönhof, M.; Helbing, D. Adaptive cruise control design for active congestion avoidance. Transp. Res. Part Emerg. Technol. 2008, 16, 668–683. [Google Scholar] [CrossRef]
- Zhou, X.; Taylor, J. DTALite: A queue-based mesoscopic traffic simulator for fast model evaluation and calibration. Cogent Eng. 2014, 1, 961345. [Google Scholar] [CrossRef]
- Di Gangi, M.; Cantarella, G.E.; Di Pace, R.; Memoli, S. Network traffic control based on a mesoscopic dynamic flow model. Transp. Res. Part Emerg. Technol. 2016, 66, 3–26. [Google Scholar] [CrossRef]
- Chinesta, F.; Cueto, E.; Abisset-Chavanne, E.; Duval, J.L.; El Khaldi, F. Virtual, digital and hybrid twins: A new paradigm in data-based engineering and engineered data. Arch. Comput. Methods Eng. 2018, 27, 105–134. [Google Scholar] [CrossRef] [Green Version]
- Lu, J. Connected and Automated Mobility Modeling on Layered Transportation Networks: Cross-Resolution Architecture of System Estimation and Optimization; Technical Report; Arizona State University: Tempe, AZ, USA, 2022. [Google Scholar]
- Delle Monache, M.L.; Liard, T.; Piccoli, B.; Stern, R.; Work, D. Traffic reconstruction using autonomous vehicles. SIAM J. Appl. Math. 2019, 79, 1748–1767. [Google Scholar] [CrossRef]
- Peherstorfer, B.; Willcox, K.; Gunzburger, M. Survey of multifidelity methods in uncertainty propagation, inference, and optimization. SIAM Rev. 2018, 60, 550–591. [Google Scholar] [CrossRef] [Green Version]
- Penwarden, M.; Zhe, S.; Narayan, A.; Kirby, R.M. Multifidelity modeling for physics-informed neural networks (pinns). J. Comput. Phys. 2022, 451, 110844. [Google Scholar] [CrossRef]
- Lu, J.; Li, C.; Wu, X.B.; Zhou, X.S. Traffic System State Identification with Integrated Traffic State, Model Parameter and Queue Profile Estimation: Nonlinear Programming Reformulation with Differentiable Traffic State Variables Across Resolutions. SSRN 2022. [Google Scholar] [CrossRef]
- Schmidt, M.; Lipson, H. Distilling free-form natural laws from experimental data. Science 2009, 324, 81–85. [Google Scholar] [CrossRef]
- Cranmer, M.; Sanchez Gonzalez, A.; Battaglia, P.; Xu, R.; Cranmer, K.; Spergel, D.; Ho, S. Discovering symbolic models from deep learning with inductive biases. Adv. Neural Inf. Process. Syst. 2020, 33, 17429–17442. [Google Scholar]
- Wang, K.; Sun, W.; Du, Q. A cooperative game for automated learning of elasto-plasticity knowledge graphs and models with AI-guided experimentation. Comput. Mech. 2019, 64, 467–499. [Google Scholar] [CrossRef] [Green Version]
- Elsken, T.; Metzen, J.H.; Hutter, F. Neural architecture search: A survey. J. Mach. Learn. Res. 2019, 20, 1997–2017. [Google Scholar]
- Chen, Y.; Friesen, A.L.; Behbahani, F.; Doucet, A.; Budden, D.; Hoffman, M.; de Freitas, N. Modular meta-learning with shrinkage. Adv. Neural Inf. Process. Syst. 2020, 33, 2858–2869. [Google Scholar]
- Thodi, B.T.; Khan, Z.S.; Jabari, S.E.; Menéndez, M. Incorporating kinematic wave theory into a deep learning method for high-resolution traffic speed estimation. IEEE Trans. Intell. Transp. Syst. 2022, 23, 17849–17862. [Google Scholar] [CrossRef]
- Fuks, O.; Tchelepi, H.A. Limitations of physics informed machine learning for nonlinear two-phase transport in porous media. J. Mach. Learn. Model. Comput. 2020, 1, 19–37. [Google Scholar] [CrossRef]
- Thodi, B.T.; Ambadipudi, S.V.R.; Jabari, S.E. Learning-based solutions to nonlinear hyperbolic PDEs: Empirical insights on generalization errors. arXiv 2023, arXiv:2302.08144. [Google Scholar]
- Mo, Z.; Di, X.; Shi, R. Robust Data Sampling in Machine Learning: A Game-Theoretic Framework for Training and Validation Data Selection. Games 2023, 14, 13. [Google Scholar] [CrossRef]
- Psaros, A.F.; Kawaguchi, K.; Karniadakis, G.E. Meta-learning PINN loss functions. J. Comput. Phys. 2022, 458, 111121. [Google Scholar] [CrossRef]
- Spirtes, P.; Glymour, C.N.; Scheines, R.; Heckerman, D. Causation, Prediction, and Search; MIT Press: Cambridge, MA, USA, 2000. [Google Scholar]
- Pearl, J. Causality; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Meng, C.; Seo, S.; Cao, D.; Griesemer, S.; Liu, Y. When Physics Meets Machine Learning: A Survey of Physics-Informed Machine Learning. arXiv 2022, arXiv:2203.16797. [Google Scholar]
- Ruan, K.; Di, X. Learning Human Driving Behaviors with Sequential Causal Imitation Learning. In Proceedings of the 36th AAAI Conference on Artificial Intelligence, Virtually, 22 February–1 March 2022. [Google Scholar]
- Ruan, K.; Zhang, J.; Di, X.; Bareinboim, E. Causal Imitation Learning Via Inverse Reinforcement Learning. In Proceedings of the 11th International Conference on Learning Representations, Kigali, Rwanda, 1–5 May 2023. [Google Scholar]
- Ji, J.; Wang, J.; Jiang, Z.; Jiang, J.; Zhang, H. STDEN: Towards Physics-guided Neural Networks for Traffic Flow Prediction. Proc. AAAI Conf. Artif. Intell. 2022, 36, 4048–4056. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. In Proceedings of the 3rd International Conference on Learning Representations (ICLR), San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Byrd, R.H.; Lu, P.; Nocedal, J.; Zhu, C. A limited memory algorithm for bound constrained optimization. SIAM J. Sci. Comput. 1995, 16, 1190–1208. [Google Scholar] [CrossRef]
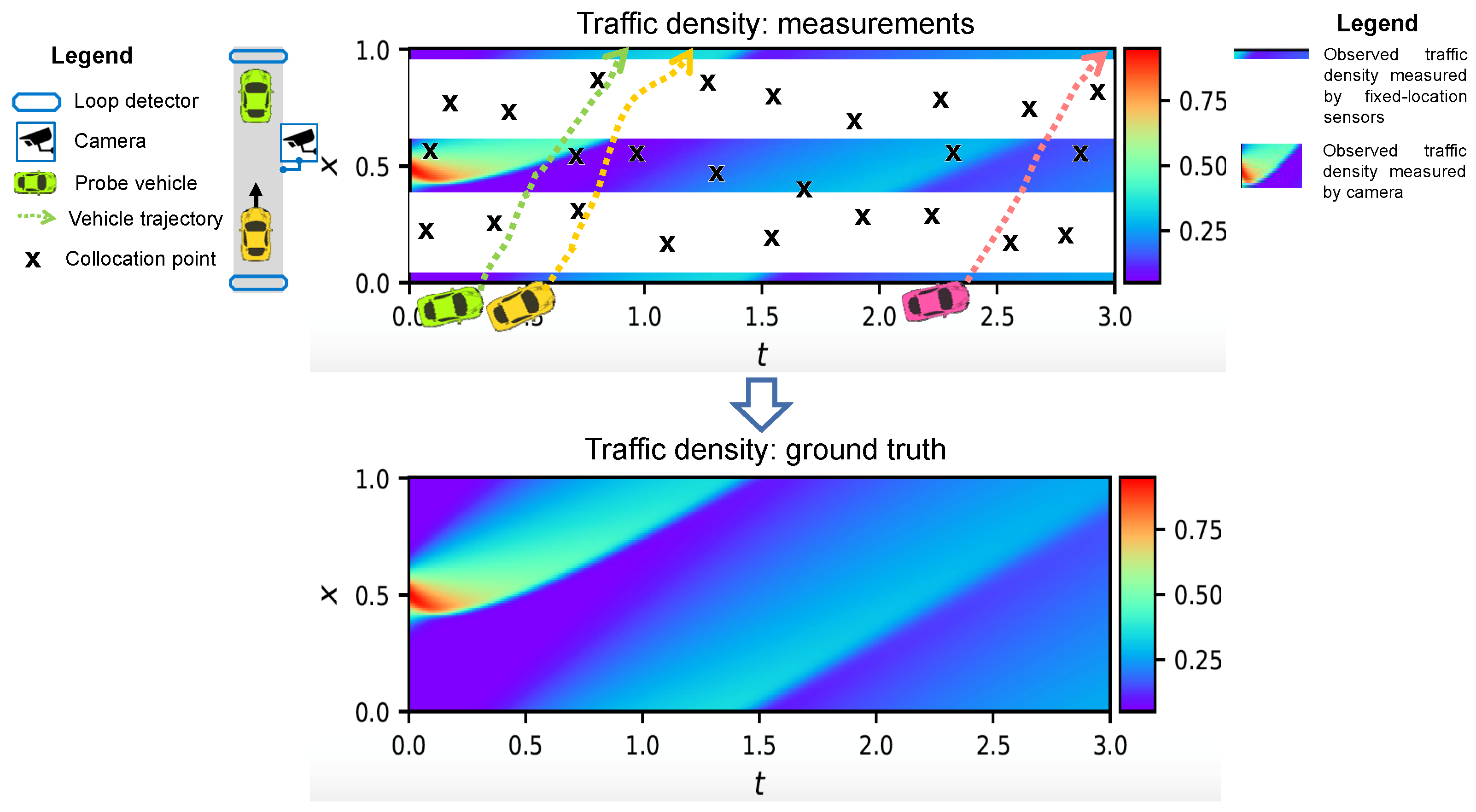
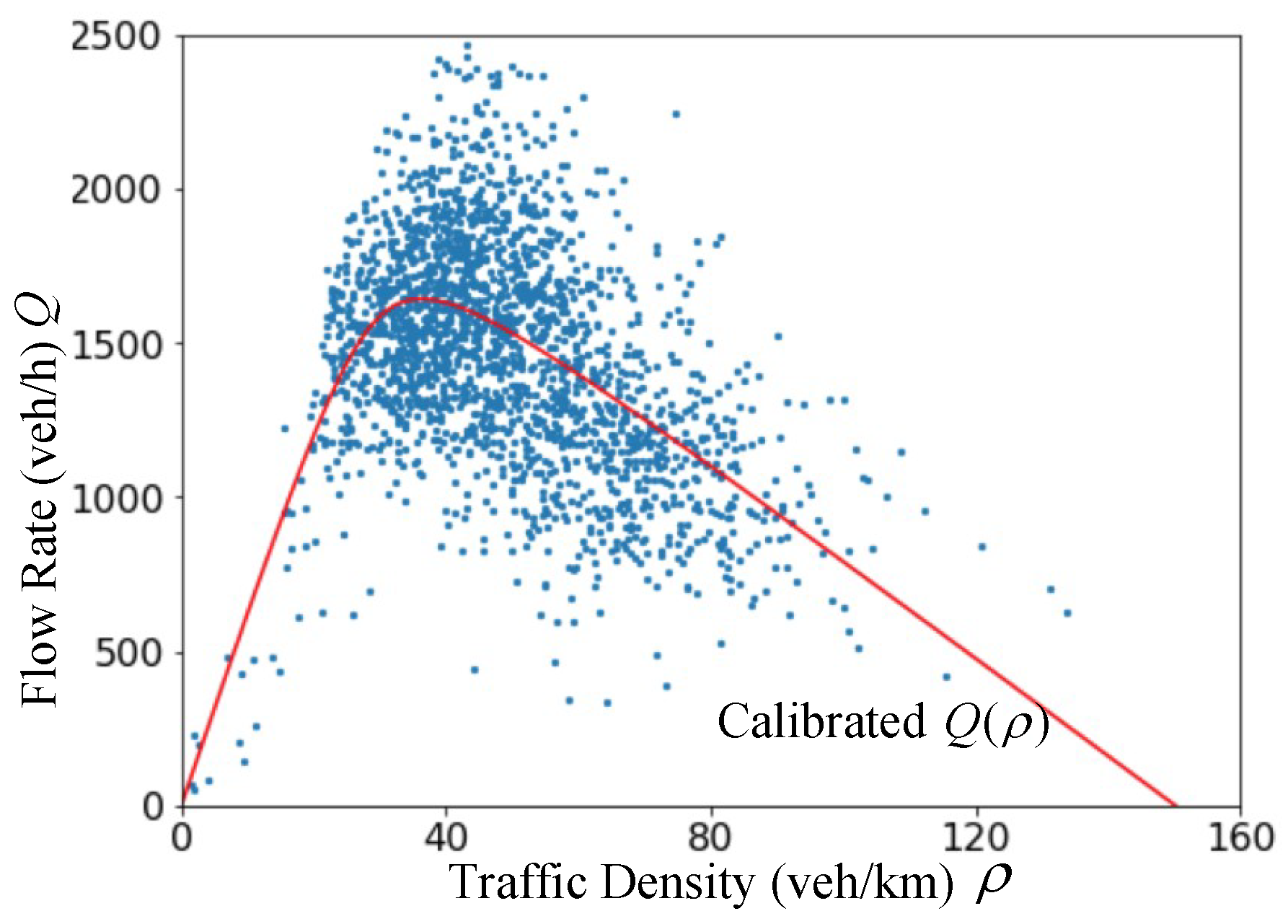
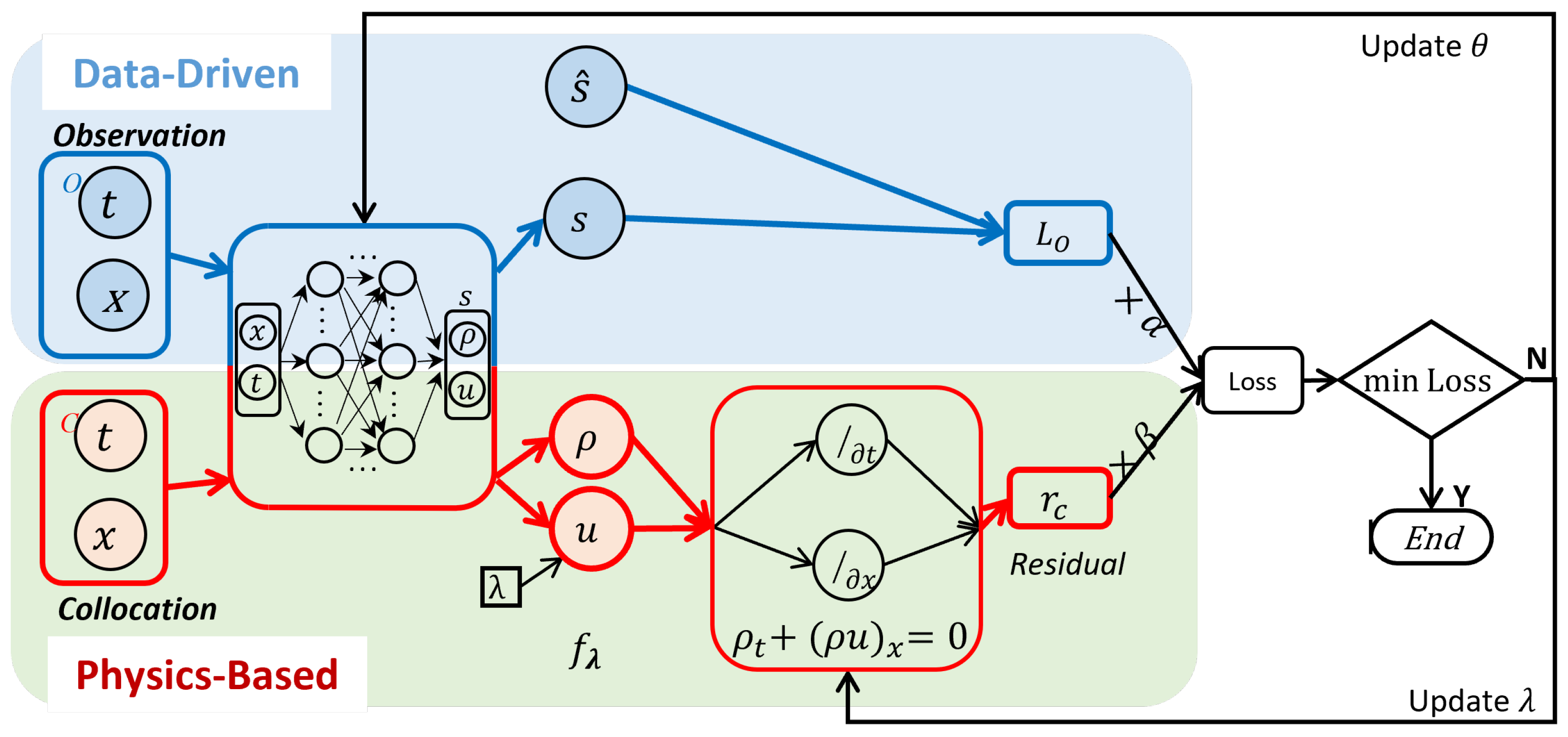
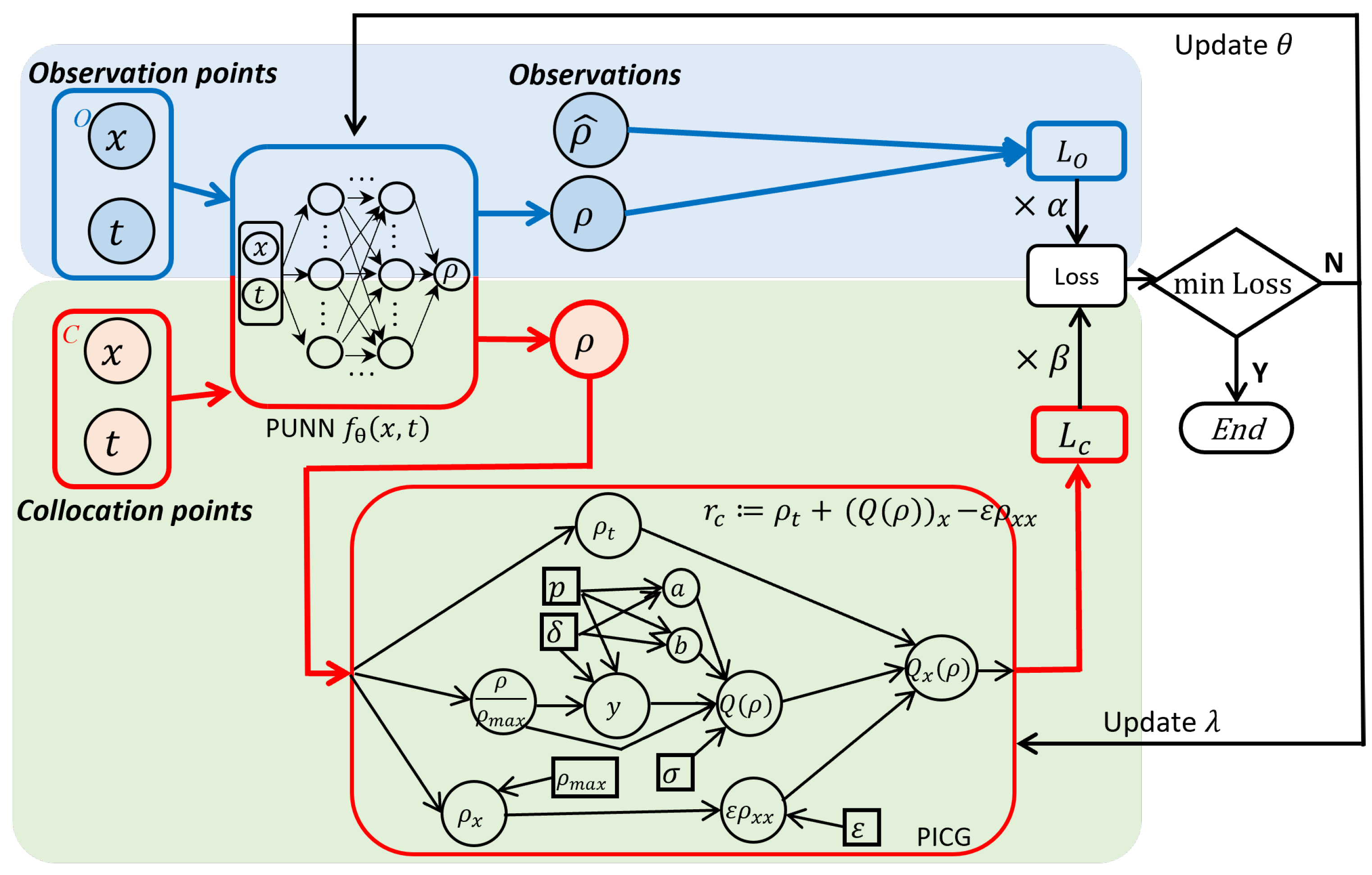
| Method | Description | ||||
|---|---|---|---|---|---|
| Max. Density | Critical Density | Max. Speed | |||
| Sequential training | Calibrate each parameter separately | Each parameter carries a certain physical meaning | Segment length divided by avg. vehicle length | Traffic density at capacity | Speed limit or max. value |
| Calibrate parameter and predict state jointly | Augment states with parameters estimated using DA [15,16,17,18] | Tuning along with other hyperparameters in DNNs | |||
| Calibrate FD | Fit parameters associated with a pre-selected FD [19,20,21,22,23,24,25] | Density at | Density at | Velocity at maximum | |
| Joint training | Calibrate FD | Fit parameters associated with a pre-selected FD along with parameters of DNNs [26,27,28] | Density at | Density at | Velocity at maximum |
| ML surrogate | Reduce variable and parameter sizes while maintaining the minimum physical relevance [29,30,31] | Parametrized in DNNs | in | ||
| Physics | Data | Descriptions | Ref. | |
|---|---|---|---|---|
| First-order model | LWR | Synthetic (Lax–Hopf method) | Integrated the Greenshields-based LWR to PIDL and validated it using loop detectors as well as randomly placed sensors. | [25] |
| LWR | Numerical, NGSIM | Presented the use of PIDL to solve Greenshields-based and three-parameter-based LWR models, and demonstrated its advantages using a real-world dataset. | [27] | |
| LWR | Numerical | Studied the general partial-state reconstruction problem for traffic flow estimation, and used PIDL encoded with LWR to counterbalance the small number of probe vehicle data. | [78] | |
| FL1, LWR | SUMO simulation | Integrated a coupled micro–macro model, combining the follow-the-leader (FL1) model and LWR model, to PIDL for TSE, which can use the velocity information from probe vehicles. | [26,30] | |
| Second-order model | LWR and ARZ | Numerical, NGSIM | Applied the PIDL-based TSE to the second-order ARZ with observations from both loop detectors and probe vehicles, and estimated both and u in parallel. | [28] |
| Proposed the idea of integrating ML surrogate (e.g., an NN) into the physics-based component in the PICG to represent the complicated FD relation. Improved estimation accuracy achieved and unknown FD relation learned. | [31] | |||
| Site | Location | Date | Length (m) | Sampling Rate (s) | Lane # |
|---|---|---|---|---|---|
| US 101 1 | LA, CA | 6/15/2005 | 640 | 0.1 | 5 |
| Model | Descriptions | Pros | Ref. | |
|---|---|---|---|---|
| PhysGAN | PI-GAN | is added to the generator loss function using the weighted sum. | The most widely used | [65,90,95,96] |
| PID-GAN | Residual is fed into the discriminator, , which is then averaged over collocation points to calculate . | Can mitigate the gradient imbalance issue | [91] | |
| Mean-GAN | Residual is averaged over the physics parameter : . | Can encode stochastic physics model | [97] | |
| PI-GAN-FDL | The relation is approximated by ML surrogates; physics loss is the same as PI-GAN. | Requires minimal physics information | [65,98] | |
| PhysFlow | PI-Flow | The normalizing flow model is used as the generator for explicit computation of the likelihood; the physics loss is the same as PI-GAN. | Simple structure; easy to train | [99] |
| PhysFlowGAN | Traffic Flow GAN | The normalizing flow model is used as the generator for explicit computation of the likelihood; a convolutional neural network is used as the discriminator to ensure high sample quality physics loss is the same as PI-GAN. | Combines the merits of PhysGAN and PhysFlow | [98] |
| PUNN-PICG Topology | PUNN Hierarchy | Shared | Separate |
|---|---|---|---|
| Sequential | [25,27,28,30,65,91,96,97,98] | [26,31,65,78,90,95,99] | |
| Parallel | [9,10] | - | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Di, X.; Shi, R.; Mo, Z.; Fu, Y. Physics-Informed Deep Learning for Traffic State Estimation: A Survey and the Outlook. Algorithms 2023, 16, 305. https://doi.org/10.3390/a16060305
Di X, Shi R, Mo Z, Fu Y. Physics-Informed Deep Learning for Traffic State Estimation: A Survey and the Outlook. Algorithms. 2023; 16(6):305. https://doi.org/10.3390/a16060305
Chicago/Turabian StyleDi, Xuan, Rongye Shi, Zhaobin Mo, and Yongjie Fu. 2023. "Physics-Informed Deep Learning for Traffic State Estimation: A Survey and the Outlook" Algorithms 16, no. 6: 305. https://doi.org/10.3390/a16060305
APA StyleDi, X., Shi, R., Mo, Z., & Fu, Y. (2023). Physics-Informed Deep Learning for Traffic State Estimation: A Survey and the Outlook. Algorithms, 16(6), 305. https://doi.org/10.3390/a16060305







