Multi-Objective PSO with Variable Number of Dimensions for Space Robot Path Optimization
Abstract
:1. Introduction
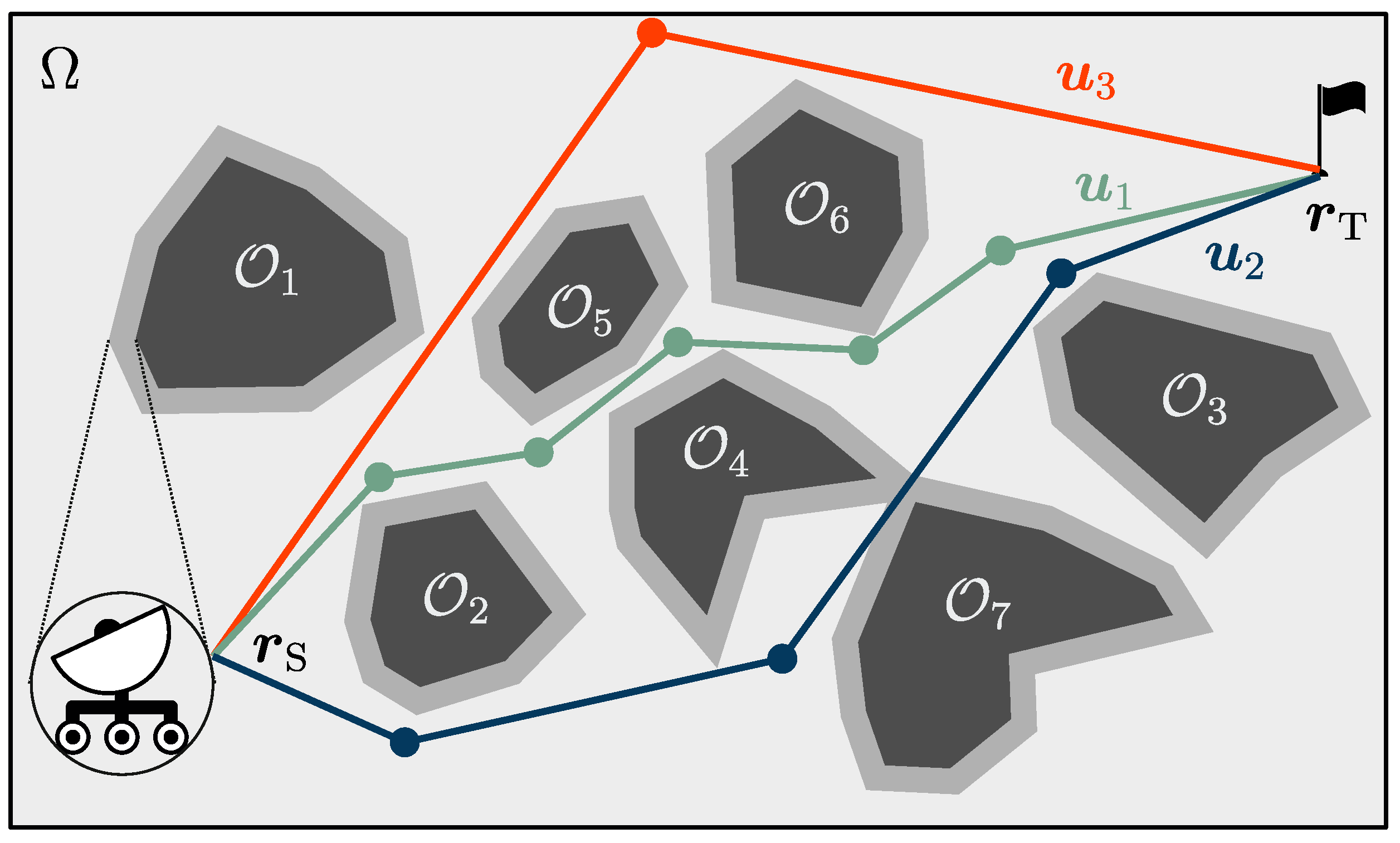
2. Problem Definition
3. Optimization Methods
3.1. Variable Number of Dimensions MOPSO
3.1.1. Conventional MOPSO
| Algorithm 1: Global best selection algorithm used in MOPSO |
Input : Probability of random global best , set of DSVs , external archive Output: Set of global best positions
|
3.1.2. VNDMOPSO
- : size of the global best, ;
- : size of the personal best, ;
- : the previous dimension of the agent (and its velocity , also).
- : probability of global best dimension, ;
- : probability of personal best dimension, .
| Algorithm 2: New dimension selection in VNDMOPSO |
Input : Probabilities , dimensions for p–th agent Output: New dimension of p–th agent
|
| Algorithm 3: VNDMOPSO general pseudocode |
Input : Set of user-defined controling parameters , objective functions , list of feasible dimensions , decision space limits Output: Non-dominated set
|
3.2. Reference Methods
3.2.1. VLMOPSO
3.2.2. VNDGDE3
3.2.3. SCMOPSO
4. Results and Discussion
4.1. Benchmark Problems
4.2. Parameter Influence
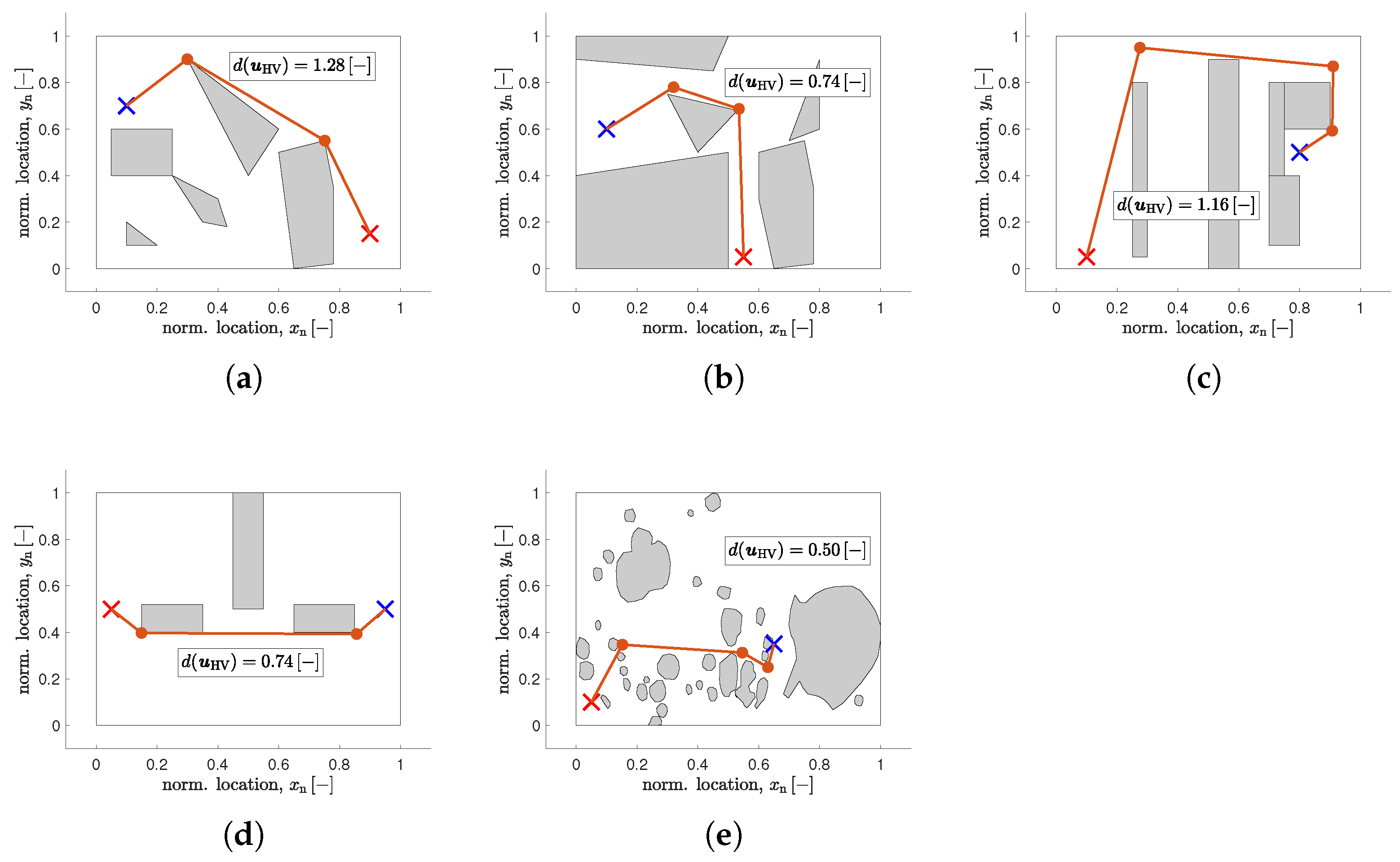
4.3. Pathfinding Problems
5. Conclusions
Supplementary Materials
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| DE | Differential evolution |
| dHV | Distance hypervolume metric |
| DSV | Decision space vector |
| EOA | Evolutionary optimization algorithm |
| GDE3 | Generalized differential evolution |
| HA | Heuristic algorithm |
| HV | Hypervolume metric |
| MO | Multi-objective |
| MOOP | Multi-objective optimization problem |
| MOPSO | Multi-objective particle swarm optimization |
| PSO | Particle swarm optimization |
| SCMOPSO | Social class MOPSO |
| SRPP | Space robot pathfinding problem |
| TP | Turning (way) point |
| VLMOPSO | Variable length MO PSO |
| VND | Variable number of dimensions |
| VNDGDE3 | Variable number of dimensions GDE3 |
| VNDMOPSO | Variable number of dimensions MOPSO |
References
- Strasser, B.; Wagner, D.; Zeitz, T. Space-Efficient, Fast and Exact Routing in Time-Dependent Road Networks. Algorithms 2021, 14, 90. [Google Scholar] [CrossRef]
- Treleaven, K.; Pavone, M.; Frazzoli, E. Asymptotically optimal algorithms for one-to-one pickup and delivery problems with applications to transportation systems. IEEE Trans. Autom. Control 2013, 58, 2261–2276. [Google Scholar] [CrossRef] [Green Version]
- Korkmaz, S.A.; Poyraz, M. Path planning for rescue vehicles via segmented satellite disaster images and GPS road map. In Proceedings of the 2016 9th International Congress on Image and Signal Processing, BioMedical Engineering and Informatics (CISP-BMEI), Taizhou, China, 15–17 October 2016; pp. 145–150. [Google Scholar]
- Yu, X.; Wang, P.; Zhang, Z. Learning-Based End-to-End Path Planning for Lunar Rovers with Safety Constraints. Sensors 2021, 21, 796. [Google Scholar] [CrossRef] [PubMed]
- Dijkstra, E.W. A note on two problems in connexion with graphs. In Edsger Wybe Dijkstra: His Life, Work, and Legacy; Numerische Mathematik; Springer: Berlin/Heidelberg, Germany, 1959; pp. 269–271. [Google Scholar]
- Hart, P.E.; Nilsson, N.J.; Raphael, B. A formal basis for the heuristic determination of minimum cost paths. IEEE Trans. Syst. Sci. Cybern. 1968, 4, 100–107. [Google Scholar] [CrossRef]
- Deb, K. Multi-Objective Optimization Using Evolutionary Algorithms; John Wiley & Sons: New York, NY, USA, 2001. [Google Scholar]
- Ajeil, F.H.; Ibraheem, I.K.; Sahib, M.A.; Humaidi, A.J. Multi-objective path planning of an autonomous mobile robot using hybrid PSO-MFB optimization algorithm. Appl. Soft Comput. 2020, 89, 106076. [Google Scholar]
- Ajeil, F.H.; Ibraheem, I.K.; Azar, A.T.; Humaidi, A.J. Grid-based mobile robot path planning using aging-based ant colony optimization algorithm in static and dynamic environments. Sensors 2020, 20, 1880. [Google Scholar]
- Wang, X.; Shi, Y.; Ding, D.; Gu, X. Double global optimum genetic algorithm–particle swarm optimization-based welding robot path planning. Eng. Optim. 2016, 48, 299–316. [Google Scholar]
- Zhang, J.H.; Zhang, Y.; Zhou, Y. Path planning of mobile robot based on hybrid multi-objective bare bones particle swarm optimization with differential evolution. IEEE Access 2018, 6, 44542–44555. [Google Scholar] [CrossRef]
- Zhang, Z.; He, R.; Yang, K. A bioinspired path planning approach for mobile robots based on improved sparrow search algorithm. Adv. Manuf. 2022, 10, 114–130. [Google Scholar] [CrossRef]
- Miettinen, K. Evolutionary Algorithms in Engineering and Computer Science; John Wiley & Sons: New York, NY, USA, 1999. [Google Scholar]
- Gonzalez, J.S.; Payan, M.B.; Riquelme-Santos, J.M. Optimization of wind farm turbine layout including decision making under risk. IEEE Syst. J. 2011, 6, 94–102. [Google Scholar] [CrossRef]
- Ghiasi, H.; Fayazbakhsh, K.; Pasini, D.; Lessard, L. Optimum stacking sequence design of composite materials Part II: Variable stiffness design. Compos. Struct. 2010, 93, 1–13. [Google Scholar]
- Sun, Y.; Xue, B.; Zhang, M.; Yen, G.G. Evolving deep convolutional neural networks for image classification. IEEE Trans. Evol. Comput. 2019, 24, 394–407. [Google Scholar] [CrossRef] [Green Version]
- Kadlec, P.; Marek, M. Microwave imaging using optimization with variable number of dimensions. IEEE Trans. Comput. Imaging 2020, 6, 1586–1594. [Google Scholar] [CrossRef]
- Ryerkerk, M.; Averill, R.; Deb, K.; Goodman, E. A survey of evolutionary algorithms using metameric representations. Genet. Program. Evolvable Mach. 2019, 20, 441–478. [Google Scholar]
- Kadlec, P.; Šeděnka, V. Particle swarm optimization for problems with variable number of dimensions. Eng. Optim. 2018, 50, 382–399. [Google Scholar]
- Burke, D.S.; De Jong, K.A.; Grefenstette, J.J.; Ramsey, C.L.; Wu, A.S. Putting more genetics into genetic algorithms. Evol. Comput. 1998, 6, 387–410. [Google Scholar] [CrossRef]
- Hutt, B.; Warwick, K. Synapsing variable-length crossover: Meaningful crossover for variable-length genomes. IEEE Trans. Evol. Comput. 2007, 11, 118–131. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential evolution-a simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95-International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Knypiński, L. Performance analysis of selected metaheuristic optimization algorithms applied in the solution of an unconstrained task. COMPEL-Int. J. Comput. Math. Electr. Electron. Eng. 2022, 41, 1271–1284. [Google Scholar] [CrossRef]
- Kiranyaz, S.; Ince, T.; Yildirim, A.; Gabbouj, M. Fractional particle swarm optimization in multidimensional search space. IEEE Trans. Syst. Man, Cybern. Part B 2009, 40, 298–319. [Google Scholar] [CrossRef] [Green Version]
- Tran, B.; Xue, B.; Zhang, M. Variable-length particle swarm optimization for feature selection on high-dimensional classification. IEEE Trans. Evol. Comput. 2018, 23, 473–487. [Google Scholar] [CrossRef]
- Schlauwitz, J.; Musilek, P. Dimension-wise particle swarm optimization: Evaluation and comparative analysis. Appl. Sci. 2021, 11, 6201. [Google Scholar] [CrossRef]
- Mohammadi, A.; Zahiri, S.H.; Razavi, S.M.; Suganthan, P.N. Design and modeling of adaptive IIR filtering systems using a weighted sum-variable length particle swarm optimization. Appl. Soft Comput. 2021, 109, 107529. [Google Scholar] [CrossRef]
- Saraf, T.O.Q.; Fuad, N.; Taujuddin, N.S.A.M. Framework of Meta-Heuristic Variable Length Searching for Feature Selection in High-Dimensional Data. Computers 2023, 12, 7. [Google Scholar] [CrossRef]
- Jubair, A.M.; Hassan, R.; Aman, A.H.M.; Sallehudin, H. Social class particle swarm optimization for variable-length Wireless Sensor Network Deployment. Appl. Soft Comput. 2021, 113, 107926. [Google Scholar]
- Mukhopadhyay, A.; Mandal, M. Identifying non-redundant gene markers from microarray data: A multiobjective variable length PSO-based approach. IEEE/ACM Trans. Comput. Biol. Bioinform. 2014, 11, 1170–1183. [Google Scholar] [CrossRef]
- Marek, M.; Kadlec, P. Another evolution of generalized differential evolution: Variable number of dimensions. Eng. Optim. 2022, 54, 61–80. [Google Scholar] [CrossRef]
- Kukkonen, S.; Lampinen, J. GDE3: The third evolution step of generalized differential evolution. In Proceedings of the 2005 IEEE Congress on Evolutionary Computation, Edinburgh, UK, 2–5 September 2005; Volume 1, pp. 443–450. [Google Scholar]
- Kadlec, P.; Marek, M.; Štumpf, M.; Šeděnka, V. PCB decoupling optimization with variable number of capacitors. IEEE Trans. Electromagn. Compat. 2018, 61, 1841–1848. [Google Scholar] [CrossRef]
- Kadlec, P.; Čapek, M.; Rỳmus, J.; Marek, M.; Štumpf, M.; Jelínek, L.; Mašek, M.; Kotalík, P. Design of a linear antenna array: Variable number of dimensions approach. In Proceedings of the 2020 30th International Conference Radioelektronika (RADIOELEKTRONIKA), Bratislava, Slovakia, 15–16 April 2020; pp. 1–6. [Google Scholar]
- Reyes-Sierra, M.; Coello, C.C. Multi-objective particle swarm optimizers: A survey of the state-of-the-art. Int. J. Comput. Intell. Res. 2006, 2, 287–308. [Google Scholar]
- Kukkonen, S.; Deb, K. A fast and effective method for pruning of non-dominated solutions in many-objective problems. In PPSN; Springer: Berlin/Heidelberg, Germany, 2006; Volume 4193, pp. 553–562. [Google Scholar]
- Marek, M.; Kadlec, P.; Čapek, M. FOPS: A new framework for the optimization with variable number of dimensions. Int. J. Microw. Comput.-Aided Eng. 2020, 30, e22335. [Google Scholar] [CrossRef]
- Van Veldhuizen, D.A.; Lamont, G.B. Evolutionary computation and convergence to a pareto front. In Proceedings of the Late Breaking Papers at the Genetic Programming 1998 Conference, Citeseer, Stanford, CA, USA, 22–25 July 1998; pp. 221–228. [Google Scholar]
- Zitzler, E. Evolutionary Algorithms for Multiobjective Optimization: Methods and Applications; Shaker Ithaca: Ithaca, NY, USA, 1999; Volume 63. [Google Scholar]
- While, L.; Bradstreet, L.; Barone, L. A fast way of calculating exact hypervolumes. IEEE Trans. Evol. Comput. 2011, 16, 86–95. [Google Scholar] [CrossRef]
- Li, H.; Deb, K. Challenges for evolutionary multiobjective optimization algorithms in solving variable-length problems. In Proceedings of the 2017 IEEE Congress on Evolutionary Computation (CEC), San Sebastián, Spain, 5–8 June 2017; pp. 2217–2224. [Google Scholar]
- Deb, K.; Thiele, L.; Laumanns, M.; Zitzler, E. Scalable multi-objective optimization test problems. In Proceedings of the 2002 Congress on Evolutionary Computation, CEC’02 (Cat. No. 02TH8600), Honolulu, HI, USA, 12–17 May 2002; Volume 1, pp. 825–830. [Google Scholar]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef] [Green Version]
- Li, H.; Zhang, Q. Multiobjective optimization problems with complicated Pareto sets, MOEA/D and NSGA-II. IEEE Trans. Evol. Comput. 2008, 13, 284–302. [Google Scholar] [CrossRef]
- U.S. Geological Survey. Apollo 11 Traverse Map. Available online: https://astrogeology.usgs.gov/search/map/Moon/Apollo/Traverse/AP11trav (accessed on 5 November 2023).









| Symbol | Explanation | Value Range |
|---|---|---|
| Number of particles (agents) | ||
| Maximal number of iterations | ||
| w | Inertia weight | |
| Cognitive learning factor | ||
| Social learning factor | ||
| Probability of adapting to dimension of global best | ||
| Probability of adapting to dimension of personal best |
| Symbol | Explanation | Value Range |
|---|---|---|
| w | Inertia weight | Decreasing from to |
| Cognitive learning factor | ||
| Social learning factor | ||
| Probability of adapting to dimension of global best | ||
| Probability of adapting to dimension of personal best |
| Settings | Feasible Dimensions, | Optimal Dimensions, |
|---|---|---|
| 1 | ||
| 2 | ||
| 3 |
| Settings | Settings | Settings | ||||
|---|---|---|---|---|---|---|
| VNDMOPSO vs. | VNDGDE3 | VLMOPSO | VNDGDE3 | VLMOPSO | VNDGDE3 | VLMOPSO |
| VNDMODTLZ1 | − | + | − | + | − | = |
| VNDMODTLZ2 | + | − | + | − | + | − |
| VNDMODTLZ3 | − | + | − | = | − | = |
| VNDMODTLZ4 | − | − | − | − | − | − |
| VNDMODTLZ5 | + | + | + | − | + | + |
| VNDMODTLZ6 | = | + | + | + | + | − |
| VNDMODTLZ7 | − | − | − | − | − | = |
| VNDMOLI1 | − | + | − | + | − | + |
| VNDMOLZ1 | − | − | + | + | + | + |
| VNDMOLZ2 | − | − | − | + | − | + |
| VNDMOLZ3 | − | + | + | + | + | + |
| VNDMOLZ4 | − | + | + | + | = | + |
| VNDMOLZ5 | = | + | + | + | + | + |
| VNDMOLZ7 | = | = | + | = | + | + |
| VNDMOLZ8 | − | = | + | + | + | + |
| VNDMOLZ9 | − | − | − | + | − | + |
| VNDMOZDT1 | + | − | − | − | − | − |
| VNDMOZDT2 | − | − | − | − | − | − |
| VNDMOZDT3 | + | + | − | − | − | − |
| VNDMOZDT4 | + | − | + | − | + | + |
| VNDMOZDT6 | − | − | − | − | + | − |
| Overall | 5 / 3 / 13 | 9 / 2 / 10 | 10 / 0 / 11 | 10 / 2 / 9 | 10 / 1 / 10 | 11 / 3 / 7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kadlec, P. Multi-Objective PSO with Variable Number of Dimensions for Space Robot Path Optimization. Algorithms 2023, 16, 307. https://doi.org/10.3390/a16060307
Kadlec P. Multi-Objective PSO with Variable Number of Dimensions for Space Robot Path Optimization. Algorithms. 2023; 16(6):307. https://doi.org/10.3390/a16060307
Chicago/Turabian StyleKadlec, Petr. 2023. "Multi-Objective PSO with Variable Number of Dimensions for Space Robot Path Optimization" Algorithms 16, no. 6: 307. https://doi.org/10.3390/a16060307
APA StyleKadlec, P. (2023). Multi-Objective PSO with Variable Number of Dimensions for Space Robot Path Optimization. Algorithms, 16(6), 307. https://doi.org/10.3390/a16060307






