Identification of Mechanical Parameters in Flexible Drive Systems Using Hybrid Particle Swarm Optimization Based on the Quasi-Newton Method

Abstract

This study presents hybrid particle swarm optimization with quasi-Newton (HPSO-QN), a hybrid optimization method for accurately identifying mechanical parameters in two-mass model (2MM) systems. These systems are commonly used to model and control high-performance electric drive systems with elastic joints, which are prevalent in modern industrial production. The proposed method combines the global exploration capabilities of particle swarm optimization (PSO) with the local exploitation abilities of the quasi-Newton (QN) method to precisely estimate the motor and load inertias, shaft stiffness, and friction coefficients of the 2MM system. By integrating these two optimization techniques, the HPSO-QN method exhibits superior accuracy and performance compared to standard PSO algorithms. Experimental validation using a 2MM system demonstrates the effectiveness of the proposed method in accurately identifying and improving the mechanical parameters of these complex systems. The HPSO-QN method offers significant implications for enhancing the modeling, performance, and stability of 2MM systems and can be extended to other systems with flexible shafts and couplings. This study contributes to the development of accurate and effective parameter identification methods for complex systems, emphasizing the crucial role of precise parameter estimation in achieving optimal control performance and stability.

1. Introduction

Drive systems play a crucial role in modern industries, such as steel mills, wind turbines, and industrial robots. Many of these systems can be represented as a model, where the motor and load inertia are connected by a shaft. In such applications, low mechanical resonance can occur due to the flexible shaft between the actuator and the load inertia. This can cause undesirable problems in the mechanical coupling of the system and decrease its performance [1,2,3,4]. To address these issues, the dynamics of these flexible systems must be modeled as a two-mass or multi-mass system when designing the control laws. However, incorrect calculations and assumptions of the parameters in these models can be problematic when relying solely on the information provided in the manufacturer’s datasheets [5,6,7]. Without knowledge of the inertia and shaft stiffness, it is difficult to effectively suppress mechanical resonance. Identifying these parameters can help suppress mechanical resonance, improve system response, and reduce tracking errors. Additionally, these mechanical parameters may not be constant over time in some practical applications.

A mechanical system with inertia disks distributed on the actuating motor and its load side, connected by a flexible shaft between them, can be considered a 2MM system. A typical 2MM drive system exhibits resonant and anti-resonant frequencies when the system’s frequency response is measured from the applied electromagnetic torque to the measured speeds of the actuating motor. Over the years, numerous methods and approaches have been developed and applied to extract the modal parameters of the system. The 2MM model has been used to describe the mechanics of various systems, including rolling mills [8], wind turbines [9], industrial robots [10], paper machines [11], and elevators [12]. Furthermore, the 2MM model has been employed in designing control laws to mitigate harmful resonances in mechanical systems and improve dynamic accuracy.

Recent years have seen a rise in the application of artificial intelligence (AI), machine learning (ML), and deep learning (DL) within the engineering and industrial electronics sectors [13,14,15]. These methodologies are now commonly used for complex tasks such as system identification, control, optimization, and fault diagnostics. For example, in power electronics, AI is utilized in system design, control, and maintenance [13]. Deep learning, a subset of ML, is making strides in fault diagnostics in electrical applications, contributing to improved system reliability [14]. Additionally, deep learning methods, such as sparse autoencoders, have been successfully employed in improving the reconstruction of fingerprint images, further expanding the scope of AI applications [16]. In fact, AI and ML technologies hold promising prospects, but their wider adoption in industry and society faces several challenges from both internal and external perspectives [15]. However, solutions are being sought, and these techniques are being incorporated into traditional engineering methods, such as model-based multivariable control systems [17]. In drive systems, AI and ML offer advanced techniques for parameter identification and system modeling, with applications like the use of dynamic neural networks for estimating nonlinear friction [18]. The intersection of AI, ML, DL, and engineering indicates a new era in industrial electronics, characterized by increased efficiency, robustness, and performance.

Parameter identification methods in the literature can be roughly divided into parametric and non-parametric methods. Parametric methods involve estimating the parameters of the 2MM system’s transfer function polynomials in the time domain. On the other hand, non-parametric methods utilize frequency response function (FRF) methods to estimate the resonant frequencies, i.e., the modal parameters of the system. Many approaches have been successfully applied for the parameter identification of 2MM systems. In [19], the authors proposed an identification method that involves solving a weighted least squares problem for an over-determined linear system derived from sampling the dynamic model along a closed-loop tracking trajectory. An experimental study was conducted on a mechanical system to validate the effectiveness of the proposed method. In [20], the authors proposed a non-linear modeling approach based on the Hammerstein structure and used recursive least squares to identify the mechanical parameters of the system, including Coulomb friction and dead zones. They found that the non-linear approach performed better than the linear approach for low-speed operation, where the non-linearities in the system had a significant impact, resulting in a reduction in the identification error.

The following examples highlight some more identification methods, emphasizing the similarities and differences amongst them. In [21], the authors studied closed-loop identification procedures for multi-mass systems by comparing different identification models, sampling periods, and model orders. Simulation and experimental results showed that reducing the sampling time can limit high-frequency noise, improve the ratio of useful signal to noise, and accurately localize the crucial points in the spectrum by limiting the sampling frequency. In [4], Ke et al. proposed an identification method that combines a Luenberger observer and the variable forgetting factor recursive least squares method to accurately estimate the mechanical parameters of a 2MM system. This method was compared with the standard forgetting factor recursive least squares method and found to achieve good results with high identification accuracy in a short amount of time. In a study by [22], a disturbance observer (DOB) method was proposed to identify the mechanical parameters of series elastic actuators (SEAs) modeled as 2MM systems. The identification process was performed with two closed-loop motor position-tracking experiments, one for identifying the motor-side parameters and spring stiffness, and one for the load-side parameters. Experimental results were provided to validate the proposed method, but the authors noted that further investigation is needed due to non-negligible errors in the Coulomb friction coefficient caused by high nonlinear frictions affecting the device. In [23], Villwock and Pacas developed an identification method in the frequency domain that combines the Welch method with the Levenberg–Marquardt algorithm to identify the parameters of 2MM and three-mass (3MM) systems. The results of this method were found to be effective for the parameter identification of 2MM and 3MM systems, as well as more complex mechanical systems. In a study by Dhaouadi and Kubo [7], a technique was presented that involves the repeated integration of data and the use of the recursive least squares method to identify the mechanical parameters of a 2MM system. Numerical results demonstrated that the estimated parameters converged to the actual transfer function parameters with high accuracy.

An intriguing method was introduced by Nowopolski and Wicher [24], where they used the standard particle swarm optimization (PSO) method to determine the mechanical parameters of a 2MM system with backlash. The PSO is an optimization technique inspired by the social behavior of birds flocking or fish schooling. It is a population-based stochastic optimization algorithm designed to find the global optimum in a problem space. In the context of parameter identification, the PSO algorithm is used to optimize a cost function to determine the best system parameters. The authors compared the results obtained using two different cost functions, and the experimental setup was excited using three different excitation signals for the identification process. However, the cost functions used resulted in relatively large errors, and the experimental results did not match the simulated responses perfectly.

There are various hybrid techniques that incorporate PSO with other optimization algorithms, with the aim of improving global search ability and convergence speed. This has been demonstrated in hybrids that involve PSO with genetic algorithms (GAs), ant colony optimization, and differential evolution. Each of these hybrids showed superior performance compared to the standard PSO, finding wide applications in fields such as engineering, finance, and image processing [25,26]. Specific strategies have been adopted to enhance the social and cooperative aspects of PSO. For instance, the integration of GA with PSO has been implemented in a few distinct ways. One approach involves using GA and PSO either sequentially or in parallel, while another strategy involves the exchange of the fittest particles between GA and PSO when run concurrently [27,28]. Some studies have even employed a two-phase mechanism, where PSO accelerates evolution, and GA ensures diversity [29]. Several innovative hybrid approaches have also been proposed. These include a fuzzy approach that utilizes simple rules for decision making [30], a hybrid algorithm known as FAPSO that combines PSO with the firefly algorithm [31], and a heuristic based on PSO and simulated annealing for resolving multi-objective problems in network-based models [32]. A unique hybrid PSO method focuses specifically on estimating the parameters of photovoltaic (PV) cells. This comes in response to the escalating demand for renewable energy and the need for accurate PV cell models [33]. In a similar vein, an adaptive simulated annealing-parallel particle swarm optimization (ASA-PPSO) approach was developed, incorporating PSO with an infix condition that applies simulated annealing (SA). Moreover, hybridizing differential evolution (DE) with PSO has been explored in various ways, one of which involves using DE to maneuver particles and thereby enhance the convergence rate of PSO [26,34].

Hybrid optimization techniques that combine the strengths of gradient-based and evolutionary algorithms have demonstrated excellent performance in finding satisfactory solutions. One such method is the PSO-descent hybrid, developed by Coelho and Mariani [35], which combines the global search ability of particle swarm optimization (PSO) with the local search capability of the quasi-Newton method. The PSO algorithm runs until convergence, and then the quasi-Newton method is applied to the best solution found. This hybrid approach has proven highly effective in solving the economic dispatch problem. Another hybrid approach, GRPSO, developed by Wang et al. [36], merges the quasi-Newton method and PSO to leverage the strengths of both algorithms. The hybrid begins by running the quasi-Newton method from a random starting point until a local minimum is achieved, then initiates a population of random particles, and runs the PSO algorithm until the global best particle surpasses the quasi-Newton method result. The PSO algorithm is then stopped, and the global best particle is used to restart the quasi-Newton method. This hybrid approach benefits from the local search capability of the quasi-Newton method and the global search ability of the PSO algorithm, enabling it to escape local minima and explore different regions of the search space. Results show that GRPSO is more efficient and reliable than other methods compared to it [36].

While global search methods, such as PSO, are effective at finding the global optimum in large search spaces, they can be less efficient when applied to local search. Gradient-based methods, on the other hand, can be faster and more efficient in finding the optimal solution in a local search space. However, gradient-based methods can struggle when there are multiple local minima or the function being optimized is non-convex. As a result, finding the global optimum using only gradient-based methods can be challenging. To address these issues, a hybrid approach that combines the strengths of both global and local search methods is often employed. In this study, a hybrid approach combining PSO and quasi-Newton was chosen because of the PSO algorithm’s ability to explore a large search space and quasi-Newton’s efficiency in finding the optimal solution in a local search space. Additionally, quasi-Newton methods are capable of handling non-linear optimization problems and can converge to the global minimum, even when the function being optimized is non-convex. Furthermore, quasi-Newton methods do not require the computation of second-order partial derivatives, making them computationally more efficient than traditional Newton methods. This is particularly important when dealing with optimization problems involving large-scale systems.

Therefore, this paper presents a novel hybrid optimization method called HPSO-QN for identifying the mechanical parameters of a 2MM system. The method combines PSO for global exploration with quasi-Newton for local exploitation and estimates the mechanical parameters, such as motor and load inertias, shaft stiffness, and viscous and Coulomb friction coefficients on both the motor and load sides of the system. This work represents a significant step forward from previous studies [2,3] that used various variants of PSO for the parameter identification of a 2MM simulation. The most effective variant of PSO was carefully selected and incorporated into the hybrid framework. We then explored different versions of local search with the quasi-Newton method to reach the globally optimal solution. The proposed method was validated using experimental results from a 2MM system, and its estimated results were compared with those identified using the frequency response function (FRF) method presented in [1].

The remainder of this paper is organized as follows. Section 2 presents the mathematical model of the 2MM system. Section 3 presents the proposed identification method. Section 4 describes the detailed experimental setup of the study. Section 5 focuses on the analysis and discussion of the results obtained. Finally, conclusions are drawn in Section 6.

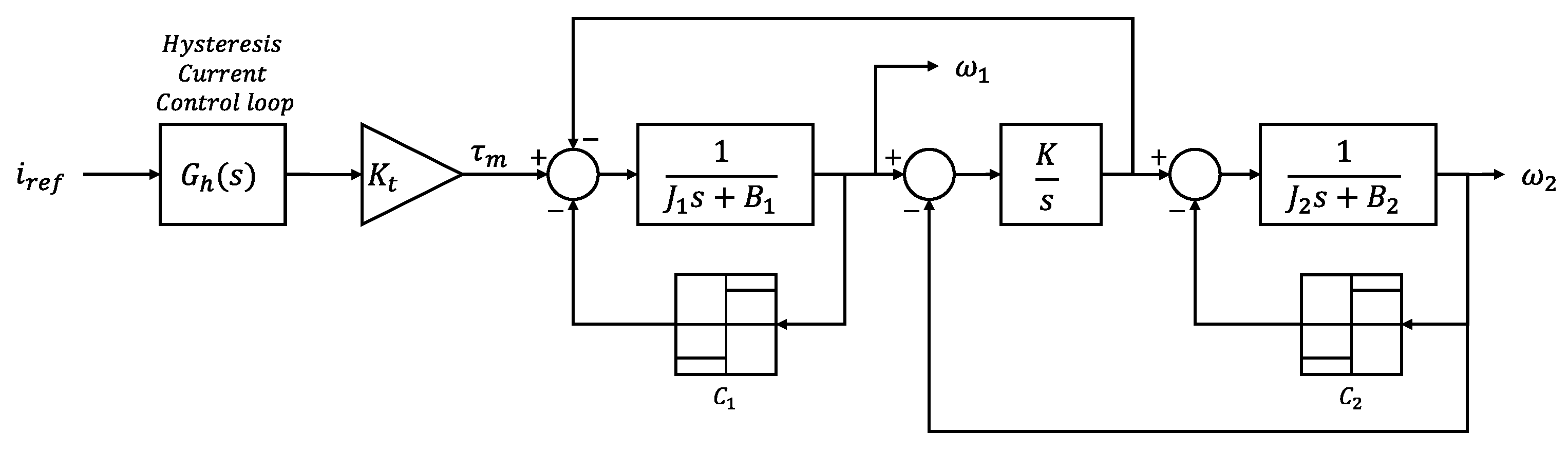
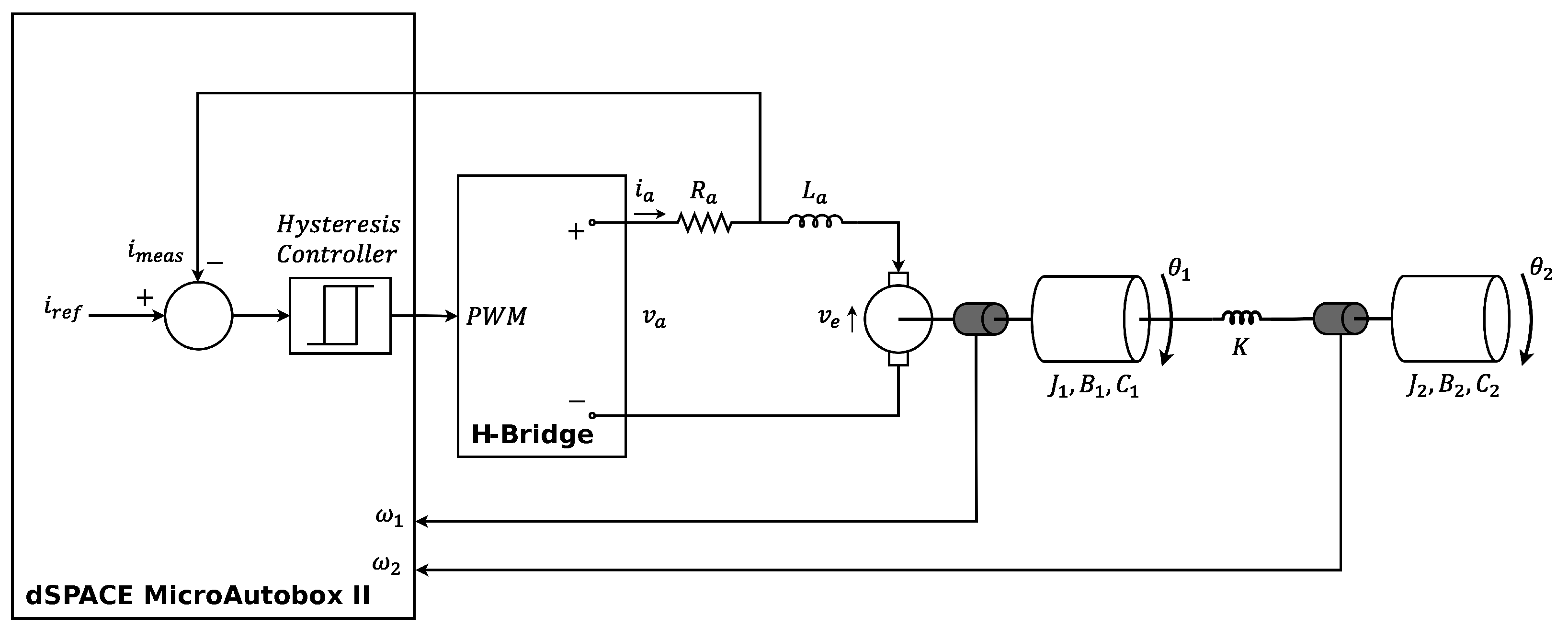
2. System Modeling

The 2MM system represents an actuating motor coupled to a mechanical system with two lumped inertias connected by a low-stiffness shaft and couplings [7,18,37,38,39,40]. The block diagram in Figure 1 shows the 2MM system with its equivalent current control loop. In this diagram, $i_{ref}$ is the reference current (A), $K_t$ is the torque constant (N·m/A), $J_1$ is the equivalent motor-side inertia (kg·m²), and $J_2$ is the equivalent load-side inertia (kg·m²). The motor-side and load-side angular velocities are represented by ${\omega }_1$ and ${\omega }_2$, respectively (rad/s). The inertias are coupled through a low-stiffness shaft $K_s$, which is subjected to torsional torque ${\tau }_s$ (N·m). Here, the Coulomb friction on both sides is taken into account, while external forces are neglected, as the system is considered to move freely. The following describes the mechanical dynamics of the 2MM system.

The mathematical model of the 2MM system is described by the following dynamic equations:

$$J_1\frac{d{\omega }_1}{dt}={\tau }_m-B_1{\omega }_1-{\tau }_s-C_{1}sign\left({\omega }_1\right)$$

(1)

$$J_2\frac{d{\omega }_2}{dt}={\tau }_s-{\tau }_l-B_2{\omega }_2-C_{2}sign\left({\omega }_2\right)$$

(2)

$${\tau }_s=K_{}({\theta }_1-{\theta }_2)$$

(3)

To aid in the identification of system parameters using the proposed method, these equations are normalized with respect to the rated speed and torque. Normalizing parameters is crucial in optimization methods, ensuring faster convergence, preventing numerical instability, and enabling the consistent comparison of system performance. It eliminates scale differences, improves interpretability, robustness, and result consistency. Additionally, normalization facilitates uniform distribution in the search space, reducing the likelihood of encountering local optima and enhancing optimization efficiency and robustness [41,42]. The normalized parameters for the motor and load side inertias are calculated as $J_{1n}=J_1({\omega }_{rated}/{\tau }_{rated})$ and $J_{2n}=J_2({\omega }_{rated}/{\tau }_{rated})$, respectively. The normalized shaft stiffness is calculated as $K_n=K_n/{\omega }_{rated}$. The normalized Coulomb and viscous friction coefficients for both the motor and load sides are calculated as $C_{1n}=C_1/{\tau }_{rated}$, $C_{2n}=C_2/{\tau }_{rated}$, $B_{1n}=B_1({\omega }_{rated}/{\tau }_{rated})$, and $B_{2n}=B_2({\omega }_{rated}/{\tau }_{rated})$. The motor and load speeds are normalized using ${\omega }_{1n}={\omega }_1/{\omega }_{rated}$ and ${\omega }_{2n}={\omega }_2/{\omega }_{rated}$. The normalized equations are denoted with a subscript ‘n’ to indicate that they are normalized with respect to the rated speed and torque of the actuator. This includes variables and parameters, such as the normalized angular velocities (${\Omega }_1$, ${\Omega }_2$), normalized angular positions (${\mathsf{\Theta }}_1$, ${\mathsf{\Theta }}_2$), normalized inertias ($J_{1n}$, $J_{2n}$), and normalized viscous damping and Coulomb friction coefficients ($B_{1n}$, $B_{2n}$, $C_{1n}$, $C_{2n}$). Additionally, the normalized motor and load torques are represented by ${\tau }_{mn}$ and ${\tau }_{ln}$, respectively, and the normalized shaft torsional torque is represented by ${\tau }_{sn}$.

To analyze the system behavior, the transfer functions of the 2MM system can be obtained by linearizing the system equations and assuming that the Coulomb friction is small and can be neglected. The transfer functions of the system are given by

$$G_1\left(s\right)=\frac{{\Omega }_1\left(s\right)}{{\tau }_{mn}\left(s\right)}=\frac{1}{J_{2n}s}\left[\frac{\frac{B_{2n}}{J_{1n}}s+\frac{K_n}{J_{1n}}}{s^2+\frac{B_{1n}+B_{2n}}{J_{1n}{J}_{2n}}s+\frac{K_n}{J_{1n}{J}_{2n}}}\right]$$

(4)

$$G_2\left(s\right)=\frac{{\Omega }_2\left(s\right)}{{\tau }_{mn}\left(s\right)}=\frac{1}{J_{1n}s}\left[\frac{\frac{B_{1n}}{J_{2n}}s+\frac{K_n}{J_{2n}}}{s^2+\frac{B_{1n}+B_{2n}}{J_{1n}{J}_{2n}}s+\frac{K_n}{J_{1n}{J}_{2n}}}\right]$$

(5)

The parameters to be identified in the 2MM system include the normalized motor and load inertias ($J_{1n}$, $J_{2n}$), the normalized torsional stiffness ($K_n$), the normalized Coulomb friction coefficients ($C_{1n}$, $C_{2n}$) and the normalized viscous damping coefficients ($B_{1n}$, $B_{2n}$). These parameters can be represented in vector notation as given below:

$$\mathit{\theta }=[J_{1n},J_{2n},K_n,C_{1n},C_{2n},B_{1n},B_{2n}]$$

(6)

The goal of parameter identification is to estimate the values of these parameters in order to accurately model the 2MM system.

3. Proposed Identification Methods

This section presents our proposed parameter identification process for the 2MM system, which involves the use of swept-sine signal excitation and error minimization through a cost function. Each step of the process is described in the following subsections.

3.1. Excitation Signal

The 2MM system is excited using a swept-sine signal, also known as a periodic chirp, with a duration $T_f$. The signal has a starting frequency $f_1$, a final frequency $f_2$, and an amplitude A. The equation for the swept sine signal is given by

$$x\left(t\right)=Asin\left(2\pi \left(\frac{1}{2}(f_2-f_1)\frac{t^2}{T_f}+f_{1}t\right)\right)$$

(7)

where t ranges from $T_0$ to $T_f$.

3.2. Cost Function

The objective of the parameter identification process is to minimize the mean square error between the actual and estimated angular velocities of the 2MM system. This is achieved through a cost function ($Fcost$) defined as follows:

$$Fcost=\frac{1}{N}\sum _{i=1}^N\left({({\Omega }_1-{\widehat{\Omega }}_1)}^2+{({\Omega }_2-{\widehat{\Omega }}_2)}^2\right)$$

(8)

where ${\widehat{\Omega }}_1$ and ${\widehat{\Omega }}_2$ represent the estimated normalized motor and load angular velocities, respectively. N denotes the number of data samples used for parameter identification.

3.3. Particle Swarm Optimization

Particle swarm optimization (PSO) is a meta-heuristic optimization algorithm that was developed by Kennedy and Eberhart in 1995 [43]. It is a population-based algorithm that simulates the social behavior observed in swarms of biological individuals, such as flocking birds and insects searching for food sources [44]. The PSO algorithm is easy to implement and has been applied to a wide range of scientific and engineering problems [44,45].

In the PSO algorithm, a swarm of particles ($N_{PSO}$) is initialized randomly within a search space defined by upper ($x_{max}$) and lower ($x_{min}$) bound limits. Each particle is evaluated against a pre-defined cost function ($Fcost$) to search for an optimal solution. The particles update their velocity vectors, which control their movement in the next iteration [43,44,45,46]. The velocity updates are influenced by two key factors: personal best ($pBest$) and global best ($gBest$). The $pBest$ represents the best solution found by an individual particle, indicating its optimal position within the search space. The $gBest$ refers to the best solution discovered by any particle in the entire swarm, representing the overall optimal position identified by the collective behavior of the swarm. The velocity and position of each particle are updated as follows [45,46]:

$$v_{k+1}\left(i\right)=v_k\left(i\right)+c_1{r}_1(pBes{t}_k\left(i\right)-x_k\left(i\right))+c_2{r}_2(gBes{t}_k-x_k\left(i\right))$$

(9)

$$x_{k+1}\left(i\right)=x_k\left(i\right)+v_{k+1}\left(i\right)$$

(10)

where i denotes the current particle; $c_1$ and $c_2$ are the acceleration coefficients for $pBest$ and $gBest$ terms; and $r_1$ and $r_2$ are random numbers generated by uniform distribution in the interval $[0, 1]$ [45,46]. The PSO offers several advantages that make it suitable for various optimization problems. It excels at quickly finding solutions, even in high-dimensional search spaces, and is capable of handling complex and noisy optimization problems [45]. Additionally, the PSO has the ability to adapt to changes in the optimization landscape, allowing it to continue searching for better solutions, even when the search space becomes more challenging [47]. However, the PSO also has some limitations. One of the main drawbacks of the PSO is its tendency to get attracted to sub-optimal solutions that are not globally optimal [48]. This can result in premature convergence, where the particles get trapped in a locally optimal solution and continue to search within reduced and limited regions of the search space. Moreover, the performance of the PSO algorithm is sensitive to the selection of control parameters, such as the inertia weight and acceleration constants. Inappropriate parameter choices can lead to poor performance and potential convergence to sub-optimal solutions [49].

To enhance the performance of PSO and address its limitations, various PSO variants have been developed, such as constriction PSO, adaptive inertia weight PSO, and hybrid PSO [50,51]. These variants incorporate additional strategies like dynamic control of the inertia weight, self-adaptive acceleration constants, and hybridization with other optimization methods. Some prior studies have explored variants such as constricted PSO with linearly decreasing inertia weight, adaptive weight factor PSO, and chaos initialized PSO for the identification of 2MM systems [2,3]. Among these, constricted PSO with a linearly decreasing inertia weight showed particularly promising performance, making it our selected base PSO variant for the hybrid framework. For more detailed information on these PSO variants and their application in 2MM system identification, readers are encouraged to refer to [2,3].

3.3.1. Linearly Decreasing Inertia Weight

The inertia weight plays a crucial role in guiding the exploration and exploitation processes in the PSO algorithm. One method for dynamically adjusting the inertia weight is the linearly decreasing time-varying inertia weight [52]. This method iteratively adjusts the inertia weight using Equation (11) as follows:

$$w_k=\frac{w_{max}-w_{min}}{k_{max}}(k_{max}-k)+w_{max}$$

(11)

Here, the suggested values for $w_{max}$ and $w_{min}$ are 0.9 and 0.4, respectively. Empirical studies have shown that this method can produce good results when the inertia weight is decreased from a high initial value (e.g., 0.9) to a lower value (e.g., 0.4) as the optimization progresses [52]. However, it is important to note that selecting an unsuitable value for the inertia weight can impede convergence or result in sub-optimal solutions.

3.3.2. Constriction Factor

The constriction factor method, also known as the constriction coefficient method, was introduced by Clerc et al. [53] to improve the convergence and stability of the PSO algorithm. It involves the use of factor ℵ, which can be calculated using Equation (12) as follows:

$$\aleph =\frac{2}{\left|2-\phi -\sqrt{{\phi }^2-4\phi }\right|}$$

(12)

where $\phi =c_1+c_2,$$\phi >4$. The constriction factor is inversely proportional to $\phi$, so when $\phi$ is set to 4.1, for example, the constriction factor becomes 0.73. This value is then multiplied by the three terms in Equation (9): the velocity, $pBest$, and $gBest$. Empirical studies have shown that the constriction factor method can improve the performance of PSO compared to the original algorithm. However, it does not offer a mechanism for preventing premature convergence, which can occur when the optimization process reaches a satisfactory solution before fully exploring the search space.

The updated velocity equation incorporating the inertia weight and the constriction factor is as follows:

$$v_{k+1}\left(i\right)=\aleph (w_k{v}_k\left(i\right)+c_1{r}_1(pBes{t}_k\left(i\right)-x_k\left(i\right))+c_2{r}_2(gBes{t}_k-x_k\left(i\right)))$$

(13)

In this research, the selected variant of PSO is referred to as the standard PSO (SPSO) for comparison with the hybrid methods. The SPSO will be integrated with the QN method to create a hybrid approach. The pseudo-code of the SPSO algorithm is presented in Algorithm 1. The algorithm will terminate when the maximum number of iterations ($k_{max}$) is reached.

Algorithm 1 SPSO.

Require:   N, $k_{max}$, $x_{min}$, $x_{max}$, $w_{min}$, $w_{max}$, $\phi$, $c_1$, and $c_2$ 1:  Set $k=0$, randomly initialize particles’ positions $x_i\left(k\right)$ and velocities $v_i\left(k\right)$ 2:  for each particle $P_i\left(k\right),i=1,2,\dots ,N$ do 3:   Set $pBes{t}_i\left(0\right)=x_i\left(0\right)$, $gBest\left(0\right)=pBes{t}_1\left(0\right)$ 4:  end for 5:  repeat 6:   set $k=k+1$ 7:   for each particle $P_i\left(k\right),i=1,2,\dots ,N$ do 8:    Evaluate $Fcost\left(x_i\left(k\right)\right)$ using Equation (8) 9:    if $Fcost\left(x_i\left(k\right)\right)<Fcost\left(pBes{t}_i\left(k\right)\right)$ then 10:     $pBes{t}_i\left(k\right)=x_i\left(k\right)$ 11:    end if 12:    if $Fcost\left(pBes{t}_i\left(k\right)\right)<Fcost\left(gBest\left(k\right)\right)$ then 13:     $gBest\left(k\right)=pBes{t}_i\left(k\right)$ 14:    end if 15:    Update velocity $v_i(k+1)$ and position $x_i(k+1)$ using Equations (13) and (10) 16:   end for 17:  until SPSO termination criterion is satisfied

3.4. Quasi-Newton Method

The quasi-Newton (QN) method is a powerful gradient-based optimization algorithm that leverages information about the curvature of a cost function to iteratively find its minimum value. It approximates the Hessian matrix at each iteration and performs a cubic line search procedure to enhance the solution obtained. The QN method is particularly useful when the direct calculation of the Hessian matrix is difficult or impractical [54,55,56,57]. By incorporating the QN method into the optimization process, the algorithm benefits from improved local optimization capabilities, increasing the likelihood of finding an optimal solution.

At each iteration, the QN method constructs a quadratic model using curvature information. The optimal solution of this quadratic model denoted as $x^{*}$ can be represented as follows:

$$x^{*}=-H^{-1}·\nabla f_k$$

(14)

where H is a positive definite symmetric matrix (the Hessian), and $\nabla f_k$ is the gradient of f at the point $x_k$ [55,56]. To update the Hessian matrix H, the QN method uses the Broyden–Fletcher–Goldfarb–Shanno (BFGS) method, which gives the following formula [55]:

$$H_{k+1}=H_k+\frac{y_k{y}_k^T}{y_k^T{s}_k}-\frac{H_k{s}_k{s}_k^T{H}_k^T}{s_k^T{H}_k{s}_k}$$

(15)

where $s_k$ and $y_k$ are calculated as follows:

$$\begin{array}{cc}\hfill s_k& =x_{k+1}-x_k\hfill \\ \hfill y_k& =\nabla f_{k+1}-\nabla f_k\hfill \end{array}$$

(16)

Here, $s_k$ represents the change in the independent variable x, and $y_k$ represents the change in the gradient. The Hessian matrix H can be initialized as any symmetric positive definite matrix, such as the identity matrix I. To avoid inverting H, the BFGS method and the Davidon–Fletcher–Powell (DFP) method use formulas that approximate the inverse Hessian at each update rather than inverting H directly. The BFGS method uses the updating formula shown above to approximate the Hessian matrix H, while the DFP method uses the same updating formula but substitutes $y_k$ for $s_k$ to calculate the approximate inverse Hessian $H^{-1}$ [55]. The inverse Hessian matrix $H_{k+1}^{-1}$ can be calculated as follows:

$$H_{k+1}^{-1}=H_k^{-1}+\frac{s_k{s}_k^T}{s_k^T{y}_k}-\frac{H_k^{-1}{y}_k{y}_k^T{H}_k^{-1}}{y_k^T{H}_k^{-1}{y}_k}$$

(17)

Equation (17) approximates the inverse Hessian matrix in the DFP method. The BFGS method uses a similar updating formula but substitutes $y_k$ for $s_k$ in the equation. Both the BFGS and DFP methods avoid directly inverting the Hessian matrix H by employing these formulas to approximate the inverse Hessian at each iteration [55,56].

At each k-th iteration, a line search is performed in the direction $d_k$, which is calculated as follows [55,56]:

$$d_k=-H_k^{-1}·\nabla f\left(x_k\right)$$

(18)

The next solution $x_{k+1}$ is calculated as follows:

$$x_{k+1}=x_k+{\alpha }_k{d}_k$$

(19)

where $x_k$ represents the current iterate, $d_k$ is the search direction, and ${\alpha }_k$ is a scalar step length parameter chosen to satisfy the Wolfe conditions [55,56].

The pseudo-code of the QN (BFGS) method is presented in the method in Algorithm 2. It utilizes the BFGS updating formula to approximate the Hessian matrix H, and the convergence tolerance $ϵ$ is used to check the stopping criteria. The line search procedure determines the step size ${\alpha }_k$ at each iteration. It is worth noting that QN methods exhibit a fast convergence rate and are relatively easy to implement. However, they require a good initial guess and are limited to finding the local minima in multimodal problems [55,56].

Algorithm 2 QN (BFGS).

Require:  Given starting point $x_0$, convergence tolerance $ϵ>0$ 1:  set $k=0$, $H_0=I$ 2:  while  $\left|\right|\nabla f_k\left|\right|>ϵ$ do 3:  Compute search direction, $d_k=-H_k·\nabla f_k$ 4:  Compute next solution, $x_{k+1}=x_k+{\alpha }_k{d}_k$ using line search 5:  Define $s_k=x_{k+1}-x_k$, $y_k=\nabla f_{k+1}-\nabla f_k$ 6:  Compute $H_{k+1}$ using Equation (15) 7:  set $k=k+1$. 8:  end while

The built-in MATLAB function ‘fminunc’ is commonly utilized for solving optimization problems [58,59]. It utilizes the QN method as the default optimization algorithm and is designed to be robust and efficient. ‘fminunc’ can handle various optimization problems, including non-smooth and non-convex functions, providing flexibility for solving different types of optimization problems [58,59].

3.5. Proposed Hybrid Methods

To overcome the limitations of the PSO method and enhance its solution refinement capabilities, we introduce a new hybrid approach, the HPSO-QN method. This method merges the global search capability of PSO with the fast convergence and local search proficiency of the quasi-Newton method. While PSO is known for its global search capability, it can be slow to converge and prone to getting trapped in locally optimal solutions. Conversely, the quasi-Newton method offers fast convergence but is limited to the local minima on multi-modal problems and is sensitive to initial conditions.

Drawing inspiration from the successes of previous hybrid techniques [35,36,60,61], our proposed hybrid approach employs both the PSO and QN algorithms to identify the mechanical parameters of the 2MM. Unlike standard PSO algorithms, this hybrid method leverages the PSO algorithm’s strength for global search and the QN method’s efficiency in local search. Initially, the PSO identifies a potential global optimal region in the search space, after which the algorithm switches to the QN method for more rapid convergence and solution refinement. This approach combines the benefits of both global and local search methods, incorporating a stopping criterion to avoid being trapped in local minima.

Diversifying the approach further, we introduce three variations of the HPSO-QN method. Each variant begins with the PSO to find an initial $gBest$ solution, which then serves as the starting point for the QN method. The key difference between these methods lies in their strategies to select particles for a second run of the PSO algorithm after the QN method has identified a minimum. These strategies provide new approaches to hybridizing the PSO and QN methods, leveraging the strengths of each, while mitigating their limitations. The following bullet points provide a brief outline of these proposed methods:

• HPSO-QN Sequential Method: PSO finds the $gBest$ solution, which is then improved by QN.
• HPSO-QN Single Local Search Method: PSO uses a stopping criterion to find the $gBest$ solution, which is then refined by the QN method.
• HPSO-QN Multi Local Search Method: SPSO is used until a stopping criterion is met, then a percentage of the best particles are selected and improved using the QN method.

3.5.1. HPSO-QN Sequential Method

In the HPSO-QN sequential method (SM), PSO is utilized to find the $gBest$ solution. The pseudo-code of the HPSO-QN SM algorithm is presented in Algorithm 3. In the same iteration, this solution serves as the starting point for the QN method. If the QN method’s solution is better than that of the PSO, the $gBest$ solution from PSO is replaced with the solution from the QN method. This method improves the $gBest$ solution obtained from the PSO algorithm with each iteration by balancing the exploration of the search space by PSO and the exploitation of the local minima by the QN method, thus enhancing both the local and global searches in each iteration.

Algorithm 3 HPSO-QN Sequential Method.

Require: $N_{PSO}$, $k_{max}$, $x_{min}$, $x_{max}$, $w_{min}$, $w_{max}$, $\phi$, $c_1$, and $c_2$ 1:  Set $k=0$, randomly initialize particles’ positions $x_i\left(k\right)$ and velocities $v_i\left(k\right)$ 2:  repeat 3:  set $k=k+1$. 4:  for each particle $P_k\left(i\right),i=1,2,..N_{PSO}$ do 5:     Evaluate $Fcost\left(x_k\left(i\right)\right)$ using Equation (8) 6:     Update $pBes{t}_k\left(i\right)$ and $gBes{t}_k$ as shown in Algorithm 1 7:     Calculate $v_{k+1}\left(i\right)$ and $x_{k+1}\left(i\right)$ using Equations (13) and (10) 8:  end for 9:  $x_0=gBes{t}_k$ 10:   $QN=fminunc(Fcost\left(x\right),x_0,$‘Algorithm’, ‘quasi-newton’) 11:   if $Fcost\left(QN\right)<Fcost\left(gBes{t}_k\right)$ then $gBes{t}_k=QN$ 12:   end if 13: until the termination criterion is met

3.5.2. HPSO-QN Single Local Search Method

In the second method, the HPSO-QN single local search method (SLSM), a stopping criterion is introduced to enhance the exploration of the search space by the PSO algorithm. This criterion allows the PSO algorithm to discover the $gBest$ solution. Once this criterion is met, the $gBest$ solution serves as the starting point for the QN method before moving on to the next PSO iteration. The QN method then performs a local search on this solution to further improve it. The stopping criterion is defined as follows:

$$\Delta Fcost=\left|\frac{(Fcost\left(gBes{t}_k\right)-Fcost\left(gBes{t}_{k-1}\right)}{Fcost\left(gBes{t}_{k-1}\right)}\right|\times 100,\Delta Fcost<F_{th}$$

(20)

Here, $F_{th}$ represents the user-defined threshold limit. This stopping criterion ensures a balance between exploration and exploitation, facilitating faster convergence and more precise solutions. By refining the PSO-found solution with QN, the chances of discovering the true global minimum are increased, resulting in more efficient search space exploration. The pseudo-code of the HPSO-QN SLSM algorithm is presented in Algorithm 4.

Algorithm 4 HPSO-QN single local search method.

Require: $N_{PSO}$, $k_{max}$, $x_{min}$, $x_{max}$, $w_{min}$, $w_{max}$, $\phi$, $c_1$, $c_2$ and $F_{th}$ 1:  Set $k=0$, randomly initialize particles’ positions $x_i\left(k\right)$ and velocities $v_i\left(k\right)$ 2:  repeat 3:   set $k=k+1$. 4:   for each particle $P_k\left(i\right),i=1,2,..N_P$ do 5:     Evaluate $Fcost\left(x_k\left(i\right)\right)$ using Equation (8) 6:     Update $pBes{t}_k\left(i\right)$ and $gBes{t}_k$ as shown in Algorithm 1 7:     Calculate $v_{k+1}\left(i\right)$ and $x_{k+1}\left(i\right)$ using Equations (13) and (10) 8:   end for 9:   if $\Delta Fcost<F_{th}$ then 10:    $x_0=gBes{t}_k$ 11:    $QN=fminunc(Fcost\left(x\right),x_0,$’Algorithm’, ’quasi-newton’) 12:    if $Fcost\left(QN\right)<Fcost\left(gBes{t}_k\right)$ then $gBes{t}_k=QN$ 13:    end if 14:  end if 15: until the termination criterion is met

3.5.3. HPSO-QN Multi Local Search Method

The third method, the HPSO-QN multi local search method (MLSM), improves upon the previous HPSO-QN SLSM by incorporating a new approach for balancing global and local search. The algorithm begins with the SPSO algorithm until a predefined stopping criterion is reached. Then, a specified percentage of the best particles is selected for the QN method, allowing the algorithm to focus on multiple promising solutions. The selected particles are determined by

$$N_{QN}=N_{PSO}\times B$$

(21)

where B represents the percentage of selected best particles and $N_{PSO}$ denotes the total number of particles in the PSO algorithm. The QN method is then applied to each selected particle, and the $gBest$ solution is replaced by the best solution found among the selected particles. This hybrid approach achieves a balance between global and local search by utilizing PSO to explore the search space and identify promising solutions, while QN fine tunes these solutions, increasing the likelihood of finding the global minimum. The pseudo-code of the HPSO-QN MLSM algorithm is presented in Algorithm 5.

Algorithm 5 HPSO-QN Multi Local Search Method.

Require: $N_{PSO}$, $N_{QN}$, $k_{max}$, $x_{min}$, $x_{max}$, $w_{min}$, $w_{max}$, $\phi$, $c_1$, $c_2$ and $F_{th}$ 1:  Set $k=0$, randomly initialize particles’ positions $x_i\left(k\right)$ and velocities $v_i\left(k\right)$ 2:  repeat 3:   set $k=k+1$. 4:   for each particle $P_k\left(i\right),i=1,2,..N_{PSO}$ do 5:     Evaluate $Fcost\left(x_k\left(i\right)\right)$ using Equation (8) 6:     Update $pBes{t}_k\left(i\right)$ and $gBes{t}_k$ as shown in Algorithm 1 7:     Calculate $v_{k+1}\left(i\right)$ and $x_{k+1}\left(i\right)$ using Equations (13) and (10) 8:   end for 9:   Select $N_{Q}N$ particles for QN local search 10:    for each particle $Q\left(j\right),j=1,2,..N_{QN}$ do 11:    $x_0\left(j\right)=pBes{t}_k\left(j\right)$ 12:    $QN\left(j\right)=fminunc(Fcost\left(x\right),x_0\left(j\right),$‘Algorithm’, ‘quasi-newton’) 13:    if $Fcost\left(QN\left(j\right)\right)<Fcost\left(gBes{t}_k\right)$ then $gBes{t}_k=QN\left(j\right)$ 14:    end if 15:  end for 16: until the termination criterion is met

The proposed methods were implemented and evaluated on a computer system with the following specifications: 16 GB of RAM, a 64-bit operating system, and an Intel(R) Xeon(R) E-2124 CPU @ 3.30GHz processor. The simulations were conducted using Matlab 2023a software [58].

4. Experimental Setup

The experimental setup for the 2MM Flexible Drive System is illustrated in Figure 2. It includes two incremental encoders for measuring the motor and load speeds, as well as a current sensor for measuring the armature current. Real-time control is achieved using the dSPACE DS1401/1512/1513 MicroAutobox II controller, which interfaces with MATLAB/Simulink and Control-Desk.

The system comprises an actuating motor on the left side, connected to an inertia disk, a flexible coupling, an encoder, and another inertia disk, forming the first mass. On the right side, there is the second mass, an inertia load connected to a load motor. The actuating motor used in this research is a Buhler DC Motor of model $1.13.075.214$. High-resolution encoders with 40,000 PPR are used to measure the angular speeds of the masses. The inertias are supported by ball bearings and interconnected by a torsional shaft.

To facilitate the identification process, an open-loop current controller with hysteresis current control was implemented in MATLAB/Simulink and later deployed to the dSPACE controller. The hysteresis current controller is sampled at a rate of 20 μs, while the speed measurements are sampled every 1 ms. Figure 3 shows the overall system block diagram, including the hysteresis current controller implementation. In current control mode, the dynamic equation does not explicitly include electrical components like resistance $R_a$ and inductance $L_a$. The current controller effectively handles these parameters to account for their impact on system dynamics.

The 2MM system was excited by periodic chirp input current signals with frequencies ranging from $f_1=1$ Hz to $f_2=40$ Hz, an amplitude current of $A=$ 3 A, and a time duration ranging from $T_0=$ 0 s to $T_f=$ 3 s. Previous research was conducted to identify the parameters of the system. These analyses involved identifying the inertias and stiffness of the system through frequency domain analysis, as well as determining the friction coefficients through time domain analysis [1,2]. In the time domain identification, the friction coefficients for both the motor and load sides were estimated individually. The approach described in [62] was utilized, which involved using a ramp function as the torque input and performing numerical analysis on speed and torque data to estimate the viscous friction coefficient and Coulomb friction coefficient. For more detailed information on the identification techniques used, interested readers are encouraged to refer to the mentioned papers [1,2,62]. The parameters identified in our previous research serve as benchmarks for comparing the results obtained from the proposed methods. In this study, we normalized these parameters using the rated values of the DC motor provided in the datasheet. This normalization improves the interpretability, robustness, and consistency of the results, as well as the numerical stability of the simulation models. The identified benchmark parameters of the 2MM system are presented in

Table 1. Benchmark parameters of the two-mass model (2MM).

Parameter	SI Units	Normalized Units
Motor Inertia ($J_1$)	$1.5602\times {10}^{-3}$ kg·m2	0.8713 s
Load Inertia ($J_2$)	$1.3966\times {10}^{-3}$ kg·m2	0.7799 s
Shaft stiffness (K)	19.4840 N·m/rad	10,881.9233 p.u.
Motor Coulomb Friction ($C_1$)	0.0182 N·m	0.0304 p.u.
Load Coulomb Friction ($C_2$)	0.0162 N·m	0.0271 p.u.
Motor Viscous Friction ($B_1$)	$3.7167\times {10}^{-3}$ N·m/rad·s	2.0759 p.u.
Load Viscous Friction ($B_2$)	$3.5530\times {10}^{-3}$ N·m/rad·s	1.9844 p.u.

, both in their SI units and normalized units.

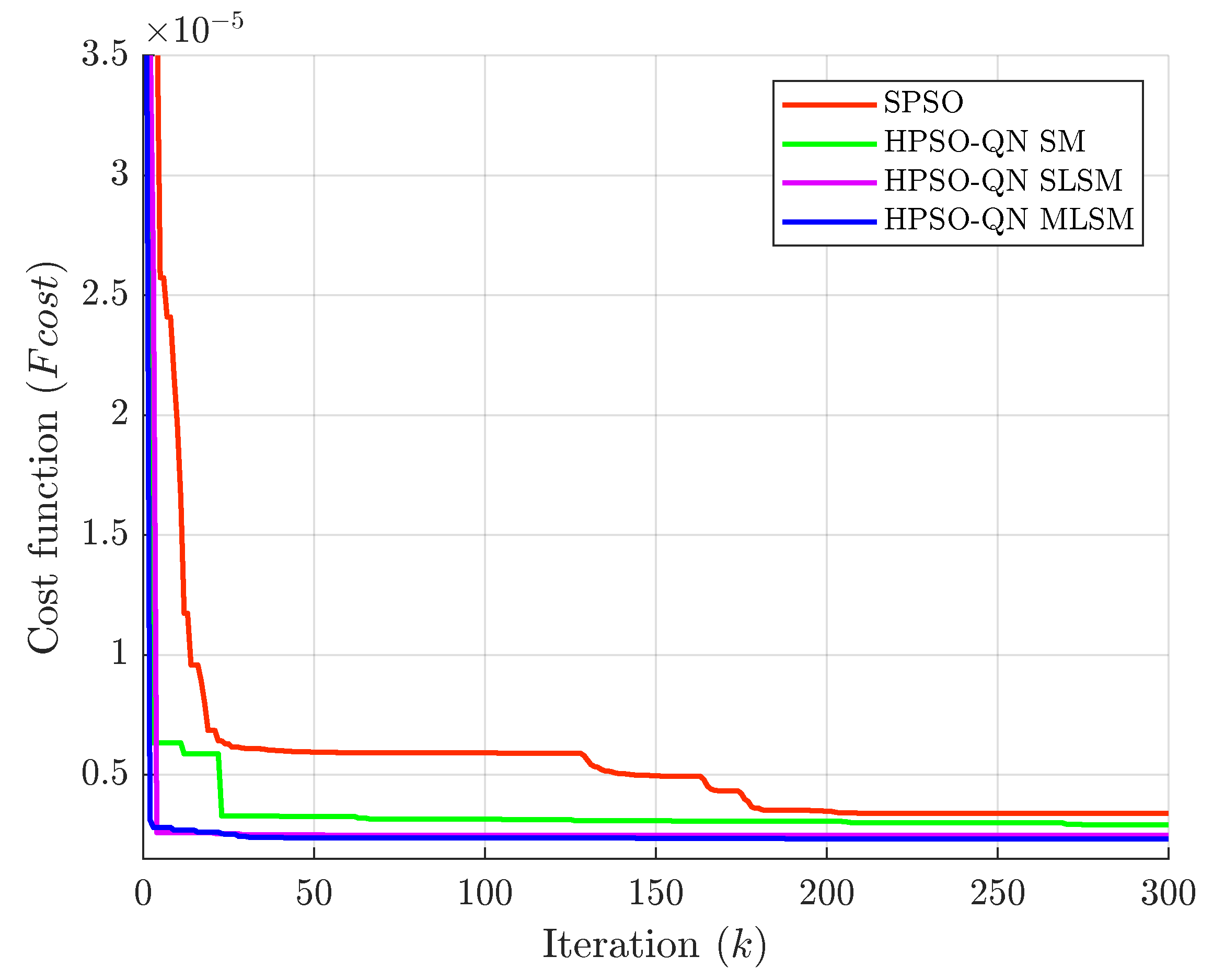
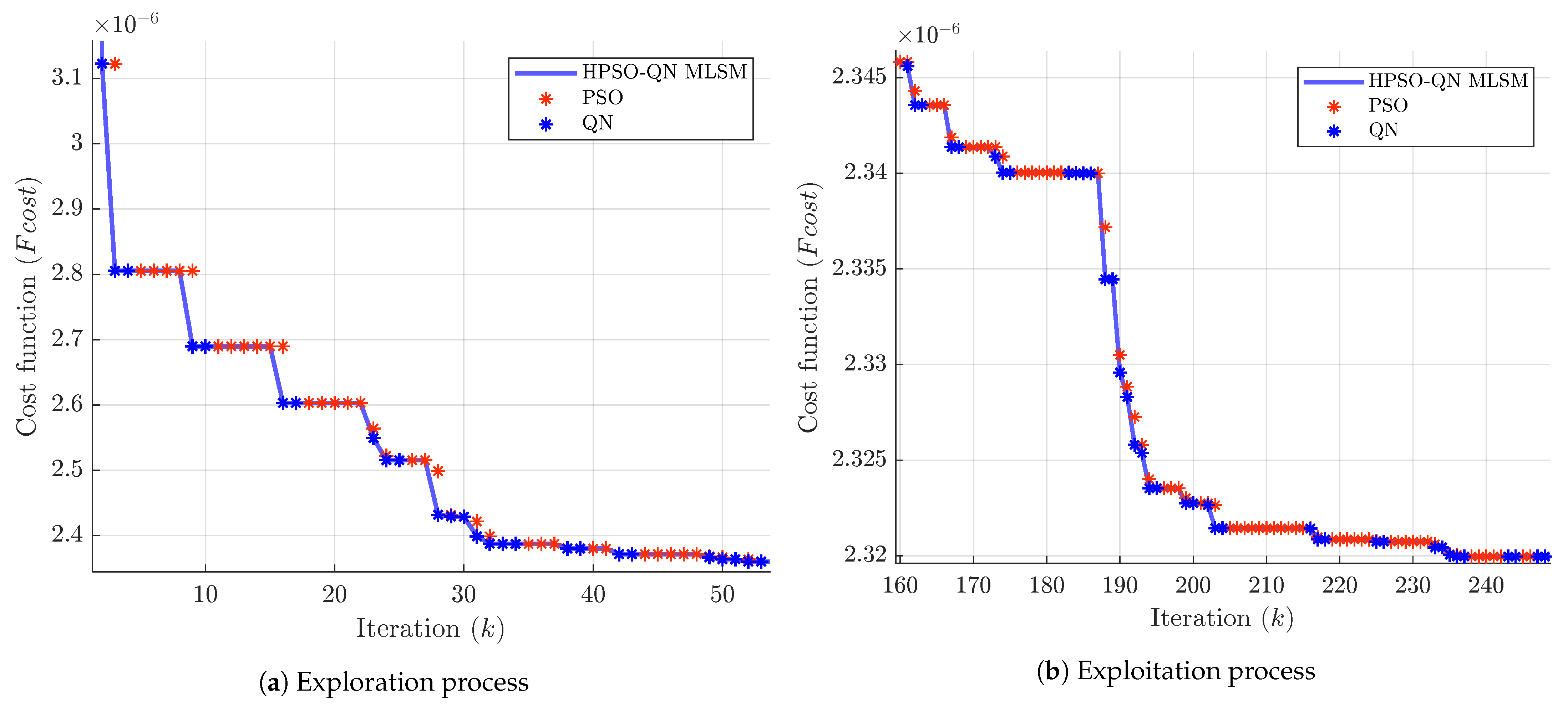
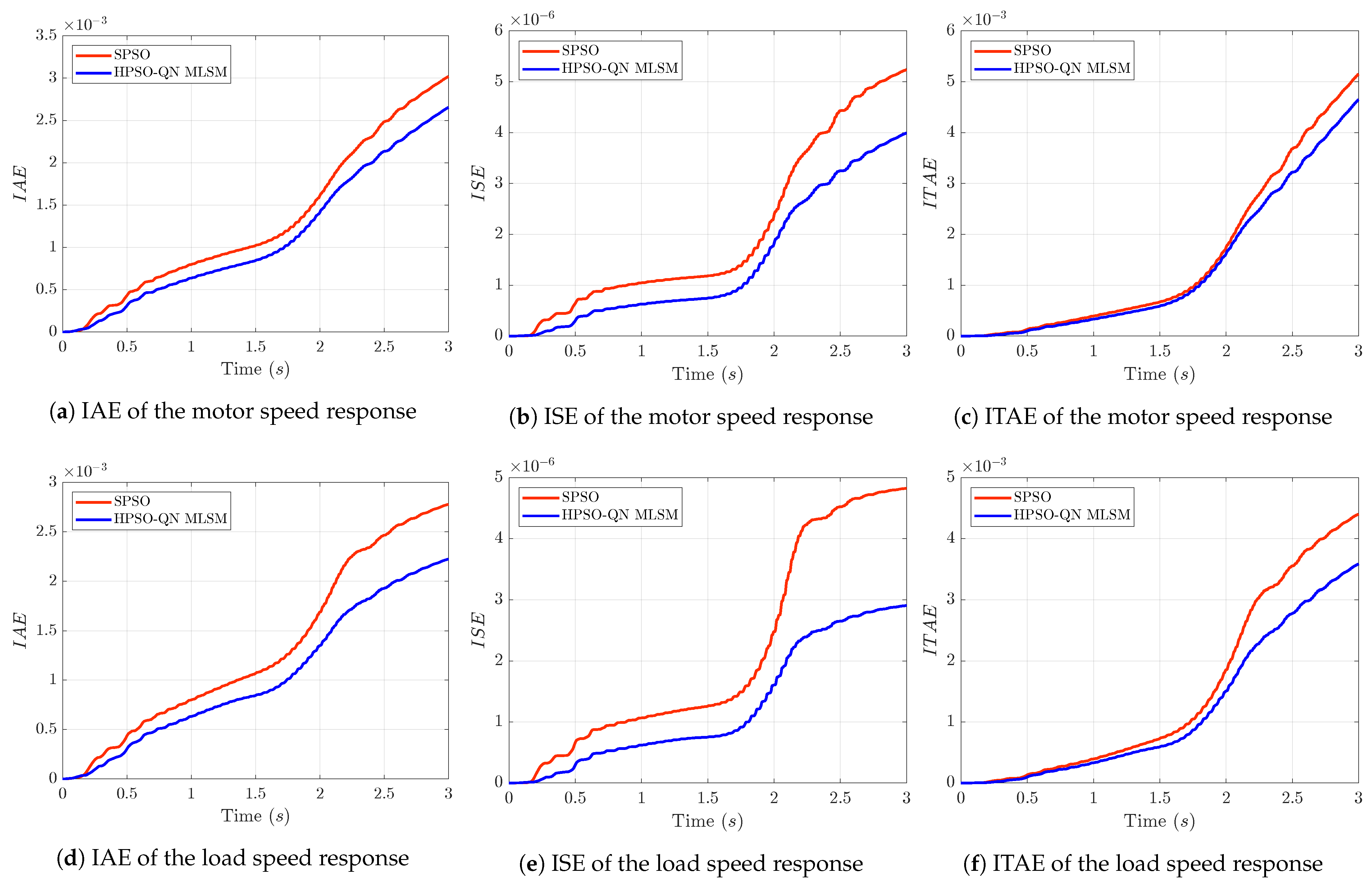
5. Results and Discussion

To evaluate the effectiveness of the proposed hybrid PSO methods, we conducted a series of simulation runs in this study. Four different algorithms were employed: SPSO, HPSO-QN SM, HPSO-QN SLSM, and HPSO-QN MLSM. Each algorithm was tested independently five times, with randomized initial positions. The proposed algorithms utilized a particle count ($N_{PSO}$) of 50 and a maximum iteration count ($k_{max}$) of 300. The choice of 300 iterations as the maximum value was determined by monitoring the convergence of the algorithm, specifically through the $Fcost$ plot analysis.

To define the search space bounds, the following upper and lower bounds for the position and velocity vectors were assigned:

$$\begin{array}{ccc}{\overrightarrow{x}}_{\min }\left(k\right)\hfill & =\hfill & \left[\begin{array}{lllllll}0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill \end{array}\right]\hfill \\ {\overrightarrow{x}}_{\max }\left(k\right)\hfill & =\hfill & \left[\begin{array}{lllllll}4\hfill & 4\hfill & 40000\hfill & 0.5\hfill & 0.5\hfill & 5\hfill & 5\end{array}\right]\hfill \end{array}$$

(22)

These bounds correspond to the following parameters:

$$\overrightarrow{x}\left(k\right)=\left[\begin{array}{ccccccc}{J}_{1n}& J_{2n}& K_n& C_{1n}& C_{2n}& B_{1n}& B_{2n}\end{array}\right]$$

(23)

To assess the effectiveness of the switching criteria for the local search methods (HPSO-QN SLSM and HPSO-QN MLSM), we evaluated different values of $F_{th}$: specifically, $5\%$, $10\%$, and $20\%$. Our findings showed that HPSO-QN SLSM achieved the lowest cost function and standard deviation of the cost function when $F_{th}$ was set to $5\%$. Furthermore, we investigated the impact of different values of B in the HPSO-QN MLSM method. We tested two scenarios: selecting either the 5 or 10 best particles for the QN local search with B set to $5\%$ and $10\%$, respectively. After evaluating the results, we observed that the lowest standard deviation of the cost function and parameters, as well as the lowest absolute percentage error (APE) of the parameters, were achieved when $F_{th}$ was set to $5\%$ and B was set to $5\%$. The results of the lowest cost function ($Fcost$) using $F_{th}=5\%$ and $BP=5\%$ are presented in

Table 2. Selected identified parameters of the 2MM system using the proposed methods with the lowest cost function.

PSO Methods	Parameters							$\mathit{F}\mathit{c}\mathit{o}\mathit{s}\mathit{t}$ $(\times {10}^{-6})$
	${\mathit{J}}_{1\mathit{n}}\left(\mathbf{s}\right)$	${\mathit{J}}_{2\mathit{n}}\left(\mathbf{s}\right)$	${\mathit{K}}_{\mathit{n}}\left({\mathbf{s}}^{-1}\right)$	${\mathit{C}}_{1\mathit{n}}$(p.u)	${\mathit{C}}_{2\mathit{n}}$(p.u)	${\mathit{B}}_{1\mathit{n}}$(p.u)	${\mathit{B}}_{2\mathit{n}}$(p.u)
SPSO	0.9211	1.1142	13,323.9963	0.0093	0.0353	1.6971	4.5508	3.3859
HPSO-QN SM	0.8642	1.0453	12,497.3021	0.0299	0.0261	0.7666	3.9063	2.9167
HPSO-QN SLSM	0.7718	0.8310	10,532.9554	0.0197	0.0303	3.6192	1.4733	2.4787
HPSO-QN MLSM	0.7987	0.8983	11,169.0221	0.0272	0.0325	0.3083	3.7556	2.3200

.

Based on these results and compared with the benchmark parameters in Table 1, the proposed HPSO-QN methods demonstrated their effectiveness in estimating the mechanical parameters of the 2MM system. The HPSO-QN MLSM method achieved the lowest cost function value of $2.32\times {10}^{-6}$ with a high degree of speed response accuracy.

Table 3. A comparison of the standard deviation of the identified parameters across five independent runs using the proposed methods.

PSO Methods	Parameters							$\mathit{F}\mathit{c}\mathit{o}\mathit{s}\mathit{t}$ $(\times {10}^{-6})$
	${\mathit{J}}_{1\mathit{n}}\left(\mathbf{s}\right)$	${\mathit{J}}_{2\mathit{n}}\left(\mathbf{s}\right)$	${\mathit{K}}_{\mathit{n}}\left({\mathbf{s}}^{-1}\right)$	${\mathit{C}}_{1\mathit{n}}$(p.u)	${\mathit{C}}_{2\mathit{n}}$(p.u)	${\mathit{B}}_{1\mathit{n}}$(p.u)	${\mathit{B}}_{2\mathit{n}}$(p.u)
SPSO	0.4199	0.3198	4356.4730	0.0142	0.0152	1.3070	1.6753	3.7320
HPSO-QN SM	0.1714	0.2817	2137.6343	0.0119	0.0146	0.9651	1.0390	2.0512
HPSO-QN SLSM	0.1927	0.3636	3548.1141	0.0171	0.0082	1.2920	1.2398	1.2274
HPSO-QN MLSM	0.0218	0.0512	461.0188	0.0052	0.0028	1.2008	1.4837	0.0787

compares the standard deviation values of the identified parameters using four different PSO methods. The HPSO-QN MLSM method consistently exhibits the lowest standard deviation values, highlighting its robustness. In contrast, the SPSO method demonstrates relatively higher standard deviation values compared to the HPSO-QN methods.

The improvement ratios of the HPSO-QN MLSM method over other methods for each identified parameter are summarized in

Table 4. Improvement ratio of the standard deviation of the HPSO-QN MLSM method compared to other methods.

PSO Methods	Parameters							$\mathit{F}\mathit{c}\mathit{o}\mathit{s}\mathit{t}$ $(\times {10}^{-6})$
	${\mathit{J}}_{1\mathit{n}}\left(\mathbf{s}\right)$	${\mathit{J}}_{2\mathit{n}}\left(\mathbf{s}\right)$	${\mathit{K}}_{\mathit{n}}\left({\mathbf{s}}^{-1}\right)$	${\mathit{C}}_{1\mathit{n}}$(p.u)	${\mathit{C}}_{2\mathit{n}}$(p.u)	${\mathit{B}}_{1\mathit{n}}$(p.u)	${\mathit{B}}_{2\mathit{n}}$(p.u)
SPSO	19.26	6.25	9.45	2.73	5.43	1.09	1.13	48.06
HPSO-QN SM	7.86	5.50	4.63	2.29	5.21	0.80	0.70	26.06
HPSO-QN SLSM	8.84	7.10	7.70	3.29	2.92	1.06	0.83	15.60

. The HPSO-QN MLSM method consistently yields substantially lower standard deviation values across all parameters compared to the other methods. For example, the standard deviation of $J_{1n}$ using the HPSO-QN MLSM is reduced by a factor of 19.26 compared to SPSO, 7.86 compared to HPSO-QN SM, and 8.84 compared to HPSO-QN SLSM. Other parameters also experience notable improvements. The standard deviation of $J_{2n}$ is reduced by factors of 6.25, 5.50, and 7.10 compared to SPSO, HPSO-QN SM, and HPSO-QN SLSM, respectively, when using the HPSO-QN MLSM method. Similarly, the $K_n$ parameter sees reduction factors of 9.45, 4.63, and 7.70. Similar improvements are observed for $C_{1n}$, $C_{2n}$, $B_{1n}$, and $B_{2n}$. It is important to note that for $B_{1n}$ and $B_{2n}$, HPSO-QN SM demonstrates slightly lower standard deviation values compared to HPSO-QN MLSM. However, HPSO-QN MLSM still outperforms the other PSO methods in terms of identifying parameters with lower standard deviation values for the majority of parameters. While the HPSO-QN SM method also shows lower standard deviation values for $B_{1n}$ and $B_{2n}$, HPSO-QN MLSM surpasses it for most parameters. Consequently, the HPSO-QN MLSM method proves to be a promising approach for parameter identification problems in similar systems.

The results in

Table 5. Performance comparison of the proposed method: average of identified parameters across five independent runs.

PSO Methods	Parameters							$\mathit{F}\mathit{c}\mathit{o}\mathit{s}\mathit{t}$ $(\times {10}^{-6})$
	${\mathit{J}}_{1\mathit{n}}\left(\mathbf{s}\right)$	${\mathit{J}}_{2\mathit{n}}\left(\mathbf{s}\right)$	${\mathit{K}}_{\mathit{n}}\left({\mathbf{s}}^{-1}\right)$	${\mathit{C}}_{1\mathit{n}}$(p.u)	${\mathit{C}}_{2\mathit{n}}$(p.u)	${\mathit{B}}_{1\mathit{n}}$(p.u)	${\mathit{B}}_{2\mathit{n}}$(p.u)
SPSO	1.2457	1.3193	16,554.7629	0.0158	0.0256	2.5953	3.0403	7.1430
HPSO-QN SM	1.0492	1.1201	14,035.9131	0.0211	0.0271	2.1197	2.7372	4.8995
HPSO-QN SLSM	0.8393	0.9980	11,961.5283	0.0289	0.0316	2.5762	1.4984	3.9044
HPSO-QN MLSM	0.8151	0.8974	11,265.7222	0.0287	0.0332	1.6844	1.7908	2.4341

offer a comparison of the proposed methods based on the average identified parameters across five independent runs. The HPSO-QN MLSM method achieved the lowest $Fcost$ value of $2.4341\times {10}^{-6}$, indicating its effectiveness in accurately estimating the mechanical parameters of the 2MM system. When comparing the average parameters obtained from HPSO-QN SM with those obtained from SPSO, the percentage difference for $J_{1n}$ is around 15.77%, while for $J_{2n}$, it is around 15.10%. The percentage difference obtained for $K_n$ is around 15.22%, and for $C_{1n}$ and $C_{2n}$, they are 33.54% and 5.86%, respectively. As for $B_{1n}$ and $B_{2n}$, the percentage differences are 18.33% and 9.97%, respectively. Regarding $Fcost$, the percentage difference obtained is 31.41% lower compared to SPSO.

When comparing HPSO-QN SLSM with HPSO-QN SM, percentage differences were around 20.01% for $J_{1n}$, 10.90% for $J_{2n}$, and 14.78% for $K_n$. The friction coefficients ($C_{1n}$, $C_{2n}$, $B_{1n}$, and $B_{2n}$) estimated by HPSO-QN SLSM showed percentage differences ranging from 20% to 45% compared to HPSO-QN SM. The percentage difference in $Fcost$ between HPSO-QN SM and HPSO-QN SLSM was around 20.31%, with HPSO-QN SLSM providing a lower value. Comparing HPSO-QN MLSM with HPSO-QN SLSM, the percentage differences obtained for $J_{1n}$, $J_{2n}$, and $K_n$ were 2.88%, 10.08%, and 5.82%, respectively. For the friction coefficients ($C_{1n}$ and $C_{2n}$), the average parameter differences between HPSO-QN MLSM and HPSO-QN SLSM were 0.69% and 5.06%, respectively. The average differences for $B_{1n}$ and $B_{2n}$ were 34.62% and 19.51%, respectively. The average $Fcost$ estimated by HPSO-QN MLSM was 37.66% lower than that estimated by HPSO-QN SLSM. Finally, comparing the average parameters obtained from HPSO-QN MLSM to the SPSO method, HPSO-QN MLSM achieved a significant improvement in $Fcost$, with a decrease of 63.92%. The percentage differences obtained for $J_{1n}$ and $J_{2n}$ were around 34.57% and 31.98%, respectively. For $K_n$, the percentage difference obtained was approximately 31.95%. The percentage differences obtained for $C_{1n}$ and $C_{2n}$ were 81.65% and 29.69%, respectively. For $B_{1n}$ and $B_{2n}$, the percentage differences obtained were 35.10% and 41.10%, respectively. These results suggest that HPSO-QN MLSM outperforms SPSO in identifying the 2MM parameters and minimizing $Fcost$.

Table 6. Performance comparison of the proposed method: absolute percentage error comparison of estimated and actual parameters.

PSO Methods	${\mathit{J}}_{1\mathit{n}}$ (%)	${\mathit{J}}_{2\mathit{n}}$ (%)	${\mathit{K}}_{\mathit{n}}$ (%)	${\mathit{C}}_{1\mathit{n}}$ (%)	${\mathit{C}}_{2\mathit{n}}$ (%)	${\mathit{B}}_{1\mathit{n}}$ (%)	${\mathit{B}}_{2\mathit{n}}$ (%)
SPSO	42.95	69.13	52.13	48.03	5.73	25.02	53.21
HPSO-QN SM	20.40	43.62	28.98	30.59	0.18	2.11	37.93
HPSO-QN SLSM	3.68	27.95	9.92	4.93	16.82	24.10	24.50
HPSO-QN MLSM	6.46	15.05	3.53	5.59	22.74	18.86	9.76

presents the accuracy of the estimated parameters compared to the benchmark parameters, measured by the absolute percentage error (APE). The APE is used as a measure of the deviation between the estimated and benchmark parameters, and it is defined as

$$APE=\frac{|Estimated-Benchmark|}{Benchmark}\times 100$$

(24)

The HPSO-QN SM method shows the lowest error for $C_{2n}$ (APE of 0.18%) and performs well for $B_{1n}$ (APE of 2.11%). The HPSO-QN SLSM method exhibits the lowest error for $J_{1n}$ (APE of 3.68%) and performs well for $C_{1n}$ (APE of 4.93%). In terms of motor-side and load-side inertias ($J_{1n}$ and $J_{2n}$) and shaft stiffness ($K_n$), the HPSO-QN MLSM method achieves the lowest error, with APE values ranging from 3.53% to 15.05%. Additionally, it performs well for $B_{2n}$ with an APE of 9.76%.

These results highlight the effectiveness of the HPSO-QN method in accurately identifying mechanical parameters, providing more reliable results compared to other methods. However, it is important to note that there is still a significant discrepancy between the estimated and actual values for the friction coefficients. This discrepancy may be attributed to factors such as measurement noise and the potential variability of these coefficients over time. Despite this limitation, the HPSO-QN method yields lower errors for the friction coefficients compared to the SPSO method.

The convergence of the proposed methods is demonstrated in Figure 4, showing the $Fcost$ versus the number of iterations for each algorithm. The plot highlights the effectiveness of the implemented switching criteria and particle selection in the hybrid method. Compared to the SPSO algorithm, which often gets trapped in the local optima, the HPSO-QN methods demonstrate faster convergence to a low-cost function in the initial stages and continue to search within that region. Moreover, the SPSO algorithm demonstrates a slower convergence speed when compared to the HPSO-QN methods.

Figure 5 compares the $Fcost$ of solutions obtained using the Hybrid PSO-QN MLSM optimization process for both exploration and exploitation processes. This graph demonstrates the effect of both methods at each iteration. It is evident that the QN method aids in escaping from the local optima and finding superior solutions during both exploration and exploitation phases, while the PSO method tends to remain stable in the optimum for a period of iterations.

The accuracy of the estimated speeds was evaluated using performance measures, such as the $IAE$, $ISE$, and $ITAE$ metrics as shown in Figure 6. These metrics provide a quantitative measure of the difference between simulated and experimental speed responses. The $IAE$, $ISE$, and $ITAE$ are defined as

$$IAE={\int }_{T_0}^{T_f}\left|e\left(t\right)\right|dt$$

(25)

$$ISE={\int }_{T_0}^{T_f}{e}^2\left(t\right)dt$$

(26)

$$ITAE={\int }_{T_0}^{T_f}t\left|e\left(t\right)\right|dt$$

(27)

The error $e\left(t\right)$ between the estimated and measured motor speeds is given by ${\Omega }_1\left(t\right)-{\widehat{\Omega }}_2\left(t\right)$, and the error between the estimated and measured load speeds is ${\Omega }_2\left(t\right)-{\widehat{\Omega }}_2\left(t\right)$. The performance of the estimated model in accurately capturing the speed responses is indicated by smaller values of these measures.

The plot indicates that the hybrid PSO-QN MLSM method achieved lower error values compared to SPSO. This demonstrates a higher degree of precision and a significant reduction in error using the hybrid PSO-QN MLSM method. The comparison highlights the accuracy and effectiveness of the hybrid PSO algorithm in estimating the mechanical parameters of the 2MM system.

Figure 7 compares the simulation results of the motor and load speeds obtained from the algorithm with the lowest $Fcost$ value to the corresponding experimental measurements for the same excitation signals. It can be observed that the speed responses of the estimated model match the measured speed.

Finally,

Table 7. Computation time for the proposed methods.

PSO Methods	Time (minutes)
SPSO	30.22
HPSO-QN SM	161.31
HPSO-QN SLSM	175.65
HPSO-QN MLSM	468.59

presents the computation time for the PSO algorithm and its variants. The HPSO-QN SM method has a longer computation time compared to SPSO due to the QN process at each PSO iteration. The HPSO-QN SLSM method introduces a stopping criterion to enhance the search for an optimal region, which increases the computation time but improves the parameter quality and performance compared to SLSM and SPSO. The HPSO-QN MLSM method selects multiple particles for QN local search, resulting in increased computation time. However, it provides optimal and consistent parameters with the lowest $Fcost$ values, indicating superior performance. Therefore, HPSO-QN MLSM is a promising approach for accurate and consistent parameter identification.

6. Conclusions

In this study, a hybrid optimization method called HPSO-QN was proposed to accurately identify the mechanical parameters of flexible 2MM drive systems using PSO methods. The research consisted of the following key aspects:

• Literature review: A comprehensive review of existing methods for parameter identification in two-mass drive systems was conducted to establish the background for the proposed research.
• System modeling and control: An accurate dynamic model of the two-mass drive system was developed, and a hysteresis current controller was implemented to aid in the mechanical identification process.
• Hybrid optimization method: The proposed hybrid PSO method, known as HPSO-QN, was implemented to identify the mechanical parameters of the 2MM drive system. Its effectiveness was evaluated using experimental data, and the HPSO-QN MLSM method exhibited the best performance in terms of accuracy and efficiency.

The following conclusions can be drawn from the results:

• The HPSO-QN MLSM method achieved the lowest cost function value of $2.32\times {10}^{-6}$ with five independent runs.
• The standard deviation values demonstrated the robustness of the HPSO-QN methods, with the HPSO-QN MLSM method having the lowest values for most parameters. The motor-side Coulomb friction parameter showed the lowest standard deviation of 0.0028 among all identified parameters.
• Comparing the proposed methods, the HPSO-QN MLSM method proved to be the most effective in terms of $Fcost$, indicating its accuracy in parameter estimation. The HPSO-QN SM method achieved the lowest cost function value of 0.18% for load-side Coulomb friction.
• The absolute percentage error (APE) values indicated that the HPSO-QN methods, particularly MLSM, exhibited low errors in estimating mechanical parameters and friction coefficients compared to the standard method.

Possible future directions include the following:

• Exploring more realistic friction models, such as the Dahl and LuGre models, to improve the estimation of viscous friction coefficients with higher APE values.
• Applying the HPSO-QN method for parameter estimation in other dynamic systems, such as battery and supercapacitor models. This could help in improving the accuracy of models used in energy systems and electric vehicles.
• Evaluating the impact of the HPSO-QN methods on the performance of control systems in real-world applications, such as robotics and automotive systems.
• Extending the HPSO-QN method to incorporate global optimization techniques, specifically multi-objective optimization, to optimize multiple objectives simultaneously.
• Extending the HPSO-QN method to estimate parameters in more complex systems, such as three-mass model systems, to capture additional dynamics.
• Utilizing the HPSO-QN method in problems of machine learning and deep learning, where high-dimensional parameter space is prevalent, which could enhance the efficiency of hyperparameter tuning.
• Investigating the potential of integrating deep learning methods with the HPSO-QN approach to enhance parameter estimation accuracy and developing hybrid models that combine data-driven and physics-based approaches.

In conclusion, the proposed HPSO-QN methods offer a promising solution for accurately estimating the mechanical parameters of 2MM systems, providing reliable and consistent results compared to other methods. Moreover, the general optimization capabilities of the HPSO-QN method indicate its potential applicability in a wide range of fields beyond mechanical systems, including energy systems, machine learning, and more. The results of this study demonstrate the effectiveness of this method in improving simulation models and optimizing control systems.