Identification of Mechanical Parameters in Flexible Drive Systems Using Hybrid Particle Swarm Optimization Based on the Quasi-Newton Method
Abstract
:1. Introduction
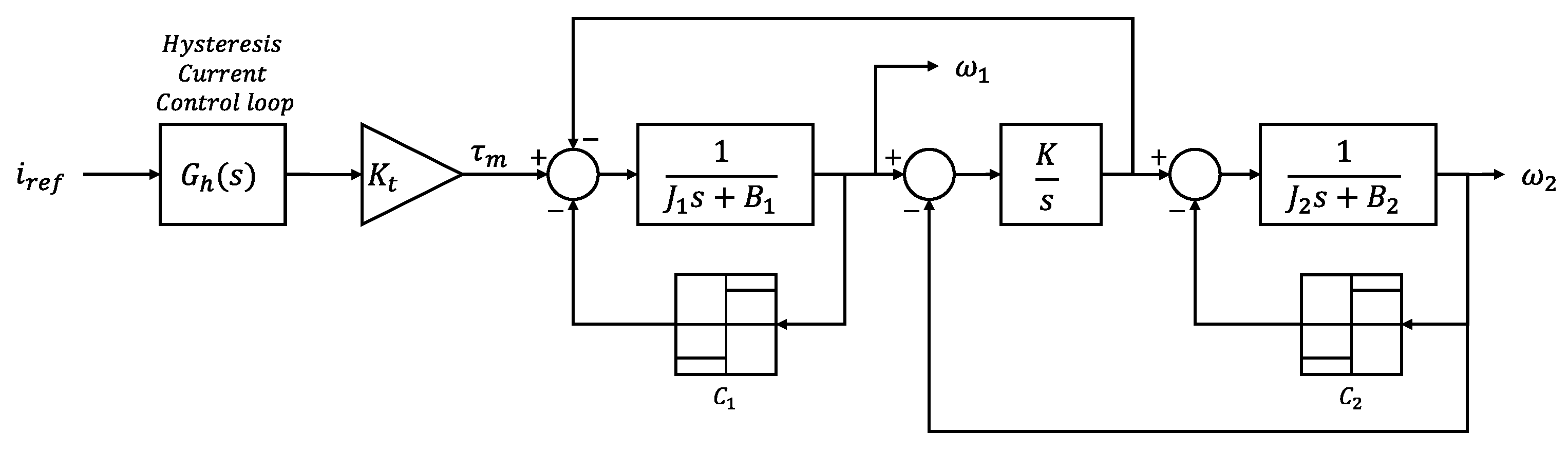
2. System Modeling
3. Proposed Identification Methods
3.1. Excitation Signal
3.2. Cost Function
3.3. Particle Swarm Optimization
3.3.1. Linearly Decreasing Inertia Weight
3.3.2. Constriction Factor
| Algorithm 1 SPSO. |
| Require: N, , , , , , , , and 1: Set , randomly initialize particles’ positions and velocities 2: for each particle do 3: Set , 4: end for 5: repeat 6: set 7: for each particle do 8: Evaluate using Equation (8) 9: if then 10: 11: end if 12: if then 13: 14: end if 16: end for 17: until SPSO termination criterion is satisfied |
3.4. Quasi-Newton Method
| Algorithm 2 QN (BFGS). |
| Require: Given starting point , convergence tolerance 1: set , 2: while
do 3: Compute search direction, 4: Compute next solution, using line search 5: Define , 6: Compute using Equation (15) 7: set . 8: end while |
3.5. Proposed Hybrid Methods
- HPSO-QN Sequential Method: PSO finds the solution, which is then improved by QN.
- HPSO-QN Single Local Search Method: PSO uses a stopping criterion to find the solution, which is then refined by the QN method.
- HPSO-QN Multi Local Search Method: SPSO is used until a stopping criterion is met, then a percentage of the best particles are selected and improved using the QN method.
3.5.1. HPSO-QN Sequential Method
| Algorithm 3 HPSO-QN Sequential Method. |
| Require: , , , , , , , , and 1: Set , randomly initialize particles’ positions and velocities 2: repeat 3: set . 4: for each particle do 5: Evaluate using Equation (8) 6: Update and as shown in Algorithm 1 8: end for 9: 10: ‘Algorithm’, ‘quasi-newton’) 11: if then 12: end if 13: until the termination criterion is met |
3.5.2. HPSO-QN Single Local Search Method
| Algorithm 4 HPSO-QN single local search method. |
| Require: , , , , , , , , and 1: Set , randomly initialize particles’ positions and velocities 2: repeat 3: set . 4: for each particle do 5: Evaluate using Equation (8) 6: Update and as shown in Algorithm 1 8: end for 9: if then 10: 11: ’Algorithm’, ’quasi-newton’) 12: if then 13: end if 14: end if 15: until the termination criterion is met |
3.5.3. HPSO-QN Multi Local Search Method
| Algorithm 5 HPSO-QN Multi Local Search Method. |
| Require: , , , , , , , , , and 1: Set , randomly initialize particles’ positions and velocities 2: repeat 3: set . 4: for each particle do 5: Evaluate using Equation (8) 6: Update and as shown in Algorithm 1 8: end for 9: Select particles for QN local search 10: for each particle do 11: 12: ‘Algorithm’, ‘quasi-newton’) 13: if then 14: end if 15: end for 16: until the termination criterion is met |
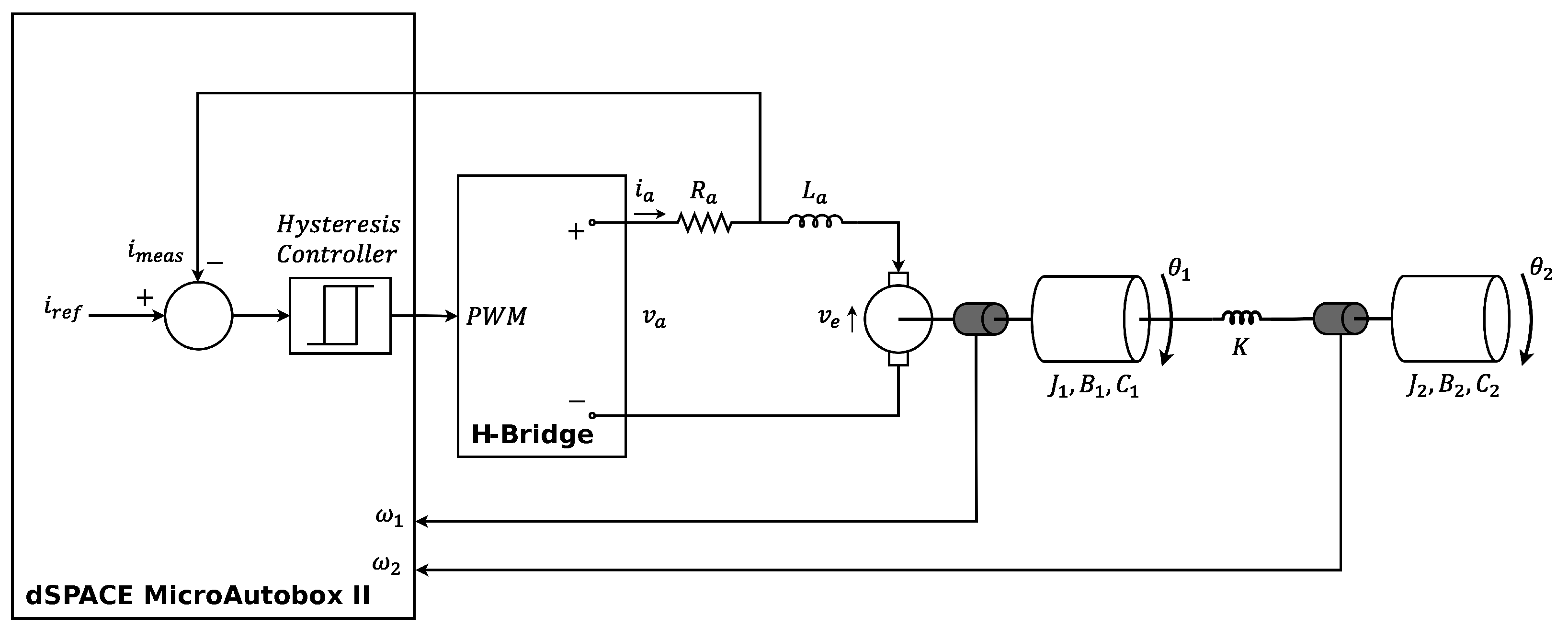
4. Experimental Setup
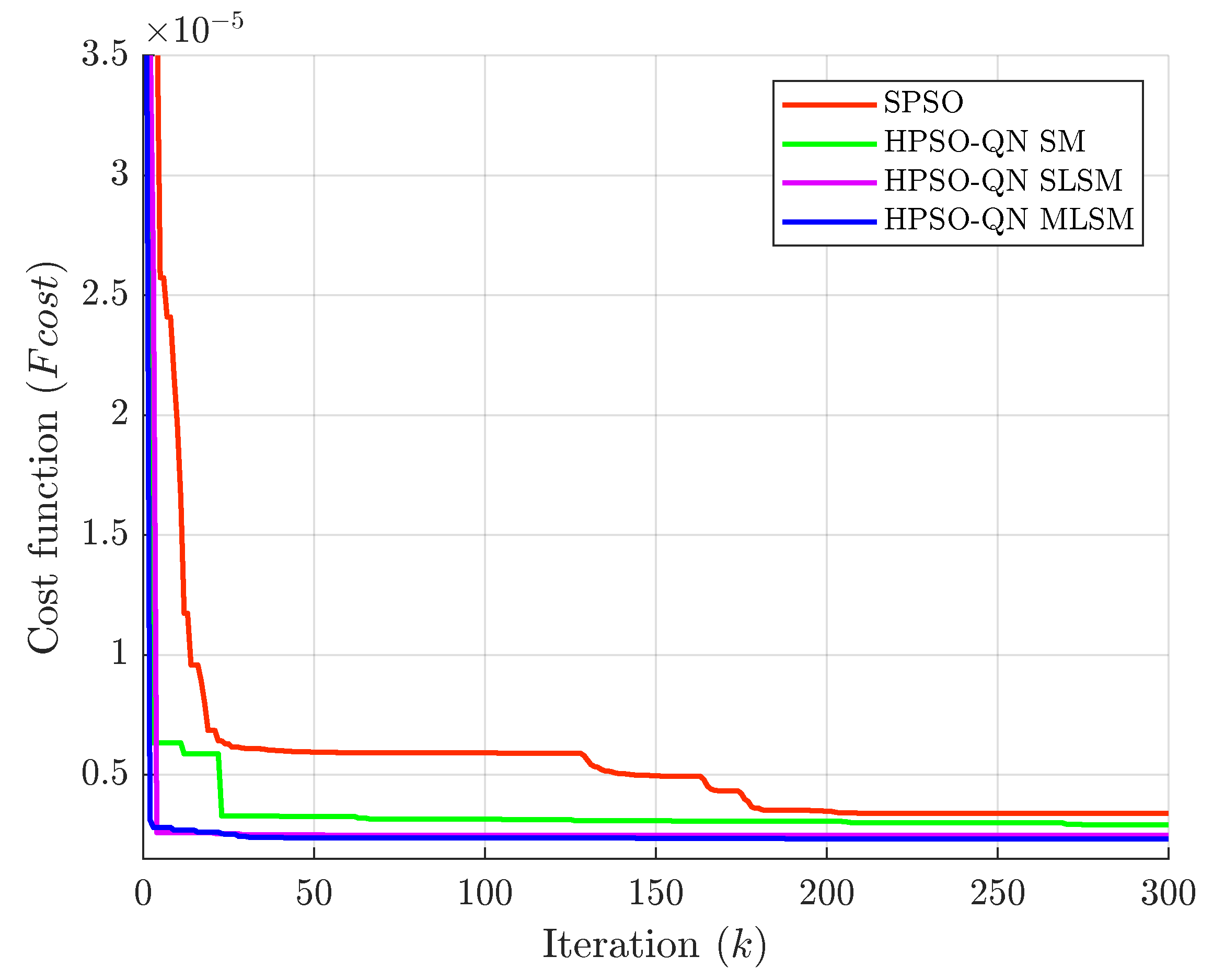
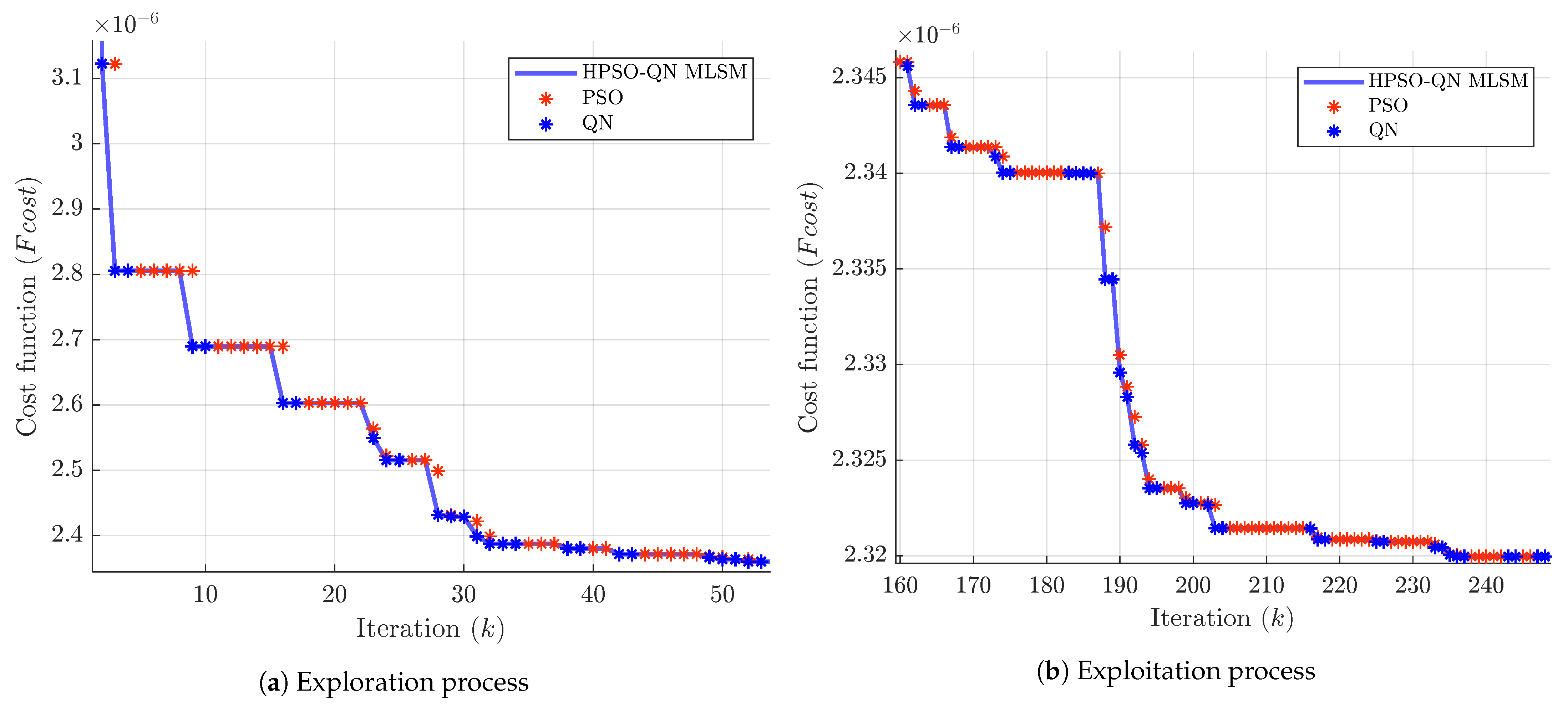
5. Results and Discussion
6. Conclusions
- Literature review: A comprehensive review of existing methods for parameter identification in two-mass drive systems was conducted to establish the background for the proposed research.
- System modeling and control: An accurate dynamic model of the two-mass drive system was developed, and a hysteresis current controller was implemented to aid in the mechanical identification process.
- Hybrid optimization method: The proposed hybrid PSO method, known as HPSO-QN, was implemented to identify the mechanical parameters of the 2MM drive system. Its effectiveness was evaluated using experimental data, and the HPSO-QN MLSM method exhibited the best performance in terms of accuracy and efficiency.
- The HPSO-QN MLSM method achieved the lowest cost function value of with five independent runs.
- The standard deviation values demonstrated the robustness of the HPSO-QN methods, with the HPSO-QN MLSM method having the lowest values for most parameters. The motor-side Coulomb friction parameter showed the lowest standard deviation of 0.0028 among all identified parameters.
- Comparing the proposed methods, the HPSO-QN MLSM method proved to be the most effective in terms of , indicating its accuracy in parameter estimation. The HPSO-QN SM method achieved the lowest cost function value of 0.18% for load-side Coulomb friction.
- The absolute percentage error (APE) values indicated that the HPSO-QN methods, particularly MLSM, exhibited low errors in estimating mechanical parameters and friction coefficients compared to the standard method.
- Exploring more realistic friction models, such as the Dahl and LuGre models, to improve the estimation of viscous friction coefficients with higher APE values.
- Applying the HPSO-QN method for parameter estimation in other dynamic systems, such as battery and supercapacitor models. This could help in improving the accuracy of models used in energy systems and electric vehicles.
- Evaluating the impact of the HPSO-QN methods on the performance of control systems in real-world applications, such as robotics and automotive systems.
- Extending the HPSO-QN method to incorporate global optimization techniques, specifically multi-objective optimization, to optimize multiple objectives simultaneously.
- Extending the HPSO-QN method to estimate parameters in more complex systems, such as three-mass model systems, to capture additional dynamics.
- Utilizing the HPSO-QN method in problems of machine learning and deep learning, where high-dimensional parameter space is prevalent, which could enhance the efficiency of hyperparameter tuning.
- Investigating the potential of integrating deep learning methods with the HPSO-QN approach to enhance parameter estimation accuracy and developing hybrid models that combine data-driven and physics-based approaches.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| 2MM | Two Mass Model |
| APE | Absolute Percentage Error |
| DC | Direct Current |
| FRF | Frequency Response Function |
| HPSO-QN | Hybrid Particle Swarm Optimization Quasi-Newton |
| IAE | Integral Absolute Error |
| ITAE | Integral Time Absolute Error |
| ISE | Integral Squared Error |
| MLSM | Multi Local Search Method |
| PSO | Particle Swarm Optimization |
| QN | Quasi-Newton |
| SM | Sequential Method |
| SLSM | Single Local Search Method |
| SPSO | Standard Particle Swarm Optimization |
References
- Dhaouadi, R.; Hafez, I. Identification of Shaft Stiffness and Inertias in Flexible Drive Systems. J. Robot. Mechatron. 2023, 35, 212–217. [Google Scholar] [CrossRef]
- Hafez, I.; Dhaouadi, R. Application of Particle Swarm Optimization for the Identification of Two-Mass Electric Drive Systems. In Proceedings of the 2022 8th International Conference on Control, Decision and Information Technologies (CoDIT), Istanbul, Turkey, 17–20 May 2022; Volume 1, pp. 758–763. [Google Scholar] [CrossRef]
- Hafez, I.; Dhaouadi, R. Parameter Identification of DC Motor Drive Systems using Particle Swarm Optimization. In Proceedings of the 2021 International Conference on Engineering and Emerging Technologies (ICEET), Istanbul, Turkey, 27–28 October 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Ke, C.; Wu, A.; Bing, C. Mechanical parameter identification of two-mass drive system based on variable forgetting factor recursive least squares method. Trans. Inst. Meas. Control 2019, 41, 494–503. [Google Scholar] [CrossRef]
- Ozmen Koca, G.; Korkmaz, D. Neural Network Based Control of a Two-Mass Drive System. Int. J. Intell. Syst. Appl. 2019, 7, 92–98. [Google Scholar] [CrossRef]
- Saarakkala, S.E.; Leppinen, T.; Hinkkanen, M.; Luomi, J. Parameter estimation of two-mass mechanical loads in electric drives. In Proceedings of the 2012 12th IEEE International Workshop on Advanced Motion Control (AMC), Sarajevo, Bosnia and Herzegovina, 25–27 March 2012; pp. 1–6. [Google Scholar] [CrossRef]
- Dhaouadi, R.; Kubo, K. Transfer function and parameters identification of a motor drive system using adaptive filtering. In Proceedings of the 4th IEEE International Workshop on Advanced Motion Control—AMC ’96-MIE, Mie, Japan, 18–21 March 1996; Volume 2, pp. 588–593. [Google Scholar] [CrossRef]
- Sadovoy, O.V.; Nazarova, O.S.; Bondarenko, V.I.; Pirozhok, A.V.; Hutsol, T.D.; Nurek, T.; Glowacki, S. Modeling and Research of Electromechanical Systems of Cold Rolling Mills; Traicon: Karnataka, India, 2020; 138p. [Google Scholar]
- Bajpai, R.S.; Goyal, M.; Gupta, R. Modeling and control of variable speed wind turbine using laboratory simulator. J. Renew. Sustain. Energy 2015, 7, 053127. [Google Scholar] [CrossRef]
- Östring, M.; Gunnarsson, S.; Norrlöf, M. Closed-loop identification of an industrial robot containing flexibilities. Control Eng. Pract. 2003, 11, 291–300. [Google Scholar] [CrossRef]
- Valenzuela, M.; Bentley, J.; Lorenz, R. Evaluation of torsional oscillations in paper machine sections. IEEE Trans. Ind. Appl. 2005, 41, 493–501. [Google Scholar] [CrossRef]
- Ryu, H.M.; Kim, S.J.; Sul, S.K.; Kwon, T.S.; Kim, K.S.; Shim, Y.S.; Seok, K.R. Dynamic load simulator for high-speed elevator system. In Proceedings of the Power Conversion Conference—Osaka 2002 (Cat. No. 02TH8579), Osaka, Japan, 2–5 April 2002; Volume 2, pp. 885–889. [Google Scholar] [CrossRef]
- Zhao, S.; Blaabjerg, F.; Wang, H. An Overview of Artificial Intelligence Applications for Power Electronics. IEEE Trans. Power Electron. 2021, 36, 4633–4658. [Google Scholar] [CrossRef]
- Sundaram, K.M.; Hussain, A.; Sanjeevikumar, P.; Holm-Nielsen, J.B.; Kaliappan, V.K.; Santhoshi, B.K. Deep Learning for Fault Diagnostics in Bearings, Insulators, PV Panels, Power Lines, and Electric Vehicle Applications—The State-of-the-Art Approaches. IEEE Access 2021, 9, 41246–41260. [Google Scholar] [CrossRef]
- Mukhamediev, R.I.; Popova, Y.; Kuchin, Y.; Zaitseva, E.; Kalimoldayev, A.; Symagulov, A.; Levashenko, V.; Abdoldina, F.; Gopejenko, V.; Yakunin, K.; et al. Review of Artificial Intelligence and Machine Learning Technologies: Classification, Restrictions, Opportunities and Challenges. Mathematics 2022, 10, 2552. [Google Scholar] [CrossRef]
- Saponara, S.; Elhanashi, A.; Gagliardi, A. Reconstruct fingerprint images using deep learning and sparse autoencoder algorithms. In Real-Time Image Processing and Deep Learning 2021; Kehtarnavaz, N., Carlsohn, M.F., Eds.; International Society for Optics and Photonics, SPIE: Bellingham, DC, USA, 2021; Volume 11736, p. 1173603. [Google Scholar] [CrossRef]
- Venkatesh, G.S.; Steven Gray, W.; Duffaut Espinosa, L.A. Combining Learning and Model Based Multivariable Control. In Proceedings of the 2019 IEEE 58th Conference on Decision and Control (CDC), Nice, France, 11–13 December 2019; pp. 1013–1018. [Google Scholar] [CrossRef]
- Jafari, A.H.; Dhaouadi, R.; Jhemi, A. Nonlinear Friction Estimation in Elastic Drive Systems Using a Dynamic Neural Network-Based Observer. J. Adv. Comput. Intell. Intell. Inform. 2013, 17, 637–646. [Google Scholar] [CrossRef]
- Pham, M.; Gautier, M.; Poignet, P. Accelerometer based identification of mechanical systems. In Proceedings of the 2002 IEEE International Conference on Robotics and Automation (Cat. No. 02CH37292), Washington, DC, USA, 11–15 May 2002; Volume 4, pp. 4293–4298. [Google Scholar] [CrossRef]
- Kara, T.; Eker, I. Experimental nonlinear identification of a two mass system. In Proceedings of the 2003 IEEE Conference on Control Applications, Istanbul, Turkey, 25 June 2003; Volume 1, pp. 66–71. [Google Scholar] [CrossRef]
- Łuczak, D.; Nowopolski, K. Identification of multi-mass mechanical systems in electrical drives. In Proceedings of the 16th International Conference on Mechatronics—Mechatronika 2014, Brno, Czech Republic, 3–5 December 2014; pp. 275–282. [Google Scholar] [CrossRef]
- Petrea, R.A.B.; Oboe, R. A DOB-based Parameter Identification method for Series Elastic Actuators without Load-Side Encoder. In Proceedings of the 2022 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM), Sapporo, Japan, 11–15 July 2022; pp. 1755–1762. [Google Scholar] [CrossRef]
- Villwock, S.; Pacas, M. Application of the Welch-Method for the Identification of Two- and Three-Mass-Systems. IEEE Trans. Ind. Electron. 2008, 55, 457–466. [Google Scholar] [CrossRef]
- Nowopolski, K.; Wicher, B. Parametric identification of electrical drive with complex mechanical structure utilizing Particle Swarm Optimization method. In Proceedings of the 2017 19th European Conference on Power Electronics and Applications (EPE’17 ECCE Europe), Warsaw, Poland, 11–14 September 2017; pp. P.1–P.10. [Google Scholar] [CrossRef]
- Sengupta, S.; Basak, S.; Peters, R.A. Particle Swarm Optimization: A Survey of Historical and Recent Developments with Hybridization Perspectives. Mach. Learn. Knowl. Extr. 2019, 1, 157–191. [Google Scholar] [CrossRef]
- Li, G.; Wang, T.; Chen, Q.; Shao, P.; Xiong, N.; Vasilakos, A. A Survey on Particle Swarm Optimization for Association Rule Mining. Electronics 2022, 11, 3044. [Google Scholar] [CrossRef]
- Robinson, J.; Sinton, S.; Rahmat-Samii, Y. Particle swarm, genetic algorithm, and their hybrids: Optimization of a profiled corrugated horn antenna. In Proceedings of the IEEE Antennas and Propagation Society International Symposium (IEEE Cat. No. 02CH37313), San Antonio, TX, USA, 16–21 June 2002; Volume 1, pp. 314–317. [Google Scholar] [CrossRef]
- Shi, X.; Lu, Y.; Zhou, C.; Lee, H.; Lin, W.; Liang, Y. Hybrid evolutionary algorithms based on PSO and GA. In Proceedings of the 2003 Congress on Evolutionary Computation, Canberra, ACT, Australia, 8–12 December 2003; Volume 4, pp. 2393–2399. [Google Scholar] [CrossRef]
- Yang, B.; Chen, Y.; Zhao, Z. A Hybrid Evolutionary Algorithm by Combination of PSO and GA for Unconstrained and Constrained Optimization Problems. In Proceedings of the 2007 IEEE International Conference on Control and Automation, Guangzhou, China, 30 May–1 June 2007; pp. 166–170. [Google Scholar] [CrossRef]
- Valdez, F.; Melin, P.; Castillo, O. Evolutionary method combining particle swarm optimization and genetic algorithms using fuzzy logic for decision making. In Proceedings of the 2009 IEEE International Conference on Fuzzy Systems, Jeju, Republic of Korea, 20–24 August 2009; pp. 2114–2119. [Google Scholar] [CrossRef]
- Xia, X.; Gui, L.; He, G.; Xie, C.; Wei, B.; Xing, Y.; Wu, R.; Tang, Y. A hybrid optimizer based on firefly algorithm and particle swarm optimization algorithm. J. Comput. Sci. 2018, 26, 488–500. [Google Scholar] [CrossRef]
- Zhao, F.; Zhang, Q.; Yu, D.; Chen, X.; Yang, Y. A Hybrid Algorithm Based on PSO and Simulated Annealing and Its Applications for Partner Selection in Virtual Enterprise. In Advances in Intelligent Computing; Huang, D.S., Zhang, X.P., Huang, G.B., Eds.; Springer: Berlin/Heidelberg, Germany, 2005; pp. 380–389. [Google Scholar]
- Singh, A.; Sharma, A.; Rajput, S.; Bose, A.; Hu, X. An Investigation on Hybrid Particle Swarm Optimization Algorithms for Parameter Optimization of PV Cells. Electronics 2022, 11, 909. [Google Scholar] [CrossRef]
- Xu, L.; Huang, C.; Li, C.; Wang, J.; Liu, H.; Wang, X. Estimation of tool wear and optimization of cutting parameters based on novel ANFIS-PSO method toward intelligent machining. J. Intell. Manuf. 2021, 32, 77–90. [Google Scholar] [CrossRef]
- dos Santos Coelho, L.; Mariani, V.C. Particle Swarm Optimization with Quasi-Newton Local Search for Solving Economic Dispatch Problem. In Proceedings of the 2006 IEEE International Conference on Systems, Man and Cybernetics, Taipei, Taiwan, 8–11 October 2006; Volume 4, pp. 3109–3113. [Google Scholar] [CrossRef]
- Wang, Y.J.; Zhang, J.S.; Zhang, Y.F. A fast hybrid algorithm for global optimization. In Proceedings of the 2005 International Conference on Machine Learning and Cybernetics, Guangzhou, China, 18–21 August 2005; Volume 5, pp. 3030–3035. [Google Scholar] [CrossRef]
- Dhaouadi, R.; Kubo, K.; Tobise, M. Two-degree-of-freedom robust speed controller for high-performance rolling mill drives. IEEE Trans. Ind. Appl. 1993, 29, 919–926. [Google Scholar] [CrossRef]
- Boukhezzar, B.; Siguerdidjane, H. Nonlinear Control of a Variable-Speed Wind Turbine Using a Two-Mass Model. IEEE Trans. Energy Convers. 2011, 26, 149–162. [Google Scholar] [CrossRef]
- Kabziński, J.; Mosiołek, P. Integrated, Multi-Approach, Adaptive Control of Two-Mass Drive with Nonlinear Damping and Stiffness. Energies 2021, 14, 5475. [Google Scholar] [CrossRef]
- Zhou, F. Drive-train torsional vibration suppression of large scale PMSG-based WECS. Prot. Control Mod. Power Syst. 2022, 7, 37. [Google Scholar] [CrossRef]
- LeCun, Y.A.; Bottou, L.; Orr, G.B.; Müller, K.R. Efficient BackProp. In Neural Networks: Tricks of the Trade: Second Edition; Montavon, G., Orr, G.B., Müller, K.R., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 9–48. [Google Scholar] [CrossRef]
- Nocedal, J.; Wright, S.J. Numerical Optimization, 2nd ed.; Springer Series in Operations Research and Financial Engineering; Springer: New York, NY, USA, 2006; Volume XXII, 664p. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar] [CrossRef]
- Kennedy, J. Swarm intelligence. In Handbook of Nature-Inspired and Innovative Computing; Springer: Berlin/Heidelberg, Germany, 2006; pp. 187–219. [Google Scholar]
- Shi, Y.; Eberhart, R. A modified particle swarm optimizer. In Proceedings of the 1998 IEEE International Conference on Evolutionary Computation Proceedings, IEEE World Congress on Computational Intelligence (Cat. No. 98TH8360), Anchorage, AK, USA, 4–9 May 1998; pp. 69–73. [Google Scholar] [CrossRef]
- Eberhart, S.Y. Particle swarm optimization: Developments, applications and resources. In Proceedings of the 2001 Congress on Evolutionary Computation (IEEE Cat. No. 01TH8546), Seoul, Republic of Korea, 27–30 May 2001; Volume 1, pp. 81–86. [Google Scholar] [CrossRef]
- Karaboga, D.; Basturk, B. A powerful and efficient algorithm for numerical function optimization: Artificial bee colony (ABC) algorithm. J. Glob. Optim. 2007, 39, 459–471. [Google Scholar] [CrossRef]
- Bonyadi, M.R.; Michalewicz, Z. Particle Swarm Optimization for Single Objective Continuous Space Problems: A Review. Evol. Comput. 2017, 25, 1–54. [Google Scholar] [CrossRef]
- Yang, X.S.; Deb, S. Cuckoo Search via Lévy flights. In Proceedings of the 2009 World Congress on Nature & Biologically Inspired Computing (NaBIC), Coimbatore, India, 9–11 December 2009; pp. 210–214. [Google Scholar] [CrossRef]
- Shami, T.M.; El-Saleh, A.A.; Alswaitti, M.; Al-Tashi, Q.; Summakieh, M.A.; Mirjalili, S. Particle Swarm Optimization: A Comprehensive Survey. IEEE Access 2022, 10, 10031–10061. [Google Scholar] [CrossRef]
- Yang, X.S.; Deb, S. Multiobjective cuckoo search for design optimization. Comput. Oper. Res. 2013, 40, 1616–1624. [Google Scholar] [CrossRef]
- Shi, Y.; Eberhart, R. Empirical study of particle swarm optimization. In Proceedings of the 1999 Congress on Evolutionary Computation-CEC99 (Cat. No. 99TH8406), Washington, DC, USA, 6–9 July 1999; Volume 3, pp. 1945–1950. [Google Scholar] [CrossRef]
- Clerc, M.; Kennedy, J. The particle swarm—Explosion, stability, and convergence in a multidimensional complex space. IEEE Trans. Evol. Comput. 2002, 6, 58–73. [Google Scholar] [CrossRef]
- Nocedal, J.; Wright, S.J. Fundamentals of unconstrained optimization. In Numerical Optimization; Springer International Publishing: Cham, Switzerland, 2006; pp. 10–29. [Google Scholar]
- Nocedal, J.; Wright, S.J. Quasi-newton methods. In Numerical Optimization; Springer International Publishing: Cham, Switzerland, 2006; pp. 135–163. [Google Scholar]
- Arora, J. Introduction to Optimum Design; Elsevier: Amsterdam, The Netherlands, 2004. [Google Scholar]
- Zhao, S.Z.; Liang, J.J.; Suganthan, P.N.; Tasgetiren, M.F. Dynamic multi-swarm particle swarm optimizer with local search for Large Scale Global Optimization. In Proceedings of the 2008 IEEE Congress on Evolutionary Computation (IEEE World Congress on Computational Intelligence), Hong Kong, China, 1–6 June 2008; pp. 3845–3852. [Google Scholar] [CrossRef]
- MathWorks Inc. MATLAB; MathWorks Inc.: Natick, MA, USA, 2023. [Google Scholar]
- Arora, J.S. 7—More on Linear Programming Methods for Optimum Design. In Introduction to Optimum Design, 2nd ed.; Arora, J.S., Ed.; Academic Press: San Diego, CA, USA, 2004; pp. 259–275. [Google Scholar] [CrossRef]
- Han, F.; Liu, Q. An Improved Hybrid PSO Based on ARPSO and the Quasi-Newton Method. In Advances in Swarm and Computational Intelligence; Tan, Y., Shi, Y., Buarque, F., Gelbukh, A., Das, S., Engelbrecht, A., Eds.; Springer International Publishing: Cham, Switzerland, 2015; pp. 460–467. [Google Scholar]
- Noel, M.M. A new gradient based particle swarm optimization algorithm for accurate computation of global minimum. Appl. Soft Comput. 2012, 12, 353–359. [Google Scholar] [CrossRef]
- Kelly, R.; Llamas, J.; Campa, R. A measurement procedure for viscous and coulomb friction. IEEE Trans. Instrum. Meas. 2000, 49, 857–861. [Google Scholar] [CrossRef]


| Parameter | SI Units | Normalized Units |
|---|---|---|
| Motor Inertia () | kg·m2 | 0.8713 s |
| Load Inertia () | kg·m2 | 0.7799 s |
| Shaft stiffness (K) | 19.4840 N·m/rad | 10,881.9233 p.u. |
| Motor Coulomb Friction () | 0.0182 N·m | 0.0304 p.u. |
| Load Coulomb Friction () | 0.0162 N·m | 0.0271 p.u. |
| Motor Viscous Friction () | N·m/rad·s | 2.0759 p.u. |
| Load Viscous Friction () | N·m/rad·s | 1.9844 p.u. |
| PSO Methods | Parameters | |||||||
|---|---|---|---|---|---|---|---|---|
| (p.u) | (p.u) | (p.u) | (p.u) | |||||
| SPSO | 0.9211 | 1.1142 | 13,323.9963 | 0.0093 | 0.0353 | 1.6971 | 4.5508 | 3.3859 |
| HPSO-QN SM | 0.8642 | 1.0453 | 12,497.3021 | 0.0299 | 0.0261 | 0.7666 | 3.9063 | 2.9167 |
| HPSO-QN SLSM | 0.7718 | 0.8310 | 10,532.9554 | 0.0197 | 0.0303 | 3.6192 | 1.4733 | 2.4787 |
| HPSO-QN MLSM | 0.7987 | 0.8983 | 11,169.0221 | 0.0272 | 0.0325 | 0.3083 | 3.7556 | 2.3200 |
| PSO Methods | Parameters | |||||||
|---|---|---|---|---|---|---|---|---|
| (p.u) | (p.u) | (p.u) | (p.u) | |||||
| SPSO | 0.4199 | 0.3198 | 4356.4730 | 0.0142 | 0.0152 | 1.3070 | 1.6753 | 3.7320 |
| HPSO-QN SM | 0.1714 | 0.2817 | 2137.6343 | 0.0119 | 0.0146 | 0.9651 | 1.0390 | 2.0512 |
| HPSO-QN SLSM | 0.1927 | 0.3636 | 3548.1141 | 0.0171 | 0.0082 | 1.2920 | 1.2398 | 1.2274 |
| HPSO-QN MLSM | 0.0218 | 0.0512 | 461.0188 | 0.0052 | 0.0028 | 1.2008 | 1.4837 | 0.0787 |
| PSO Methods | Parameters | |||||||
|---|---|---|---|---|---|---|---|---|
| (p.u) | (p.u) | (p.u) | (p.u) | |||||
| SPSO | 19.26 | 6.25 | 9.45 | 2.73 | 5.43 | 1.09 | 1.13 | 48.06 |
| HPSO-QN SM | 7.86 | 5.50 | 4.63 | 2.29 | 5.21 | 0.80 | 0.70 | 26.06 |
| HPSO-QN SLSM | 8.84 | 7.10 | 7.70 | 3.29 | 2.92 | 1.06 | 0.83 | 15.60 |
| PSO Methods | Parameters | |||||||
|---|---|---|---|---|---|---|---|---|
| (p.u) | (p.u) | (p.u) | (p.u) | |||||
| SPSO | 1.2457 | 1.3193 | 16,554.7629 | 0.0158 | 0.0256 | 2.5953 | 3.0403 | 7.1430 |
| HPSO-QN SM | 1.0492 | 1.1201 | 14,035.9131 | 0.0211 | 0.0271 | 2.1197 | 2.7372 | 4.8995 |
| HPSO-QN SLSM | 0.8393 | 0.9980 | 11,961.5283 | 0.0289 | 0.0316 | 2.5762 | 1.4984 | 3.9044 |
| HPSO-QN MLSM | 0.8151 | 0.8974 | 11,265.7222 | 0.0287 | 0.0332 | 1.6844 | 1.7908 | 2.4341 |
| PSO Methods | (%) | (%) | (%) | (%) | (%) | (%) | (%) |
|---|---|---|---|---|---|---|---|
| SPSO | 42.95 | 69.13 | 52.13 | 48.03 | 5.73 | 25.02 | 53.21 |
| HPSO-QN SM | 20.40 | 43.62 | 28.98 | 30.59 | 0.18 | 2.11 | 37.93 |
| HPSO-QN SLSM | 3.68 | 27.95 | 9.92 | 4.93 | 16.82 | 24.10 | 24.50 |
| HPSO-QN MLSM | 6.46 | 15.05 | 3.53 | 5.59 | 22.74 | 18.86 | 9.76 |
| PSO Methods | Time (minutes) |
|---|---|
| SPSO | 30.22 |
| HPSO-QN SM | 161.31 |
| HPSO-QN SLSM | 175.65 |
| HPSO-QN MLSM | 468.59 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hafez, I.; Dhaouadi, R. Identification of Mechanical Parameters in Flexible Drive Systems Using Hybrid Particle Swarm Optimization Based on the Quasi-Newton Method. Algorithms 2023, 16, 371. https://doi.org/10.3390/a16080371
Hafez I, Dhaouadi R. Identification of Mechanical Parameters in Flexible Drive Systems Using Hybrid Particle Swarm Optimization Based on the Quasi-Newton Method. Algorithms. 2023; 16(8):371. https://doi.org/10.3390/a16080371
Chicago/Turabian StyleHafez, Ishaq, and Rached Dhaouadi. 2023. "Identification of Mechanical Parameters in Flexible Drive Systems Using Hybrid Particle Swarm Optimization Based on the Quasi-Newton Method" Algorithms 16, no. 8: 371. https://doi.org/10.3390/a16080371
APA StyleHafez, I., & Dhaouadi, R. (2023). Identification of Mechanical Parameters in Flexible Drive Systems Using Hybrid Particle Swarm Optimization Based on the Quasi-Newton Method. Algorithms, 16(8), 371. https://doi.org/10.3390/a16080371






