Entropy and the Kullback–Leibler Divergence for Bayesian Networks: Computational Complexity and Efficient Implementation
Abstract
1. Introduction
- Deriving efficient formulations of Shannon’s entropy and the Kullback–Leibler divergence for Gaussian BNs and conditional linear Gaussian BNs.
- Exploring the computational complexity of both for all common types of BNs.
- Providing step-by-step numeric examples for all computations and all common types of BNs.
- Using asymptotic estimates voids the theoretical properties of many machine learning algorithms: Expectation-Maximisation is not guaranteed to converge [5], for instance.
- The number of samples required to estimate the Kullback–Leibler divergence accurately on the tails of the global distribution of both BNs is also an issue [22], especially when we need to evaluate it repeatedly as part of some machine learning algorithm. The same is true, although to a lesser extent, for Shannon’s entropy as well. In general, the rate of convergence to the true posterior in Monte Carlo particle filters is proportional to the number of variables squared [23].
2. Bayesian Networks
3. Common Distributional Assumptions for Bayesian Networks
3.1. Discrete BNs
- Sum over variables to produce the joint probability table for , which contains cells. The value of each cell is the sum of probabilities.
- Normalise the columns of the joint probability table for over each of the configurations of values of , which involves summing O(l) probabilities and dividing them by their total.
3.2. Gaussian BNs
- Composing the global distribution. We can create an lower triangular matrix from the regression coefficients in the local distributions such that gives after rearranging rows and columns. In particular, we:
- Arrange the nodes of in the (partial) topological ordering induced by , denoted .
- The ith row of (denoted ], i = 1, …, N) is associated with X(i). We compute its elements from the parameters of X(i) | aswhere ] are the rows of that correspond to the parents of X(i). The rows of are filled following the topological ordering of the BN.
- Compute .
- Rearrange the rows and columns of to obtain .
Intuitively, we construct by propagating the node variances along the paths in while combining them with the regression coefficients, which are functions of the correlations between adjacent nodes. As a result, gives after rearranging the rows and columns to follow the original ordering of the nodes.The elements of the mean vector are similarly computed as iterating over the variables in topological order. - Decomposing the global distribution. Conversely, we can derive the matrix from by reordering its rows and columns to follow the topological ordering of the variables in and computing its Cholesky decomposition. Thencontains the regression coefficients in the elements corresponding to (Here is a diagonal matrix with the same diagonal elements as and is the identity matrix.) Finally, we compute the intercepts as by reversing the equations we used to construct above.
3.3. Conditional Linear Gaussian BNs
- Discrete are only allowed to have discrete parents (denoted ), and are assumed to follow a multinomial distribution parameterised with CPTs. We can estimate their parameters in the same way as those in a discrete BN.
- Continuous are allowed to have both discrete and continuous parents (denoted , ). Their local distributions arewhich is equivalent to a mixture of linear regressions against the continuous parents with one component for each configuration of the discrete parents:If has no discrete parents, the mixture reverts to a single linear regression like that in (4). The parameters of these local distributions are usually estimated by maximum likelihood like those in a GBN; we have used hierarchical regressions with random effects in our recent work [38] for this purpose as well. Bayesian and regularised estimators are also an option [5].
3.4. Inference
4. Shannon Entropy and Kullback–Leibler Divergence
4.1. Discrete BNs
- Identify a clique containing both and . Such a clique is guaranteed to exist by the family preservation property [5] (Definition 10.1).
- Compute the marginal distribution of by summing over the remaining variables in the clique.
- is the probability assigned by to given that the variables that are parents of in take value j;
- is the element of the CPT of in .
- Transform into its junction tree.
- Compute the entropy .
- For each node :
- (a)
- Identify , the parents of in .
- (b)
- Obtain the distribution of the variables from the junction tree of , consisting of the probabilities .
- (c)
- Read the from the local distribution of in .
- Use the and the to compute (10).
| e | f | e | f | e | f | e | f | |||||||
| g | g | g | g | |||||||||||
| h | h | h | h | |||||||||||
- 1.
- We identify the parents of each node in :
- 2.
- We construct a junction tree from and we use it to compute the distributions , , and .
a b c d a b e f e f g h - 3.
- We compute the cross-entropy terms for the individual variables in and :which sum up to .
- 4.
- We compute , which matches the value we previously computed from the global distributions.
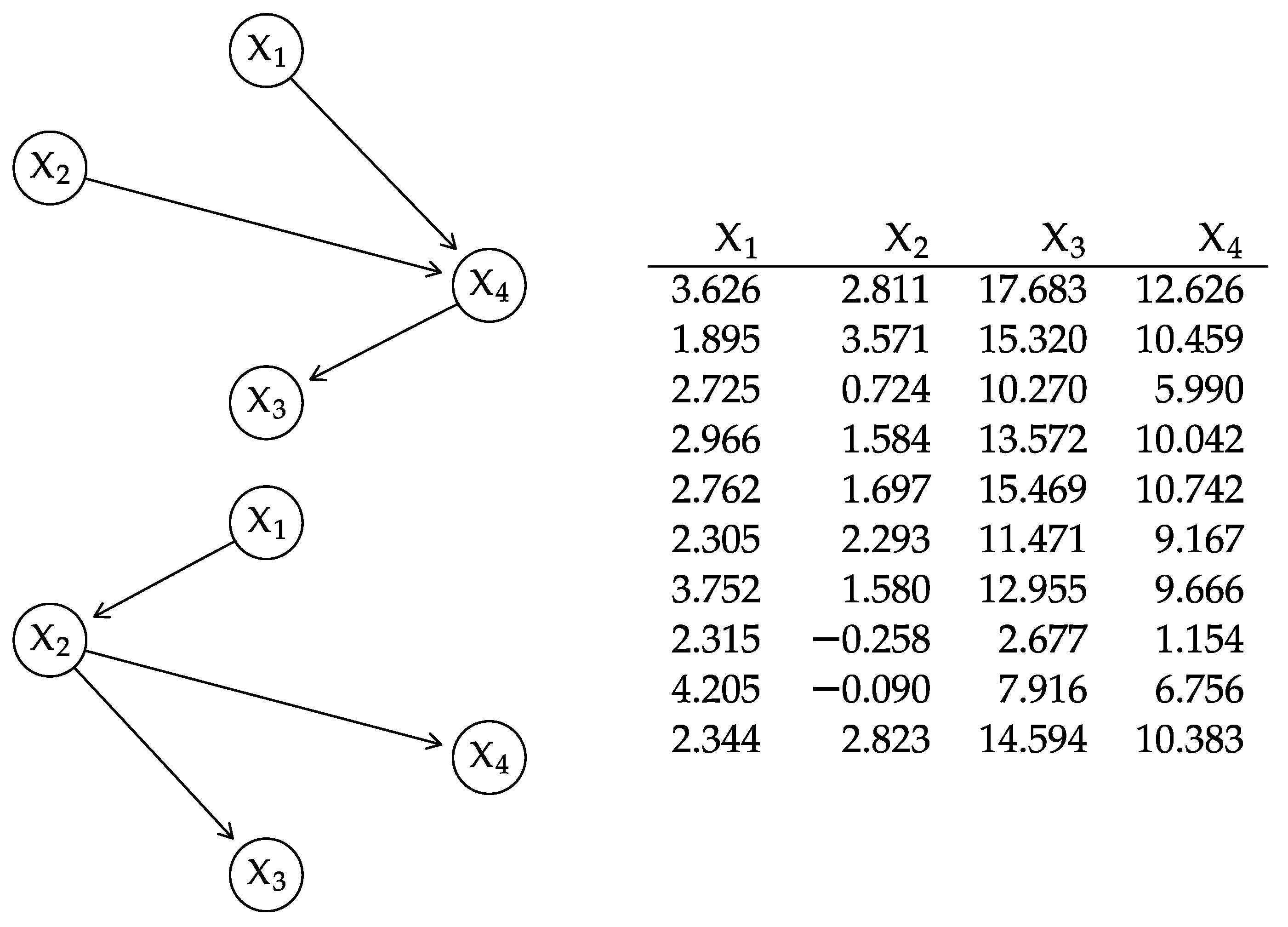
4.2. Gaussian BNs
- Composing the global distribution from the local ones. We avoid computing and , thus reducing this step to complexity.
- Computing the trace . We can reduce the computation of the trace as follows.
- We can replace and in the trace with any reordered matrix [53] (Result 8.17): we choose to use and where is defined as before and is with the rows and columns reordered to match . Formally, this is equivalent to where P is a permutation matrix that imposes the desired node ordering: since both the rows and the columns are permuted in the same way, the diagonal elements of are the same as those of and the trace is unaffected.
- We have .
- As for , we can write where is the lower triangular matrix with the rows re-ordered to match . Note that is not lower triangular unless and have the same partial node ordering, which implies .
- Computing the determinants and . From (13), each determinant can be computed in .
- Computing the quadratic term . Decomposing leads towhere and are the mean vectors re-ordered to match . The computational complexity is still because is available from previous computations.
- , , , are the estimated intercepts and regression coefficients;
- and are the vectorsthe fitted values computed from the data observed for , , ;
- and are the residual variances in and .
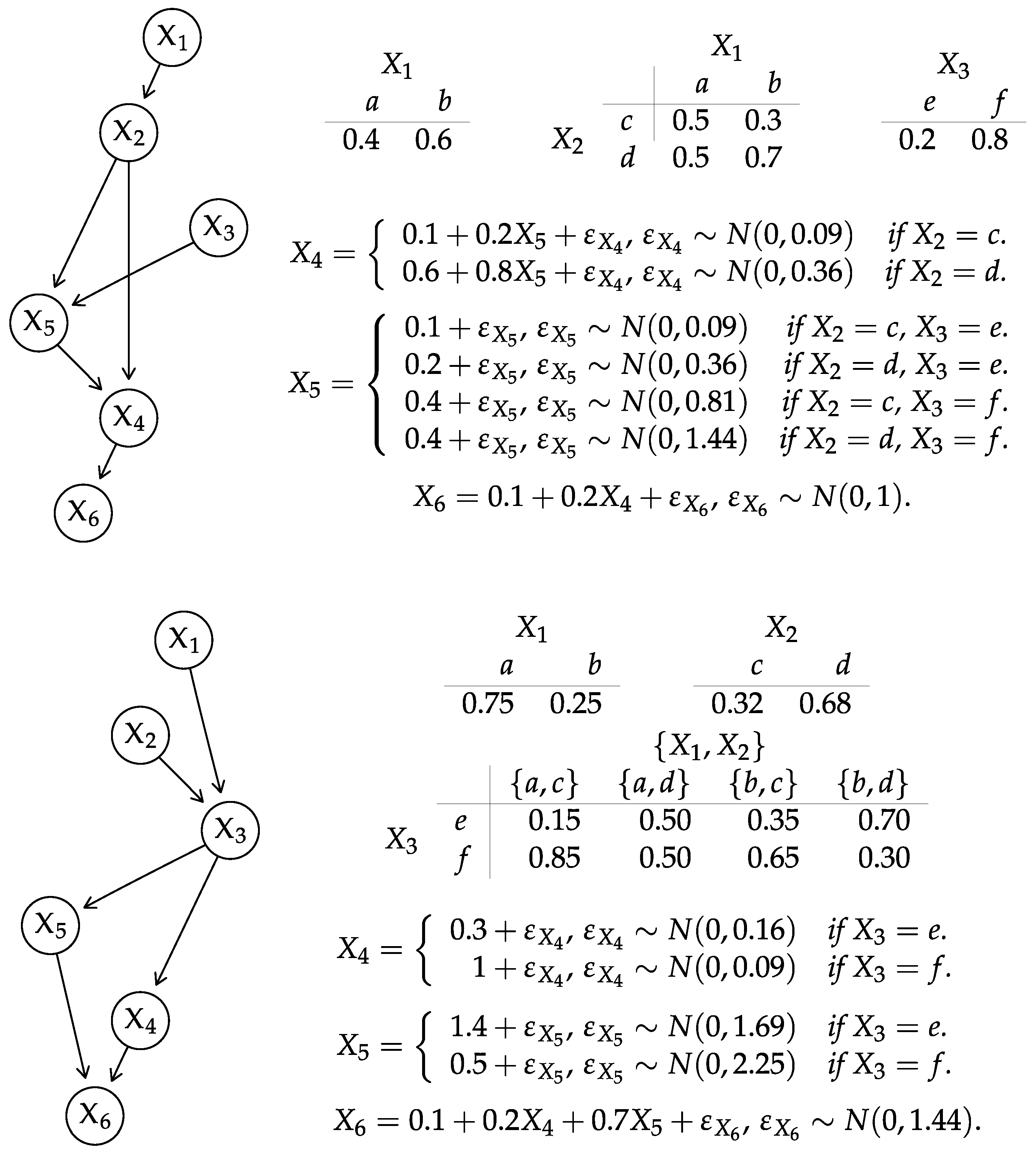
4.3. Conditional Gaussian BNs
- We can reduce to where . In other words, the continuous nodes are conditionally independent on the discrete nodes that are not their parents () given their parents (). The same is true for . The number of distinct terms in the summation in (26) is then given by which will be smaller than in sparse networks.
- The conditional distributions and are multivariate normals (not mixtures). They are also faithful to the subgraphs spanning the continuous nodes , and we can represent them as GBNs whose parameters can be extracted directly from and . Therefore, we can use the results from Section 4.2 to compute their Kullback–Leibler divergences efficiently.
- the maximum clique size w in the subgraph spanning ;
- the number of arcs from discrete nodes to continuous nodes in both and and the overlap between and .
5. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Computational Complexity Results
| Composing and decomposing the global distributions | ||
| discrete BNs | Section 3.1 | |
| GBNs | Section 3.2 | |
| CLGBNs | Section 3.3 | |
| Computing Shannon’s entropy | ||
| discrete BNs | Section 4.1 | |
| O(N) | GBNs | Section 4.2 |
| CLGBNs | Section 4.3 | |
| Computing the Kullback–Leibler divergence | ||
| discrete BNs | Section 4.1 | |
| GBNs | Section 4.2 | |
| CLGBNs | Section 4.3 | |
| Sparse Kullback–Leibler divergence | ||
| GBNs | Section 4.2 | |
| CLGBNs | Section 4.3 | |
| Approximate Kullback–Leibler divergence | ||
| GBNs | Section 4.2 | |
| Efficient empirical Kullback–Leibler divergence | ||
| GBNs | Section 4.2 | |
Appendix B. Additional Examples
| e | f | e | f | e | f | e | f | |||||||
| g | g | g | g | |||||||||||
| h | h | h | h | |||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||
- 1.
- We construct the moral graph of , which contains the same arcs (but undirected) as its DAG plus .
- 2.
- We identify two cliques and and a separator .
- 3.
- We connect them to create the junction tree .
- 4.
- We initialise the cliques with the respective distributions , and .
- 5.
- We compute and .
References
- Scutari, M.; Denis, J.B. Bayesian Networks with Examples in R, 2nd ed.; Chapman & Hall: Boca Raton, FL, USA, 2021. [Google Scholar]
- Castillo, E.; Gutiérrez, J.M.; Hadi, A.S. Expert Systems and Probabilistic Network Models; Springer: Berlin/Heidelberg, Germany, 1997. [Google Scholar]
- Cowell, R.G.; Dawid, A.P.; Lauritzen, S.L.; Spiegelhalter, D.J. Probabilistic Networks and Expert Systems; Springer: Berlin/Heidelberg, Germany, 1999. [Google Scholar]
- Pearl, J. Probabilistic Reasoning in Intelligent Systems: Networks of Plausible Inference; Morgan Kaufmann: Burlington, MA, USA, 1988. [Google Scholar]
- Koller, D.; Friedman, N. Probabilistic Graphical Models: Principles and Techniques; MIT Press: Cambridge, MA, USA, 2009. [Google Scholar]
- Murphy, K.P. Dynamic Bayesian Networks: Representation, Inference and Learning. Ph.D. Thesis, Computer Science Division, UC Berkeley, Berkeley, CA, USA, 2002. [Google Scholar]
- Spirtes, P.; Glymour, C.; Scheines, R. Causation, Prediction, and Search; MIT Press: Cambridge, MA, USA, 2000. [Google Scholar]
- Pearl, J. Causality: Models, Reasoning and Inference, 2nd ed.; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Borsboom, D.; Deserno, M.K.; Rhemtulla, M.; Epskamp, S.; Fried, E.I.; McNally, R.J.; Robinaugh, D.J.; Perugini, M.; Dalege, J.; Costantini, G.; et al. Network Analysis of Multivariate Data in Psychological Science. Nat. Rev. Methods Prim. 2021, 1, 58. [Google Scholar]
- Carapito, R.; Li, R.; Helms, J.; Carapito, C.; Gujja, S.; Rolli, V.; Guimaraes, R.; Malagon-Lopez, J.; Spinnhirny, P.; Lederle, A.; et al. Identification of Driver Genes for Critical Forms of COVID-19 in a Deeply Phenotyped Young Patient Cohort. Sci. Transl. Med. 2021, 14, 1–20. [Google Scholar]
- Requejo-Castro, D.; Giné-Garriga, R.; Pérez-Foguet, A. Data-driven Bayesian Network Modelling to Explore the Relationships Between SDG 6 and the 2030 Agenda. Sci. Total Environ. 2020, 710, 136014. [Google Scholar] [PubMed]
- Zilko, A.A.; Kurowicka, D.; Goverde, R.M.P. Modeling Railway Disruption Lengths with Copula Bayesian Networks. Transp. Res. Part C Emerg. Technol. 2016, 68, 350–368. [Google Scholar]
- Gao, R.X.; Wang, L.; Helu, M.; Teti, R. Big Data Analytics for Smart Factories of the Future. CIRP Ann. 2020, 69, 668–692. [Google Scholar]
- Blei, D.M.; Kucukelbir, A.; McAuliffe, J.D. Variational Inference: A Review for Statisticians. J. Am. Stat. Assoc. 2017, 112, 859–877. [Google Scholar]
- Dempster, A.P.; Laird, N.M.; Rubin, D.B. Maximum Likelihood From Incomplete Data via the EM Algorithm. J. R. Stat. Soc. (Ser. B) 1977, 39, 1–22. [Google Scholar] [CrossRef]
- Minka, T.P. Expectation Propagation for Approximate Bayesian Inference. In Proceedings of the 17th Conference on Uncertainty in Artificial Intelligence (UAI), Seattle, WA, USA, 2–5 August 2001; pp. 362–369. [Google Scholar]
- van der Maaten, L.; Hinton, G. Visualizing Data Using t-SNE. J. Mach. Learn. Res. 2008, 9, 2579–3605. [Google Scholar]
- Becht, E.; McInnes, L.; Healy, J.; Dutertre, C.A.; Kwok, I.W.H.; Ng, L.G.; Ginhoux, F.; Newell, E.W. Dimensionality Reduction for Visualizing Single-Cell Data Using UMAP. Nat. Biotechnol. 2019, 37, 38–44. [Google Scholar] [CrossRef]
- Murphy, K.P. Probabilistic Machine Learning: An Introduction; MIT Press: Cambridge, MA, USA, 2022. [Google Scholar]
- Murphy, K.P. Probabilistic Machine Learning: Advanced Topics; MIT Press: Cambridge, MA, USA, 2023. [Google Scholar]
- Moral, S.; Cano, A.; Gómez-Olmedo, M. Computation of Kullback–Leibler Divergence in Bayesian Networks. Entropy 2021, 23, 1122. [Google Scholar] [CrossRef]
- Hershey, J.R.; Olsen, P.A. Approximating the Kullback Leibler Divergence Between Gaussian Mixture Models. In Proceedings of the 32nd IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Honolulu, HI, USA, 15–20 April 2007; Volume IV, pp. 317–320. [Google Scholar]
- Beskos, A.; Crisan, D.; Jasra, A. On the Stability of Sequential Monte Carlo Methods in High Dimensions. Ann. Appl. Probab. 2014, 24, 1396–1445. [Google Scholar] [CrossRef]
- Scutari, M. Learning Bayesian Networks with the bnlearn R Package. J. Stat. Softw. 2010, 35, 1–22. [Google Scholar] [CrossRef]
- Heckerman, D.; Geiger, D.; Chickering, D.M. Learning Bayesian Networks: The Combination of Knowledge and Statistical Data. Mach. Learn. 1995, 20, 197–243. [Google Scholar] [CrossRef]
- Chickering, D.M.; Heckerman, D. Learning Bayesian Networks is NP-Hard; Technical Report MSR-TR-94-17; Microsoft Corporation: Redmond, WA, USA, 1994. [Google Scholar]
- Chickering, D.M. Learning Bayesian Networks is NP-Complete. In Learning from Data: Artificial Intelligence and Statistics V; Fisher, D., Lenz, H., Eds.; Springer: Berlin/Heidelberg, Germany, 1996; pp. 121–130. [Google Scholar]
- Chickering, D.M.; Heckerman, D.; Meek, C. Large-sample Learning of Bayesian Networks is NP-hard. J. Mach. Learn. Res. 2004, 5, 1287–1330. [Google Scholar]
- Scutari, M.; Vitolo, C.; Tucker, A. Learning Bayesian Networks from Big Data with Greedy Search: Computational Complexity and Efficient Implementation. Stat. Comput. 2019, 25, 1095–1108. [Google Scholar] [CrossRef]
- Cussens, J. Bayesian Network Learning with Cutting Planes. In Proceedings of the 27th Conference on Uncertainty in Artificial Intelligence (UAI), Barcelona, Spain, 14–17 July 2011; pp. 153–160. [Google Scholar]
- Suzuki, J. An Efficient Bayesian Network Structure Learning Strategy. New Gener. Comput. 2017, 35, 105–124. [Google Scholar] [CrossRef]
- Scanagatta, M.; de Campos, C.P.; Corani, G.; Zaffalon, M. Learning Bayesian Networks with Thousands of Variables. Adv. Neural Inf. Process. Syst. (Nips) 2015, 28, 1864–1872. [Google Scholar]
- Hausser, J.; Strimmer, K. Entropy Inference and the James-Stein Estimator, with Application to Nonlinear Gene Association Networks. J. Mach. Learn. Res. 2009, 10, 1469–1484. [Google Scholar]
- Agresti, A. Categorical Data Analysis, 3rd ed.; Wiley: Hoboken, NJ, USA, 2012. [Google Scholar]
- Geiger, D.; Heckerman, D. Learning Gaussian Networks. In Proceedings of the 10th Conference on Uncertainty in Artificial Intelligence (UAI), Seattle, WA, USA, 29–31 July 1994; pp. 235–243. [Google Scholar]
- Pourahmadi, M. Covariance Estimation: The GLM and Regularization Perspectives. Stat. Sci. 2011, 26, 369–387. [Google Scholar]
- Lauritzen, S.L.; Wermuth, N. Graphical Models for Associations between Variables, Some of which are Qualitative and Some Quantitative. Ann. Stat. 1989, 17, 31–57. [Google Scholar] [CrossRef]
- Scutari, M.; Marquis, C.; Azzimonti, L. Using Mixed-Effect Models to Learn Bayesian Networks from Related Data Sets. In Proceedings of the International Conference on Probabilistic Graphical Models, Almería, Spain, 5–7 October 2022; Volume 186, pp. 73–84. [Google Scholar]
- Lauritzen, S.L.; Spiegelhalter, D.J. Local Computation with Probabilities on Graphical Structures and their Application to Expert Systems (with discussion). J. R. Stat. Soc. Ser. B (Stat. Methodol.) 1988, 50, 157–224. [Google Scholar]
- Lauritzen, S.L.; Jensen, F. Stable Local Computation with Conditional Gaussian Distributions. Stat. Comput. 2001, 11, 191–203. [Google Scholar] [CrossRef]
- Cowell, R.G. Local Propagation in Conditional Gaussian Bayesian Networks. J. Mach. Learn. Res. 2005, 6, 1517–1550. [Google Scholar]
- Namasivayam, V.K.; Pathak, A.; Prasanna, V.K. Scalable Parallel Implementation of Bayesian Network to Junction Tree Conversion for Exact Inference. In Proceedings of the 18th International Symposium on Computer Architecture and High Performance Computing, Ouro Preto, Brazil, 17–20 October 2006; pp. 167–176. [Google Scholar]
- Pennock, D.M. Logarithmic Time Parallel Bayesian Inference. In Proceedings of the 14th Conference on Uncertainty in Artificial Intelligence (UAI), Pittsburgh, PA, USA, 31 July–4 August 2023; pp. 431–438. [Google Scholar]
- Namasivayam, V.K.; Prasanna, V.K. Scalable Parallel Implementation of Exact Inference in Bayesian Networks. In Proceedings of the 12th International Conference on Parallel and Distributed Systems (ICPADS), Minneapolis, MN, USA, 12–15 July 2006; pp. 1–8. [Google Scholar]
- Malioutov, D.M.; Johnson, J.K.; Willsky, A.S. Walk-Sums and Belief Propagation in Gaussian Graphical Models. J. Mach. Learn. Res. 2006, 7, 2031–2064. [Google Scholar]
- Cheng, J.; Druzdzel, M.J. AIS-BN: An Adaptive Importance Sampling Algorithm for Evidential Reasoning in Large Bayesian Networks. J. Artif. Intell. Res. 2000, 13, 155–188. [Google Scholar] [CrossRef]
- Yuan, C.; Druzdzel, M.J. An Importance Sampling Algorithm Based on Evidence Pre-Propagation. In Proceedings of the 19th Conference on Uncertainty in Artificial Intelligence (UAI), Acapulco, Mexico, 7–10 August 2003; pp. 624–631. [Google Scholar]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory, 2nd ed.; Wiley: Hoboken, NJ, USA, 2006. [Google Scholar]
- Csiszár, I.; Shields, P. Information Theory and Statistics: A Tutorial; Now Publishers Inc.: Delft, The Netherlands, 2004. [Google Scholar]
- Gómez-Villegas, M.A.; Main, P.; Susi, R. Sensitivity of Gaussian Bayesian Networks to Inaccuracies in Their Parameters. In Proceedings of the 4th European Workshop on Probabilistic Graphical Models (PGM), Cuenca, Spain, 17–19 September 2008; pp. 265–272. [Google Scholar]
- Gómez-Villegas, M.A.; Main, P.; Susi, R. The Effect of Block Parameter Perturbations in Gaussian Bayesian Networks: Sensitivity and Robustness. Inf. Sci. 2013, 222, 439–458. [Google Scholar] [CrossRef]
- Görgen, C.; Leonelli, M. Model-Preserving Sensitivity Analysis for Families of Gaussian Distributions. J. Mach. Learn. Res. 2020, 21, 1–32. [Google Scholar]
- Seber, G.A.F. A Matrix Handbook for Stasticians; Wiley: Hoboken, NJ, USA, 2008. [Google Scholar]
- Stewart, G.W. Matrix Algorithms, Volume I: Basic Decompositions; SIAM: Philadelphia, PA, USA, 1998. [Google Scholar]
- Cavanaugh, J.E. Criteria for Linear Model Selection Based on Kullback’s Symmetric Divergence. Aust. N. Z. J. Stat. 2004, 46, 197–323. [Google Scholar] [CrossRef]
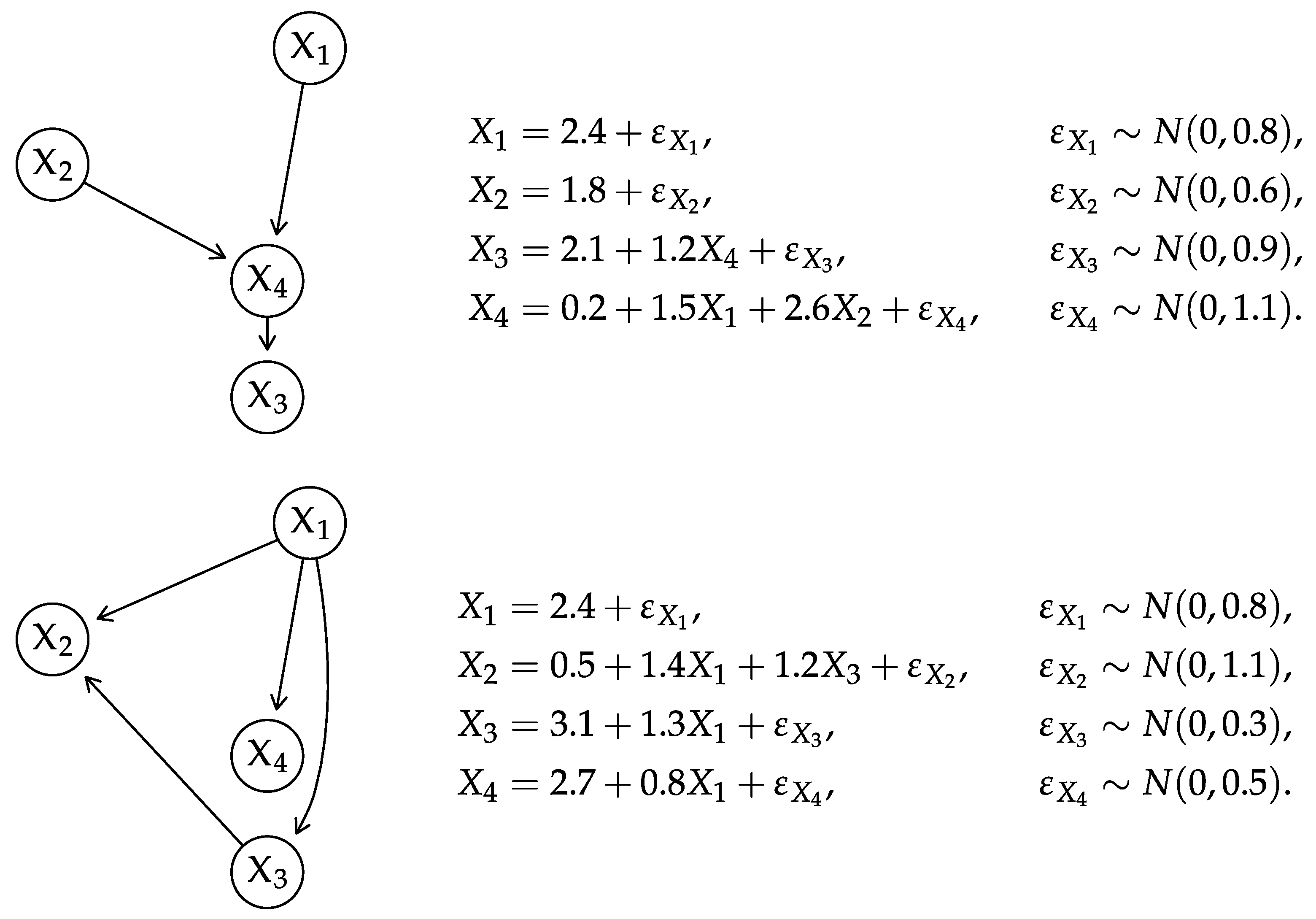
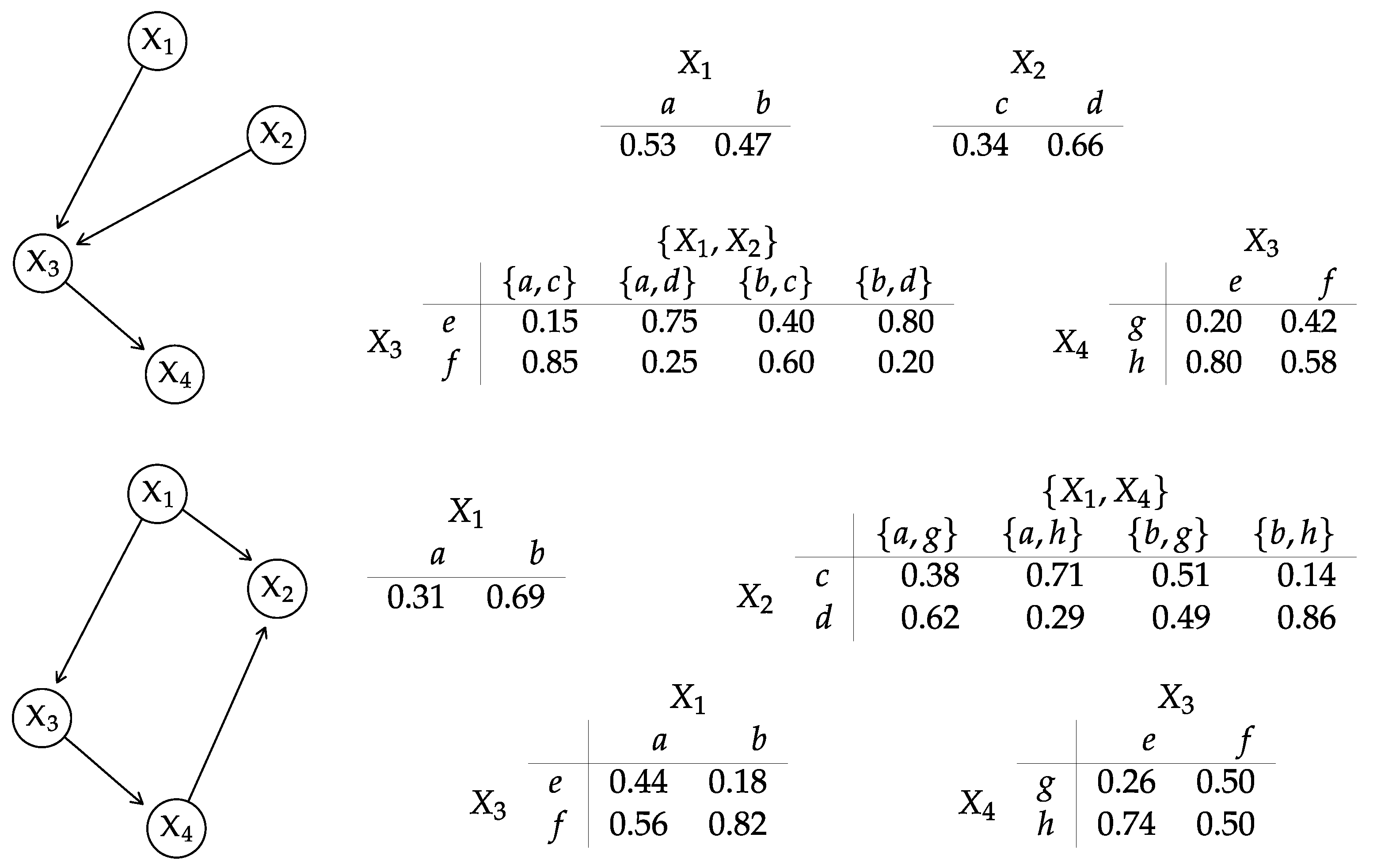
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Scutari, M. Entropy and the Kullback–Leibler Divergence for Bayesian Networks: Computational Complexity and Efficient Implementation. Algorithms 2024, 17, 24. https://doi.org/10.3390/a17010024
Scutari M. Entropy and the Kullback–Leibler Divergence for Bayesian Networks: Computational Complexity and Efficient Implementation. Algorithms. 2024; 17(1):24. https://doi.org/10.3390/a17010024
Chicago/Turabian StyleScutari, Marco. 2024. "Entropy and the Kullback–Leibler Divergence for Bayesian Networks: Computational Complexity and Efficient Implementation" Algorithms 17, no. 1: 24. https://doi.org/10.3390/a17010024
APA StyleScutari, M. (2024). Entropy and the Kullback–Leibler Divergence for Bayesian Networks: Computational Complexity and Efficient Implementation. Algorithms, 17(1), 24. https://doi.org/10.3390/a17010024







