Hybrid Sparrow Search-Exponential Distribution Optimization with Differential Evolution for Parameter Prediction of Solar Photovoltaic Models

Abstract

It is difficult to determine unknown solar cell and photovoltaic (PV) module parameters owing to the nonlinearity of the characteristic current–voltage (I-V) curve. Despite this, precise parameter estimation is necessary due to the substantial effect parameters have on the efficacy of the PV system with respect to current and energy results. The problem’s characteristics make the handling of algorithms susceptible to local optima and resource-intensive processing. To effectively extract PV model parameter values, an improved hybrid Sparrow Search Algorithm (SSA) with Exponential Distribution Optimization (EDO) based on the Differential Evolution (DE) technique and the bound-constraint modification procedure, called ISSAEDO, is presented in this article. The hybrid strategy utilizes EDO to improve global exploration and SSA to effectively explore the solution space, while DE facilitates local search to improve parameter estimations. The proposed method is compared to standard optimization methods using solar PV system data to demonstrate its effectiveness and speed in obtaining PV model parameters such as the single diode model (SDM) and the double diode model (DDM). The results indicate that the hybrid technique is a viable instrument for enhancing solar PV system design and performance analysis because it can predict PV model parameters accurately.

1. Introduction

Due to the pressing necessity of safeguarding the environment against pollution, researchers have been diligently engaged in constructing a diverse range of precise models aimed at generating effective renewable energy (RE) alternatives to conventional fossil fuel-derived energy [1,2]. The utilization of traditional energy sources has led to the emergence of environmental contamination, which stands as a prominent concern within the realm of environmental challenges. The utilization of alternate renewable energy sources has garnered significant attention recently as a potential solution to this problem. The most economically viable sources of renewable energy include wind, solar, tidal, wave, and nuclear power, among others. The aforementioned sources possess a diverse range of applications in practical domains such as photovoltaic (PV) systems, wireless sensors, hot water delivery, and agriculture. Solar power has garnered significant recognition from institutions, governments, and researchers in recent times related to its enduring advantages in generating electricity via PV energy, while avoiding environmental harm, in contrast in the context of the effects of fossil fuels [1,2,3].

PV systems are indispensable to facilitate the worldwide advancement of renewable energy by effectively transforming solar energy into electrical power [4,5]. However, the presence of external elements, such as dust accumulation in the PV grid’s extensive systems, poses challenges to the efficient energy supply of PV systems. Particles in the air, as well as uncertain weather and changing temperatures, have a negative effect on the performance of solar cells, which makes them less efficient overall. To solve these problems, one possible answer is to find accurate PV models that make solar cell energy generation as efficient as possible. To utilize a PV system effectively, at first, current–voltage (I-V) characteristics of the system should be well determined both theoretically and practically, and this requires good mathematical modeling for the system. In the most prevalent iterations, solar PV systems may simply be represented by using a current source paralleled with a diode and two resistors of which one is shunt and the other is connected in series [6].

In the context of PV parallel circuits, the creation of a single-diode model (SDM) involves the combination of a single diode with two resistors as shown in Figure 1. The augmentation of diodes in the PV models leads to an amplification of unidentified parameters, hence resulting in a heightened level of complexity inside the model. In a PV equivalent circuit, SDM encompasses five unidentified characteristics related to PV behavior. Conversely, The double-diode model (DDM) includes seven unidentified parameters, and subsequent models follow a similar pattern, DDM is formed by pairing two diodes, as shown in Figure 2. Diode models integrate a number of variables, including saturation current, series/parallel resistance, shunt-resistant current, and shunt resistor. These parameters are not known and need to be computed and obtained from the data on the I-V characteristic curve. The comprehensive consideration of these components is essential to the effectiveness of solar cell process models, as imprecise estimations of these parameters can lead to substantial discrepancies in the manufacturing process. Consequently, the estimation of these features is a crucial endeavor that enhances the optimization of the PV system. Mathematical models for PV systems frequently use implicit, non-linear, multi-variable, and multi-modal equations [7].

According to the researchers, the resolution of PV models continues to pose a challenging issue. In order to address this, they put forward a number of approaches aimed at extracting, assessing, and simulating PV parameters with the objectives of timeliness, accuracy, and reliability [4,5,8]. In recent decades, multiple attempts have been made to comprehend, optimize, and estimate the PV parameters derived from various mathematical models of PV systems. Numerous approaches have been put out in scholarly works to address and evaluate the intricacy of non-linearities in PV models, aiming to achieve both precision and efficiency. The simplification of equations has been found to have a detrimental impact on the accuracy and effectiveness of the results. A recent study [4] identified a limitation in the ability of this strategy to accurately extract parameters when compared to the I-V characteristic method. The method that relies on I-V characteristic curves aims to reduce the disparities between the current data obtained from experiments and the current data generated through simulations in order to identify the PV system parameters. Through the utilization of this methodology, the parameters can be resolved and discerned through diverse means.

Within the technical literature, there exist three distinct categories of solutions in which I-V curves are utilized for the purpose of extracting and identifying PV parameters. These include analytical methods, numerical procedures, and solutions utilizing meta-heuristic techniques. Several methodologies can be used to extract PV parameters from experimental data obtained from the characteristics of the I-V curve. The utilization of these techniques is characterized by their relative ease of use, requiring only a single iteration of the computation to successfully accomplish the given task.

Analytical solutions for most models can be obtained under Standard Test Conditions (STC) within a specific context through occasional utilization of the Lambert W function [9]. Using the SDM and the DDM, refs. [10,11] developed an analytical method to precisely determine the PV parameters of various silicon solar cells. This method exhibits a high level of precision, with an error rate of less than $10\%$ for the majority of solar cells. Calculations were conducted for identifying the parameters via key points such as maximum power point ($M_{PP}$) ($V_{MP}$, $I_{MP}$) and values resulting from the slops of the measured curves for the short-circuit current Isc and open-circuit voltage $V_{oc}$ points. Using the values of ($V_{MP}$, $I_{MP}$), and $V_{oc}$ points on the I-V characteristic curve, subsequently, the ideality factor n was determined, and the remaining PV parameters were obtained. The analytical approach utilized in study [12] did not consider the effects of series and shunt resistances, although it relied on a comprehensive analysis of many data sheets. Despite the simplicity of this proposed approach, its accuracy is compromised under conditions of low irradiance. Ref. [13] proposed the exclusion of the shunt resistance in various operational scenarios as a method for deriving four PV parameters from the manufacturing data sheet without using all of the characteristics included in the I-V characteristic curve. This lead to a series resistance value that exhibited a non-physically negative characteristic. Ref. [14] extracted the five parameters of the SDM at the STC of irradiance (1000 W/m²) and temperature (25 ${}^{\circ }$C). This was accomplished by implementing the four-parameter model and fitting the I-V curve with a piecewise linear fit procedure, which required identifying the points corresponding to short-circuit and open-circuit conditions. By establishing a correlation between the diode ideality factor (n) and the open-circuit voltage ($V_{oc}$), ref. [15] proposed a method for deriving the equations of the SDM. This method allowed for access to five PV parameters of the SDM under STC. The analytical solutions for determining the PV parameters have demonstrated notable efficacy and expediency, rendering them readily applicable in practical settings. However, there are assumptions, approximations, exclusions, and simplifications. The user’s text does not contain any information to rewrite. The equations of the suggested PV models, derived by analytical methods, have been identified as the primary cause for the low precision and efficiency observed in the extraction of PV parameters [16].

Several research publications have employed numerical methods to extract PV parameters [17]. By utilizing iterative algorithms, these strategies seek to achieve a closer alignment between the simulated and experimental I-V characteristic curves, resulting in more precise results. Researchers often utilize the Newton–Raphson approach as a prevalent process for iteratively solving the exponential model [17]. Similarly, the Levenberg–Marquardt method is utilized for solving the I-V curve [8,17]. Additionally, the Lambert W function can be used to manage the explicit relationship between current and voltage. This argument’s fundamental premise asserts that a suboptimal initial condition may result in convergence and inaccuracy. Initial values are assumed for diode’s forward current $I_s$, reverse saturation current $I_{sh}$, and ideality factor n. Upon successful implementation of the iterative method, the photo-generated current, $I_{ph}$, and the current flowing through the series resistor, $I_s$, are determined. The efficacy of these numerical algorithms is notable in identifying local optima, although their ability to detect global optima presents a significant challenge. However, these strategies necessitate more computational resources and often yield suboptimal parameter values. This phenomenon occurs due to the sensitivity of these methods to the simulated algorithm, as they heavily depend on the original prediction. The phenomenon of the local optimum poses a significant challenge for solution-seeking processes. The utilization of these strategies is limited to the resolution of differential and convex models [5,18].

Several authors have found that the previously described procedures for deriving PV parameters from equivalent circuit models are not the most effective. The meta-heuristic approaches have demonstrated superior performance in the extraction and evaluation of PV parameters, especially when compared to analytical and numerical approaches that rely on strict requirements, assumptions, or initial estimates. In recent years, a variety of meta-heuristic techniques inspired by natural phenomena have been used to determine PV characteristics. The aforementioned algorithms demonstrated greater precision and efficacy than previous methods. For the preponderance of meta-heuristic procedures, the issue of computational time remains a challenge. In addition, the outcome is uncertain due to the probabilistic nature of these approaches. Various optimization strategies have been employed to extract parameters from PV models, including teaching–earning-based optimization, cuckoo search, artificial bee colonies, and particle swarm optimization [5]. Utilizing meta-heuristic techniques that seek to minimize the difference between the deduced current derived from experimental data and simulation data can effectively determine PV parameters. The aforementioned methodologies show advantages in the acquisition and analysis of PV properties. However, there is room for enhancement in terms of computational time efficiency.

Differential Evolution (DE) is a highly regarded evolutionary technique that has been extensively employed to solve numerous optimization problems. The DE technique has been subject to several modifications in order to effectively tackle the challenges associated with parameter extraction in the PV model. In the study conducted in [19], a penalty-based DE technique was introduced. This method aims to identify feasible solutions while simultaneously enhancing the overall quality of the solutions. This strategy has been shown to be effective in terms of both precision and computational efficiency. Ref. [20] developed an adaptive DE technique that integrated changes to the DE technique’s governing parameters based on the fitness value. A more advanced and adaptable DE method was introduced in the study conducted in [21] in order to extract PV parameter values. The authors proposed a strategy for population reduction that involves a dynamic approach and a mechanism for sorting crossover rates. In order to forecast the parameters of solar cells, a multitude of researchers have developed multiple iterations of the successful history-based adaptive differential evolution DE (SHADE) algorithm. Ref. [4] introduced a novel technique known as memetic adaptive differential evolution DE (MADE) in order to improve the precision, convergence speed, and robustness of parameter estimation in the PV model.

In the study conducted in [22], the modified DE method incorporated the Lambert W function and a meta-heuristic step. This approach aimed to identify the optimal mutation factor and crossover parameters for individual I-V characteristics. In recent times, a variety of hybrid strategies have been introduced with the purpose of obtaining the parameters of PV models. Ref. [22] integrated reinforcement learning with DE in the study. The evaluation of the fitness function value occurs primarily during the reduplication process, wherein it serves to calculate the reward for adjusting parameters. Using reinforcement learning techniques, the parameter value is then modified in order to obtain the optimal algorithmic parameters for the provided environmental model. Study [23] proposed the utilization of a gaining–sharing knowledge-based approach (GSK) for the purpose of determining the parameters of a solar PV model. The program demonstrates competitiveness in effectively tackling optimization difficulties by simulating the process of gathering and exchanging information across the entirety of the human life cycle. There are two crucial stages that are necessary. The junior level is characterized by a beginner to intermediate skill level, whereas the senior level is characterized by an intermediate to expert skill level.

1.1. Motivations

Numerous algorithms have been proposed for dealing with the issue of obtaining the parameters of the PV model. However, the task of reliably and accurately determining the values of these parameters remains a significant challenge. The hypothesis known as the “No-Free-Lunch” principle [7,24,25] posits that no individual algorithm possesses the capacity to achieve optimal solutions for all optimization issues, hence potentially offering a sufficient explanation to the posed inquiry. This phenomenon arises as a result of the reality that while a methodology may demonstrate exceptional efficacy in addressing a particular problem, it cannot be guaranteed that it will achieve comparable levels of success in addressing other challenges. Therefore, it is imperative to continue conducting research in order to identify an effective meta-heuristic approach. Numerous creative compositions draw inspiration from the “No-Free-Lunch” notion, a concept that also permits the adaptation of pre-existing algorithms to address novel problem domains.

In this research, a novel strategy called ISSAEDO (Improved Hybrid SSA and EDO with DE technique and bound-constraint adjustment) is proposed for successfully deriving the PV parameter values for multiple PV models, which is discussed in Section 3.

The Exponential Distribution Algorithm (EDO) is a proposed method utilized for the determination of optimal parameters according to an exponential distribution, which is explained in detail in Section 3.2. The exponential distribution is a probability distribution that characterizes the inter-event period in a Poisson process when events transpire continuously and autonomously at a consistent average rate. Exponential distribution is characterized by a sole parameter, denoted as $\lambda$, which represents the rate parameter. In order to maximize exponential distribution, the optimal value for parameter $\lambda$ that corresponds to the dataset under consideration must be determined. Various optimization techniques, such as maximum likelihood estimation (MLE) or least squares optimization, can be employed to accomplish this task.

The MLE method is frequently employed as a means of optimizing exponential distribution. The task at hand is to determine the optimal value of $\lambda$ that maximizes the likelihood function, which is a mathematical function that characterizes the likelihood of witnessing the supplied data given a specific value of $\lambda$. Numerical optimization approaches, such as gradient descent or the Newton–Raphson method, can be employed to carry out this task. An alternative method for optimizing the exponential distribution involves the utilization of least squares optimization. This entails the minimization of the total of the squared discrepancies between the actual data and the anticipated values, assuming an exponential distribution with a specified $\lambda$ value. Numerical optimization algorithms, such as the Levenberg–Marquardt algorithm, can also be employed for this purpose. In general, the proposed EDO demonstrates utility in the context of fitting data to an exponential distribution and determining the optimal parameter value of lambda ($\lambda$).

The suggested EDO algorithm, shown in Section 3.2 incorporates two distinct approaches: exploitation and exploration. To enhance the current solutions, the approach incorporates three fundamental concepts throughout the exploitation phase: the attribute of memorylessness, the utilization of a guiding solution, and the presence of exponential variance among exponential random variables. To emulate the memory-less characteristic, it is assumed that the initial population solely comprised individuals who were successful and attained high levels of fitness. A distinct matrix, known as memory-less, was constructed to retain the newly generated solutions irrespective of their fitness in relation to the winners from the original population. Consequently, the matrix devoid of memory documents the outcomes of various solution types, distinguishing between victors and losers. According to the lower memory property, the history of prior failures is disregarded and not retained, as they are seen to be autonomous and unrelated to the present. Therefore, the individuals who did not succeed can contribute to improving future solutions.

The proposed EDO method possesses several advantages that distinguish it as a helpful instrument for data analysis, setting it apart from the majority of optimization algorithms. These advantages have motivated us to propose its utilization in this study. The EDO method use numerical optimization methods to efficiently determine the ideal parameters for exponential distribution. The EDO technique demonstrates versatility in its ability to handle diverse datasets and effectively represent various event types that adhere to an exponential distribution. Through the identification of the most suitable parameters for exponential distribution, the optimizer is able to effectively represent the inherent probability distribution of the data. This capability holds significant value in the realm of forecasting and anticipating forthcoming occurrences. The EDO is a widely comprehended and user-friendly probability distribution, wherein the parameters of the distribution possess unambiguous interpretations. An illustration of this concept is rate parameter $\lambda$, which signifies the anticipated quantity of occurrences during a given timeframe.

In contrast, the technique known as Sparrow Search Algorithm (SSA) is a distinctive form of swarm intelligence optimization. The bird’s swarm algorithm can be considered a logical extension of the principles obtained from the social interactions and behaviors observed in bird swarms. Sparrows of different species are often known for their sociable nature, which is explained in detail in Section 3.1. The individuals are geographically distributed across many regions worldwide and have a preference for inhabiting areas with human populations. Moreover, many avian species exhibit omnivorous feeding habits, predominantly consuming a diet consisting of weeds or grain seeds. The sparrow population’s foraging and anti-predation habits have been influential in the development of their heightened intelligence and resilient memory, distinguishing them from numerous other avian species of smaller size. The Sparrow Search Algorithm balances exploration and exploitation by incorporating random movements and information sharing among sparrows. This allows the algorithm efficient search for the solution space and convergence towards promising solutions.The algorithm combines both global and local search strategies. Sparrows explore new regions in the search space (global search) while also exploiting promising areas (local search). This balanced approach helps in finding optimal solutions.The algorithm’s simplicity in terms of implementation is an advantage. It does not require complex mathematical operations, making it accessible for both beginners and researchers, and it has fewer control parameters compared to some other optimization algorithms. This can simplify the tuning process and make the algorithm more user friendly.

The ISSAEDO algorithm, which has been recommended, was subjected to evaluation by comparison to several established algorithms across two distinct PV models, namely SDM and DDM. Based on the obtained results, the ISSAEDO algorithm has been identified as a highly competitive meta-heuristic approach. It demonstrates strong performance and competitiveness in terms of escaping local optima and exploring the global optimum.

1.2. Contributions

The study presented a novel EDO algorithm that enhances the derivation of PV parameter values for various PV models using DE and a bound-constraint modification procedure. The primary contributions of this work can be described as follows:

• ISSAEDO is a novel approach proposed to effectively identify the appropriate values for PV model parameters by enhancing the SSA and EDO algorithms using a DE technique and a bound-constraint adjustment procedure, which is defined accurately in Section 3.3.1 and Section 3.3.2.
• The DE technique is used to support diversity in populations and provide a comprehensive examination of the search space, thereby reducing the possibility of the ISSAEDO algorithm parallel to a local optimum.
• In order to establish the adequacy of the proposed ISSAEDO, the appropriate parameter values for two separate PV models, namely the SDM and the DDM, are specified.
• The ISSAEDO algorithm is assessed using recognized and competitive methodologies for the estimation of unknown parameters in PV systems. The results illustrate the strength and accuracy of the ISSAEDO in acquiring the coefficients of PV models.

1.3. Structure

The following section describes the proposed framework for organizing the article’s structure. The mathematical simulation of PV models and the objective function utilized are elucidated in Section 2. In Section 3, the suggested ISSAEDO algorithm provides a concise summary of the core EDO and SSA algorithms, the DE technique, and the bound-constraint modification technique. The results of the experiments are presented in Section 4, accompanied by a thorough analysis of the comparisons made with several established competing methodologies. Furthermore, Section 5 presents visual representations to complement the aforementioned discourse. Lastly, Section 6 presents concluding remarks and discusses potential avenues for future research.

2. PV Model Modeling and Problem Formulation

PV modeling involves the development of mathematical models that accurately depict the behavior of PV systems across different scenarios. The utilization of models enables the examination of PV system performance, the enhancement of system operation, and the advancement of novel PV systems. PV models can be categorized into various classifications.

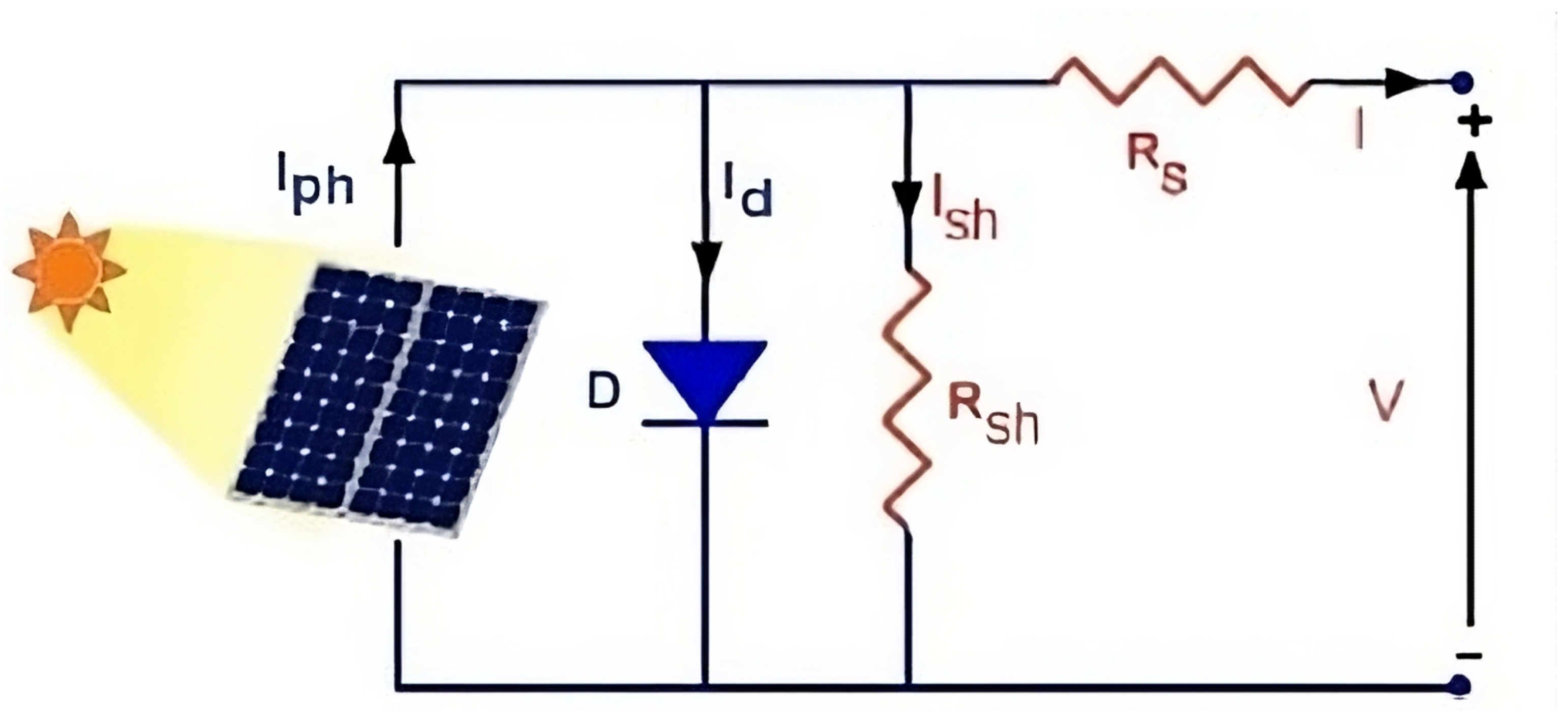
• SDM: The I-V characteristics of a PV cell or module are commonly described by a widely employed and uncomplicated model. The proposed model includes a single diode to represent the current passage through the PV cell or module, joining other elements such as series and shunt resistances.
• DDM: The proposed expansion involves the integration of a second diode through the SDM system, which aims to reduce the negative impacts of recombination losses occurring in the PV cell or module. In various experimental conditions, the model has the capability to generate predictions of the I-V characteristic with enhanced accuracy.
• Analytical models: The behavior of PV systems is described by mathematical formulas in these models. These models can be utilized for the purpose of analyzing and enhancing the operational efficiency of PV systems.
• Empirical models: The models are derived from empirical data and can be utilized for approximating the performance of PV systems. In cases where there is an absence of comprehensive information related to the PV system, these models are commonly used.
• Computational models: Numerical approaches are employed to simulate the behavior of PV systems. These models have the capability of predicting and enhancing the efficiency of PV systems across a variety of situations.

The process of PV modeling involves the identification of the model’s parameters, which can be obtained through the analysis of experimental data. After its construction, the model can be utilized to analyze the efficiency of the PV system influenced by several factors, including temperature, irradiance, and load. Additionally, the models can be used to optimize the efficacy of PV systems. This involves determining the most effective tilt and configuration of solar cells to maximize energy production.

The SDM and the DDM are two circuit models that are frequently employed in the academic field to illustrate the correlation between current (I) and voltage (V) in solar and PV cells. These models are considered congruent in their representation of these cells’ electrical behavior. This section provides a concise overview of the SDM and the DDM in order to demonstrate the I-V characteristics of PV devices. The objective function utilized for determining the parameters of both models is also provided.

2.1. Solar Cells

PV cells, often known as solar cells, are electronic devices designed to convert solar energy into electrical energy. Semiconductor elements, such as silicon, are utilized in the construction of these devices. These materials possess the ability to absorb photons emitted by sunlight, thus liberating electrons and facilitating the flow of electric current. Solar panels are commonly interconnected in both series and parallel configurations to enhance their voltage and electrical output. Solar panels possess a diverse array of applications, encompassing the generation of electricity for both residential and commercial purposes, the provision of power in distant settings, and the facilitation of portable electronic devices such as calculators and mobile phones.

The efficiency and affordability of solar cells are consistently advancing, rendering them an increasingly attractive option for harnessing clean and sustainable energy. Every aspect of the I-V spectrum of a cell or component is represented by equivalent circuit models using a series of sequential functions that are determined based on predefined operational constraints.

2.1.1. SDM Modelling

The SDM is widely regarded as a fundamental circuit model that is frequently employed and constructed based on physical principles [26]. The SDM is widely utilized due to its simplicity in integration and comprehensiveness in characterizing the inherent features of fixed solar cells. The SDM consists of a solitary current source, a solitary diode, a solitary shunt resistor $R_{sh}$, and a solitary series resistor $R_s$, as depicted in Figure 1.

A series resistor is used to offset the voltage loss across the solar cell’s gearbox resistors. The shunt resistor is used to ascertain the influence of leakage current through the p-n diode interface and restrictions, as well as the shunt resistor that develops within the solar cell [27]. The current mathematical expression of the SDM cell is [28]

$$I=I_{ph}-I_d-I_{sh},$$

(1)

$$I_d=I_{sd}\left[exp\left(\frac{V+R_s·I}{\gamma ·V_t}\right)-1\right],$$

(2)

$$V_t=\frac{K·T}{Q},$$

(3)

$$I_{sh}=\frac{V+R_s·I}{R_{sh}},$$

(4)

where $I_{ph}$ is the symbol for the photo-current, $I_d$ is the symbol for the diode current, and $I_{sh}$ is the symbol for the shunt resistor current. Many internal parameters can be altered to improve the output characteristics of the diode, which is fabricated using semiconductor components. The utilization of the SDM equation and Kirchhoff’s law of voltage enables the manipulation of the fundamental parameters of a diode. Symbol $I_{sd}$ indicates the diode’s reverse overload current. Variable V represents the cell’s output voltage. Parameter $\gamma$ represents the intrinsic typical operator of the diode. Lastly, $V_t$ refers to heat conduction voltage. The calculation can be performed using Equation (3). Symbol K represents the Boltzmann constant, which has a value of $1.3806503\times {10}^{-23}$ J/K. Variable T represents the temperature of the junction, measured in Kelvin. Additionally, Symbol Q represents the charge of an electron, which is equal to $1.60217646\times {10}^{-19}$ ${}^{\circ }$C. Consequently, the present value of the cell’s output, denoted as I, may be reformulated utilizing Equations (1)–(4) as stated in work [29].

$$I=I_{ph}-I_{sd}\left[exp\left(\frac{V+R_s·I}{\gamma ·V_t}\right)-1\right]-\frac{V+R_s·I}{R_{sh}}.$$

(5)

The determination of the five unknown parameters ($I_{ph},I_{sd},\gamma ,R_s,R_{sh}$) from the solar cell I-V data is necessary, as given in Equation (5). The choice of suitable parameters has a significant impact on the output and efficacy of a solar cell.

2.1.2. DDM Modelling

One limitation of SDM is its failure to consider the impact of ongoing waste recombination within the reduction zone. In seeking this objective, the researchers introduced the DDM, which is characterized by its ability to calculate the recombination current loss in the depletion region by the incorporation of an extra diode. It is believed that the DDM offers greater precision compared to the SDM [30].

The circuit design that represents the DDM is depicted in Figure 2. In DDM, the photo-produced current source is implemented using a pair of diodes. The diode labeled as $D_1$ is responsible for generating the propagation current within the $p\text{-}n$ junction, while the diode denoted as $D_2$ specifically deals with the consequences of recombination in the region of the junction associated with space freight age, as discussed in [31]. In the domain of direct current (DC) electrical systems, the current output of a cell, denoted as I, can be ascertained by employing the subsequent equation:

$$I=I_{ph}-I_{d_1}-I_{d_2}-I_{sh},$$

(6)

$$I_{d_1}=I_{s{d}_1}\left[exp\left(\frac{V+R_s·I}{{\gamma }_1·V_t}\right)-1\right],$$

(7)

$$I_{d_2}=I_{s{d}_2}\left[exp\left(\frac{V+R_s·I}{{\gamma }_2·V_t}\right)-1\right].$$

(8)

Variables $I_{d_1}$ and $I_{d_2}$ denote the currents flowing through the first and second diodes, respectively. The currents responsible for propagation and saturation effects in diodes $D_1$ and $D_2$ are represented by symbols $I_{s{d}_1}$ and $I_{s{d}_2}$, respectively. The initial and subsequent abstract characteristic operators of diodes $D_1$ and $D_2$, respectively, are denoted as ${\gamma }_1$ and ${\gamma }_2$. Based on the information provided, the current output (I) of the cell as determined by the DDM can be expressed in an alternative formulation.

$$I=I_{ph}-I_{s{d}_1}\left[exp\left(\frac{V+R_s·I}{{\gamma }_1·V_t}\right)-1\right]-I_{s{d}_2}\left[exp\left(\frac{V+R_s·I}{{\gamma }_2·V_t}\right)-1\right]-\frac{V+R_s·I}{R_{sh}}.$$

(9)

As demonstrated in Equation (9), there exist seven unidentified parameters $(I_{ph},I_{s{d}_1},$$I_{s{d}_2},{\gamma }_1,{\gamma }_2,R_s,R_{sh})$ that necessitate estimation through the utilization of the measured I-V data of the solar cell.

2.2. PV Models’ Objective Function

The primary objective of the extraction phase in the determination of coefficients for various PV models using optimization algorithms is to evaluate the effectiveness of each parameter and identify the most optimal value of each parameter for the specific problem being studied. This method aims to minimize the difference between estimated and measured current data by minimizing error as much as feasible. In order to evaluate the proposed coefficients, the objective function must be established and optimized. The objective function is designed to minimize the difference between the estimated and measured current values to the maximum extent possible. The utilization of the root mean squared error (RMSE) as the objective function is the primary focus of this study. The RMSE is a metric used to evaluate the level of dispersion among predicted and measured results [8,28].

$$RMSE\left(\varkappa \right)=\sqrt{\frac{1}{N}\sum _{i=1}^N{\left[f(V_i,I_i,\varkappa )-\widehat{f}(V_i,I_i,\varkappa )\right]}^2}.$$

(10)

In the given context, symbol N represents the measured current, $\varkappa$ denotes the coefficients that are to be differentiated, and $f(V,I,\varkappa )$ represents the error function. In the context of the SDM framework, the error function is formulated as follows:

$$f(V,I,\varkappa )=I_{ph}-I_{sd}\left[exp\left(\frac{V+R_s·I}{\gamma ·V_t}\right)-1\right]-\frac{V+R_s·I}{R_{sh}}-I,$$

(11)

where $\varkappa =[I_{ph},I_{sd},\gamma ,R_s,R_{sh}]$. For the DDM, the error function is presented as

$$f(V,I,\varkappa )=I_{ph}-I_{s{d}_1}\left[exp\left(\frac{V+R_s·I}{{\gamma }_1·V_t}\right)-1\right]-I_{s{d}_2}\left[exp\left(\frac{V+R_s·I}{{\gamma }_2·V_t}\right)-1\right]-\frac{V+R_s·I}{R_{sh}·N_s}-I,$$

(12)

where $\varkappa =[I_{ph},I_{s{d}_1},I_{s{d}_2},{\gamma }_1,{\gamma }_2,R_s,R_{sh}]$. Finally, the algorithm with the lowest RMSE value is considered preferable.

3. Proposed Improved Hybrid SSA with an EDO (ISSAEDO) Algorithm

This section presents a brief summary of the ISSAEDO algorithm. The initial presentation displays the original SSA algorithm. In addition to this, modifications are implemented to the initial iteration of EDO.

3.1. Sparrow Search Algorithm (SSA)

The SSA [32] under consideration is a meta-heuristic optimization approach that draws inspiration from the gathering behavior of sparrows. The SSA is derived from a collective of bird genera known as sparrows, which indicate browsing behavior in their immediate environment. Every sparrow represents a potential solution to an optimization problem. The SSA method simulates the food-seeking behaviors of sparrows in order to identify the optimal solution to an optimization problem. At the initial phase of the procedure, a population of sparrows is generated in a random manner. Each sparrow serves as a representative of a candidate solution to the optimization problem, with its position indicating the specific parameters associated with that solution. The fitness of the sparrows is then evaluated, which is estimated by the desired value of the optimal problem. The program subsequently works through a sequence of iterations wherein the sparrows seek improved solutions by adjusting their position according to a set of principles that simulate sparrow foraging behavior. The following rules are as follows:

• Exploration: In order to discover novel solutions, sparrows execute random examinations of the search space.
• Exploitation: Some sparrows display an ability to implement and modify the most optimal solutions currently available, with the aim of enhancing their performance.
• Memory: Each separate sparrow possesses the ability to identify its own optimal location as well as the most advantageous one identified by the whole group up until that point.
• Learning: Sparrows demonstrate adaptive behavior by changing their space position according to their memory and the optimal position determined by the collective behavior of the swarm.

The sparrow’s position inside the SSA procedure is associated with a prospective resolution to the optimization problem, while its fitness is an indication of the importance of the solution it represents. The system operates by employing a set of equations that represent sparrow searching behavior, wherever the positions of the birds are dynamically modified based on their fitness levels in an attractive manner.

The SSA possesses the benefit of requesting a limited number of parameters and demonstrating a simplicity of implementation. The methodology includes the identification of three key parameters: the population size, the maximum number of repetitions, and the parameters dealing with the Levy flight. By contrast, alternative meta-heuristic methods may require additional parameter modification or a greater number of parameters to be provided. One additional advantage of the SSA method is its demonstrated effectiveness in addressing optimization problems of both continuous and discrete nature. This holds particular significance in actual situations where the characteristics of the optimization problem remain unknown.

A mathematical model can be developed for constructing the SSA, drawing on the previous overview of the sparrows. In order to improve simplicity, the following sparrow behaviors and their corresponding requirements are currently being introduced:

• Designers often perform as very active reserves, providing explorers with access to gathering sites or instruction. Their primary responsibility is to identify regions characterized by significant food resources. The measurement of an individual’s fitness levels is used to evaluate the level of their energy reserves.
• Upon perceiving the presence of an attacker, sparrows immediately initiate a series of chirping expressions, working as an immediate warning signal. In case the alarm boundary exceeds the established safety limits, it is important for the producers to immediately instruct all hunters to relocate to a secure location.
• The potential for a sparrow to change into a producer function is dependent on its ability to actively search for suitable food sources. However, it is important to note that regardless of individual variations, the overall proportion of producers and hunters within the sparrow population remains constant.
• The species of birds demonstrating the most increased energy levels would be classified as producers. Numerous individuals who experience starvation are inclined to travel to different areas to seek food as a means of locating a source of food.
• Scavengers exhibit an ability to leave behind the producer organism that offers the most optimal food resources during their seeking activities. Certain scavengers engage in continuous surveillance of producers and compete for resources, strategically positioning themselves to enhance their own survival rate.
• In response to a perceived threat, sparrows located at the periphery of the group exhibit rapid movement into a designated safe area, thereby assuming a more advantageous position. Conversely, sparrows situated within the core of the group display aimless wandering behavior, likely driven by their desire to maintain proximity to their fellow group members.

The utilization of virtual sparrows in the simulation experiment can be employed as a means to locate food resources. The matrix presented here serves as a visual representation of the spatial distribution of sparrows.

$$X=\left[\begin{array}{ccccc}{x}_{1,1}& x_{1,2}& \dots & \dots & x_{1,d}\\ x_{2,1}& x_{2,2}& \dots & \dots & x_{2,d}\\ ⋮& ⋮& ⋮& ⋮& ⋮\\ x_{n,1}& x_{n,2}& \dots & \dots & x_{n,d}\end{array}\right].$$

(13)

In this context, variable n denotes the quantity of sparrows that are subject to optimization, while variable d reflects the dimension of the variables that are to be enhanced. The vector can be used to represent the fitness value of all sparrows.

$$F_X=\left[\begin{array}{c}f\left(\begin{array}{ccccc}{x}_{1,1}& x_{1,2}& \dots & \dots & x_{1,d}\end{array}\right)\\ f\left(\begin{array}{ccccc}{x}_{2,1}& x_{2,2}& \dots & \dots & x_{2,d}\end{array}\right)\\ \begin{array}{c}⋮⋮⋮⋮⋮\end{array}\\ f\left(\begin{array}{ccccc}{x}_{n,1}& x_{n,2}& \dots & \dots & x_{n,d}\end{array}\right)\end{array}\right].$$

(14)

Variable n represents the quantity of sparrows, whereas each row in matrix $F_X$ corresponds to the fitness value of an individual sparrow. Within the framework of the SSA, producers possessing superior fitness values are accorded primary precedence in the pursuit of sustenance. Moreover, producers assume responsibility for procuring sustenance and overseeing the collective mobility of the populace. Consequently, producers possess the ability to explore a broader range of food sources compared to scroungers. The producer’s location undergoes a change in each iteration, in accordance with Rules (1) and (2).

$$X_{i,j}^{t+1}=\left\{\begin{array}{c}{X}_{i,j}^t\exp \left(\frac{-i}{\alpha {\mathrm{iter}}_{max}}\right)\mathrm{if}{R}_2<ST\hfill \\ X_{i,j}^t+Q·L\mathrm{if}{R}_2\ge ST\hfill \end{array}\right..$$

(15)

We let t denote current iteration. For $j=1,2,\dots ,d$, the value of the jth dimension of the $i^{th}$ sparrow at iteration t is denoted as $X_{i,j}^t$. Variable $ite{r}_{max}$ represents a constant value denoting the maximum number of iterations. Variable $\alpha$ is a random number that belongs to interval $(0,1]$. Variables $R_2$ (where $R_2$ is within the range of [0, 1]) and $ST$ (where $ST$ is within the range of [0.5, 1.0]) denote the alarm value and the safety threshold, respectively. Variable Q is a stochastic quantity that follows a normal distribution. Matrix L is a $1\times d$ matrix in which every member is equal to 1. When the value of $R_2$ is less than $ST$, indicating the absence of predators in the vicinity, the producer transitions into the wide search mode. If condition $R_2\le ST$ is satisfied, it can be inferred that a subset of sparrows is aware of the presence of a predator, necessitating the immediate relocation of all sparrows to alternative secure habitats.

In contrast, individuals classified as scroungers are required to adhere to Rules (4) and (5). As previously said, certain individuals diligently monitor the activities of producers. Upon learning of the producer’s fortuitous discovery of delectable sustenance, individuals opt to relinquish their present positions in order to engage in a competitive pursuit for nourishment. In the event of their victory, they are granted quick access to the sustenance provided by the producer. In the absence of alternative actions, individuals persist in adhering to the established rules (5). The subsequent equation represents the formula for updating the position of the scrounger:

$$X_{i,j}^{t+1}=\left\{\begin{array}{c}Q·\exp \left(\frac{X_{worst}^t-X_{i,j}^t}{j^2}\right)\mathrm{if}j>\frac{n}{2}\hfill \\ X_p^{t+1}+|X_{i,j}^t-X_p^{t+1}|·A^{+}·L\mathrm{otherwise}\hfill \end{array}\right..$$

(16)

We let $X_P$ represent the ideal position occupied by the producer, and we let $X_{worst}$ reflect the current global worst placement. We let A be a matrix of size $1\times d$ where each element is randomly assigned a value of either 1 or $-1$. Matrix $A^{+}$ is defined as the product of the transpose of A and the inverse of the product of A and its transpose, i.e., $A^{+}=A^T{\left(A{A}^T\right)}^{-1}$. When $i>\frac{n}{2}$, it implies that the ith individual with the lowest fitness value is more likely to be experiencing starvation. The sparrows in the simulation experiments, which demonstrate an awareness of the potential hazards, constitute a proportion ranging from $10\%$ to $20\%$ of the overall population. The spatial distribution of these sparrows is generated randomly within the population. The mathematical model can be represented as follows, in accordance with Rule (6).

$$X_{i,j}^{t+1}=\left\{\begin{array}{c}{X}_{best}^t+\beta |X_{i,j}^t-X_{best}^t|\mathrm{if}{f}_i>f_g\hfill \\ X_{i,j}^t+K·\left(\frac{|X_{i,j}^t-X_{best}^t|}{(f_i-f_w)+ϵ}\right)\mathrm{if}{f}_i=f_g\hfill \end{array}\right..$$

(17)

Symbol $X_{best}$ represents the present global ideal location. $beta$ is a random variable that follows a normal distribution with a mean of 0 and a standard deviation of 1. K is a random number that falls within the interval of $[-1,1]$. Variable $f_i$ represents the current sparrow’s fitness level. Variables $f_g$ and $f_w$ represent, correspondingly, the present international greatest and lowest fitness values. Symbol $ϵ$ represents the minimum constant required to prevent division by zero errors. To facilitate comprehension, condition $f_i>f_g$ denotes the sparrow’s position at the periphery of the group. Variable $X_{b}est$ represents the precise coordinates of the population’s central point, which is deemed secure in its immediate vicinity. Equation $f_i=f_g$ indicates that sparrows positioned in the middle of the population are aware of the potential risks and, as a result, must relocate closer to their conspecifics. Symbol K represents the direction in which the sparrow walks and functions as the step size control coefficient. The pseudo-code presented in Algorithm 1 summarizes the fundamental stages of the original SSA, taking into account the model’s idealization and practicability.

Algorithm 1 The original SSA algorithm

Input:   G—the maximum iterations   $PD$—the number of producers   $SD$—the number of scroungers   $R_2$—the alarm value   n—the number of sparrows Output:   $X_{best}$—the comprehensive best position discovered while searching   $f\left(X_{best}\right)$—the comprehensive best fitness discovered, which should be decreased   1: Start   2:     Initializes a population of n sparrows and define their relevant parameters;   3:     Rank the individuals in an ascending order based on their fitness function values $f\left(X\right)$;   4:     while $(t<G)$ do   5:         Rank the fitness values and find the current best individual and the current worst individual;   6:         $R_2\leftarrow$ a random value in [0; 1];   7:         for producer $i=1:PD$ do   8:               upgrade the current producer’s position through Equation (15) to obtain $X_i^{t+1}$;   9:         for sparrow $i=(PD+1):n$ do 10:               upgrade the current sparrow’s position through Equation (16) to obtain $X_i^{t+1}$; 11:         for scrounger $i=1:SD$ do 12:               upgrade the current scrounger’s position through Equation (17) to obtain $X_i^{t+1}$; 13:         $f\left(X_i^{t+1}\right)\leftarrow$ Assess the value of fitness function for $X_i^{t+1}$; 14:        if $f\left(X_i^{t+1}\right)<f(X_i^t$) then ▹ Update the previous position if the present novel position is better than it 15:               $X_i^t\leftarrow X_i^{t+1}$;     $f\left(X_i^t\right)\leftarrow f(X_i^{t+1}$); 16:         Re-arrange the positions ascendingly based on their fitness function values $f\left(X\right)$; 17:         Locate the best position $X_{best}^{t+1}$ and its best fitness value $f\left(X_{best}^{t+1}\right)$ at completion of the present iteration t + 1; 18:         $X_{best}\leftarrow X_{best}^{t+1}$;      $f\left(X_{best}\right)\leftarrow f\left(X_{best}^{t+1}\right)$; 19:         $t\leftarrow t+1$; 20: End

3.2. Exponential Distribution Optimization (EDO) Algorithm

The exponential distribution model provided the basis for inspiration. Exponential distribution is a type of continuous probability distribution that is commonly used to model the time it takes for an event to happen. An algorithm, also referred to as an exponential distribution algorithm, is a set of instructions or a computer program specifically designed to produce random numbers following exponential distribution. Exponential distribution is a commonly employed probability distribution for modeling the time intervals between events that transpire at a consistent rate, in a random and independent manner.

There exist multiple methodologies for generating random numbers that follow exponential distribution. The inverse transform method involves the generation of a random variable, u, that follows a uniform distribution on the interval $[0,1]$. This random variable is subsequently transformed using the inverse cumulative distribution function (CDF) of exponential distribution. The CDF of an exponential distribution can be expressed as follows: $F\left(x\right)=1-{\exp }^{(-\lambda x)}$, where $\lambda$ represents the rate parameter and x denotes the time variable. The inverse of the CDF can be expressed as follows: $F^{-1}\left(u\right)=-log\left(\frac{1-u}{\lambda }\right)$, where u represents a random variable that follows a uniform distribution between 0 and 1. The aforementioned methodology has the potential to be perpetually extended in order to generate a set of random integers that adhere to exponential distribution. There are other methodologies available for generating random numbers that follow exponential distribution. Presented below are a few illustrations of various methodologies.

• Inverse Transform Method: The CDF of an exponential distribution can be mathematically reversed to derive the corresponding quantile function, which serves as the fundamental principle for this approach. The quantile function is a mathematical tool that provides the value of a random variable at which a specified probability is surpassed. The quantile function for the exponential distribution can be expressed as $Q\left(p\right)=-log\left(\frac{1-p}{\lambda }\right)$, where p represents the probability and $\lambda$ denotes the rate parameter. In order to generate a random number from an exponential distribution, the process involves generating a uniform random number, u, that falls within the range of 0 to 1. Subsequently, the inverse quantile function formula is applied to derive the corresponding exponential random variable. The aforementioned methodology has the potential to be extended indefinitely in order to generate a random set of numbers that adhere to exponential distribution.
• Box–Muller Transform: This approach is designed to produce random numbers from a normal distribution, but it can also be used to generate random numbers from exponential distribution.
• Acceptance–Rejection Method: The proposed approach involves the generation of random numbers from a less complex distribution, followed by a decision-making process where these numbers are accepted or rejected based on a comparison with the probability density function (PDF) of the exponential distribution. One commonly chosen alternative for a simpler distribution is uniform distribution.

The selection of these approaches may be influenced by the characteristics of the data and the computational resources at hand, leading to their preference in particular situations. The EDO algorithm operates in the following manner:

• A pair of uniform random numbers $(u_1,u_2)$ is generated between 0 and 1.
• Exponential random variable x can be computed as $x=-log\left(\frac{u_1}{\lambda }\right)$.
• If formula $u_2\le \frac{f\left(x\right)}{M}$ holds, where $f\left(x\right)$ represents the probability density function (PDF) of the exponential distribution and M is a constant such that $\frac{f\left(x\right)}{M}\le 1$ for all values of x, then the value of x can be accepted as a random number generated from exponential distribution. Alternatively, if x does not meet the criteria, it should be discarded and the process should be repeated. The computing cost of the acceptance–rejection approach can be significant, particularly when the ratio of the probability density function (PDF) $\frac{f\left(x\right)}{g\left(x\right)}$ is high, where $g\left(x\right)$ represents the PDF of the less complex distribution. Nevertheless, the utilization of this approach can prove beneficial in cases where the inverse transform method is either inapplicable or presents implementation challenges.
• The Box–Muller transform is a method used to generate a pair of independent standard normal random variables $(Z_1,Z_2)$.
• Exponential random variable x can be computed as x = $-log\left(\frac{u}{\lambda }\right)$, where u = $exp\left(\frac{-z_1}{z_2}\right)$. If $Z_2\le (\lambda -0.5)\times \left(log\left(\frac{x}{\lambda }\right)+\frac{1}{\lambda }\right)$, then x can be accepted as a random number from exponential distribution. In the event that x does not meet the criteria, it is necessary to decline its acceptance and thereafter initiate the process again.

The Box–Muller transform demonstrates computational efficiency; nonetheless, it requires the generation of normal random variables, a task that is comparatively more challenging than generating uniform random variables. The utilization of an EDO is a technique or instrument employed to enhance the characteristics of exponential distribution. Exponential distribution is a commonly employed probability distribution for the purpose of modeling the time intervals between events that transpire at a consistent rate, in a random and independent manner.

Exponential distribution is a probability distribution that characterizes the time intervals between occurrences in a posteriori point process. The tool possesses numerous characteristics that contribute to its effectiveness across a diverse array of applications.

• Memoryless property: The memoryless property of exponential distribution indicates the probability that an event occurring is not influenced by the time passed since the previous event. This characteristic can prove advantageous in depicting situations characterized by random or randomly generated events, where the timing between these events has significance.
• Flexibility: Exponential distribution, being a continuous probability distribution, has the capability to imitate continuous variables. This is advantageous in cases where the optimization problem involves continuous variables, such as in certain machine learning models.
• Simple parameterization: Exponential distribution is characterized by simple parameterization consisting of a single parameter, namely the rate parameter. In specific optimization scenarios, the simplicity of this probability distribution can facilitate its handling when contrasted with more intricate distributions.
• Widely used: Exponential distribution is widely recognized as a prominent probability distribution that enjoys comprehensive comprehension among researchers and practitioners across several academic domains. This suggests that those seeking to implement this concept in their professional endeavors can access a considerable amount of scholarly literature and resources. Certainly, we provide additional advantages of exponential distribution.
• Probability density function: Exponential distribution possesses a readily comprehensible probability density function, rendering it amenable to statistical analysis. This approach can prove advantageous in the pursuit of analytical solutions, particularly in theoretical investigations or the development of novel algorithms.
• Computational efficiency: Exponential distribution is known for its rapid sampling and assessment capabilities, rendering it a valuable tool in simulation research and computational modeling. The inverse transform method is a technique that can be employed to generate samples from exponential distribution with low computational requirements.
• Parameter estimation: The MLE is a straightforward approach utilized to estimate the parameters of exponential distribution based on observed data. The utilization of real-world data believed to be derived from an exponential distribution can be advantageous as it facilitates the estimation of distribution parameters based on the data.
• Relationship to other distributions: Exponential distribution shows close relationships with other probability distributions, such as Gamma distribution and Weibull distribution. Exponential distribution can be utilized as a fundamental element in models that involve complex structures and incorporate several probability distributions.

The proposed EDO utilizes the following methodologies in order to effectively investigate the global optimal search space.

• Initially, a collection of solutions is generated through a random process, encompassing a diverse spectrum of values. The search process can be described as having exponential distributions, which means that the positions of all solutions can be considered as random variables that follow exponential distribution.
• To replicate the memoryless characteristic, a matrix is created and initialized with the identical value as the initial population.
• By employing the exploratory and exploitative phases of the suggested approach, all solutions gradually converge towards the global optimum.
• During the exploitation phase, the memoryless matrix is employed to simulate the memoryless property. This property allows for previously generated solutions, regardless of their past, to serve as influential members in updating new solutions, thereby preserving their established knowledge. Consequently, the responses are categorized into two distinct groups: those deemed as winners and those classified as losers. Furthermore, the utilization of the mean, exponential rate, and variance of the exponential distribution is observed in several contexts. The victorious entity progresses toward the guiding solution in order to explore the global optimum in its vicinity, whereas the defeated entity travels toward the victorious entity.
• In order to enhance the exploration phase, the mean solution and two randomly chosen winners from the initial population are employed for the update process. The average response and variability exhibit significant deviation from the optimal global solution at the outset. The discrepancy between the average response and the universally optimal solution is progressively diminished through the process of optimization until it reaches a minimum value. The switch parameter mentioned above is employed with a probability of 0.5 to determine whether to execute the exploration phase or the exploitation phase.

  $$V_i^{time+1}=\left\{\begin{array}{c}\left\{\begin{array}{c}a·(memoryles{s}_i^{time}-{\sigma }^2)\hfill \\ +b·Xguid{e}^{time},\hfill \\ ifXwinner{s}_i^{time}=memoryles{s}_i^{time}\hfill \\ \\ b·(memoryles{s}_i^{time}-{\sigma }^2)\hfill \\ +log\left(\varphi \right)·Xwinner{s}^{time},otherwise\hfill \end{array}\right.\hfill \\ \\ Xwinner{s}_i^{time}-M^{time}\hfill \\ +(c·Z_1+(1-c)·Z_2),otherwise.\hfill \end{array}\right.$$

  (18)
• After being generated, the perimeter of each newly obtained solution is analyzed. The user’s responses are then stored in a matrix with no memory.
• The original population is updated by including new solutions obtained through the utilization of a greedy method during both exploitation and exploration stages. If the new solution proves to be successful, the original population undergoes updates. In the event that the newly proposed solution demonstrates efficacy, it results in the modification of the original population.
• After the conclusion of the optimization technique, it is observed that all of the solutions converge towards the global optimum solution. The anticipated values for the mean and variance of the optimal solution are expected to be low, while the value of the scale parameter is projected to be high.

Following an overview of the procedures involved in the proposed EDO algorithm as described earlier, Algorithm 2 presents the pseudo-code that delineates the original EDO method.

Algorithm 2 The original EDO algorithm

Input:   N—the population size   $Maxtime$—the maximum time   $lb$—the lower bound   $ub$—the upper bound Output:   $X{winners}_{best}$—the optimal solutions obeying the exponential solution   1: Start   2:     Initialize a population of N solutions representing the multiple Exponential Distribution models $X{winners}_i(i=1,2,\dots ,N)$ using Equation (11);   3:     Define fitness vector to store the fitness of all solutions obeying the Exponential Distribution;   4:     Find the best fitness ($bestfitness$) and $X{winners}_{best}$;   5:     $time=1$;   6:     Construct the memory-less matrix such that $memoryless=Xwinners$;   7:     while $(time<Maxtime)$ do   8:         Define V matrix of size S;   9:         Rank the solutions in $Xwinners$ population in ascending order of their fitness values; 10:         Calculate $X{guide}^{time}=(Xwinner{s}_{best1}^{time}+X{winners}_{best2}^{time}+Xwinner{s}_{best3}^{time})/3$; 11:         Define the EDO adaptive parameters $a,b,c,d$ and f; 12:         for $i=1:N$ do 13:            if $\alpha <0.5$ then                      ▹ Apply exploitation phase 14:                if $Xwinner{s}_i^{time}=memoryles{s}_i^{time}$ then 15:                    Update $V_i^{time+1}=a(memorules{s}_i^{time}-{\sigma }^2)+bXguid{e}^{time}$; 16:                else 17:                    Generate $\varphi \in \left[0.1\right]$; 18:                    Updata $V_i^{time+1}=b(memoryles{s}_i^{time}-{\sigma }^2)+log\left(\varphi \right)Xwinner{s}_i^{time}$; 19:            else 20:                Updata $V_i^{time+1}=Xwinner{s}_i^{time}-M^{time}+(c{Z}_1+(1-c)Z_2)$; 21:            Check bounds of $V_i^{time+1}$; 22:         Copy V to $memoryless$ matrix; 23:         Define $newFitness$ vector to store the fitness of all solutions of $memoryless$ matrix; 24:         for $i=1:N$ do 25:            if $(newFitnes{s}_i=Fitnes{s}_i)$ then 26:                Update $Xwinner{s}_i=V_i$ and $Fitnes{s}_i=newFitnes{s}_i$; 27:            if $(Fitnes{s}_i<bestfitness)$ then 28:                Update $Xwinner{s}_{best}=Xwinner{s}_i$ and $bestfitness=Fitnes{s}_i$; 29:         $time++$; 30: End

3.3. Proposed Improved Hybrid SSA with the EDO (ISSAEDO) Algorithm

This section introduces a novel approach called ISSAEDO which combines an improved SSA and the EDO method based on the DE technique, along with a bound-constraint adjustment mechanism. The hybrid method that has been suggested facilitates the accurate and dependable determination of the ideal values for various PV models.

3.3.1. DE Technique

The DE technique, proposed by Storn and Price in 1997 [33], is an effective population-based heuristic algorithm that employs an evolutionary process to identify the optimal solution for an optimization problem. This particular solution is notable for its simplicity in construction and comprehension, as well as its versatility in addressing various optimization problems, leading to favorable results within a fair timeframe. DE employs four fundamental processes, namely initialization, mutation, crossover, and selection, in order to identify the optimal solution for an optimization problem. The primary aim of the initialization step is to ensure comprehensive coverage of the whole search space. This is achieved by randomly setting the initial population within the specified boundaries. Subsequently, the population undergoes the processes of mutation, crossing over, and selection, which serves to augment its characteristics.

• Mutation step
  The objective of this procedure, alternatively referred to as a differential mutation, is to generate a mutated vector, ${\upsilon }_i,$ for every solution vector in each iteration. The modified vector ${\upsilon }_i$ is generated by a random selection process, where three nominee vectors $X_{r_1},X_{r_2},X_{r_3}$ are chosen from a range of options ranging from 1 to population size. The process involves computing the difference between two of the selected nominee vectors, namely $X_{r_2}$ and $X_{r_3}$, and afterward merging the obtained results. After multiplying the third nominee vector, Xr1, by a mutation weighting factor (W) within the interval [0, 1] [34], it is subsequently added to the aforementioned difference. The numerical expression for I${\upsilon }_i$ is as follows:

  $$\overrightarrow{{\upsilon }_i}={\overrightarrow{X}}_{r1}+W({\overrightarrow{X}}_{r2}-{\overrightarrow{X}}_{r3}).$$

  (19)
  One distinguishing factor between DE and other evolutionary processes lies in this particular stage.
• Crossover step
  To ensure the preservation of population diversity, the DE technique use this particular phase to adapt the differential mutation search strategy. The offspring vector $u_i$ is generated using a crossover operation that combines values from the objective vector $X_i$ and the altered vector ${\upsilon }_i$. Based on the principles of binomial and exponential operators, the prevailing and fundamental crossover search operators can be enumerated as follows:

  $$u_{i,d}=\left\{\begin{array}{c}{\upsilon }_{i,d},\mathrm{if}\mathrm{rand}\le C_R\mathrm{or}d=j_{\mathrm{rand}}\hfill \\ X_{i,d},\mathrm{otherwise}\hfill \end{array}\right.$$

  (20)
  Random numbers $j_{\mathrm{rand}}$ are selected from the range $[1,2,\dots ,D_X]$, while rand is picked from the interval $[0,1]$. This selection ensures that the modified vector will have at least one dimension. Variable $C_R$, often assigned a high value $(C_R=0.9)$, is the user-specified crossover rate that determines the probability of crossing over each element. A comparison is performed between variables $C_R$ and rand, as elucidated in Equation (20). If the value of rand is less than or equal to $C_R$, then the calculation of $u_i$ is derived from the value of ${\upsilon }_i$. If this condition is not met, $X_i$ infers $u_i$.
• Selection step
  The final stage of the DE cycle is the selection phase. In this stage, the fitness function values of the offspring vector $f\left(u_i\right)$ to the corresponding target vector $f\left(X_i\right)$ are compared to determine the solution that is more appropriate for future iteration. The procedure for determining a winner is explained as

  $$X_i=\left\{\begin{array}{c}{u}_i,\mathrm{if}f\left(u_i\right)<f\left(X_i\right)\hfill \\ X_i,\mathrm{otherwise}\hfill \end{array}\right..$$

  (21)
  In the case where the fitness function, denoted as $f\left(u_i\right)$, generates a value lower than that of the target vector, $f\left(X_i\right)$, the offspring vector, $u_i$, is reassigned to be equal to the target vector, $X_i$. Alternatively, the previous target vector, denoted as $X_i$, remains unchanged.

3.3.2. Bound-Constraint Adjustment Approach

During the initial iterations, it is possible that the decision variables generated by meta-heuristic algorithms may not be incorporated into the search process. The bound-constraint adjustment strategy is commonly employed to address this problem and eliminate infeasible decision variables. The random method is considered a crucial process in the context of bound-constrained adjustment. The proposed methodology involves replacing the choice variables that fall outside the specified boundaries with randomly generated values that lie within the boundaries. This analytical process is illustrated by the following equation:

$$X_{i,d}^{amend}=\left\{\begin{array}{c}{X}_{i,d},\mathrm{if}{X}_d^{LB}\le X_{i,d}\le X_d^{UB}\hfill \\ X_d^{LB}+rand(0,1)\times (X_d^{UB}-X_d^{LB}),\hfill \\ \mathrm{if}{X}_{i,d}<X_d^{LB}\hfill \\ X_d^{LB}+rand(0,1)\times (X_d^{UB}-X_d^{LB}),\hfill \\ \mathrm{if}{X}_d^{UB}<X_{i,d}.\hfill \end{array}\right.$$

(22)

The decision variable’s valid value is denoted as $X_{i,d}^{amend}$, while $X_i,d$ represents the value that surpasses the variable’s boundaries. The lower and upper bounds of the variable are denoted as $X_d^{LB}$ and $X_d^{UB}$, respectively. Additionally, the function rand $(0,1)$ generates a random number between 0 and 1 with a uniform distribution. The fundamental characteristic of the random process is its capacity to sustain diversity within a given population, rendering it an indispensable attribute.

The ISSAEDO algorithm aims to address the challenge of local optima and avoiding falling into it encountered in parameter extraction from PV models through its hybrid nature and the integration of multiple optimization techniques. We used the DE technique and a bound constraint for this reason; in addition, these strategies are also beneficial in a population-based optimization algorithm that excels at global exploration of the solution space. It maintains a population of candidate solutions and employs mutation, crossover, and selection operations to explore the search space more extensively. It was chosen for its global search capabilities, while bound constraint handling techniques are crucial for ensuring that solutions generated by the optimization algorithm are feasible and adhere to problem-specific constraints. Combination of these techniques can enhance the robustness of optimization algorithms, making them more effective in finding high-quality solutions for a variety of problems.

3.3.3. The Exhaustive ISSAEDO Algorithm

An improved ISSAEDO technique was produced by combining the SSA algorithm and the EDO algorithm, combined with the DE technique and the bound constraint modification procedure in SSA and EDO. By integrating EDO and DE within the SSA framework, the ISSAEDO algorithm combines the strengths of each technique. EDO helps guide the search based on the properties of exponential distribution, while DE enhances exploration and diversification. Together, these techniques aim to improve the accuracy and efficiency of parameter extraction in solar PV models by efficiently exploring the search space and converging towards optimal solutions.

The created ISSAEDO algorithm’s pseudo-code may be found in Algorithm 3. In addition, Figure 3 presents a flowchart of the ISSAEDO algorithm so that expected readers can become familiar with the basic processes of the ISSAEDO algorithm. Here is a high-level overview of how the ISSAEDO algorithm integrates EDO and DE within the SSA framework through these steps:

• The population of sparrow solutions with random values within the defined search space is initialized. Each solution represents a set of parameters for the solar PV model.
• The SSA component of the algorithm is responsible for the exploration and exploitation of the search space. It simulates the foraging behavior of sparrows to iteratively improve solutions.
• The sparrows move within the search space by adjusting their positions based on their current positions, the best solution found so far, and random exploration.
• The exploration phase allows the algorithm searching for new regions of the search space, while the exploitation phase focuses on intensifying the search around promising solutions.
• The EDO component utilizes the properties of the exponential distribution to optimize the parameters.
• The exponential distribution has a probability density function that can be used to model the likelihood of occurrence of events. In the context of optimization, it can guide the search towards regions that are more likely to contain optimal solutions.
• The EDO component incorporates the exponential distribution into the SSA framework to enhance the exploration and exploitation abilities of the algorithm.
• The algorithm adapts the parameters of exponential distribution, such as the rate parameter, during the optimization process to improve the convergence towards optimal solutions.
• The DE component is another optimization technique employed within the ISSAEDO algorithm.
• DE operates on a population of candidate solutions and iteratively improves them through a combination of mutation, recombination, and selection.
• During the DE phase, a set of new candidate solutions is generated by perturbing and recombining the existing solutions in the population.
• The new solutions are then compared with the original solutions, and selection is performed based on their fitness or objective function values.
• DE introduces additional variation and diversity into the optimization process, allowing for a more thorough exploration of the search space.

Algorithm 3 ISSAEDO algorithm

Input:   M—overall number of individuals (population size)   $G_{max}$—maximum number of iterations   D—dimensions of individuals’ positions   $X^{LB}$—lower bounds of individuals’ positions   $X^{UB}$—upper bounds of individuals’ positions   $C_R$—crossover rate   W—weighting factor Output:   $X_{opt}$—the global optimum position discovered while searching   $f\left(X_{opt}\right)$—the best fitness discovered, which should be decreased   1: Start   2:      Initialize population P with n sparrows;   3:     Evaluate fitness of each sparrow in P using the solar PV model; Set best${}_{\mathrm{sparrow}}$ = the sparrow with the best fitness in P; Set generation count $g=1$;   4:     while $g<G_{max}$ do   5:         Generate new population Q using the following steps:   6:         Perform SSA with probability $p_s$ to generate new solutions;   7:          For every solution obtained by SSA, perform EDO;   8:          For every solution obtained by EDO, perform DE;   9:         Randomly initialize remaining solutions in Q; 10:         Evaluate fitness of each sparrow in Q using the solar PV model 11:         Set best sparrow ${}_Q=$ the sparrow with the best fitness in Q; 12:         If best sparrow${}_Q$ has better fitness than best sparrow, set best sparrow = best sparrow${}_Q$; 13:         Set $P=Q$ 14:          Increment g by 1; 15:         Return the best sparrow as the optimized parameters for the solar PV model;              $f\left(X_{opt}\right)\leftarrow f\left(X_{opt}^{g+1}\right)$; 16: End

Figure 3. Flowchart of the ISSAEDO algorithm.

Figure 3. Flowchart of the ISSAEDO algorithm.

3.4. Computational Complexity of the ISSAEDO Algorithm

The overall proposed ISSAEDO algorithm’s computational complexity ($O\left(ISSAEDO\right)$) can be determined by computing the complexity of each step individually, which can be summarized in five essential steps, namely population initialization, position upgrading, random position amendment appreciation of fitness function, and DE strategy.

We let D be the dimensional space of the problem, N be the total number of candidate positions (population size), we let T equal of maximum time, and we let population of M equal the population of N in all allowed iterations. Let us point out the complications as follows:

• $O($Population initialization$)=O(N).$
• $O($Position upgrading$)=O(N\times T\times D).$
• $O($Random Position Amendment$)=O(N\times T\times D).$
• $O($Appreciation of fitness function$)=O(N\times T).$
• $O($DE strategy$)=O(N\times T\times D).$

By combining these complexities to get the overall computational complexity:

$$\begin{array}{cc}\hfill O\left(ISSAEDO\right)& =O\left(\mathrm{Population}\mathrm{initialization}\right)+O\left(\mathrm{Position}\mathrm{Upgrading}\right)\hfill \\ \hfill & +O\left(\mathrm{Random}\mathrm{Position}\mathrm{Amendment}\right)+O\left(\mathrm{DE}\mathrm{strategy}\right)+\hfill \\ \hfill & +O\left(\mathrm{Appreciation}\mathrm{of}\mathrm{Fitness}\mathrm{Function}\right)\hfill \\ \hfill & =O\left(N\right)+O(N\times T\times D)+O(N\times T\times D)+O(N\times T)+O(N\times T\times D).\hfill \end{array}$$

Grouping similar terms, we obtain

$$O\left(ISSAEDO\right)=O(N+N\times T+N\times T\times D).$$

Therefore, the overall computational complexity of the ISSAEDO algorithm is

$$O(N+N\times T+N\times T\times D).$$

According to the flowchart and assumption within each algorithm, the following can be obtained as follows:

• M is the population size.
• $G\left(Max\right)$ is the maximum number of iterations.
• $O\left(E\right)$ is the time complexity for the single solution evaluation.
• $O\left(S\right)$ assumed that the SSA algorithm per iteration is a standard which is this one.
• $O\left(D\right)$ assumed the same for the EDO algorithm.
• $O\left(DE\right)$ assumed the same for the EDO algorithm per iteration as well.

The Overall Time Complexity would be:

$$O\left(G\right(Max)\ast (ME+S+D+DE\left)\right)$$

Since M is the population size, each one will be evaluated once per iteration, if we Suppose the evaluation takes $O\left(E\right)$, so this entire step takes $O\left(ME\right)$.

4. PV Models Results and Experimental Analysis

Obtaining the parameters for the two PV models (SDM, DDM), this section presents computational experiments comparing the ISSAEDO algorithm to several competing meta-heuristic algorithms. The PV models are described in

Table 1. Details of different PV models.

Parameter	SDM	DDM
Type	Poly-crystalline	Poly-crystalline
Number of cells in zeros $\left(N_s\right)$	1	1
Number of cells in parallel $\left(N_p\right)$	1	1
Size	57 mm diameter	57 mm diameter
Test temperature (T)	33 ${}^{\circ }$C	33 ${}^{\circ }$C

. The details of the I-V for SDM and DDM are given in [35]. In addition,

Table 2. Search boundary of parameters for different PV models.

Parameter	SDM/DDM
	LB	UB
$I_{ph}\left(A\right)$	0	1
$I_{sd}$, $I_{sd1}$, $I_{sd2}$ ($\mu A$)	0	1
$R_s\left(\mathsf{\Omega }\right)$	0	0.5
$R_{sh}\left(\mathsf{\Omega }\right)$	0	100
$\gamma$, ${\gamma }_1$, ${\gamma }_2$	1	2

displays the search range for all undiscovered parameters.

Research was conducted using the Python programming language in a computing environment equipped with a Dual Xeon Gold 5115 2.4 GHz CPU and 128 GB of RAM. The operating system used was Microsoft Windows Server 2019. It should be noted that the execution of each method was repeated a total of thirty times, and the resulting data included the minimum, maximum, mean, and standard deviation (STD) values. In order to maintain a consistent and equitable evaluation, all algorithms under consideration were executed until reaching the specified stopping condition ($G_{max}$) as outlined in

Table 3. Stopping condition ($G_{max}$) of different PV models.

Parameter	SDM	DDM
$G_{max}$	12,000	25,000

for the different PV models employed. The variable values of the competing approaches were obtained from the articles associated with each strategy. To ensure a robust comparison, the community sizes for all comparison methodologies were uniformly set to 25, as per the suggested strategy. ISSAEDO performance was juxtaposed with contemporary that of methodologies. These methodologies were implemented on the identical personal computer as the previously designated configurations.

• Memetic Adaptive DE (MADE) Algorithm [4];
• Differential Evolution (DE) method with an adaptation approach (SaDE) [36];
• DE with an ensemble of parameters and mutation strategies (EPSDE) [37];
• DE with composite trial vector generation strategies (CoDE) [38];
• A Multi-Population Ensemble DE (MPEDE) [39];
• An Enhanced adaptive DE method with population adaptation strategy (jDE) [40];
• Adaptive DE with optional external Archive (JADE) [41];
• A Performance Guided JAYA (PGJAYA) [42];
• An enhanced JAYA (IJAYA) [43];
• Multiple Learning Backtracking Search Approach (MLBSA) [44].

The experimental results are thoroughly examined in the following subsections, with boldface numbers indicating the best results.

4.1. SDM Results

This subsection provides an explanation and analysis of the findings acquired from the presented ISSAEDO algorithm, as well as a comparison to the SDM algorithm.

Table 4. Optimal parameters extracted from the presented ISSAEDO and the comparative algorithms for the SDM.

Algorithm	${\mathit{I}}_{\mathit{ph}}$ (A)	${\mathit{I}}_{\mathit{sd}}$ ($\mathsf{\mu }$A)	${\mathit{R}}_{\mathit{s}}\left(\mathsf{\Omega }\right)$	${\mathit{R}}_{\mathit{sh}}\left(\mathsf{\Omega }\right)$	$\mathit{\gamma }$	RMSE
ISSAEDO	0.7607755300	0.3230207850	0.0363770930	53.7185252000	1.4811835800	9.8602187789E-04
MADE	0.7607755332	0.3230000000	0.0363770930	53.7185005600	1.4811835853	9.8602187789E-04
SaDE	0.7606306974	0.3881272938	0.0356323074	59.7703987550	1.4998983522	9.8767260000E-04
EPSDE	0.7607755303	0.3230208010	0.0363770928	53.7185218340	1.4811835873	9.8602190000E-04
CoDE	0.7606228498	0.3630150610	0.0358942084	57.1533115200	1.4930535768	1.0143800000E-03
MPEDE	0.7607800000	0.3230200000	0.0363770000	53.7190000000	1.4812000000	9.8602190000E-04
jDE	0.7607755293	0.3230073030	0.0363772593	53.7178992130	1.4811793730	9.8602190000E-04
JADE	0.7607772391	0.3249853860	0.0363544613	54.0345027540	1.4817918886	9.8626910000E-04
PGJAYA	0.7607719946	0.3206643324	0.0364105809	53.6010407450	1.4804454483	9.8615000000E-04
IJAYA	0.7607138662	0.3176309309	0.0364462526	53.6012765710	1.4794893522	9.8737780000E-04
MLBSA	0.7607764255	0.3230719859	0.0363765964	53.7177979230	1.4811995702	9.8602210000E-04

displays the values of the derived parameters and their corresponding RMSE results. Table 4 shows the values of the five unknown parameters: $I_{ph}$, $I_{sd}$, $R_s$, $R_{sh}$ and $\gamma$. Based on the RMSE values reported in Table 4, the presented ISSADEO acquired the best RMSE value (9.86021877E-04). MADE produced the second-best value for RMSE $\left(9.8602187789E04\right)$.

The statistical outcomes (the minimum, maximum, mean, and standard deviation) derived from the presented ISSAEDO and competitive algorithms are shown in

Table 5. Statistical outcomes achieved by the presented ISSAEDO and its peers for SDM.

Algorithm	RMSE
	Minimum	Maximum	Mean	STD
ISSAEDO	9.8602188E-04	9.8602188E-04	9.8602188E-04	1.7950565E-14
MADE	9.8602188E-04	9.8602191E-04	9.8602189E-04	6.4252315E-12
SaDE	9.8767260E-04	1.8884850E-03	1.1952670E-03	2.0847960E-04
EPSDE	9.8602190E-04	1.3563180E-03	1.0257090E-03	8.3009550E-05
CoDE	1.0143800E-03	1.2244620E-03	1.1046240E-03	5.8656380E-05
MPEDE	9.8602190E-04	9.8602190E-04	9.8602190E-04	4.3589640E-12
jDE	9.8602190E-04	1.4239390E-03	1.1186400E-03	1.2769220E-04
JADE	9.8626910E-04	1.1812090E-03	1.0460130E-03	5.3216160E-05
PGJAYA	9.8615000E-04	1.4631150E-03	1.0607400E-03	1.0901850E-04
IJAYA	9.8737780E-04	1.5932340E-03	1.1949590E-03	2.0842070E-04
MLBSA	9.8602210E-04	1.2345460E-03	1.0561590E-03	7.9342520E-05

. In comparison to state-of-the-art approaches, the provided ISSAEDO algorithm achieves the best minimum RMSE values for the SDM. The MADE method is the only one that earns the best maximum RMSE and lowest STD values. The provided ISSAEDO algorithm is the only one that achieves the best mean RMSE values. This demonstrates that, when compared to previous algorithms, the given ISSAEDO is capable of achieving consistent and dependable solutions.

In addition, the parameters obtained from the given ISSAEDO were employed to calculate the measured voltages, simulated current, and Individual Absolute Error (IAE) for the SDM. These values were subsequently used to generate characteristic curves. The comparison between the measured model data and simulation data obtained from the reported ISSAEDO for the SDM is depicted in Figure 4. The voltages that were measured and the IAE curves are compared in Figure 5. The simulation data exhibit a high level of compatibility with the model data presented in this figure, suggesting that the estimated values of the unknown parameters obtained through the employed ISSAEDO approach are characterized by a remarkable level of precision.

4.2. DDM Results

This section presents the results of the implemented ISSAEDO algorithm and other competitive approaches in addressing the DDM problem.

Table 6. Optimal parameters extracted from the presented ISSAEDO and the comparative algorithms for the DDM.

Algorithm	${\mathit{I}}_{\mathit{ph}}$ (A)	${\mathit{I}}_{\mathit{sd}1}$ ($\mathsf{\mu }$A)	${\mathit{R}}_{\mathit{s}}\left(\mathsf{\Omega }\right)$	${\mathit{R}}_{\mathit{sh}}\left(\mathsf{\Omega }\right)$	${\mathit{\gamma }}_1$	${\mathit{I}}_{\mathit{sd}2}$ ($\mathsf{\mu }$A)	${\mathit{\gamma }}_2$	RMSE
ISSAEDO	0.7607810790	0.2259739760	0.0367404315	55.4854436000	1.4510166600	0.7493498910	2.0000000000	9.8248485179E-04
MADE	0.7607810797	0.2260000000	0.0367404211	55.4854055726	1.4510173879	0.7493000000	1.9999999997	9.8248485587E-04
SaDE	0.7605529097	0.4019423717	0.0352812892	63.8865930751	1.5048179780	0.1090051418	1.9074684965	9.8458640000E-04
EPSDE	0.7607839281	0.7398515250	0.0367635704	55.4482499718	1.9812650310	0.2200262130	1.4489316075	9.8272390000E-04
CoDE	0.7606657463	0.7169618000	0.0359843956	56.2001315362	1.8307575470	0.3482198660	1.4889528267	1.0104260000E-03
MPEDE	0.7607800000	0.7493400000	0.0367400000	55.4850000000	2.0000000000	0.2259700000	1.4510000000	9.8248490000E-04
jDE	0.7608080110	0.2262055410	0.0367193581	55.2789940264	1.4513068866	0.7028794990	1.9818923230	9.8285900000E-04
JADE	0.7607724100	0.1939047400	0.0365249693	54.2950340976	1.7341490459	0.2446544550	1.4607843563	9.8519020000E-04
PGJAYA	0.7607837732	0.4630972107	0.0367145383	55.3345161445	1.7858272830	0.1849328798	1.4386695529	9.8525850000E-04
IJAYA	0.7607756123	0.4719030929	0.0366006720	55.1172649192	1.9439093713	0.2468714629	1.4589209674	9.8343310000E-04
MLBSA	0.7607813802	0.2375023013	0.0366501347	54.9172957588	1.4558677128	0.4640968779	1.9157161435	9.8348930000E-04

displays the values of the derived parameters as well as the accompanying RMSE results. The values of the seven unknown parameters are shown in Table 6: $I_{ph}$, $I_{sd1}$, $R_s$, $R_{sh}$, ${\gamma }_1$, $I_{sd2}$, ${\gamma }_2$. Based on the RMSE values displayed in Table 6, the presented ISSADEO has the best RMSE value of (9.82484851E-04). MADE has the second best RMSE value of (9.8248485587E-04).

The statistical outcomes (the minimum, maximum, mean, and standard deviation) retrieved from the presented ISSAEDO and competitive algorithms are shown in

Table 7. Statistical outcomes achieved by ISSAEDO and its peers for DDM.

Algorithm	RMSE
	Minimum	Maximum	Mean	STD
ISSAEDO	9.8248485E-04	9.8602238E-04	9.8408156E-04	1.4185686E-06
MADE	9.8248486E-04	9.8910305E-04	9.8511840E-04	1.8182667E-06
SaDE	9.8458640E-04	1.7089030E-03	1.2130700E-03	1.9964670E-04
EPSDE	9.8272390E-04	2.5031770E-03	1.5854020E-03	4.5970190E-04
CoDE	1.0104260E-03	1.7836150E-03	1.3436560E-03	1.9219140E-04
MPEDE	9.8248490E-04	9.8673210E-04	9.8461020E-04	1.4732270E-06
jDE	9.8285900E-04	1.6377260E-03	1.0650130E-03	1.5496370E-04
JADE	9.8519020E-04	2.8240180E-03	1.6014520E-03	4.4163080E-04
PGJAYA	9.8525850E-04	1.4380610E-03	1.0345370E-03	8.8557680E-05
IJAYA	9.8343310E-04	1.7581600E-03	1.1920610E-03	2.0934500E-04
MLBSA	9.8348930E-04	1.0282400E-03	9.9315490E-04	1.3358040E-05

. In comparison to state-of-the-art approaches, the provided ISSAEDO algorithm achieves the best minimum RMSE values for the DDM. The MADE method is the only one that earns the best maximum RMSE and lowest STD values. The provided ISSAEDO algorithm is the only one that achieves the best mean RMSE values. This demonstrates that, when compared to previous algorithms, the given ISSAEDO is capable of achieving consistent and dependable solutions.

In addition, the parameters obtained from the given ISSAEDO were employed to compute the measured voltages, simulated current, and IAE for the DDM. These values were subsequently graphed as characteristic curves. The comparison between the observed model data and simulation data obtained from the ISSAEDO for the DDM is depicted in Figure 6. The voltages that were measured and the IAE curves are compared in Figure 7. The simulation data demonstrate a high level of agreement with the model data presented in this figure, suggesting that the estimated values of the unknown parameters obtained using the given ISSAEDO are highly accurate.

4.3. Various ISSAEDO’s Components Results

Comparing the proposed ISSAEDO to the unique versions of DE and SSA demonstrates that this combination enhances the performance of the ISSAEDO algorithm.

Table 8. Optimum parameters obtained by the diverse components of the ISSAEDO for SDM.

Algorithm	${\mathit{I}}_{\mathit{ph}}$ (A)	${\mathit{I}}_{\mathit{sd}}$ ($\mathsf{\mu }$A)	${\mathit{R}}_{\mathit{s}}\left(\mathsf{\Omega }\right)$	${\mathit{R}}_{\mathit{sh}}\left(\mathsf{\Omega }\right)$	$\mathit{\gamma }$	RMSE
SSA	0.7611237070	0.2553533450	0.0372915872	46.3936672000	1.4578304200	1.1351825925E-03
EDO	0.1494502860	0.6416363660	0.2519534990	85.2178070000	1.4772455100	8.7962970619E-03
SSAEDO	0.9631364110	0.0491793204	0.2857274100	79.7732647000	1.3100563200	1.5303729578E-03
DE	0.7607755300	0.3230207970	0.0363770928	53.7185230000	1.4811835900	9.8602187789E-04
SSADE	0.7607755240	0.3230210790	0.0363770907	53.7186219000	1.4811836700	9.8602187790E-04
EDODE	0.3842538840	0.0994869333	0.1675509700	65.4048061000	1.0850875100	9.9793333516E-04
ISSAEDO	0.7607755300	0.3230207850	0.0363770930	53.7185252000	1.4811835800	9.8602187789E-04

and

Table 9. Comparative summary of the diverse components of the ISSAEDO for SDM.

Algorithm	RMSE
	Minimum	Maximum	Mean	STD
SSA	1.1351826E-03	4.9923896E-02	1.6412148E-02	1.2306843E-02
EDO	8.7962971E-03	4.9100913E-02	2.6817953E-02	1.0819581E-02
SSAEDO	1.5303730E-03	1.4939081E-02	4.3928599E-03	3.2682416E-03
DE	9.8602188E-04	9.8634410E-04	9.8603281E-04	5.7814328E-08
SSADE	9.8602188E-04	1.3052765E-03	1.0047413E-03	5.7919392E-05
EDODE	9.9793333E-04	1.7105545E-02	3.2587436E-03	3.8058891E-03
ISSAEDO	9.8602188E-04	9.8602188E-04	9.8602188E-04	1.7950565E-14

indicate the values of the determined parameters and their corresponding RMSE values for all implemented models. According to the RMSE values provided in

Table 10. Optimum parameters obtained by the diverse components of the ISSAEDO for DDM.

Algorithm	${\mathit{I}}_{\mathit{ph}}$ (A)	${\mathit{I}}_{\mathit{sd}1}$ ($\mathsf{\mu }$A)	${\mathit{R}}_{\mathit{s}}\left(\mathsf{\Omega }\right)$	${\mathit{R}}_{\mathit{sh}}\left(\mathsf{\Omega }\right)$	${\mathit{\gamma }}_1$	${\mathit{I}}_{\mathit{sd}2}$ ($\mathsf{\mu }$A)	${\mathit{\gamma }}_2$	RMSE
SSA	0.7607292070	0.0962466377	0.0335449530	66.7972347000	1.8260237200	0.6065940090	1.5498233600	1.8536310762E-03
EDO	0.3920021250	0.1988300750	0.2727070710	96.9255478000	1.2826811200	0.1131069910	1.8711319500	6.5929103094E-03
SSAEDO	0.7607600010	0.4846699400	0.0360174473	63.7180802000	1.5358508900	0.0024107608	1.2508950300	1.2588395188E-03
DE	0.7607818090	0.2236078160	0.0367528712	55.5095539000	1.4501308800	0.7684338980	1.9999712500	9.8248876571E-04
SSADE	0.7607811140	0.2259500230	0.0367405577	55.4853989000	1.4510077100	0.7495405350	1.9999999800	9.8248485256E-04
EDODE	0.7607741680	0.1465861030	0.0363745501	53.7224790000	1.4883549700	0.1771543740	1.4760443000	9.8602722237E-04
ISSAEDO	0.7607810790	0.2259739760	0.0367404315	55.4854436000	1.4510166600	0.7493498910	2.0000000000	9.8248485179E-04

and

Table 11. Comparative summary of the diverse components of the ISSAEDO for DDM.

Algorithm	RMSE
	Minimum	Maximum	Mean	STD
SSA	1.8536311E-03	3.1783778E-02	7.9238393E-03	6.3513919E-03
EDO	6.5929103E-03	4.0223204E-02	2.3216000E-02	9.0087144E-03
SSAEDO	1.2588395E-03	1.0135373E-02	3.5780324E-03	1.9048191E-03
DE	9.8248877E-04	9.8608817E-04	9.8496762E-04	1.1333581E-06
SSADE	9.8248485E-04	9.8948889E-04	9.8552284E-04	1.5032988E-06
EDODE	9.8602722E-04	8.8772632E-03	2.8693984E-03	2.1017978E-03
ISSAEDO	9.8248485E-04	9.8602238E-04	9.8408156E-04	1.4185686E-06

, the suggested ISSEADO had the lowest RMSE values across all tested models. DE, on the other hand, had the lowest RMSE values across all two test models (SDM and DDM). Finally, for one of the test models, SSA produced the lowest RMSE values. This demonstrates that the algorithm exhibits a higher degree of stability and reliability in generating solutions compared to the algorithms employed by its individual components.

4.4. Results of the Proposed ISSAEDO Compared with Other Recent Algorithms

This subsection compares the performance of the proposed ISSAEDO against various current algorithms, including an improved gaining–sharing knowledge (IGSK) [8], a modified teaching–learning-based optimization (MTLBO) [45], a Memory-based Improved Gorilla Troops Optimizer (MIGTO) [46], reinforcement learning-based differential evolution (DERL) [22], self-adaptive ensemble-based DE (SEDE) [47], Opposition-based JAYA with population reduction (EJAYA) optimization algorithm [48], and hybrid adaptive teaching–learning-based optimization with DE (ATLDE) [49], which were carried out under the same experimental settings.

Table 12. Comparison of the optimal parameters extracted from the proposed ISSAEDO with other recent results for the SDM.

Algorithm	${\mathit{I}}_{\mathit{ph}}$ (A)	${\mathit{I}}_{\mathit{sd}}$ ($\mathsf{\mu }$A)	${\mathit{R}}_{\mathit{s}}\left(\mathsf{\Omega }\right)$	${\mathit{R}}_{\mathit{sh}}\left(\mathsf{\Omega }\right)$	$\mathit{\gamma }$	RMSE
ISSAEDO	0.7607755300	0.3230207850	0.0363770930	53.7185252000	1.4811835800	9.8602187789E-04
IGSK	0.760775530000	0.323000000000	0.036377092600	53.718525318300	1.481183592100	9.8602187789E-04
MTLBO	0.760775530000	0.323000000000	0.036377090000	53.718525100000	1.481183590000	9.8602190000E-04
MIGTO	0.760775529978	0.323020838966	0.036377092476	53.718529820618	1.481183599063	9.8602187789E-04
DERL	0.760775530476	0.323020835362	0.036377092315	53.718526836059	1.481183597903	9.8602187789E-04
SEDE	0.760918670367	0.342699806830	0.036159060560	54.374637365047	1.487135632586	9.8602419564E-04
EJAYA	0.760775530234	0.323020820235	0.036377092603	53.718527449147	1.481183593200	9.8602187789E-04
ATLDE	0.766113038531	0.976041045494	0.028905212893	35.699281625311	1.606957864299	5.0558093207E-03

presents the five unknown parameter values $I_{ph}$, $I_{sd}$, $R_s$, $R_{sh}$, $\gamma$, and RMSE for SDM. Based on the values of RMSE shown in Table 12, ISSAEDO, IGSK, MIGTO, DERL, and EJAYA obtained the lowest RMSE value (9.8602187789E-04).

Table 13. Statistical outcomes achieved by ISSAEDO and recent methods for SDM.

Algorithm	RMSE
	Minimum	Maximum	Mean	STD	CPU Time (s)
ISSAEDO	9.8602188E-04	9.8602188E-04	9.8602188E-04	1.7950565E-14
IGSK	9.86021880E-04	9.86021880E-04	9.86021880E-04	3.5821018E-17	5.34
MTLBO	9.8602190E-04	9.8602190E-04	9.8602190E-04	1.9092749E-17	—
MIGTO	9.86021880E-04	9.86021880E-04	9.86021880E-04	1.4800000E-17	3.15
DERL	9.86021880E-04	9.86021880E-04	9.86021880E-04	7.7778590E-17	2.89
SEDE	9.8602420E-04	1.0460447E-03	9.9286093E-04	1.2097805E-05	2.51
EJAYA	9.86021880E-04	9.86021880E-04	9.86021880E-04	3.5158347E-13	10.26
ATLDE	5.0558093E-03	2.6010278E-02	1.2918977E-02	3.8927359E-03	0.69

presents the minimum, maximum, mean, and STD of the RMSE values of the proposed ISSAEDO and their counterpart algorithms. The approaches (ISSAEDO, IGSK, MIGTO, DERL, and EJAYA) were capable of reaching the best minimum, best maximum, and best mean RMSE results for the SDM in comparison with other algorithms. The presented ISSADEO obtained the minimum STD value. Therefore, the presented ISSAEDO has the potential to produce stable and reliable results when compared to other methods. Finally, ATLDE demonstrated the minimum execution time.

Table 14. Comparison of the optimal parameters extracted from the proposed ISSAEDO with other recent results for the DDM.

Algorithm	${\mathit{I}}_{\mathit{ph}}$ (A)	${\mathit{I}}_{\mathit{sd}1}$ ($\mathsf{\mu }$A)	${\mathit{R}}_{\mathit{s}}\left(\mathsf{\Omega }\right)$	${\mathit{R}}_{\mathit{sh}}\left(\mathsf{\Omega }\right)$	${\mathit{\gamma }}_1$	${\mathit{I}}_{\mathit{sd}2}$ ($\mathsf{\mu }$A)	${\mathit{\gamma }}_2$	RMSE
ISSAEDO	0.7607810790	0.2259739760	0.0367404315	55.4854436000	1.4510166600	0.7493498910	2.0000000000	9.8248485179E-04
IGSK	0.760781078800	0.749300000000	0.036740428600	55.485434254300	2.000000000000	0.226000000000	1.451016892800	9.8248485179E-04
MTLBO	0.760781000000	0.749300000000	0.036740430000	55.485447000000	1.999999900000	0.225970000000	1.451016000000	9.8248490000E-04
MIGTO	0.760781079716	0.225974098430	0.036740429798	55.485441004589	1.451016706890	0.749349388682	1.999999999997	9.8248485179E-04
DERL	0.760781427162	0.769331473053	0.036755411997	55.511061446498	1.999999885032	0.223397967779	1.450045266267	9.8249599338E-04
SEDE	0.759974384717	0.521351239996	0.033000678297	64.299061995503	1.579409410340	0.167338150195	1.841165682244	9.8262738626E-04
EJAYA	0.760786512297	0.230273700314	0.036721466099	55.329778672223	1.452584868825	0.711749061850	1.999999965157	9.8249988436E-04
ATLDE	0.766288413557	0.762958757469	0.026086596318	33.403749313859	1.630211622282	0.991549225520	1.719109201673	3.2186265367E-03

presents the values of the seven unknown parameters Iph, Isd1, Rs, Rsh, $\gamma$1, Isd2, $\gamma$2, and RMSE for DDM. Based on the values of RMSE shown in Table 14, ISSAEDO only obtained the lowest RMSE value (9.8248485179E-04).

Table 15. Statistical outcomes achieved by ISSAEDO and recent methods for the DDM.

Algorithm	RMSE
	Minimum	Maximum	Mean	STD	CPU Time (s)
ISSAEDO	9.8248485E-04	9.8602238E-04	9.8408156E-04	1.4185686E-06
IGSK	9.8248485E-04	9.86021880E-04	9.8272774E-04	8.9578942E-06	14.08
MTLBO	9.8250260E-04	9.8248490E-04	9.8248550E-04	3.3000000E-09	—
MIGTO	9.8266170E-04	9.8602187E-04	9.8266170E-04	7.7100000E-06	5.32
DERL	9.8249600E-04	1.0091744E-03	9.8634733E-04	4.4372558E-06	3.82
SEDE	9.8262739E-04	1.1069935E-03	1.0092765E-03	3.9080194E-05	0.22
EJAYA	9.8249988E-04	9.8613006E-04	9.9057738E-04	1.7720444E-06	12.02
ATLDE	3.2186265E-03	1.4438034E-02	7.9795069E-03	2.9918516E-03	1.38

shows the statistical outcomes (the minimum, maximum, mean, and STD) extracted from the presented ISSAEDO and the competitive algorithms. The proposed ISSAED, and IGSK algorithms are capable of reaching the best least RMSE values for the DDM compared to the state-of-the-art methods. The MTLBO is the only algorithm that achieved the best maximum RMSE values, the best mean RMSE values, and minimum STD values. Finally, ATLDE achieved the minimum execution time.

5. Discussion

This paper introduces a novel approach referred to as ISSAEDO, the hybrid algorithm ISSAEDO combining SSA, EDO, and DE techniques. Hybridization aims to leverage the strengths of individual methods while compensating for their weaknesses, offers strengths and precision in the acquisition of coefficients for PV models. The enhanced global and local search capabilities, robustness to noise and uncertainty, convergence speed, ability to handle complex models, flexibility, general applicability, and integration potential with advanced techniques make this model a valuable tool for researchers and statisticians working on PV system modeling and analysis. One notable characteristic of the SSA, EDO algorithm is its simplicity in parameter specification, requiring only two parameters: population size and stopping criterion. These parameters are commonly found in other meta-heuristic algorithms. As a result, it can be readily applied to a wide range of optimization issues. Furthermore, the DE is employed in the Self-Adaptive, SSA, EDO algorithm to enhance population diversity and facilitate extensive search space exploration, hence preventing the SSA, EDO from converging to a local optimum. In the course of experimental investigations, ISSAEDO is subjected to a comparative analysis with various established meta-heuristic algorithms. The empirical evidence and statistical analysis indicate that ISSAEDO exhibits superior performance compared to other algorithms in the extraction of parameters from PV models, including SDM and DDM, in both practical and statistical contexts. As a result, the performance of the proposed algorithm is evaluated by utilizing two authentic manufacturer’s data sheets, namely TFST40 and MCSM55, in order to showcase its practical use. Furthermore, a comparison is made between the measured model data and simulation data acquired by the use of ISSAEDO. The findings indicate a high level of similarity between the extracted data and the model data, suggesting that the unknown parameter values acquired by the current ISSAEDO algorithm are very accurate. Furthermore, the statistical analysis of Wilcoxon’s rank-sum test is performed at a significance level of 0.05 in order to evaluate the importance of the reported ISSAEDO in comparison to its counterparts.

In conclusion, a comparative analysis is conducted with the proposed ISSAEDO algorithm and the original iterations of DE, SSA, and EDO algorithms in order to demonstrate the enhanced performance achieved by the amalgamation of these methodologies. The RMSE values collected indicate that the suggested ISSAEDO algorithm consistently delivers the lowest RMSE outcomes across all utilized models. The EDO algorithm demonstrates the lowest RMSE values in this study. This illustrates that the described ISSAEDO possesses the capacity to attain solutions that are stable and dependable in comparison to the algorithms of its individual components.

ISSAEDO may have potential limitations and compromises. For example, it may exhibit sensitivity to the set of initial solutions, algorithm performance may vary based on the quality and diversity of initial solutions, and poor initialization may lead to convergence to suboptimal solutions. The effectiveness of ISSAEDO may be affected by characteristics of the problem, such as dimensions, multimedia, and the presence of restrictions Like many optimization algorithms, ISSAEDO may have parameters that need to be adjusted for optimal performance. The behavior of the algorithm can be sensitive to the values of these parameters, and finding the right combination of parameter values may require additional effort. Also, the complexity of combining these algorithms can affect the efficiency of ISSAEDO in terms of computational resources and time. There is a possibility that the hybrid algorithm will have difficulty maintaining diversity in the population. It is important to know that ISSAEDO represents a new hybridization of optimization techniques. Users should be aware of potential limitations and carefully consider its applicability to specific problem areas by performing comprehensive experiments and sensitivity analysis in understanding the strengths and weaknesses of the algorithm in different scenarios. We can address it in the future in different research to develop this research with different modifications.

6. Conclusions and Future Work

The hybrid ISSAEDO approach strikes a balance as follows: SSA for the Global Exploration algorithm aids in global exploration. By simulating the foraging behavior of sparrows, SSA enables the simulation of the search space and facilitates the discovery of new regions that potentially harbor optimal solutions. The EDO for Biasing Search algorithm leverages the exponential distribution’s properties to direct the search towards locations that are more probable to contain optimal solutions. Adaptive adjustments are made to exponential distribution parameters throughout the optimization procedure.EDO achieves a balance between exploration and exploitation by directing the algorithm towards areas that demonstrate promise. DE enhances candidate solutions iteratively via selection, recombination, and mutation on a population of such solutions. By integrating SSA, EDO, and DE, the ISSAEDO algorithm strikes a harmonious equilibrium between local search and global exploration. Exploration is facilitated by SSA and EDO through the adaptation of the search process in accordance with exponential distribution properties. In contrast, DE places emphasis on local search as a means to enhance and refine the solutions acquired via the remaining components. Adopting a hybrid approach, this method facilitates an exhaustive investigation of the solution space by effectively managing exploration to circumvent local optima and exploitation to enhance solutions within regions that show promise. It is crucial to acknowledge that the precise equilibrium attained by the hybrid approach may be contingent upon parameter configurations, the attributes of the problem, and the interaction among the optimization elements. The hybrid approach must be meticulously crafted and fine-tuned in order to achieve an optimal equilibrium between local and global search within the solution space. This is what our manuscript aims to achieve.

According to statistical analysis, the ISSEADO algorithm shows superior performance in terms of convergence speed, accuracy and reliability compared to other widely recognized algorithms. Hence, the proposed methodologies represent appropriate and effective methods for deriving photovoltaic model parameters.

In the next plan, the proposed ISSAEDO algorithm will be extended to other equivalent problems, like optimal power flow and maximum power point tracking. Also, the ISSAEDO algorithm will be adjusted to be able to deal with multi-objective PV problems with constraints. Moreover, the ISSAEDO algorithm will be put through its paces by solving more practical models of PV modules.

As a comprehensive future outlook, PV technology holds significant importance in technology and scientific research. Its role in providing renewable energy, enhancing energy independence, mitigating climate change, and driving economic growth cannot be overstated. By addressing PV in scientific research, researchers and statisticians can contribute to the advancement of solar cell technology, paving the way for further progress in the field and enabling a sustainable and clean energy future, Overall, continued scientific research and innovation in PV technology are essential for realizing the full potential of solar energy, driving down costs, and ensuring a sustainable and resilient energy future.