Abstract
In automated storage and retrieval systems (AS/RSs), the utilization of intelligent algorithms can reduce the makespan required to complete a series of input/output operations. This paper introduces a simulation optimization algorithm designed to minimize the makespan in a realistic AS/RS commonly found in the steel sector. This system includes weight and quality constraints for the selected items. Our hybrid approach combines discrete event simulation with biased-randomized heuristics. This combination enables us to efficiently address the complex time dependencies inherent in such dynamic scenarios. Simultaneously, it allows for intelligent decision making, resulting in feasible and high-quality solutions within seconds. A series of computational experiments illustrates the potential of our approach, which surpasses an alternative method based on traditional simulated annealing.
1. Introduction
Warehousing involves the storage of raw materials, components, work in progress (WIP), and finished goods. It has consistently been recognized as a crucial element within the supply chain and within logistics. A well-designed and effectively managed warehousing system can yield significant benefits, such as reducing the risk of running out of stock, mitigating the bullwhip effect, and decreasing the lead time of the final products [1]. Over recent decades, advancements in automation have led to the proliferation of fully automated solutions like automated storage and retrieval systems (AS/RSs) and automated vehicle storage and retrieval systems (AVS/RSs) across various industrial environments [2]. An AS/RS comprises two essential components: (i) a storage area that can be subdivided and (ii) multiple automated machines responsible for material movement within and outside the storage area. Compared to traditional manual warehouses, AS/RSs offer undeniable advantages, including labor savings, an increased storage capacity, a reduced throughput time, and a decreased occurrence of errors, damage, and risks for operators. However, the success of AS/RS implementation relies on the efficiency and alignment of the control policies with the needs of the industrial system. A well-designed AS/RS must autonomously address various challenges, such as scheduling retrieval and storage operations, assigning stock items to customer orders, allocating delivery trucks to output points, and determining routing for operations involving storage and retrieval machines, among others [3].
Despite their complexity, and owing to their numerous benefits, AS/RSs have rapidly gained traction across diverse sectors in recent decades. One industry where AS/RSs are becoming increasingly prevalent is the steel industry. According to an analysis by the World Steel Association (https://www.worldsteel.org/, accessed on 15 January 2024), this industry is at the heart of global development. In 2017, the steel industry achieved sales of USD trillion and generated USD 500 billion in value. For every USD 1 added within the steel industry, an additional USD of value-added activity is supported across other sectors of the global economy due to purchases of raw materials, goods, energy, and services. This generates over USD trillion in value. In terms of employment, this analysis study confirmed that the steel industry employs more than 6 million people, and for every 2 jobs in the steel sector, 13 more jobs are supported throughout its supply chain, resulting in a total of around 40 million jobs. AS/RSs used in the steel sector significantly differ from those implemented in other environments, such as AS/RSs for pallets [2], miniloads [4], shuttle-based AS/RSs [5], etc. These differences predominantly stem from the fact that, in the steel sector, the systems are designed to handle unconventional stock-keeping units and typically heavier and bulkier items (e.g., slabs, blooms, billets, tubes and bundles, metal sheet bundles, etc.). Consequently, solutions proposed for other AS/RSs are often impractical for systems intended for the steel sector. One of the most prevalent AS/RSs in the steel sector is the shuttle–lift–crane (SLC)-based AS/RS (SLC-AS/RS) (Figure 1): a fully automated system specifically designed for storing bundles of long metal bars or tubes, wherein the stored items themselves act as the unit loads (i.e., the bundles themselves).

Figure 1.
A picture of a shuttle–lift–crane AS/RS.
To the best of the authors’ knowledge, the SLC-AS/RS has received limited attention in the scientific literature despite its significance in this industry. Thus, this paper contributes to partially filling this gap. Managing the handling of metal bar bundles involves several constraints related to the weight and quality of goods, complicating operational decisions. Previous work by Bertolini et al. [6] addressed the allocation problem using simulated annealing (SA), albeit limited to improving the retrieval phase. In this paper, the authors expand on the aforementioned work by enhancing both the retrieval and storage operations. Here, the problem is approached using a simulation optimization methodology that combines discrete event simulation (DES) principles with a biased-randomized (BR) algorithm [7]. While the DES component handles intricate time dependencies among different events, the BR component facilitates intelligent decision making. The resulting BR-DES is then integrated into a multi-start framework, enabling the generation of multiple high-quality solutions within short computing times.
The remainder of this paper is organized as follows: Section 2 provides an overview of related work. Section 3 offers a detailed description of the AS/RS under analysis. Section 4 introduces the optimization problem to be solved. Section 5 details the deterministic heuristic used by the authors to evaluate solutions. The proposed biased-randomized algorithm, along with its integration into a multi-start framework, is described in Section 6. The obtained solutions for different instances are compared with those generated by previous approaches in Section 7. Finally, conclusions and future research directions are presented in Section 8.
2. Related Work
Automated storage and retrieval systems have long been a focal point in the scientific community. A comprehensive overview of AS/RS literature was first presented by Roodbergen and Vis [2] after over 30 years of research in the field. These authors were the first to spotlight design and control issues addressed in AS/RSs, encompassing design decisions, storage assignment, batching, dwell location, sequencing of storage and retrieval requests, and performance measurement. Recently, Bertolini et al. [8] extended the review, focusing on papers published between 2009 and 2019. Over the years, numerous aspects related to AS/RSs have been meticulously studied, while new areas of interest, such as environmental aspects and energy consumption, have emerged [9,10]. Moreover, as AS/RSs have become more widespread across different sectors, many challenges initially addressed in classical AS/RSs for pallets have now been extended to modern systems. These new systems introduce new issues due to varying physical designs, collaborative machine operations, and limitations associated with handled unit loads. Among the most researched AS/RS typologies are shuttle-based AS/RSs [5], mini-loads [11], autonomous vehicle AS/RSs [12], split platform AS/RSs [13], and tier-to-tier AS/RSs [14]. Thus, Ekren and Heragu [15] discusses the significance of material handling, specifically focusing on unit load storage and retrieval systems. The paper highlights the evolution of crane-based automation technologies since the 1970s, leading to the widespread use of AS/RSs in distribution and production environments. Roy et al. [16] analyze the adoption of autonomousvehicle-based AS/RSs as an alternative to traditional automated systems for unit-load operations. These authors model the system as a multi-class semi-open queuing network with class switching and propose a decomposition-based approach to evaluate system performance. Ekren et al. [12] employ a matrix-geometric method to model and analyze an autonomous vehicle AS/RS as a semi-open queuing network. Their model accounts for waiting times, and it can solve the network and derive key performance measures. Liu et al. [17] focus on the travel time analysis of a split-platform AS/RS with a dual command cycle operating mode and an input/output dwell point policy. The study introduces a continuous travel time model and validates its accuracy through computer simulations. Liu et al. [13] investigate travel time models for split-platform AS/RSs, where machines employ independent horizontal shuttles and vertical lifts. The paper presents two dual command travel time models, which are validated through computer simulations. Hu et al. [18] analyze the travel time of a novel AS/RS designed for extra heavy loads like sea container cargo, where conventional stacker cranes may be insufficient. A travel time model is presented under the stay dwell point policy and validated through computer simulations. In addition, the authors provide guidelines for optimizing the design of a rectangular-in-time AS/RS rack. Cai et al. [19] model and evaluate an autonomous vehicle AS/RS with tier-to-tier vehicles utilizing a semi-open queuing network. Various storage/retrieval requests are represented as different customer classes in the model. Due to the time-consuming nature of analyzing multiple configurations through computer simulations, this paper employed analytical methods. This research also compared two synchronization policies. Finally, Zou et al. [14] also model and analyze tier-captive autonomous vehicle storage and retrieval systems, introducing a parallel processing policy where arrival transactions can simultaneously request both the lift and the vehicle. An approximation method, based on decomposing the fork-join network, is developed to estimate system performance. Simulation models validated the effectiveness of analytical models, showing that the fork-join network accurately estimates system performance under the parallel processing policy. Although other typologies, like the adoption of two storage and retrieval machines sharing the same path, have been highlighted [20], the steel sector has been notably neglected throughout this technical and scientific evolution. Noteworthy contributions specifically aimed at improving AS/RS performance in the steel sector include works by Bertolini et al. [6] and Zammori et al. [21].
This work introduces novelty in two key areas: (i) the system considered and (ii) the proposed algorithm. The system under consideration is known as the shuttle–lift–crane automated storage and retrieval system (SLC-AS/RS), widely deployed in the steel industry and occasionally used in the wood industry to preserve tree trunks. A detailed system description is provided in Section 3. Apart from the aforementioned works by Bertolini et al. [6] and Zammori et al. [21], we are pioneers in offering an optimization technique for such systems. The proposed solution, described in Section 6, is based on a discrete-event heuristic (DEH). The DEH combines a swift heuristic algorithm for decision making with discrete event simulation to evaluate the impact of decisions within a complex system characterized by high levels of parallelism and resource interaction. While similar approaches have proven efficient in various contexts, such as those seen in Arnau et al. [22], the application of a DEH to automated storage and retrieval systems is novel.
3. Modeling an Automated Warehouse in the Steel Sector
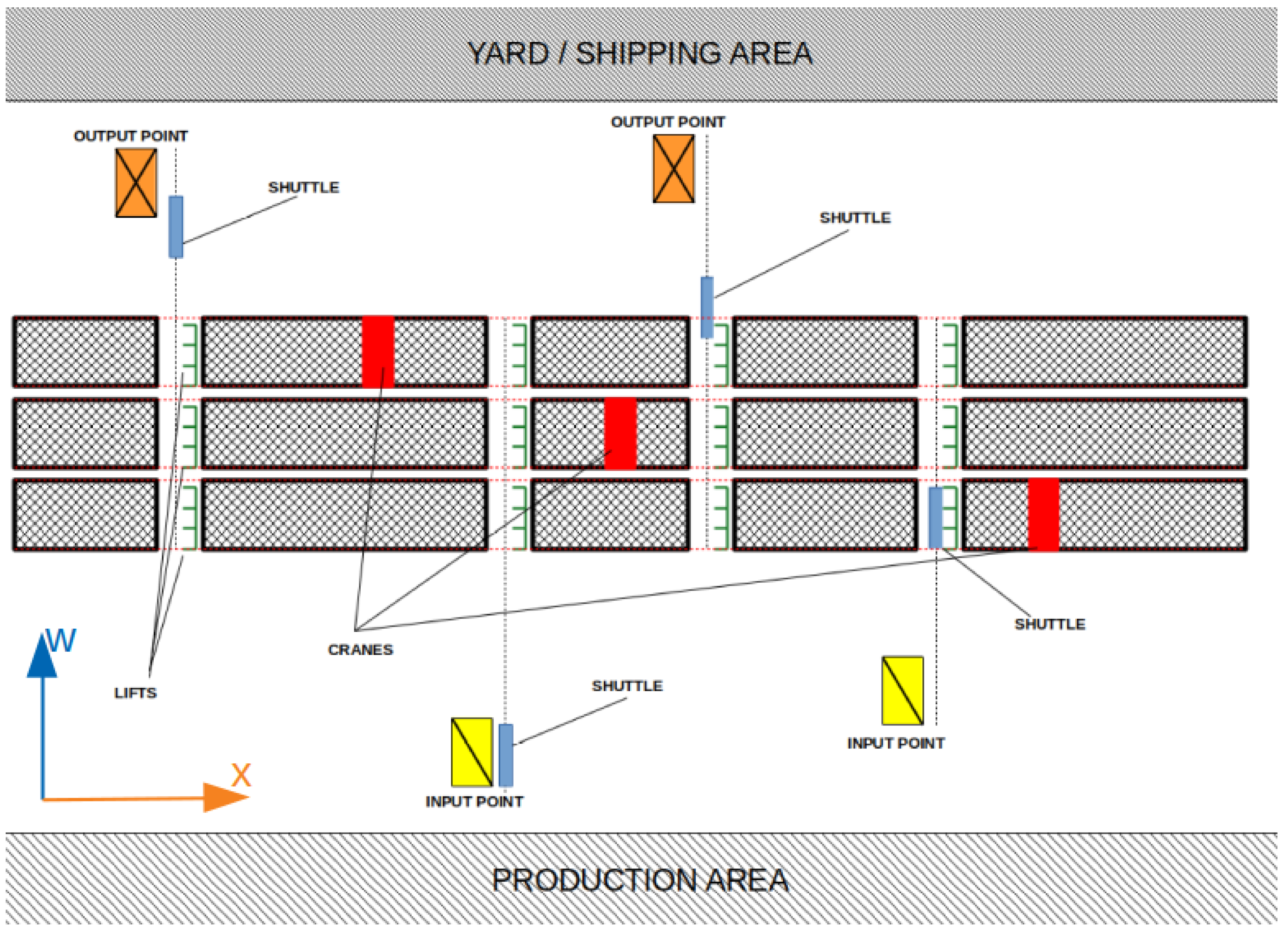
The shuttle–lift–crane automated storage and retrieval system is a prevalent storage solution in the steel industry, specifically designed to store bundles of long metal bars or tubes ranging from ten to twelve meters in length and weighing between 1000 and 5000 kg. Notably, this system does not involve picking individual bundles. Rather, each bundle enters and exits the warehouse without any alterations. As a result, the SLC-AS/RS does not employ loading units or boxes to store items since the bundles themselves serve as the unit loads. Typically, the overall storage area of an SLC-AS/RS is divided into several bearing metal structures known as racks. Each rack can reach heights of up to 20 to 25 m, widths of 12 m (depending on the stored tubes or bars’ length), and lengths exceeding 100 m. To facilitate understanding this complex system, a schematic representation is provided in Figure 2, displaying a system comprising three racks and two input and two output locations.
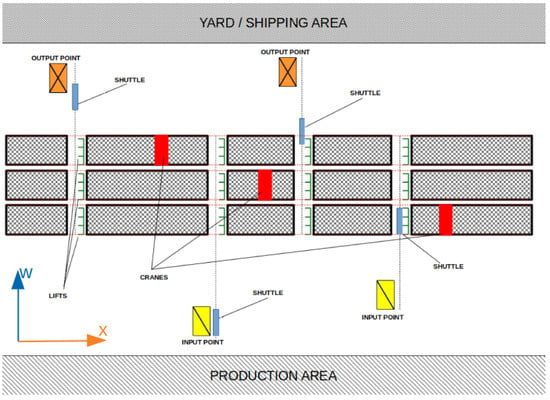
Figure 2.
Schematic representation of ann SLC-AS/RS.
Unlike standard AS/RSs for pallets, each rack in the SLC-AS/RS is divided into perpendicular aisles, crossing the rack lengthwise (x-axis) and splitting it into multiple sections. Storage locations, composed of metal shelves, line both sides of these aisles, accommodating multiple bundles of varying types and lengths, as depicted in Figure 3. Consequently, these storage locations are not standardized, and previous allocations can affect the possibility of utilizing specific storage spaces. This unique aspect of the SLC-AS/RS could be formulated as a one-dimensional cutting stock problem to minimize the number of storage locations used.

Figure 3.
Example of bundle allocation in a single storage location.
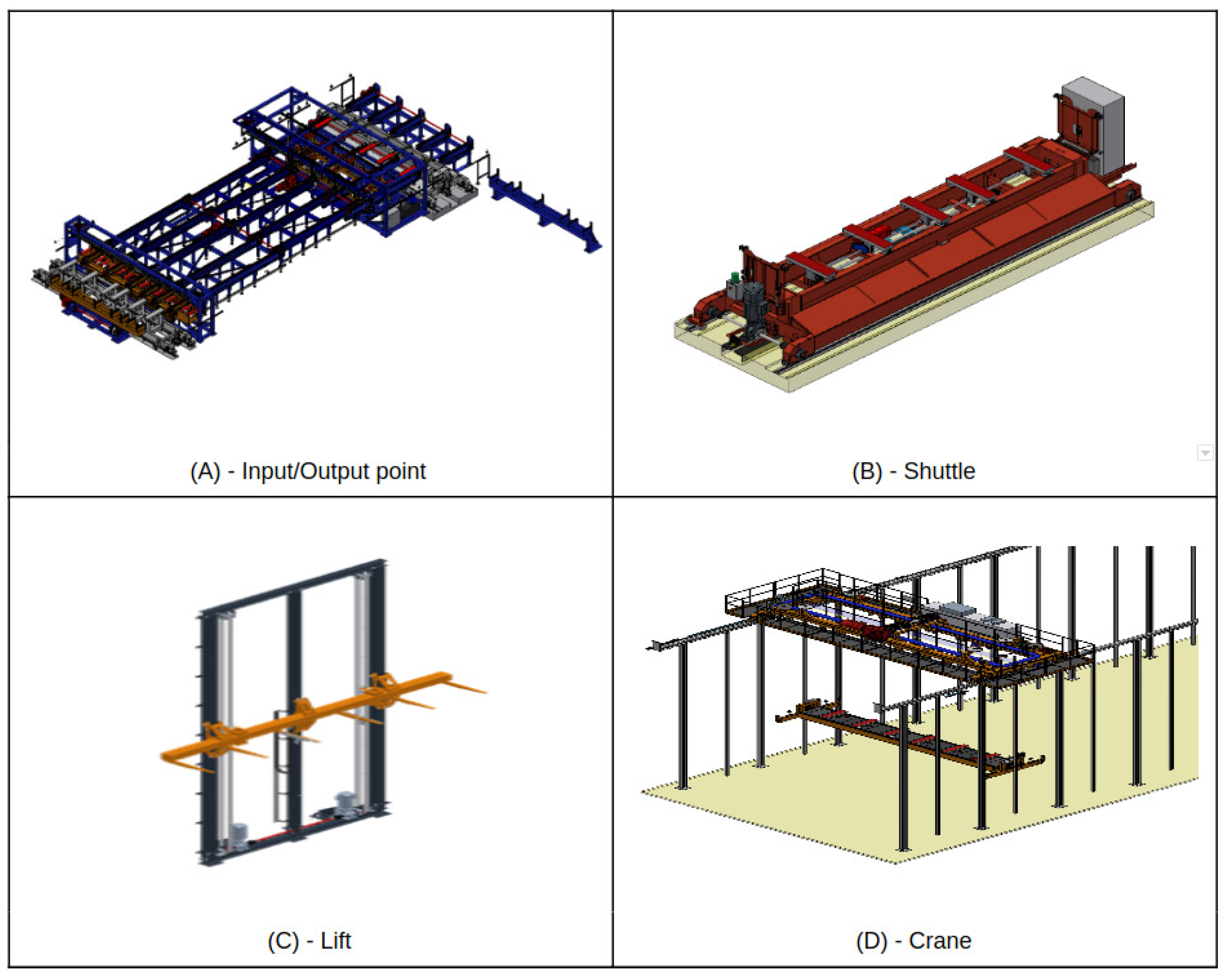
Resource-wise, an SLC-AS/RS encompasses four categories: (i) input/output (I/O) points; (ii) shuttles; (iii) lifts; and (iv) cranes. Each shuttle serves all racks but only one I/O point, while each lift serves a single crane and shuttle. Conversely, each crane serves every lift within its rack. A detailed breakdown of these machines is provided below:
- I/O points: Chain conveyors serve as buffers between the system and external processes, such as truck loading or production lines. Input points, equipped with sensors for bundle alignment and weight control, are also depicted in Figure 4A.
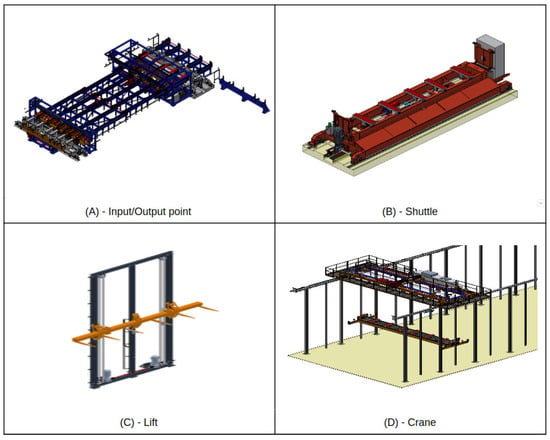 Figure 4. Main elements of a shuttle–lift–crane AS/RS.
Figure 4. Main elements of a shuttle–lift–crane AS/RS. - Shuttles: Vehicles handle horizontal movements, transporting bundles between I/O points and racks. They can transport one or two bundles, depending on single-depth or double-deep storage, as illustrated in Figure 4B.
- Lifts: Responsible for vertical movements and transporting bundles between shuttles and the top of racks or cranes. Figure 4C showcases an example of these lifts.
- Cranes: Essential for storage and retrieval operations, moving bundles between lifts and shelves or vice versa. Each rack houses one crane capable of three-axis movements, as detailed in Figure 4D.
For a comprehensive understanding of the SLC-AS/RS operations and cycle time computation, refer to Zammori et al. [21]. In this work, we focus on the behavior and interactions of machines during input and output operations. The operation begins when the entering bundle reaches an input point. If the shuttle is not near the input point, it is recalled, the bundle is loaded upon arrival, and then proceeds to the assigned rack. Once the bundle is loaded onto the lift, it is transported to the top of the rack and requested by the crane for storage. The crane then moves the bundle to the designated storage location. Similarly, we will consider the process for retrieval or output operations. The operation is sent to the crane, which retrieves the required bundle from the storage location and transports it to the corresponding lift for output.
4. Detailed Problem Description
This section provides an accurate description of the problem being studied in this paper, which includes the main assumptions and description of the stock-keeping units, a description of the customers’ orders and storage facilities, and a formal model.
4.1. Main Assumptions and Stock-Keeping Units Description
We consider an SLC-AS/RS with single, deep storage locations, featuring one single crane on each rack and only one shuttle for each I/O point. Due to the latter two aspects, there is no need to consider anti-collision policies. Additionally, since each shuttle is associated with exactly one I/O point, shuttles linked to an input point solely perform input operations, while those connecting racks to an output point exclusively execute output operations. As previously mentioned, the stock-keeping units (SKUs) comprise bundles of metal bars, hereafter denoted as . Each SKU i is defined by the following attributes: (i) a unique code, ; (ii) a specific quality level, , influenced by factors like the geometric dimensional tolerances of the bar, chemical purity of the material, and the presence of surface damages; (iii) a weight and length ; and (iv) the rack where the bundle is located, along with its position inside the rack, denoted as .
4.2. Customers’ Orders and Storage Requests
All customer orders, denoted as output requests, , possess the following attributes: (i) an arrival time, ; (ii) a required product identified by a unique code, ; (iii) a specified required quantity, ; (iv) a minimum quality level of the material, ; and (v) an indicator specifying the I/O point used, . Distinguishing customer orders from storage orders (input requests ) involves an additional attribute, . In the former case, holds a value of zero, whereas in the latter case, it holds a value of one. The interpretation of the remaining attributes varies based on . For instance, in a customer order, , , and signify the product, quantity, and required quality level, respectively. Conversely, in a storage request, they represent the product, weight, and quality of the incoming bundle, respectively.
In an SLC-AS/RS, processing customers’ orders differs slightly from traditional AS/RS setups for pallets. Typically, customers specify a particular product type, along with a quantity in kilograms and a desired quality level. The fulfillment of this request necessitates one or more bundles, ensuring that the overall quantity and quality of retrieved bundles closely match the required specifications. This resembles a knapsack problem embedded within the larger issue at hand.
4.3. Mathematical Formalization and Scope of the Algorithm
The primary objective of the proposed approach is to minimize the makespan, denoted as the time required to complete a given set of operations. Here, represents the operations to fulfil requests, denotes the set of machines (such as shuttles, lifts, and cranes), and signifies the time at which machine finishes operation j. The objective function can be formally defined as:
where A is a newly introduced variable subject to the following constraints:
For each storage request, represented by , we define an input operation. Similarly, for each customer order , one or more retrieval operations are defined based on the required quantity and stock availability. The algorithm does not handle the assignment of input/output points to requests, as this decision relies on external factors. Specifically, the input point depends on the production line from which the entering bundle originates, while the output point is chosen by the truck driver, typically opting for the first available one. The sequence in which requests are processed is highly constrained. For input requests, rearranging the order of entry bundles once they have reached the input point and placed on the conveyor is time-consuming due to their substantial weight (over five tons) and length (up to twelve meters). Altering the sequencing of input requests involves significant expenses, typically requiring at least two operators and a forklift or a bridge crane. Hence, changing the sequence of input requests should be minimized. Regarding output requests, due to the bulkiness of the bundles, they cannot be temporarily stored in a loading area or yard (as with classic pallets). Therefore, output requests should generally adhere to first-in-first-out (FIFO) logic. Postponing an output request is rare and only considered when the required product (in the required quantity) is not in stock.
The constraints for assigning bundles to output operations and empty spaces to input operations can be formalized as follows. For a storage operation , the only requirement is that the space accommodating the entering bundle must be of sufficient length. Thus, if represents the length of , denotes the length of a generic space, and is a decision variable equal to one only if space is assigned to operation j, the following constraint must be satisfied:
Conversely, for a customer order, quantity and quality constraints are essential. For each customer order , the difference between the required and retrieved quantities must fall within certain limits:
where represents the set of in-stock bundles selected to fulfil customer order k, and △ denotes an acceptable deviation from the required quantity. Regarding the quality constraint, must have an average quality level equal to or higher than the required quality :
where refers to the cardinality of set .
5. Evaluation of the Solutions
The solution generated by the proposed algorithm includes a set of operations , encompassing both input and output operations aimed at fulfilling the requests. Each input operation corresponds to an empty storage location where the entry bundle will be stored. Similarly, every output operation is linked to a bundle in stock for retrieval. Sorting the operations by their scheduled execution time enables the computation of the makespan through a discrete event simulation. This simulation can accommodate stochastic processing times and is applicable irrespective of the system’s complexity. Notably, the deterministic simulation considered here naturally extends to a stochastic one. During each simulation run, deterministic processing times can be substituted with randomly generated times using corresponding probability distributions. The specific probability distributions employed to model these random processing times are derived from fitted historical data. To elucidate the computation of the makespan analytically, a simple example is provided below, showcasing machines and operations:
- , , and represent the crane, shuttle, and lift necessary for operation j, dependent on its associated operation and the bundle it involves.
- denotes the most recent operation involving machines r, s, and l. Similarly, signifies the most recent operation involving only r, while indicates the most recent operation involving crane r and shuttle s.
Key events occurring during the simulation of each operation are defined as follows:
- represents the moment when operation j becomes available for machine m.
- signifies the start time when machine m initiates work on operation j.
- indicates the completion time when machine m finishes work on operation j.
- and denote the first and second positions that crane must visit to execute operation j. If j is an input operation, represents the interchange point between lift and crane , while denotes the storage location. Conversely, for an output operation, corresponds to the storage location, while indicates the interchange point between lift and crane .
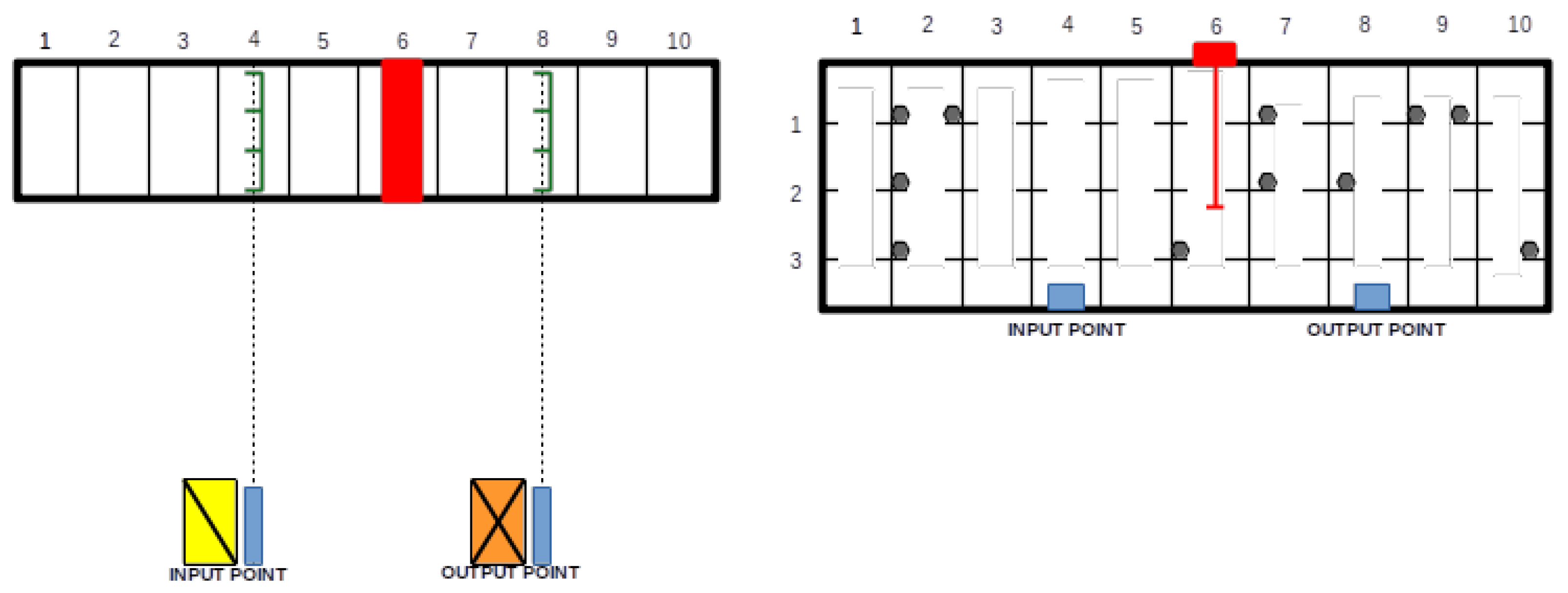
An illustration of the SLC-AS/RS under consideration is depicted in Figure 5. The layout assumes a configuration with one crane and two lifts within the rack (with one lift designated for each I/O point). The warehouse comprises ten aisles, each spanning a length of one meter. For the input shuttle, traversal of the rack occurs through the fourth aisle, while the output shuttle navigates along the eighth aisle. Within each aisle, storage consists of three levels, each standing at a height of one meter. The crane’s movement follows a uniform, linear trajectory, covering one meter per second in both length and height. The unidirectional travel time for the lifts is presumed to be 3 s, while the upload and download times are estimated at 5 s. Additionally, the one-way travel time for shuttles to reach the rack is set at 6 s. The operations to be executed include:
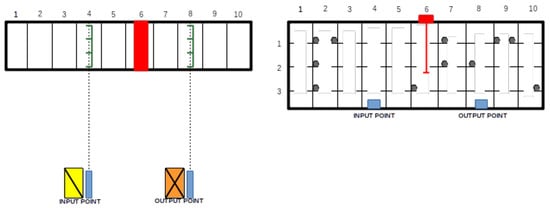
Figure 5.
Planar (left) and frontal (right) view of the SLC-AS/RS considered.
- .
- .
- .
- .
- .
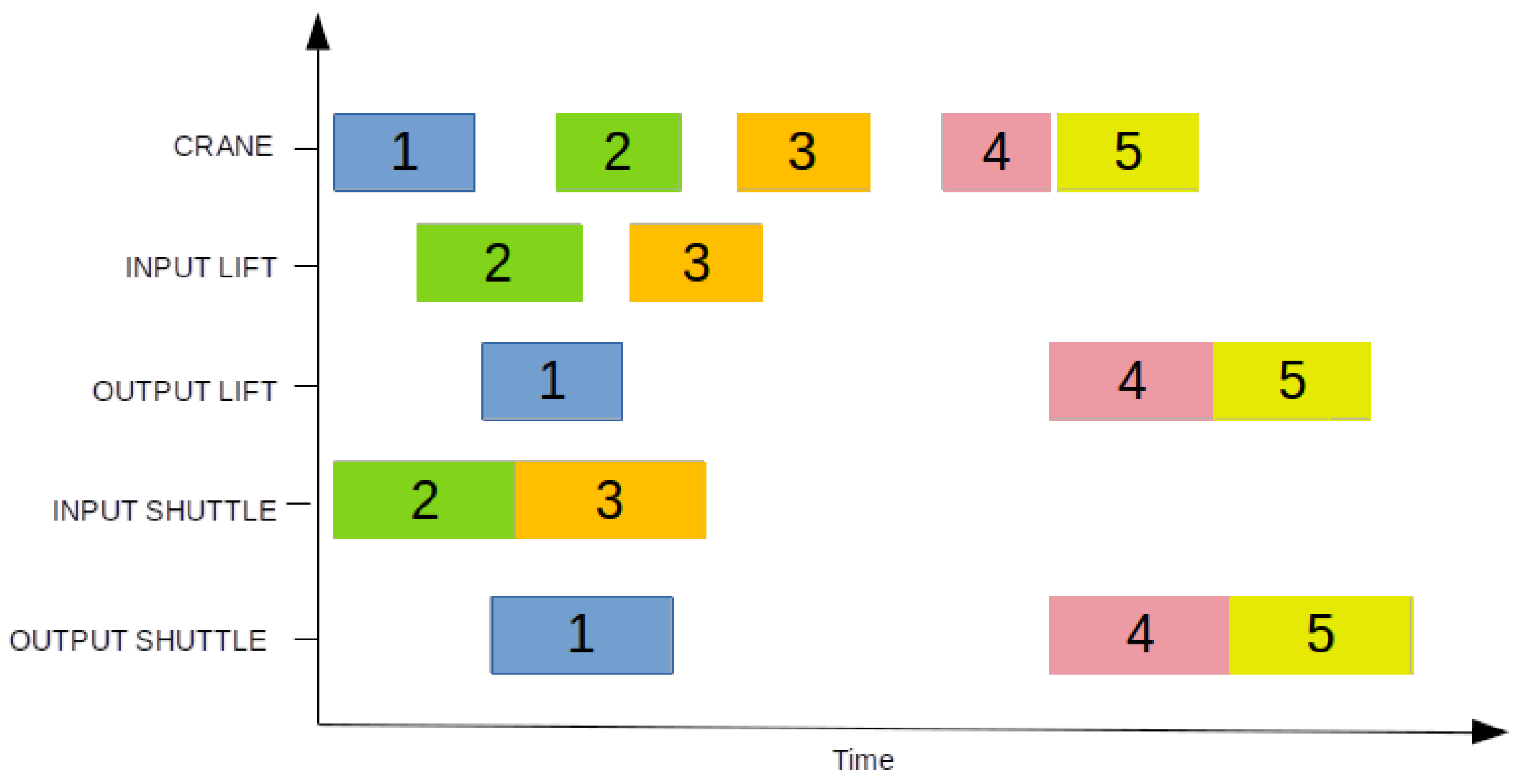
In a properly executed simulation, the timing for each event (in seconds) is detailed in Table 1. Additionally, a Gantt chart depicting the sequence of operations is presented in Figure 6.

Table 1.
Timing of the events (in seconds) associated with each of the operations in the showcased simulation.
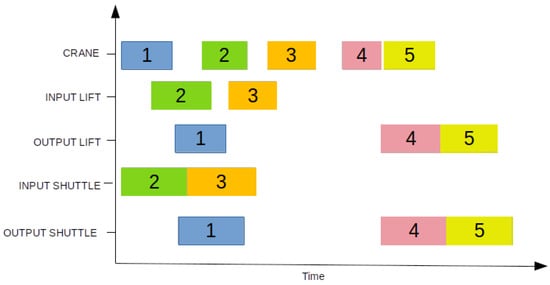
Figure 6.
Schematic representation of operations in the presented example.
6. The Proposed Simulation Optimization Algorithm
This section delineates the hybrid algorithmic approach utilized to address the aforementioned problem. This approach combines biased randomization with discrete-event heuristics; consequently, both concepts are described in the following subsections.
6.1. Biased-Randomized Heuristics
The algorithm proposed can be classified as a biased-randomized heuristic. BR algorithms are part of the family of random search methods extensively employed for addressing large-scale NP-hard optimization problems. As described by Dominguez et al. [7], in a BR algorithm, solution-building elements are arranged in a list based on logical criteria specific to the optimization problem at hand. Subsequently, during each iteration of the solution-construction process, a new element is selected from this list according to a probability distribution. The probability of selection increases with a higher position of the element in the sorted list. This approach aims to introduce slight modifications to the greedy constructive path, facilitating exploration beyond local optima by traversing ‘similar’ paths (retaining most of the heuristic logic) within shorter computing times.
Two of the earliest biased-randomized procedures were proposed by Arcus [23] and Tonge [24], known as biased random sampling (BRS), and used to bias the selection of randomly generated solutions. Subsequently, numerous priority-rule-based heuristics have been developed. Before the advent of BR techniques utilizing skewed probability distributions like the geometric one, probabilistic tabu search (PTS) was introduced by Glover [25] and expanded upon again by Glover [26]. Another metaheuristic framework implementing similar concepts is ant colony optimization (ACO), pioneered by Dorigo and Gambardella [27]. However, many of these approaches define probabilities using empirical distributions. An alternative approach advocates employing theoretical probability distributions. Consequently, some authors have advocated for the implementation of skewed theoretical probability distributions to devise BR algorithms. Overall, the primary advantages of utilizing a theoretical probability distribution over empirical ones include: (i) the reduced computing times required for generating random numbers (employing analytical expressions instead of loops); and (ii) simplification of the fine-tuning process (which might become intricate when using empirical probability distributions due to the numerous parameters and their ranges). Among the most commonly used theoretical probability distributions in BR algorithms is the geometric distribution, chosen likely due to its flexibility, simplicity, and dependence on a single parameter. The algorithm’s dependence on a single parameter streamlines the fine-tuning process, avoiding time-consuming complexities.
6.2. Adding Discrete Event Simulation Principles to BR
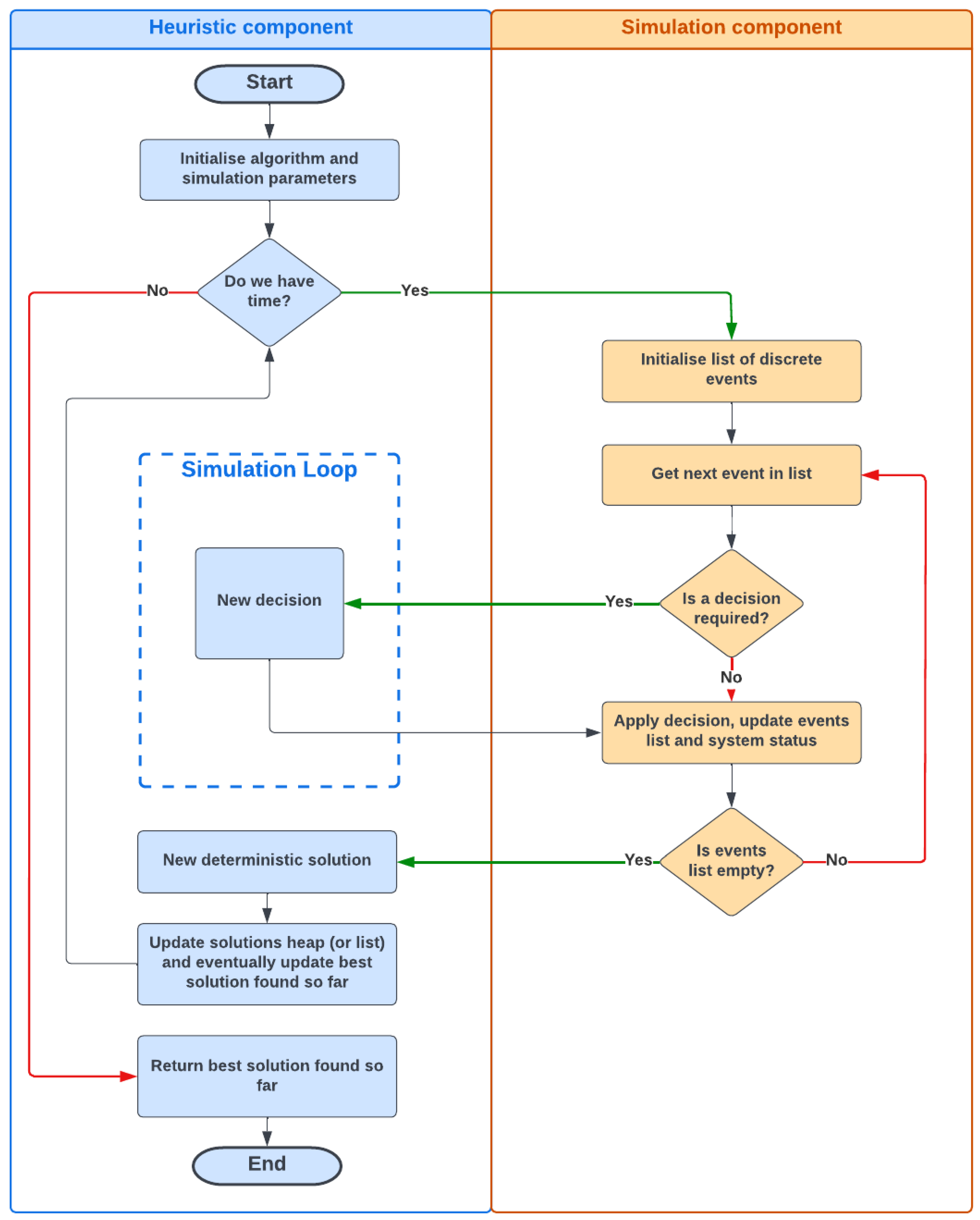
To synchronize the various events within the warehouse, the BR heuristic is enhanced with a discrete event simulation. Employing DES allows for a consistent and reliable evaluation of the impacts of BR decisions. Given the system’s high parallelism and synchronization complexities, measuring the makespan of a set of operations would be infeasible without DES. Consequently, during the deterministic discrete event simulation of the system, a BR process is employed at each decision stage to select the next building element from a list of candidates. This hybrid BR-DES approach facilitates the rapid generation of a range of feasible solutions (in terms of event synchronization) guided by the logic of the constructive heuristic, ensuring potentially favorable solutions in terms of quality. The integration of BR with DES is depicted in Figure 7. The entire algorithm can be visualized as a multi-start framework, where, until the computational time does not surpass a predefined threshold, new, random but oriented solutions are continually generated from scratch. This architecture comprises two distinct components: the BR heuristic, which includes a Monte Carlo simulation that makes random but oriented decisions, and the discrete event simulation. Each new solution is created by running the simulation, delegating decisions to BR within what we term the algorithm simulation loop. Subsequently, the new solution is compared with the best solution obtained so far and this is replaced if superior.
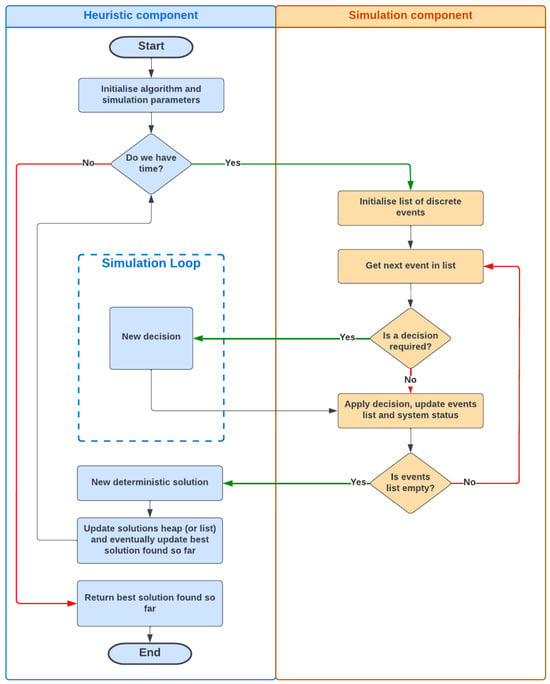
Figure 7.
Flowchart of a generic discrete-event heuristic.
Within the simulation loop, key decisions made by BR include the sequencing of input and output operations, the selection of retrieved bundles to fulfil customer orders, and the allocation of storage locations for entering bundles. Specifically, input and output requests are jointly processed using an FIFO criterion. For each request, the algorithm strives to deliver a satisfactory and feasible solution—such as assigning a storage location for input operations or a set of bundles for output operations. If the solution found is deemed infeasible, the request is postponed, and the subsequent input request is processed. For instance, when represents an input request and the solution is infeasible, all subsequent input requests originating from the same input point are deferred. This strategy minimizes changes to the input request queue, crucial due to the complexities of handling large metal bar bundles, as detailed in Section 4. Specifically, if the non-feasible input request involves storing a bundle of type , all subsequent inputs are postponed until after the next output request requiring retrieval of the same bundle type. This action, as exemplified in Table 2, ensures sufficient space is created by the output request, guaranteeing fulfillment of the previously postponed non-feasible request k.

Table 2.
List of requests before (left) and after (right) the postponement process.
If the non-feasible request pertains to an output, it is deferred until after the subsequent input that introduces the required product type into the system. The pseudo-code outlining the overall BR-DES algorithm is presented in Algorithm 1. The parameters within the algorithm should be interpreted as follows: requests denotes the list containing both input and output orders to be processed; racks signifies the list of warehouse racks; and beta represents the vector of parameters utilized for the geometric distributions employed in the various BR processes.
| Algorithm 1 Pseudo-code of the proposed BR-DES algorithm. | |
| input: requests, racks, beta | |
| ▹ init final solution | |
| while length(requests) > 0 do | |
| ▹ init solution to current request | |
| if type() == Input then | |
| else if type() == Output then | |
| end if | |
| if isFeasible() then | |
| ▹ request postponed | |
| else | |
| end if | |
| end while | |
| return | |
For an input operation, the objective is to identify an available space within the warehouse to accommodate the incoming bundle. The space must be sufficiently long, aligning with the bundle’s type (code). To determine a viable solution, all racks are taken into consideration. During each iteration, racks are prioritized based on the availability of their respective cranes, with one of these racks chosen through a BR procedure. This phase is crucial for ensuring an equitable distribution of workload among all cranes. Specifically, the BR procedure incorporates a geometric probability distribution, as proposed in Hatami et al. [28]. If x denotes the position occupied by a candidate in the previously sorted list and represents the parameter of the geometric probability distribution, then the probability of selecting candidate x is calculated as follows:
When the chosen rack contains feasible storage locations, one of them is randomly selected using a uniform distribution. The decision is recorded in the emerging solution, and a new operation is scheduled to update the system’s state. However, if the selected rack lacks feasible space, it is eliminated from the list of potential racks, and the BR rack-selection process is reiterated. If the list of potential racks becomes empty without finding a solution, a non-feasible solution is returned. In such cases, the BR-DES procedure postpones the input request. The pseudo-code for processing input operations is presented in Algorithm 2.
| Algorithm 2 Pseudo-code for input processing | |
| input: , , , | |
| copy | ▹ list of racks to consider |
| ▹ solution to the current request | |
| whileanddo | |
| sort | ▹ sort racks prioritizing the busiest |
| ones | |
| findBR | ▹ select a rack by using BR |
| feasiblePlaces | ▹ feasible storage locations |
| if then | |
| randomUniformChoice | ▹ pick a random storage location |
| new | |
| scheduleOperation | ▹ schedule the new operation to carry out |
| else | ▹ if rack has no feasible solution, remove it |
| remove | |
| end if | |
| end while | |
| return | |
For output operations, constructing a solution involves selecting multiple bundles. Upon choosing a bundle, the system’s state must be updated to accurately select the subsequent bundle. However, the solution cannot be deemed feasible until all required bundles have been retrieved. Therefore, before initiating solution construction, the system’s state is saved to enable restoration to a previous state if the solution is found to be non-feasible. The construction process operates iteratively. If, at any stage, quantity constraints are violated and no feasible bundles remain, the process is halted, the system state is restored, and a non-feasible warning is issued. Similarly, if the construction process adheres to quantity constraints but violates quality constraints, the system state is restored and a non-feasible warning is issued. For a bundle to be considered feasible, its weight, in addition to the weight of the current solution, must not surpass a predefined threshold. Bundles from prior input operations are only considered if the respective input operation has concluded. If no feasible bundles exist in the selected rack, the rack is eliminated from the list of potential racks, and the process begins anew with another rack. Conversely, if feasible bundles are available, they are arranged by decreasing the weight and then by the difference between their quality and the required quality level. Bundles with quality levels closer to the required level are given priority. Once the bundles are sorted, one of them is selected using a new geometric distribution (note that the parameter value used here may differ from the one used for rack selection). Subsequently, the solution’s weight, total quality, and the count of retrieved items are updated. The system state is also updated, and the list of possible racks is reset. This process continues iteratively until a feasible solution is achieved. The pseudo-code for processing output operations is detailed in Algorithm 3.
| Algorithm 3 Pseudo-code for output processing. | |
| input: , , , | |
| copy | ▹ save the state of the solution |
| ▹ solution to the current request | |
| copy | ▹ list of racks to consider |
| ▹ total weight of retrieved bundles | |
| ▹ total quality of retrieved bundles | |
| ▹ number of retrieved bundles | |
| while and do | |
| sort | ▹ sort racks prioritizing the busiest |
| ones | |
| findBR | ▹ select a rack by using BR |
| feasibleBundles | ▹ feasible bundles in rack |
| if then | |
| sort | ▹ sort bundles by weight |
| sort | ▹ sort bundles by quality |
| findBR | ▹ select a bundle by using BR |
| ▹ update weight | |
| ▹ update quality | |
| ▹ update number of retrieved bundles | |
| new | ▹ instantiate a retrieve |
| scheduleOperation | ▹ schedule a retrieval operation |
| add | |
| copy | ▹ restore the set of possible racks |
| else | |
| remove | |
| end if | |
| end while | |
7. Computational Experiments
The BR-DES algorithm was implemented in Python and executed using the CPython interpreter. The testing was conducted on a standard personal computer equipped with an Intel QuadCore CPU running at GHz and 8 GB RAM with the Ubuntu operating system. When constructing the experimental data sets, the quality level of each bundle was randomly generated using a uniform probability distribution between 1 (minimum level) and 10 (maximum level). Then, the quality of a solution was computed as the average of the quality of the retrieved bundles. The input quantity was randomly generated using a uniform probability distribution between 700 and 1300, expressed in kilograms. We assume that two bundles enter together as input, each with an average weight of 500 kg. Finally, since a customer might require many bundles, the output quantity was randomly generated using a uniform probability distribution between 700 and 10,000, expressed in kilograms. Table 3 displays the data corresponding to Instance 1, where type 0 represents an input point and type 1 refers to an output point. Both the desired quality and quantity are provided as reference values. These reference values will be compared with those associated with the solution provided by each algorithm to calculate the mismatch. Similar data for the remaining instances, as well as the algorithm code, are available at https://github.com/mattianeroni/Shuttle-Lift-Crane-AS-RS (accessed on 15 January 2024).

Table 3.
Example of an instance data set—Instance 1.
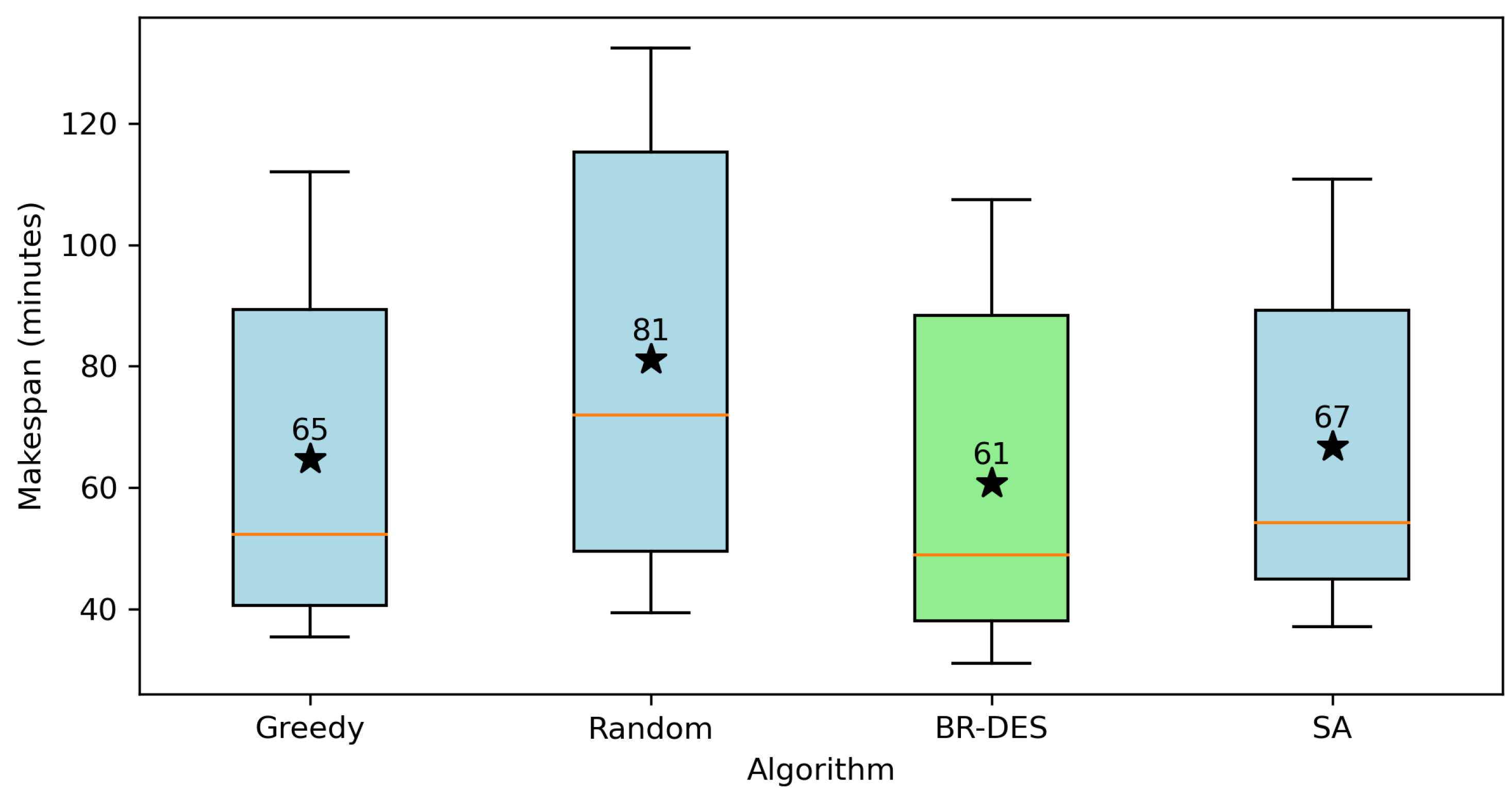
As can be seen in Table 4 and Table 5, our algorithm demonstrates an efficient performance, since it is capable of providing competitive solutions in just a few seconds, while other approaches require noticeably longer times without reaching the same solution quality. To validate the proposed methodology, a comparison with three distinct approaches is presented. The selected benchmark approaches are as follows: (i) a random algorithm utilizing a uniform probability distribution to select from different possibilities at each step of the solution-construction process; (ii) a greedy heuristic that consistently chooses the top-listed element in the candidates’ list, sorted based on a minimum time criterion; and (iii) the simulated annealing method proposed by Bertolini et al. [6] for a similar problem, adapted for the specific problem considered in this study by incorporating new constraints. The random approach serves as a lower-bound benchmark and was obtained by implementing the proposed BR-DES while substituting the geometric distribution with a uniform distribution. This adjustment was achieved by setting the beta value to 0 in the BR-DES algorithm. However, when employing such low beta values, the algorithm often failed to find a feasible solution. To address this limitation, we utilized a geometric probability distribution with a slightly higher beta value of , allowing the algorithm to discover feasible solutions in most test scenarios, although not all. On the other hand, the greedy algorithm presents a practical solution for warehouse system managers and was acquired by implementing the proposed BR-DES with a beta value of 1. The SA algorithm by Bertolini et al. [6] is currently the only algorithm explicitly tailored for this type of automated warehouse system (i.e., an SLC-AS/RS). While theoretically serving as a solid benchmark, the original SA algorithm did not consider any constraints regarding the sequence of request processing. To ensure a fair comparison, we integrated these constraints into the SA algorithm.

Table 4.
Comparison of makespans (in minutes) achieved by the greedy, random, BR-DES, and SA approaches for each instance (row).

Table 5.
Computational times (in seconds) associated with each of the approaches (greedy, random, BR-DES, and SA) for each instance (row).
For the comparison, we employed the actual layout of an SLC-AS/RS consisting of three racks, each containing 500 storage locations, with two input and two output points. In the computational experiments, 12 different request lists were used, each varying in size (30, 60, 90, and 150 requests). Every algorithm was executed three times on each request list to monitor both its average performance and its variability. The comparison primarily focuses on the total makespan, expressed in minutes (Table 4), and computational time (Table 5). Additionally, we monitored the overall mismatch between the quantities and quality levels required by customers (Table 6). The parameters of the proposed algorithm, namely the betas of the geometric distribution used in the selection of racks () and bundles (), were adjusted in each iteration according to trimmed Gaussian distributions. The means of these Gaussian distributions ( and ) were determined through a series of empirical experiments, exploring combinations of and with a step of . Both were set with a standard deviation of . Regarding SA, the same parameter values as proposed in Bertolini et al. [6] were employed. All BR-DES and SA results were acquired after exploring 1000 solutions. The makespan results are presented in Table 4. As anticipated, our proposed algorithm consistently outperforms the greedy and random approaches, as well as the SA algorithm, in all instances. Notably, the random and greedy approaches often fail to find feasible solutions, whereas our algorithm consistently obtains feasible solutions in all scenarios.

Table 6.
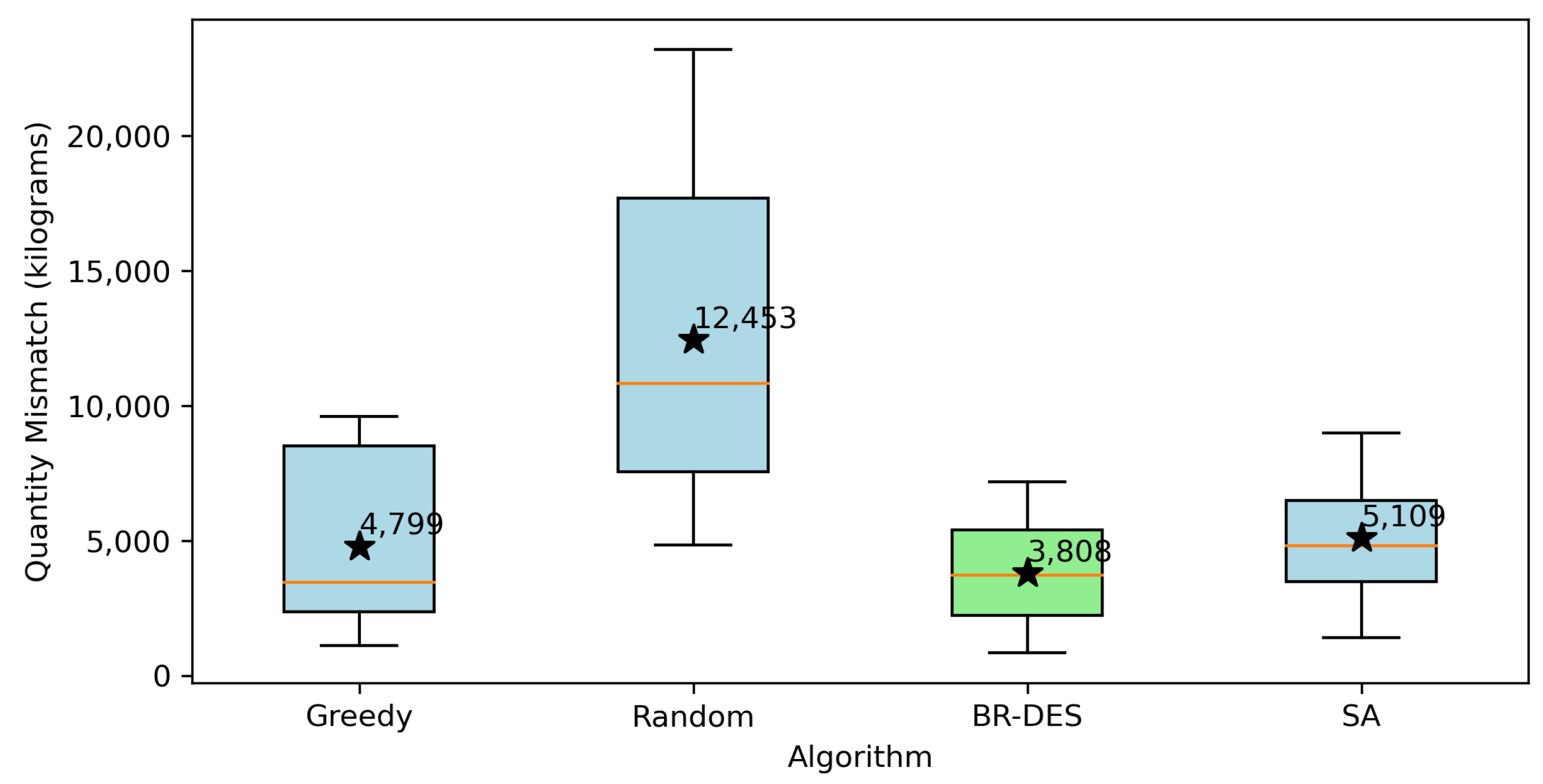
Mismatches in quantity (kilograms) and quality levels between the required and retrieved items for each approach (greedy, random, BR-DES, and SA) and instance (row).
An additional noteworthy aspect is the greater variability exhibited by the SA algorithm when compared to the BR-DES algorithm. This variability is due to the SA algorithm’s exploration of infeasible solutions across numerous iterations, as it is not guided by a discrete event list. In contrast, BR-DES operates based on a discrete event list, allowing for feasibility and making informed decisions at each stage. Consequently, it requires considerably less computational time to achieve comparable or superior solutions compared to those generated by the SA algorithm. Computational times are displayed in Table 5. Notably, our BR-DES consistently outperforms the SA algorithm in terms of solution quality as well as computational efficiency. Throughout the tests, we closely monitored the deviation, encompassing both quantity and quality indicators, between the optimal solution derived by the algorithms and the customer-requested specifications. Table 5 presents the aggregate discrepancy observed after fulfilling all the requests. Each algorithm underwent three executions for each instance. In these terms, BR-DES emerges as the superior approach. The top solutions obtained by BR-DES for each instance are significantly approximate to the customers’ specified requirements, both in terms of quality and quantity. Following closely, the SA algorithm constitutes the second-best alternative. At times, the greedy algorithm produces commendable solutions. However, this achievement often prolongs the makespan. Minimizing the divergence between the proposed solution and the customers’ stipulations holds immense significance. Even as the primary objective revolves around reducing the makespan, meticulous adherence to the aforementioned quality and quantity requisites significantly augments customer satisfaction.
Figure 8 and Figure 9 visually juxtapose the considered approaches with regards to makespan and quantity mismatch. Since the greedy and random approaches fail to produce feasible solutions for Instances 10 to 12, only Instances 1 to 9 are considered in these figures. Notice that the BR-DES algorithm outperforms all other approaches both in terms of the makespan and the quantity mismatch.
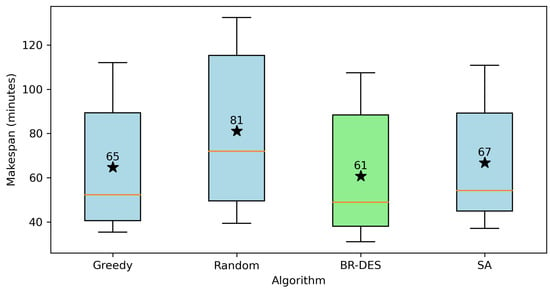
Figure 8.
Makespan comparison of different approaches.
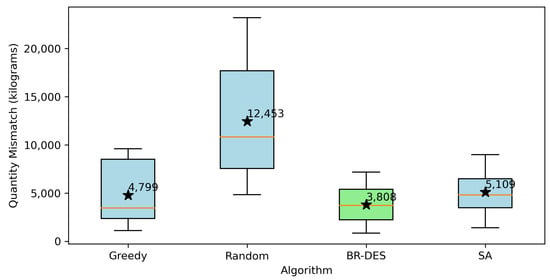
Figure 9.
Quantity mismatch comparison of different approaches.
8. Conclusions and Future Perspectives
This paper has discussed a complex and realistic warehouse automated storage and retrieval system (AS/RS) in the steel industry sector. The peculiar characteristics of this sector, notably the considerable size and weight of items and bundles stored and retrieved, alongside stringent quality constraints, constitute a challenge when enhancing the system performance. Traditional approaches such as developing a simulation model or employing classical optimization methods, albeit viable, present limitations to providing optimal solutions within reasonable computational time frames. Hence, this paper advocates a novel hybrid simulation optimization algorithm. It combines the precision of discrete event simulations, crucial in managing time dependencies within the system’s sequential operations, with a biased-randomized heuristic. This combination, encapsulated within a multi-start framework, swiftly generates a multitude of promising, high-quality solutions in seconds, outperforming the more traditional simulated annealing (SA) metaheuristic. Although the SA algorithm is a robust approach, it struggles to adequately address the intricate time dependencies among events in the warehouse system.
Our approach boasts adaptability, a key advantage for accommodating novel scenarios. Based on simulation principles, it holds the potential to evolve into a simheuristic [28], adept at tackling stochastic versions of the problem. This adaptability extends to various AS/RS configurations, thus illustrating its versatility. Furthermore, the computational experiments conducted confirm the capacity of our approach in providing feasible and high-quality solutions for optimization problems characterized by complex constraints, especially those entailing intricate time dependencies among decisions.
From a managerial perspective, the proposed approach can enhance decision-making processes, particularly in managing the complexities of AS/RS operations characterized by time-dependent sequences and stringent constraints. The BR-DES algorithm is specifically tailored to the challenges of steel storage systems, including large item sizes, substantial weights, and strict quality constraints. From a business impact perspective, the algorithm contributes to improving the operational efficiency by rapidly generating high-quality solutions, resulting in a reduced makespan and optimized resource utilization. This, in turn, can lead to savings in labor, energy, and equipment usage. The algorithm’s focus on reducing the discrepancy between the proposed solutions and customer specifications ensures an enhanced customer satisfaction, thereby positively impacting customer relations.
The following points outline the potential directions for future research: (i) extending our approach to achieve full automation, enabling the algorithm to make decisions autonomously without human intervention; (ii) improving the algorithm’s handling of weight and quality constraints, particularly in more constrained scenarios, to enhance its effectiveness even further; and (iii) expanding the approach to encompass scenarios involving random times and stochastic availability of items, broadening its applicability to diverse, less deterministic environments.
Author Contributions
Conceptualization, M.B. and M.N.; methodology, A.A.J. and M.N.; software, M.N.; writing—original draft preparation, M.N., A.A.J. and M.B.; writing—review and editing, A.A.J. and M.B. All authors have read and agreed to the published version of the manuscript.
Funding
This work was partially funded by the Horizon Europe program (HORIZON-CL4-2022-HUMAN-01-14-101092612 SUN and HORIZON-CL4-2021-TWIN-TRANSITION-01-07-101057294 AIDEAS), as well as by the Generalitat Valenciana (PROMETEO/2021/065).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
All data and code is available at https://github.com/mattianeroni/Shuttle-Lift-Crane-AS-RS (last accessed on 15 January 2024).
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Zhang, G.; Lai, K. Combining path relinking and genetic algorithms for the multiple-level warehouse layout problem. Eur. J. Oper. Res. 2006, 169, 413–425. [Google Scholar] [CrossRef]
- Roodbergen, K.J.; Vis, I.F. A survey of literature on automated storage and retrieval systems. Eur. J. Oper. Res. 2009, 194, 343–362. [Google Scholar] [CrossRef]
- Chen, L.; Langevin, A.; Riopel, D. The storage location assignment and interleaving problem in an automated storage/retrieval system with shared storage. Int. J. Prod. Res. 2010, 48, 991–1011. [Google Scholar] [CrossRef]
- Foley, R.D.; Hackman, S.T.; Park, B.C. Back-of-the-envelope miniload throughput bounds and approximations. IIE Trans. 2004, 36, 279–285. [Google Scholar] [CrossRef]
- Kosanić, N.Ž.; Milojević, G.Z.; Zrnić, N. A survey of literature on shuttle based storage and retrieval systems. FME Trans. 2018, 46, 400–409. [Google Scholar] [CrossRef]
- Bertolini, M.; Esposito, G.; Mezzogori, D.; Neroni, M. Optimizing retrieving performance of an automated warehouse for unconventional stock keeping units. Procedia Manuf. 2019, 39, 1681–1690. [Google Scholar] [CrossRef]
- Dominguez, O.; Juan, A.A.; Faulin, J. A biased-randomized algorithm for the two-dimensional vehicle routing problem with and without item rotations. Int. Trans. Oper. Res. 2014, 21, 375–398. [Google Scholar] [CrossRef]
- Bertolini, M.; Neroni, M.; Uckelmann, D. A survey of literature on automated storage and retrieval systems from 2009 to 2019. Int. J. Logist. Syst. Manag. 2023, 44, 514–552. [Google Scholar] [CrossRef]
- Liu, S.; Wang, Q.; Sun, J. Integrated optimization of storage allocations in automated storage and retrieval system of bearings. In Proceedings of the 25th Chinese Control and Decision Conference, Guiyang, China, 25–27 May 2013; pp. 4267–4271. [Google Scholar]
- Wang, W.; Tang, X.; Shao, Z. Study on energy consumption and cable force optimization of cable-driven parallel mechanism in automated storage/retrieval system. In Proceedings of the Second International Conference on Soft Computing and Machine Intelligence, Dubai, United Arab Emirates, 23–25 November 2016; pp. 144–150. [Google Scholar]
- Lerher, T.; Sraml, M.; Potr, I. Simulation analysis of mini-load multi-shuttle automated storage and retrieval systems. Int. J. Simul. Model. 2015, 14, 48–59. [Google Scholar] [CrossRef]
- Ekren, B.Y.; Heragu, S.S.; Krishnamurthy, A.; Malmborg, C.J. Matrix-geometric solution for semi-open queuing network model of autonomous vehicle storage and retrieval system. Comput. Ind. Eng. 2014, 68, 78–86. [Google Scholar] [CrossRef]
- Liu, T.; Gong, Y.; De Koster, R.B. Travel time models for split-platform automated storage and retrieval systems. Int. J. Prod. Econ. 2018, 197, 197–214. [Google Scholar] [CrossRef]
- Zou, B.; Xu, X.; Gong, Y.; De Koster, R. Modeling parallel movement of lifts and vehicles in tier-captive vehicle-based warehousing systems. Eur. J. Oper. Res. 2016, 254, 51–67. [Google Scholar] [CrossRef]
- Ekren, B.; Heragu, S. A New Technology for Unit-Load Automated Storage System: Autonomous Vehicle Storage and Retrieval System; Springer: London, UK, 2012; pp. 285–339. [Google Scholar]
- Roy, D.; Krishnamurthy, A.; Heragu, S.S.; Malmborg, C.J. Performance analysis and design trade-offs in warehouses with autonomous vehicle technology. IIE Trans. 2012, 44, 1045–1060. [Google Scholar] [CrossRef]
- Liu, T.; Xu, X.; Qin, H.; Lim, A. Travel time analysis of the dual command cycle in the split-platform AS/RS with I/O dwell point policy. Flex. Serv. Manuf. J. 2016, 28, 442–460. [Google Scholar] [CrossRef]
- Hu, Y.H.; Huang, S.Y.; Chen, C.; Hsu, W.J.; Toh, A.C.; Loh, C.K.; Song, T. Travel time analysis of a new automated storage and retrieval system. Comput. Oper. Res. 2005, 32, 1515–1544. [Google Scholar] [CrossRef]
- Cai, X.; Heragu, S.S.; Liu, Y. Modeling and evaluating the AVS/RS with tier-to-tier vehicles using a semi-open queueing network. IIE Trans. 2014, 46, 905–927. [Google Scholar] [CrossRef]
- Carlo, H.J.; Vis, I.F.A. Sequencing dynamic storage systems with multiple lifts and shuttles. Int. J. Prod. Econ. 2012, 140, 844–853. [Google Scholar] [CrossRef]
- Zammori, F.; Neroni, M.; Mezzogori, D. Cycle time calculation of shuttle-lift-crane automated storage and retrieval system. IISE Trans. 2021, 54, 40–59. [Google Scholar] [CrossRef]
- Arnau, Q.; Barrena, E.; Panadero, J.; de la Torre, R.; Juan, A.A. A biased-randomized discrete-event heuristic for coordinated multi-vehicle container transport across interconnected networks. Eur. J. Oper. Res. 2022, 302, 348–362. [Google Scholar] [CrossRef]
- Arcus, A.L. A computer method of sequencing operations for assembly lines. Int. J. Prod. Res. 1965, 4, 259–277. [Google Scholar] [CrossRef]
- Tonge, F.M. Assembly line balancing using probabilistic combinations of heuristics. Manag. Sci. 1965, 11, 727–735. [Google Scholar] [CrossRef]
- Glover, F. Tabu search—Part I. ORSA J. Comput. 1989, 1, 190–206. [Google Scholar] [CrossRef]
- Glover, F. Tabu search—Part II. ORSA J. Comput. 1990, 2, 4–32. [Google Scholar] [CrossRef]
- Dorigo, M.; Gambardella, L.M. Ant colony system: A cooperative learning approach to the traveling salesman problem. IEEE Trans. Evol. Comput. 1997, 1, 53–66. [Google Scholar] [CrossRef]
- Hatami, S.; Calvet, L.; Fernandez-Viagas, V.; Framinan, J.M.; Juan, A.A. A simheuristic algorithm to set up starting times in the stochastic parallel flowshop problem. Simul. Model. Pract. Theory 2018, 86, 55–71. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).