Theoretical Study of the Wear of a Reduced-Diameter Wheel for Freight Wagons, Based on Its Diameter

Abstract

This paper presents the development of a numerical analysis model designed to estimate the lifespan of reduced-diameter wheels used in freight wagons based on their diameter, under quasi-static conditions. These wheels are increasingly being used in combined transport applications, where they are installed in various bogie configurations and subjected to different operational environments. However, due to the unique characteristics of reduced-diameter wheels, their lifespan has been scarcely studied. To accurately build this model, an in-depth investigation of the rolling phenomenon was required, addressing key issues in the track–vehicle interaction and establishing relationships between these factors. After constructing the rail–wheel interaction model, it was applied to calculate the lifespan of wheels with standard, medium, and reduced diameters under identical conditions for comparison. This approach makes it possible to determine the lifespan of reduced-diameter wheels relative to standard ones, as well as to observe how lifespan changes with wheel diameter, and it is observed how lifespan diminishes non-linearly with decreasing diameters. The underlying reasons for this variation are explained through a comprehensive understanding of the rolling phenomenon, enabled by the full analysis.

1. Introduction

The goal of this study is to address the wear issue associated with reduced-diameter wheels, which unlike standard-diameter wheels, may experience different wear patterns due to their increased angular contact with the rail for the same mileage. To achieve this, a calculation model was developed to estimate the lifespan of a wheel based on a key operational factor: the nominal wheel diameter.

In response to evolving logistic needs and emerging transportation models, the rail motorway model has gained popularity in recent years. This model is detailed in a recent publication by the authors [1] and depicted in Figure 1:

Notwithstanding the adoption of this model, it does generate some inconveniences, which are commented upon in the same reference. These inconveniences are why the usage of reduced-diameter wheels was recommended, as it is explained in that reference and shown in Figure 2, which is also based on the Spanish regulation on railway height gauges [2]:

A standard wheel typically has a diameter of around 920 mm, whereas a reduced-diameter wheel measures between one-half and one-third of that size. This poses a new problem: if a wheel whose diameter has been halved must roll the same distance as an ordinary-diameter wheel, then the former will have to revolve twice around its rotation axis. Also, its contact angle with the rail will be higher due to its smaller size, and it will have less material to support and withstand the same load. Taking this information into account, it can be foreseen that the reduced-diameter wheel is likely to experience more intense wear and rolling contact fatigue (RCF) than the ordinary-diameter wheel. However, this is only a prediction and must be proved and validated mathematically, taking into account as many factors as possible:

• Wheel factors: geometry (diameter, conicity, tread width, contact angle), machining (roughness), material (properties), load, and previous wear.
• Wagon factors: configuration (bogies or axles distribution and type of bogies), type of suspension, braking system, running speed, and load distribution (axle load).
• Railway superstructure factors: track gauge, line layout (curve radii, windiness, sagitta, gradient, etc.), layout quality (excess or deficiency in cant, transition curves, etc.), type of rail (welded or with joints), track materials (properties) and track previous degradation (previous rail wear, specially).
• External factors: Temperature, humidity, wind, rain, snow, and weather in general. The presence of moisture, leaves, and pollutants (saltpeter, oil, etc.) is important here too.

The process involves creating a mathematical model based on behavioral equations derived from existing models that explain wheel degradation, each incorporating a set of assumptions. While the analytical model should account for as many influencing factors as possible, it must also be constrained in size to ensure computational efficiency. This means that additional assumptions will be made to exclude factors with minimal impact on wheel degradation.

This study focuses on the Spanish conventional railway network due to the current push for rail motorways in Spain, which faces certain implementation challenges. Specifically, the conventional network has a restrictive loading gauge [3], leading to the use of reduced-diameter wheels. Additionally, the tight curves and steep gradients of this network cause significant wear on these wheels.

These wheels are part of wheelsets, which consist of an axle and a pair of wheels. Typically, wheelsets are configured in two-axle (two-wheelset) bogies. According to the same source, two bogies are sufficient for a flat-bed wagon used in rail motorways, making this type of railway vehicle the focus of the wheel degradation analysis. Consequently, this study will concentrate on freight transport within the Spanish national railway network, which has a specific track gauge of 1668 mm. External factors that are highly variable and difficult to predict will be excluded from this analysis.

This research paper can be compared to other advanced studies on wheel wear calculation, but it differs in several notable ways. In this paragraph, these differences are discussed in detail: To start with, Refs. [4,5,6,7] focus on polygonal wheel wear, which is a relevant problem in high-speed railway lines, but they do not include RCF and abrasive-adhesive wear, which cause significant trouble in rail freight transportation. Ref. [8] correlates RCF and abrasive-adhesive wear through analytical models and proves the results experimentally, although it does not give insight into wheel life, not even for ordinary-diameter wheels. Ref. [9] is very specific as it focuses on the wheel wear caused under different braking modes, without covering the wear appearing when the vehicle is not braking. Refs. [10,11] are very specific as they focus on the effect of wheel diameter difference, i.e., when the wheels in a wheelset do not have the same diameter, and wheel life is not studied (only numerical simulations and experiments for 200,000 km). Refs. [12,13] focus on the optimization of the reprofiling cycles for wheels, although their diameter is not varied and the strategy is drawn up only for ordinary-diameter ones. Ref. [14] develops a wheel–rail contact model which considers many structural elements of the vehicle and the infrastructure; however, it does not consider reduced-diameter wheels either. To end with, Ref. [15] reviews as many numerical models for rail–wheel contact as possible, while Ref. [16] compares different wear indicators for quantifying wheel wear in rail freight operations; even so, the former does not discuss numerical models for reduced-diameter wheels, and the latter does not apply the wear indicators to them.

The primary contribution of this work is addressing the wear issue of reduced-diameter wheels, a topic that has been scarcely explored due to the unique characteristics of these wheels. This study offers an in-depth analysis of the kinematics and dynamics of wheels, wheelsets, and bogies, providing valuable insights into why wheel lifespan varies with diameter and the nature of this dependency.

Unlike previous research, this study proposes several realistic scenarios based on rail motorways and varies wheel diameter during the analysis process. By maintaining consistent or equivalent parameters throughout, this study enables meaningful comparisons across different scenarios.

2. Methods and Materials

This work follows a deductive methodology:

First, the rail–wheel contact problem was analyzed based on the theory of contact friction mechanics, which has been developed since the late 18th century.

Second, various contact models were evaluated for their accuracy and computational efficiency. The models selected for this study include Hertz’s solution, Polach’s method, the center of friction, energy transfer, and the fatigue index.

Next, these selected models were applied to address key issues in the vehicle–track interaction. The interface between the vehicle and track was parameterized for this analysis.

While each model comes with its own set of assumptions, additional hypotheses were introduced to define the problem scope. These assumptions are crucial for incorporating important factors and excluding others that have minimal impact on the solution.

Each model is represented by a set of equations, allowing for their interrelation through geometrical and mathematical connections. This enabled the creation of a numerical analysis model in the form of an algorithm. The algorithm was implemented using equation-solving software, which solves all equations once the necessary data are provided.

The results, presented as the wear depth of each wheel on a given bogie, also predict the onset of rolling contact fatigue (RCF). When the wear depth on a wheel reaches a predefined threshold, all the wheels on the bogie are reprofiled, and the wear cycle restarts (the algorithm is re-executed). Notably, key parameters such as nominal wheel diameter can be adjusted as needed.

Finally, the results for wheels of different diameters are compared, and conclusions are drawn regarding their behavior and the influence of wheel diameter.

2.1. Abbreviations List

The abbreviations used in this article can be found in

Table A1. Latin symbol abbreviations. Source: [1].

Abbreviation	Definition	Unit (SI)	Abbreviation	Definition	Unit (SI)
$a$	Longitudinal semi-axis of Hertz’s ellipse	$\mathrm{m}$	$n_{dec}$	Degree of the function deceleration-time	$\mathrm{\varnothing }$
$a_{lat}$	Lateral acceleration experienced by the vehicle	$\mathrm{m}·{\mathrm{s}}^{-2}$	$n_{ejes}$	Number of axles on the vehicle	$\mathrm{\varnothing }$
$A$	Relative longitudinal curvature	${\mathrm{m}}^{-1}$	$n_{ejes}^{\prime }$	Number of axles on the bogie	$\mathrm{\varnothing }$
$A_c$	Hertz’s ellipse area	${\mathrm{m}}^2$	$n_H$	Lateral Hertz’s coefficient	$\mathrm{\varnothing }$
$A_f$	Ratio between the minimum friction coefficient (infinite slip speed) and the maximum (null slip)	$\mathrm{\varnothing }$	$N$	Reaction force of the rail on the wheel on the normal contact direction (normal force)	$\mathrm{N}$
$b$	Lateral semi-axis of Hertz’s ellipse	$\mathrm{m}$	$N_{br}| N_p$	Reaction force of the rail on the wheel in the normal direction to the contact area at the (tread flange) at a wheel experiencing flange–rail contact	$\mathrm{N}$
$b_i| b_e$	Distance from track center to the rolling radius of the (inner | outer) wheel in relation to the curve	$\mathrm{m}$	$N_e| N_i$	Normal force acting on the (outer| inner) wheel in relation to the curve	$\mathrm{N}$
$b_o$	Distance from track center to rolling radius	$\mathrm{m}$	$N_r| N_t$	Normal force component in the radial |tangential direction (the tangential one is perpendicular to the radial one)	$\mathrm{N}$
$B$	Relative lateral curvature	${\mathrm{m}}^{-1}$	$N_{\perp }| N_{\parallel }$	Normal force component acting on the wheel (perpendicularly|tangentially) to contact area	$\mathrm{N}$
$B_f$	Exponential constant at friction law	$\mathrm{s}·{\mathrm{m}}^{-1}$	$o$	Existing offset between the track gauge minus the flange—rail play and the distance between the nominal radius center of the wheelset wheels	$\mathrm{m}$
$c$	Effective size of contact patch	$\mathrm{m}$	$o_p$	Horizontal distance between the center of the flange contact area center and the center of the wheel	$\mathrm{m}$
$C$	Contact tangential stiffness	$\mathrm{N}·{\mathrm{m}}^{-3}$	$p_{z_o}$	Maximum contact normal pressure	$\mathrm{P}\mathrm{a}$
$C_S$	Contact tangential stiffness for the pure spin case	$\mathrm{N}·{\mathrm{m}}^{-3}$	$Q_i| Q_f$	Initial | final metric point	$\mathrm{m}$
$C_{11}\left|C_{22}\right|C_{33}$	Longitudinal| lateral | vertical Kalker’s coefficient	$\mathrm{\varnothing }$	$r_e| r_i$	Theorical rolling radius of the (outer| inner) wheel in relation to the curve	$\mathrm{m}$
$C_{11}^{\prime }| C_{22}^{\prime }$	Kalker’s coefficient (longitudinal |lateral) corrected according to non-dimensional slip components	$\mathrm{\varnothing }$	$r_e^{*}| r_i^{*}$	Rolling radius of the (outer | inner) wheel in relation to the curve including the displacement due to the yaw angle	$\mathrm{m}$
$C_{23}|{ C}_{32}$	$\mathrm{Kalker}’\mathrm{s} \mathrm{coefficients} \mathrm{on} y_c{z}_c$ plane	$\mathrm{\varnothing }$	$r_o$	Nominal rolling radius	$\mathrm{m}$
$D$	Nominal wheel diameter	$\mathrm{m}$	$r_p$	Wheel radius measured until the flange contact patch	$\mathrm{m}$
$e$	Total bogie wheelbase (measured from its leading to trailing wheelset)	$\mathrm{m}$	$r_{rr}$	Real rolling radius	$\mathrm{m}$
$e^{\prime }$	Partial bogie wheelbase (measured between 2 next wheelsets)	$\mathrm{m}$	$r_H$	Vertical Hertz’s coefficient	$\mathrm{\varnothing }$
$E$	Equivalent Young’s modulus of the materials in contact	$\mathrm{P}\mathrm{a}$	$R$	Curve radius (measured from its center to the track axis)	$\mathrm{m}$
$E_1| E_2$	Young’s modulus of the rail | wheel	$\mathrm{P}\mathrm{a}$	$R_{x_1}$	Rail lateral radius	$\mathrm{m}$
${\mathcal{f}}_i$	Sagitta of the inner rail in relation to the curve	$\mathrm{m}$	$R_{x_2}$	Wheel lateral radius	$\mathrm{m}$
$F$	Magnitude of tangential force vector	$\mathrm{N}$	$R_{y_1}$	Rail longitudinal radius	$\mathrm{m}$
$F_f$	Braking force	$\mathrm{N}$	$R_{y_2}$	Longitudinal wheel radius	$\mathrm{m}$
$F_t$	Traction force	$\mathrm{N}$	$s$	Magnitude of non-dimensional slip vector	$\mathrm{\varnothing }$
$F_x| F_y$	Longitudinal | lateral tangential force	$\mathrm{N}$	$s_x| s_y$	Longitudinal | lateral non-dimensional slip	$\mathrm{\varnothing }$
$F_x^{\prime }| F_y^{\prime }$	$\mathrm{Longitudinal} | \mathrm{lateral} \tan \mathrm{gential} \mathrm{force} \mathrm{translated} \mathrm{to} \mathrm{the} \mathrm{reference} \mathrm{frame} \overline{\mathcal{u}}\overline{\mathcal{v}}\overline{\mathcal{w}}$	$\mathrm{N}$	$s_C$	Magnitude of non-dimensional slip corrected with the spin contribution	$\mathrm{\varnothing }$
$F_{y,C}$	Lateral tangential force (lateral force) corrected with the spin contribution	$\mathrm{N}$	$s_{y,C}$	Lateral non-dimensional slip corrected with the spin contribution	$\mathrm{\varnothing }$
$F_{y,S}$	Increase in lateral force due to spin	$\mathrm{N}$	$T\gamma /A_c$	Wear index for the USFD law	$\mathrm{N}·{\mathrm{m}}^{-2}$
$F_{máx,RCF}$	Maximum tangential force before rolling contact fatigue appears	$\mathrm{N}$	${\mathcal{u}}_f$	$\mathrm{Coordinate} \mathrm{in} \mathrm{the} \overline{\mathcal{u}}$$\mathrm{axis} \mathrm{of} \mathrm{the} \mathrm{wheel} \mathrm{contact} \mathrm{area}, \mathrm{in} \mathrm{the} \mathrm{reference} \mathrm{frame} \overline{\mathcal{u}}\overline{\mathcal{v}}\overline{\mathcal{w}}$	$\mathrm{m}$
$F{I}_{surf}$	Fatigue index	$\mathrm{\varnothing }$	${\mathcal{u}}_{fl}$	$\mathrm{Coordinate} \mathrm{in} \mathrm{the} \overline{\mathcal{u}}$$\mathrm{axis} \mathrm{of} \mathrm{the} \mathrm{flange} \mathrm{outer} \mathrm{part}, \mathrm{in} \mathrm{the} \mathrm{frame} \overline{\mathcal{u}}\overline{\mathcal{v}}\overline{\mathcal{w}}$	$\mathrm{m}$
$g$	Gravity acceleration	$\mathrm{m}·{\mathrm{s}}^{-2}$	${\mathcal{v}}_f$	$\mathrm{Coordinate} \mathrm{in} \mathrm{the} \overline{\mathcal{v}}$$\mathrm{axis} \mathrm{of} \mathrm{the} \mathrm{wheel} \mathrm{contact} \mathrm{area}, \mathrm{in} \mathrm{the} \mathrm{frame} \overline{\mathcal{u}}\overline{\mathcal{v}}\overline{\mathcal{w}}$	$\mathrm{m}$
$G$	Equivalent shear modulus of the materials in contact	$\mathrm{P}\mathrm{a}$	${\mathcal{v}}_{fl}$	$\mathrm{Coordinate} \mathrm{in} \mathrm{the} \overline{\mathcal{v}}$$\mathrm{axis} \mathrm{of} \mathrm{the} \mathrm{flange} \mathrm{outer} \mathrm{part}, \mathrm{in} \mathrm{the} \mathrm{frame} \overline{\mathcal{u}}\overline{\mathcal{v}}\overline{\mathcal{w}}$	$\mathrm{m}$
$G_1|{ G}_2$	Shear module of the rail | wheel	$\mathrm{P}\mathrm{a}$	$v_x| v_y$	Longitudinal| lateral creepage	$\mathrm{\varnothing }$
$h_r$	Real cant of the railway line	$\mathrm{m}$	$V$	Vehicle speed	$\mathrm{m}·{\mathrm{s}}^{-1}$
$H_{CdG}$	$\mathrm{Center} \mathrm{of} \mathrm{gravity} \mathrm{of} {\lambda }_{eje}$ height over the rolling plane		$V_f| V_i$	Final | initial vehicle speed	$\mathrm{m}·{\mathrm{s}}^{-1}$
$H_{tara}$	$\mathrm{Center} \mathrm{of} \mathrm{gravity} \mathrm{of} {\lambda }_{tara}$ height over the rolling plane	$\mathrm{m}$	$w_x|{ w}_y$	Longitudinal| lateral slip speed	$\mathrm{m}·{\mathrm{s}}^{-1}$
$H_u$	$\mathrm{Center} \mathrm{of} \mathrm{gravity} \mathrm{of} {\lambda }_u$ height over the rolling plane	$\mathrm{m}$	$w_w$	Wheel width	$\mathrm{m}$
$H_{USFD}$	Total wheel wear depth (USFD law)	$\mathrm{m}$	$W_{R, USFD}$	Wear rate (USFD law)	$\mathrm{k}\mathrm{g}·{\mathrm{m}}^{-1}·{\mathrm{m}}^{-2}$
$i$	Railway line gradient/slope	$‰$	$y$	Wheelset uncentering	$\mathrm{m}$
$J$	Track gauge	$\mathrm{m}$	$y^{*}$	Total wheelset uncentering	$\mathrm{m}$
$k$	Wheel semi-conicity or inclination	$\mathrm{m}$	$y_{lím}^{*}$	Available play for the bogie leading wheelset when it uncenters towards the outside of a curve	$\mathrm{m}$
$k_A| k_S$	Reduction coefficient for the initial slope of the traction curve at the stick | slip region	$\mathrm{\varnothing }$	$y_{lím,diag}^{*}$	Available play for the bogie trailing wheelset when it uncenters towards the inside of a curve	$\mathrm{m}$
$K_M$	$\mathrm{Auxiliary} \mathrm{coefficient} \mathrm{for} \mathrm{the} \mathrm{calculation} \mathrm{of} F_{y,S}$	$\mathrm{\varnothing }$	$\dot{y}$	Wheelset uncentering rate	$\mathrm{m}·{\mathrm{s}}^{-1}$
$L_{rr}$	Length really rolled by a wheel	$\mathrm{N}$	${\dot{y}}^{*}$	Total wheelset uncentering rate	$\mathrm{m}·{\mathrm{s}}^{-1}$
$m_H$	Longitudinal Hertz’s coefficient	$\mathrm{m}$	$Z_w$	Number of wheels on the bogie	$\mathrm{\varnothing }$
$M_z$	Spin torque	$\mathrm{N}·\mathrm{m}$

for those with Latin symbols (Appendix A) and in

Table A2. Greek symbol abbreviations. Source: [1].

Abbreviation	Definition	Unit (SI)	Abbreviation	Definition	Unit (SI)
${\alpha }_{fn}$	Fraction of the force normal to the wheel falling on the flange contact patch	$\mathrm{\varnothing }$	${\mu }_o$	Initial friction coefficient or maximum (null slip speed)	$\mathrm{\varnothing }$
${\beta }_{rp}$	Gradient angle	$\mathrm{r}\mathrm{a}\mathrm{d}$	$\nu$	Equivalent Poisson’s ratio of the materials in contact	$\mathrm{\varnothing }$
${\gamma }_o$	Wheel contact angle	$\mathrm{r}\mathrm{a}\mathrm{d}$	${\nu }_1|{ \nu }_2$	Poisson’s ratio of the rail | wheel	$\mathrm{\varnothing }$
${\delta }_o$	Maximum indentation between the two bodies in contact	$\mathrm{m}$	$\xi$	Gauge widening (at tight curves)	$\mathrm{m}$
${\delta }_P$	$\mathrm{Auxiliary} \mathrm{coefficient} \mathrm{for} \mathrm{the} \mathrm{obtention} \mathrm{of} \mathrm{coefficient} K_M$	$\mathrm{\varnothing }$	$\rho$	Density of the wheel material	$\mathrm{k}\mathrm{g}·{\mathrm{m}}^{-3}$
$\epsilon$	Tangential stress gradient at the stick region	$\mathrm{\varnothing }$	$\varsigma$	Longitudinal displacement angle of the contact patch	rad
${\epsilon }_S$	Tangential stress gradient at the stick region for the pure spin case	$\mathrm{\varnothing }$	${\tau }_{máx}$	Maximum tangential stress transmitted	$\mathrm{P}\mathrm{a}$
${\zeta }_h| {\zeta }_v$	Load (horizontal | vertical) on the flange contact patch	$\mathrm{N}$	${\tau }_{lím}$	Tangential yield stress of the wheel material	$\mathrm{P}\mathrm{a}$
$\eta$	Play between the flange and the rail	$\mathrm{m}$	$\mathsf{\Phi }$	Tilt angle	$\mathrm{r}\mathrm{a}\mathrm{d}$
$\theta$	Hertz’s angle	rad	$\dot{\mathsf{\Phi }}$	Variation angle of tilt angle	$\mathrm{r}\mathrm{a}\mathrm{d}·{\mathrm{s}}^{-1}$
${\vartheta }_r$	Real cant angle	rad	$\phi$	Spin (rotational creepage)	$\mathrm{r}\mathrm{a}\mathrm{d}·{\mathrm{m}}^{-1}$
${\lambda }_{eje}$	Axle load	$\mathrm{k}\mathrm{g}$	$\psi$	Yaw angle	$\mathrm{r}\mathrm{a}\mathrm{d}$
${\lambda }_{tara}$	Vehicle tare	$\mathrm{k}\mathrm{g}$	$\dot{\psi }$	Variation rate of yaw angle	$\mathrm{r}\mathrm{a}\mathrm{d}·{\mathrm{s}}^{-1}$
${\lambda }_u$	Payload transported by the vehicle	$\mathrm{k}\mathrm{g}$	${\omega }^{\prime }$	Angular slip speed when braking per unit length	$\mathrm{r}\mathrm{a}\mathrm{d}·{\mathrm{s}}^{-1}·{\mathrm{m}}^{-1}$
$\mu$	Dynamic friction coefficient (or adhesion coefficient)	$\mathrm{\varnothing }$

for those with Greek symbols (Appendix A).

2.2. Hypotheses

The ensuing hypotheses were considered, in addition to the application assumptions of Hertz’s solution, Polach’s method, and the wear calculation:

(a)

It is quasi-static, i.e., it does neither regard dynamic loads nor the vibrations derived from them, based on other quasi-static analyses [17,18].

(b)

The method relies on global calculations for the contact patch without dividing it into finite elements.

(c)

It is stationary, meaning it does not account for changes in variables over time. In transition curves, where these variations are more significant, average values are calculated.

(d)

It ignores any rail wear and the prior wear of the wheels, meaning it does not update the contact parameters as the profile changes, since this profile is consistently renewed.

(e)

It is applied to all the bogie wheels. For each wheel, the parameters and wear calculations are stored separately, as the wear varies among the different bogie wheels [18].

(f)

It is applied to a single bogie of a wagon. Typically, a wagon comprises two bogies, which can generally rotate independently of one another.

(g)

It overlooks the tractive and compressive forces that certain wagons transfer to one another through couplings while navigating curves, due to the inherent coupling slacks [19].

(h)

It considers that the track bed stiffness is infinite and its damping is null, so that its deformation does not affect the contact patch shape, as is usually the case in these analyses [17,18].

(i)

It disregards non-holonomic bonds/ties, which is usually the case in these analyses [17,18].

(j)

It can account for up to two contact patches on the same wheel: one on the tread and the other on the flange [17].

(k)

In Kalker’s and Polach’s equations, the spin is assumed to be positive when it is clockwise, as it must comply with the sign convention applied for creepage. This spin is later passed on to the energy transfer model employed.

(l)

Creepage is derived from the kinematic analyses of the wheelset rather than from the non-dimensional slips, which involve partial derivatives typically not used in global calculations.

(m)

Throughout this study, the radial deformation ${\delta }_o$ is considered negligible compared to the wheel radius $r_o$ (${\delta }_o \ll r_o$). Additionally, since $\mathsf{\Phi }\ll {\gamma }_o$ (specifically, $\mathsf{\Phi } \ll \psi \ll {\gamma }_o$, based on the values obtained in Ref. [17]), the influence of $\mathsf{\Phi }$ on ${\gamma }_o$ can also be disregarded.

(n)

However, the influence of $\dot{\mathsf{\Phi }} \left(=\mathrm{d}\mathsf{\Phi }/dt\right)$ on the wear occurring at transition curves is taken into account, as it contributes to a slight increase in wear.

(o)

The displacements from the bogie suspensions and anti-yaw mechanisms are not considered in the kinematic analysis.

(p)

The variation in wheel and rail curvatures at transition curves is ignored because although the location of the rail–wheel contact shifts across the widths of the wheel and rail (affecting their curvatures), these changes are typically minimal. When the variations are significant, the most unfavorable values are used directly (for example, the curvatures at the flange–rail contact when such contact is expected to occur at a specific transition curve).

(q)

Defects like cracks, spalling, squats, or flats are disregarded, and only adhesive and abrasive wear are considered [20,21].

(r)

RCF is only anticipated without calculating the extent of the damage caused, often involving subsurface cracks [20].

(s)

The bogie wheels are assumed to be non-powered, which means $F_t=0$ at the contact patches.

(t)

The bogie wheels are assumed to have disk brakes that do not cause wear on the wheels [17].

(u)

The railway vehicle is expected to navigate curves (both circular and transitional) at a constant speed, applying brakes (if necessary) before entering the curve, resulting in $F_f=0$ during the curve. An exception to this occurs when the vehicle is traveling downhill, as outlined in the next hypothesis.

(v)

It is assumed that the railway vehicle brakes slightly when descending, and reducing or cutting off traction is insufficient to maintain a constant speed while navigating curves: when the slope is less than 10‰, the vehicle brakes will be off; when the slope is between 10 and 15‰, the brakes will brake 5% of the accelerating force at each wheelset; and when the slope is greater than 15‰, the brakes will brake 10% of the accelerating force.

(w)

The infrastructure parameters or conditions modifying the wear conditions, such as warp, rail deflection, joints, running on turnouts/switches and other track devices, and track irregularities are not observed [22].

(x)

No manufacturing or assembly tolerances for any component are considered.

(y)

By neglecting rail deflection and manufacturing or assembly tolerances, it can be assumed that the longitudinal rail curve radius ($R_{y,1}$) approaches infinity, causing the associated curvature ($1/R_{y,1}$) to approach zero (which is treated as such).

(z)

It is assumed that the bogie wheels do not derail or become blocked (this was numerically verified in Ref. [17]). Furthermore, they are expected not to displace laterally under conditions of cant deficiency or excess, as well as low static friction, and to remain free from hunting oscillations within the considered speed ranges (this was numerically demonstrated in Ref. [17]).

2.3. Calculation Process

An algorithm was developed, consisting of input data blocks, calculation blocks, and two output blocks, as illustrated in Figure 3. Each of the referenced equation blocks is linked with the corresponding article title, under which it is described in detail:

• At the top of the algorithm, the input data (represented by green blocks) was entered to the calculation blocks. The data is arranged in blocks that are added before going down to the main branches. These blocks gather information on the wheelset and bogie geometry, vehicle speed, railway line geometry, wheel geometry, load characteristics, rail geometry and contact materials properties.
• On the left, in the 3 central blocks (in light blue), the kinematic parameters for the wheelsets are obtained through relations dependent on the line geometry after inputting information on the wheelset and bogie geometry, vehicle speed, railway line geometry and wheel geometry. After that, the uncentering of each wheelset is saturated through equations dependent on the line geometry and finally, creepages are obtained through kinematics equations.
• On the right, in the 6 central blocks (in dark blue), the normal force on each wheel is computed by means of dynamics equations after entering data on the vehicle speed, line geometry, load characteristics, and some results coming from the left main branch after the saturation of uncentering. Afterwards, the geometric and normal contact problems are solved by means of Hertz’s solution, for which data on the wheel and rail geometries and the contact materials properties is needed. The results of Hertz’s solution and the creepages computed in the left main branch allows for the application of Polach’s method. This solution can be applied either with constant or variable friction. At the end of this branch, the flange–rail contact is characterized by equilibrium equations.
• At the bottom of the algorithm (purple blocks), the wheel wear is computed through the energy transfer model, and the appearance of RCF is predicted with the fatigue index model.
• Regarding the symbology, the orange symbol with a diagonal cross indicates the addition of values, the orange symbol with a Greek cross represents a disjunction, the gray symbol signifies that only one flow is input, and the yellow symbol denotes a bifurcation:

2.4. Calculation Model

This subsection defines the calculation model, starting with the definition of the reference frames and continuing with the mathematical description of each equation block shown in Figure 3 (Section 2.3).

2.4.1. Reference Frames Definition

Four reference frames were established for the kinematic and dynamic analyses detailed in the following sections. These frames are outlined below and depicted in Figure 4 for a wheelset (the entire bogie does not need a specific reference frame):

• Absolute reference frame $XYZ$, clockwise, fixed, with its origin located on the rolling plane, anchored at the start of the track and centered between the rails.
• Track reference frame $\tilde{x}\tilde{y}\tilde{z}$, clockwise, moving at the vehicle’s speed, with its origin located on the rolling plane along the centerline of the track, maintaining the $\tilde{\mathrm{x}}$ axis always tangent to that line.
• Axle reference frame $\stackrel{̿}{x}\stackrel{̿}{y}\stackrel{̿}{z}$, clockwise, moving at the axle speed, with its origin located at the center of gravity of the wheelset.
• Contact area reference frame $x_c{y}_c{z}_c$, clockwise, moving at the speed of the contact area, with its origin positioned at the center of that area.

2.4.2. Obtention of the Kinematic Parameters

Refs. [18,19,20,23,24,25] explain how to obtain the kinematic parameters for the wheelsets through relations dependent on the railway line geometry. Ref. [17] collects these relations and applies them to all of the possible geometries that can be found in a railway line: straight or circular sections, where the circular section can either be a circular curve or a transition curve (clothoid, quadratic parabola, or cubic parabola).

As for the curves, a circular curve is that whose radius holds constant, while the transition curves are those whose radii are variable: the radius of a clothoid, also called an Euler or Cornu spiral, is inversely proportional to the distance run, while the radii of quadratic and cubic parabolas depend on the distance as per those mathematical functions.

The parameters obtained at these geometries are listed next according to the order in which the relations were collected and generalized in Ref. [17]:

• Uncentering and its change rate.
• Average uncentering and its change rate.
• Yaw angle and its change rate.
• Average sinus of yaw angle and of yaw angle change rate.
• Average yaw angle.
• Combination of the uncentering and yaw angle effects.
• Angle of longitudinal displacement of the contact area.
• Tilt and its change rate.

An example of the parameters’ obtention is given next: uncentering. This parameter ($y$) can be defined as the distance between the track center and the wheelset center of gravity. Uncentering happens because of wheel conicity: wheels are slightly tapered to make wheel negotiation possible for wheelsets, which lack a differential. In this way, the wheel whose position is inner in relation to the curve can roll with a lower rolling radius than the nominal radius, while the opposite is true for the wheel whose position is outer in relation to the curve. Therefore, in the end, the outer wheel rolls a longer distance than the inner one, and the wheelset can negotiate the curve with a lower slip.

The uncentering parameter is associated with some track and wheelset parameters, which are shown in Figure 5, except for the (equivalent) conicity ($k$), which is an intrinsic parameter of each wheel. These parameters can be interrelated by computing the linear velocities of each wheel and equating them or by applying the Thales’s Theorem to the triangles drawn in Figure 5. The formula for uncentering is named after F. J. Redtenbacher, who developed it in the 19th century:

$$y={\displaystyle \frac{r_o{b}_o}{kR}}$$

(1)

2.4.3. Saturation of Uncentering

According to Refs. [18,20,23,25], the total uncentering of a wheelset ($y$*) can be calculated by adding the original uncentering and the uncentering coming from wheelset rotation (that of the bogie pivot with respect to the tangent line to the track centerline). This is shown in Figure 6a and the formulae are presented after it.

The reason why uncentering must be saturated is because there exists a geometrical constraint; the total uncentering cannot be greater than the addition of half the track play/slack (the flangeway clearance) and the existing gauge widening (equal or different to 0). When the total uncentering reaches that value, then the flange belonging to the outer wheel touches the outer rail. Ref. [17] explains this in detail and defines all of the track and wheelset/bogie parameters involved. These parameters are listed below (SC—Parameters are found at straight sections and curves, while C—Parameters are only found at curves under the current hypotheses), most of which are shown in Figure 6b, and the formulae are presented after it:

• SC—Rolling radius ($r_o$).
• SC—Track gauge ($J\to 1668$ for Iberian gauge).
• SC—Rail inclination ($1: no\to 1:20$ for Iberian gauge).
• SC—Track play/slack ($\eta )$.
• C—Curve radius ($R$).
• C—Gauge widening ($\xi$).
• C—Curve sagitta ($\mathcal{f}$).
• C—Total uncentering ($y^{*}$) and uncentering limit ($y_{lim}^{*}$ or $y_{\mathrm{l}\mathrm{i}\mathrm{m}}$).
• C—Outer | inner wheel rolling radius ($r_e | r_i$).
• C—Yaw ($\psi$) and tilt angles ($\mathsf{\Phi }$).
• C—Angle of longitudinal displacement of the contact area ($\varsigma$).

$$y^{*} \left(1^{st} wheelset\right)=y+e{\displaystyle \frac{\pi \left|\psi \right|}{360}}$$

(2)

$$y^{*} \left(2^{nd} wheelset\right)=y-e{\displaystyle \frac{\pi \left|\psi \right|}{360}}$$

(3)

$$y_{lim}^{*}={\displaystyle \frac{\eta }{2}}+\xi$$

(4)

$$y^{*}=y_{\mathrm{l}\mathrm{i}\mathrm{m}}^{*} \text{(if the former was greater before)}$$

(5)

2.4.4. Obtention of the Creepages

As explained in Ref. [23], creepages are the rigid slip velocities divided by the vehicle speed, so they are non-dimensional (although the spin creepage is dimensional: “rad/m”):

$$v_x=\mathsf{\Delta }{V}_x/V$$

(6)

$$v_y=\mathsf{\Delta }{V}_y/V$$

(7)

$$\phi =\mathsf{\Phi }/V$$

(8)

Refs. [20,23,24] explain how to calculate creepage from kinematic parameters, whereas Ref. [17] collects this information and proves the formulae. The whole process is briefly explained next, starting with longitudinal creepage, continuing with lateral creepage and ending with spin creepage.

Longitudinal creepage has three main contributions, which are represented in Figure 7 and added thereafter:

• Difference between the nominal wheel radius and the real rolling one (generating $V_x^I$).
• Application of tractive or braking torques to the wheel (generating $V_x^{II}$).
• Variation of yaw angle (generating $V_x^{III}$).

$$\mathsf{\Delta }{V}_x=V_x^I+V_x^{III}+V_x^{III}$$

(9)

$$\mathsf{\Delta }{V}_x=-\mathsf{\Delta }r \omega -r_o{\omega }^{\prime }\pm b_o\dot{\psi }$$

(10)

$$v_x={\displaystyle \frac{-\mathsf{\Delta }r}{r_o}}+{\displaystyle \frac{-r_o{\omega }^{\prime }\pm b_o\dot{\psi } }{V}}$$

(11)

As for lateral creepage, this is composed of three contributions, which are represented in Figure 8 and added thereafter:

• Not null yaw angle (generating $\mathsf{\Delta }{V}_y^I$).
• Adoption of a new equilibrium position by the wheelset (generating $\mathsf{\Delta }{V}_y^{II}$).
• Not null tilt angle (generating $\mathsf{\Delta }{V}_y^{III}$).

$$\mathsf{\Delta }{V}_y=V_y^I+V_y^{III}+V_y^{III}$$

(12)

$$\mathsf{\Delta }{V}_y=-Vsin\psi cos{\gamma }_o+\dot{y}\cos {\gamma }_o-r_i\dot{\mathsf{\Phi }}\cos {\gamma }_o$$

(13)

$$v_y=\left(-sin\psi +{\displaystyle \frac{\dot{y}-r_i\dot{\mathsf{\Phi }}}{V}}\right)\mathrm{c}\mathrm{o}\mathrm{s}{\gamma }_o$$

(14)

Finally, spin creepage is made up of two contributions, which are shown in Figure 9 and added afterwards:

• Conicity (generating $\mathsf{\Delta }{\mathsf{\Phi }}^I$, alternatively known as the camber effect [20]).
• Variation of yaw angle (generating $\mathsf{\Delta }{\mathsf{\Phi }}^{II}$).

$$\mathsf{\Delta }\mathsf{\Phi }=\mathsf{\Delta }{\mathsf{\Phi }}^I+\mathsf{\Delta }{\mathsf{\Phi }}^{II}$$

(15)

$$\mathsf{\Delta }\mathsf{\Phi }=\pm \omega sen{\gamma }_o+\dot{\psi }\cos {\gamma }_o$$

(16)

$$\phi =\pm {\displaystyle \frac{sen {\gamma }_o}{r_o}}+{\displaystyle \frac{\dot{\psi } cos{\gamma }_o}{V}}$$

(17)

2.4.5. Obtention of the Normal Force on Each Wheel

The normal force is applied by the rail on the wheel in response to the opposing force exerted by the wheel on the rail, which results from gravity and other acceleration components, such as centrifugal force. Refs. [3,18,19,24,26,27,28,29,30,31,32] give some insight on how to calculate the normal force on each wheel.

Nevertheless, the most significant reference is [17], as it addresses the gaps in previous research and determines the normal force on each wheel based on these factors:

• Axle load (${\lambda }_{eje}$), which is obtained from the payload, tare and number of axles.
• Center of gravity of the axle load ($H_{CdG}$), considering the contribution of each load.
• Gradient angle (${\beta }_{rp}$), which is directly inferred from the inclination ($i$).
• Cant angle (${\vartheta }_r$), which depends on the cant and the distance between contact areas.
• Lateral acceleration ($a_{lat}$), which considers the effect of cant excess or deficiency.
• Wheel contact angle (${\gamma }_o$) and longitudinal displacement angle of the contact patch ($\varsigma$).

In that Ref., the normal force on the outer and inner wheels in relation to a curve ($N_e$ and $N_i$, respectively) was calculated and subsequently decomposed into their perpendicular and parallel components ($N_{\perp }$ and $N_{\parallel }$). It is important to note that in a straight section, $N_e$ and $N_i$ would be equal ($N$). This process is summarized in Figure 10, with the resulting formulae provided below it:

$${\lambda }_{eje}={\displaystyle \frac{{\lambda }_u+{\lambda }_{tara}}{n_{ejes}}}$$

(18)

$$H_{CdG}={\displaystyle \frac{{\frac{1}{n_{ejes}}(\lambda }_u{H}_u+{\lambda }_{tara}{H}_{tara}) }{\frac{1}{n_{ejes}}\left({\lambda }_u+{\lambda }_{tara}\right)}}$$

(19)

$${\beta }_{rp}=arctan\left({\displaystyle \frac{i}{1000}}\right)$$

(20)

$${\vartheta }_r=arcsen \left({\displaystyle \frac{h_r}{2b_o}}\right)$$

(21)

$$a_{lat}={\displaystyle \frac{V^2}{R+y}}-{\displaystyle \frac{h_r^{\prime }}{2b_o}} g cos{\beta }_r$$

(22)

$$N_e={\displaystyle \frac{{\lambda }_{eje}}{2}}\left(1+{\displaystyle \frac{y}{b_o}}\right)g cos{\vartheta }_r cos{\beta }_{rp}+{\displaystyle \frac{{\lambda }_{eje}}{2b_o}}{a}_{lat}{H}_{CdG}$$

(23)

$$N_i={\displaystyle \frac{{\lambda }_{eje}}{2}}\left(1-{\displaystyle \frac{y}{b_o}}\right)g cos{\vartheta }_r cos{\beta }_{rp}-{\displaystyle \frac{{\lambda }_{eje}}{2b_o}}{a}_{lat}{H}_{CdG}$$

(24)

$$N_{\perp }={ N}_{e|i}\cos \left(\varsigma \right)\cos \left({\gamma }_o\right)$$

(25)

$$N_{\parallel }=N_{e|i}\cos \left(\varsigma \right)\sin \left({\gamma }_o\right)$$

(26)

2.4.6. Solution of the Geometric and Normal Contact Problems

An isolated wheel transmits its own weight and load to the rail via a common interface: the contact area. This contact area must be greater than zero to avoid infinite normal stress. To compute wear and identify its location, both the contact area and normal stress need to be determined. The first is a geometric problem, while the second pertains to normal contact.

As explained in Ref. [23], contact between two bodies can be either non-conformal or conformal. In non-conformal contact, the contact area is relatively small compared to the bodies’ characteristic sizes. In contrast, conformal contact occurs when the geometry of one body adapts to that of the other, resulting in a larger contact area—this can happen when the wheel and rail are worn enough that their geometries align.

Ref. [23] also notes that if the materials in contact are quasi-identical, the problem simplifies significantly. The quasi-identity requires a relationship between the shear modulus and Poisson’s ratio, which is satisfied in wheel–rail contact since both are made of the same material (steel).

Both the geometric and normal contact problems are solved simultaneously, and the theories for addressing them are discussed in Refs. [18,20,23]:

• Hertzian contact theory. This theory was the first satisfactory analysis for the stresses appearing at the contact zone between 2 elastic solid bodies and solves the geometric problem at the same time if a series of hypotheses are fulfilled. According to this theory, the contact area is the intersection of two perfect paraboloids: a perfect ellipse.
• Kik–Piotrowski theory. This is a quasi-Hertzian theory and is also based on the virtual interpenetration between surfaces. It assumes the same pressure distribution in the longitudinal direction as Hertz, but not in the lateral direction as the curvature is not always constant in that direction. It is interesting to point out that this theory disregards the real shape of the bodies and replaces them by elastic half-spaces, which allows employing Boussinesq’s influence functions.
• Ayasse–Chollet. This is also a quasi-Hertzian theory, a variant of the previous one.
• Stiff approach. This theory is based on a stiff contact in which there is a theoretical contact point for which a series of constraints is imposed.

As stated in Ref. [17], which collects the theories, the Herztian contact theory is the most common due to its high accuracy, low computing effort and because the hypotheses it brings are fulfilled for most of the cases. Here is the list:

• The bodies in contact are homogeneous, isotropic, and linearly elastic.
• Displacements are assumed to be infinitesimal, significantly smaller than the characteristic dimensions of the bodies.
• The surfaces of the bodies are smooth in the contact zone, meaning they have no roughness.
• Each body can be modeled as an elastic half-space, necessitating non-conformal contact.
• The surfaces of the bodies can be approximated by quadratic functions near the point of maximum interpenetration, indicating that the curvatures (the second derivatives of the functions) are constant.
• The distance between the undeformed profiles of both bodies at the maximum interpenetration point can be modeled as a paraboloid.
• The contact between the bodies occurs without friction, allowing only normal pressure to be transmitted.

In Figure 11, the most representative images of this model are presented. After that, the main formulae are shown, which come from the aforementioned references and also from Refs. [33,34,35]:

$$A={\displaystyle \frac{1}{2}}\left({\displaystyle \frac{1}{{R_y}_1}}+{\displaystyle \frac{1}{{R_y}_2}}\right)$$

(27)

$$B={\displaystyle \frac{1}{2}}\left({\displaystyle \frac{1}{{R_x}_1}}+{\displaystyle \frac{1}{{R_x}_2}}\right)$$

(28)

$${R_y}_2={\displaystyle \frac{r}{cos{\gamma }_o}}$$

(29)

$$A_c=\pi ab$$

(30)

$$a=m_H{\left({\displaystyle \frac{3}{2}}N{\displaystyle \frac{1-{\nu }^2}{E}}{\displaystyle \frac{1}{A+B}}\right)}^{{\displaystyle \frac{1}{3}}}$$

(31)

$$b=n_H{\left({\displaystyle \frac{3}{2}}N{\displaystyle \frac{1-{\nu }^2}{E}}{\displaystyle \frac{1}{A+B}}\right)}^{{\displaystyle \frac{1}{3}}}$$

(32)

$${\displaystyle \frac{1-{\nu }^2}{E}}={\displaystyle \frac{1}{2}}\left({\displaystyle \frac{1-{\nu }_1^2}{E_1}}+{\displaystyle \frac{1-{\nu }_2^2}{E_2}}\right)$$

(33)

$$cos\theta ={\displaystyle \frac{\left|B-A\right|}{A+B}}$$

(34)

$${p_z}_o={\displaystyle \frac{3F_z}{2\pi ab}}$$

(35)

$${\delta }_o=r_H{\left({\left({\displaystyle \frac{3}{2}}N{\displaystyle \frac{1-{\nu }^2}{E}}\right)}^2\left(A+B\right)\right)}^{{\displaystyle \frac{1}{3}}}$$

(36)

2.4.7. Solution of the Tangential Contact Problem

The Hertzian model does not take into account the forces and torques resulting from friction. As a result of the relative motion between the wheel and rail in both the longitudinal and lateral directions, as well as around the vertical axis ($z_c$), opposing forces and torques are generated. These are linked to tangential stresses and deformations at the contact area, particularly in the slip region of the contact ellipse, which consists of one stick and one slip region. There are two methods for calculating these variables:

• Analytical. The values are calculated for the entire contact patch as a whole. A series of analytical equations are employed, allowing the tangential problem to be decoupled from the geometric and normal problems due to the satisfaction of non-conformity and quasi-identity conditions.
• Finite element. The values of the variables are calculated locally and then summed to obtain the global values. To achieve this, the contact patch is divided into a mesh.

In this study, an analytical approach is chosen because it enables addressing the problem with an algorithm that achieves a favorable balance between accuracy and computational effort.

For computing these tangential forces and the spin torque as well, a series of models was proposed throughout the last hundred years. In Refs. [18,20,23], these models are reviewed:

• Carter’s theory. This was the first theory ever. Carter coined the term “creepage” as “the ratio of the distance gained by a surface with respect to the other divided by the distance run“. He stated that the longitudinal dimension of Hertz’s ellipse in the unworn profiles was, in general, greater than the lateral one, but as a consequence of wear, the profiles flattened, giving rise to a uniform-width strip. He assumed that the wheel and rail profiles could be approximated by two parallel-axis cylinders, so the problem was reduced to a plane stress problem, i.e., bi-dimensional.
• Johnson’s theory. Johnson published the first contact theory for circular contacts. In this theory, the stick region is circle-shaped, and it touches the leading edge at a single point, although he later showed that this hypothesis leads to a contradiction: tangential stress does not oppose slip at the slip region adjacent to the leading edge. He also derived relations between creepages that were decreasingly small and tangential forces. Finally, he showed that the spin effect also contributes to lateral force.
• Johnson–Vermeulen’s theory. Johnson worked later with Vermeulen and both extended the theory of circular contacts under pure creepage (no spin) conditions to cases of elliptical contact. They used the solution for slipping contacts with microslip derived by Deresiewick for elliptical contact, with the only difference being that the stick region touches the leading edge at a single point with the purpose of reducing the erroneous area for a rolling contact case. However, in this theory, there was still a region where the friction law was not fulfilled.
• Kalker’s theory. At first, Kalker established a linear relation between the tangential forces and decreasingly small creepages. At such a restrictive situation, it is possible to assume that the whole contact area is in adhesion (there is no slip region). This first linear theory was also known as “non-slip theory” in which the friction law and the friction coefficient were discarded. Due to the lack of saturation of this theory (Coulomb–Amonton’s law would be the only saturation), this theory was improved with linear and cubic saturation approaches (CONTACT and SHE methods, respectively).
• Polach’s theory. Even with the improvements, Kalker’s theory was not enough for computing the lateral tangential force accurately when the spin grows beyond a certain threshold. Polach proposed a method to tackle this problem: (1) Tangential forces computation considering null spin. (2) Tangential forces computation considering pure spin. (3) Addition of the forces computed in steps (1) and (2) and saturation according to the traction limit. For this method, Polach assumed that the ellipse semi-axis in the rolling direction ($a$) tends to zero, so the position of the spin center tends to the ellipse center. He extended this assumption to higher semi-axes ratios ($a/b$).

Ref. [17] gathers all of these theories and draws the conclusion that Polach’s method is the most suitable for considering the spin effect on the variables, inasmuch that it is accurate and its computational effort is low. Refs. [36,37] give further insight on the method, which is based on Kalker’s coefficients [38].

In Figure 12, the evolution of the stick and slip regions at the contact patch for a case of pure longitudinal creepage is shown, as well as the four contact patches appearing at a four-wheeled bogie without flange–rail contact. At these contact patches, all of the possible creepages, forces, and torques are illustrated. Underneath Figure 12, the most representative formulae of Polach’s method are shown. It must be noted that for calculations with a variable friction coefficient, the coefficient $k_A$ is introduced in order to correct the slope of the traction curve:

$$s_i={\displaystyle \frac{\mu N_{\perp }}{Gab{ C}_{jj}}}{v}_i, i,j=x,1; i,j=y,2$$

(37)

$$\left\{\begin{array}{lll}{s}_{y,C}=& s_y+\left(-\phi \right)a,& \left|s_y+\left(-\phi \right)a\right|>\left|s_y\right|\\ s_{y,C}=& s_y,& \left|s_y+\left(-\phi \right)a\right|\le \left|s_y\right|\end{array}\right.$$

(38)

$$F=-{\displaystyle \frac{2\mu N_{\perp }}{\pi }}\left({\displaystyle \frac{\epsilon }{1+{\epsilon }^2}}+arctan\epsilon \right)$$

(39)

$$F_i=F{\displaystyle \frac{s_i}{s}}, i=x,y$$

(40)

$$F_{y,S}=-{\displaystyle \frac{9}{16}}a \mu N_{\perp } K_M\left[1+\mathrm{6,3} \left(1-e^{-{\displaystyle \frac{a}{b}}}\right)\right]{\displaystyle \frac{\left(-\phi \right)}{s_C}}$$

(41)

$$F_{y,C}=F_y+F_{y,S}$$

(42)

$$F=-{\displaystyle \frac{2\mu N_{\perp }}{\pi }}\left({\displaystyle \frac{k_A\epsilon }{1+{\left(k_A\epsilon \right)}^2}}+arctan{(k}_S\epsilon )\right)$$

(43)

$$\mu ={\mu }_o\left[\left(1-A_f\right)e^{-{wB}_f}+A_f\right]$$

(44)

$$w_i=s_{i}V i=x,y$$

(45)

2.4.8. Characterization of Flange–Rail Contact

Flange–rail contact is an aggressive interaction that occurs on tight or narrow curves where gauge widening is insufficient for smooth negotiation. In this scenario, the wheel flange presses laterally against the rail, which in turn exerts a reaction force on the wheel, increasing pressure on the flange, a region with small radii. Even when flange–rail contact is present, the typical tread–rail contact does not disappear (at least under the assumptions considered here), making it crucial to understand the load on each contact point.

To determine the reaction force exerted by the rail on the flange, Ref. [28] introduces the center of friction model. This model posits that for each bogie negotiating a curve, there exists a point where, if a wheel were mounted, it would rotate ideally without slipping. This point is known as the center of friction, and identifying it allows for the calculation of forces acting on the flange–rail contact through force and torque balances.

According to this model, there can be one flange–rail contact (free motion) or two flange–rail contacts (restricted motion). The latter situation occurs in the tightest curves when both wheels of a diagonal pair touch the rails.

Regarding load distribution at each contact, Ref. [39] explains the Sauvage model. This model states that the total indentation (${\delta }_o$) is the sum of the indentation at the tread–rail contact (${\delta }_{br}$) and at the flange–rail contact (${\delta }_{pe}$). Since these indents depend on the normal force, it is possible to derive the normal force at the tread contact ($N_{br}$) and the flange contact ($N_p$). However, this method is heuristic unless supported by a robust finite-element analysis to determine the precise values of ${\delta }_{br}$ and ${\delta }_{pe}$.

Ref. [17] compiles both models and simplifies the Sauvage model by introducing the load distribution coefficient (${\alpha }_{fn}$), which ranges from 0.5 (indicating equal normal load for both contacts) to 1 (where the tread contact would be unloaded). Typical values for this coefficient, derived from the Sauvage model results, fall between 0.7 and 0.8.

Figure 13 illustrates the parts of the center of friction model. It can be noted that the motion is restricted when both the wheels $W_1$ and $W_4$ touch the rail, receiving the reactions ${\zeta }_{h.1}$ and ${\zeta }_{h.4}$ from the rails, respectively. Otherwise, when the motion is free, only the wheel $W_1$ touches the rail and ${\zeta }_{h.4}$ is null. Below Figure 13, the main equations of this model and the normal force distribution by means of ${\alpha }_{fn}$ are presented:

$${\zeta }_v={\alpha }_{fn}{N}_e$$

(46)

$$N_p={\zeta }_v cos{\gamma }_o+{\zeta }_h sen{\gamma }_o$$

(47)

$$\left(-F_t|+F_f\right)=-{\sum }_{i=1}^{i=Z_w+2}{F}_{x,i}^{\prime }$$

(48)

$${\zeta }_{h,1}-{\zeta }_{h,Z_w}={\sum }_{i=1}^{i=Z_w+2}{F}_{y,i}^{\prime }$$

(49)

$${\zeta }_{h,1}{\mathcal{u}}_{fl,1}-{\zeta }_{h,Z_w}{\mathcal{u}}_{fl,4}={\sum }_{i=1}^{i=Z_w+2}\left(F_{y,i}^{\prime } {\mathcal{u}}_{f,i}\right)+{\sum }_{i=1}^{i=Z_w+2}\left(F_{x,i }^{\prime }{\mathcal{v}}_{f,i}\right)$$

(50)

2.4.9. Calculation of Wear

Wear significantly damages wheels, drastically reducing their lifespan. This wear occurs due to both abrasive and adhesive processes, and there are models based on wear rates that help determine the wear depth and characterize the damage [23]. Abrasive wear results from the relative movement and roughness of the wheel and rail surfaces, leading to friction and the subsequent loss of material from both. In contrast, adhesive wear arises from plastic deformation and the cohesive forces (such as Van der Waals, electrostatic, or chemical) that develop between the surfaces, resulting in material transfer from one surface to the other [40].

For characterizing wheel wear, Ref. [18] proposed the following hypotheses:

• The equations are parameterized for abrasive wear rather than adhesive wear for several reasons: (1) Plastic deformation occurs, but modeling it accurately is challenging without finite-element methods, which are computationally intensive. (2) It is reasonable to assume that abrasive wear is the primary contributor. (3) When the mathematical tools are calibrated with experimental data, both wear phenomena are inherently included in the resulting wear law.
• The various mathematical tools analyze the wear on the wheel profile, where the wear calculated at each moment is cumulative.
• Wear is considered to be uniform, i.e., the focus is on the variation of the transverse profile rather than on pattern formation in the longitudinal (circumferential) direction. Therefore, the wear measured at a specific position and time is extrapolated to the entire circumference.
• There are no pollutants present at the contact interface. The impact of pollutants is accounted for by adjusting the friction coefficient or by introducing new wear laws.

Regarding these hypotheses, the models examined in Refs. [18,23] can be applied to characterize wheel wear:

• Energy transfer models. These models compute the energy dissipated at the wheel–rail interface and associate it with the wear rate, which can be ultimately associated with the wear depth. There are various models, each with its own wear law: Zoroby’s model, which is based on the energy flow; the model developed by the British Railway Research (BRR), which is based on a non-continuous wear law depending on the wear regime (mild, transition, severe); and the model developed by the University of Sheffield (USFD), which is based on a continuous wear law divided into several regimes (mild, severe, catastrophic).
• Reye–Archand–Khruschchov (RAK) model. This is the simplest model and characterizes the abrasive wear appearing at the slip zone of the contact area. In this model, the volume of material lost is expressed as a function of the slip speed, normal force, hardness of the wheel material (steel), and a coefficient coming from a wear chart divided in wear zones depending on the normal pressure and the slip speed.

In Ref. [17], energy transfer models and the RAK model are collected and assessed. The RAK model is hard to implement because it requires a high computational accuracy; if pressure or slip speed is miscalculated, then the RAK coefficient may be wrong and be in another order of magnitude. As for the energy transfer models, the one with the easiest implementation and lowest computational effort is the USFD model since its wear law is continuous, so small errors do not lead to great errors in the end.

There are also other models that compute wheel wear by considering dynamic loading, especially in the event of the train running on a turnout/switch [41,42]. However, this is neither considered nor introduced in the current paper as clarified in the hypotheses list.

Figure 14 presents the wear calculation according to the USFD, which can be removed by reprofiling when its depth reaches a determinate threshold [21,43,44]. The main equations of the USFD model are presented next; the wear rate ($W_{R,USFD}$) for the mild, severe, and catastrophic regimes as a function of the wear index ($T\gamma /A_c$, with $A_c$ expressed in [mm²]) and the wear depth ($H_{USFD}$, expressed in [µm]):

$${\displaystyle \frac{T\gamma }{A_c}}={\displaystyle \frac{\left|F_x{v}_x\right|+\left|F_y{v}_y\right|+\left|M_z\phi \right|}{A_c}}$$

(51)

$$\left\{\begin{array}{c}{W}_{R, USFD}=5.3 {\displaystyle \frac{T\gamma }{A_c}}, for {\displaystyle \frac{T\gamma }{A_c}}\le 10.4\\ W_{R,USFD}=55.0, for 10.4<{\displaystyle \frac{T\gamma }{A_c}}\le 77.2 \\ W_{R,USFD}=55.0+61.9\left({\displaystyle \frac{T\gamma }{A_c}}-77.2\right), for {\displaystyle \frac{T\gamma }{A_c}}>77.2\end{array}\right.$$

(52)

$$H_{USFD}=W_{R,USFD} {\displaystyle \frac{a L_{rr} }{\rho \pi r_{rr}}}{10}^3$$

(53)

2.4.10. Prediction of RCF

Under high axle loads, stress distribution around the contact patch can lead to fatigue cracks on the wheel surface or within it. To predict the occurrence of rolling contact fatigue (RCF), the fatigue index model developed by Ref. [45], as presented by Ref. [23], proves effective. The fatigue index ($F{I}_{surf}$) is calculated as the utilized friction term (${\mu }_u$) minus the shakedown limit ($L_{RCF}$). By comparing this value to zero, three scenarios can be identified:

• If $F{I}_{suf}<0$, RCF alone is insufficient to initiate cracks because the tangential force is controlled by moderated (utilized) friction.
• If $F{I}_{suf}=0$, this represents the limiting condition. Cracks do not form because the shear stress at yield (${\tau }_{lim}$) has not yet been exceeded.
• If $F{I}_{suf}>0$, RCF triggers surface cracks due to the increased tangential force resulting from higher (utilized) friction.

The formation of an RCF prediction is presented next. The maximum force above which RCF appears ($F_{max,RCF}$) results from equating $F{I}_{suf}$ to zero (that is, in the limit situation):

$$F{I}_{surf}={\mu }_u-L_{RCF}$$

(54)

$$F{I}_{surf}={\displaystyle \frac{\sqrt{F_x^2+F_y^2}}{N}}-{\displaystyle \frac{{\tau }_{lim}}{p_{z_o}}}$$

(55)

$$F_{max,RCF}={\displaystyle \frac{2}{3}}{\tau }_{lim}\pi ab$$

(56)

2.5. Choice of the Calculation Software

After defining the architecture and specifics of the algorithm, it needs to be implemented in a program designed for solving equations. Given the extensive input data, including numerous equations, relationships, functions, procedures, and subroutines, only software capable of efficiently handling this volume of data was considered. After evaluating several options—Mathematica, Matlab, and Engineering Equation Solver (EES)—the choice was made in favor of EES [46]. This program is preferred because it allows for the creation of algorithms with any architecture using functions, procedures, and subroutines defined in its programming language, F-Chart, a variant of Pascal.

EES internally reorganizes user-defined equation blocks, processes the necessary inputs, and produces the requested outputs through iterative methods. The results are obtained after a variable number of iterations, determined by adjustable stopping criteria such as relative residuals (which can be as low as 10⁻¹⁰) or an iteration limit. The specific version used for these results is Engineering Equation Solver Professional V9.457-3D (EES). In addition to solving algorithms, this software also offers the capability to generate parametric tables and graphs based on the equations.

2.6. Calculation Scenarios

The objective is to calculate the wear as a function of the nominal diameter for various wheels and compare the results, for which the calculation scenarios and input data must be previously set.

In Ref. [17], a review of various types of bogies revealed that bogies equipped with reduced-diameter wheels require more wheels to support the same load. This is because smaller wheels can handle lower axle loads compared to standard-sized wheels, due to their reduced material strength. Consequently, more wheels are needed to distribute the same load across the bogie. Additionally, the minimum diameter after reprofiling cycles is more restrictive for reduced-diameter wheels to ensure operational safety.

For comparison, these commercial bogies, used or proposed on rail motorways, are examined:

• Y—25. This bogie has four wheels (two wheelsets) and supports a total load of 45 tons (22.5 tons per axle) at a maximum speed of 120 km/h. The total wheelbase ($e$) is variable, and the wheels are typically braked by brake shoes. The nominal wheel diameter ($D$) ranges from 920 mm (original maximum) to 840 mm (operational minimum).
• Saas-z 703. This bogie also features four wheels (two wheelsets) and supports a total load of 32 tons (16 tons per axle) at a maximum speed of 100 km/h. The wheelbase ($e$) is variable, and the wheels are braked by brake disks. The nominal wheel diameter ($D$) ranges from 680 mm to 630 mm.
• Graz Pauker 702. This bogie has eight wheels (four wheelsets) and supports a total load of 20 tons (5 tons per axle) at a maximum speed of 100 km/h. The wheelbase ($e$) is variable, and the nominal wheel diameter ($D$) ranges from 355 mm to 335 mm.

While these bogies differ significantly, comparisons should be made under consistent conditions, focusing solely on the parameter being assessed—in this case, the nominal diameter ($D$). However, achieving identical conditions for comparison is challenging [17]:

• Axle load (${\lambda }_{eje}$). Maintaining a constant axle load across all scenarios would result in some wheels being overloaded and others underloaded. For instance, axle loads of 22.5 tons would be unrealistic for 680 mm and 355 mm wheels, whereas loads as low as 5 tons would be feasible but would place extreme stress on the smallest wheels. To ensure comparable conditions, the axle load that generates a normal pressure of 1235 MPa is chosen. This value is common since maximum axle loads usually induce between 1100 and 1300 MPa on the wheel, with 1235 MPa being a mean value, even if it exceeds the manufacturer’s limit for the smallest wheels.
• Flange radius ($r_p$). This is the sum of the nominal rolling radius ($r_o$, which is half of $D$) and a constant. Therefore, $r_p$ decreases in proportion to $D$.

As a result, some data will vary depending on the wheel in question. These scenario-dependent data are detailed in Ref. [17] and are summarized in

Table 1. Specific input values for each of the three scenarios.

Variable	Value for 920-mm Wheels Scenario	Value for 680-mm Wheels Scenario	Value for 355-mm Wheels Scenario
$D$ (m)	0.920	0.680	0.355
$n_{ejes}$ $(\mathrm{\varnothing }$)	4	4	8
$r_p$ (m)	0.467–0.475	0.347–0.355	0.185–0.193
${\lambda }_{eje}$ (kg)	18,784	15,325	6996

:

The remaining conditions, such as the wheelbase, are kept consistent and are detailed in Section 2.7. Only realistic, feasible, and plausible values are used, and variations in geometry and friction, including the effect of speed on dry friction, are considered.

Given these parameters, three scenarios are defined: wheels with diameters of 920 mm, 680 mm, and 355 mm. For each scenario, the input data are initially entered into the system. The program then executes the algorithm for each segment of the railway line, reversing direction upon reaching the end station. When the wear depth of the wheel reaches a specified threshold, the wheel is reprofiled, and the scenario begins anew with a wheel of a smaller diameter. This process continues until the wheel reaches the minimum-allowed diameter after a set number of reprofiling cycles, at which point the scenario concludes. The results are recorded in wheel diameter versus mileage curves, which are detailed in Section 3.

The wear depth threshold is set as low as possible because wheel profiles are not updated during wear and must be replaced diligently. A practical threshold value is 1 mm for all scenarios (this value is used as a stopping criterion rather than an input parameter). Reprofiling requires the lathe to remove slightly more material, approximately 1.5 mm. When converted from radial to diametral data, this conversion results in values of 2 mm and 3 mm.

Finally, Figure 15 depicts the placement of the $\overline{\mathcal{u}}\overline{\mathcal{v}}\overline{\mathcal{w}}$ reference frame for the bogies, which is essential for the center of friction model. It shows the wheels entering a curve, with wheels $W_1$ and $W_2$ alternating between leading and trailing positions. Additionally, Figure 15 illustrates the geometric adjustment of the wheel and rail profiles, paying particular attention to the flange–rail contact:

2.7. Input Data

As illustrated in Figure 3, the algorithm requires input related to several factors: wheelset and bogie geometry, wheel and rail geometries, material properties in contact, load characteristics, railway line geometry, and vehicle speed. The vehicle speed can be aligned with the railway line’s specifications if the vehicle operates at the maximum allowable speed for that infrastructure.

For the three scenarios, the wheel profile follows the 1/40 standard and is made from ER8 steel, while the rail profile adheres to the 60E1 standard and is made from R260 steel [47]. Most wheelset and bogie characteristics, sourced from the bogie comparison in Ref. [17], are consistent across all scenarios. Similarly, parameters for friction variation with speed, based on Polach’s method (which incorporates variable friction under dry conditions), are the same. These common input parameters are in

Table A3. Input values common to the three scenarios (920, 680, and 355-mm wheels). Source: [1].

Variable	Value	Variable	Value	Variable	Value
$A_f$ $(\mathrm{\varnothing }$)	0.400	$k \left(flange\right)$ $(\mathrm{\varnothing }$)	1.235–2.747	${\gamma }_o \left(tread\right)$ (◦)	1.432
$B_f$ (s/m)	0.600	$k_A$ $(\mathrm{\varnothing }$)	1	${\gamma }_o \left(trea{d}^{\prime }\right)$ (◦)	1.432
$e$ (m)	1.800	$k_S$ $(\mathrm{\varnothing }$)	0.400	${\gamma }_o \left(flange\right)$ (◦)	51–70
$E_1$ (Pa)	$2.100\times {10}^{11}$	$R_{x_1} \left(tread\right)$ (m)	$300\times {10}^{-3}$	$\eta$ (m)	$0.007$
$E_2$ (Pa)	$2.100\times {10}^{11}$	$R_{x_1}\left(trea{d}^{\prime }\right)$ (m)	$80\times {10}^{-3}$	${\lambda }_{tara}$ (kg)	20,000
$g$ (m·s−2)	$9.810$	$R_{x_1}\left(flange\right)$ (m)	$13\times {10}^{-3}$	$\mu$ $(\mathrm{\varnothing }$)	0.400
$G_1$ (Pa)	$81.712\times {10}^9$	$R_{x_2} \left(tread\right)$ (m)	$5\times {10}^7$	${\mu }_o$ $(\mathrm{\varnothing }$)	0.550
$G_2$ (Pa)	$81.712\times {10}^9$	$R_{x_2} \left(trea{d}^{\prime }\right)$ (m)	$5\times {10}^7$	${\nu }_1$ $(\mathrm{\varnothing }$)	$0.285$
$H_{tara}$ (m)	0.512	$R_{x_2} \left(flange\right)$ (m)	$(13 or 20)\times {10}^{-3}$	${\nu }_2$ $(\mathrm{\varnothing }$)	$0.285$
$H_{CdG}$ (m)	1.573	$n_{dec}$ $(\mathrm{\varnothing }$)	0	$\rho$ (kg·m−3)	$7850$
$J$ (m)	$1.668$	$o$ (m)	$0.075$	${\tau }_{lím}$ (Pa)	$3.120\times {10}^8$
$k \left(tread\right)$ $(\mathrm{\varnothing }$)	0.025	$w_w$ (m)	0.140
$k \left(trea{d}^{\prime }\right)$ $(\mathrm{\varnothing }$)	0.025	${\alpha }_{fn}$ $(\mathrm{\varnothing }$)	0.750

Notes: (1) Tread’ is the tread of the wheel opposed to the wheel experiencing flange–rail contact. (2) Some values are expressed as ranges since flange–rail contact geometry is a little different at every contact. (3) $5·{10}^7$ means that the value tends to infinity (∞ is not accepted on EES).

(Appendix B).

Regarding railway line parameters, calculations for the three scenarios use data from a hypothetical railway line. Railway line design parameters are referenced from Refs. [26,48,49,50], though not all are used for wear calculations. In Ref. [17], a railway line is defined segment by segment with the following parameters:

• Initial and final metric points ($Q_{in}$ and $Q_f$, respectively).
• Stretch type: RECTA (straight), CIR (circular curve), CLO (clothoid), PARACUAD (quadratic parabola), or PARACUB (cubic parabola).
• Curve direction: NING (the stretch is straight), IZDA (curve to the left), or DCHA (curve to the right).
• Bogie position on the curve: NING (the stretch is straight), ENT (the bogie is entering the curve), or SAL (the bogie is exiting the curve).
• Curve radius ($R$), cant ($h_r$), and inclination ($i$).
• Initial and final maximum allowed speeds ($V_{in}$ and $V_{fn}$, respectively).

Constant values, such as the track gauge (1.668 m), remain uniform across all segments. Gauge widening is defined as a piecewise function imported from Ref. [26], with the parameter $\xi$ varying by curve radius ($R$). For instance, $\xi$ is zero for curves with R greater than 300 m and 20 mm for curves with $R$ between 100 and 150 m.

Additional parameters, such as those for transition curves, are pre-defined, while others are derived from the provided values. For example, the distance between two metric points is simply the difference between them.

The 333 defined stretches from Ref. [17] are available in the Supplementary Materials. The curve radii range from a minimum of 265 m (where the ratio $e/R_{min}$ is less than 0.01, indicating restricted movement) to a maximum approaching infinity in straight sections (∞ is not accepted in EES, so it is approximated as 5$\times$10⁷), with 200–800 m radii being the most common. For added realism, fictional names are used: station 1 is Albarque, station 2 is Zacarín, and there is an intermediate station named Milbello.

Finally, the Supplementary Materials includes details on incorporating Hertz’s and Kalker’s coefficients through polynomials and the 150 equations not displayed in this document due to space constraints but are part of the algorithm [51].

3. Results

After running the algorithm, the diameter versus mileage curves are obtained, with the diameter measured in millimeters (mm) and distance traveled in kilometers (km). Detailed results are discussed in Section 4, but here are some key figures:

• The 920-mm wheels can travel up to 124,275 km before their diameter reduces to 840 mm. These wheels lose 2 mm in diameter with each reprofiling cycle, at which point they are replaced for safety and operational reasons.
• The 680-mm wheels are able to travel for 75,648 km before reaching their minimum allowed diameter of 630 mm. In practice, this is the point at which the wheels are retired. However, if the wear and reprofiling cycles are extended as though the minimum diameter could be 600 mm (similar to the difference between 680 and 600 being analogous to the difference between 920 and 840), the wheels would theoretically last 118,683 km.
• The 355-mm wheels are capable of traveling 26,983 km before their diameter reaches the minimum allowed size of 335 mm. This is the practical end of their service life. If wear and reprofiling cycles were extended as if the final diameter could be 275 mm (with the difference being similar to that of the 920 to 840 scenario), the wheels would theoretically travel 101,433 km.

Additionally, the worn wheel profile is represented by mapping the wear depths onto the zones of a real wheel profile. This wear is determined after a randomly chosen distance traveled, using coordinates for the vertical position ($z_{p,f}$) and horizontal position ($y_{p,f}$). The worn profiles indicate that flange wear is much more significant compared to the minimal tread wear. This is expected due to the aggressive nature of flange–rail contact and the prevalence of tight curves on the railway line. The algorithm shows that in most flange–rail contacts, rolling contact fatigue (RCF) occurs due to high normal pressures and tangential stresses.

Figure 16 presents the diameter versus mileage curves and the worn wheel profile, with the latter shown in the lower right corner. The first plot demonstrates that wheels start with a nominal diameter of 920 mm at the tread. Upon reaching the wear depth limit (1 mm in radius or 2 mm in diameter), the wheel is sent for lathing. This process begins with a nearly new diameter of 920 mm at the tread and ends with a diameter of 917 mm. Consequently, 3 mm of material is removed (1.5 mm per side when viewed in cross-section). The wheel then exits the workshop with a diameter of 917 mm, wears down to 915 mm, and is reprofiled from 917 mm to 914 mm, and so forth:

4. Discussion

An algorithm capable of calculating wheel wear was designed in this work. As seen in Figure 16, it was found that a 920-mm wheel installed on a Y–25 bogie can travel for 124,275 km, a 680-mm wheel mounted on a Saas-z 702 bogie can travel for 75,648 km, while a 355-mm wheel assembled on a Graz Pauker can travel for 26,985 km. Should the last two wheels undergo the same number of reprofiling cycles as the first one then their results would be greater than that of the 920-mm wheel: 118,683 and 101,433 km, respectively.

To fully understand these results, it is essential to examine specific aspects uncovered during the overall analysis of this work. This includes a detailed review of the underlying equation blocks that ultimately produce the diameter–mileage curves:

• Comparing the real life ends (124,275; 75,648; and 26,985 km) in percentual terms with respect to the first value, it is obtained that the 680-mm wheels’ life is 30.13% shorter and the 355-mm wheels’ life is 78.29% shorter.
• Due to the elevated life shortening of 355-mm wheels, operators prefer using bigger wheels. For example, in Ref. [17], 380-mm wheels, which are mounted on the Saadkms690 bogie, are presented, which can be reprofiled until reaching 335 mm and the difference between both values (45 mm) is 25 mm higher than for 355-mm wheels (20 mm). Escalating the life of 355-mm wheels heuristically with the ratio 45/20, the result is 43,176 km, only 65.26% shorter than 920-mm wheels’ life. This is very advantageous despite the elevation in 25 mm of the loading plane height, so replacing 355-mm wheels by 380-mm wheels will ultimately depend on the application (semi-trailers’ heights and tunnels and bridges’ loading gauges).
• The distance difference between reprofiling (the reprofiling span) is very variable when reprofiling a same wheel and, obviously, when moving across wheels, so adopting arithmetic mean values is required. The mean value is 4,603 km for 920-mm wheels, 4,396 km for 680-mm ones, and 3,757 km for 355-mm ones.
• Should the wagons perform $n$ routes Albarque–Zacarín–Albarque (75.272 km) a week, then reprofiling the periodicity should be $Reprofiling span·\left(7/(75.272n)\right)$. Using the average value of 4250 km, the approximate result obtained is $56·\left(7/n\right)$.
• If all of the wheels were reprofiled the same number of cycles (always eliminating 80 mm in diameter), then the wheels’ life (fictional, as eliminating 80 mm would be against the manufacturers and operators’ regulations) would be: 118,683 km for 680-mm wheels and 101,433 km for 355-mm wheels. The former value is 4.50% lower than that of 920-mm wheels (124,275 km), while the latter value is 18.38% lower.
• These trends are summarized in Figure 17, where it can be seen that neither the behavior of the real life end nor that of the fictional life end are linear:
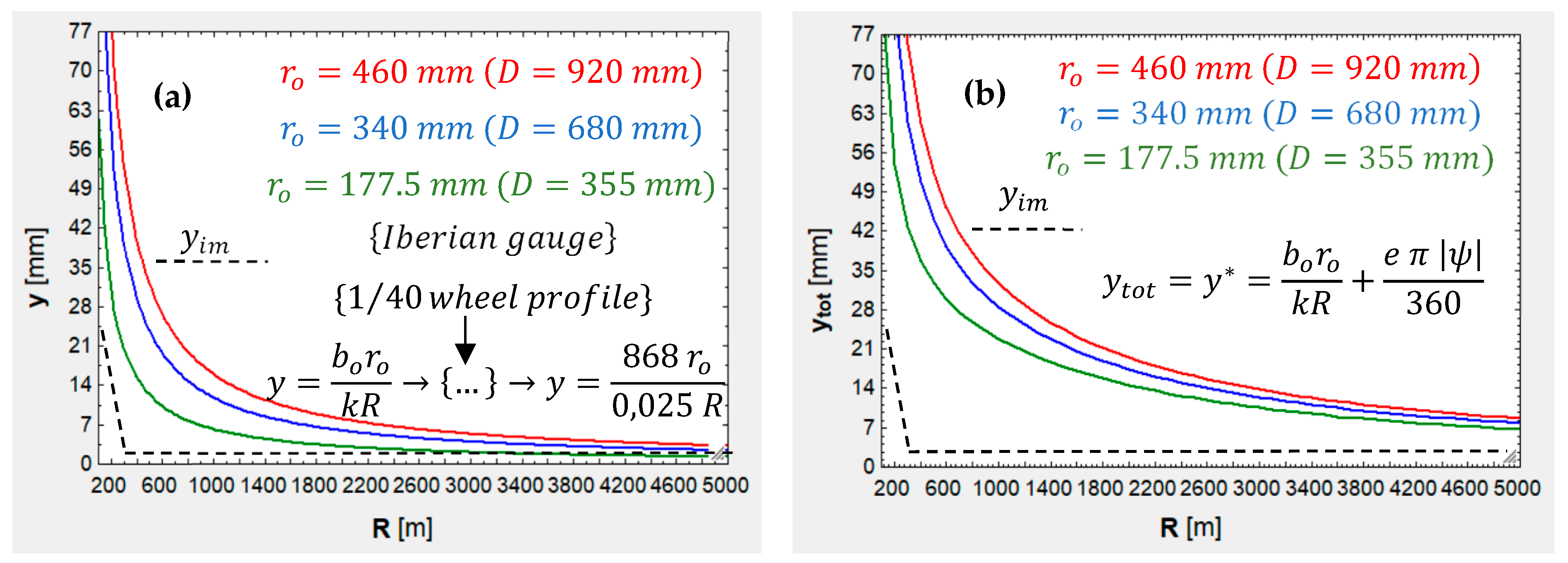
• This non-linear behavior responds to the different kinematic response of reduced-diameter wheels when negotiating curves. As demonstrated by Redtenbacher’s formula, uncentering is proportional to wheel radius (to wheel diameter in turn, as the radius is half), so not only do reduced-diameter wheels uncenter less than ordinary-diameter ones, but also their flanges will push against the rails less intensely. Moreover, the bogies where reduced-diameter wheels are mounted are less loaded, which will further reduce the force exerted by the rail on the flange (coming from force and torque balances). Figure 18a illustrates the partial uncentering (differential effect) for the three scenarios and shows how saturation ($y_{lim}$) is reached at a lower radius threshold for reduced-diameter wheels, while Figure 18b shows the total uncentering (adding bogie rotation) in the worst case (leading wheelset, outer wheel), but even in this case, flange–rail contact is less aggressive owing to dynamics:
• The results for the three scenarios were obtained for a 1235-MPa normal pressure at the tread contact area with the rail when the wheels run on straight tracks, attaining such a value by adjusting the axle load for each scenario. Pressures existing at the flanges were not equated due to the variability of the force exerted by the rail on the flange on the curve radius, which would make it very difficult to obtain unique axle load values.
• It is necessary to limit axle load on reduced-diameter wheels, as their contact area with the rail is reduced as well, and the normal pressure is proportional to the load–area ratio. This reduction in the contact area responds to the decrease in the longitudinal radius ${R_y}_2$, which is proportional to the wheel diameter. With a lower ${R_y}_2$ value, a greater longitudinal relative curvature ($A$) is obtained, which diminishes the intersection between the theoretical paraboloids and, as a result, the contact patch size (as $A$ diminishes, the longitudinal semi-axis (a) does as well).
• Flange wear is between 10 and 1000 times more intense than tread wear, so the former was taken for elaborating the curves. This is due to the fact that lateral radii are very reduced for flange–rail contact ($R_{x_1}=13-36$ mm, $R_{x_2}=36$ mm), opposing tread–rail contact radii ($R_{x_1}=80-300$ mm, $R_{x_2}\to \infty$), increasing in turn the relative lateral curvature ($B$), which diminishes the intersection between the theoretical paraboloids and, as a result, the contact patch size (as $B$ diminishes, the longitudinal semi-axis (b) does as well). This size is smaller than that of the tread contact patch.
• Wheel diameter is more influential on tread wear than on flange wear. This owes to the fact that the radius $R_{y_2}$ (proportional to wheel diameter) is dominating, along with the radius $R_{x_1}$ (which is in the same order of magnitude), at the tread ($R_{y_2}~R_{x,1}$ and ${R_{y_1},R}_{x_2}\to \infty$). In contrast, at the flange, $R_{y_2}$ is not the dominating radius, being dominated by $R_{x_1}$ and $R_{x_2}$ values, which are in a lower order of magnitude ($R_{x_1}~R_{x,2}<R_{y_2}$ and $R_{y_1}\to \infty$), and $R_{x_1}$ and $R_{x_2}$ hold constant independently of the wheel diameter.
• RCF is predicted for every flange–rail contact (except for isolated cases where the 355-mm wheel is negotiating a curve with a radius closely below 1850 m, this value being the threshold radius in this case) as a consequence of the high normal pressure (5–7 GPa) at the flange contact area with the rail. Although the contact patch size is smaller than that of the tread contact patch, such a high pressure is withstandable by the material since indentation is elevated (0.2–0.3 mm) and pressure can stack in many layers (isobaric surfaces), as in hydrostatics.
• RCF effects can be mitigated by setting a reduced wear depth limit and in the current work, it was due to the hypothesis established. In the real operation, it is the economical factor the one prioritized, which forces to find the trade-off between the crack growth and wear depth limit.
• As a consequence of RCF and the fatigue induced during reprofiling (which leaves residual stresses) and also for operational safety reasons, operators’ internal regulations forbid eliminating more than 80 mm in diameter for a 920-mm wheel, more than 60 for a 680-mm one, and more than 20 for a 355-mm one.
• Last,

  Table A4. Extent of RCF and wear on the three different wheels when flange–rail contact occurs. Source: own elaboration and [1].

  Variable	920-mm Wheel	680-mm Wheel	355-mm Wheel
  $D$ (m)	0.920	0.680	0.355
  $R$ (m)	265	265	265
  $F_{surf}$ $(\varnothing$)	0.433	0.426	0.409
  $p_{z_o}$ $(\mathrm{P}\mathrm{a}$)	$6.401 \times$ 109	$6.599 \times$ 109	$6.584 \times$ 109
  $T\gamma \left(\mathrm{N}\right)$	468.088	367.463	367.887
  $a \left(\mathrm{m}\mathrm{m}\right)$	10.030	8.249	6.276
  $b \left(\mathrm{m}\mathrm{m}\right)$	0.636	0.611	0.881
  $A_c \left(\mathrm{m}{\mathrm{m}}^2\right)$	20.031	15.834	17.360
  $T\gamma /A_c$ $(\mathrm{N}/{\mathrm{m}\mathrm{m}}^2$)	23.368	23.207	21.192
  $W_{R,USFD}\left({\displaystyle \frac{\mu g}{m·m{m}^2}}\right)$	55	55	55
  $H_{USFD} \left(\mu m\right)$	2.295	2.427	3.538
  $F_x$ (N)	1274	1034	1009
  $F_y$ (N)	41,159	32,931	34,760
  $M_z$ (N·m)	197.200	112.100	55.280
  $v_x$ $(\varnothing$)	$-3.013 \times$ 10−3	$-2.917 \times$ 10−3	$-2.581 \times$ 10−3
  $v_y$ $(\varnothing$)	$-5.760 \times$ 10−3	$-5.760 \times$ 10−3	$-5.760 \times$ 10−3
  $\phi \left({\displaystyle \frac{rad}{m}}\right)$	1.152	−1.559	−2.986
  $N$ (N)	85,465	69,622	76,224

  Note: Values for the flange.

  (Appendix C) gathers the RCF and wear results for the three different wheels when negotiating the tightest curve, the one with the 265-m radius. As it can be seen, even though the forces and RCF are less aggressive for reduced-diameter wheels, the wear depth increases as the wheel diameter decreases because the reduced-diameter wheels must revolve more times around its diameter so as to cover the same linear distance. However, the increase in wear depth is not simply inversely proportional to diameter (Figure 17 shows the same non-linear trend).

5. Conclusions

Through mathematical modeling, the physical problem of the wear of reduced-diameter railway wheels was tackled. The algorithm which was constructed allowed emphasizing the importance of diameter in the wear problem.

The algorithm links several calculation models and methods, balancing accuracy with computational efficiency. It accounts for key factors affecting wheel wear, including both vehicle-related and superstructure-related elements. By incorporating additional boundary conditions and assumptions, the algorithm can compute wear for wheels of various diameters.

In this instance, wheel wear calculations were employed to generate diameter-mileage curves for various scenarios: 920-mm diameter wheels on the Y-25 bogie, 680-mm diameter wheels on the Saas-z 702 bogie, and 355-mm diameter wheels on the Graz Pauker 702 bogie. In light of these results, when analyzing the evolution of one particular wheel (920, 680, or 355 mm), the wheel degradation worsens as the diameter diminishes, so the reprofiling span shortens as a consequence. This result agrees with the initial assumption of the paper: “presumably, reduced-diameter wheels do not undergo the same degradation as the ordinary-diameter wheels due to its greater angular contact with the rail (number of revolutions)”. The results also prove that smaller wheels can travel for shorter mileages than bigger wheels, as expected.

Notwithstanding, the trend observed when extrapolating the results of 680-mm and 355-mm wheels as though they could be reprofiled as 980-mm exhibits non-linear behavior, i.e., halving the diameter does not imply that the lifespan will halve as well. The comprehension of wheel, wheelset and bogie kinematics, and dynamics (which this work has enabled), allows finding the root causes responsible for this behavior:

• Contemplating kinematics, reduced-diameter wheels navigate curves more smoothly than standard-diameter wheels due to their lower uncentering, which results in less frequent flange contact with the rails and a lower threshold radius.
• Contemplating dynamics, the contact between the flange and the rail is gentler with reduced-diameter wheels. When the flanges of these wheels make contact with the rails, the interaction is less forceful due to the reduced uncentering forces. Additionally, because bogies using reduced-diameter wheels carry less load, the force exerted by the rails on the flange is lower. As a result, the balance of forces and torques leads to reduced rail–flange forces.

As a continuation of this research study, many actions can be implemented besides those commented upon in reference [1]:

• Repetition of the results for other track gauges present around the world.
• Computation of the speed effects through finite elements, proving more accurate results by obtaining the elastic distortions for every different speed.
• Computation of the exact load distribution between the tread and the flange in the event of simultaneous contacts. Finite elements would allow for knowing the real deformations, strains, stresses, and forces at both areas.
• Inclusion of more superstructure factors modifying wheel (and rail) wear, such as warp, rail deflection, joints, irregularities and cant excess and deficiency under low static friction conditions.
• Inclusion of dynamic loads, especially those appearing as the wheels traverse a turnout/switch.
• Inclusion of impacts between the wheels and the superstructure, especially those of the wheels with the switch frogs and track devices.
• Inclusion of other types of wheel damage shortening wheel life, such as cracks, flats and spalling.
• Extension of the algorithm to cover any other bogies belonging to the wagon (wagons have at least one more bogie).