Performance Analysis and Parallel Scalability of Numerical Methods for Fractional-in-Space Diffusion Problems with Adaptive Time Stepping
Abstract
:1. Introduction
2. Fractional-in-Space Parabolic Equation
2.1. Continuous Problem
2.2. Finite Element Approximation in Space
2.3. Backward Euler Discretization in Time
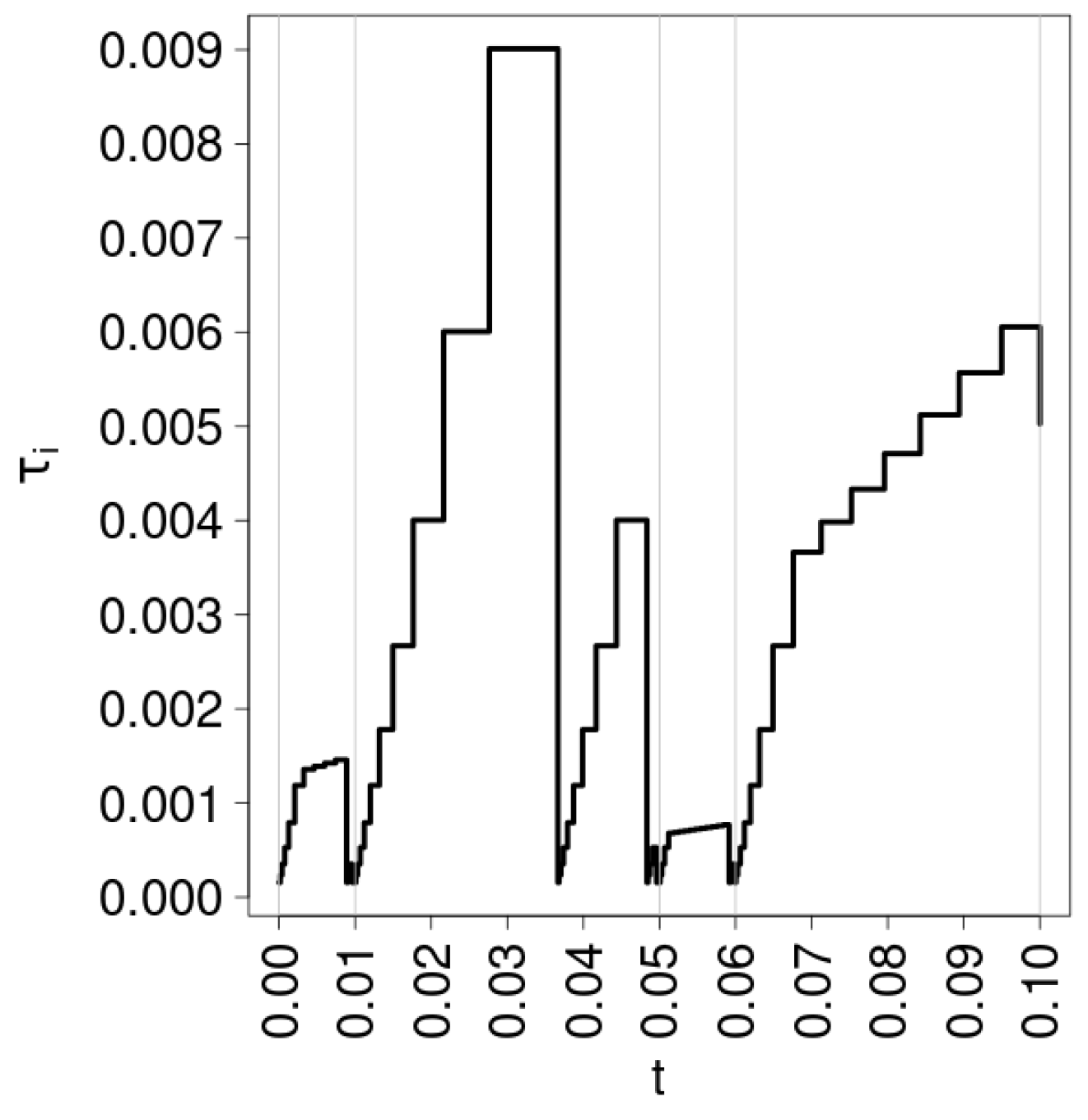
2.4. Adaptive Forward–Backward Euler Discretization in Time
Algorithm for Time Step Selection
- Prognostic solution. Calculation of in using the forward Euler scheme (8).
- Prognostic error. The prognostic solution is used to compute the prognostic truncation error given by (9).
- Step size selection. The time step is selected based on the prognostic error and the parameter that defines the desired accuracy.
3. Hierarchical Semi-Separable Compression
3.1. Basic Relations and Algorithmic Steps
- Hierarchical semi-separable compression. The matrix A is divided in four blocks, and the off-diagonal blocks are approximated by a product of three matrices (also called generators) as follows:For a suitable matrix A (with low off-diagonal blocks), U generators have few columns, B are small and square or rectangular, and V have few rows. The diagonal blocks D can also be compressed in a similar way and so on recursively until a threshold for the smallest block to be compressed is reached. The maximum rank r of the off-diagonal blocks occurring in the HSS compression of A is calculated. The computational efficiency of the compression can be roughly measured by comparing r to the size of the matrix N. For suitable problems . In general, HSS compression is approximate, where random sampling is applied to calculate the generators. The user must supply a relative threshold and an absolute one . The computational complexity of the HSS compression is .
- ULV-like factorization. A special form of LU factorization called ULV-like factorization can be applied to the thus compressed matrix H. The compression implemented within STRUMPACK uses the structure of the generators, unlike the original ULV factorization, which uses orthogonal transformations [30]. The computational complexity of ULV-like factorization is .
- Solving a factorized matrix system. A system of linear algebraic equations with matrix H can be solved by ULV-like factorization with computational complexity .
3.2. Modified Algorithm for Diagonally Perturbed Matrices
| Algorithm 1 Algorithm for diagonally perturbed matrices with HSS compression | |
| Input: K, , , , , , , | |
| Output: | |
| H = compress(K) | ▹ Apply HSS compression on the stiffness matrix |
| while do | |
| ▹ Increase prognostic step | |
| ▹ Compute prognostic solution | |
| ▹ Compute truncation error | |
| ▹ Calculate time step | |
| if then | ▹ Apply size limitations to new time step |
| else if then | |
| else if or then | |
| end if | |
| if then | |
| end if | |
| if then | |
| ▹ Perturb the diagonal of H with and | |
| ULV = factor(H) | ▹ Calculate the ULV factorization of H |
| end if | |
| ▹ Compute right hand side | |
| = solve(ULV, ) | ▹ Compute the solution at time |
| , | ▹ Prepare parameters for next time step |
| if then | |
| ▹ Restore original compressed matrix | |
| end if | |
| end while | |
4. Computational Complexity of the Time Stepping Algorithms
5. Test Problem for Numerical Experiments
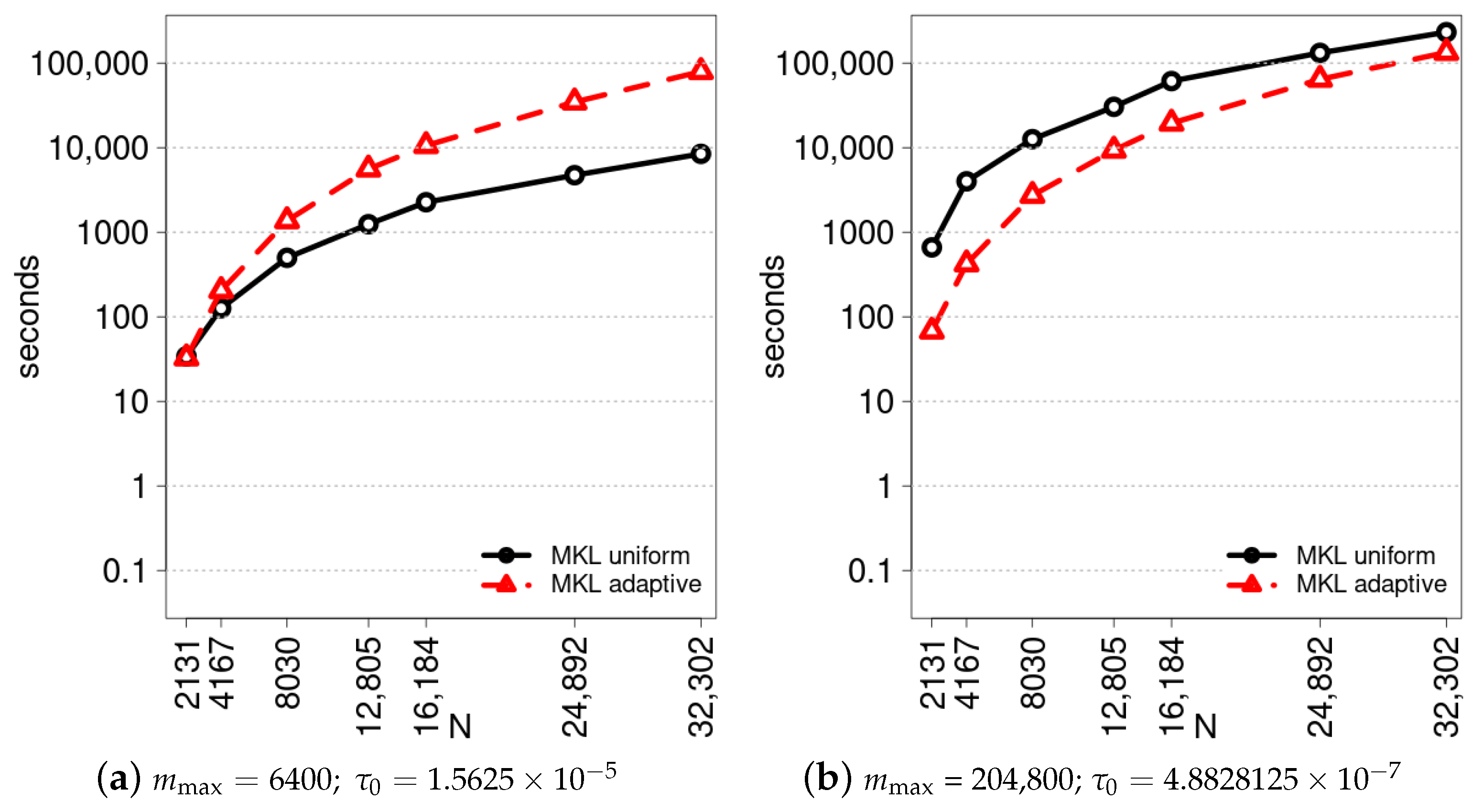
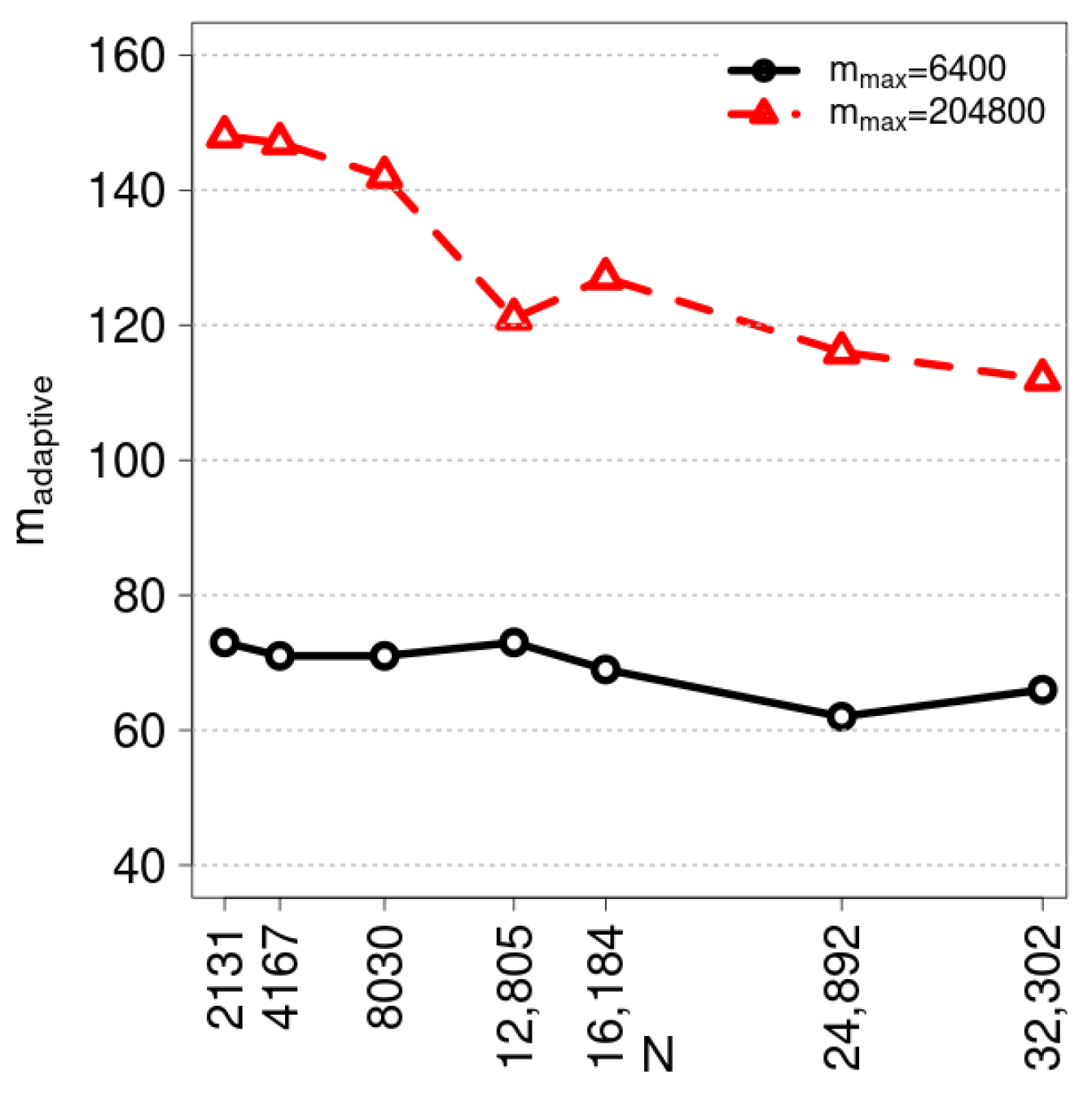
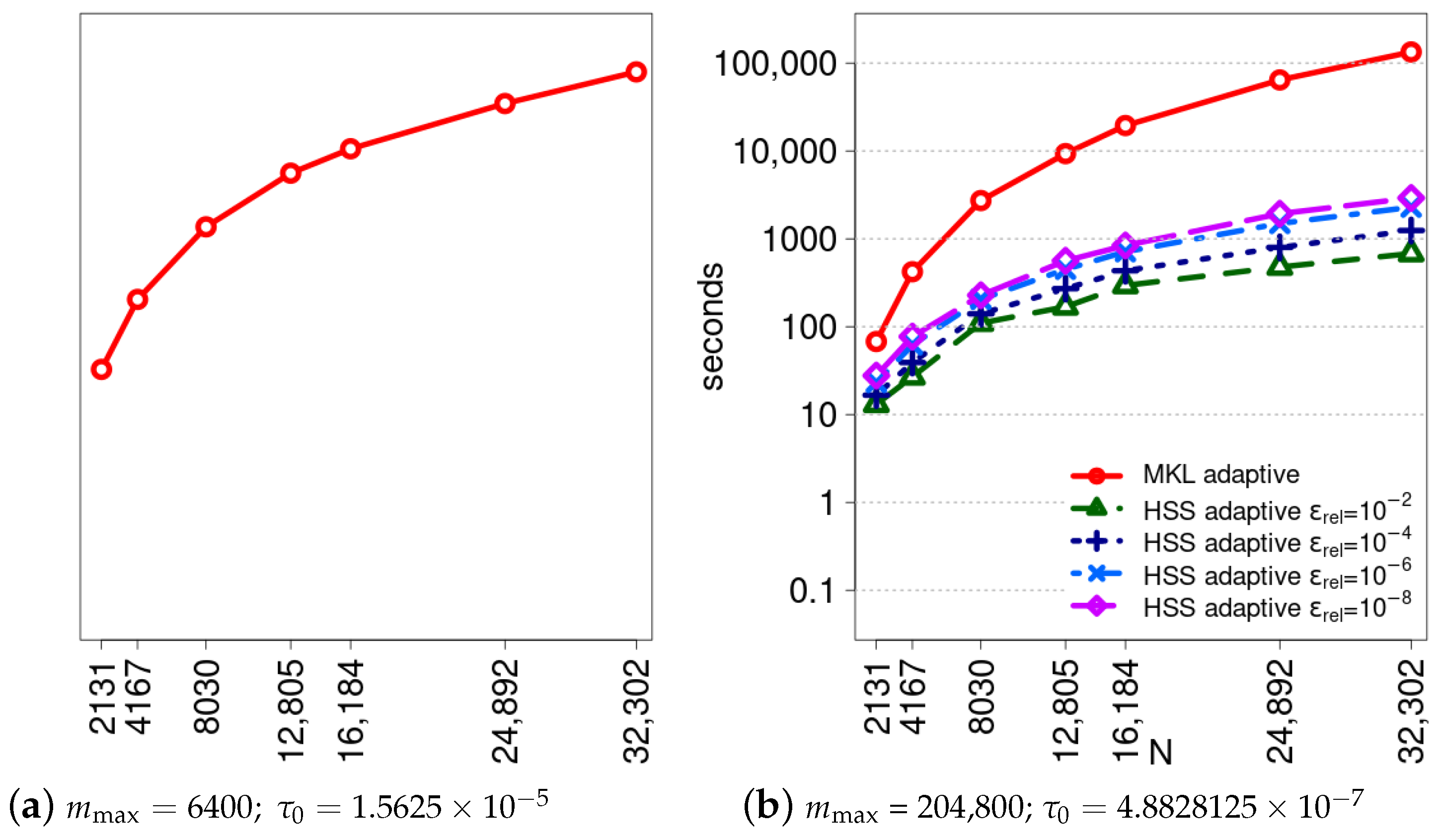
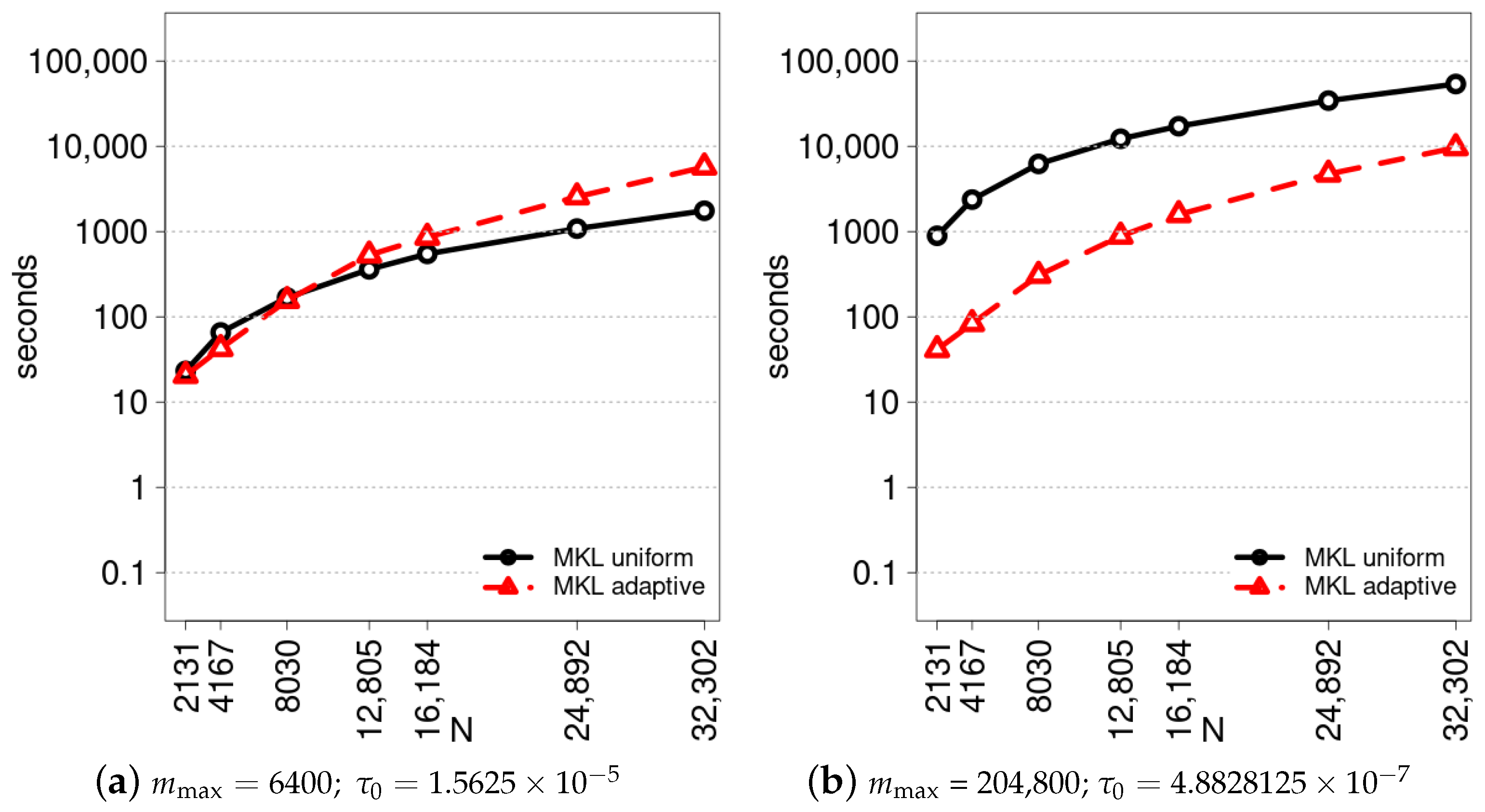
6. Comparative Analysis of Sequential Performance
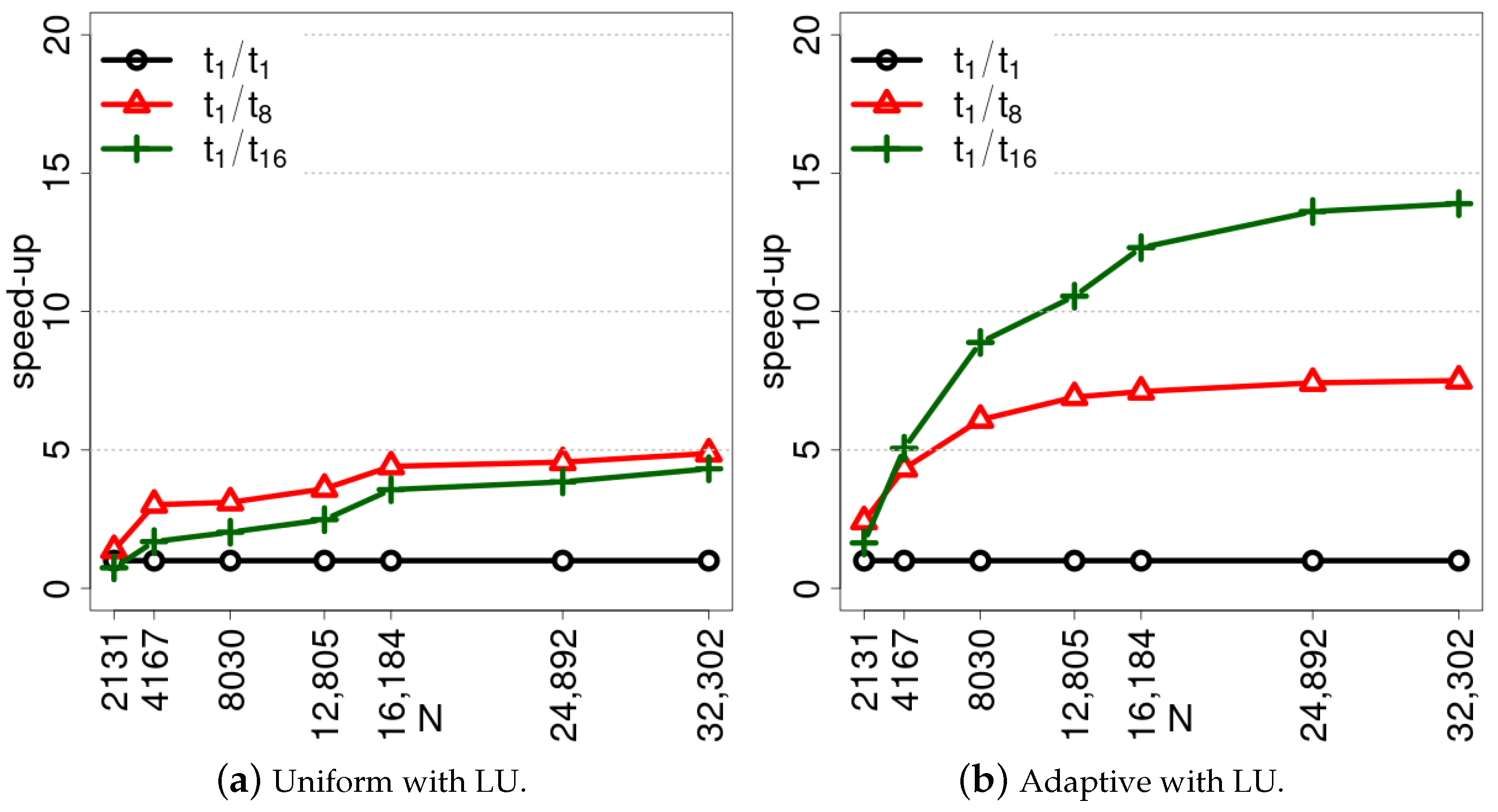
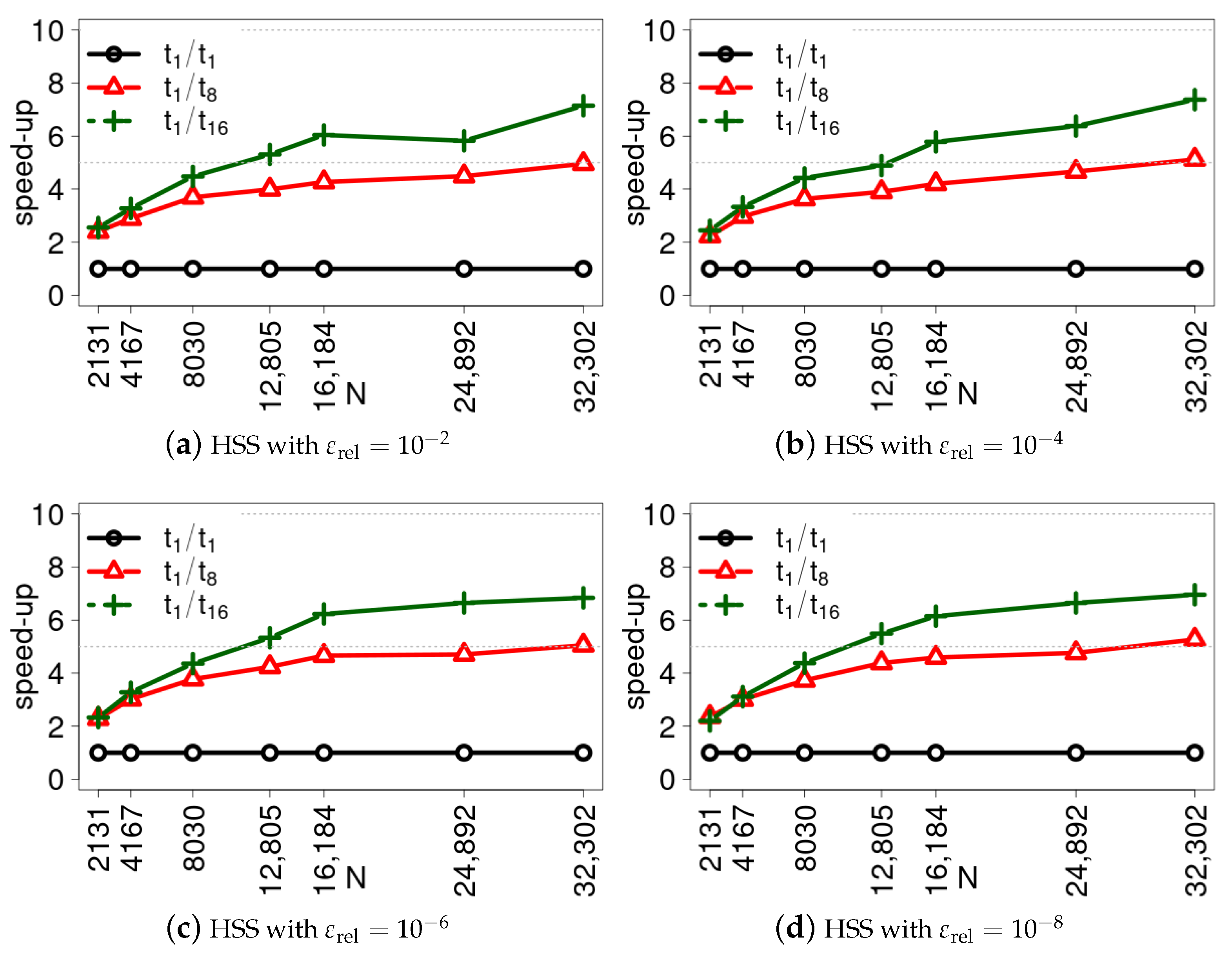
7. Parallel Scalability
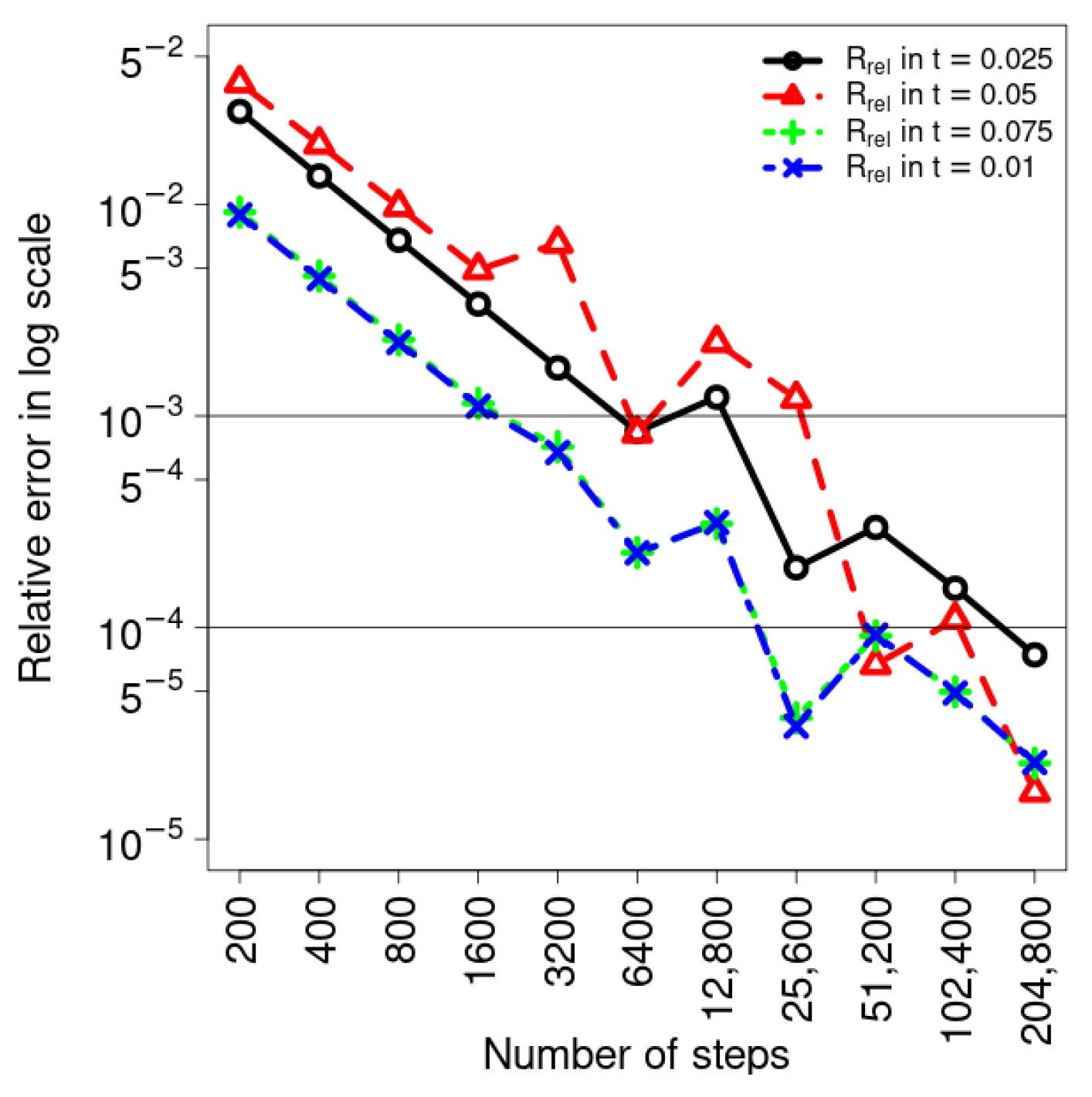
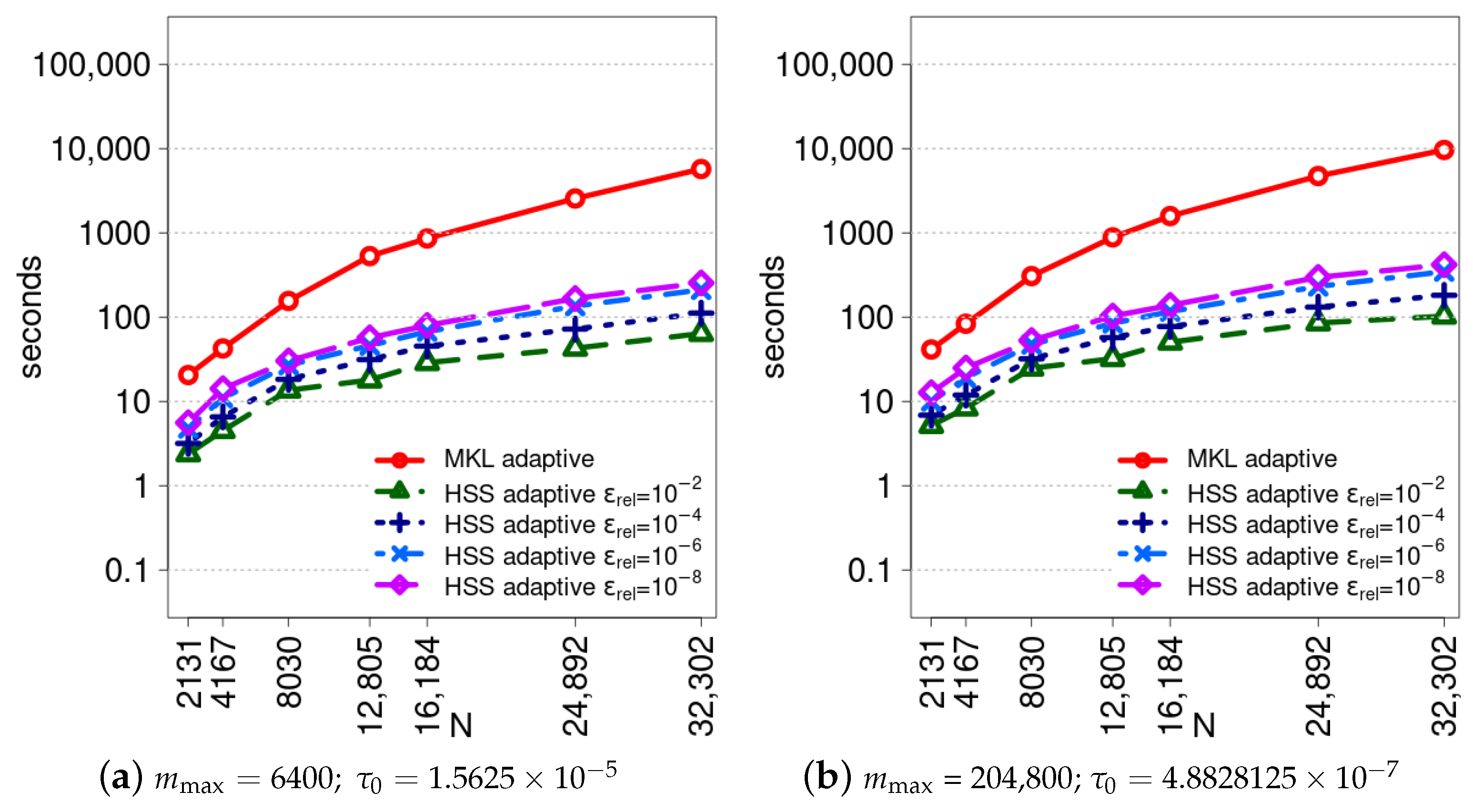
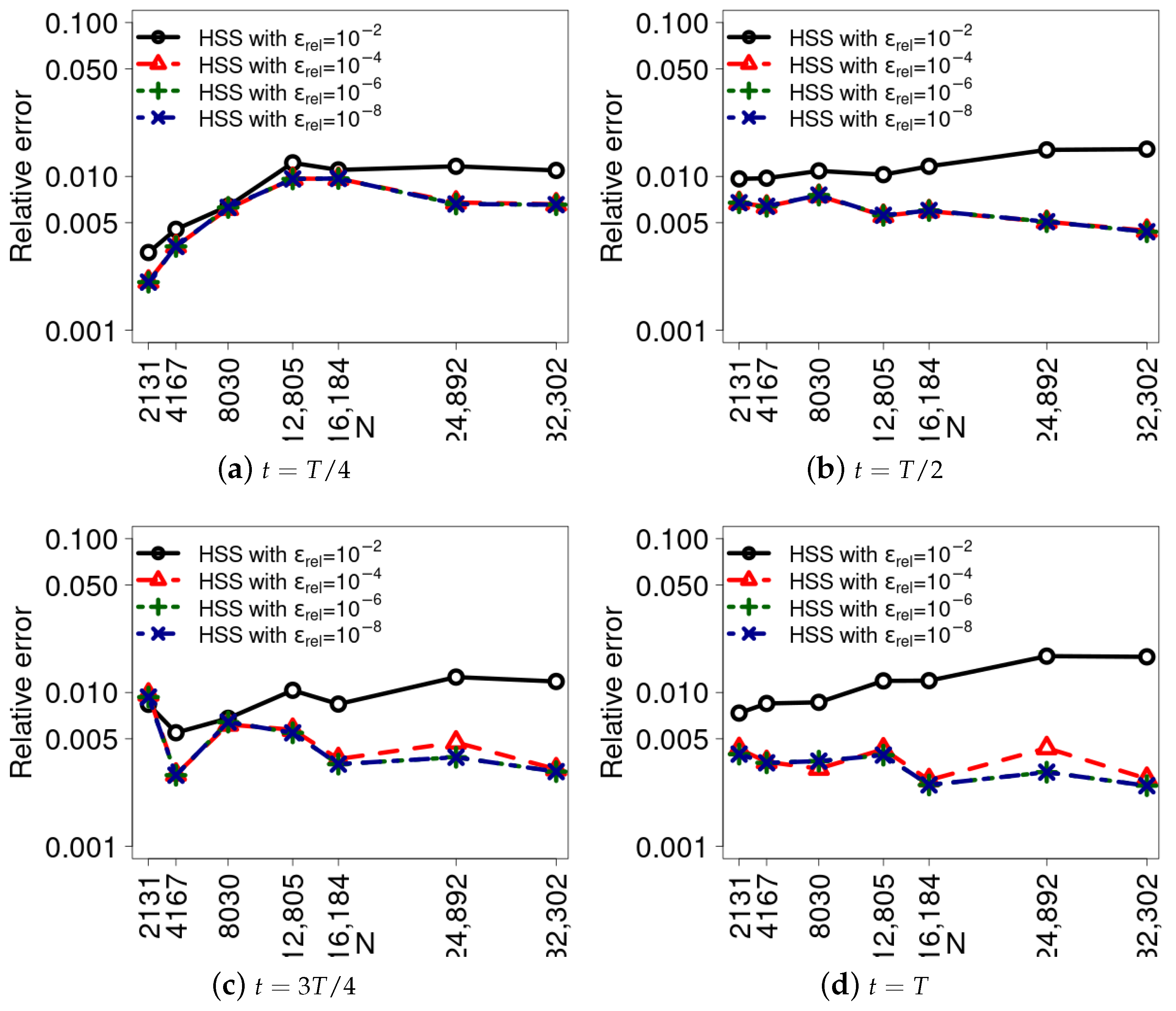
8. Analysis of Relative Errors of the HSS Compression Solver
9. Discussion
10. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Binder, K.; Bennemann, C.; Baschnagel, J.; Paul, W. Anomalous diffusion of polymers in supercooled melts near the glass transition. In Anomalous Diffusion from Basics to Applications; Pękalski, A., Sznajd-Weron, K., Eds.; Springer: Berlin/Heidelberg, Germany, 1999; pp. 124–139. [Google Scholar]
- Langlands, T.; Henry, B.; Wearne, S. Fractional Cable Equation Models for Anomalous Electrodiffusion in Nerve Cells: Finite Domain Solutions. SIAM J. Appl. Math. 2011, 71, 1168–1203. [Google Scholar] [CrossRef]
- Taitelbaum, H. Diagnosis using photon diffusion: From brain oxygenation to the fat of the atlantic salmon. In Anomalous Diffusion from Basics to Applications; Pękalski, A., Sznajd-Weron, K., Eds.; Springer: Berlin/Heidelberg, Germany, 1999; pp. 160–174. [Google Scholar]
- Rosasco, L.; Belkin, M.; Vito, E.D. On Learning with Integral Operators. J. Mach. Learn. Res. 2010, 11, 905–934. [Google Scholar]
- Chaturapruek, S.; Breslau, J.; Yazdi, D.; Kolokolnikov, T.; McCalla, S. Crime modeling with Lèvy flights. SIAM J. Appl. Math. 2013, 73, 1703–1720. [Google Scholar] [CrossRef]
- Sun, H.; Zhang, Y.; Baleanu, D.; Chen, W.; Chen, Y. A new collection of real world applications of fractional calculus in science and engineering. Commun. Nonlinear Sci. Numer. Simul. 2018, 64, 213–231. [Google Scholar] [CrossRef]
- Kwaśnicki, M. Ten equivalent definitions of the fractional laplace operator. Fract. Calc. Appl. Anal. 2017, 20, 7–51. [Google Scholar] [CrossRef]
- Lischke, A.; Pang, G.; Gulian, M.; Song, F.; Glusa, C.; Zheng, X.; Mao, Z.; Cai, W.; Meerschaert, M.M.; Ainsworth, M.; et al. What is the fractional Laplacian? A comparative review with new results. J. Comput. Phys. 2020, 404, 109009. [Google Scholar] [CrossRef]
- Harizanov, S.; Margenov, S.; Popivanov, N. Spectral Fractional Laplacian with Inhomogeneous Dirichlet Data: Questions, Problems, Solutions. In Advanced Computing in Industrial Mathematics; Georgiev, I., Kostadinov, H., Lilkova, E., Eds.; Springer: Cham, Switzerland, 2021; pp. 123–138. [Google Scholar] [CrossRef]
- Bonito, A.; Lei, W.; Pasciak, J.E. The approximation of parabolic equations involving fractional powers of elliptic operators. J. Comput. Appl. Math. 2017, 315, 32–48. [Google Scholar] [CrossRef]
- Markus Melenk, J.; Rieder, A. An exponentially convergent discretization for space–time fractional parabolic equations using hp-FEM. IMA J. Numer. Anal. 2022, 43, 2352–2376. [Google Scholar] [CrossRef]
- Nochetto, R.H.; Otárola, E.; Salgado, A.J. A PDE Approach to Space-Time Fractional Parabolic Problems. SIAM J. Numer. Anal. 2016, 54, 848–873. [Google Scholar] [CrossRef]
- Vabishchevich, P.N. Splitting schemes for non-stationary problems with a rational approximation for fractional powers of the operator. Appl. Numer. Math. 2021, 165, 414–430. [Google Scholar] [CrossRef]
- Vabishchevich, P.N. Numerical Solution of Non-stationary Problems for a Space-Fractional Diffusion Equation. Fract. Calc. Appl. Anal. 2016, 19, 116–139. [Google Scholar] [CrossRef]
- Čiegis, R.; Starikovičius, V.; Suboč, O.; Čiegis, R. On Construction of Partially Dimension-Reduced Approximations for Nonstationary Nonlocal Problems of a Parabolic Type. Mathematics 2023, 11, 1984. [Google Scholar] [CrossRef]
- Danczul, T.; Hofreither, C.; Schöberl, J. A unified rational Krylov method for elliptic and parabolic fractional diffusion problems. Numer. Linear Algebra Appl. 2023, 30, e2488. [Google Scholar] [CrossRef]
- Khristenko, U.; Wohlmuth, B. Solving time-fractional differential equations via rational approximation. IMA J. Numer. Anal. 2022, 43, 1263–1290. [Google Scholar] [CrossRef]
- Yang, Y.; Huang, J. Double fast algorithm for solving time-space fractional diffusion problems with spectral fractional Laplacian. Appl. Math. Comput. 2024, 475, 128715. [Google Scholar] [CrossRef]
- Acosta, G.; Bersetche, F.M.; Borthagaray, J.P. Finite Element Approximations for Fractional Evolution Problems. Fract. Calc. Appl. Anal. 2019, 22, 767–794. [Google Scholar] [CrossRef]
- Slavchev, D.; Margenov, S. Performance Study of Hierarchical Semi-separable Compression Solver for Parabolic Problems with Space-Fractional Diffusion. In Large-Scale Scientific Computing; Lirkov, I., Margenov, S., Eds.; Springer: Cham, Switzerland, 2022; pp. 71–80. [Google Scholar]
- Acosta, G.; Borthagaray, J. A Fractional Laplace Equation: Regularity of Solutions and Finite Element Approximations. SIAM J. Numer. Anal. 2017, 55, 472–495. [Google Scholar] [CrossRef]
- Slavchev, D.; Margenov, S. On the Application of a Hierarchically Semi-separable Compression for Space-Fractional Parabolic Problems with Varying Time Steps. In Numerical Methods and Applications; Georgiev, I., Datcheva, M., Georgiev, K., Nikolov, G., Eds.; Springer: Cham, Switzerland, 2023; pp. 289–301. [Google Scholar]
- Blaheta, R.; Byczanski, P.; Kohut, R.; Starỳ, J. Algorithms for Parallel Fem Modelling of Thermo-Mechanical Phenomena Arising from the Disposal of the Spent Nuclear Fuel. In Elsevier Geo-Engineering Book Series; Elsevier: Amsterdam, The Netherlands, 2004; Volume 2, pp. 395–400. [Google Scholar]
- Georgiev, K.; Kosturski, N.; Margenov, S.; Starỳ, J. On adaptive time stepping for large-scale parabolic problems: Computer simulation of heat and mass transfer in vacuum freeze-drying. J. Comput. Appl. Math. 2009, 226, 268–274. [Google Scholar] [CrossRef]
- Vabishchevich, P.N.; Vasil’ev, A.O. Time step selection for the numerical solution of boundary value problems for parabolic equations. Comput. Math. Math. Phys. 2017, 57, 843–853. [Google Scholar] [CrossRef]
- Hackbusch, W. A Sparse Matrix Arithmetic Based on H-Matrices. Part I: Introduction to H-Matrices. Computing 1999, 62, 89–108. [Google Scholar] [CrossRef]
- Hackbusch, W.; Grasedyck, L.; Börm, S. An introduction to hierarchical matrices. Math. Bohem. 2002, 127, 229–241. [Google Scholar] [CrossRef]
- Martinsson, P.G. A Fast Randomized Algorithm for Computing a Hierarchically Semiseparable Representation of a Matrix. SIAM J. Matrix Anal. Appl. 2011, 32, 1251–1274. [Google Scholar] [CrossRef]
- Xia, J.; Chandrasekaran, S.; Gu, M.; Li, X.S. Fast algorithms for hierarchically semiseparable matrices. Numer. Lin. Alg. Appl. 2010, 17, 953–976. [Google Scholar] [CrossRef]
- Rouet, F.H.; Li, X.; Ghysels, P.; Napov, A. A Distributed-Memory Package for Dense Hierarchically Semi-Separable Matrix Computations Using Randomization. ACM Trans. Math. Softw. 2016, 42, 1–35. [Google Scholar] [CrossRef]
- Slavchev, D.; Margenov, S.; Georgiev, I. On the application of recursive bisection and nested dissection reorderings for solving fractional diffusion problems using HSS compression. AIP Conf. Proc. 2020, 2302, 120008. [Google Scholar] [CrossRef]
- Rebrova, E.; Chávez, G.; Liu, Y.; Ghysels, P.; Li, X.S. A Study of Clustering Techniques and Hierarchical Matrix Formats for Kernel Ridge Regression. In Proceedings of the 2018 IEEE International Parallel and Distributed Processing Symposium Workshops (IPDPSW), Vancouver, BC, Canada, 21–25 May 2018; pp. 883–892. [Google Scholar] [CrossRef]
- Dongarra, J.J.; Luszczek, P.; Petitet, A. The LINPACK Benchmark: Past, present and future. Concurr. Comput. Pract. Exp. 2003, 15, 803–820. [Google Scholar] [CrossRef]
- Georgiev, K.; Margenov, S. Numerical Methods for Fractional Diffusion-Reaction Problems Based on Operator Splitting and BURA. In Advanced Computing in Industrial Mathematics; Georgiev, I., Kostadinov, H., Lilkova, E., Eds.; Springer: Cham, Switzerland, 2023; pp. 73–84. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Margenov, S.; Slavchev, D. Performance Analysis and Parallel Scalability of Numerical Methods for Fractional-in-Space Diffusion Problems with Adaptive Time Stepping. Algorithms 2024, 17, 453. https://doi.org/10.3390/a17100453
Margenov S, Slavchev D. Performance Analysis and Parallel Scalability of Numerical Methods for Fractional-in-Space Diffusion Problems with Adaptive Time Stepping. Algorithms. 2024; 17(10):453. https://doi.org/10.3390/a17100453
Chicago/Turabian StyleMargenov, Svetozar, and Dimitar Slavchev. 2024. "Performance Analysis and Parallel Scalability of Numerical Methods for Fractional-in-Space Diffusion Problems with Adaptive Time Stepping" Algorithms 17, no. 10: 453. https://doi.org/10.3390/a17100453
APA StyleMargenov, S., & Slavchev, D. (2024). Performance Analysis and Parallel Scalability of Numerical Methods for Fractional-in-Space Diffusion Problems with Adaptive Time Stepping. Algorithms, 17(10), 453. https://doi.org/10.3390/a17100453







