Mission Planning of UAVs and UGV for Building Inspection in Rural Area
Abstract
:1. Introduction
2. Establishment of Mathematical Model
- Each UAV on the UGV possesses uniform characteristics, with identical cruising speeds during flight and equal battery capacities.
- UAVs take off with full battery capacity, and when battery levels are low, they return to the UGV for battery replacement, disregarding the time for takeoff, landing, ascent, descent, and battery replacement.
- Constrained by the distribution of task points and the precision requirements of UAV positioning, the UGV needs to remain stationary at the parking point until all UAVs complete their inspection tasks.
- During the flight between the start and the destination, the time variations caused by altitude changes have been incorporated into the operational time of each task.
3. Design of Planning Algorithm for Cooperative Inspection
3.1. Determination of the Parking Point Location
3.2. Mission Planning Algorithm Based on ACO-GA
3.2.1. Encoding and Decoding of Individual Solutions
3.2.2. Selection Method Based on ACO
3.2.3. Crossover Method
3.2.4. Mutation Method
3.2.5. Computing Fitness Values and Updating Pheromones
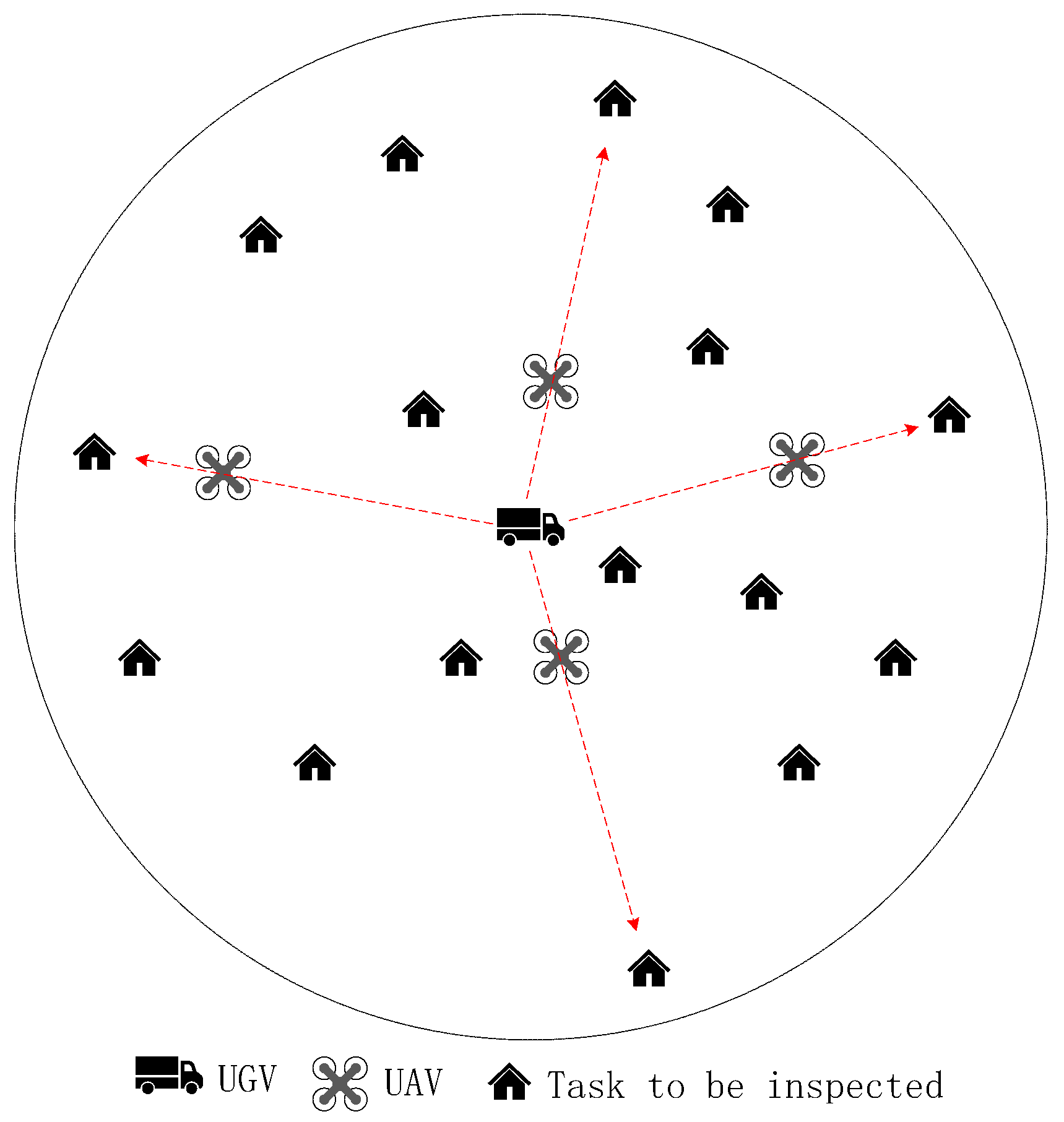
4. Simulation Studies
4.1. Optimization Results of ACO-GA
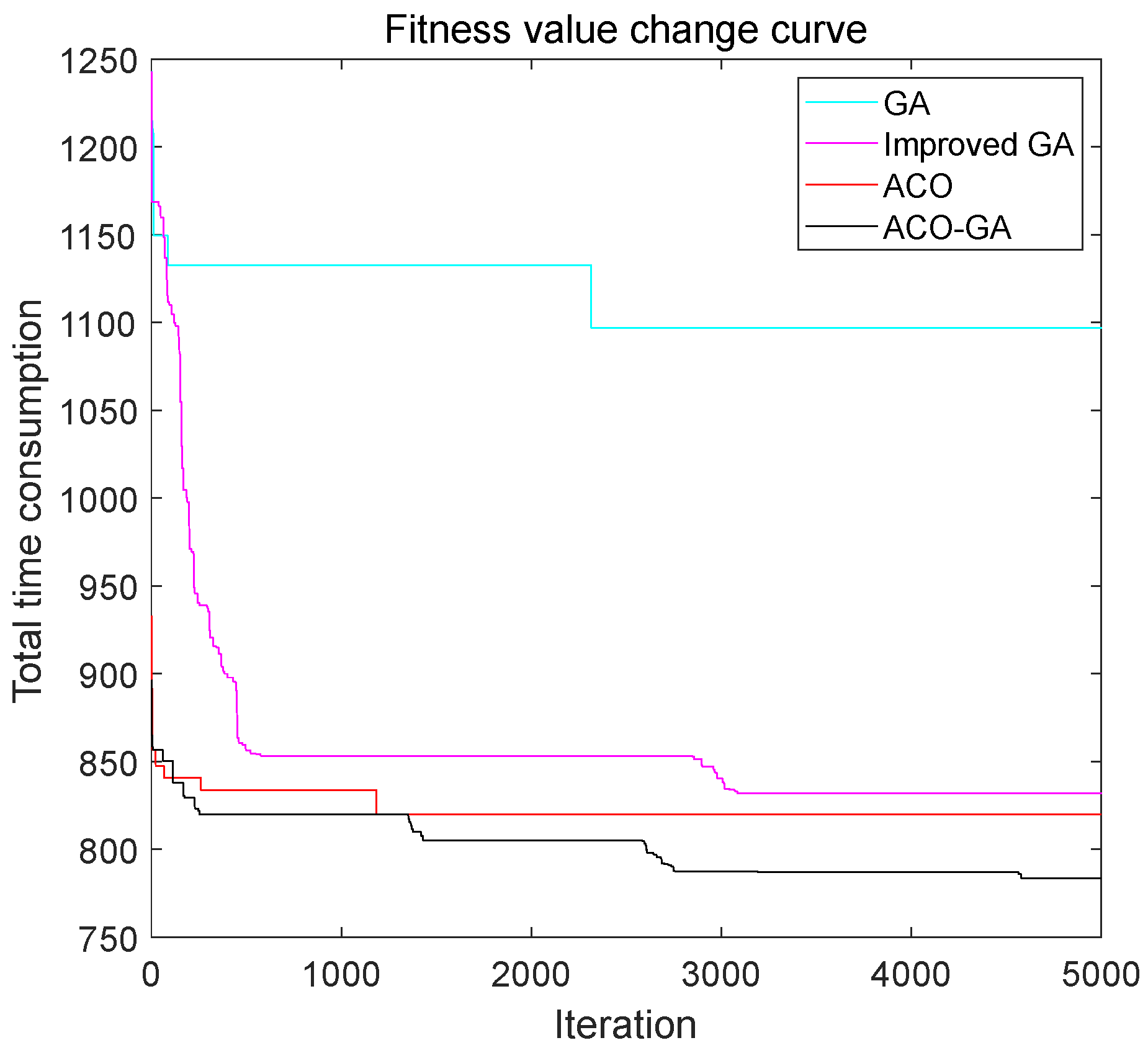
4.2. Comparison with Other Algorithm Optimization Results
4.3. Influence of the Number of UAVs on the Task Allocation Scheme
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ye, F.; Chen, J.; Sun, Q.; Tian, Y.; Jiang, T. Decentralized task allocation for heterogeneous multi-UAV system with task coupling constraints. J. Supercomput. 2021, 77, 111–132. [Google Scholar] [CrossRef]
- Beloev, I.H. A review on current and emerging application possibilities for unmanned aerial vehicles. Acta Technol. Agric. 2016, 19, 70–76. [Google Scholar] [CrossRef]
- Yan, J.; Zhang, X.; Shen, S.; He, X.; Xia, X.; Li, N.; Wang, S.; Yang, Y.; Ding, N. A Real-Time Strand Breakage Detection Method for Power Line Inspection with UAVs. Drones 2023, 7, 574. [Google Scholar] [CrossRef]
- Wu, M.; Chen, W.; Tian, X. Optimal Energy Consumption Path Planning for Quadrotor UAV Transmission Tower Inspection Based on Simulated Annealing Algorithm. Energies 2022, 15, 8036. [Google Scholar] [CrossRef]
- Tang, G.; Wang, C.; Zhang, Z.; Men, S. UAV Path Planning for Container Terminal Yard Inspection in a Port Environment. J. Mar. Sci. Eng. 2024, 12, 128. [Google Scholar] [CrossRef]
- Shang, Z.; Bradley, J.; Shen, Z. A co-optimal coverage path planning method for aerial scanning of complex structures. Expert Syst. Appl. 2020, 158, 113535. [Google Scholar] [CrossRef]
- Zhang, R.; Li, H.; Duan, K.; You, S.; Liu, K.; Wang, F.; Hu, Y. Automatic Detection of Earthquake-Damaged Buildings by Integrating UAV Oblique Photography and Infrared Thermal Imaging. Remote Sens. 2020, 12, 2621. [Google Scholar] [CrossRef]
- Ruiz, R.D.B.; Lordsleem, A.C., Jr.; Rocha, J.H.A.; Irizarry, J. Unmanned aerial vehicles (UAV) as a tool for visual inspection of building facades in AEC+ FM industry. Constr. Innov. 2022, 22, 1155–1170. [Google Scholar] [CrossRef]
- Radmanesh, M.; Sharma, B.; Kumar, M.; French, D. PDE solution to UAV/UGV trajectory planning problem by spatio-temporal estimation during wildfires. Chin. J. Aeronaut. 2021, 34, 601–616. [Google Scholar] [CrossRef]
- Wu, Y.; Wu, S.; Hu, X. Cooperative path planning of UAVs & UGVs for a persistent surveillance task in urban environments. IEEE Internet Things J. 2020, 8, 4906–4919. [Google Scholar]
- Song, J.; Zhao, K.; Liu, Y. Survey on Mission Planning of Multiple Unmanned Aerial Vehicles. Aerospace 2023, 10, 208. [Google Scholar] [CrossRef]
- Wang, Z.; Li, M.; Li, J.; Cao, J.; Wang, H. A task allocation algorithm based on market mechanism for multiple robot systems. In Proceedings of the 2016 IEEE International Conference on Real-Time Computing and Robotics (RCAR), Angkor Wat, Cambodia, 6–10 June 2016; pp. 150–155. [Google Scholar]
- Peng, Q.; Wu, H.; Xue, R. Review of dynamic task allocation methods for UAV swarms oriented to ground targets. Complex Syst. Model. Simul. 2021, 1, 163–175. [Google Scholar] [CrossRef]
- Wu, Y.; Liang, T.; Gou, J.; Tao, C.; Wang, H. Heterogeneous Mission Planning for Multiple UAV Formations via Metaheuristic Algorithms. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 3924–3940. [Google Scholar] [CrossRef]
- Wu, Y. A survey on population-based meta-heuristic algorithms for motion planning of aircraft. Swarm Evol. Comput. 2021, 62, 100844. [Google Scholar] [CrossRef]
- Guangtong, X.; Li, L.; Long, T.; Wang, Z.; Cai, M. Cooperative multiple task assignment considering precedence constraints using multi-chromosome encoded genetic algorithm. In Proceedings of the 2018 AIAA Guidance, Navigation, and Control Conference, Kissimmee, FL, USA, 8–12 January 2018; p. 1859. [Google Scholar]
- Chen, J.; Ling, F.; Zhang, Y.; You, T.; Liu, Y.; Du, X. Coverage path planning of heterogeneous unmanned aerial vehicles based on ant colony system. Swarm Evol. Comput. 2022, 69, 101005. [Google Scholar] [CrossRef]
- Huo, L.; Zhu, J.; Wu, G.; Li, Z. A Novel Simulated Annealing Based Strategy for Balanced UAV Task Assignment and Path Planning. Sensors 2020, 20, 4769. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.-Z.; Li, J.-W.; Hu, B.; Zhang, J.-D. An improved PSO algorithm for solving multi-UAV cooperative reconnaissance task decision-making problem. In Proceedings of the 2016 IEEE International Conference on Aircraft Utility Systems (AUS), Beijing, China, 10–12 October 2016; pp. 434–437. [Google Scholar]
- Lee, M.-T.; Chen, B.-Y.; Lai, Y.-C. A Hybrid Tabu Search and 2-opt Path Programming for Mission Route Planning of Multiple Robots under Range Limitations. Electronics 2020, 9, 534. [Google Scholar] [CrossRef]
- Zhang, Y.-Z.; Hu, B.; Li, J.-W.; Zhang, J.-D. Heterogeneous multi-UAVs cooperative task assignment based on GSA-GA. In Proceedings of the 2016 IEEE International Conference on Aircraft Utility Systems (AUS), Beijing, China, 10–12 October 2016; pp. 423–426. [Google Scholar]
- Zhu, W.; Li, L.; Teng, L.; Yonglu, W. Multi-UAV reconnaissance task allocation for heterogeneous targets using an opposition-based genetic algorithm with double-chromosome encoding. Chin. J. Aeronaut. 2018, 31, 339–350. [Google Scholar]
- Han, H.; Bai, X.; Han, H.; Hou, Y.; Qiao, J. Self-adjusting multitask particle swarm optimization. IEEE Trans. Evol. Comput. 2021, 26, 145–158. [Google Scholar] [CrossRef]
- Gou, Q.; Li, Q. Task assignment based on PSO algorithm based on logistic function inertia weight adaptive adjustment. In Proceedings of the 2020 3rd International Conference on Unmanned Systems (ICUS), Harbin, China, 27–28 November 2020; pp. 825–829. [Google Scholar]
- Ebadinezhad, S. DEACO: Adopting dynamic evaporation strategy to enhance ACO algorithm for the traveling salesman problem. Eng. Appl. Artif. Intell. 2020, 92, 103649. [Google Scholar] [CrossRef]
- Shang, K.; Karungaru, S.; Feng, Z.; Ke, L.; Terada, K. A GA-ACO hybrid algorithm for the multi-UAV mission planning problem. In Proceedings of the 2014 14th International Symposium on Communications and Information Technologies (ISCIT), Incheon, Republic of Korea, 24–26 September 2014; pp. 243–248. [Google Scholar]
- Jia, Z.; Xiao, B.; Qian, H. Improved Mixed Discrete Particle Swarms based Multi-task Assignment for UAVs. In Proceedings of the 2023 IEEE 12th Data Driven Control and Learning Systems Conference (DDCLS), Xiangtan, China, 12–14 May 2023; pp. 442–448. [Google Scholar]
- Jiang, C.; Wan, Z.; Peng, Z. A new efficient hybrid algorithm for large scale multiple traveling salesman problems. Expert Syst. Appl. 2020, 139, 112867. [Google Scholar] [CrossRef]









| Parameter | Parameter Values |
|---|---|
| Numbers of UAVs m | 5 |
| Maximum time of flight tmax | 900 s |
| Flight speed v | 15 m/s |
| Number of task points n | 46 |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Number of populations NP | 200 | Mutation probability Pe | 0.5 |
| Maximum number of iterations G | 5000 | Enhancement factor α,β | 1.5 |
| Crossover probability Pm | 0.9 | Pheromone enhancement coefficient Q | 100 |
| Task Point | Coordinates | Operating Time | Task Point | Coordinates | Operating Time | Task Point | Coordinates | Operating Time |
|---|---|---|---|---|---|---|---|---|
| 1 | (6.3, 928.1) | 75 s | 17 | (1155.5, 790.9) | 90 s | 33 | (1487.8, 1049.2) | 46 s |
| 2 | (72.5, 708.3) | 61 s | 18 | (1171.9, 1166.5) | 35 s | 34 | (1500.9, 1092.8) | 39 s |
| 3 | (242.7, 92.0) | 45 s | 19 | (1183.9, 1216.3) | 57 s | 35 | (1493.0, 1415.2) | 38 s |
| 4 | (335.6, 1380.9) | 76 s | 20 | (1209.0, 1270.7) | 36 s | 36 | (1526.8, 1235.1) | 83 s |
| 5 | (489.2, 989.3) | 87 s | 21 | (1218.8, 817.6) | 88 s | 37 | (1603.3, 2174.9) | 65 s |
| 6 | (533.2, 529.4) | 40 s | 22 | (1245.3, 805.9) | 30 s | 38 | (1688.6, 1677.0) | 63 s |
| 7 | (569.1, 779.7) | 62 s | 23 | (1233.7, 939.8) | 77 s | 39 | (1753.9, 1035.0) | 39 s |
| 8 | (606.0, 1532.8) | 66 s | 24 | (1278.9, 902.9) | 79 s | 40 | (1862.3, 1479.5) | 82 s |
| 9 | (958.4, 1128.3) | 75 s | 25 | (1284.2, 1665.1) | 83 s | 41 | (1877.0, 1186.6) | 68 s |
| 10 | (985.8, 1949.2) | 57 s | 26 | (1315.5, 963.6) | 35 s | 42 | (1941.7, 621.0) | 51 s |
| 11 | (1063.1, 990.7) | 35 s | 27 | (1343.1, 993.25) | 54 s | 43 | (2008.3, 615.7) | 61 s |
| 12 | (1067.0, 1048.7) | 44 s | 28 | (1332.4, 1800.0) | 46 s | 44 | (2005.1, 925.1) | 54 s |
| 13 | (1063.6, 1048.7) | 85 s | 29 | (1369.2, 996.8) | 78 s | 45 | (2017.6, 621.4) | 35 s |
| 14 | (1104.9, 977.8) | 39 s | 30 | (1381.7, 854.5) | 56 s | 46 | (2011.5, 891.1) | 45 s |
| 15 | (1103.1, 1053.4) | 80 s | 31 | (1425.0, 1195.1) | 85 s | Parking position | ||
| 16 | (1104.9, 1090.6) | 63 s | 32 | (1440.1, 1024.0) | 41 s | (1206.5, 1103.9) |
| Serial Number | UAV1 | UAV2 | UAV3 | UAV4 | UAV5 |
|---|---|---|---|---|---|
| Operating time (s) | 708 | 577 | 504 | 586 | 545 |
| Flight time (s) | 75.88 | 209.02 | 277.46 | 194.49 | 221.11 |
| Total time (s) | 783.88 | 786.02 | 781.46 | 780.49 | 766.11 |
| Algorithm | ACO-GA | GA | Improved GA | ACO |
|---|---|---|---|---|
| Average (s) | 787.69 | 1110.42 | 825.40 | 825.51 |
| Maximum (s) | 790.04 | 1141.97 | 843.05 | 829.17 |
| Minimum (s) | 785.88 | 1048.86 | 805.13 | 819.98 |
| Standard deviation (s) | 2.07 | 32.39 | 13.20 | 4.47 |
| Mean computation time (s) | 316.39 | 253.11 | 290.61 | 456.99 |
| Number of UAVs | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|
| Average time consuming (s) | 1686.17 | 1060.20 | 787.69 | 698.63 | 614.55 |
| Average cost (¥) | 1165.85 | 1304.08 | 1143.85 | 1319.18 | 1480.19 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, X.; Wu, Y.; Xu, S. Mission Planning of UAVs and UGV for Building Inspection in Rural Area. Algorithms 2024, 17, 177. https://doi.org/10.3390/a17050177
Chen X, Wu Y, Xu S. Mission Planning of UAVs and UGV for Building Inspection in Rural Area. Algorithms. 2024; 17(5):177. https://doi.org/10.3390/a17050177
Chicago/Turabian StyleChen, Xiao, Yu Wu, and Shuting Xu. 2024. "Mission Planning of UAVs and UGV for Building Inspection in Rural Area" Algorithms 17, no. 5: 177. https://doi.org/10.3390/a17050177
APA StyleChen, X., Wu, Y., & Xu, S. (2024). Mission Planning of UAVs and UGV for Building Inspection in Rural Area. Algorithms, 17(5), 177. https://doi.org/10.3390/a17050177






