An Integer-Fractional Gradient Algorithm for Back Propagation Neural Networks
Abstract
:1. Introduction
2. Method
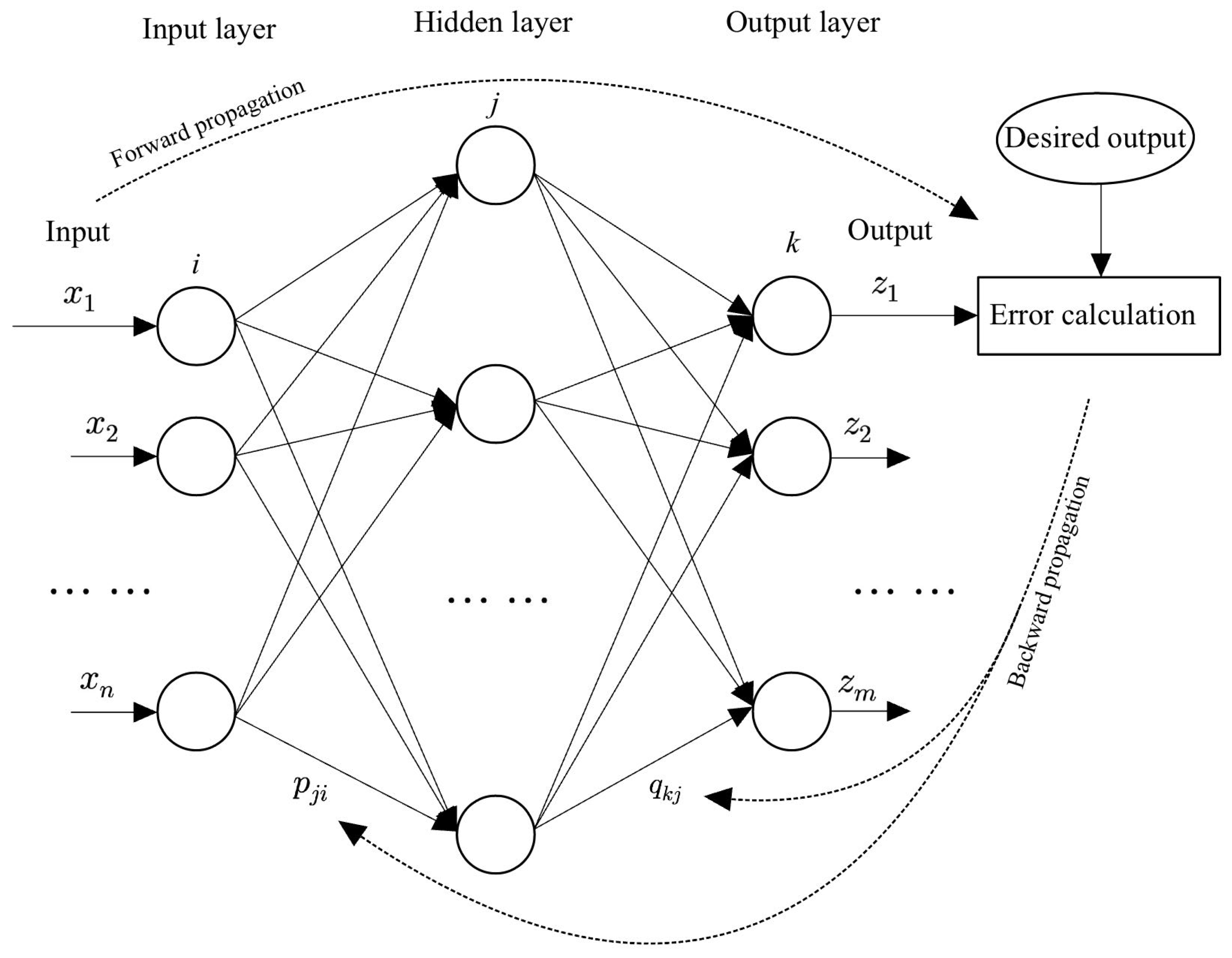
2.1. Network Structure
2.2. Fractional Parameter Update
2.3. Algorithms
| Algorithm 1 BPNN |
|
| Algorithm 2 FBPNN |
|
| Algorithm 3 MIFBPNN |
|
3. Convergence Analysis
4. Numerical Experiments
4.1. Experiment Preparation
4.2. Optimal Parameters Tuning
4.3. Training for Different Training Sets’ Sizes
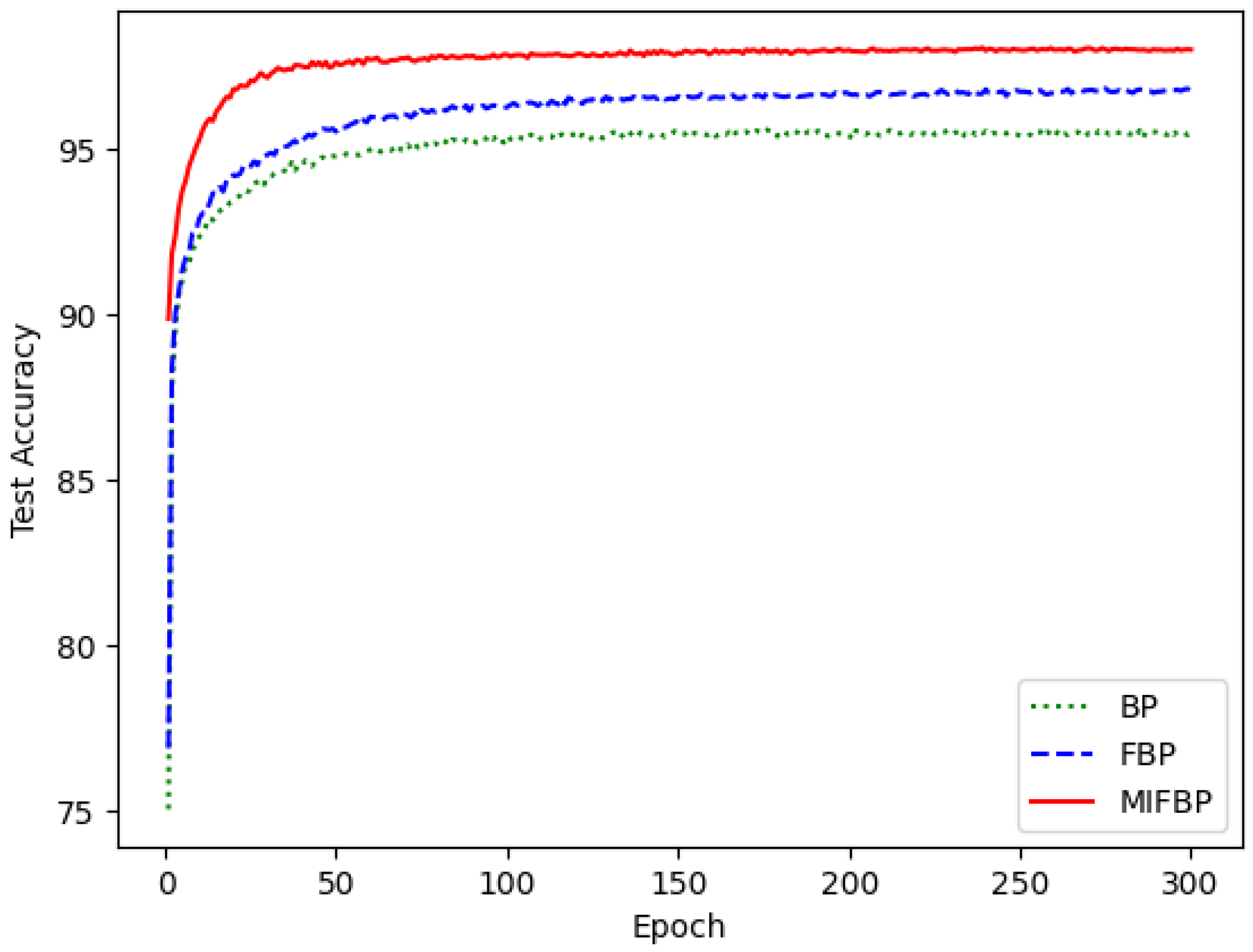
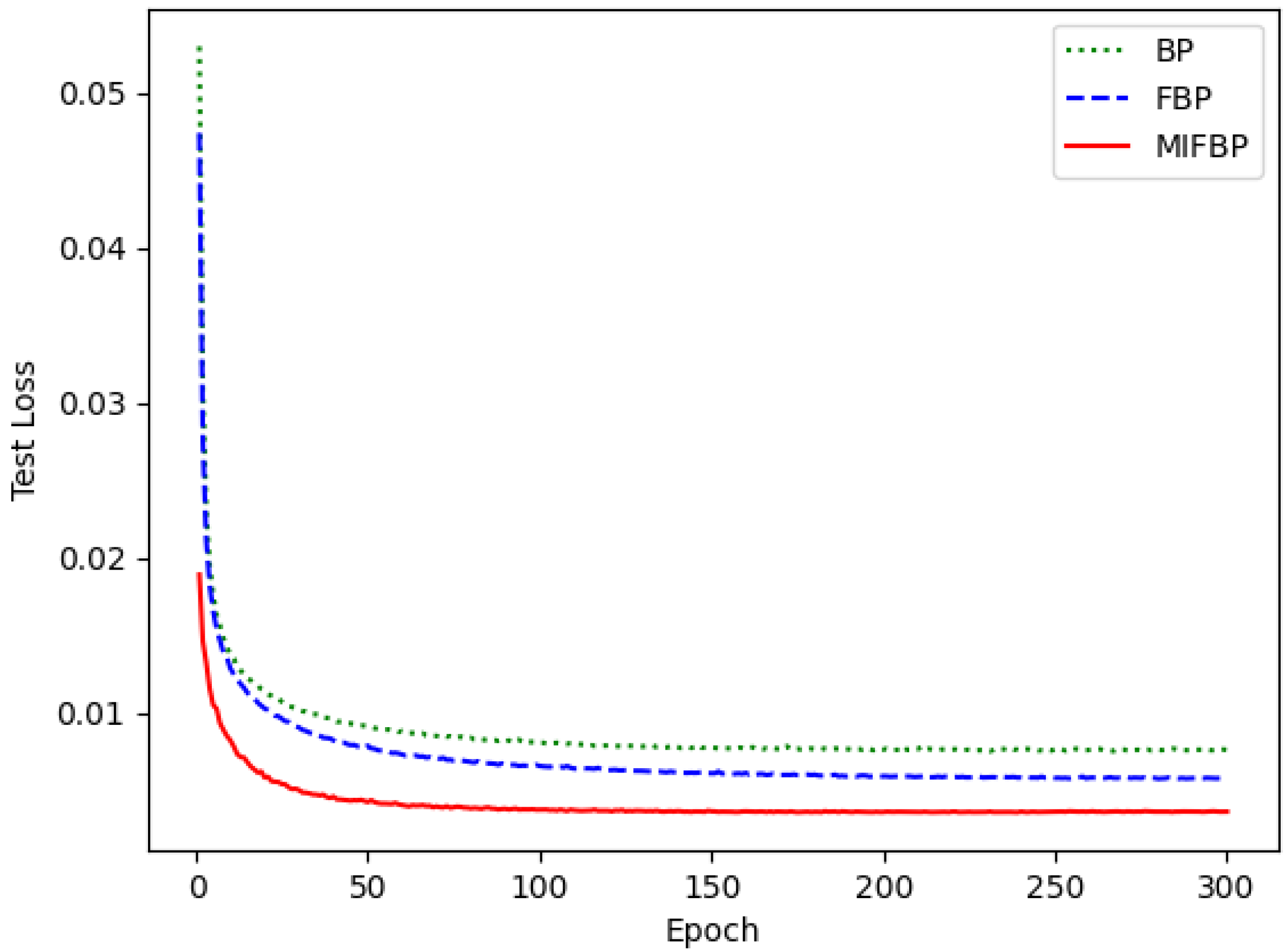
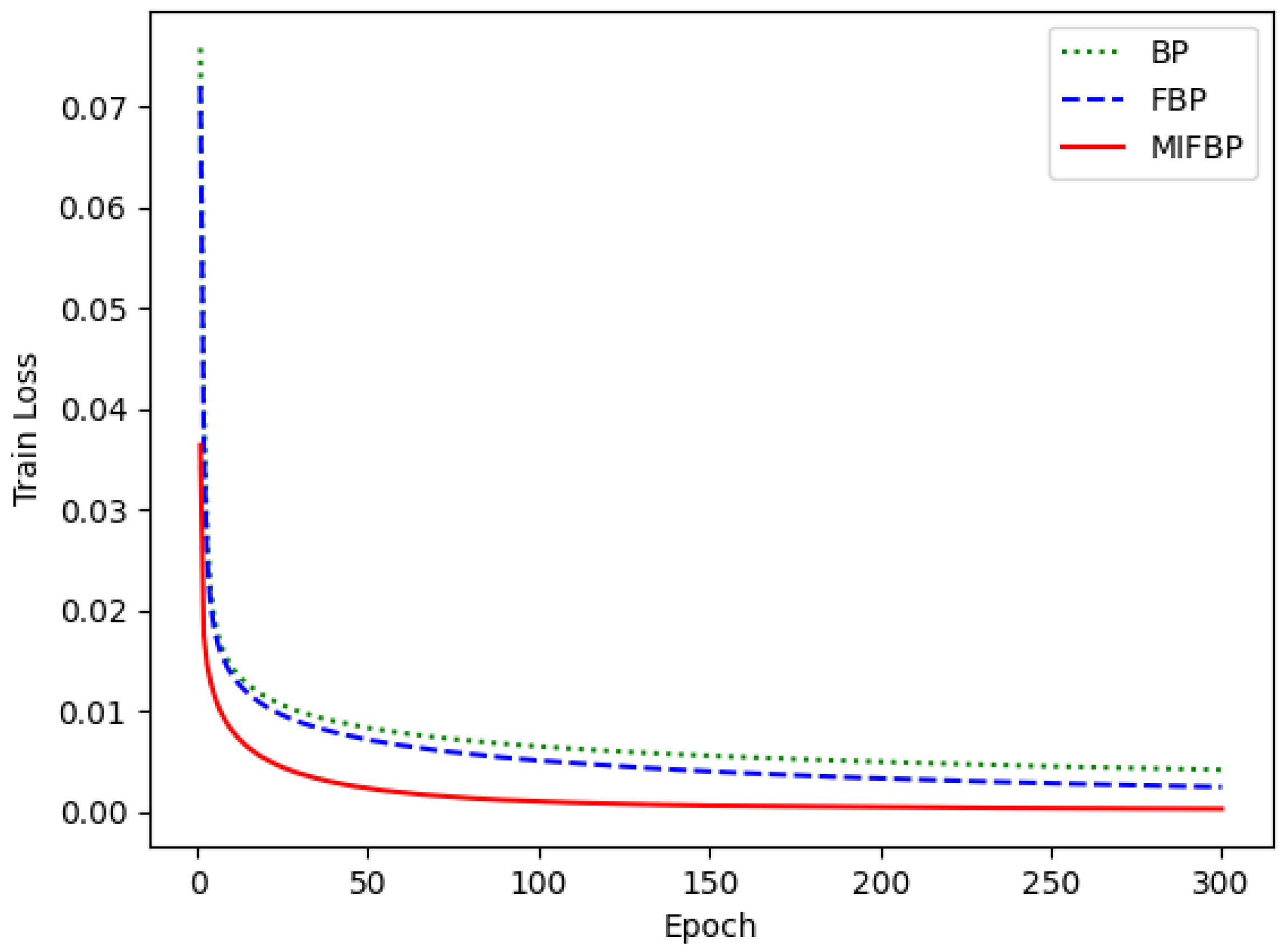
4.4. Training Performances of Different Neural Networks
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Edwards, C.J. The Historical Development of the Calculus; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Oldham, K.; Spanier, J. The Fractional Calculus Theory and Applications of Differentiation and Integration to Arbitrary Order; Academic Press: Cambridge, MA, USA, 1974. [Google Scholar]
- Hahn, D.W.; Özisik, M.N. Heat Conduction; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Matlob, M.A.; Jamali, Y. The concepts and applications of fractional order differential calculus in modeling of viscoelastic systems: A primer. Crit. Rev. Biomed. Eng. 2019, 47, 249–276. [Google Scholar] [CrossRef] [PubMed]
- Dehestani, H.; Ordokhani, Y.; Razzaghi, M. Fractional-order Legendre–Laguerre functions and their applications in fractional partial differential equations. Appl. Math. Comput. 2018, 336, 433–453. [Google Scholar] [CrossRef]
- Yuxiao, K.; Shuhua, M.; Yonghong, Z. Variable order fractional grey model and its application. Appl. Math. Model. 2021, 97, 619–635. [Google Scholar] [CrossRef]
- Kuang, Z.; Sun, L.; Gao, H.; Tomizuka, M. Practical fractional-order variable-gain supertwisting control with application to wafer stages of photolithography systems. IEEE/ASME Trans. Mechatronics 2021, 27, 214–224. [Google Scholar] [CrossRef]
- Liu, C.; Yi, X.; Feng, Y. Modelling and parameter identification for a two-stage fractional dynamical system in microbial batch process. Nonlinear Anal. Model. Control 2022, 27, 350–367. [Google Scholar] [CrossRef]
- Wang, S.; Li, W.; Liu, C. On necessary optimality conditions and exact penalization for a constrained fractional optimal control problem. Optim. Control Appl. Methods 2022, 43, 1096–1108. [Google Scholar] [CrossRef]
- Bhrawy, A.H.; Ezz-Eldien, S.S.; Doha, E.H.; Abdelkawy, M.A.; Baleanu, D. Solving fractional optimal control problems within a Chebyshev–Legendre operational technique. Int. J. Control 2017, 90, 1230–1244. [Google Scholar] [CrossRef]
- Saxena, S. Load frequency control strategy via fractional-order controller and reduced-order modeling. Int. J. Electr. Power Energy Syst. 2019, 104, 603–614. [Google Scholar] [CrossRef]
- Mohammadi, H.; Kumar, S.; Rezapour, S.; Etemad, S. A theoretical study of the Caputo–Fabrizio fractional modeling for hearing loss due to Mumps virus with optimal control. Chaos Solitons Fractals 2021, 144, 110668. [Google Scholar] [CrossRef]
- Aldrich, C. Exploratory Analysis of Metallurgical Process Data with Neural Networks and Related Methods; Elsevier: Amsterdam, The Netherlands, 2002. [Google Scholar]
- Bhattacharya, U.; Parui, S.K. Self-adaptive learning rates in backpropagation algorithm improve its function approximation performance. In Proceedings of the ICNN’95-International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; IEEE: Piscataway, NJ, USA, 1995; Volume 5, pp. 2784–2788. [Google Scholar]
- Niu, H.; Chen, Y.; West, B.J. Why do big data and machine learning entail the fractional dynamics? Entropy 2021, 23, 297. [Google Scholar] [CrossRef]
- Xu, C.; Liao, M.; Li, P.; Guo, Y.; Xiao, Q.; Yuan, S. Influence of multiple time delays on bifurcation of fractional-order neural networks. Appl. Math. Comput. 2019, 361, 565–582. [Google Scholar] [CrossRef]
- Pakdaman, M.; Ahmadian, A.; Effati, S.; Salahshour, S.; Baleanu, D. Solving differential equations of fractional order using an optimization technique based on training artificial neural network. Appl. Math. Comput. 2017, 293, 81–95. [Google Scholar] [CrossRef]
- Asgharnia, A.; Jamali, A.; Shahnazi, R.; Maheri, A. Load mitigation of a class of 5-MW wind turbine with RBF neural network based fractional-order PID controller. ISA Trans. 2020, 96, 272–286. [Google Scholar] [CrossRef] [PubMed]
- Fei, J.; Wang, H.; Fang, Y. Novel neural network fractional-order sliding-mode control with application to active power filter. IEEE Trans. Syst. Man Cybern. Syst. 2021, 52, 3508–3518. [Google Scholar] [CrossRef]
- Zhang, Y.; Xiao, M.; Cao, J.; Zheng, W.X. Dynamical bifurcation of large-scale-delayed fractional-order neural networks with hub structure and multiple rings. IEEE Trans. Syst. Man Cybern. Syst. 2020, 52, 1731–1743. [Google Scholar] [CrossRef]
- Cao, J.; Stamov, G.; Stamova, I.; Simeonov, S. Almost periodicity in impulsive fractional-order reaction–diffusion neural networks with time-varying delays. IEEE Trans. Cybern. 2020, 51, 151–161. [Google Scholar] [CrossRef] [PubMed]
- Bao, C.; Pu, Y.; Zhang, Y. Fractional-order deep backpropagation neural network. Comput. Intell. Neurosci. 2018, 2018, 7361628. [Google Scholar] [CrossRef] [PubMed]
- Han, X.; Dong, J. Applications of fractional gradient descent method with adaptive momentum in BP neural networks. Appl. Math. Comput. 2023, 448, 127944. [Google Scholar] [CrossRef]
- Prasad, K.; Krushna, B. Positive solutions to iterative systems of fractional order three-point boundary value problems with Riemann–Liouville derivative. Fract. Differ. Calc. 2015, 5, 137–150. [Google Scholar] [CrossRef]
- Hymavathi, M.; Ibrahim, T.F.; Ali, M.S.; Stamov, G.; Stamova, I.; Younis, B.; Osman, K.I. Synchronization of fractional-order neural networks with time delays and reaction-diffusion terms via pinning control. Mathematics 2022, 10, 3916. [Google Scholar] [CrossRef]
- Wu, Z.; Zhang, X.; Wang, J.; Zeng, X. Applications of fractional differentiation matrices in solving Caputo fractional differential equations. Fractal Fract. 2023, 7, 374. [Google Scholar] [CrossRef]
| Accuracy | 93.79% | 94.15% | 94.50% | 95.20% | 95.22% | 95.30% | 95.65% | 95.60% | 95.45% |
| Training epoch | 246 | 297 | 245 | 257 | 217 | 191 | 163 | 197 | 203 |
| Accuracy | 96.28% | 95.86% | 95.87% | 95.76% | 96.01% | 96.65% | 96.13% | 95.93% | 95.70% |
| Training epoch | 79 | 75 | 55 | 63 | 70 | 68 | 67 | 73 | 57 |
| , | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Accuracy | 97.52% | 97.64% | 97.34% | 97.30% | 97.27% | 97.41% | 97.46% | 97.49% | 97.36% |
| Training epoch | 63 | 71 | 54 | 55 | 50 | 51 | 47 | 56 | 55 |
| Training Dataset Size | BP | FBP | MIFBP | |||
|---|---|---|---|---|---|---|
| Accuracy | Training Epoch | Accuracy | Training Epoch | Accuracy | Training Epoch | |
| 10,000 | 91.69% | 124 | 92.99% | 86 | 94.55% | 79 |
| 20,000 | 93.71% | 176 | 93.29% | 76 | 96.06% | 64 |
| 30,000 | 93.81% | 140 | 93.85% | 68 | 96.94% | 69 |
| 40,000 | 94.20% | 109 | 94.23% | 58 | 97.17% | 55 |
| 50,000 | 95.23% | 157 | 95.69% | 71 | 97.28% | 61 |
| 60,000 | 95.65% | 163 | 96.95% | 68 | 97.64% | 71 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Xu, H.; Li, Y.; Lin, G.; Zhang, L.; Tao, C.; Wu, Y. An Integer-Fractional Gradient Algorithm for Back Propagation Neural Networks. Algorithms 2024, 17, 220. https://doi.org/10.3390/a17050220
Zhang Y, Xu H, Li Y, Lin G, Zhang L, Tao C, Wu Y. An Integer-Fractional Gradient Algorithm for Back Propagation Neural Networks. Algorithms. 2024; 17(5):220. https://doi.org/10.3390/a17050220
Chicago/Turabian StyleZhang, Yiqun, Honglei Xu, Yang Li, Gang Lin, Liyuan Zhang, Chaoyang Tao, and Yonghong Wu. 2024. "An Integer-Fractional Gradient Algorithm for Back Propagation Neural Networks" Algorithms 17, no. 5: 220. https://doi.org/10.3390/a17050220
APA StyleZhang, Y., Xu, H., Li, Y., Lin, G., Zhang, L., Tao, C., & Wu, Y. (2024). An Integer-Fractional Gradient Algorithm for Back Propagation Neural Networks. Algorithms, 17(5), 220. https://doi.org/10.3390/a17050220







