Semi-Self-Supervised Domain Adaptation: Developing Deep Learning Models with Limited Annotated Data for Wheat Head Segmentation
Abstract
:1. Introduction
Background
2. Data and Methodology
2.1. Data
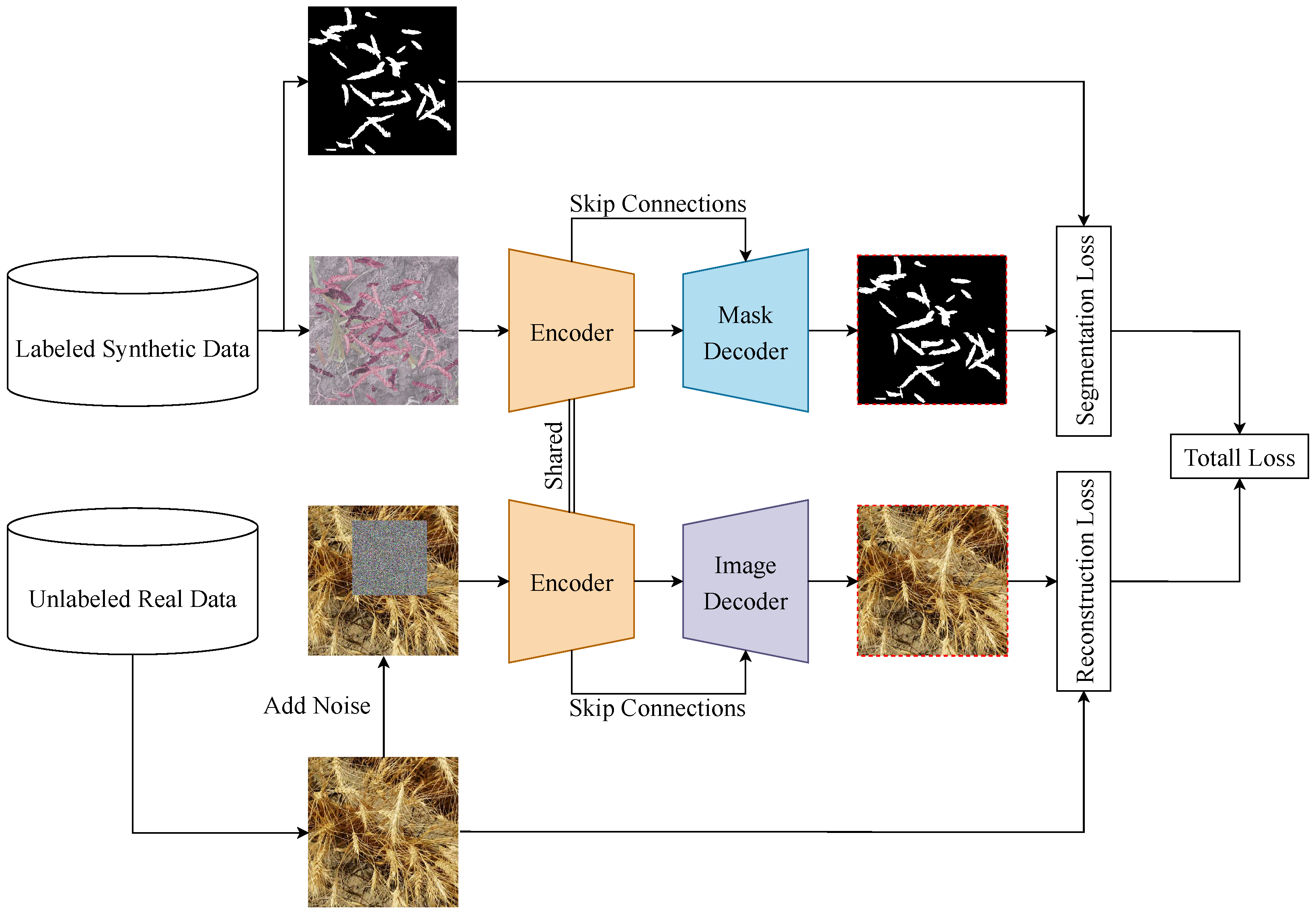
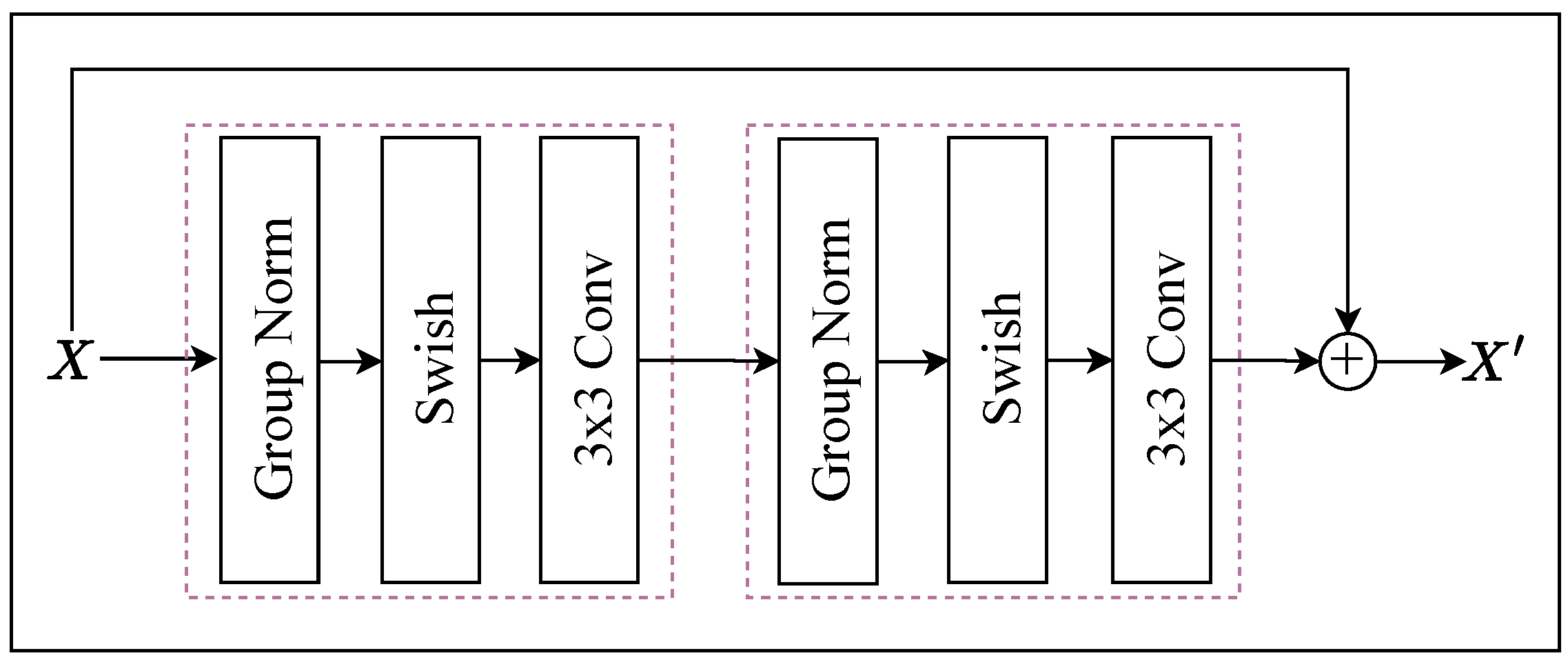
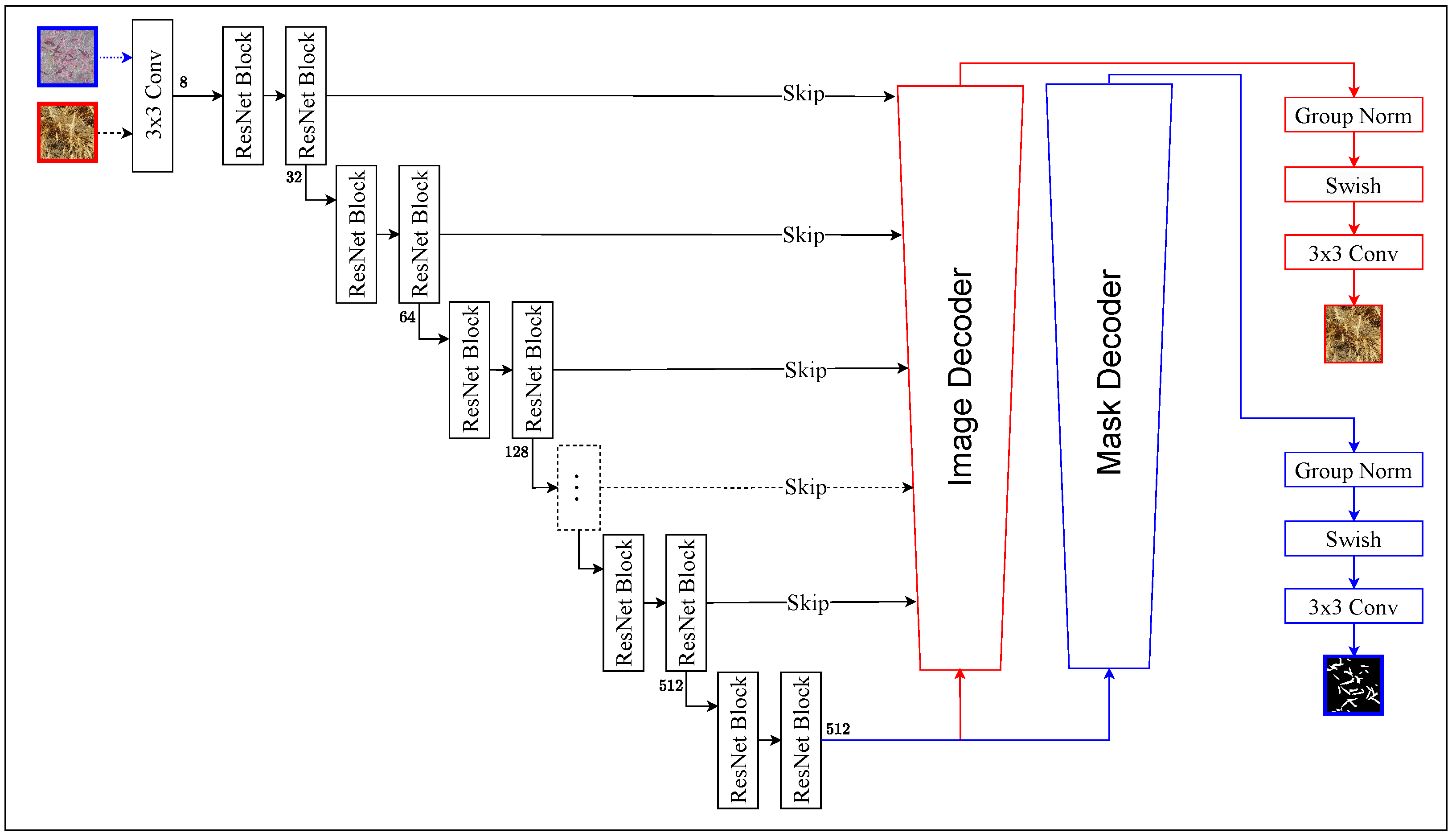
2.2. Model Architecture
2.3. Model Training and Evaluation
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Oliver, M.A.; Bishop, T.F.; Marchant, B.P. Precision Agriculture for Sustainability and Environmental Protection; Routledge: Abingdon, UK, 2013. [Google Scholar]
- Tan, M.; Le, Q. EfficientNet: Rethinking Model Scaling for Convolutional Neural Networks. In Proceedings of the International Conference on Machine Learning, Long Beach, CA, USA, 9–15 June 2019; pp. 6105–6114. [Google Scholar]
- Najafian, K.; Jin, L.; Kutcher, H.R.; Hladun, M.; Horovatin, S.; Oviedo-Ludena, M.A.; De Andrade, S.M.P.; Wang, L.; Stavness, I. Detection of Fusarium Damaged Kernels in Wheat Using Deep Semi-Supervised Learning on a Novel WheatSeedBelt Dataset. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Paris, France, 2–6 October 2023; pp. 660–669. [Google Scholar]
- Wang, C.Y.; Bochkovskiy, A.; Liao, H.Y.M. YOLOv7: Trainable bag-of-freebies sets new state-of-the-art for real-time object detectors. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 7464–7475. [Google Scholar]
- Najafian, K.; Ghanbari, A.; Stavness, I.; Jin, L.; Shirdel, G.H.; Maleki, F. A Semi-Self-Supervised Learning Approach for Wheat Head Detection using Extremely Small Number of Labeled Samples. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Virtual, 11–17 October 2021; pp. 1342–1351. [Google Scholar]
- Mo, Y.; Wu, Y.; Yang, X.; Liu, F.; Liao, Y. Review the state-of-the-art technologies of semantic segmentation based on deep learning. Neurocomputing 2022, 493, 626–646. [Google Scholar] [CrossRef]
- Najafian, K.; Ghanbari, A.; Sabet Kish, M.; Eramian, M.; Shirdel, G.H.; Stavness, I.; Jin, L.; Maleki, F. Semi-Self-Supervised Learning for Semantic Segmentation in Images with Dense Patterns. Plant Phenomics 2023, 5, 0025. [Google Scholar] [CrossRef] [PubMed]
- Kirillov, A.; Mintun, E.; Ravi, N.; Mao, H.; Rolland, C.; Gustafson, L.; Xiao, T.; Whitehead, S.; Berg, A.C.; Lo, W.Y.; et al. Segment Anything. arXiv 2023, arXiv:2304.02643. [Google Scholar]
- He, K.; Gkioxari, G.; Dollár, P.; Girshick, R. Mask R-CNN. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 2980–2988. [Google Scholar] [CrossRef]
- Hafiz, A.M.; Bhat, G.M. A survey on instance segmentation: State of the art. Int. J. Multimed. Inf. Retr. 2020, 9, 171–189. [Google Scholar] [CrossRef]
- Champ, J.; Mora-Fallas, A.; Goëau, H.; Mata-Montero, E.; Bonnet, P.; Joly, A. Instance segmentation for the fine detection of crop and weed plants by precision agricultural robots. Appl. Plant Sci. 2020, 8, e11373. [Google Scholar] [CrossRef] [PubMed]
- Sinha, S.; Gehler, P.; Locatello, F.; Schiele, B. TeST: Test-Time Self-Training Under Distribution Shift. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision (WACV), Waikoloa, HI, USA, 2–7 January 2023; pp. 2759–2769. [Google Scholar]
- Hu, Q.; Guo, Y.; Xie, X.; Cordy, M.; Papadakis, M.; Ma, L.; Le Traon, Y. CodeS: Towards code model generalization under distribution shift. In Proceedings of the International Conference on Software Engineering (ICSE): New Ideas and Emerging Results (NIER), Melbourne, Australia, 14–20 May 2023. [Google Scholar]
- Hwang, D.; Misra, A.; Huo, Z.; Siddhartha, N.; Garg, S.; Qiu, D.; Sim, K.C.; Strohman, T.; Beaufays, F.; He, Y. Large-scale ASR Domain Adaptation using Self- and Semi-supervised Learning. In Proceedings of the ICASSP 2022—2022 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Singapore, 23–27 May 2022; pp. 6627–6631. [Google Scholar]
- Pan, F.; Shin, I.; Rameau, F.; Lee, S.; Kweon, I.S. Unsupervised Intra-domain Adaptation for Semantic Segmentation through Self-Supervision. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 14–19 June 2020; pp. 3764–3773. [Google Scholar]
- Rani, V.; Nabi, S.T.; Kumar, M.; Mittal, A.; Kumar, K. Self-supervised Learning: A Succinct Review. Arch. Comput. Methods Eng. 2023, 30, 2761–2775. [Google Scholar] [CrossRef] [PubMed]
- Zbontar, J.; Jing, L.; Misra, I.; LeCun, Y.; Deny, S. Barlow Twins: Self-Supervised Learning via Redundancy Reduction. In Proceedings of the 38th International Conference on Machine Learning, Virtual Event, 18–24 July 2021; Meila, M., Zhang, T., Eds.; Proceedings of Machine Learning Research (PMLR). Volume 139, pp. 12310–12320. [Google Scholar]
- Ramesh, A.; Dhariwal, P.; Nichol, A.; Chu, C.; Chen, M. Hierarchical Text-Conditional Image Generation with CLIP Latents. arXiv 2022, arXiv:2204.06125. [Google Scholar]
- Rombach, R.; Blattmann, A.; Lorenz, D.; Esser, P.; Ommer, B. High-Resolution Image Synthesis with Latent Diffusion Models. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 10684–10695. [Google Scholar]
- Croitoru, F.A.; Hondru, V.; Ionescu, R.T.; Shah, M. Diffusion Models in Vision: A Survey. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 10850–10869. [Google Scholar] [CrossRef] [PubMed]
- Chen, T. On the Importance of Noise Scheduling for Diffusion Models. arXiv 2023, arXiv:2301.10972. [Google Scholar]
- Nichol, A.Q.; Dhariwal, P. Improved Denoising Diffusion Probabilistic Models. In Proceedings of the International Conference on Machine Learning. PMLR, Virtual Event, 18–24 July 2021; pp. 8162–8171. [Google Scholar]
- David, E.; Serouart, M.; Smith, D.; Madec, S.; Velumani, K.; Liu, S.; Wang, X.; Pinto, F.; Shafiee, S.; Tahir, I.S.; et al. Global Wheat Head Detection 2021: An Improved Dataset for Benchmarking Wheat Head Detection Methods. Plant Phenomics 2021, 22, 9846158. [Google Scholar] [CrossRef] [PubMed]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Ramachandran, P.; Zoph, B.; Le, Q.V. Searching for Activation Functions. arXiv 2017, arXiv:1710.05941. [Google Scholar]
- Buslaev, A.; Iglovikov, V.I.; Khvedchenya, E.; Parinov, A.; Druzhinin, M.; Kalinin, A.A. Albumentations: Fast and flexible image augmentations. Information 2020, 11, 125. [Google Scholar] [CrossRef]
- Wazir, S.; Fraz, M.M. HistoSeg: Quick attention with multi-loss function for multi-structure segmentation in digital histology images. In Proceedings of the 2022 12th International Conference on Pattern Recognition Systems (ICPRS), Saint-Etienne, France, 7–10 June 2022; pp. 1–7. [Google Scholar]
- Beheshti, S.; Hashemi, M.; Sejdic, E.; Chau, T. Mean Square Error Estimation in Thresholding. IEEE Signal Process. Lett. 2010, 18, 103–106. [Google Scholar] [CrossRef]
- Hore, A.; Ziou, D. Image Quality Metrics: PSNR vs. SSIM. In Proceedings of the 2010 20th International Conference on Pattern Recognition, Istanbul, Turkey, 23–26 August 2010; pp. 2366–2369. [Google Scholar]
- Johnson, J.; Alahi, A.; Fei-Fei, L. Perceptual Losses for Real-Time Style Transfer and Super-Resolution. In Proceedings of the Computer Vision–ECCV 2016: 14th European Conference, Amsterdam, The Netherlands, 11–14 October 2016; Proceedings, Part II 14. Springer: Cham, Switzerland, 2016; pp. 694–711. [Google Scholar]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. PyTorch: An Imperative Style, High-Performance Deep Learning Library. In Proceedings of the Advances in Neural Information Processing Systems 32, Vancouver, BC, Canada, 8–12 December 2019; pp. 8024–8035. [Google Scholar]
- Loshchilov, I.; Hutter, F. Decoupled Weight Decay Regularization. arXiv 2017, arXiv:1711.05101. [Google Scholar]
- Yang, B.; Lei, Y.; Li, X.; Li, N.; Nandi, A.K. Label Recovery and Trajectory Designable Network for Transfer Fault Diagnosis of Machines with Incorrect Annotation. IEEE/CAA J. Autom. Sin. 2024, 11, 932–945. [Google Scholar] [CrossRef]



| Model | Evaluation Method | Dice | IoU |
|---|---|---|---|
| [7] | Internal test set | 0.709 | 0.565 |
| Internal test set | 0.773 | 0.638 | |
| Internal test set | 0.807 | 0.686 | |
| S [7] | External test set | 0.367 | 0.274 |
| External test set | 0.551 | 0.427 | |
| External test set | 0.648 | 0.526 |
| Domain | Model | Dice Score | Domain | Model | Dice Score |
|---|---|---|---|---|---|
 | 0.731 |  | 0.711 | ||
| 0.660 | 0.644 | ||||
| 0.692 | 0.759 | ||||
 | 0.848 |  | 0.290 | ||
| 0.815 | 0.193 | ||||
| 0.857 | 0.271 | ||||
 | 0.309 |  | 0.601 | ||
| 0.764 | 0.599 | ||||
| 0.812 | 0.769 | ||||
 | 0.240 |  | 0.583 | ||
| 0.503 | 0.795 | ||||
| 0.431 | 0.748 | ||||
 | 0.794 |  | 0.156 | ||
| 0.715 | 0.286 | ||||
| 0.698 | 0.356 | ||||
 | 0.389 |  | 0.582 | ||
| 0.479 | 0.492 | ||||
| 0.605 | 0.667 | ||||
 | 0.509 |  | 0.884 | ||
| 0.655 | 0.648 | ||||
| 0.625 | 0.805 | ||||
 | 0.859 |  | 0.501 | ||
| 0.674 | 0.488 | ||||
| 0.671 | 0.686 | ||||
 | 0.539 |  | 0.629 | ||
| 0.586 | 0.496 | ||||
| 0.579 | 0.520 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ghanbari, A.; Shirdel, G.H.; Maleki, F. Semi-Self-Supervised Domain Adaptation: Developing Deep Learning Models with Limited Annotated Data for Wheat Head Segmentation. Algorithms 2024, 17, 267. https://doi.org/10.3390/a17060267
Ghanbari A, Shirdel GH, Maleki F. Semi-Self-Supervised Domain Adaptation: Developing Deep Learning Models with Limited Annotated Data for Wheat Head Segmentation. Algorithms. 2024; 17(6):267. https://doi.org/10.3390/a17060267
Chicago/Turabian StyleGhanbari, Alireza, Gholam Hassan Shirdel, and Farhad Maleki. 2024. "Semi-Self-Supervised Domain Adaptation: Developing Deep Learning Models with Limited Annotated Data for Wheat Head Segmentation" Algorithms 17, no. 6: 267. https://doi.org/10.3390/a17060267
APA StyleGhanbari, A., Shirdel, G. H., & Maleki, F. (2024). Semi-Self-Supervised Domain Adaptation: Developing Deep Learning Models with Limited Annotated Data for Wheat Head Segmentation. Algorithms, 17(6), 267. https://doi.org/10.3390/a17060267







