Multithreading-Based Algorithm for High-Performance Tchebichef Polynomials with Higher Orders
Abstract
:1. Introduction
2. Background and Literature Review
2.1. Background of the Tchebichef Polynomials
2.2. Literature Review
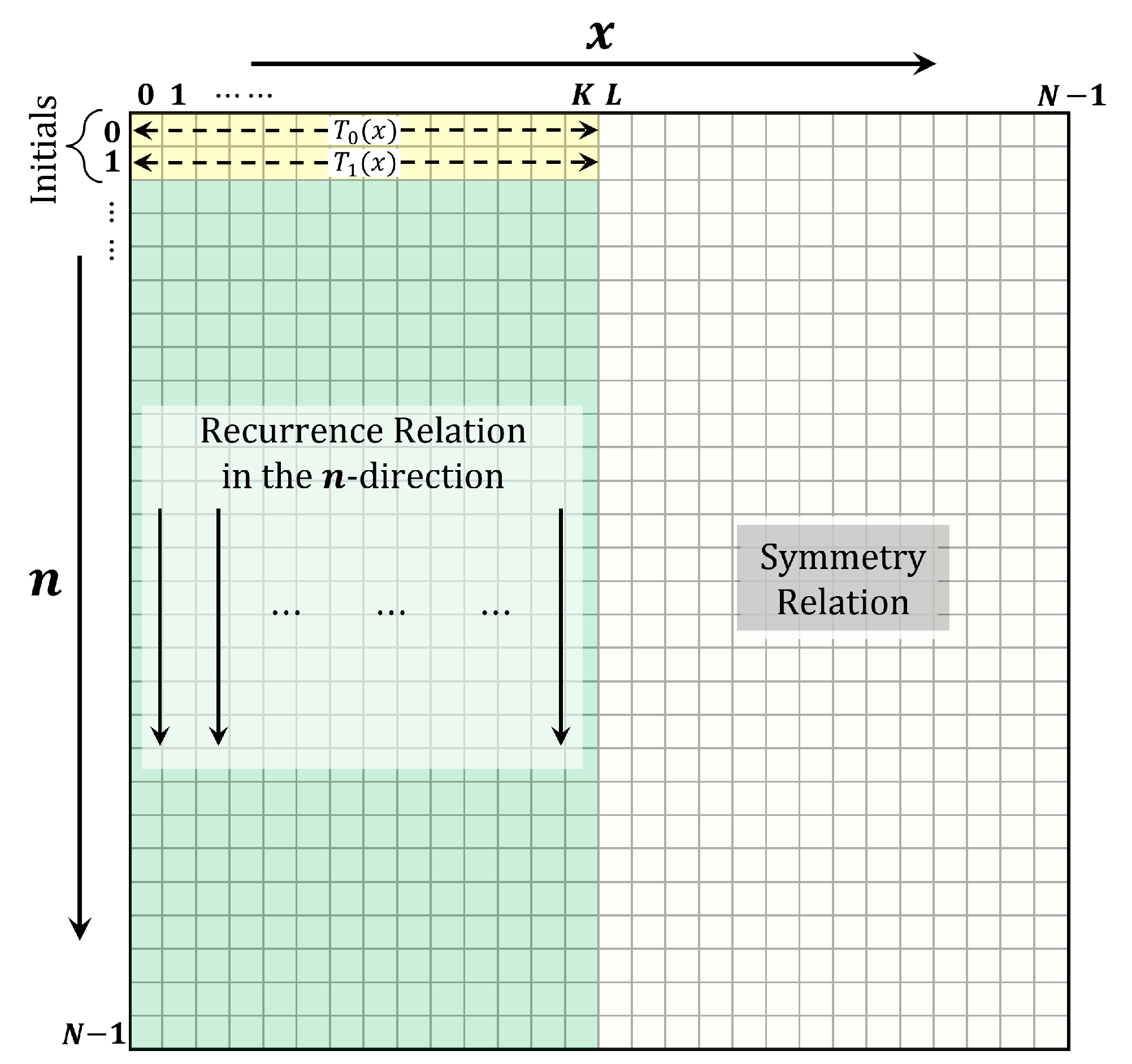
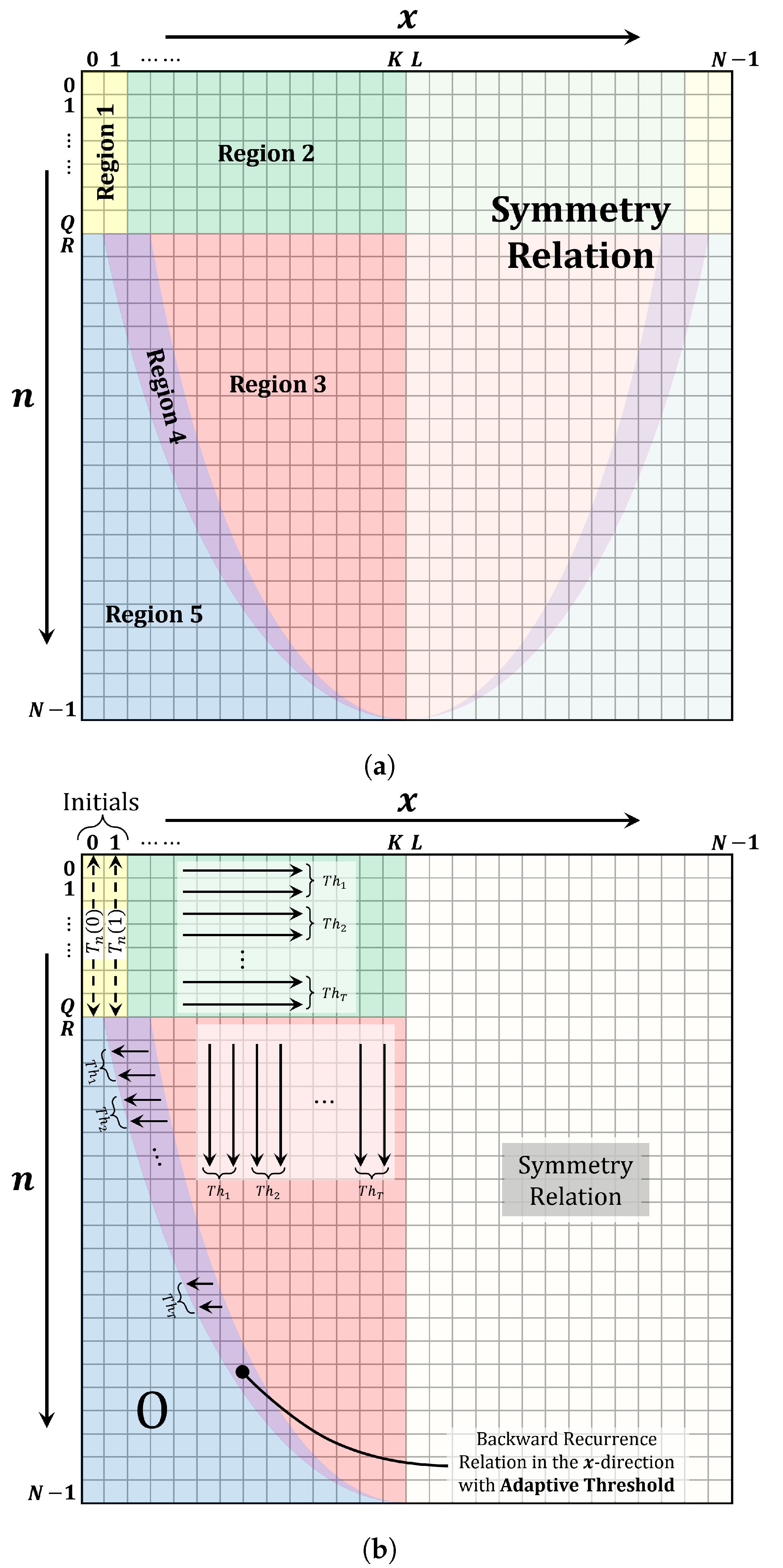
3. The Proposed Multithreaded Algorithm
- Compute the value of using (17).
- Compute the coefficient values of over the range and using (18), where .
- Compute the value of over the range and using (19).
| Algorithm 1: The code framework for the proposed multithreaded algorithm. |
 |
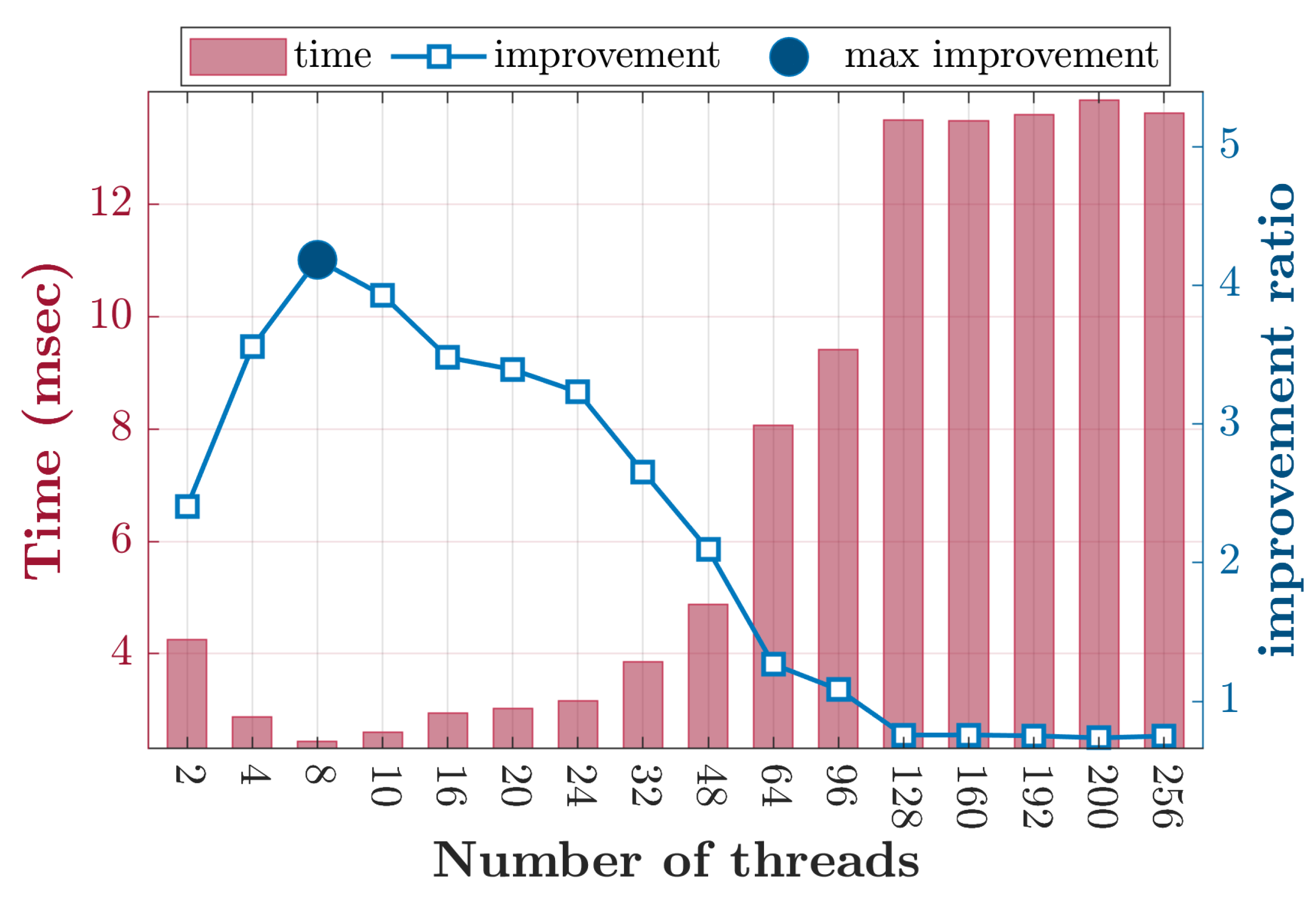
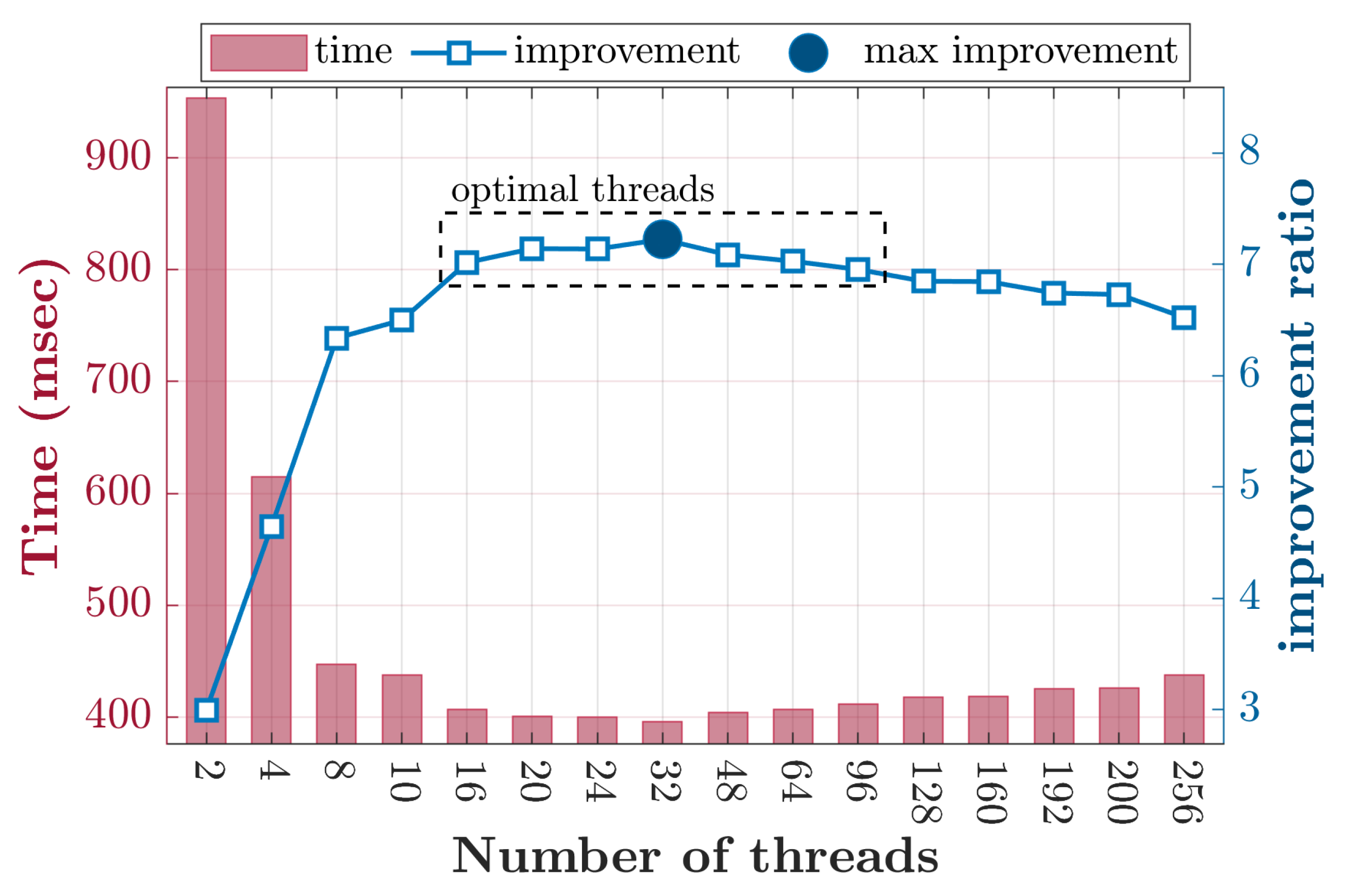
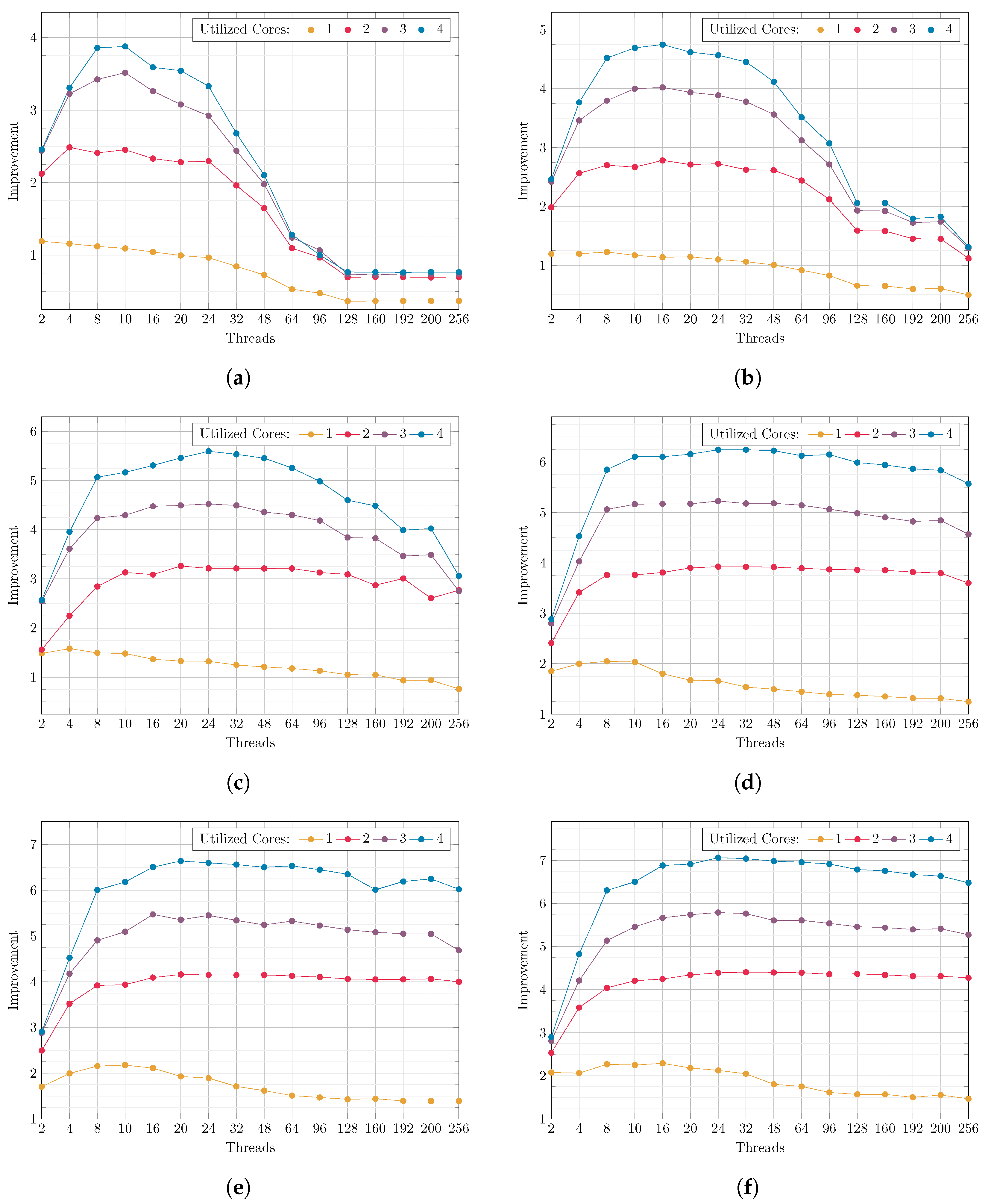
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| OPs | Orthogonal polynomials |
| TTRR | Three-term recurrence relation |
| DCT | Discrete cosine transform |
| TPs | Tchebichef polynomials |
| TTRRn | Three-term recurrence relation with respect to n-direction |
| TTRRx | Three-term recurrence relation with respect to x-direction |
| TTRRnx | Three-term recurrence relation with respect to n- and x-direction |
| TTRRnxa | Three-term recurrence relation with respect to n- and x-direction with adaptive threshold |
| GSOP | g Gram–Schmidt orthonormalization process |
| BS | Bunch size |
| T | Thread |
| RAM | Random access memory |
References
- Abd-Elhameed, W.M.; Al-Harbi, M.S. Some formulas and recurrences of certain orthogonal polynomials generalizing Chebyshev polynomials of the third-kind. Symmetry 2022, 14, 2309. [Google Scholar] [CrossRef]
- Sun, L.; Chen, Y. Numerical analysis of variable fractional viscoelastic column based on two-dimensional Legendre wavelets algorithm. Chaos Solitons Fractals 2021, 152, 111372. [Google Scholar] [CrossRef]
- AbdelFattah, H.; Al-Johani, A.; El-Beltagy, M. Analysis of the stochastic quarter-five spot problem using polynomial chaos. Molecules 2020, 25, 3370. [Google Scholar] [CrossRef]
- Alhaidari, A.D.; Taiwo, T. Energy spectrum design and potential function engineering. Theor. Math. Phys. 2023, 216, 1024–1035. [Google Scholar] [CrossRef]
- Yang, J.; Zeng, Z.; Kwong, T.; Tang, Y.Y.; Wang, Y. Local Orthogonal Moments for Local Features. IEEE Trans. Image Process. 2023, 32, 3266–3280. [Google Scholar] [CrossRef]
- Markel, J.; Gray, A. Roundoff noise characteristics of a class of orthogonal polynomial structures. IEEE Trans. Acoust. Speech Signal Process. 1975, 23, 473–486. [Google Scholar] [CrossRef]
- Ma, R.; Shi, L.; Huang, Z.; Zhou, Y. EMP signal reconstruction using associated-Hermite orthogonal functions. IEEE Trans. Electromagn. Compat. 2014, 56, 1242–1245. [Google Scholar] [CrossRef]
- Abdulhussain, S.H.; Mahmmod, B.M.; Flusser, J.; AL-Utaibi, K.A.; Sait, S.M. Fast overlapping block processing algorithm for feature extraction. Symmetry 2022, 14, 715. [Google Scholar] [CrossRef]
- Abdulqader, D.A.; Hathal, M.S.; Mahmmod, B.M.; Abdulhussain, S.H.; Al-Jumeily, D. Plain, edge, and texture detection based on orthogonal moment. IEEE Access 2022, 10, 114455–114468. [Google Scholar] [CrossRef]
- Levenshtein, V.I. Krawtchouk polynomials and universal bounds for codes and designs in Hamming spaces. IEEE Trans. Inf. Theory 1995, 41, 1303–1321. [Google Scholar] [CrossRef]
- Zeng, J. Linearization of Meixner, Krawtchouk, and Charlier polynomial products. SIAM J. Math. Anal. 1990, 21, 1349–1368. [Google Scholar] [CrossRef]
- Karakasis, E.G.; Papakostas, G.A.; Koulouriotis, D.E.; Tourassis, V.D. Generalized dual Hahn moment invariants. Pattern Recognit. 2013, 46, 1998–2014. [Google Scholar] [CrossRef]
- Mahmmod, B.M.; Flayyih, W.N.; Fakhri, Z.H.; Abdulhussain, S.H.; Khan, W.; Hussain, A. Performance enhancement of high order Hahn polynomials using multithreading. PLoS ONE 2023, 18, e0286878. [Google Scholar] [CrossRef]
- Zhu, H.; Shu, H.; Liang, J.; Luo, L.; Coatrieux, J.L. Image analysis by discrete orthogonal Racah moments. Signal Process. 2007, 87, 687–708. [Google Scholar] [CrossRef]
- Mahmmod, B.M.; Abdulhussain, S.H.; Suk, T.; Alsabah, M.; Hussain, A. Accelerated and improved stabilization for high order moments of Racah polynomials. IEEE Access 2023, 11, 110502–110521. [Google Scholar] [CrossRef]
- Veerasamy, M.; Jaganathan, S.C.B.; Dhasarathan, C.; Mubarakali, A.; Ramasamy, V.; Kalpana, R.; Marina, N. Legendre Neural Network Method for Solving Nonlinear Singular Systems. In Intelligent Technologies for Sensors; Apple Academic Press: Palm Bay, FL, USA, 2023; pp. 25–37. [Google Scholar]
- Boelen, L.; Filipuk, G.; Van Assche, W. Recurrence coefficients of generalized Meixner polynomials and Painlevé equations. J. Phys. A Math. Theor. 2010, 44, 035202. [Google Scholar] [CrossRef]
- Vasileva, M.; Kyurkchiev, V.; Iliev, A.; Rahnev, A.; Kyurkchiev, N. Associated Hermite Polynomials. Some Applications. Int. J. Differ. Equ. Appl. 2023, 22, 1–17. [Google Scholar]
- Schweizer, W.; Schweizer, W. Laguerre Polynomials. In Special Functions in Physics with MATLAB; Springer: Cham, Switzerland, 2021; pp. 211–214. [Google Scholar]
- Mukundan, R.; Ong, S.; Lee, P. Image analysis by Tchebichef moments. IEEE Trans. Image Process. 2001, 10, 1357–1364. [Google Scholar] [CrossRef]
- Li, J.; Wang, P.; Ni, C.; Zhang, D.; Hao, W. Loop Closure Detection for Mobile Robot based on Multidimensional Image Feature Fusion. Machines 2022, 11, 16. [Google Scholar] [CrossRef]
- Teague, M.R. Image analysis via the general theory of moments. J. Opt. Soc. Am. 1980, 70, 920–930. [Google Scholar] [CrossRef]
- Jahid, T.; Karmouni, H.; Hmimid, A.; Sayyouri, M.; Qjidaa, H. Fast computation of Charlier moments and its inverses using Clenshaw’s recurrence formula for image analysis. Multimed. Tools Appl. 2019, 78, 12183–12201. [Google Scholar] [CrossRef]
- den Brinker, A.C. Stable calculation of Krawtchouk functions from triplet relations. Mathematics 2021, 9, 1972. [Google Scholar] [CrossRef]
- den Brinker, A.C. Stable Calculation of Discrete Hahn Functions. Symmetry 2022, 14, 437. [Google Scholar] [CrossRef]
- Aldakheel, E.A.; Khafaga, D.S.; Fathi, I.S.; Hosny, K.M.; Hassan, G. Efficient Analysis of Large-Size Bio-Signals Based on Orthogonal Generalized Laguerre Moments of Fractional Orders and Schwarz–Rutishauser Algorithm. Fractal Fract. 2023, 7, 826. [Google Scholar] [CrossRef]
- Costas-Santos, R.S.; Soria-Lorente, A.; Vilaire, J.M. On Polynomials Orthogonal with Respect to an Inner Product Involving Higher-Order Differences: The Meixner Case. Mathematics 2022, 10, 1952. [Google Scholar] [CrossRef]
- Fernández-Irisarri, I.; Mañas, M. Pearson equations for discrete orthogonal polynomials: II. Generalized Charlier, Meixner and Hahn of type I cases. arXiv 2021, arXiv:2107.02177. [Google Scholar]
- Bourzik, A.; Bouikhalen, B.; El-Mekkaoui, J.; Hjouji, A. A comparative study and performance evaluation of discrete Tchebichef moments for image analysis. In Proceedings of the 6th International Conference on Networking, Intelligent Systems & Security, Larache, Morocco, 24–26 May 2023; pp. 1–7. [Google Scholar]
- Mukundan, R. Some Computational Aspects of Discrete Orthonormal Moments. IEEE Trans. Image Process. 2004, 13, 1055–1059. [Google Scholar] [CrossRef]
- Abdulhussain, S.H.; Ramli, A.R.; Al-Haddad, S.A.R.; Mahmmod, B.M.; Jassim, W.A. On Computational Aspects of Tchebichef Polynomials for Higher Polynomial Order. IEEE Access 2017, 5, 2470–2478. [Google Scholar] [CrossRef]
- Camacho-Bello, C.; Rivera-Lopez, J.S. Some computational aspects of Tchebichef moments for higher orders. Pattern Recognit. Lett. 2018, 112, 332–339. [Google Scholar] [CrossRef]
- Abdulhussain, S.H.; Mahmmod, B.M.; Baker, T.; Al-Jumeily, D. Fast and accurate computation of high-order Tchebichef polynomials. Concurr. Comput. Pract. Exp. 2022, 34, e7311. [Google Scholar] [CrossRef]
- Kumar, R.; Tullsen, D.M.; Jouppi, N.P. Core architecture optimization for heterogeneous chip multiprocessors. In Proceedings of the 15th International Conference on Parallel Architectures and Compilation Techniques, Seattle, WA, USA, 16–20 September 2006; pp. 23–32. [Google Scholar]
- Schildermans, S.; Shan, J.; Aerts, K.; Jackrel, J.; Ding, X. Virtualization overhead of multithreading in X86 state-of-the-art & remaining challenges. IEEE Trans. Parallel Distrib. Syst. 2021, 32, 2557–2570. [Google Scholar]
- Thomadakis, P.; Tsolakis, C.; Chrisochoides, N. Multithreaded runtime framework for parallel and adaptive applications. Eng. Comput. 2022, 38, 4675–4695. [Google Scholar] [CrossRef]
- Kim, E.; Choi, S.; Kim, C.G.; Park, W.C. Multi-Threaded Sound Propagation Algorithm to Improve Performance on Mobile Devices. Sensors 2023, 23, 973. [Google Scholar] [CrossRef] [PubMed]
- Wei, X.; Ma, L.; Zhang, H.; Liu, Y. Multi-core-, multi-thread-based optimization algorithm for large-scale traveling salesman problem. Alex. Eng. J. 2021, 60, 189–197. [Google Scholar] [CrossRef]
- Luan, G.; Pang, P.; Chen, Q.; Xue, S.; Song, Z.; Guo, M. Online thread auto-tuning for performance improvement and resource saving. IEEE Trans. Parallel Distrib. Syst. 2022, 33, 3746–3759. [Google Scholar] [CrossRef]
- Donoho, D.L. Compressed sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions: With Formulas, Graphs, and Mathematical Tables; Dover Publications: New York, NY, USA, 1964. [Google Scholar]
- Foncannon, J.J. Irresistible integrals: Symbolics, analysis and experiments in the evaluation of integrals. Math. Intell. 2006, 28, 65–68. [Google Scholar] [CrossRef]
- Gautschi, W. Computational aspects of three-term recurrence relations. SIAM Rev. 1967, 9, 24–82. [Google Scholar] [CrossRef]
- Lewanowicz, S. Recurrence relations for hypergeometric functions of unit argument. Math. Comput. 1985, 45, 521–535. [Google Scholar] [CrossRef]







Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-sudani, A.H.; Mahmmod, B.M.; Sabir, F.A.; Abdulhussain, S.H.; Alsabah, M.; Flayyih, W.N. Multithreading-Based Algorithm for High-Performance Tchebichef Polynomials with Higher Orders. Algorithms 2024, 17, 381. https://doi.org/10.3390/a17090381
Al-sudani AH, Mahmmod BM, Sabir FA, Abdulhussain SH, Alsabah M, Flayyih WN. Multithreading-Based Algorithm for High-Performance Tchebichef Polynomials with Higher Orders. Algorithms. 2024; 17(9):381. https://doi.org/10.3390/a17090381
Chicago/Turabian StyleAl-sudani, Ahlam Hanoon, Basheera M. Mahmmod, Firas A. Sabir, Sadiq H. Abdulhussain, Muntadher Alsabah, and Wameedh Nazar Flayyih. 2024. "Multithreading-Based Algorithm for High-Performance Tchebichef Polynomials with Higher Orders" Algorithms 17, no. 9: 381. https://doi.org/10.3390/a17090381
APA StyleAl-sudani, A. H., Mahmmod, B. M., Sabir, F. A., Abdulhussain, S. H., Alsabah, M., & Flayyih, W. N. (2024). Multithreading-Based Algorithm for High-Performance Tchebichef Polynomials with Higher Orders. Algorithms, 17(9), 381. https://doi.org/10.3390/a17090381





