A Survey on Variable Neighborhood Search for Sustainable Logistics
Abstract
1. Introduction
- Economic sustainability refers to the ability of an economic system to support long-term growth while ensuring the efficient use of resources and financial stability. It requires careful management to avoid negative impacts on social, environmental, or cultural factors. It emphasizes the efficient allocation of resources to ensure that industries, businesses, and economies can continue to function in a sustainable manner, while also providing opportunities for future generations to prosper.
- Environmental sustainability focuses on managing and conserving natural resources in a responsible manner to prevent ecosystem degradation and ensure that these resources remain available for future generations. This dimension of sustainability involves reducing pollution, conserving biodiversity, minimizing waste, and promoting renewable energy sources and sustainable practices in industries such as transportation, manufacturing, and agriculture. The ultimate objective is to protect the health of the planet and maintain its ecological balance for the well-being of future generations.
- Social sustainability is about creating and maintaining societies that promote social equity, justice, and well-being for all individuals. This pillar focuses on ensuring access to basic services such as education, healthcare, and employment opportunities, as well as fostering inclusive and resilient communities. Social sustainability emphasizes the importance of respecting human rights, cultural diversity, and social progress, ensuring that future generations inherit a world characterized by equality, fairness, and peace.
- In which specific areas of sustainable logistics is VNS most commonly applied, and what types of problems does it address most effectively?
- Which VNS variants are utilized most frequently to solve these sustainable logistics problems?
- How is VNS commonly hybridized with other optimization methods to tackle complex logistics challenges, and which hybridization approaches have proven to be the most effective?
- How are multiobjective logistics problems, which often involve trade-offs between different sustainability aspects, addressed when employing VNS?
- Which aspects of sustainability are most frequently considered when applying VNS to solve logistics problems, and how are these aspects integrated into the optimization process?
2. VNS: Concept, Versions, and Extensions
3. Review Methodology
- Formulation of the search question and choice of keywords.
- Definition of inclusion and extrusion criteria.
- Search in databases.
- Paper selection; discussion and analysis of the results.
- Reporting of the results.
3.1. Question Formulation and Keywords Definition
3.2. Definition of Inclusion and Exclusion Criteria
3.3. Search in Databases
3.4. The Selection of the Most Relevant Papers
3.5. Analysis, Synthesis, and Results Reporting: Classification Methodology
4. Results and Findings
4.1. VNS Version Analysis
4.2. Hybridization Analysis
4.3. Multiobjective Analysis
4.4. Uncertainty and Dynamism Analysis
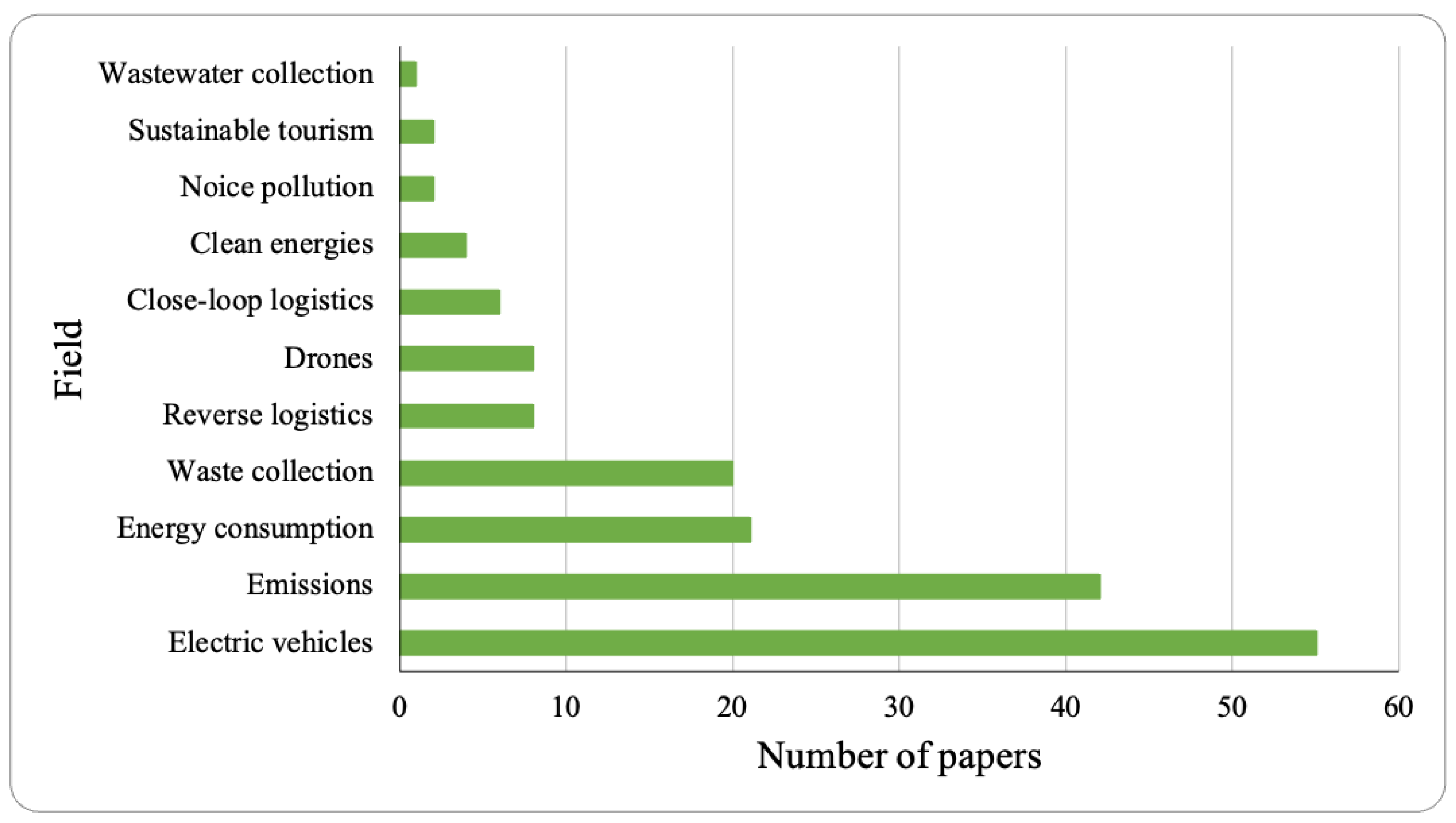
4.5. Sustainability Analysis
4.5.1. Economic Criteria
4.5.2. Environmental Criteria
- Electric vehicles: This category includes papers that explore the use of electric vehicles (EVs), which are pivotal in reducing the environmental impact of logistics by minimizing reliance on fossil fuels.
- Emissions: Papers in this group focus on strategies to minimize emissions, such as carbon dioxide, nitrogen oxides, and particulate matter, from transportation and logistics operations, highlighting the importance of cleaner and greener practices.
- Waste collection: This category encompasses studies dedicated to optimizing waste collection systems, improving efficiency while ensuring sustainable waste management practices.
- Energy consumption: Papers classified here address the reduction in energy consumption within logistics operations. Some of these studies involve mixed fleets that combine traditional and alternative energy sources, with a focus on improving overall energy efficiency.
- Drones: This field includes research that explores the use of electric drones for logistics, which offers the potential for lower emissions and greater efficiency in last-mile delivery, particularly in urban or remote areas.
- Reverse logistics: Papers in this category focus on reverse logistics processes, which involve the return of goods from consumers to producers, and emphasize sustainable practices such as recycling and reusing products.
- Closed-loop logistics: This category includes studies that look into closed-loop logistics systems, which are designed to ensure products are reused or recycled, minimizing waste and reducing the need for raw materials.
- Clean energies: This field encompasses papers exploring the use of clean energy sources such as wind farms, biomass energy, and photovoltaic (solar) energy within logistics, aiming to reduce the environmental footprint of operations.
- Sustainable Tourism: Studies in this category focus on the intersection of logistics and sustainable tourism, addressing how transportation and logistics systems can support environmentally responsible travel practices.
- Noise pollution: This group includes papers that address the issue of noise pollution, which is an often-overlooked aspect of sustainability in logistics, focusing on strategies to reduce noise emissions from transportation vehicles and operations.
- Wastewater collection: Finally, papers related to wastewater collection explore logistics systems that are designed to manage and transport wastewater in a sustainable manner, minimizing environmental impact and optimizing infrastructure.
4.5.3. Social Criteria
5. Research Trends and Gaps
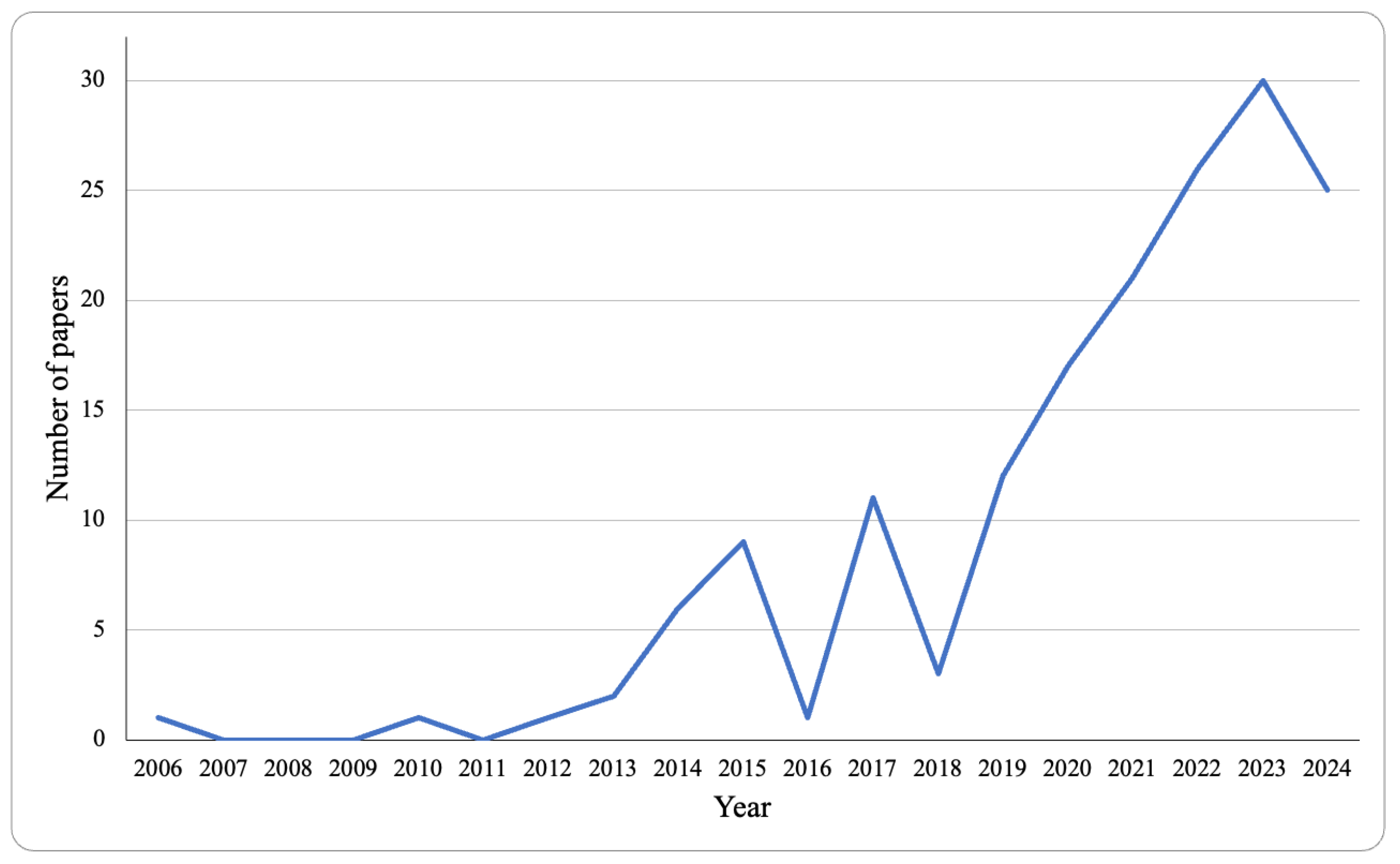
- Growth in publications. As illustrated in Figure 1, there has been a notable rise in the number of publications on VNS in sustainable logistics since 2019. This trend reflects the increasing awareness and recognition of optimization methods like VNS in addressing complex and pressing challenges in logistics systems while promoting sustainability. The rapid growth in interest highlights the broadening application of VNS techniques in response to the global demand for more sustainable and efficient logistics practices.
- Dominance of operational research and computer science journals. The majority of studies in this field are published in journals related to operations research, computer science, and engineering. Journals such as Computers & Operations Research and Computers & Industrial Engineering are particularly prominent, as depicted in Figure 2.
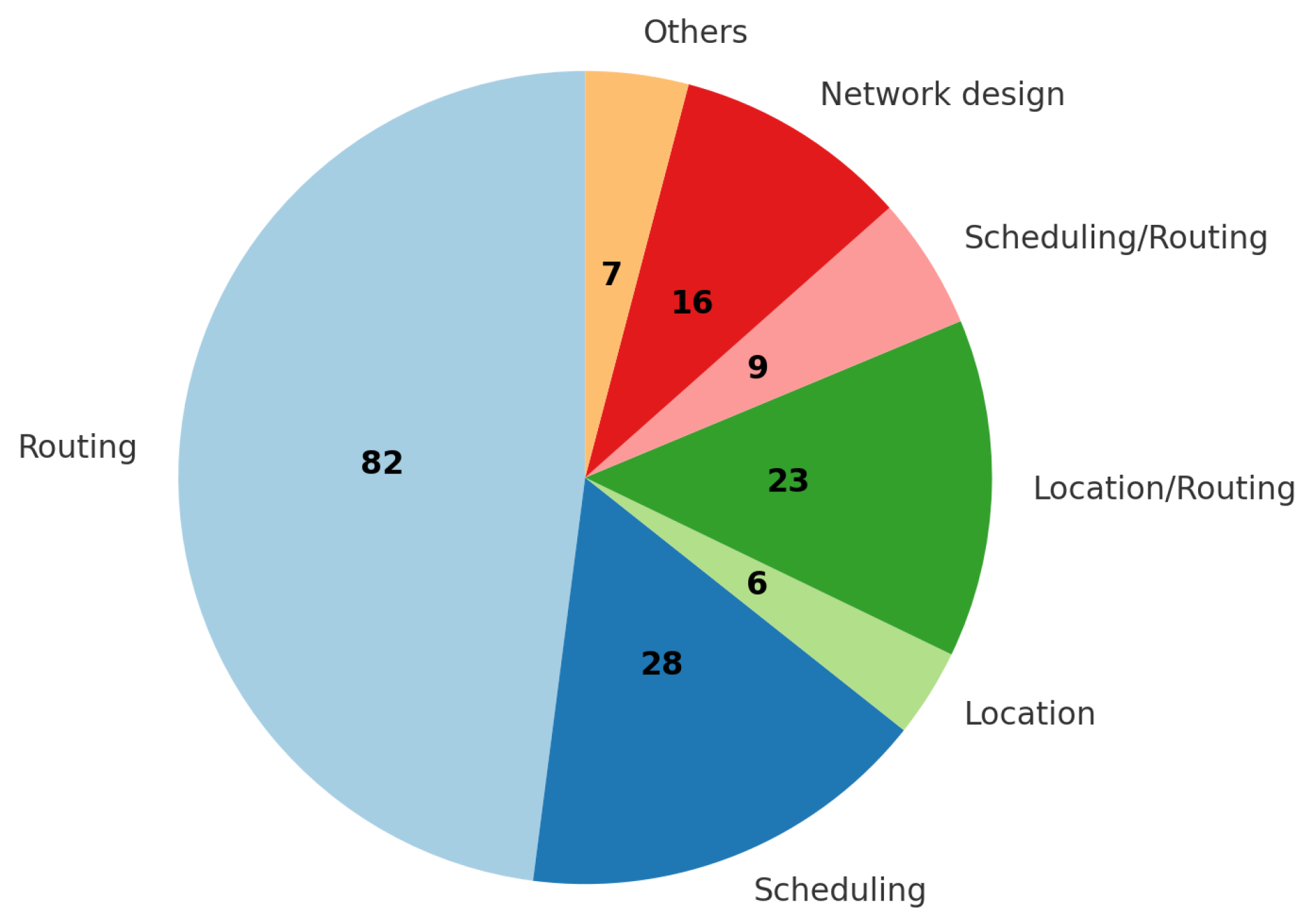
- Focus on routing and scheduling. The optimization problems most frequently addressed in the reviewed studies are routing and scheduling. As shown in Figure 3, the majority of papers using VNS target these two areas, underlining their centrality in sustainable logistics. These problems are essential for reducing transportation costs, improving efficiency, and minimizing environmental impacts, all of which are core elements of sustainable logistics practices.
- Multiobjective optimization. An expanding body of research focuses on multiobjective problems where VNS is applied to simultaneously optimize conflicting objectives. These studies are vital for developing logistics systems that not only minimize costs but also integrate sustainability considerations such as emissions reduction, energy efficiency, and resource conservation. Multiobjective approaches remain highly relevant as they enable decision-makers to balance economic, environmental, and social goals in logistics systems.
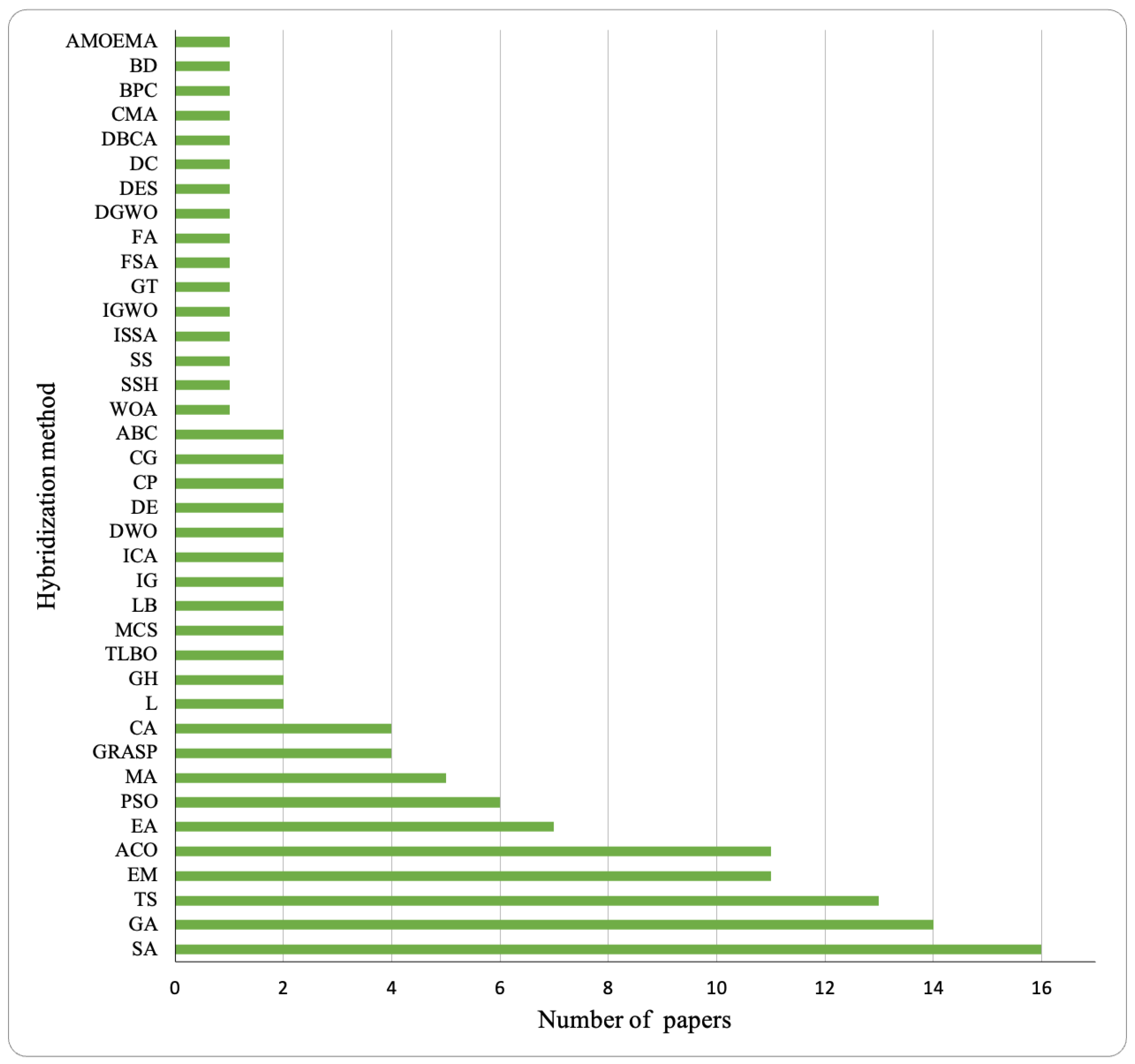
- Hybridization with other methods. A significant trend is the hybridization of VNS with other optimization techniques. As indicated in Figure 5, methods such as SA, TS, and GA are commonly combined with VNS to improve solution quality. This hybridization enhances flexibility and facilitates the exploration of complex optimization problems.
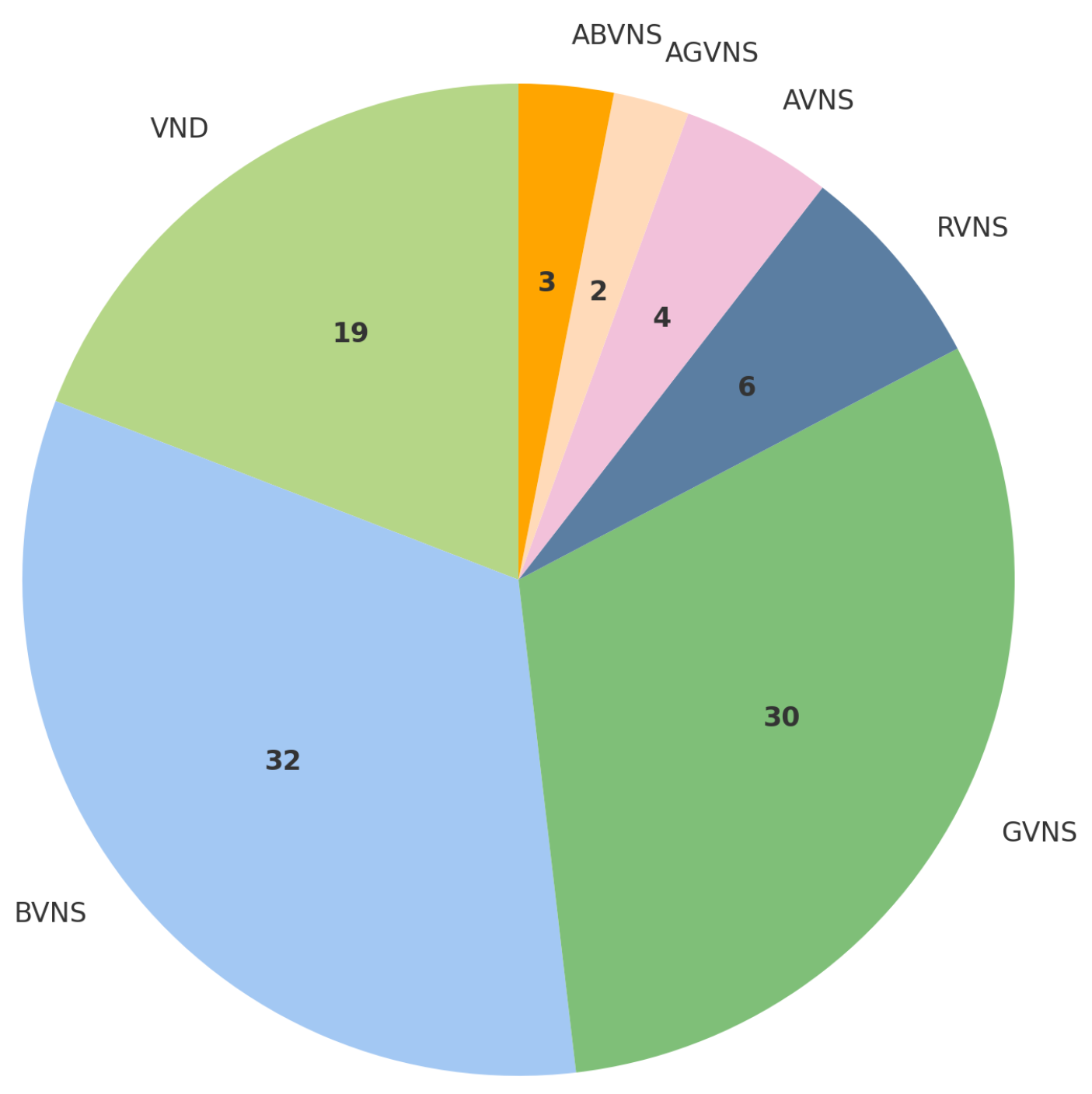
- Prevalence of VNS variants. GVNS and BVNS remain the most widely used VNS variants, with a growing interest in the use of AVNS over the past few years.
- Lack of focus on uncertainty and dynamism. While uncertainty and dynamism are critical factors in sustainable logistics, few studies incorporate these elements into VNS-based models. Uncertainty in demand, travel times, and environmental conditions, as well as the dynamic nature of logistics networks, can substantially impact optimization algorithms. Future research could explore robust optimization techniques and dynamic adaptation mechanisms to make VNS more applicable to real-world logistics challenges.
- Limited exploration of social sustainability. Although economic and environmental sustainability are often addressed in VNS-based logistics optimization, the social dimension remains underrepresented. Social factors, such as worker well-being, job creation, and safety, require more attention in the literature. Including these social metrics in optimization models is essential to ensuring logistics practices are socially responsible and equitable.
- Innovation in hybridization techniques. While VNS has been successfully combined with various methods, further innovation in hybridization strategies is needed. Incorporating emerging technologies such as machine learning and reinforcement learning into VNS frameworks has received limited attention but holds significant potential for advancing sustainable logistics.
- VNS variants. The proliferation of VNS variants and terminologies necessitates a more structured classification. Additionally, some researchers label their methods as VNS when applying neighborhood-based searches, even when they primarily use local search strategies. A systematic clarification of these methodologies would enhance understanding and consistency in the field.
- Broader integration of sustainability metrics. While environmental sustainability remains a central focus, optimization models often lack comprehensive metrics. Factors such as resource efficiency, waste minimization, and community impact should be incorporated into future models to provide holistic solutions.
- Need for comprehensive benchmarks and standardization. A major challenge in applying VNS to sustainable logistics is the absence of standardized benchmarks and performance metrics. Standardizing problem definitions, datasets, and evaluation metrics would improve the comparability of results across studies and facilitate a clearer understanding of the strengths and limitations of VNS approaches.
- Emerging areas of application. New application domains for VNS in sustainable logistics are emerging, including renewable energy logistics, last-mile delivery using drones, and sustainable tourism optimization. Exploring and adapting VNS techniques to these novel challenges will expand their applicability and foster innovation in logistics research.
6. Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Correction Statement
Abbreviations
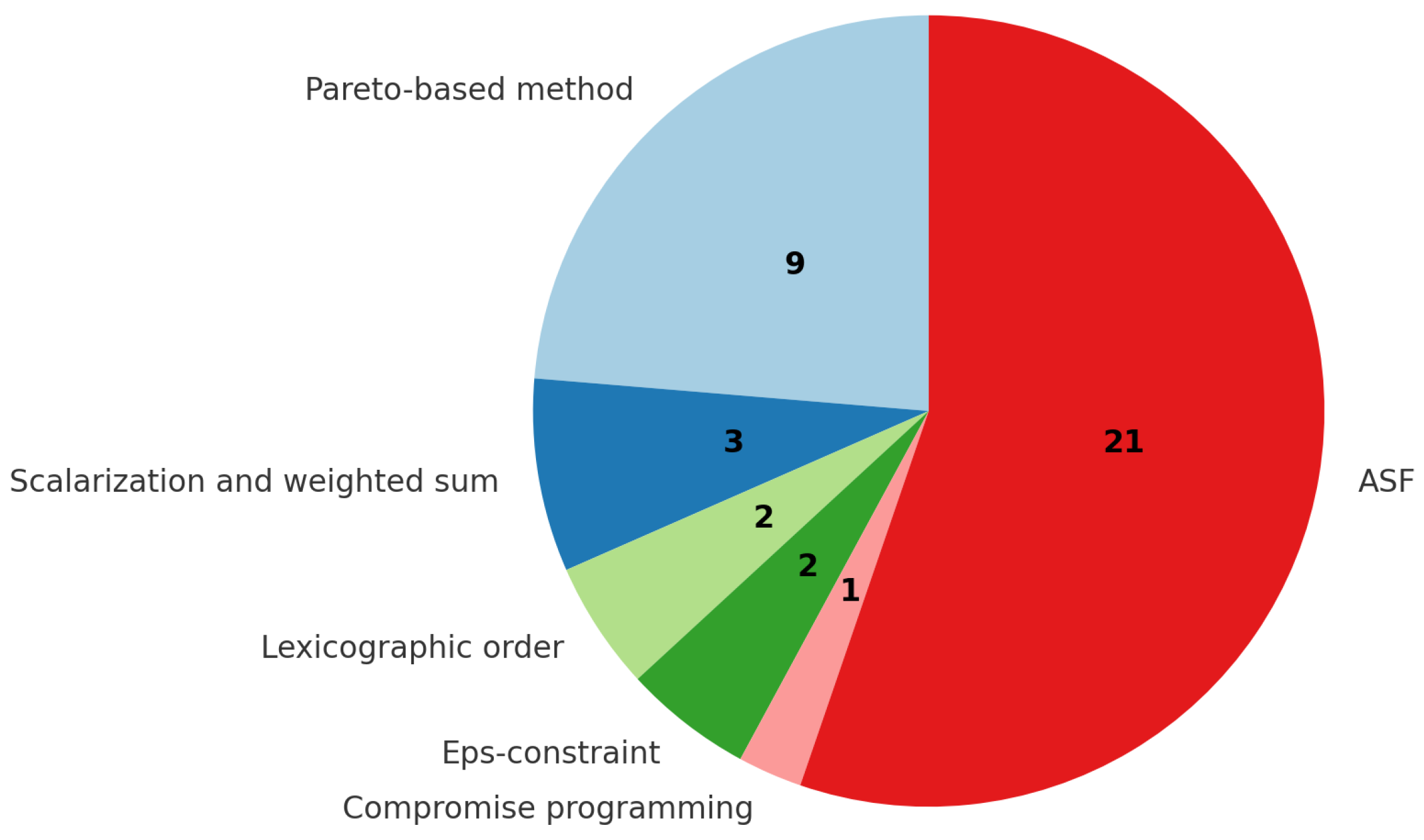
| ABC | Artificial Bee Colony |
| ACO | Ant Colony Optimization |
| ASF | Achievement Scalarizing Functions |
| ABVNS | Adaptive Basic Variable Neighborhood Search |
| AGVNS | Adaptive General Variable Neighborhood Search |
| ALNS | Adaptive Large Neighborhood Search |
| AVNS | Adaptive Variable Neighborhood Search |
| BD | Benders Decomposition |
| BPC | Branch-and-Price-and-Cut |
| BVNS | Basic Variable Neighborhood Search |
| CA | Cellular Automata |
| CG | Column Generation |
| CMA | Cellular Memetic Algorithm |
| CP | Compromise Programming |
| DBCA | Density-Based Clustering Algorithm |
| DC | Divide and Conquer |
| DE | Differential Evolution |
| DES | Discrete Event Simulation |
| DGWO | Discrete Genetic-Grey Wolf Optimization Algorithm |
| DWO | Discrete Whale Optimization |
| EA | evolutionary algorithms |
| EM | Exact Method |
| EMA | Electro-Magnetism Algorithm |
| FA | Firefly Algorithm |
| FSA | Fish Swarm Algorithm |
| GA | Genetic Algorithm |
| GH | Greedy heuristic |
| GRASP | Greedy randomized adaptive search procedure |
| GT | Game Theory |
| GVNS | General Variable Neighborhood Search |
| ICA | Imperialist Competitive Algorithm |
| IG | Iterated Greedy |
| IGWO | Improved Gray Wolf Optimization Algorithm |
| ISSA | Improved Sparrow Search Algorithm |
| L | Learning |
| LB | Local Branching |
| MA | Memetic Algorithm |
| MCS | Monte Carlo Simulation |
| MO | multiobjective |
| PSO | Particle Swarm Optimization |
| RVNS | Reduced Variable Neighborhood Search |
| SA | Simulated Annealing |
| SLP | Sustainable Logistic Problem |
| SLR | Systematic Literature Review |
| SS | Scatter Search |
| SSH | Space-Saving Heuristic |
| SVNS | Skewed Variable Neighborhood Search |
| TLBO | Teaching-Learning-Based Optimization |
| TS | Tabu Search |
| VNS | Variable Neighborhood Search |
| VND | Variable Neighborhood Descent |
| WOA | Whale Optimization Algorithm |
Appendix A. Summary of Papers Reviewed
| Ref. | Decision Problem | Field | U | D | SS | Objective | MO | VNS Variant | Hybrid |
|---|---|---|---|---|---|---|---|---|---|
| [99] | Location/Scheduling | Electric vehicles | Min number of charging points | GVNS | |||||
| [112] | Location | Electric vehicles | Max profit | GVNS | GHs | ||||
| [71] | Location | Electric vehicles | Min cost/Max coverage | ✓ | Sequential VND | SS | |||
| [101] | Location | Electric vehicles | Min distance | GVNS | |||||
| [100] | Location | Reversed logistics | Min travel cost | BVNS | |||||
| [54] | Location | Emissions | ✓ | Min travel cost | BVNS | EM, MCS | |||
| [27] | Location/Routing | Emissions | Min cost/Min environmental impact | ✓ | AGVNS | PSO | |||
| [14] | Location/Routing | Electric vehicles | Min cost | AVNS | TS | ||||
| [20] | Location/Routing | Electric vehicles | Min cost | AVNS | |||||
| [31] | Location/Routing/Inventory | Emissions | Min cost * | ABVNS | |||||
| [91] | Location/Routing | Electric vehicles | ✓ | Min cost | BVNS | PSO | |||
| [23] | Location/Routing/Inventory | Emissions | Min cost * | AVNS | |||||
| [24] | Location/Routing/Inventory | Emissions | Min cost * | AGVNS | |||||
| [113] | Location/Routing | Electric vehicles | Min cost | BVNS | |||||
| [36] | Location/Routing | Electric vehicles | Min cost | SGVNS | |||||
| [114] | Location/Routing | Clean energies | Min cost | BVNS | TS | ||||
| [92] | Location/Routing | Emissions | ✓ | Min cost * | RVNS | ICA | |||
| [15] | Location/Routing | Emissions | Min cost * | AGVNS | ALNS | ||||
| [60] | Location/Routing | Electric vehicles | Min cost | VND | ACO | ||||
| [115] | Location/Routing | Electric vehicles | Min cost | BVNS | |||||
| [116] | Location/Routing | Electric vehicles | Min cost | GVNS | |||||
| [117] | Location/Routing/Inventory | Emissions | Min cost | BVNS, GVNS with cyclicVND, pipeVND | |||||
| [118] | Location/Routing | Waste collection | Min cost | BVNS | MA | ||||
| [119] | Location/Routing | Electric vehicles | Min cost | BVNS | |||||
| [120] | Location/Routing | Electric vehicles | Min time | GVNS | |||||
| [121] | Location/Routing | Clean energies | Min cost | GVNS | GA | ||||
| [122] | Location/Routing | Clean energies | Min cost | GVNS | |||||
| [123] | Location/Routing | Waste collection | Min cost | BVNS | |||||
| [124] | Location/Routing | Electric vehicles | Min distance | BVNS | GA | ||||
| [125] | Location/Routing | Waste collection | Min cost | VND | |||||
| [87] | Scheduling | Wind farm | Min cost/Min completion period | ✓ | BVNS | CP, SA | |||
| [126] | Scheduling | Emissions | Min CO2 emission | VND/RVNS | |||||
| [72] | Scheduling | Noise pollution | Min makespan/Min noise pollution | ✓ | BVNS | CA | |||
| [127] | Scheduling | Energy consumption | Min cost | RVNS | DWO | ||||
| [89] | Scheduling | Cross-docking | Min energy consumption/Min cost | ✓ | BVNS | SA, TS | |||
| [128] | Scheduling | Energy consumption | Min cost | BVNS | DWO | ||||
| [73] | Scheduling | Energy consumption | Min makespan/Min energy consumption | ✓ | VND | MAs | |||
| [61] | Scheduling | Emissions/Noise pollution | Min completion time/Min energy consumption | ✓ | BVNS | IGWO, PSO | |||
| [129] | Scheduling | Energy consumption | Max net revenue | GVNS | |||||
| [74] | Scheduling | Energy consumption | Min makespan/Min worker cost/Min green indicator | ✓ | VND | EA | |||
| [130] | Scheduling | Energy consumption | Min cost | BVNS | DGWO | ||||
| [68] | Scheduling | Energy consumption | Min energy consumption/Min surplus stocks | ✓ | RVNS | TLBO | |||
| [131] | Scheduling | Emissions | Min carbon emissions | RVNS | |||||
| [98] | Scheduling | Energy consumption | ✓ | Min energy consumption | BVNS | ||||
| [75] | Scheduling | Energy consumption | Min makespan/Min energy consumption | ✓ | VND | TLBO | |||
| [76] | Scheduling | Energy consumption | Min makespan/Min energy cost | ✓ | VND | EA | |||
| [132] | Scheduling | Electric vehicles | Min cost | GVNS | BD | ||||
| [133] | Scheduling | Clean energy | Min electricity consumption | BVNS | TS | ||||
| [77] | Scheduling | Energy consumption | Min makespan/Min energy consumption | ✓ | VND | CMA | |||
| [78] | Scheduling | Energy consumption | Min makespan/Min equipment load/Min energy consumption/Min delay time/Min processing quality | ✓ | VND | EA | |||
| [134] | Scheduling | Energy consumption | Min cost | VND | ISSA | ||||
| [16] | Scheduling | Energy consumption | Min makespan/Min energy consumption | ✓ | AVNS | ||||
| [79] | Scheduling | Energy consumption | Min makespan/Min energy consumption | ✓ | VND | ||||
| [30] | Scheduling | Energy consumption | Min energy consumption/Min earliness and tardiness | ✓ | AVNS | ABC | |||
| [102] | Scheduling | Energy consumption | Min energy consumption | GVNS | GA, EM | ||||
| [80] | Scheduling | Energy consumption | Min makespan/Min energy consumption | ✓ | VND | GA | |||
| [81] | Scheduling | Energy consumption | Min tardiness/Min energy cost/Min carbon trading cost | ✓ | GVNS | EA, L | |||
| [82] | Scheduling | Energy consumption | ✓ | Min makespan/Min maximum occupational repetitive action index/Max minimum level of satisfaction of all workers/Min energy consumption | ✓ | BVNS | GA, L | ||
| [83] | Scheduling/Routing | Emissions | Min tardiness/Min energy consumption | ✓ | BVNS | EA | |||
| [135] | Scheduling/Routing | Emissions | Min cost * | VND | GA, SA | ||||
| [136] | Scheduling/Routing | Electric vehicles | Min travel time | BVNS and VND | EA | ||||
| [137] | Scheduling/Routing | Emissions | Max profit | BVNS | |||||
| [22] | Scheduling/Routing | Electric vehicles | Min travel time | AGVNS | |||||
| [138] | Scheduling/Routing | Electric vehicles | ✓ | Min cost | BVNS | BPC, CG | |||
| [52] | Scheduling/Routing | Wind farm | Min cost | BVNS | EM | ||||
| [139] | Scheduling/Routing | Electric vehicles | Min cost | BVNS | |||||
| [18] | Scheduling/Routing | Electric vehicles | Min cost | AVNS | GRASP | ||||
| [34] | Network design | Reversed logistics | Min cost/Min tardiness/Min pollution | ✓ | Parallel BVNS with SVNS | ||||
| [84] | Network design | Closed-loop logistics | ✓ | Min cost/Min environmental impact/Max job opportunities | ✓ | RVNS | ICA | ||
| [62] | Network design | Reversed logistics | Min cost/Min tardiness | ✓ | BVNS | ||||
| [28] | Network design (and order allocation) | Emissions | ✓ | Min cost/Min environmental impact | ✓ | ABVNS | Adaptive MO-EMA | ||
| [19] | Network design | Closed-loop logistics | Max total net present value | ABVNS | GA | ||||
| [29] | Network design | Emissions | ✓ | Min cost/Min environmental impact and social impacts | ✓ | ABVNS | PSO, EMA, ABC, GA | ||
| [63] | Network design | Reversed logistics | Min cost/Min tardiness | ✓ | RVNS | ||||
| [64] | Production/Distribution/ Inventory/Allocation/Location | Emissions | ✓ | Min cost/Max social factors | ✓ | BVNS | ACO, FSA, FA | ||
| [140] | Network design | Emissions | Max profit | GVNS | GT | ||||
| [110] | Network design | Emissions | Min cost * | GVNS | SA | ||||
| [88] | Network design | Closed-loop logistics | Min cost/Min carbon emissions | ✓ | BVNS | CP | |||
| [65] | Network design | Closed-loop logistics | Min cost/Max crop yield and phosphorus use | ✓ | BVNS | WOA | |||
| [17] | Network design | Emissions | Min cost * | Two-Level AVNS | |||||
| [66] | Network design | Wastewater collection | Min cost/Min energy comsuption | ✓ | BVNS | DC | |||
| [141] | Network design | Emissions | Min cost/Min emissions | BVNS | GA | ||||
| [85] | Network design | Electric vehicles | Min avg travel time/Min number of stations | ✓ | MO-VNS | ||||
| [142] | Routing | Waste Collection | Min time | VND | |||||
| [143] | Routing | Waste Collection | Min time/distance | VND | TS | ||||
| [144] | Routing | Waste Collection | Min time | BVNS | SA | ||||
| [145] | Routing | Waste Collection | Min cost | BVNS | EM | ||||
| [146] | Routing | Electric vehicles | Min distance | BVNS | TS, SA | ||||
| [147] | Routing | Waste Collection | Min cost | BVNS | SA | ||||
| [93] | Routing | Closed-loop logistics | ✓ | Min cost | GVNS | ||||
| [148] | Routing | Reversed logistics | Min distance | GVNS | |||||
| [40] | Routing | Electric vehicles | Min time | VNS Branching | LB | ||||
| [149] | Routing | Electric vehicles | Min distance | VND | |||||
| [51] | Routing | Emissions | Min cost | BVNS | EM | ||||
| [57] | Routing | Emissions | Min cost * | VND | ACO | ||||
| [96] | Routing | Waste Collection | ✓ | Min cost | BVNS | MCS | |||
| [150] | Routing | Electric vehicles | Min time | VNS Branching | LB | ||||
| [151] | Routing | Emissions | Min fuel consumption | GVNS | |||||
| [94] | Routing | Waste Collection | ✓ | Min time | BVNS | ||||
| [152] | Routing | Emissions | Min carbon emissions | GVNS | |||||
| [97] | Routing | Electric vehicles | ✓ | Min distance | GVNS | ||||
| [153] | Routing | Electric vehicles | Min cost | GVNS | |||||
| [154] | Routing | Electric vehicles | Min distance | GVNS | |||||
| [86] | Routing | Emissions | Min emissions/Min delay | ✓ | GVNS | ||||
| [35] | Routing | Emissions | ✓ | Min traveling time + traveling distance + environmental cost + social cost | SVNS | ||||
| [155] | Routing | Emissions | Min cost | GVNS | EA | ||||
| [156] | Routing | Waste collection | ✓ | Max social welfare | BVNS | TS | |||
| [70] | Routing | Waste collection | Min total and maximum distance | ✓ | GVNS | IG | |||
| [157] | Routing | Emissions | Min cost | BVNS | PSO | ||||
| [158] | Routing | Electric vehicles | Min cost | GVNS | SSH | ||||
| [159] | Routing | Electric vehicles | Min cost | IVNS | |||||
| [160] | Routing | Electric vehicles | Min energy compsuption | GVNS | |||||
| [161] | Routing | Emissions | Min distance | GVNS | TS | ||||
| [162] | Routing | Emissions | Min cost | VNS | GA, TS | ||||
| [163] | Routing | Emissions | Min distance | VND | ACO | ||||
| [164] | Routing | Waste collection | Min cost | GVNS | |||||
| [165] | Routing | Electric vehicles | Min cost | GVNS | |||||
| [166] | Routing | Electric vehicles | Min cost | BVNS | TS | ||||
| [105] | Routing | Electric vehicles | Min time + TW deviation + unscheduled visits + overtime | VND | |||||
| [167] | Routing | Electric vehicles | Min cost | GVNS | |||||
| [90] | Routing | Emissions | Max number of customers served by PDs and ODs/Max usage rate of professional vehicles/Min unfairness of PD routes/Min cost of operating cost ODs | ✓ | Memory-based GVNS | ||||
| [168] | Routing | Emissions | Min cost | VND | ACO | ||||
| [169] | Routing | Waste collection | Min cost | BVNS | ACO | ||||
| [21] | Routing | Waste collection | Min cost | AVNS | |||||
| [69] | Routing | Sustainable tourism | Max profit/Min cost/Min emissions | ✓ | GVNS | ||||
| [43] | Routing | Drones | Min cost | ILS | |||||
| [170] | Routing | Electric vehicles | Min distance | BVNS | TS | ||||
| [55] | Routing | Electric vehicles | Min cost | BVNS | EM | ||||
| [171] | Routing | Electric vehicles and drones | Min energy consumption | VND | ACO | ||||
| [172] | Routing | Electric vehicles | Min distance | RVNS | |||||
| [173] | Routing | Electric vehicles | Min distance | GVNS | |||||
| [174] | Routing | Waste Collection | Min cost | GVNS | SA | ||||
| [104] | Routing | Emissions | Min cost * | RVNS | |||||
| [37] | Routing | Emissions | Min cost | GVNS | |||||
| [38] | Routing | Emissions | ✓ | Min cost | RVNS | SA | |||
| [175] | Routing | Sustainable tourism | ✓ | Max number of tourists | BVNS | DE | |||
| [176] | Routing | Drones | Min energy consumption | VND | GRASP | ||||
| [67] | Routing | Drones | Min completion time/Min costs/Min truck emission/Min penalty | ✓ | GVNS | SA | |||
| [177] | Routing | Drones | Min final arrival time at the depot | RVNS | |||||
| [178] | Routing | Emissions | Min cost | GVNS | |||||
| [179] | Routing | Electric vehicles | Min cost | GVNS | DBCA | ||||
| [108] | Routing | Electric vehicles | Min energy consumption + number of vehicles | GVNS | SA | ||||
| [56] | Routing | Electric vehicles | Min cost | BVNS | EM | ||||
| [106] | Routing | Electric vehicles | Min travel time + penalty for missing time windows | GVNS | |||||
| [180] | Routing | Electric vehicles | Min cost + number of vehicles | BVNS | SA | ||||
| [25] | Routing | Electric vechiles | Min cost | AGVNS | |||||
| [109] | Routing | Electric vehicles | Min energy consumption + number of vehicles | GVNS | BSO, ACO | ||||
| [181] | Routing | Emissions | Min emissions/Min vehicle cost/Min fuel consumption/Min delay | ✓ | VND | PSO | |||
| [182] | Routing | Emissions | Min carbon emissions | GVNS | GA | ||||
| [183] | Routing | Emissions | Min carbon emissions | BVNS | |||||
| [26] | Routing | Waste collection | Min cost | AVNS | SA | ||||
| [184] | Routing | Electric vehicles and drones | Min final completition time | GVNS | |||||
| [95] | Routing | Electric vehicles | ✓ | Min recharging | GVNS | TS, SA, CG | |||
| [53] | Routing | Electric vehicles | Min cost | GVNS | EM | ||||
| [185] | Routing | Electric vehicles | Min maximum distance traveled | VND | GA, GH | ||||
| [53] | Routing | Electric vehicles | Min cost | GVNS | EM | ||||
| [186] | Routing | Electric vehicles | Min cost | GVNS | |||||
| [107] | Routing | Emissions | Min cost * | Sequential VND | GA | ||||
| [187] | Routing | Electric vehicles | Min cost | GVNS | ACO | ||||
| [103] | Routing | Drones | Min cost * | Randomized VNS | |||||
| [184] | Routing | Drones | Min completion time | BVNS | |||||
| [188] | Routing | Waste collection | Min cost | GVNS | GA, SA | ||||
| [58] | Routing | Emissions | Min cost | GVNS | ACO | ||||
| [59] | Routing | Waste collection | Min cost | VND | ACO | ||||
| [189] | Routing/Packing | Energy consumption | Min cost | BVNS | GRASP | ||||
| [190] | Layout | Wind farm | Min annual production cost per unit power | BVNS | GRASP | ||||
| [191] | Inventory | Reverse logistics | Min cost | BVNS | TS, DES | ||||
| [192] | Lot sizing | Closed-loop logistics | Min cost | GVNS | |||||
| [193] | Lot sizing | Reverse logistics | Min cost | GVNS variants | |||||
| [194] | Lot sizing | Reverse logistics | Min cost | VND | |||||
| [195] | Layout | Wind farm | Min transportation cost | BVNS | EM | ||||
| [196] | Layout | Wind farm | Max power production—wakes and foundation costs | BVNS |
References
- Ma, L.; Ghorbani, Y.; Kongar-Syuryun, C.B.; Khayrutdinov, M.M.; Klyuev, R.V.; Petenko, A.; Brigida, V. Dynamics of backfill compressive strength obtained from enrichment tails for the circular waste management. Resour. Conserv. Recycl. Adv. 2024, 23, 200224. [Google Scholar] [CrossRef]
- Zheng, Z.; Zhu, Y.; Zhang, Y.; Yin, P. The impact of China’s regional economic integration strategy on the circular economy: Policy effects and spatial spillovers. J. Environ. Manag. 2025, 373, 123669. [Google Scholar] [CrossRef]
- Mladenović, N. A variable neighborhood algorithm—A new metaheuristic for combinatorial optimization. In Proceedings of the Optimization Days, Montreal, QC, Canada, 10–12 May 1995; Volume 12, p. 234. [Google Scholar]
- Mladenović, N.; Hansen, P. Variable neighborhood search. Comput. Oper. Res. 1997, 24, 1097–1100. [Google Scholar] [CrossRef]
- Hansen, P.; Mladenović, N. Variable neighborhood search for the p-median. Locat. Sci. 1997, 5, 207–226. [Google Scholar] [CrossRef]
- Hansen, P.; Mladenović, N. Variable neighborhood search: Principles and applications. Eur. J. Oper. Res. 2001, 130, 449–467. [Google Scholar] [CrossRef]
- Hansen, P.; Mladenović, N.; Brimberg, J.; Pérez, J.A.M. Variable Neighborhood Search; Springer: Cham, Switzerland, 2019; pp. 57–97. [Google Scholar] [CrossRef]
- Brimberg, J.; Salhi, S.; Todosijević, R.; Urošević, D. Variable Neighborhood Search: The power of change and simplicity. Comput. Oper. Res. 2023, 155, 106221. [Google Scholar] [CrossRef]
- Hansen, P.; Mladenović, N.; Pérez, J.A.M. Variable neighbourhood search: Methods and applications. 4OR 2008, 6, 319–360. [Google Scholar] [CrossRef]
- Hansen, P.; Mladenović, N.; Pérez, J.A.M. Variable neighbourhood search: Methods and applications. Ann. Oper. Res. 2010, 175, 367–407. [Google Scholar] [CrossRef]
- Hansen, P.; Mladenović, N.; Todosijević, R.; Hanafi, S. Variable neighborhood search: Basics and variants. EURO J. Comput. Optim. 2017, 5, 423–454. [Google Scholar] [CrossRef]
- Hu, B.; Raidl, G.R. Variable neighborhood descent with self-adaptive neighborhood-ordering. In Proceedings of the 7th EU/MEeting on Adaptive, Self-Adaptive, and Multi-Level Metaheuristics, Málaga, Spain, 16–17 November 2006. [Google Scholar]
- Polacek, M.; Benkner, S.; Doerner, K.F.; Hartl, R.F. A Cooperative and Adaptive Variable Neighborhood Search for the Multi Depot Vehicle Routing Problem with Time Windows. Bus. Res. 2008, 1, 207–218. [Google Scholar] [CrossRef]
- Wang, L.Y.; Song, Y.-B. Multiple Charging Station Location-Routing Problem with Time Window of Electric Vehicle. J. Eng. Sci. Technol. Rev. 2015, 8, 190–201. [Google Scholar]
- Theeraviriya, C.; Ruamboon, K.; Praseeratasang, N. Solving the multi-level location routing problem considering the environmental impact using a hybrid metaheuristic. Int. J. Eng. Bus. Manag. 2021, 13, 18479790211017353. [Google Scholar] [CrossRef]
- Hamida, M.B.; Azzouz, A.; Said, L.B. An Adaptive Variable Neighborhood Search Algorithm to Solve Green Flexible Job Shop Problem. In Proceedings of the 2023 9th International Conference on Control, Decision and Information Technologies (CoDIT), Rome, Italy, 3–6 July 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 1403–1408. [Google Scholar] [CrossRef]
- Mogale, D.G.; De, A.; Ghadge, A.; Tiwari, M.K. Designing a sustainable freight transportation network with cross-docks. Int. J. Prod. Res. 2023, 61, 1455–1478. [Google Scholar] [CrossRef]
- Cebeci, E.; Yücel, E.; Koç, Ç. The home health care routing with heterogeneous electric vehicles and synchronization. OR Spectr. 2024. [Google Scholar] [CrossRef]
- Hasani, A.; Zegordi, S.H.; Nikbakhsh, E. Robust closed-loop global supply chain network design under uncertainty: The case of the medical device industry. Int. J. Prod. Res. 2015, 53, 1596–1624. [Google Scholar] [CrossRef]
- Hof, J.; Schneider, M.; Goeke, D. Solving the battery swap station location-routing problem with capacitated electric vehicles using an AVNS algorithm for vehicle-routing problems with intermediate stops. Transp. Res. Part B Methodol. 2017, 97, 102–112. [Google Scholar] [CrossRef]
- Erdem, M. Optimisation of sustainable urban recycling waste collection and routing with heterogeneous electric vehicles. Sustain. Cities Soc. 2022, 80, 103785. [Google Scholar] [CrossRef]
- Liu, W.; Dridi, M.; Ren, J.; Hassani, A.H.E.; Li, S. A double-adaptive general variable neighborhood search for an unmanned electric vehicle routing and scheduling problem in green manufacturing systems. Eng. Appl. Artif. Intell. 2023, 126, 107113. [Google Scholar] [CrossRef]
- Karakostas, P.; Sifaleras, A.; Georgiadis, M.C. Adaptive variable neighborhood search solution methods for the fleet size and mix pollution location-inventory-routing problem. Expert Syst. Appl. 2020, 153, 113444. [Google Scholar] [CrossRef]
- Karakostas, P.; Sifaleras, A.; Georgiadis, M.C. Adaptive GVNS Heuristics for Solving the Pollution Location Inventory Routing Problem. In Learning and Intelligent Optimization; Matsatsinis, N.F., Marinakis, Y., Pardalos, P., Eds.; Springer: Cham, Switzerland, 2020; pp. 157–170. [Google Scholar] [CrossRef]
- Erdem, M. Optimisation of the electric truck route for milk collection problem: A real case study. Transp. Lett. 2023, 15, 193–210. [Google Scholar] [CrossRef]
- Luo, K.; Zhao, W.; Zhang, R. A multi-day waste collection and transportation problem with selective collection and split delivery. Appl. Math. Model. 2024, 126, 753–771. [Google Scholar] [CrossRef]
- Govindan, K.; Jafarian, A.; Khodaverdi, R.; Devika, K. Two-echelon multiple-vehicle location–routing problem with time windows for optimization of sustainable supply chain network of perishable food. Int. J. Prod. Econ. 2014, 152, 9–28. [Google Scholar] [CrossRef]
- Govindan, K.; Jafarian, A.; Nourbakhsh, V. Bi-objective integrating sustainable order allocation and sustainable supply chain network strategic design with stochastic demand using a novel robust hybrid multi-objective metaheuristic. Comput. Oper. Res. 2015, 62, 112–130. [Google Scholar] [CrossRef]
- Govindan, K.; Jafarian, A.; Nourbakhsh, V. Designing a sustainable supply chain network integrated with vehicle routing: A comparison of hybrid swarm intelligence metaheuristics. Comput. Oper. Res. 2019, 110, 220–235. [Google Scholar] [CrossRef]
- Tong, H.; Zhu, J. A customer-oriented method to support multi-task green scheduling with diverse time-of-use prices in Cloud Manufacturing. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2023, 237, 911–924. [Google Scholar] [CrossRef]
- Karakostas, P.; Sifaleras, A.; Georgiadis, M.C. Basic VNS Algorithms for Solving the Pollution Location Inventory Routing Problem; Springer: Cham, Switzerland, 2019; pp. 64–76. [Google Scholar] [CrossRef]
- Hansen, P.; Mladenović, N. First vs. best improvement: An empirical study. Discret. Appl. Math. 2006, 154, 802–817. [Google Scholar] [CrossRef]
- Hansen, P.; Jaumard, B.; Mladenović, N.; Parreira, A.D. Variable neighbourhood search for maximum weight satisfiability problem. Cah. Du GERAD 2000, 62, 1–27. [Google Scholar]
- Eskandarpour, M.; Zegordi, S.H.; Nikbakhsh, E. A parallel variable neighborhood search for the multi-objective sustainable post-sales network design problem. Int. J. Prod. Econ. 2013, 145, 117–131. [Google Scholar] [CrossRef]
- Reyes-Rubiano, L.; Calvet, L.; Juan, A.A.; Faulin, J.; Bové, L. A biased-randomized variable neighborhood search for sustainable multi-depot vehicle routing problems. J. Heuristics 2020, 26, 401–422. [Google Scholar] [CrossRef]
- Affi, M.; Derbel, H.; Jarboui, B.; Siarry, P. A Skewed General Variable Neighborhood Search Approach for Solving the Battery Swap Station Location-Routing Problem with Capacitated Electric Vehicles; Springer: Cham, Switzerland, 2020; pp. 75–89. [Google Scholar] [CrossRef]
- Fan, X.; Yao, G.; Yang, Y. Multi-Compartment Vehicle Routing Problem Considering Traffic Congestion under the Mixed Carbon Policy. Appl. Sci. 2023, 13, 10304. [Google Scholar] [CrossRef]
- Chen, T.; Chu, F.; Zhang, J.; Sun, J. Sustainable collaborative strategy in pharmaceutical refrigerated logistics routing problem. Int. J. Prod. Res. 2023, 62, 5036–5060. [Google Scholar] [CrossRef]
- Hansen, P.; Mladenović, N.; Urošević, D. Variable neighborhood search and local branching. Comput. Oper. Res. 2006, 33, 3034–3045. [Google Scholar] [CrossRef]
- Bruglieri, M.; Pezzella, F.; Pisacane, O.; Suraci, S. A Variable Neighborhood Search Branching for the Electric Vehicle Routing Problem with Time Windows. Electron. Notes Discret. Math. 2015, 47, 221–228. [Google Scholar] [CrossRef]
- Mladenović, N.; Hansen, P. A tutorial on variable neighborhood search. Les Cah. Du GERAD 2003, 711, 2440. [Google Scholar]
- Lourenço, H.R.; Martin, O.C.; Stützle, T. Iterated Local Search: Framework and Applications; Springer: Cham, Switzerland, 2019; pp. 129–168. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, Z.; Hu, X.; Xue, G.; Guan, X. Truck—Drone hybrid routing problem with time-dependent road travel time. Transp. Res. Part C Emerg. Technol. 2022, 144, 103901. [Google Scholar] [CrossRef]
- Todosijević, R.; Benmansour, R.; Hanafi, S.; Mladenović, N.; Artiba, A. Nested general variable neighborhood search for the periodic maintenance problem. Eur. J. Oper. Res. 2016, 252, 385–396. [Google Scholar] [CrossRef]
- Brimberg, J.; Mladenović, N.; Todosijević, R.; Urošević, D. A general framework for nested variable neighborhood search. Electron. Notes Discret. Math. 2017, 58, 159–166. [Google Scholar] [CrossRef]
- Mladenović, N.; Todosijević, R.; Urošević, D. Two level general variable neighborhood search for attractive traveling salesman problem. Comput. Oper. Res. 2014, 52, 341–348. [Google Scholar] [CrossRef]
- Durach, C.F.; Kembro, J.; Wieland, A. A New Paradigm for Systematic Literature Reviews in Supply Chain Management. J. Supply Chain Manag. 2017, 53, 67–85. [Google Scholar] [CrossRef]
- Aloui, A.; Hamani, N.; Derrouiche, R.; Delahoche, L. Systematic literature review on collaborative sustainable transportation: Overview, analysis and perspectives. Transp. Res. Interdiscip. Perspect. 2021, 9, 100291. [Google Scholar] [CrossRef]
- Sifaleras, A.; Konstantaras, I. A Survey on Variable Neighborhood Search Methods for Supply Network Inventory; Springer International Publishing: Cham, Switzerland, 2020; pp. 71–82. [Google Scholar] [CrossRef]
- Lan, S.; Fan, W.; Yang, S.; Pardalos, P.M.; Mladenovic, N. A survey on the applications of variable neighborhood search algorithm in healthcare management. Ann. Math. Artif. Intell. 2021, 89, 741–775. [Google Scholar] [CrossRef]
- Wang, K.; Shao, Y.; Zhou, W. Matheuristic for a two-echelon capacitated vehicle routing problem with environmental considerations in city logistics service. Transp. Res. Part D Transp. Environ. 2017, 57, 262–276. [Google Scholar] [CrossRef]
- Irawan, C.A.; Ouelhadj, D.; Sperstad, I.B.; Jones, D. A combined tactical and operational framework for maintenance scheduling and routing in offshore wind farms. J. Oper. Res. Soc. 2023, 74, 2241–2260. [Google Scholar] [CrossRef]
- İslim, R.B.; Çatay, B. An effective matheuristic approach for solving the electric traveling salesperson problem with time windows and battery degradation. Eng. Appl. Artif. Intell. 2024, 132, 107943. [Google Scholar] [CrossRef]
- Imran, A.; Utomo, E.W.; Ramadhan, F.; Desrianty, A.; Helianty, Y.; Mustofa, F.H. A Simulation-Based Optimisation for the Stochastic Green Capacitated p-Median Problem. J. Ind. Eng. Manag. 2022, 15, 552–565. [Google Scholar] [CrossRef]
- Seyfi, M.; Alinaghian, M.; Ghorbani, E.; Çatay, B.; Sabbagh, M.S. Multi-mode hybrid electric vehicle routing problem. Transp. Res. Part E Logist. Transp. Rev. 2022, 166, 102882. [Google Scholar] [CrossRef]
- Çatay, B.; Sadati, İ. An improved matheuristic for solving the electric vehicle routing problem with time windows and synchronized mobile charging/battery swapping. Comput. Oper. Res. 2023, 159, 106310. [Google Scholar] [CrossRef]
- Jabir, E.; Panicker, V.V.; Sridharan, R. Design and development of a hybrid ant colony-variable neighbourhood search algorithm for a multi-depot green vehicle routing problem. Transp. Res. Part D Transp. Environ. 2017, 57, 422–457. [Google Scholar] [CrossRef]
- Wang, Y.; Wei, Z.; Luo, S.; Zhou, J.; Zhen, L. Collaboration and resource sharing in the multidepot time-dependent vehicle routing problem with time windows. Transp. Res. Part E Logist. Transp. Rev. 2024, 192, 103798. [Google Scholar] [CrossRef]
- Sahib, T.M.; Mohd-Mokhtar, R.; Mohd-Kassim, A. A comparative study utilizing hybridized ant colony optimization algorithms for solving dynamic capacity of vehicle routing problems in waste collection system. Teknomekanik 2024, 7, 38–61. [Google Scholar] [CrossRef]
- Leite, M.R.C.O.; Bernardino, H.S.; Gonçalves, L.B. Solving a Bilevel Problem with Station Location and Vehicle Routing Using Variable Neighborhood Descent and Ant Colony Optimization; Springer International Publishing: Cham, Switzerland, 2021; pp. 211–223. [Google Scholar] [CrossRef]
- Guo, H.; Li, J.; Yang, B.; Mao, X.; Zhou, Q. Green scheduling optimization of ship plane block flow line considering carbon emission and noise. Comput. Ind. Eng. 2020, 148, 106680. [Google Scholar] [CrossRef]
- Eskandarpour, M.; Nikbakhsh, E.; Zegordi, S.H. Variable neighborhood search for the bi-objective post-sales network design problem: A fitness landscape analysis approach. Comput. Oper. Res. 2014, 52, 300–314. [Google Scholar] [CrossRef]
- Yıldız, G.B.; Soylu, B. A multiobjective post-sales guarantee and repair services network design problem. Int. J. Prod. Econ. 2019, 216, 305–320. [Google Scholar] [CrossRef]
- Goodarzian, F.; Taleizadeh, A.A.; Ghasemi, P.; Abraham, A. An integrated sustainable medical supply chain network during COVID-19. Eng. Appl. Artif. Intell. 2021, 100, 104188. [Google Scholar] [CrossRef]
- Shokouhifar, M.; Sohrabi, M.; Rabbani, M.; Molana, S.M.H.; Werner, F. Sustainable Phosphorus Fertilizer Supply Chain Management to Improve Crop Yield and P Use Efficiency Using an Ensemble Heuristic–Metaheuristic Optimization Algorithm. Agronomy 2023, 13, 565. [Google Scholar] [CrossRef]
- Balamurugan, J.; Kasthuri, N.; Sudarsan, J.; Reddy, A.B.; Someshwar, S.; Sakhare, D.; Sampathkumar, V. An efficient wastewater collection model for groundwater resource protection in smart cities. Groundw. Sustain. Dev. 2024, 25, 101091. [Google Scholar] [CrossRef]
- Teimoury, E.; Rashid, R. A hybrid variable neighborhood search heuristic for the sustainable time-dependent truck-drone routing problem with rendezvous locations. J. Heuristics 2023, 30, 1–41. [Google Scholar] [CrossRef]
- Jin, W.; He, Z.; Peng, T. A JIT part supply scheduling strategy with electric transport device between central receiving store and supermarkets in the automobile industry considering energy. eTransportation 2021, 9, 100126. [Google Scholar] [CrossRef]
- Divsalar, G.; Divsalar, A.; Jabbarzadeh, A.; Sahebi, H. An optimization approach for green tourist trip design. Soft Comput. 2022, 26, 4303–4332. [Google Scholar] [CrossRef]
- Delgado-Antequera, L.; Caballero, R.; Sánchez-Oro, J.; Colmenar, J.M.; Martí, R. Iterated greedy with variable neighborhood search for a multiobjective waste collection problem. Expert Syst. Appl. 2020, 145, 113101. [Google Scholar] [CrossRef]
- Yazdekhasti, A.; Jazi, M.A.; Ma, J. Electric vehicle charging station location determination with consideration of routing selection policies and driver’s risk preference. Comput. Ind. Eng. 2021, 162, 107674. [Google Scholar] [CrossRef]
- Lu, C.; Gao, L.; Pan, Q.; Li, X.; Zheng, J. A multi-objective cellular grey wolf optimizer for hybrid flowshop scheduling problem considering noise pollution. Appl. Soft Comput. 2019, 75, 728–749. [Google Scholar] [CrossRef]
- Jin, L.; Zhang, C.; Fei, X. Realizing energy savings in integrated process planning and scheduling. Processes 2019, 7, 120. [Google Scholar] [CrossRef]
- Gong, G.; Chiong, R.; Deng, Q.; Han, W.; Zhang, L.; Lin, W.; Li, K. Energy-efficient flexible flow shop scheduling with worker flexibility. Expert Syst. Appl. 2020, 141, 112902. [Google Scholar] [CrossRef]
- Song, C. A Hybrid Multi-Objective Teaching-Learning Based Optimization for Scheduling Problem of Hybrid Flow Shop with Unrelated Parallel Machine. IEEE Access 2021, 9, 56822–56835. [Google Scholar] [CrossRef]
- Zeng, Z.; Chen, X.; Wang, K. Energy Saving for Tissue Paper Mills by Energy-Efficiency Scheduling under Time-of-Use Electricity Tariffs. Processes 2021, 9, 274. [Google Scholar] [CrossRef]
- Wang, Y.; Peng, W.; Lu, C.; Xia, H. A Multi-Objective Cellular Memetic Optimization Algorithm for Green Scheduling in Flexible Job Shops. Symmetry 2022, 14, 832. [Google Scholar] [CrossRef]
- Sang, Y.; Tan, J. Many-Objective Flexible Job Shop Scheduling Problem with Green Consideration. Energies 2022, 15, 1884. [Google Scholar] [CrossRef]
- Zhang, W.; Geng, H.; Li, C.; Gen, M.; Zhang, G.; Deng, M. Q-learning-based multi-objective particle swarm optimization with local search within factories for energy-efficient distributed flow-shop scheduling problem. J. Intell. Manuf. 2023. [Google Scholar] [CrossRef]
- Li, Y.; Hu, R.; Wu, X.; Qian, B.; Zhang, Z.Q. Learning Variable Neighborhood Search Algorithm for Solving the Energy-Efficient Flexible Job-Shop Scheduling Problem; Springer Nature: Singapore, 2023; pp. 241–250. [Google Scholar] [CrossRef]
- Li, P.; Xue, Q.; Zhang, Z.; Chen, J.; Zhou, D. Multi-objective energy-efficient hybrid flow shop scheduling using Q-learning and GVNS driven NSGA-II. Comput. Oper. Res. 2023, 159, 106360. [Google Scholar] [CrossRef]
- Destouet, C.; Tlahig, H.; Bettayeb, B.; Mazari, B. Multi-objective sustainable flexible job shop scheduling problem: Balancing economic, ecological, and social criteria. Comput. Ind. Eng. 2024, 195, 110419. [Google Scholar] [CrossRef]
- Hassanzadeh, A.; Rasti-Barzoki, M. Minimizing total resource consumption and total tardiness penalty in a resource allocation supply chain scheduling and vehicle routing problem. Appl. Soft Comput. 2017, 58, 307–323. [Google Scholar] [CrossRef]
- Devika, K.; Jafarian, A.; Nourbakhsh, V. Designing a sustainable closed-loop supply chain network based on triple bottom line approach: A comparison of metaheuristics hybridization techniques. Eur. J. Oper. Res. 2014, 235, 594–615. [Google Scholar] [CrossRef]
- Iliopoulou, C.; Tassopoulos, I.X.; Kepaptsoglou, K. Multi-objective planning of electric bus systems in cities with trolleybus infrastructure networks. Sustain. Cities Soc. 2024, 103, 105227. [Google Scholar] [CrossRef]
- Ren, X.; Huang, H.; Feng, S.; Liang, G. An improved variable neighborhood search for bi-objective mixed-energy fleet vehicle routing problem. J. Clean. Prod. 2020, 275, 124155. [Google Scholar] [CrossRef]
- Irawan, C.A.; Jones, D.; Ouelhadj, D. Bi-objective optimisation model for installation scheduling in offshore wind farms. Comput. Oper. Res. 2017, 78, 393–407. [Google Scholar] [CrossRef]
- Irawan, C.A.; Abdulrahman, M.D.A.; Salhi, S.; Luis, M. An efficient matheuristic algorithm for bi-objective sustainable closed-loop supply chain networks. IMA J. Manag. Math. 2022, 33, 603–636. [Google Scholar] [CrossRef]
- Chargui, T.; Bekrar, A.; Reghioui, M.; Trentesaux, D. Multi-objective sustainable truck scheduling in a rail-road physical internet cross-docking hub considering energy consumption. Sustainability 2019, 11, 3127. [Google Scholar] [CrossRef]
- Cao, L.; Ye, C.; Cheng, R.; Wang, Z. Memory-based variable neighborhood search for green vehicle routing problem with passing-by drivers: A comprehensive perspective. Complex Intell. Syst. 2022, 8, 2507–2525. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.; Chen, M.; Zhang, W. A novel location-routing problem in electric vehicle transportation with stochastic demands. J. Clean. Prod. 2019, 221, 567–581. [Google Scholar] [CrossRef]
- Araghi, M.E.T.; Tavakkoli-Moghaddam, R.; Jolai, F.; Molana, S.M.H. A green multi-facilities open location-routing problem with planar facility locations and uncertain customer. J. Clean. Prod. 2021, 282, 124343. [Google Scholar] [CrossRef]
- Hu, Z.H.; Sheu, J.B.; Zhao, L.; Lu, C.C. A dynamic closed-loop vehicle routing problem with uncertainty and incompatible goods. Transp. Res. Part C Emerg. Technol. 2015, 55, 273–297. [Google Scholar] [CrossRef]
- Qi, M.; Xiong, W.; Zhou, Q.; Hua, S. Robust Periodic Vehicle Routing Problem with Service Time Uncertainty. In Proceedings of the 2018 IEEE International Conference on Industrial Engineering and Engineering Management (IEEM), Bangkok, Thailand, 16–19 December 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1431–1435. [Google Scholar] [CrossRef]
- Jeong, J.; Ghaddar, B.; Zufferey, N.; Nathwani, J. Adaptive robust electric vehicle routing under energy consumption uncertainty. Transp. Res. Part C Emerg. Technol. 2024, 160, 104529. [Google Scholar] [CrossRef]
- Gruler, A.; Quintero-Araújo, C.L.; Calvet, L.; Juan, A.A. Waste collection under uncertainty: A simheuristic based on variable neighbourhood search. Eur. J. Ind. Eng. 2017, 11, 228–255. [Google Scholar] [CrossRef]
- Lu, J.; Wang, L. A Bi-Strategy Based Optimization Algorithm for the Dynamic Capacitated Electric Vehicle Routing Problem. In Proceedings of the 2019 IEEE Congress on Evolutionary Computation (CEC), Wellington, New Zealand, 10–13 June 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 646–653. [Google Scholar] [CrossRef]
- Kong, M.; Xu, J.; Zhang, T.; Lu, S.; Fang, C.; Mladenovic, N. Energy-efficient rescheduling with time-of-use energy cost: Application of variable neighborhood search algorithm. Comput. Ind. Eng. 2021, 156, 107286. [Google Scholar] [CrossRef]
- Koháni, M.; Babčan, S. Variable Neighborhood Search for the Electric Bus Charging Stations Location Design Problem. In Proceedings of the 13th International Conference on Operations Research and Enterprise Systems. SCITEPRESS-Science and Technology Publications, Rome, Italy, 24–26 February 2024; pp. 317–324. [Google Scholar] [CrossRef]
- Fard, A.M.F.; Hajaghaei-Keshteli, M. A tri-level location-allocation model for forward/reverse supply chain. Appl. Soft Comput. 2018, 62, 328–346. [Google Scholar] [CrossRef]
- Cintrano, C.; Toutouh, J.; Alba, E. Citizen Centric Optimal Electric Vehicle Charging Stations Locations in a Full City: Case of Malaga; Springer: Cham, Switzerland, 2021; pp. 247–257. [Google Scholar] [CrossRef]
- Li, D.; Zheng, T.; Li, J.; Teymourifar, A. A Hybrid Framework Integrating Machine-learning and Mathematical Programming Approaches for Sustainable Scheduling of Flexible Job-shop Problems. Chem. Eng. Trans. 2023, 103, 385–390. [Google Scholar] [CrossRef]
- Xiao, Q.; Gao, J. The Multi-Visit Vehicle Routing Problem with Drones under Carbon Trading Mechanism. Sustainability 2024, 16, 6145. [Google Scholar] [CrossRef]
- Chen, W.; Zhang, D.; Woensel, T.V.; Xu, G.; Guo, J. Green vehicle routing using mixed fleets for cold chain distribution. Expert Syst. Appl. 2023, 233, 120979. [Google Scholar] [CrossRef]
- Bac, U.; Erdem, M. Optimization of electric vehicle recharge schedule and routing problem with time windows and partial recharge: A comparative study for an urban logistics fleet. Sustain. Cities Soc. 2021, 70, 102883. [Google Scholar] [CrossRef]
- Matijević, L. General variable neighborhood search for electric vehicle routing problem with time-dependent speeds and soft time windows. Int. J. Ind. Eng. Comput. 2023, 14, 275–292. [Google Scholar] [CrossRef]
- Su, Y.; Zhang, S.; Zhang, C. A lightweight genetic algorithm with variable neighborhood search for multi-depot vehicle routing problem with time windows. Appl. Soft Comput. 2024, 161, 111789. [Google Scholar] [CrossRef]
- Stamadianos, T.; Kyriakakis, N.A.; Marinaki, M.; Marinakis, Y. A hybrid simulated annealing and variable neighborhood search algorithm for the close-open electric vehicle routing problem. In Annals of Mathematics and Artificial Intelligence; Springer: Berlin/Heidelberg, Germany, 2023. [Google Scholar] [CrossRef]
- Stamadianos, T.; Kyriakakis, N.A.; Marinaki, M.; Marinakis, Y. The close-open mixed-fleet electric vehicle routing problem. Clean. Logist. Supply Chain 2023, 9, 100125. [Google Scholar] [CrossRef]
- Shojaei, M.; Fakhrmoosavi, F.; Zockaie, A.; Ghamami, M.; Mittal, A.; Fishelson, J. Sustainable Transportation Networks Incorporating Green Modes for Urban Freight Delivery. J. Transp. Eng. Part A Syst. 2022, 148, 6. [Google Scholar] [CrossRef]
- Todosijević, R.; Urošević, D.; Mladenović, N.; Brimberg, J. Less Is More Approach. In Discrete Diversity and Dispersion Maximization: A Tutorial on Metaheuristic Optimization; Springer: Cham, Switzerland, 2023; pp. 191–220. [Google Scholar]
- Biesinger, B.; Hu, B.; Stubenschrott, M.; Ritzinger, U.; Prandtstetter, M. Optimizing Charging Station Locations for Electric Car-Sharing Systems; Springer International Publishing: Cham, Switzerland, 2017; Volume 10197, pp. 157–172. [Google Scholar] [CrossRef]
- Almouhanna, A.; Quintero-Araujo, C.L.; Panadero, J.; Juan, A.A.; Khosravi, B.; Ouelhadj, D. The location routing problem using electric vehicles with constrained distance. Comput. Oper. Res. 2020, 115, 104864. [Google Scholar] [CrossRef]
- Cao, J.X.; Wang, X.; Gao, J. A two-echelon location-routing problem for biomass logistics systems. Biosyst. Eng. 2021, 202, 106–118. [Google Scholar] [CrossRef]
- Corrêa, V.H.V.; dos Santos, A.G.; Nogueira, T.H. Strategies for Electric Location-routing Problems Considering Short and Long Term Horizons. In Proceedings of the International Conference on Enterprise Information Systems, ICEIS-Proceedings, Virtual, 26–28 April 2021; Science and Technology Publications, Lda: Setubal, Portugal, 2021; Volume 1, pp. 795–802. [Google Scholar] [CrossRef]
- Stumpe, M.; Rößler, D.; Schryen, G.; Kliewer, N. Study on sensitivity of electric bus systems under simultaneous optimization of charging infrastructure and vehicle schedules. EURO J. Transp. Logist. 2021, 10, 100049. [Google Scholar] [CrossRef]
- Karakostas, P.; Sifaleras, A.; Georgiadis, M.C. Variable neighborhood search-based solution methods for the pollution location-inventory-routing problem. Optim. Lett. 2022, 16, 211–235. [Google Scholar] [CrossRef]
- Hu, W.; Dong, J.; Xu, N. Multi-period planning of integrated underground logistics system network for automated construction-demolition-municipal waste collection and parcel delivery: A case study. J. Clean. Prod. 2022, 330, 129760. [Google Scholar] [CrossRef]
- Olsen, N.; Kliewer, N. Location Planning of Charging Stations for Electric Buses in Public Transport Considering Vehicle Scheduling: A Variable Neighborhood Search Based Approach. Appl. Sci. 2022, 12, 3855. [Google Scholar] [CrossRef]
- Vukićević, M.; Ratli, M.; Rivenq, A.; Zrikem, M. Covering delivery problem with electric vehicle and parcel lockers: Variable neighborhood search approach. Comput. Oper. Res. 2023, 157, 106263. [Google Scholar] [CrossRef]
- Irawan, C.A.; Salhi, S.; Chan, H.K. A continuous location and maintenance routing problem for offshore wind farms: Mathematical models and hybrid methods. Comput. Oper. Res. 2022, 144, 105825. [Google Scholar] [CrossRef]
- Irawan, C.A.; Starita, S.; Chan, H.K.; Eskandarpour, M.; Reihaneh, M. Routing in offshore wind farms: A multi-period location and maintenance problem with joint use of a service operation vessel and a safe transfer boat. Eur. J. Oper. Res. 2023, 307, 328–350. [Google Scholar] [CrossRef]
- Gläser, S.; Stücken, M. Introduction of an underground waste container system–model and solution approaches. Eur. J. Oper. Res. 2021, 295, 675–689. [Google Scholar] [CrossRef]
- Innis, C.; Chen, P. Location-Routing Problem for Electric Delivery Vehicles with Mobile Charging Trailers. In Proceedings of the 2024 American Control Conference (ACC), Toronto, ON, Canada, 10–12 July 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 3007–3012. [Google Scholar] [CrossRef]
- Noreña-Zapata, D.; Restrepo-Vallejo, J.C.; Morillo-Torres, D.; Gatica, G. A Novel Exact and Heuristic Solution for the Periodic Location-Routing Problem Applied to Waste Collection. Processes 2024, 12, 1557. [Google Scholar] [CrossRef]
- Zhou, Y.; Liret, A.; Liu, J.; Ferreyra, E.; Rana, R.; Kern, M. Decision Support System for Green Real-Life Field Scheduling Problems; Springer: Cham, Switzerland, 2017; pp. 355–369. [Google Scholar] [CrossRef]
- Luan, F.; Cai, Z.; Wu, S.; Liu, S.Q.; He, Y. Optimizing the Low-Carbon Flexible Job Shop Scheduling Problem with Discrete Whale Optimization Algorithm. Mathematics 2019, 7, 688. [Google Scholar] [CrossRef]
- Jiang, T.; Zhang, C.; Sun, Q.M. Green Job Shop Scheduling Problem with Discrete Whale Optimization Algorithm. IEEE Access 2019, 7, 43153–43166. [Google Scholar] [CrossRef]
- Kong, M.; Pei, J.; Liu, X.; Lai, P.C.; Pardalos, P.M. Green manufacturing: Order acceptance and scheduling subject to the budgets of energy consumption and machine launch. J. Clean. Prod. 2020, 248, 119300. [Google Scholar] [CrossRef]
- Gu, J.; Jiang, T.; Zhu, H.; Zhang, C. Low-Carbon Job Shop Scheduling Problem with Discrete Genetic-Grey Wolf Optimization Algorithm. J. Adv. Manuf. Syst. 2020, 19, 1–14. [Google Scholar] [CrossRef]
- Zhu, S.; Gao, J.; He, X.; Zhang, S.; Jin, Y.; Tan, Z. Green logistics oriented tug scheduling for inland waterway logistics. Adv. Eng. Inform. 2021, 49, 101323. [Google Scholar] [CrossRef]
- Varga, J.; Raidl, G.R.; Limmer, S. Computational Methods for Scheduling the Charging and Assignment of an On-Site Shared Electric Vehicle Fleet. IEEE Access 2022, 10, 105786–105806. [Google Scholar] [CrossRef]
- Li, H.; Wang, S.; Zhen, L.; Wang, X. Data-driven optimization for automated warehouse operations decarbonization. Ann. Oper. Res. 2022, 343, 1129–1156. [Google Scholar] [CrossRef]
- Luan, F.; Li, R.; Liu, S.Q.; Tang, B.; Li, S.; Masoud, M. An Improved Sparrow Search Algorithm for Solving the Energy-Saving Flexible Job Shop Scheduling Problem. Machines 2022, 10, 847. [Google Scholar] [CrossRef]
- Fan, H.; Yu, J.; Liu, X. Tramp ship routing and scheduling with speed optimization considering carbon emissions. Sustainability 2019, 11, 6367. [Google Scholar] [CrossRef]
- Erdem, M. The multi-period electric home healthcare routeing and scheduling problem with nonlinear charging. S. Afr. J. Ind. Eng. 2020, 31, 92–106. [Google Scholar] [CrossRef]
- De, A.; Wang, J.; Tiwari, M.K. Fuel Bunker Management Strategies within Sustainable Container Shipping Operation Considering Disruption and Recovery Policies. IEEE Trans. Eng. Manag. 2021, 68, 1089–1111. [Google Scholar] [CrossRef]
- Yin, Y.; Liu, X.; Chu, F.; Wang, D. An exact algorithm for the home health care routing and scheduling with electric vehicles and synergistic-transport mode. Ann. Oper. Res. 2023. [Google Scholar] [CrossRef]
- Zhou, S.; Zhang, D.; Ji, B.; Zhou, S.; Li, S.; Zhou, L. A MILP model and heuristic method for the time-dependent electric vehicle routing and scheduling problem with time windows. J. Clean. Prod. 2024, 434, 140188. [Google Scholar] [CrossRef]
- Amini, H.; Kianfar, K. A variable neighborhood search based algorithm and game theory models for green supply chain design. Appl. Soft Comput. 2022, 119, 108615. [Google Scholar] [CrossRef]
- Jahed, A.; Molana, S.M.H.; Tavakkoli-Moghaddam, R.; Valizadeh, V. Designing an integrated sustainable-resilient mix-and-match vaccine supply chain network. Ann. Oper. Res. 2024. [Google Scholar] [CrossRef]
- Pia, A.D.; Filippi, C. A variable neighborhood descent algorithm for a real waste collection problem with mobile depots. Int. Trans. Oper. Res. 2006, 13, 125–141. [Google Scholar] [CrossRef]
- Benjamin, A.M.; Beasley, J.E. Metaheuristics for the waste collection vehicle routing problem with time windows, driver rest period and multiple disposal facilities. Comput. Oper. Res. 2010, 37, 2270–2280. [Google Scholar] [CrossRef]
- Hemmelmayr, V.; Doerner, K.F.; Hartl, R.F.; Rath, S. A heuristic solution method for node routing based solid waste collection problems. J. Heuristics 2013, 19, 129–156. [Google Scholar] [CrossRef]
- Hemmelmayr, V.C.; Doerner, K.F.; Hartl, R.F.; Vigo, D. Models and algorithms for the integrated planning of bin allocation and vehicle routing in solid waste management. Transp. Sci. 2014, 48, 103–120. [Google Scholar] [CrossRef]
- Schneider, M.; Stenger, A.; Goeke, D. The electric vehicle-routing problem with time windows and recharging stations. Transp. Sci. 2014, 48, 500–520. [Google Scholar] [CrossRef]
- Henke, T.; Speranza, M.G.; Wäscher, G. The multi-compartment vehicle routing problem with flexible compartment sizes. Eur. J. Oper. Res. 2015, 246, 730–743. [Google Scholar] [CrossRef]
- Djikanovic, J.; Joksimovic, D.; Vujosevic, M. Application of Variable Neighbourhood Search Method for Vehicle-Routing Problems in an Integrated Forward and Reverse Logistic Chain. Acta Polytech. Hung. 2015, 12, 51–70. [Google Scholar]
- Roberti, R.; Wen, M. The Electric Traveling Salesman Problem with Time Windows. Transp. Res. Part E Logist. Transp. Rev. 2016, 89, 32–52. [Google Scholar] [CrossRef]
- Bruglieri, M.; Mancini, S.; Pezzella, F.; Pisacane, O.; Suraci, S. A three-phase matheuristic for the time-effective electric vehicle routing problem with partial recharges. Electron. Notes Discret. Math. 2017, 58, 95–102. [Google Scholar] [CrossRef]
- Affi, M.; Derbel, H.; Jarboui, B. Variable neighborhood search algorithm for the green vehicle routing problem. Int. J. Ind. Eng. Comput. 2018, 9, 195–204. [Google Scholar] [CrossRef]
- Tayachi, D.; Boukadi, H. A variable neighborhood search to reduce carbon dioxide emissions in the capacitated vehicle routing problem. In Proceedings of the 2019 6th International Conference on Control, Decision and Information Technologies (CoDIT), Paris, France, 23–26 April 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 297–301. [Google Scholar] [CrossRef]
- Rezgui, D.; Siala, J.C.; Aggoune-Mtalaa, W.; Bouziri, H. Application of a variable neighborhood search algorithm to a fleet size and mix vehicle routing problem with electric modular vehicles. Comput. Ind. Eng. 2019, 130, 537–550. [Google Scholar] [CrossRef]
- Li, L.; Li, T.; Wang, K.; Gao, S.; Chen, Z.; Wang, L. Heterogeneous fleet electric vehicle routing optimization for logistic distribution with time windows and simultaneous pick-up and delivery service. In Proceedings of the 2019 16th International Conference on Service Systems and Service Management (ICSSSM), Shenzhen, China, 13–15 July 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Peng, B.; Wu, L.; Yi, Y.; Chen, X. Solving the multi-depot green vehicle routing problem by a hybrid evolutionary algorithm. Sustainability 2020, 12, 2127. [Google Scholar] [CrossRef]
- Shao, S.; Xu, S.X.; Huang, G.Q. Variable neighborhood search and tabu search for auction-based waste collection synchronization. Transp. Res. Part B Methodol. 2020, 133, 1–20. [Google Scholar] [CrossRef]
- De, A.; Wang, J.; Tiwari, M.K. Hybridizing basic variable neighborhood search with particle swarm optimization for solving sustainable ship routing and bunker management problem. IEEE Trans. Intell. Transp. Syst. 2020, 21, 986–997. [Google Scholar] [CrossRef]
- Zhu, X.; Yan, R.; Huang, Z.; Wei, W.; Yang, J.; Kudratova, S. Logistic Optimization for Multi Depots Loading Capacitated Electric Vehicle Routing Problem from Low Carbon Perspective. IEEE Access 2020, 8, 31934–31947. [Google Scholar] [CrossRef]
- Lu, J.; Chen, Y.; Hao, J.K.; He, R. The Time-dependent Electric Vehicle Routing Problem: Model and solution. Expert Syst. Appl. 2020, 161, 113593. [Google Scholar] [CrossRef]
- Wang, L.; Gao, S.; Wang, K.; Li, T.; Li, L.; Chen, Z. Time-Dependent Electric Vehicle Routing Problem with Time Windows and Path Flexibility. J. Adv. Transp. 2020, 2020, 1DUMMMY. [Google Scholar] [CrossRef]
- Sadati, M.E.H.; Çatay, B. A hybrid variable neighborhood search approach for the multi-depot green vehicle routing problem. Transp. Res. Part E Logist. Transp. Rev. 2021, 149, 102293. [Google Scholar] [CrossRef]
- Fan, H.; Zhang, Y.; Tian, P.; Lv, Y.; Fan, H. Time-dependent multi-depot green vehicle routing problem with time windows considering temporal-spatial distance. Comput. Oper. Res. 2021, 129, 105211. [Google Scholar] [CrossRef]
- Islam, M.A.; Gajpal, Y. Optimization of conventional and green vehicles composition under carbon emission cap. Sustainability 2021, 13, 6940. [Google Scholar] [CrossRef]
- Zhao, W.; Zhang, R.; Yuan, X.; Luo, K. An improved variable neighborhood search algorithm for the solid waste collection and transportation problem with split deliveries. In Proceedings of the 2021 11th International Conference on Information Science and Technology, ICIST 2021, Chengdu, China, 21–23 May 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 659–667. [Google Scholar] [CrossRef]
- Wang, D.; Zhou, H. A two-echelon electric vehicle routing problem with time windows and battery swapping stations. Appl. Sci. 2021, 11, 10779. [Google Scholar] [CrossRef]
- Lin, B.; Ghaddar, B.; Nathwani, J. Electric vehicle routing with charging/discharging under time-variant electricity prices. Transp. Res. Part C Emerg. Technol. 2021, 130, 103285. [Google Scholar] [CrossRef]
- Zhou, Y.; Huang, J.; Shi, J.; Wang, R.; Huang, K. The electric vehicle routing problem with partial recharge and vehicle recycling. Complex Intell. Syst. 2021, 7, 1445–1458. [Google Scholar] [CrossRef]
- Jabir, E.; Panicker, V.V.; Sridharan, R. Environmental friendly route design for a milk collection problem: The case of an Indian dairy. Int. J. Prod. Res. 2022, 60, 912–941. [Google Scholar] [CrossRef]
- Roy, A.; Manna, A.; Kim, J.; Moon, I. IoT-based smart bin allocation and vehicle routing in solid waste management: A case study in South Korea. Comput. Ind. Eng. 2022, 171, 108457. [Google Scholar] [CrossRef]
- Sadati, M.E.H.; Akbari, V.; Çatay, B. Electric vehicle routing problem with flexible deliveries. Int. J. Prod. Res. 2022, 60, 4268–4294. [Google Scholar] [CrossRef]
- Kyriakakis, N.A.; Stamadianos, T.; Marinaki, M.; Marinakis, Y. The electric vehicle routing problem with drones: An energy minimization approach for aerial deliveries. Clean. Logist. Supply Chain 2022, 4, 100041. [Google Scholar] [CrossRef]
- Yilmaz, Y.; Kalayci, C.B. Variable Neighborhood Search Algorithms to Solve the Electric Vehicle Routing Problem with Simultaneous Pickup and Delivery. Mathematics 2022, 10, 3108. [Google Scholar] [CrossRef]
- Akbay, M.A.; Kalayci, C.B.; Blum, C.; Polat, O. Variable Neighborhood Search for the Two-Echelon Electric Vehicle Routing Problem with Time Windows. Appl. Sci. 2022, 12, 1014. [Google Scholar] [CrossRef]
- Zhao, T.; Lu, S.; Kong, M.; Cheng, H.; Liu, X. Green scheduling of packaging in the global logistics distribution centre with a dominant job and deterioration effects. Int. J. Logist. Res. Appl. 2025, 28, 98–120. [Google Scholar] [CrossRef]
- Thumrongvut, P.; Sethanan, K.; Pitakaso, R.; Jamrus, T.; Golinska-Dawson, P. Application of Industry 3.5 approach for planning of more sustainable supply chain operations for tourism service providers. Int. J. Logist. Res. Appl. 2023, 26, 1578–1601. [Google Scholar] [CrossRef]
- Kyriakakis, N.A.; Aronis, S.; Marinaki, M.; Marinakis, Y. A GRASP/VND algorithm for the energy minimizing drone routing problem with pickups and deliveries. Comput. Ind. Eng. 2023, 182, 109340. [Google Scholar] [CrossRef]
- Yanpirat, N.; Silva, D.F.; Smith, A.E. Sustainable last mile parcel delivery and return service using drones. Eng. Appl. Artif. Intell. 2023, 124, 106631. [Google Scholar] [CrossRef]
- Li, Y.; Sun, Z. Repositioning shared bikes under low-carbon policies. Comput. Ind. Eng. 2023, 184, 109594. [Google Scholar] [CrossRef]
- Euchi, J.; Yassine, A. A hybrid metaheuristic algorithm to solve the electric vehicle routing problem with battery recharging stations for sustainable environmental and energy optimization. Energy Syst. 2023, 14, 243–267. [Google Scholar] [CrossRef]
- Moradi, N.; Sadat, İ.; Çatay, B. Last mile delivery routing problem using autonomous electric vehicles. Comput. Ind. Eng. 2023, 184, 109552. [Google Scholar] [CrossRef]
- Li, K.; Li, D.; Ma, H.Q. An improved discrete particle swarm optimization approach for a multi-objective optimization model of an urban logistics distribution network considering traffic congestion. Adv. Prod. Eng. Manag. 2023, 18, 211–224. [Google Scholar] [CrossRef]
- Lou, P.; Zhou, Z.; Zeng, Y.; Fan, C. Vehicle routing problem with time windows and carbon emissions: A case study in logistics distribution. Environ. Sci. Pollut. Res. 2024, 31, 41600–41620. [Google Scholar] [CrossRef]
- Ferreira, K.M.; de Queiroz, T.A.; Munari, P.; Toledo, F.M.B. A variable neighborhood search for the green vehicle routing problem with two-dimensional loading constraints and split delivery. Eur. J. Oper. Res. 2024, 316, 597–616. [Google Scholar] [CrossRef]
- Zhu, T.; Boyles, S.D.; Unnikrishnan, A. Battery Electric Vehicle Traveling Salesman Problem with Drone. Networks Spat. Econ. 2024, 24, 49–97. [Google Scholar] [CrossRef]
- Fazeli, S.S.; Venkatachalam, S.; Smereka, J.M. Efficient algorithms for electric vehicles’ min-max routing problem. Sustain. Oper. Comput. 2024, 5, 15–28. [Google Scholar] [CrossRef]
- Souza, A.L.; Papini, M.; Penna, P.H.; Souza, M.J. A flexible variable neighbourhood search algorithm for different variants of the Electric Vehicle Routing Problem. Comput. Oper. Res. 2024, 168, 106713. [Google Scholar] [CrossRef]
- Wang, H.; Chen, S.; Li, M.; Zhu, C.; Wang, Z. Demand-Driven Charging Strategy Based Distributed Routing Optimization Under Traffic Restrictions in Internet of Electric Vehicles. IEEE Internet Things J. 2024, 11, 35917–35927. [Google Scholar] [CrossRef]
- Masmoudi, M.A.; Baldacci, R.; Mancini, S.; Kuo, Y.H. Multi-compartment waste collection vehicle routing problem with bin washer. Transp. Res. Part E Logist. Transp. Rev. 2024, 189, 103681. [Google Scholar] [CrossRef]
- Rojas-Saavedra, J.E.; Álvarez Martínez, D.; Escobar, J.W. Boosting sustainable development goals: A hybrid metaheuristic approach for the heterogeneous vehicle routing problem with three-dimensional packing constraints and fuel consumption. Ann. Oper. Res. 2023. [Google Scholar] [CrossRef]
- Yin, P.Y.; Wang, T.Y. A GRASP-VNS algorithm for optimal wind-turbine placement in wind farms. Renew. Energy 2012, 48, 489–498. [Google Scholar] [CrossRef]
- Zolfagharinia, H.; Hafezi, M.; Farahani, R.Z.; Fahimnia, B. A hybrid two-stock inventory control model for a reverse supply chain. Transp. Res. Part E Logist. Transp. Rev. 2014, 67, 141–161. [Google Scholar] [CrossRef]
- Sifaleras, A.; Konstantaras, I. General variable neighborhood search for the multi-product dynamic lot sizing problem in closed-loop supply chain. Electron. Notes Discret. Math. 2015, 47, 69–76. [Google Scholar] [CrossRef]
- Sifaleras, A.; Konstantaras, I.; Mladenović, N. Variable neighborhood search for the economic lot sizing problem with product returns and recovery. Int. J. Prod. Econ. 2015, 160, 133–143. [Google Scholar] [CrossRef]
- Sifaleras, A.; Konstantaras, I. Variable neighborhood descent heuristic for solving reverse logistics multi-item dynamic lot-sizing problems. Comput. Oper. Res. 2017, 78, 385–392. [Google Scholar] [CrossRef]
- Irawan, C.A.; Song, X.; Jones, D.; Akbari, N. Layout optimisation for an installation port of an offshore wind farm. Eur. J. Oper. Res. 2017, 259, 67–83. [Google Scholar] [CrossRef]
- Cazzaro, D.; Pisinger, D. Variable neighborhood search for large offshore wind farm layout optimization. Comput. Oper. Res. 2022, 138, 105588. [Google Scholar] [CrossRef]

| Criteria | Justification | |
|---|---|---|
| Inclusion | Papers published between 2006 and August 2024 | To focus on the most recent publications. |
| Publications in peer-reviewed journals, conference papers and chapters | To concentrate on high-quality articles and other documents for a broader and more comprehensive literature search. | |
| The measure of environmental or social impact is explicit either in the objective function or in the constraints of the model, or comes implicitly due to the kind of vehicles used (electric, hybrid, ⋯) | This criterion ensures that the research specifically addresses sustainability aspects, which is central to our study. By including models that consider environmental or social impacts, we can better evaluate the effectiveness and practicality of various logistics solutions in promoting sustainable practices. The focus on vehicle types further emphasizes the operational choices that contribute to reduced emissions and overall environmental benefits. | |
| Exclusion | Studies in a language other than English | English is the predominant language of scientific research, ensuring a wider scope of high-quality and peer-reviewed papers. Additionally, limiting the review to English-language papers facilitates consistent and accurate analysis by all researchers involved. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
de Armas, J.; Moreno-Pérez, J.A. A Survey on Variable Neighborhood Search for Sustainable Logistics. Algorithms 2025, 18, 38. https://doi.org/10.3390/a18010038
de Armas J, Moreno-Pérez JA. A Survey on Variable Neighborhood Search for Sustainable Logistics. Algorithms. 2025; 18(1):38. https://doi.org/10.3390/a18010038
Chicago/Turabian Stylede Armas, Jesica, and José A. Moreno-Pérez. 2025. "A Survey on Variable Neighborhood Search for Sustainable Logistics" Algorithms 18, no. 1: 38. https://doi.org/10.3390/a18010038
APA Stylede Armas, J., & Moreno-Pérez, J. A. (2025). A Survey on Variable Neighborhood Search for Sustainable Logistics. Algorithms, 18(1), 38. https://doi.org/10.3390/a18010038







