Development of Optimal Size Range of Modules for Driving of Automatic Sliding Doors
Abstract
:1. Introduction
- There is no analysis of the problem of choosing an optimal size range, as a result of which the characteristic features that must be taken into account when solving it are determined.
- In a significant part of the publications, mathematical models are presented for solving mainly single-parameter problems. The use of multi-parameter models in practice is limited. This leads to the use of simplified models that do not adequately describe the real problem and, as a consequence, a decrease in the quality of the selected solutions and the need for additional costs for adjustment and corrections in their implementation, based on the intuition, experience and professional knowledge of the designer.
- Another problem is related to the insufficiently justified choice of the optimality criterion. As such, the total costs with various components included are most often used. In some works, the choice of the optimal size range is carried out based on the criterion of maximum profit for a certain period of time, but this criterion does not take into account the contradictory requirements of manufacturers and users, but only the interests of the manufacturer. A limited number of studies take into account the degree of compliance of the selected variant of the size range with the one determined by the market research, as well as the batch volume (production program) of the elements of the size range and the “time” factor when determining costs. This approach is generally correct, but determining the economic consequences of the discrepancy between demand and supply is associated with a number of difficulties and unresolved problems, which limits its application.
- In a significant part of the works, pre-defined product demand is used, and there is no information on how to determine it, while in others, a uniform distribution of demand is assumed, or it is not taken into account. In this way, it is impossible to take into account the differences in demand for individual sizes, which will inevitably affect the final solution.
- The methods for solving the problem are characterized by great diversity. In a number of cases, they are inappropriate and/or ineffective. The used method of full combination is applicable with a limited number of elements in the size ranges. The random search method reaches a solution that is close to the optimal one, but is not the optimal solution itself. Very often, this leads to the need for corrections of the selected solution and reduction in the efficiency of its implementation. In other works, classical methods of differential and variational calculus are applied, but their applicability is limited due to the special requirements for the objective function and the search function—differentiability, uniqueness of the extremum, etc. The adaptive method for constructing an optimal size range has not been widely used, since it has low convergence, and the issue of its applicability to multiparameter problems has not been clarified. In some works, the results of the application of cluster analysis and evolutionary algorithms for selecting an optimal parametric range have been shown and analyzed. Their application is difficult, since they lack an accurate formulation of the problem being solved, information about the metric used, etc. In addition, evolutionary algorithms have the disadvantage of all methods with a stochastic solution search procedure—their black-box behavior, which makes it difficult to interpret the results obtained from them. In a number of works, the determination of the optimal parametric range is carried out using the dynamic programming method. Regardless of its advantages, its effective application requires the development of recurrence relations that take into account the characteristic features of the problem being solved.
- In the known works dedicated to size range optimization, a procedure for studying the sensitivity of the optimal solution is not provided.
- Stage 1.
- Selection of basic parameters.
- Stage 2.
- Determining demand.
- Stage 3.
- Selection of optimality criterion.
- Stage 4.
- Development of a cost model.
- Stage 5.
- Building a mathematical model.
- Stage 6.
- Selection of a mathematical method.
- Stage 7.
- Algorithmic and software support.
- Stage 8.
- Solving the problem—choosing the optimal size range.
- Stage 9.
- Studying the sensitivity of the optimal solution.
2. Solving the Problem
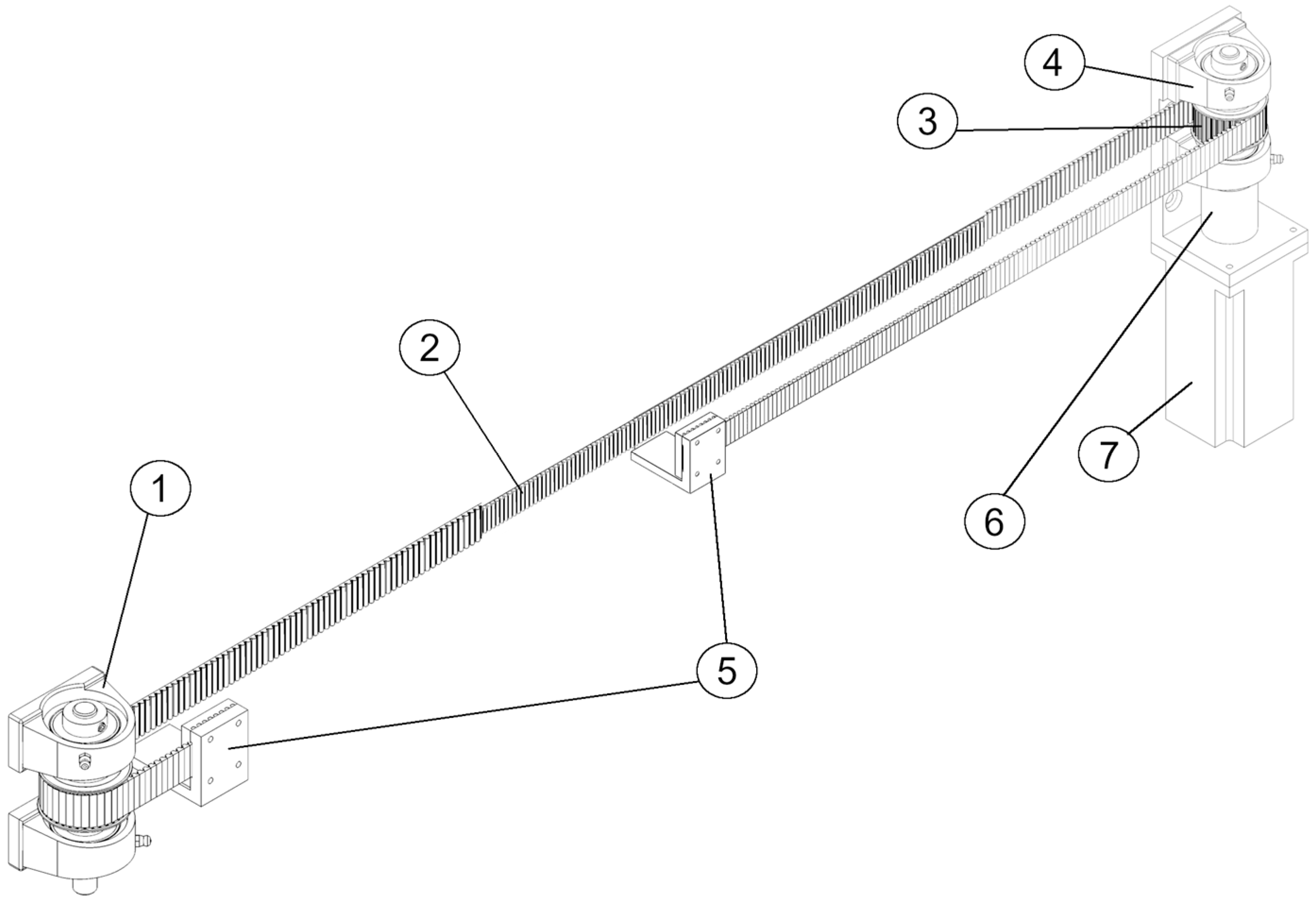
2.1. Stage 1. Selection of Basic Parameters
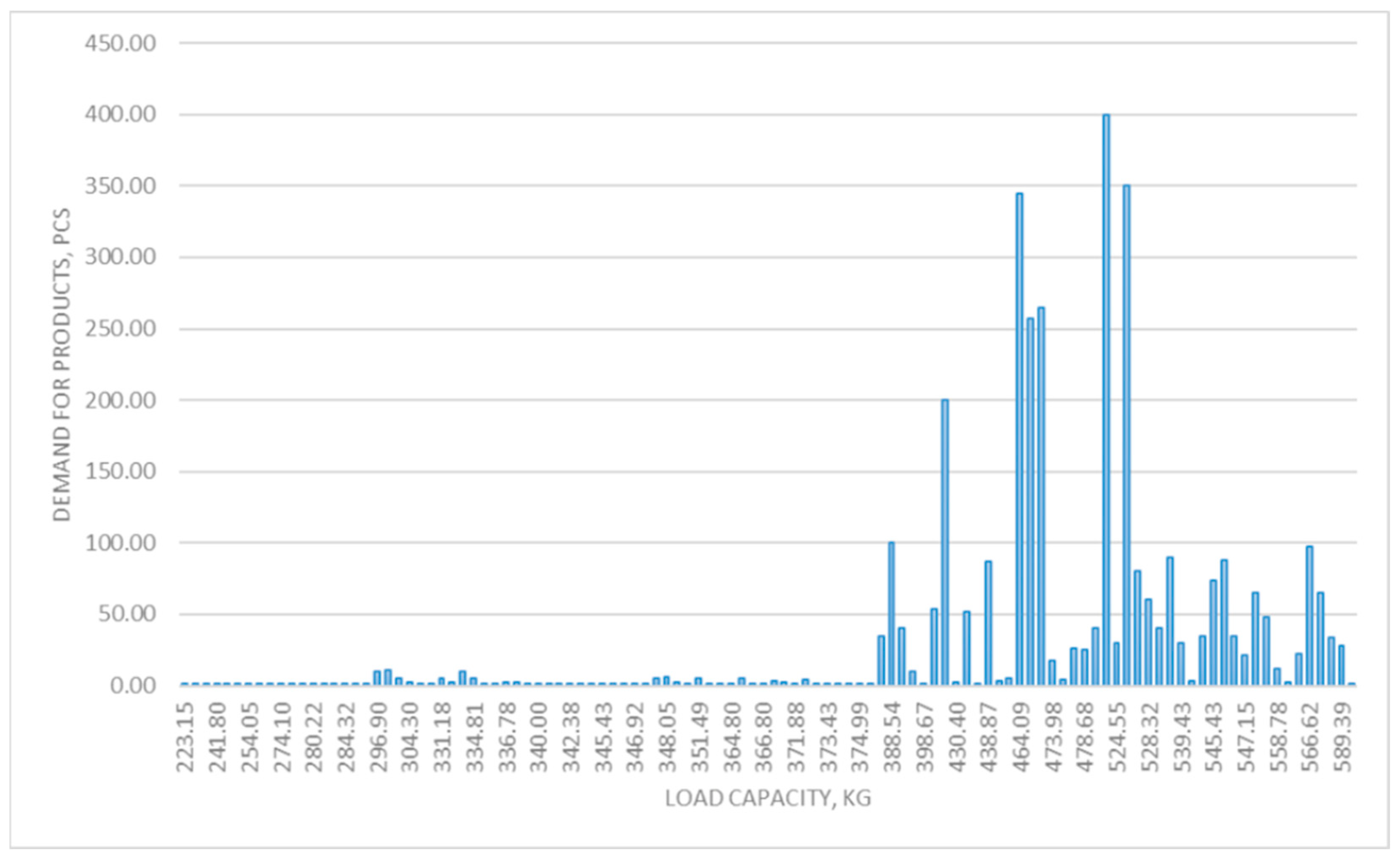
2.2. Stage 2. Determining Demand
2.3. Stage 3. Selection of Optimality Criterion
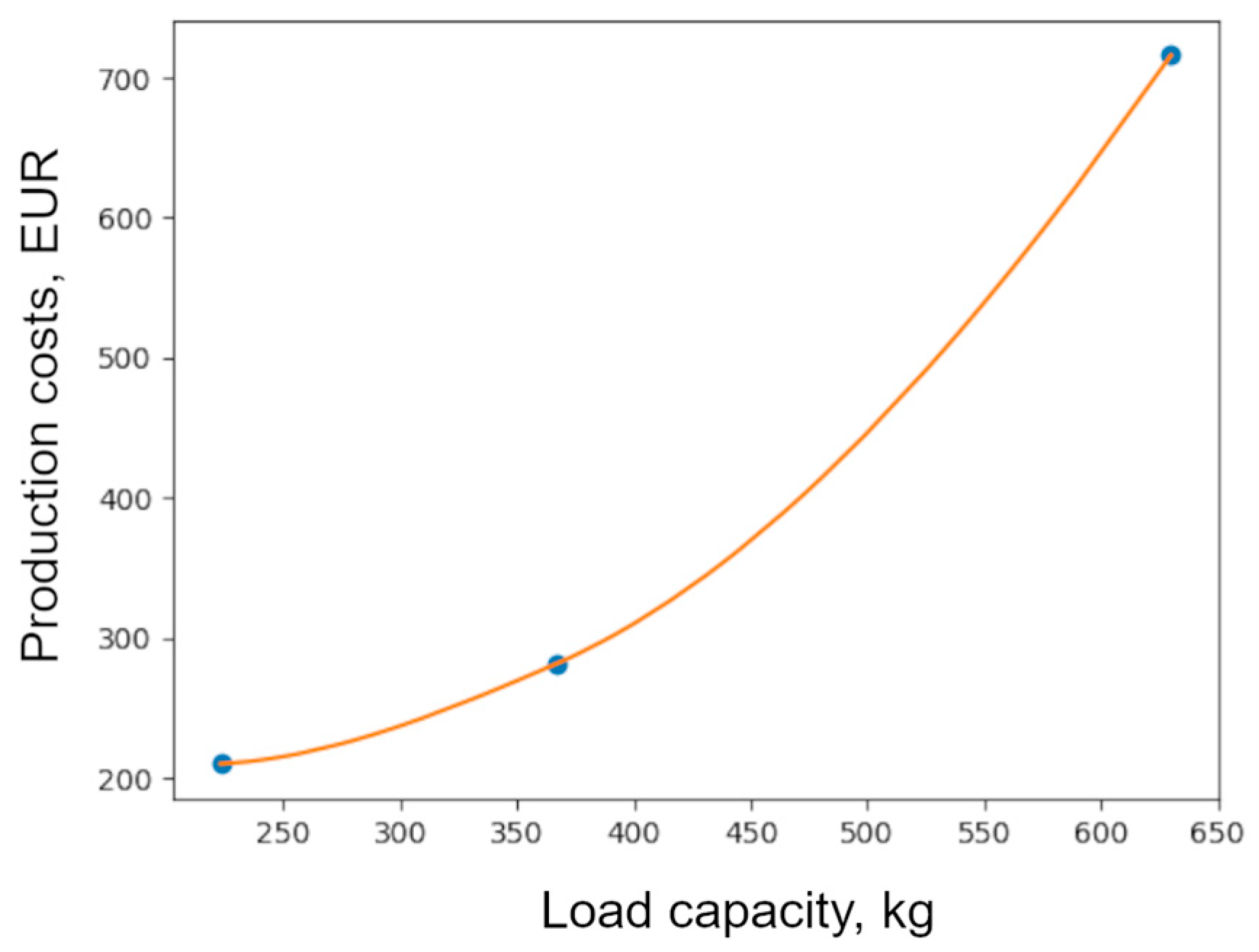
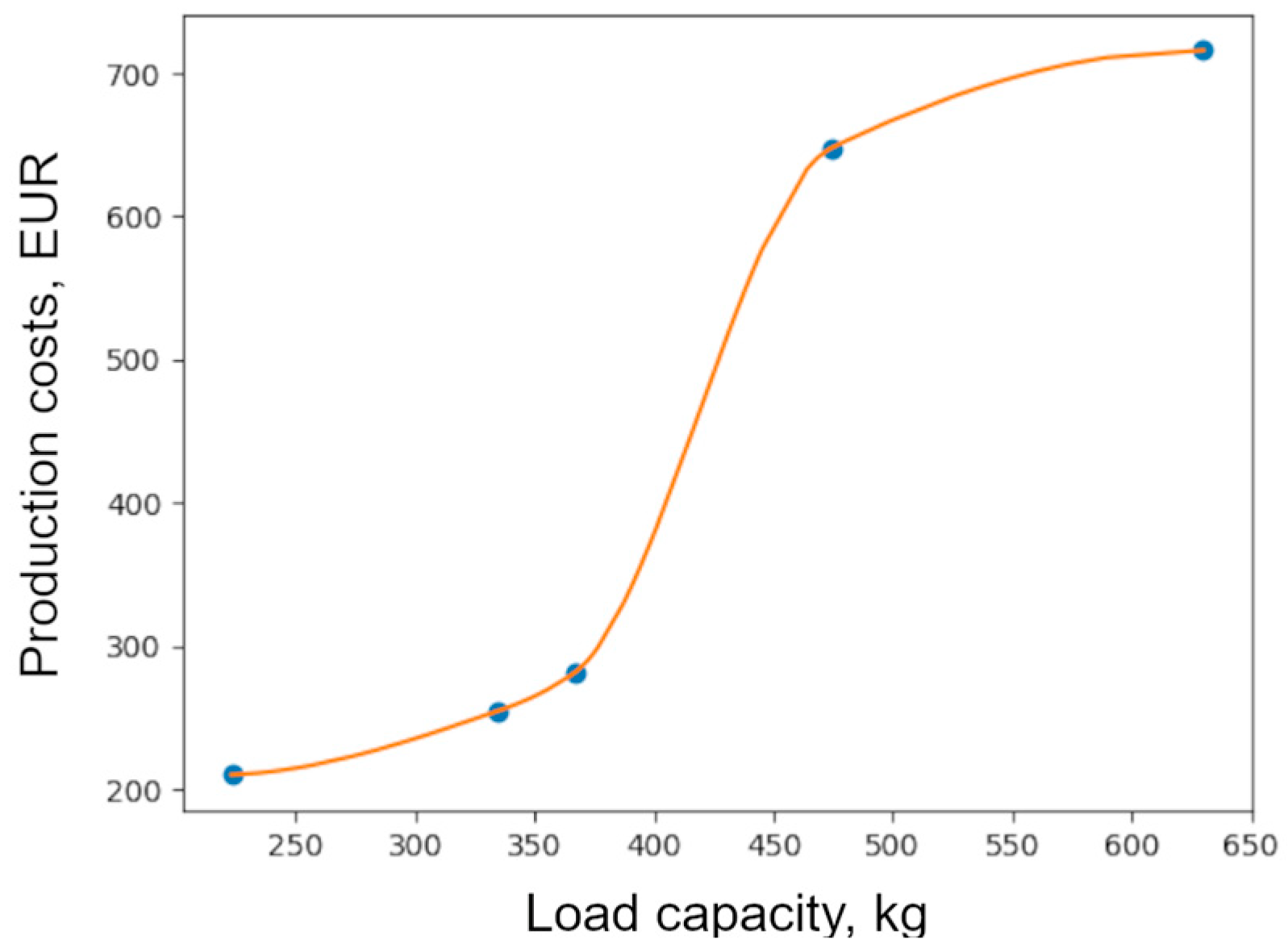
2.4. Stage 4. Development of a Cost Model
2.5. Stage 5. Building a Mathematical Model
2.6. Stage 6. Selection of a Mathematical Method
2.7. Stage 7. Algorithmic and Software Support
2.7.1. Full Combination Algorithm
2.7.2. Algorithm Implementing the Dynamic Programming Method
2.7.3. Software Applications
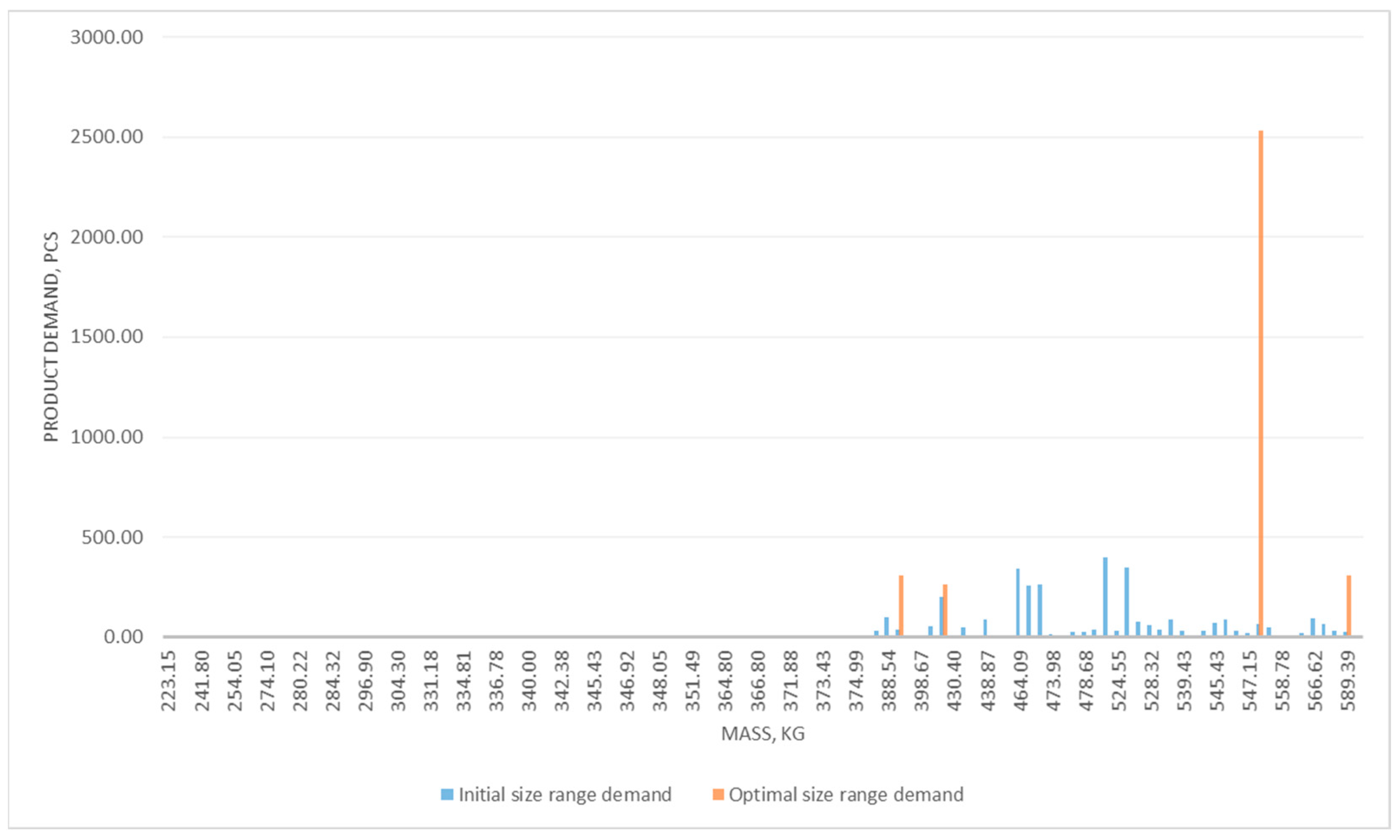
2.8. Stage 8. Solving the Problem—Choosing the Optimal Size Range
- Reduction of the number of sizes from 110 to 5, i.e., by approximately 96%;
- Reduction of total costs compared to the size range including all possible sizes by €571,317.56, or by 39.5%;
- Reduction of total costs compared to a range including only one (largest) size by 34%, which is the most common case in practice.
2.9. Stage 9. Studying the Sensitivity of the Optimal Solution
- The demand function, the coefficients taking into account the scale of production, and the learning rate must be determined as accurately as possible, since they have a significant impact on the optimal solution;
- Changing the production program does not have a significant impact on the number and type of elements in the optimal size range, as its change leads only to a change in the amount of total costs.
3. Conclusions
- The demand for modules for driving automatic sliding doors is determined as a function of their load capacity.
- A mathematical model of the problem for choosing an optimal size range is developed.
- The analytical dependence of the optimality criterion “total costs” is proposed, including the main variable production costs and additional costs in the field of operation, which take into account the discrepancy between the required and offered standard sizes.
- The functional dependence between the total costs and the influencing parameters has been determined using an established interpolation method.
- Recurrence relations for calculating the total costs based on the Bellman optimality principle have been derived.
- Algorithms and the corresponding software applications have been developed to solve the problem.
- The optimal size range of modules for driving automatic sliding doors is determined, which is characterized by a reduction in the number of elements in the initial range, determined after the market research, by 96%; a reduction in total costs compared to the initial range by 39.5%; and with the range including only the largest size, which is the most common case in practice, by 34%.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
Appendix C
Appendix C.1
| Algorithm A1: Full combination algorithm |
| Step 1. Entering input information: , , . The following sets are defined: the set , , which is used to store the indices of the current combination of elements in the currently analyzed size range; the set , which is used to calculate the element demand for the currently analyzed size range, , . Step 2. . If follows Step 3, otherwise follows Step 61. (Step 3 to Step 6—generate first combination of element indices for current size ranges containing number of elements ) Step 3. . Step 4. If follows Step 5, otherwise follows Step 7. Step 5. . Step 6. . Follows Step 4. Step 7. . (Step 8 to Step 22—calculating the demand of the elements that make up the current size range) Step 8. If follows Step 9, otherwise follows Step 19. Step 9. . Step 10. If follows Step 11, otherwise follows Step 16. Step 11. . Step 12. If follows Step 13, otherwise follows Step 15. Step 13. . Step 14. . Follows Step 12. Step 15. . Follows Step 10. Step 16. If follows Step 17, otherwise follows Step 23. Step 17. . Step 18. . Follows Step 16. Step 19. . Step 20. If follows Step 21, otherwise follows Step 23. Step 21. . Step 22. . Follows Step 20. (Step 23 to Step 26—calculation of production costs of the current size range) Step 23. , . Step 24. If follows Step 25, otherwise follows Step 27. Step 25. . Step 26. . Follows Step 24. (Step 27 to Step 37—calculation of additional costs of the current size range) Step 27. , . Step 28. If follows Step 29, otherwise follows Step 34. Step 29. . Step 30. If follows Step 31, otherwise follows Step 33. Step 31. . Step 32. . Follows Step 30. Step 33. . Follows Step 28. Step 34. . Step 35. If follows Step 36, otherwise follows Step 38. Step 36. . Step 37. . Follows Step 35. (Step 38—calculate the total cost for the current size range) Step 38. . (Step 39 to Step 41—checking for global optimum) Step 39. If follows Step 40, otherwise follows Step 41. Step 40. If follows Step 41, otherwise follows Step 42. Step 41. . The indices from the set for which is satisfied are stored in the set , which contains the indices of the elements of the optimal size range. If from previous iterations of the algorithm the set contains indices, then its elements are completely replaced by the elements , . (Step 42 to Step 44—checking for local optimum, i.e., for the set of size ranges with the same number of sizes ) Step 42. If follows Step 43, otherwise follows Step 44. Step 43. If , follows Step 44, otherwise follows Step 45. Step 44. . (Step 45 to Step 58—generate next combination of element indices for next current size range) Step 45. , . Step 46. If follows Step 47, otherwise follows Step 49. Step 47. If follows Step 49, otherwise follows Step 48. Step 48. , . Follows Step 46. Step 49. If follows Step 60, otherwise follows Step 50. Step 50. . Step 51. If follows Step 52, otherwise follows Step 55. Step 52. If follows Step 53, otherwise follows Step 54. Step 53. . Follows Step 55. Step 54. . Follows Step 51. Step 55. , . Step 56. If follows Step 57, otherwise follows Step 59. Step 57. . Step 58. , . Follows Step 56. Step 59. , . Follows Step 8. Step 60. , . At this stage in , and are recorded, respectively, the optimal value for the total costs found up to the current iteration of the algorithm, the optimal value for the total costs for size ranges with number of elements and the indices of the elements constituting the size range with total costs . Follows Step 2. Step 61. The optimum for total costs is , and the elements of the optimal size range are . End. |
Appendix C.2
| Algorithm A2: Algorithm implementing the dynamic programming method |
| Step 1. Entering input information: , , . The following matrices are defined: of the minimum costs , , and the indices of the elements (sizes) that participate in the size ranges with minimum costs , . Step 2. , . Step 3. Calculating , after which . Step 4. . If follows Step 5, otherwise return to Step 3. Step 5. . If follows Step 12, otherwise follows Step 6. Step 6. . Step 7. . Step 8. Calculating . If , then and . Step 9. . If follows Step 10, otherwise follows Step 8. Step 10. . If follows Step 11, otherwise follows Step 7. Step 11. . If follows Step 12, otherwise follows Step 6. Step 12. , , . Step 13. If , then and . Step 14. . If follows Step 15, otherwise follows Step 13. Step 15. The optimal size range having total costs , is , . The indices of its members, elements of the initial size range, are determined by the matrix , starting from the last to the first: , , where . End. |
References
- Dormakaba. Meeting All Your Access Needs; Product Brochure; Dormakaba: Rümlang, Swithzerland, 2022. [Google Scholar]
- Alumil. Available online: https://www.alumil.com/international/aluminium-systems/all-architectural-aluminium-systems/minimal-sliding-insulated-system-supreme-s650-phos (accessed on 5 March 2025).
- Record. Available online: https://record-bg.com/ (accessed on 5 March 2025).
- GEZE. Available online: https://www.geze.com/en/products-solutions/sliding_doors/automatic_sliding_doors/slimdrive/c_36770 (accessed on 5 March 2025).
- Pahl, G.; Beitz, W. Konstruktionslehre. Methoden und Anwendung; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Vietor, T.; Stechert, C. Produktarten zur Rationalisierung des Entwicklungsund Konstruktionsprozesses. In Pahl/Beitz Konstruktionslehre; Feldhusen, V.J.H., Grote, K.-H., Eds.; Springer: Berlin, Germany, 2013; pp. 817–871. [Google Scholar]
- Mueller, D. A cost calculation model for the optimal design of size ranges. J. Eng. Des. 2011, 22, 467–485. [Google Scholar] [CrossRef]
- Dashenko, A.; Belousov, A. Design of Automated Lines; Graduate School: Moscow, Russia, 1983. (In Russian) [Google Scholar]
- Zhang, M.; Tseng, M. A product and process modeling based approach to study cost implications of product variety in mass customization. IEEE Trans. Eng. Manag. 2007, 54, 130–144. [Google Scholar] [CrossRef]
- Zaharinov, V.; Malakov, I.; Hasansabri, H. Choosing of an Optimal Structural Variant of a Basic Size of a Size Range of Modules. Ann. DAAAM Proc. Int. DAAAM Symp. 2023, 34, 62–71. [Google Scholar]
- Dichev, D.; Kogia, F.; Koev, H.; Diakov, D. Method of Analysis and correction of the Error from Nonlinearity of the Measurement Instruments. J. Eng. Sci. Technol. Rev. 2016, 9, 116–121. [Google Scholar] [CrossRef]
- Dichev, D.; Zhelezarov, I.; Dicheva, R.; Diakov, D.; Nikolova, H.; Cvetanov, G. Algorithm for estimation and correction of dynamic errors. In Proceedings of the 30th International Scientific Symposium Metrology and Metrology Assurance, Sozopol, Bulgaria, 7–11 September 2020. [Google Scholar] [CrossRef]
- Kamberov, K.; Todorov, G.; Zlatev, B. Virtual Prototyping-Based Development of Stepper Motor Design. Actuators 2024, 13, 512. [Google Scholar] [CrossRef]
- Mitev, P. Development of a Training Station for the Orientation of Dice Parts with Machine Vision. Eng. Proc. 2024, 70, 57. [Google Scholar] [CrossRef]
- Nikolov, S.; Dimitrova, R.; Tsolov, S.; Dimitrov, L. Classification of Parallel Kinematics Robots. AIP Conf. Proc. 2024, 3063, 060001. [Google Scholar] [CrossRef]
- Todorov, G.; Kralov, I.; Kamberov, K.; Zahariev, E.; Sofronov, Y.; Zlatev, Z. An Assessment of the Embedding of Francis Turbines for Pumped Hydraulic Energy Storage. Water 2024, 16, 2252. [Google Scholar] [CrossRef]
- Simpson, T.W. Product platform design and customization. Artif. Intell. Eng. Des. Anal. Manuf. 2004, 18, 3–20. [Google Scholar] [CrossRef]
- Ginsburg, A.; Börjesson, F.; Erixon, G. Size ranges in modular products—A financial approach. In Proceedings of the 7th Workshop on Product Structuring–Product Platform Development, Göteborg, Sweden, 24–25 March 2004; pp. 141–150. [Google Scholar]
- Lotz, J.; Freund, T.; Würtenberger, J.; Kloberdanz, H. Uncertainty in size range development—An analysis of potential for a new scaling approach. Proc. Int. Des. Conf. 2016, 84, 341–350. [Google Scholar]
- Chaymae, B.; Abdellah, E.B. Reconfigurable Manufacturing Systems: Enhancing Efficiency via Product Family Optimization. J. Manuf. Mater. Process. 2025, 9, 39. [Google Scholar] [CrossRef]
- Cetin, O.; Saitou, K. Decomposition-based assembly synthesis for structural modularity. ASME J. Mech. Des. 2003, 126, 234–243. [Google Scholar] [CrossRef]
- Kipp, T.; Krause, D. Computer aided size range development–data mining vs. optimization. In Proceedings of the ICED 09, the 17th International Conference on Engineering Design, Vol. 4, Product and Systems Design, Palo Alto, CA, USA, 24–27 August 2009; Design Society: Glasgow, UK, 2009; pp. 179–190. [Google Scholar]
- Lotz, J. Beherrschung von Unsicherheit in der Baureihenentwicklung. Ph.D. Thesis, TU Darmstadt, Darmstadt, Germany, 2018. [Google Scholar]
- Kokkolaras, M.; Fellini, R.; Kim, H.; Michelena, N.; Papalambros, P. Extension of the target cascading formulation to the design of product families. Struct. Multidiscipilnary Optim. 2002, 24, 293–301. [Google Scholar] [CrossRef]
- Yu, T.; Yassine, A.A.; Goldberg, D.E. A Genetic Algorithm for Developing Modular Product Architectures. In Proceedings of the ASME 2003 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference. Volume 3b: 15th International Conference on Design Theory and Methodology, Chicago, IL, USA, 2–6 September 2003; pp. 515–524. [Google Scholar] [CrossRef]
- Malakov, I.; Zaharinov, V.; Tzenov, V. Size ranges optimization. Procedia Eng. 2015, 100, 791–800. [Google Scholar] [CrossRef]
- Groover, M. Automation, Production Systems and Computer-Integrated Manufacturing, 2nd ed.; Prentice Hall: Hoboken, NJ, USA, 2001; ISBN 9780130889782. [Google Scholar]
- Du, Z.; Li, J.; Li, J. Hybrid Multi-Objective Artificial Bee Colony for Flexible Assembly Job Shop with Learning Effect. Mathematics 2025, 13, 472. [Google Scholar] [CrossRef]
- Mädler Catalogue 43, Catalogue, 1 ed., Mädler. 2025. Available online: https://blaetterkatalog.maedler.de/blaetterkatalog/index.html?catalog=MAEDLER_Katalog43_EN&lang=en#page_1 (accessed on 6 April 2025).
- Exoror. Available online: https://www.exoror.com/ (accessed on 6 April 2025).
- Fritsch, F.N.; Butland, J. A method for constructing local monotone piecewise cubic interpolants. SIAM J. Sci. Comput. 1984, 5, 300–304. [Google Scholar] [CrossRef]
- Bellman, R. Dynamic Programming; Princeton University Press: New York, NY, USA, 1957. [Google Scholar]
- Zaharinov, V.; Malakov, I.; Hasansabri, H. Determining the Influence of Model Parameters on the Choosing of an Optimal Size Range of Linear Modules for Automated Sliding Doors. In Proceedings of the 2024 XXXIV International Scientific Symposium Metrology and Metrology Assurance (MMA), Sozopol, Bulgaria, 7–11 September 2024; pp. 1–6. [Google Scholar]

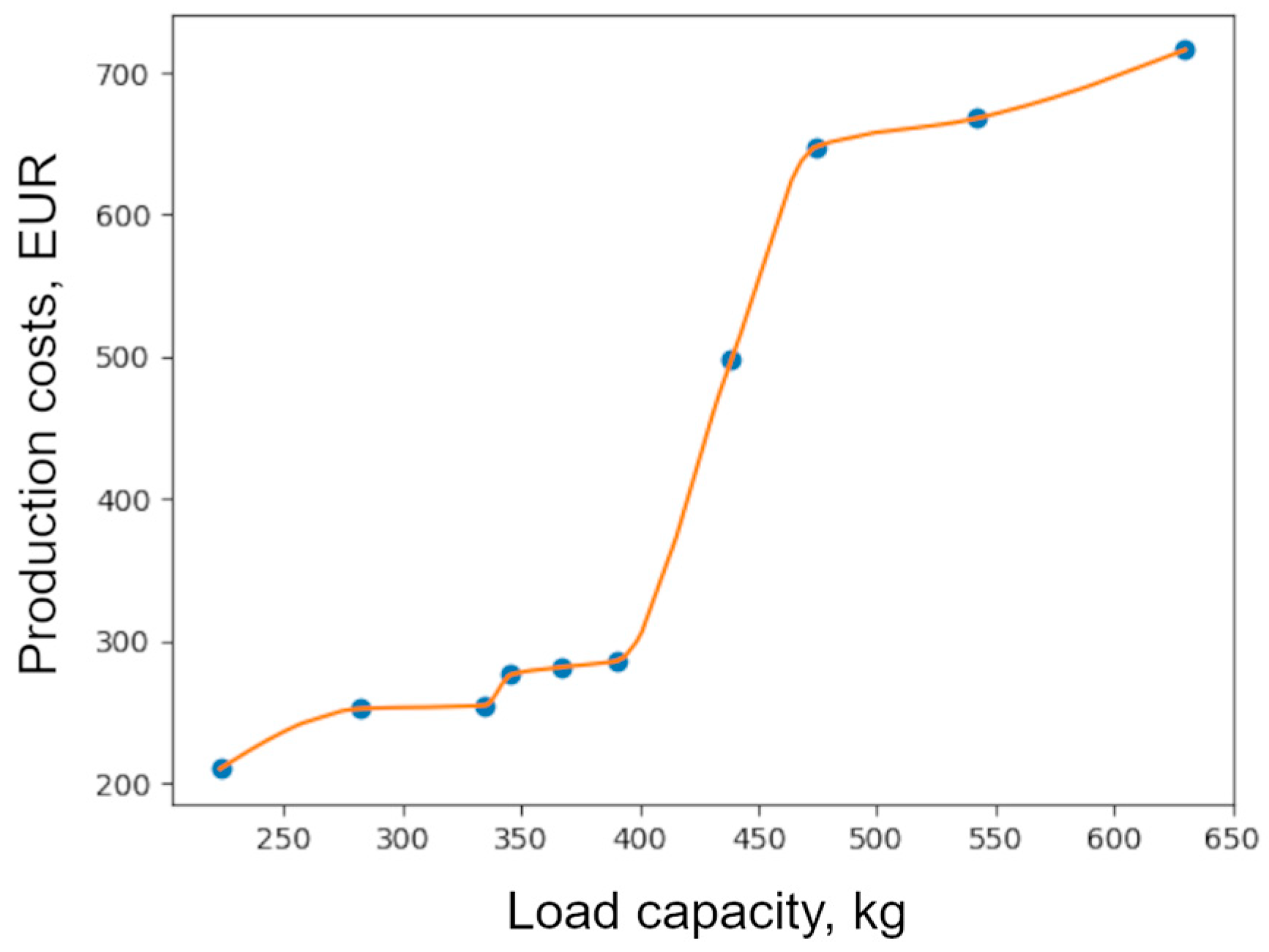
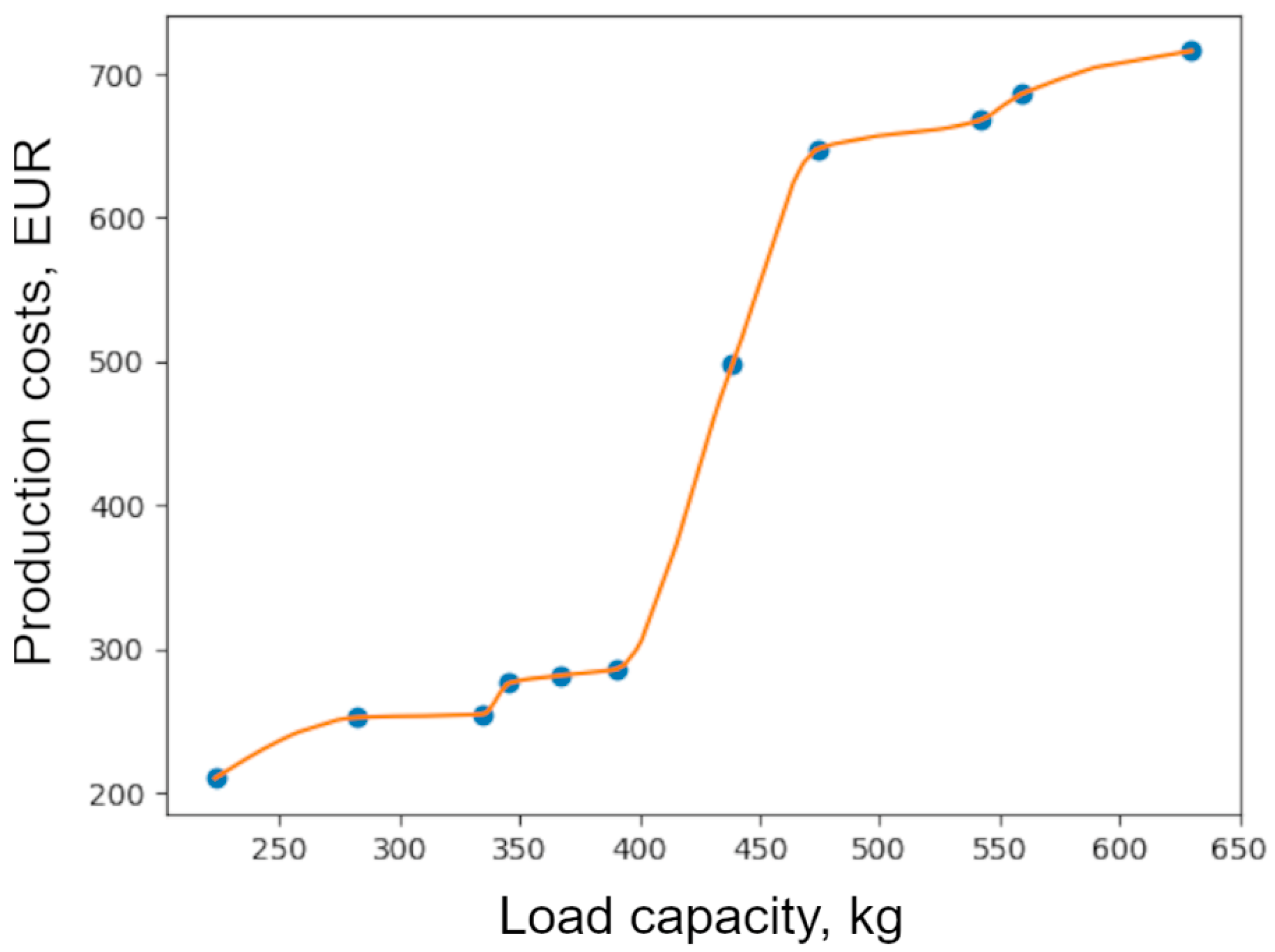
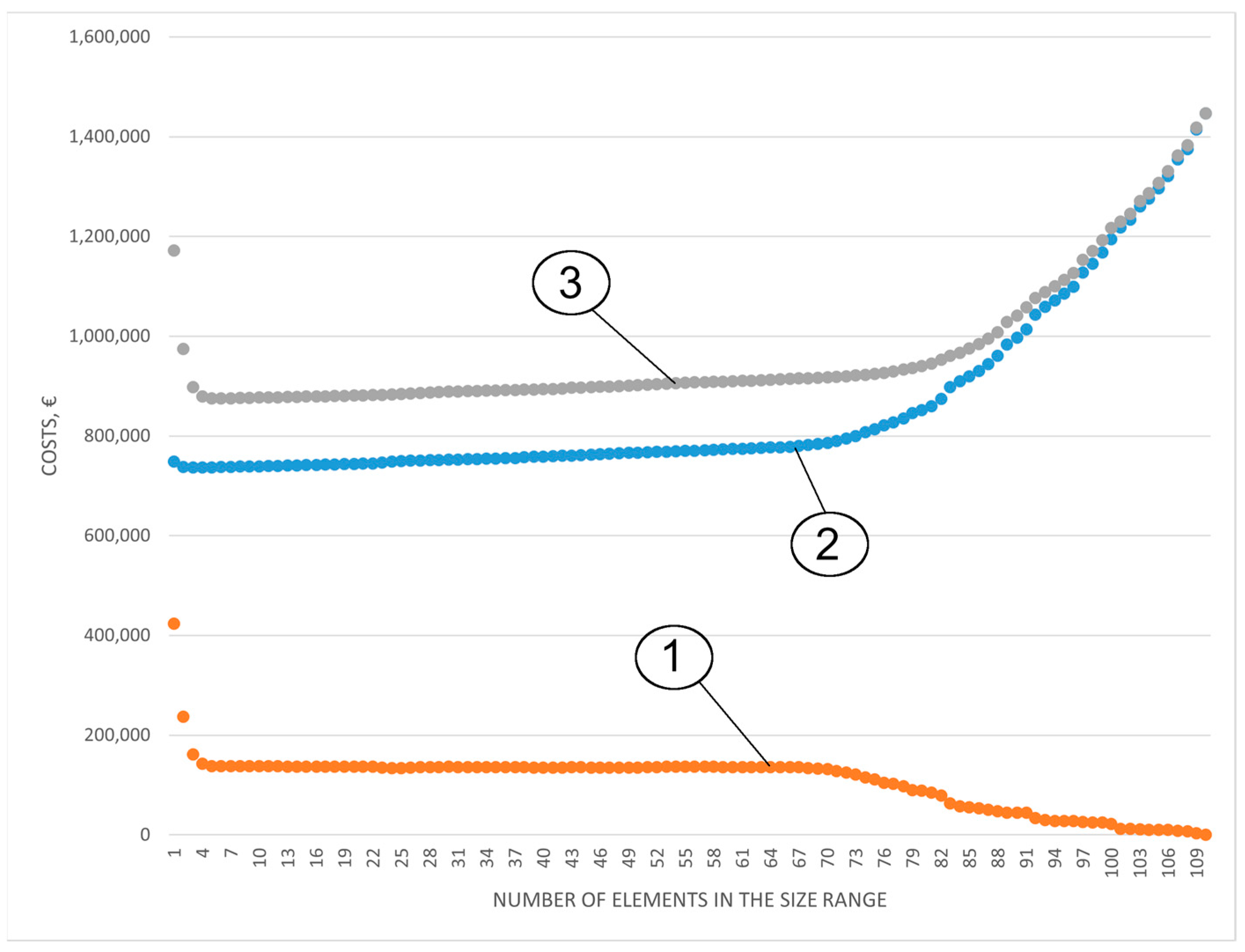
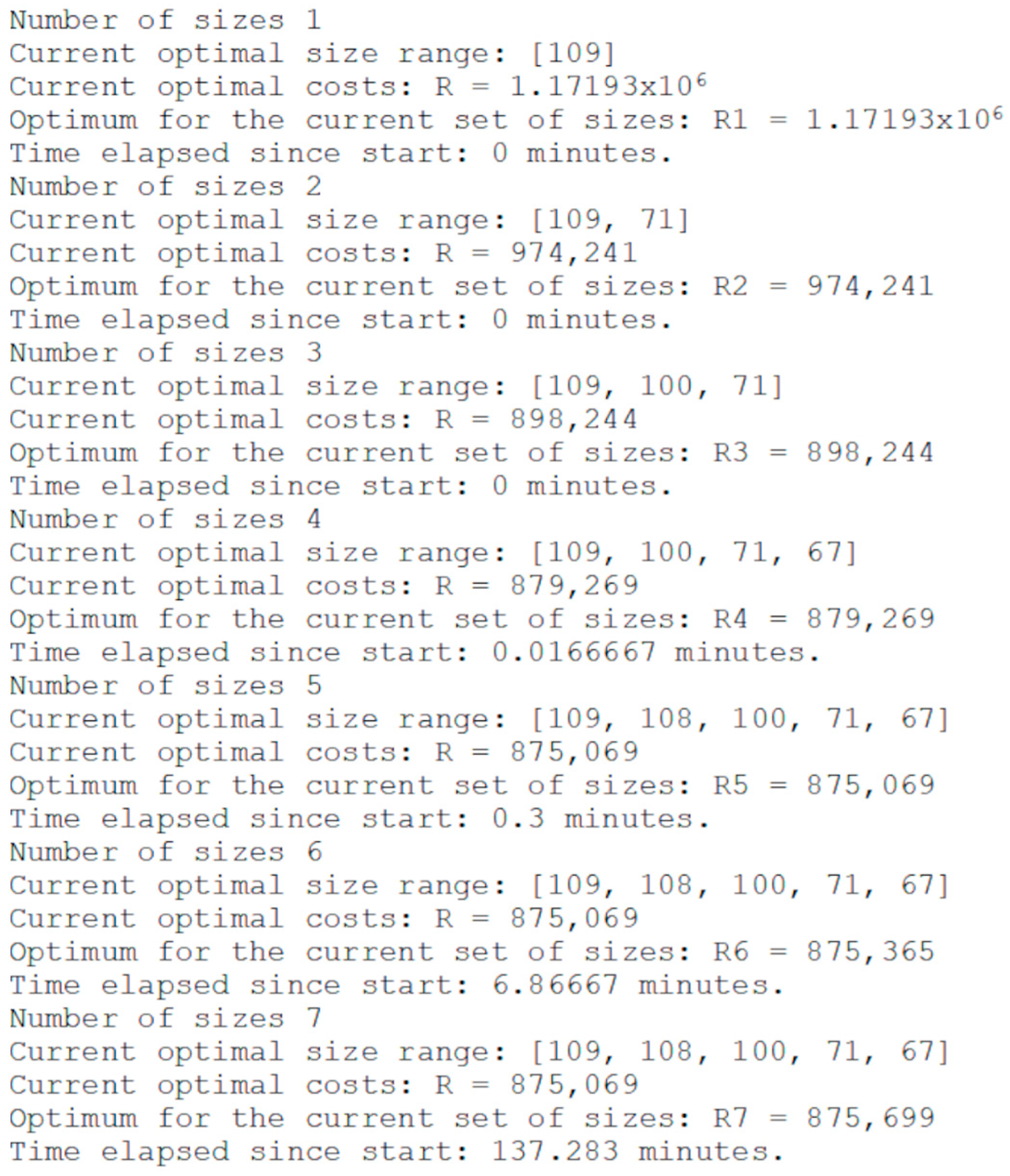

| Indicator | Optimal Size Range |
|---|---|
| , € | 875,069, 19 |
| 5 | |
| , € | 1,446,386, 75 |
| , % | 39.5% |
| No | Size | Size | Demand |
|---|---|---|---|
| 1 | |||
| 2 | |||
| 3 | |||
| 4 | |||
| 5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Malakov, I.; Zaharinov, V.; Hasansabri, H. Development of Optimal Size Range of Modules for Driving of Automatic Sliding Doors. Algorithms 2025, 18, 248. https://doi.org/10.3390/a18050248
Malakov I, Zaharinov V, Hasansabri H. Development of Optimal Size Range of Modules for Driving of Automatic Sliding Doors. Algorithms. 2025; 18(5):248. https://doi.org/10.3390/a18050248
Chicago/Turabian StyleMalakov, Ivo, Velizar Zaharinov, and Hasan Hasansabri. 2025. "Development of Optimal Size Range of Modules for Driving of Automatic Sliding Doors" Algorithms 18, no. 5: 248. https://doi.org/10.3390/a18050248
APA StyleMalakov, I., Zaharinov, V., & Hasansabri, H. (2025). Development of Optimal Size Range of Modules for Driving of Automatic Sliding Doors. Algorithms, 18(5), 248. https://doi.org/10.3390/a18050248






