A Benchmarking Algorithm to Determine Minimum Aggregation Delay for Data Gathering Trees and an Analysis of the Diameter-Aggregation Delay Tradeoff

Abstract

Aggregation delay is the minimum number of time slots required to aggregate data along the edges of a data gathering tree (DG tree) spanning all the nodes in a wireless sensor network (WSN). We propose a benchmarking algorithm to determine the minimum possible aggregation delay for DG trees in a WSN. We assume the availability of a sufficient number of unique CDMA (Code Division Multiple Access) codes for the intermediate nodes to simultaneously aggregate data from their child nodes if the latter are ready with the data. An intermediate node has to still schedule non-overlapping time slots to sequentially aggregate data from its own child nodes (one time slot per child node). We show that the minimum aggregation delay for a DG tree depends on the underlying design choices (bottleneck node-weight based or bottleneck link-weight based) behind its construction. We observe the bottleneck node-weight based DG trees incur a smaller diameter and a larger number of child nodes per intermediate node; whereas, the bottleneck link-weight based DG trees incur a larger diameter and a much lower number of child nodes per intermediate node. As a result, we observe a complex diameter-aggregation delay tradeoff for data gathering trees in WSNs.

1. Introduction

Wireless Sensor Networks (WSNs) are typically deployed for monitoring environmental data such as temperature, pressure, humidity, etc. Sensor nodes operate under limited battery charge and transmission range. Hence, the data sensed at one or more sensor nodes cannot be directly propagated to the control center (a.k.a. sink); multi-hop data propagation is the norm. Various algorithms for determining communication topologies (like cluster [1], grid [2], chain [3], connected dominating set [4], tree [5], etc.) that support the many-to-one reporting style have been proposed in the literature. Among these, the data gathering trees (DG trees) have been considered energy-efficient due to the use of the minimum number of links for data transmission and reception [5,6,7].

In this research, we focus on the delay incurred for data aggregation along the edges of a DG tree. We define the aggregation delay as the minimum number of time slots it takes for the data to be aggregated in a data gathering tree (DG tree) spanning all the nodes of the network. Various algorithms (e.g., [8,9,10,11,12,13]) have been proposed to determine the aggregation delay for DG trees and all of these assume limited availability of the communication channels and focus on scheduling the channels for the different nodes to minimize the aggregation delay. In this paper, we consider a channel availability model such that the intermediate nodes at the same level or different levels could simultaneously aggregate data from their respective child nodes using different CDMA (Code Division Multiple Access) codes [14]. An intermediate node has to schedule non-overlapping time slots (one for each of its child nodes: Time Division Multiple Access, TDMA) to aggregate data from its child nodes. Given a DG tree with sufficient availability of communication channels with unique CDMA codes, we propose a benchmarking algorithm to determine the minimum aggregation delay at every intermediate node (including the root node) of the DG tree.

We run the proposed algorithm on four broad categories of DG trees typically used for data aggregation in WSNs [5,15,16,17,18,19,20]: The Maximum Bottleneck Node Weight-based Data Gathering trees (MaxBNW-DG trees) are the ones for which the bottleneck node weight (minimum node weight) of the path from any node to the root node is the maximum; the Minimum Bottleneck Node Weight-based Data Gathering trees (MinBNW-DG trees) are the ones for which the bottleneck node weight (maximum node weight) of the path from any node to the root node is the minimum. The Maximum Bottleneck Link Weight-based Data Gathering trees (MaxBLW-DG trees) are the ones for which the bottleneck link weight (minimum link weight) of the constituent links of a path from any node to the root node is the maximum; the Minimum Bottleneck Link Weight-based Data Gathering trees (MinBLW-DG trees) are the ones for which the bottleneck link weight (maximum link weight) of the constituent links of a path from any node to the root node is the minimum. MaxBNW-DG trees could be used to determine DG trees with a larger residual energy per intermediate node such that the minimum node energy of the path from any node to the root node is the maximum (e.g., [15,16]). The MinBNW-DG trees could be used to determine DG trees in mobile sensor networks with lower velocity for the intermediate nodes such that the maximum node velocity of the path from any node to the root node is the minimum (e.g., [17]). MaxBLW-DG trees could be used to determine DG trees with a larger trust score for each link on the tree such that the minimum trust score for any of the constituent links of a path from any node to the root node is the maximum (e.g., [18]); the MinBLW-DG trees could be used to determine DG trees with maximum of the square of the link distance (measure of the transmission energy loss) for any of the constituent links for a path from any node to the root node is the minimum (e.g., [19]).

Most of the work conducted in the literature focus on deriving bounds for the aggregation delay for the data gathering trees as a function of various networking parameters (like density, diameter, node degree, etc.). To the best of our knowledge, we have not come across any work that has analyzed the aggregation delay for data gathering trees as a function of the structure of the data gathering tree itself. We hypothesize that there could be two distinct types of data gathering trees depending on the way they are constructed (bottleneck node-weight based and bottleneck link-weight based). Our hypothesis is confirmed through the simulations. We observe the bottleneck node-weight based data gathering trees to incur a smaller diameter and a larger number of child nodes per intermediate node, thereby incurring a larger aggregation delay compared to that of the bottleneck link-weight based data gathering trees that incur a relatively larger diameter and a fewer number of child nodes per intermediate node. We thus see a diameter-aggregation delay tradeoff for data gathering trees in sensor networks and this has been hitherto not reported in the literature.

The rest of the paper is organized as follows: Section 2 discusses related work on the lower and upper bounds for aggregation delay in sensor networks and highlights our contributions. Section 3 presents the system model and presents in detail the Maximum Bottleneck Node Weight-based data gathering (MaxBNW-DG) algorithm. The section also presents the modifications to the MaxBNW-DG algorithm to determine the MinBNW-DG, MaxBLW-DG and MinBLW-DG trees, as defined above. Section 4 presents in detail the algorithms to determine the diameter of the DG tree and the minimum aggregation delay for a DG tree. Section 5 presents results of simulation studies conducted on the four categories of DG trees and discusses the results obtained for the diameter, aggregation delay, hop count per path and the distribution of the child nodes per intermediate node and the leaf nodes as well analyzes the tradeoffs. Section 6 concludes the paper and discusses plans for future work.

2. Related Work and Our Contributions

In this section, we first present the existing work in the literature on algorithms related to aggregation delay for data gathering trees in sensor networks. We then motivate the need for analyzing the aggregation delay as a function of the type of the data gathering trees and thereby also exploring the diameter-aggregation delay tradeoff. Most of the work conducted in the literature focus on deriving theoretical bounds for the minimum and maximum aggregation delay as a function of the network parameters such as the number of nodes, maximum node degree, diameter of the network, transmission range of the nodes, etc., without considering the type of data gathering trees that are determined. For example, the paper [8] proposes O(∆ + D/2) as the upper bound for aggregation delay where ∆ is the maximum node degree and D is the diameter of the network (in terms of the number of hops), and in [10], the authors showed that the upper bound for aggregation latency in a multi-sink scenario is O(∆ + k*D/2), where k is the number of sinks. In [21], the authors show that the lower bound for the aggregation delay is max{D/2, ${\log }_2^n$}, where n is the number of nodes in the network. However, the aforementioned works do not analyze the possible differences in the minimum or maximum aggregation delays due to the type of the underlying data gathering trees involved.

To the best of our knowledge, ours is the first such work to show that for a given network, the minimum aggregation delay principally depends on the type of the data gathering tree (bottleneck node weight-based or bottleneck link weight-based) and could be significantly different for the two categories of data gathering trees. Likewise, the focus of tradeoff analysis has been on the aggregation delay—energy consumption tradeoff (e.g., [22,23,24]) as a function of the underlying interference models, availability of the channels and the channel scheduling schemes used. To the best of our knowledge, ours is the first such work to analyze the diameter-aggregation delay tradeoff as a function of the type of the underlying data gathering tree (bottleneck node weight-based or bottleneck link weight-based) involved.

Some of the works in the literature (e.g., [25]) focus on developing distributed algorithms to minimize the aggregation delay as much as possible (given a set of available channels). A common trend among these distributed algorithms is to first construct a spanning tree of the network based on a link or node criterion, determine a connected dominating set (CDS) [26] of the nodes (a CDS is a set of nodes such that every node in the network is either in this set or is a neighbor of the nodes in this set) in the spanning tree, form a data gathering tree of the nodes that are part of the CDS and construct a TDMA-schedule of the nodes that are part of the CDS to aggregate data according to the availability of the channels. Our approach in the paper is different. Given a graph with node weights or link weights, we directly construct a bottleneck node weight or bottleneck link weight-based data gathering tree of the network. We make use of the observation made in [27] that the intermediate nodes of a bottleneck node weight or bottleneck link weight based DG tree are also the nodes constituting a CDS constructed with the objective of optimizing the bottleneck node weight or bottleneck link weight.

Our contributions in this paper are twofold: First, we propose a benchmarking algorithm that, given a DG tree, (with sufficient number of communication channels with unique CDMA codes) determines the minimum aggregation delay at every intermediate node (including that of the root node) of the DG tree. To the best of our knowledge, we have not come across a benchmarking algorithm that gives the minimum aggregation delay for any intermediate node vis-à-vis its position in the DG tree. The aggregation delays obtained with our centralized benchmarking algorithm will serve as a lower bound for the aggregation delays determined with the distributed algorithms proposed in the literature. Second, for a given WSN graph, we observe the bottleneck link-weight based data gathering trees to incur a lower aggregation delay, but a larger diameter; on the other hand, the bottleneck node-weight based data gathering trees incur a larger aggregation delay but a smaller diameter. Ours is the first work to comprehensively analyze the diameter-aggregation delay tradeoff for sensor networks and show that the tradeoff depends on the type of the underlying data gathering trees used (bottleneck node-weight based or bottleneck link-weight based).

3. Generic Algorithm to Determine Maximum Bottleneck Node Weight-Based Data Gathering Trees

In this section, we present an algorithm to determine maximum bottleneck node weight-based data gathering trees (MaxBNW-DG trees) that could work with any notion of node weights. We then illustrate the generic nature of the algorithm by explaining how it could be easily adapted and be used for determining minimum bottleneck node weight-based data gathering trees as well as the maximum and minimum bottleneck link-weight based data gathering trees.

3.1. System Model

In this subsection, we present the graph model considered for the sensor networks, the channel availability model for the nodes and an overview of the data aggregation process. We assume a wireless sensor network (WSN) to be modeled as a weighted undirected graph G = (V, E, W_V, W_E) of a set of vertices (V) and edges (E); the link weights (W_E) may or may not be related to node weights (W_V). The link weights and node weights are positive real numbers. We assume each node in the graph has a weight; if two or more nodes have the same weight during the execution of the algorithms (described in Section 3.2, Section 3.3, Section 3.4 and Section 3.5), ties are broken arbitrarily. We do not anticipate frequently encountering ties, as the node weights (as well as link weights) are real numbers (and not integers). We use higher precisions for the real numbers (of length allowed by the programming environment) in the simulations. In addition, in the simulations, since we run multiple iterations of the algorithms for the same operating condition and average the results, our conjecture is that the arbitrary breaking of the ties is the best way to avoid any bias towards excessive usage of any particular node. For example, if the ties are broken in favor of the node with a smaller ID or larger ID, then such nodes get overused all the time in situations of a tie and the results could be biased.

Each vertex in the graph corresponds to a node in the WSN. There exists an undirected edge between two vertices if the Euclidean distance between the corresponding nodes in the network is within the transmission range of the nodes. We assume the transmission range of the nodes to be identical. A data-gathering tree (DG tree) of a WSN graph is rooted at a particular node (referred to as the leader node) and spans all the vertices of the graph and aggregation of data proceeds from the leaf nodes towards the leader node. An intermediate node waits for aggregated data or individual data (depending on the case) coming from its immediate child nodes, aggregates its own data with it and forwards the aggregated data to its own upstream node in the tree. We assume the energy level at the sensor nodes to be sufficient enough throughout the network session and that there would be no failure of nodes due to energy exhaustion (this way, we could extract the best possible and/or expected performance from the benchmarking algorithms with respect to the metrics that they are designed to optimize). We assume the sensor nodes to be both TDMA (Time Division Multiple Access) and CDMA (Code Division Multiple Access) enabled [14]. An intermediate node assigns TDMA time slots to its immediate child nodes so that they can send the aggregated data to their parent node, one at a time, without any collision. However, two intermediate nodes at the same level or different levels of the DG tree could simultaneously gather data from their respective child nodes by using different CDMA codes.

3.2. Description of the MaxBNW-DG Algorithm

The underlying theme behind the MaxBNW-DG algorithm is to give preference for nodes with larger weights to serve as intermediate nodes. The bottleneck weight of a path between two nodes is the minimum of the weights of the nodes on the path (including those of the end nodes). Each node prefers to join the DG tree through a neighbor that has the largest bottleneck weight path to the root node. The bottleneck weight of the path that connects a node to the root node of the DG tree is referred to as the Tree-join-weight. We maintain three lists during the execution of the algorithm: Candidate-Nodes-List, Optimized-Nodes-List and Parent-Node-List. The bottleneck path weights of the vertices in the Candidate-Nodes-List are referred to as the Estimated-join-weights (an estimate of the optimal bottleneck weight of the path to the root node) and when a vertex is removed from the Candidate-Nodes-List and included in the Optimized-Nodes-List, we set its Tree-join-weight to the value of the Estimated-join-weight of the vertex at the time of its removal from the Candidate-Nodes-List. The Candidate-Nodes-List is implemented as a priority queue (maximum heap) [26]. The Parent-Node-List keeps track of the predecessor node for every node in the DG tree. Algorithm 1 presents the pseudo code for the MaxBNW-DG algorithm.

Algorithm 1. Pseudo Code for the Algorithm to Determine Maximum Bottleneck Node Weight-DG Trees.
Input: Graph G = (V, E, WV, WE)
Output: $T_{Max}^{BNW}(V,E_T)$ where ET is the set of edges in the MaxBNW-DG tree
Auxiliary Variables: Optimized-Nodes-List, Candidate-Nodes-List, Parent-Node-List
Estimated-join-weight, Tree-join-weight, Leader Node
Initialization: Optimized-Nodes-List = ϕ; Candidate-Nodes-List = ϕ, Parent-Node-List = ϕ, ET = ϕ
$\forall u\in V$: Estimated-join-weight(u) = -1, Tree-join-weight(u) = -1
Begin MaxBNW-DG Algorithm
1	Leader Node s = {u | $\underset{u\in V}{Maximum}(W_V(u))$}
2	Parent-Node-List(s) = NULL
3	Candidate-Nodes-List = Candidate-Nodes-List $\cup$ {s}
4	Estimated-join-weight(s) = WV(s)
5	while (Candidate-Nodes-List ≠ ϕ) do
6	Node u = {i | $\underset{i\in Candidate-Nodes-List}{Maximum}$ (Estimated-join-weights(i)}
7	Candidate-Nodes-List = Candidate-Nodes-List - {u}
8	Optimized-Nodes-List = Optimized-Nodes-List $\cup$ {u}
9	Tree-join-weight(u) = Estimated-join-weight(u)
10	for ( Node v $\in$ Neighbors(u) AND v $\notin$ Optimized-Nodes-List) do
11	if (Estimated-join-weight(v) < Minimum(WV(v), Tree-join-weight(u) ) ) then
12	Estimated-join-weight(v) = Minimum(WV(v), Tree-join-weight(u) )
13	Parent-Node-List(v) = u
14	end if
15	end for
16	end while
17	if (Candidate-Nodes-List = ϕ AND | Optimized-Nodes-List | < | V | ) then
18	return NULL; // the graph is not connected
19	end if
20	if (Candidate-Nodes-List = ϕ AND | Optimized-Nodes-List | = | V | ) then
21	for (Node u $\in$ V AND u ≠ Leader Node ) do
22	ET = ET $\cup$ {(u, Parent-Node-List(u))}
23	end for
24	end if
25	return $T_{Max}^{BNW}(V,E_T)$
End MaxBNW-DG Algorithm

The algorithm proceeds in iterations; in each iteration, we explore the neighborhood (i.e., visit the neighbor nodes) of a vertex that currently has the largest Estimated-join-weight among the vertices in the Candidate-Nodes-List. As part of this procedure, the vertex is also removed from the Candidate-Nodes-List and added to the Optimized-Nodes-List; we say the vertex has been optimized (i.e., its Estimated-join-weight cannot be further increased) and set its Tree-join-weight to be its Estimated-join-weight value at the time of exploring its neighbors and removal from the Candidate-Nodes-List. Thus, the Optimized-Nodes-List includes vertices whose neighborhood has been already explored and the Tree-join-weight of a vertex at the time of its inclusion in the Optimized-Nodes-List is the best possible bottleneck path weight with which the node can be part of the DG tree.

The root node of the DG tree (also called the leader node) is the vertex with the largest weight among the vertices in the graph. The leader node is on the largest bottleneck weight path to itself. Initially, the leader node has an Estimated-join-weight corresponding to its individual weight and the Estimated-join-weight of the other vertices in the graph is set to −1. We start the algorithm by including the leader node as the only vertex in the Candidate-Nodes-List and explore its neighbors. In each iteration, as we explore the neighborhood of a vertex u with the largest Estimated-join-weight (that is also the Tree-join-weight for node u, pending u's removal from the Candidate-Nodes-List) among the vertices in the Candidate-Nodes-List, we examine whether the Estimated-join-weight values for each of the neighbors (say, v) of u could be improved further by making u as the parent node of v. We do this by first checking whether the currently Estimated-join-weight of node v is still less than both the individual weight of node v and the Tree-join-weight of node u, and if found so, we set the Estimated-join-weight of node v to the minimum of the individual weight of node v and the Tree-join-weight of node u as well as set node u to be the parent (predecessor) for node v in the DG tree. We continue the iterations until the Candidate-Nodes-List gets empty (by this time, all the vertices in the graph are in the Optimized-Nodes-List if the graph is connected) and every node other than the leader node would have a parent node in the tree. If the graph is not connected, the Candidate-Nodes-List gets empty when there is still at least one vertex that is not yet in the Optimized-Nodes-List; the vertices not included in the Optimized-Nodes-List are not in the same connected component of the leader node.

3.3. Modifications to the MaxBNW-DG Algorithm to Determine MinBNW-DG Tree

A MinBNW-DG tree is the one for which the bottleneck node weight on a path is defined as the maximum of the node weights (instead of the minimum of the node weights as in a MaxBNW-DG tree) and the objective would be to determine a DG tree for which the bottleneck node weight for a path from any node to the root node is the minimum. Accordingly, we start with the node having the minimum node weight and accommodate nodes in the increasing order of the Tree-join-weight; we modify the pseudo code of the MaxBNW-DG algorithm as shown in Algorithm 2: the lines that are not explicitly shown are the same as in the MaxBNW-DG algorithm.

Algorithm 2. Pseudo Code for the Algorithm to Determine Minimum Bottleneck Node Weight-DG Trees.
Input: Graph G = (V, E, WV, WE)
Output: $T_{Min}^{BNW}(V,E_T)$ where ET is the set of edges in the MaxBNW-DG tree
Auxiliary Variables: Optimized-Nodes-List, Candidate-Nodes-List, Parent-Node-List
Estimated-join-weight, Tree-join-weight, Leader Node
Initialization: Optimized-Nodes-List = ϕ; Candidate-Nodes-List = ϕ, Parent-Node-List = ϕ, ET = ϕ
$\forall u\in V$: Estimated-join-weight(u) = ∞, Tree-join-weight(u) = ∞
Begin MaxBNW-DG Algorithm
1	Leader Node s = {u | $Minimum(W_V(u))$}
2...4	(as in the pseudo code for the MaxBNW-DG algorithm, refer Algorithm 1)
5	while (Candidate-Nodes-List ≠ ϕ) do
6	Node u = {i | $\underset{i\in Candidate-Nodes-List}{Minimum}$ (Estimated-join-weights(i)}
7...8	(as in the pseudo code for the MaxBNW-DG algorithm, refer Algorithm 1)
10	for ( Node v $\in$ Neighbors(u) AND v $\notin$ Optimized-Nodes-List) do
11	if (Estimated-join-weight(v) > Maximum(WV(v), Tree-join-weight(u) ) ) then
12	Estimated-join-weight(v) = Maximum(WV(v), Tree-join-weight(u) )
13	Parent-Node-List(v) = u
14	end if
15	end for
16...24	(as in the pseudo code for the MaxBNW-DG algorithm, refer Algorithm 1)
25	return $T_{Min}^{BNW}(V,E_T)$
End MinBNW-DG Algorithm

3.4. Modifications to the MaxBNW-DG Algorithm to Determine the MaxBLW-DG Tree

A MaxBLW-DG tree is the one for which the bottleneck link weight (minimum of the weights of the constituent links) for a path from any node to the root node is the maximum. In this section, we illustrate the modification of the MaxBNW-DG algorithm to determine a MaxBLW-DG tree. Instead of starting with a node having the largest or smallest weight, we could start with an arbitrarily chosen node and set its Tree-join-weight to ∞ and initialize the Estimated-join-weights of the other vertices to −1. Assuming the graph has positive edge weights, the objective would be then to increase the Estimated-join-weights of the other vertices as much as possible and eventually join a vertex to the DG tree through an incident edge that has the largest weight (that is also the Tree-join-weight of the vertex). We modify the pseudo code of the MaxBNW-DG algorithm as in Algorithm 3 to obtain the MaxBLW-DG tree.

Algorithm 3. Pseudo Code for the Algorithm to Determine Minimum Bottleneck Node Weight-DG Trees.
Input: Graph G = (V, E, WV, WE)
Output: $T_{Max}^{BLW}(V,E_T)$ where ET is the set of edges in the MaxBNW-DG tree
Auxiliary Variables: Optimized-Nodes-List, Candidate-Nodes-List, Parent-Node-List
Estimated-join-weight, Tree-join-weight, Leader Node
Initialization: Optimized-Nodes-List = ϕ; Candidate-Nodes-List = ϕ, Parent-Node-List = ϕ, ET = ϕ
$\forall u\in V$: Estimated-join-weight(u) = -1, Tree-join-weight(u) = -1
Begin MaxBNW-DG Algorithm
1	Leader Node s is arbitrarily chosen among the vertices in V
2...3	(as in the pseudo code for the MaxBNW-DG algorithm, refer Algorithm 1)
4	Estimated-join-weight(s) = ∞
5	while (Candidate-Nodes-List ≠ ϕ) do
6	Node u = {i | $\underset{i\in Candidate-Nodes-List}{Maximum}$ (Estimated-join-weights(i)}
7...9	(as in the pseudo code for the MaxBNW-DG algorithm, refer Algorithm 1)
10	for ( Node v $\in$ Neighbors(u) AND v $\notin$ Optimized-Nodes-List) do
11	if (Estimated-join-weight(v) < WE(u-v)) then
12	Estimated-join-weight(v) = WE(u-v)
13	Parent-Node-List(v) = u
14	end if
15	end for
16...24	(as in the pseudo code for the MaxBNW-DG algorithm, refer Algorithm 1)
25	return $T_{Max}^{BLW}(V,E_T)$
End MaxBNW-DG Algorithm

3.5. Modifications to the MaxBNW-DG Algorithm to Determine the MinBLW-DG Tree

For a MinBLW-DG tree, we define the bottleneck link weight for a path as the maximum of the weights of the constituent links of the path. The objective would be then to determine a DG tree for which the bottleneck link weight for a path from any node to the root node of the MinBLW-DG tree is the minimum. Accordingly, we start with an arbitrarily chosen node as the root node of the MinBLW-DG tree and set its Tree-join-weight to −∞ and initialize the Estimated-join-weight for every other vertex to ∞. In each iteration of the algorithm, we attempt to decrease the Estimated-join-weight of the vertices as much as possible and eventually join a vertex to the MinBLW-DG tree through an incident edge that has the smallest weight (that also becomes the Tree-join-weight of the vertex). Algorithm 4 illustrates modifications to the pseudo code of the MaxBNW-DG algorithm to determine the MinBLW-DG trees.

Algorithm 4. Pseudo Code for the Algorithm to Determine Minimum Bottleneck Node Weight-DG Trees.
Input: Graph G = (V, E, WV, WE)
Output: $T_{Min}^{BLW}(V,E_T)$ where ET is the set of edges in the MinBNW-DG tree
Auxiliary Variables: Optimized-Nodes-List, Candidate-Nodes-List, Parent-Node-List
Estimated-join-weight, Tree-join-weight, Leader Node
Initialization: Optimized-Nodes-List = ϕ; Candidate-Nodes-List = ϕ, Parent-Node-List = ϕ, ET = ϕ
$\forall u\in V$: Estimated-join-weight(u) = ∞, Tree-join-weight(u) = ∞
Begin MinBNW-DG Algorithm
1	Leader Node s is arbitrarily chosen among the vertices in V
2...3	(as in the pseudo code for the MaxBNW-DG algorithm, refer Algorithm 1)
4	Estimated-join-weight(s) = -∞
5	while (Candidate-Nodes-List ≠ ϕ) do
6	Node u = {i | $\underset{i\in Candidate-Nodes-List}{Minimum}$ (Estimated-join-weights(i)}
7...9	(as in the pseudo code for the MaxBNW-DG algorithm, refer Algorithm 1)
10	for ( Node v $\in$ Neighbors(u) AND v $\notin$ Optimized-Nodes-List) do
11	if (Estimated-join-weight(v) > WE(u-v)) then
12	Estimated-join-weight(v) = WE(u-v)
13	Parent-Node-List(v) = u
14	end if
15	end for
16...24	(as in the pseudo code for the MaxBNW-DG algorithm, refer Algorithm 1)
25	return $T_{Min}^{BLW}(V,E_T)$
End MaxBNW-DG Algorithm

4. Algorithms to Determine the Diameter of the DG Tree and Minimum Delay for Data Aggregation

In this section, we describe algorithms to determine the diameter of a data gathering (DG) tree and the minimum delay for data aggregation spanning across all the nodes of the DG tree. We also discuss the time complexity of the benchmarking algorithm to determine minimum aggregation delay as well as present its proof of correctness. Finally, we illustrate examples to compute the minimum aggregation delay and illustrate the relationship between aggregation delay and metrics such as the tree diameter and the number of child nodes per intermediate node (further analyzed through simulations, Section 5).

The diameter of a DG tree (also referred to as the height of the tree) is the maximum distance from any leaf node to the root of the tree [26]. We first identify the level of each node in the DG tree, with the root node (leader node) set to be at level 0, its immediate child nodes at level 1 and so on. Two intermediate nodes at a particular level or different levels can simultaneously communicate with their respective child nodes at the same time using different CDMA (Code Division Multiple Access) codes [14] to avoid any interference. An intermediate node could only communicate sequentially with its immediate downstream nodes using TDMA (Time Division Multiple Access) time slots (one data aggregation per time unit).

4.1. Algorithm to Determine Diameter of a Data Gathering Tree

In this subsection; we present an algorithm (see Algorithm 5 for the pseudo code) to compute the diameter of a data gathering tree; using the MaxBNW-DG tree as reference. The algorithm can be used to determine the diameter of any DG tree rooted at a particular node. We perform Breadth First Search (BFS) [26] on the edges of the DG tree to determine the diameter of the tree as well as the level (distance) of the vertices from the root node of the tree. As part of this procedure; we use the auxiliary variables; Neighbor-List storing the neighbors of each of the vertices in the DG tree; Nodes-Explored storing the list of nodes whose neighborhood is already explored as part of BFS; Candidate-Nodes-List containing the list of nodes (maintained in a First-in First-out basis; the front vertex in the list is extracted using a dequeue operation) that are visited while exploring the neighborhood of some other vertices; but their own neighborhood is not yet explored; and Node-Level that stores the level (distance) of a node from the root node of the DG tree. In addition to the Diameter of the DG tree; the algorithm outputs the Child-Nodes-List that contains the list of child nodes (if any) for each node in the DG tree and a two-dimensional data structure referred to as Nodes-At-Levels that stores a list of nodes at each level of the DG tree. The Node-Level for the root node/leader node is 0. In each iteration of the BFS algorithm, we remove (dequeue) the vertex in the front of the Candidate-Nodes-List and add it to the Nodes-Explored list as well as explore its neighbors. If a neighbor node v that has not been visited (explored) so far is visited for the first time as part of the exploration of the neighborhood of a node u; we add node v to the Candidate-Nodes-List and Nodes-Explored list as well as set Node-Level[v] = Node-Level[u] + 1 and set node u to be the parent node for node v in the DG tree. We also add node v to the list of nodes at level Node-Level[v]. If the value for Node-Level[v] is greater than the currently known diameter of the DG tree; we set the diameter of the tree to Node-Level[v]; implying we have found a node that is farther away from the leader node of the DG tree. The complexity of the algorithm to determine the diameter of a DG tree is the complexity incurred with running the BFS algorithm on the |V| − 1 edges of the DG tree spanning over all the |V| vertices of the graph. Hence; the time complexity of the algorithm to determine the diameter of a DG tree is Θ (|V|).

4.2. Algorithm to Determine the Minimum Aggregation Delay of a Data Gathering Tree

In this subsection, we present the benchmarking algorithm to determine the minimum aggregation delay for a data gathering tree. Algorithm 6 presents the pseudo code that makes use of the diameter of the DG tree and the list of nodes at various levels of the tree to determine the delay for data aggregation. An intermediate node cannot forward an aggregated data to its upstream node unless it gets the aggregated data from all its immediate downstream child nodes. We assume it takes one time unit for a child node to send aggregated data to its parent node. We assume the leaf nodes of the DG tree (at all the levels) to have data readily available at time unit 0 (hence, the delay at any leaf node is 0). The delay at an intermediate node u, Delay[u], is iteratively computed over all its child nodes as shown in lines 6–8 of Algorithm 6 and explained here: We first sort the delays of the child nodes of u and maintain Sorted-Delay-Child-Nodes[u]. We maintain a temporary estimate of the delay (initialized to zero) at the intermediate node u using a running variable Temp-Delay[u] that is incremented as follows for each child node of u considered in the increasing order of their delays: For a child node v $\in$ Child-Nodes-List[u], Temp-Delay[u] = Maximum(Temp-Delay[u] + 1, Delay[v] + 1), as we assume it takes one time unit for data to reach from a child node to the immediate parent node. The increment of the Temp-Delay[u] by 1 within the Maximum function takes into consideration scenarios when the delay at the child node v would be smaller than the Temp-Delay already computed at the parent node u due to data aggregation delays involving the siblings of node v (i.e., the other child nodes of node u). The delay associated with an intermediate node u, Delay[u], is the final value of Temp-Delay[u] after going through the delay-based sorted list of the child nodes of u. The above procedure is repeated at all the intermediate nodes, including the leader node. The aggregation delay at the leader node is considered to be the aggregation delay of the entire DG tree. The overall time complexity of the algorithm to compute the aggregation delay of a DG tree is dominated by the time incurred to sort the delays of the child nodes of the intermediate nodes at the different levels.

Algorithm 5. Pseudo Code for an Algorithm to Determine the Diameter of a Data Gathering Tree.
Input: DG Tree $T_{Max}^{BNW}(V,E_T)$, Leader Node s
Output: Diameter, Nodes-At-Levels, Child-Nodes-List
Auxiliary Variables: Nodes-Explored; Candidate-Nodes-List, Child-Nodes-List;
Neighbor-List; Node-Level
Initialization: $\forall i\in V$: Neighbor-List[i] = ϕ, Node-Level[i] = 0; Child-Nodes-List[i] = ϕ
Nodes-At-Levels = ϕ; Diameter = 0; Nodes-Explored = ϕ; Candidate-Nodes-List = ϕ
Begin Algorithm Diameter-DG Tree
1	for (edge (u, v) $\in$ ET) do
2	Neighbor-List[u] = Neighbor-List[u] $\cup$ {v}
3	Neighbor-List[v] = Neighbor-List[v] $\cup$ {u}
4	end for
5	Candidate-Nodes-List = {s}
6	Node-Level[s] = 0
7	Nodes-At-Levels[0].add({s}) // adds the leader node s to the list of nodes at level 0
8	Nodes-Explored = Nodes-Explored $\cup$ {s}
9	while (Candidate-Nodes-List ≠ ϕ) do
10	Node u = Dequeue(Candidate-Nodes-List) // removes u from Candidate-Nodes-List
11	for ( Node v $\in$ Neighbor-List(u) AND v $\notin$ Nodes-Explored) do
12	Node-Level[v] = Node-Level[u] + 1
13	Nodes-At-Levels[Node-Level[v]].add({v})
14	Child-Nodes-List(u) = Child-Nodes-List(u) $\cup$ {v}
15	Nodes-Explored = Nodes-Explored $\cup$ {v}
16	Candidate-Nodes-List = Candidate-Nodes-List $\cup$ {v}
17	if (Diameter < Node-Level[v]) then
18	Diameter = Node-Level[v]
19	end if
20	end for
21	end while
22	return Diameter, Nodes-At-Levels, Child-Nodes-List
End Algorithm Diameter-DG Tree

4.3. Time Complexity and Proof of Correctness

In this subsection, we discuss the time complexity and proof of correctness for the benchmarking algorithm to determine minimum aggregation delay of a data gathering tree. In the worst case, an intermediate node could have the rest of the nodes as its child nodes and it would take Θ(|V|*log|V|) time to sort the delays of the |V|−1 child nodes. To calculate the Temp-Delay values and the delay at each of the nodes, we spend one time unit for each edge at its upstream node. Hence, the overall time complexity of the algorithm to compute the aggregation delay of the DG tree is Θ(|V|*log|V|).

The proof of correctness of the algorithm to determine the minimum aggregation delay for a DG tree simply follows from line 7 of the pseudo code (see Algorithm 6): For every intermediate node u, the estimate of the delay in each iteration of the loop (lines 6–8) while aggregating data received from a child node v is the maximum of the two values: one more than the current estimate of the delay at node u and one more than the aggregation delay at node v. The increment by one for both the parameters of the maximum function is the minimum possible increment that can be assigned to transmit data on a link. An intermediate node has to merely wait for data if none of its child nodes are ready with the data. However, if all the child nodes are ready with the data, the intermediate node aggregates data at a rate of just spending one additional time unit per child node.

Algorithm 6. Pseudo Code for an Algorithm to Determine the Minimum Aggregation Delay of a Data Gathering Tree.
Input: Diameter, Nodes-At-Levels, Child-Nodes-List, Leader Node s
Output: Delay[s]
Auxiliary Variables: Temp-Delay; Sorted-Delay-Child-Nodes
Initialization: $\forall i\in V$: Delay[i] = 0, Temp-Delay[i] = 0, Sorted-Delay-Child-Nodes[i] = ϕ
Begin Algorithm Aggregation-Delay-DG Tree
1	for (Node-level = Diameter to 0) do
2	for (Node u $\in$ Nodes-At-Levels.get(Node-level) ) do
3	for (Node v $\in$ Child-Nodes-List[u]) do
4	Insert (v, Delay[v]) at appropriate entry in Sorted-Delay-Child-Nodes[u]
5	end for
6	for (tuple (v, Delay[v]) in Sorted-Delay-Child-Nodes[u]) do
7	Temp-Delay[u] = Maximum(Temp-Delay[u] + 1, Delay[v] + 1)
8	end for
9	Delay[u] = Temp-Delay[u]
10	end for
11	end for
12	return Delay[s]End Algorithm Aggregation-Delay-DG Tree

4.4. Examples to Compute the Minimum Aggregation Delay of Data Gathering Trees

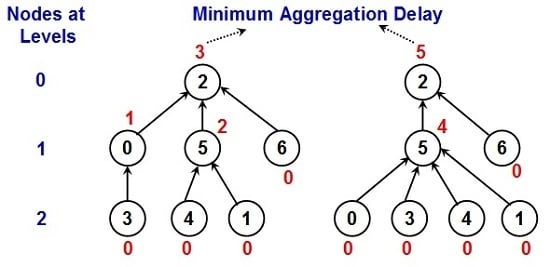
Figure 1 illustrates examples to compute the minimum aggregation delay of two different data gathering trees that have the same diameter. In both the examples, the number inside the circle indicates the node ID and the number outside the circle indicates the minimum aggregation delay for the node. DG trees that have a larger fraction of leaf nodes (and hence fewer intermediate nodes) are more likely to have a larger number of child nodes per intermediate node. For such DG trees, it would take relatively more time slots for an intermediate node to sequentially aggregate data from its child nodes (especially for intermediate nodes at higher levels), resulting in a larger aggregation delay at the leader node. Hence, even if two DG trees have the same diameter (as shown in Figure 1), it could take a relatively longer time to aggregate data from the DG tree that has a larger number of child nodes per intermediate node. This is the trend of performance that is also observed with the DG trees in the simulations, especially for networks of high–very high node density.

Figure 1. Examples to Determine the Minimum Aggregation Delay for a Data Gathering Tree.

Figure 1. Examples to Determine the Minimum Aggregation Delay for a Data Gathering Tree.

5. Simulations

In this section, we present the simulation environment and examine the results of the simulation study conducted on the four categories of data gathering trees with respect to five performance metrics (see Section 5.1 for the list of metrics), including the aggregation delay-the primary metric of interest in this paper. We evaluate results of statistical tests conducted on the values obtained for the performance metrics and arrive at significant conclusions. We explore the contributions of the other four performance metrics for minimizing the aggregation delay as well as analyze the performance tradeoffs. We also calculate the margin of error values for the minimum aggregation delay (confidence interval: 95%). Finally, we discuss the impact of the algorithm design choices on the structure of the two categories of data gathering trees (bottleneck node-weight based and bottleneck link-weight based trees) and their performance.

We conduct simulations in a discrete-event simulator implemented in Java. We implemented the algorithms to determine the four types of data gathering trees (MaxBNW-DG, MinBNW-DG, MaxBLW-DG and MinBLW-DG trees) described in Section 3 and the algorithms to determine the diameter and minimum aggregation delay for data gathering trees described in Section 4. We conducted the simulations with networks of 50 nodes and 100 nodes, with the transmission ranges of the nodes varied from 25 m to 50 m, in increments of 5 m. The network dimensions are 100 m × 100 m. These are the usual parameters considered for simulation in sensor networks (e.g., refer [1,3,5,6,8]). The average number of neighbors per node is given by πR²/A, where R is the transmission range and A is the network area. We consider the 50-node network to be of moderate to high node density (20 to 40 neighbors per node on average) and the 100-node network to be of high to very high node density (40 to 80 neighbors per node on average).

We assume an ideal medium access control (MAC) channel protocol [28] for the underlying wireless channel (i.e., there are no collisions during channel access). We also assume the number of unique CDMA codes to be sufficient enough for the intermediate nodes at the same level or different levels to simultaneously aggregate data from their respective child nodes, if the latter are ready with the data. Such idealistic assumptions have been successfully applied in the literature for wireless ad hoc networks and sensor networks (e.g., [29,30,31,32,33]) to extract optimal performance from the benchmarking algorithms run in the higher layers and to delineate the effects of the design choices.

Figure 2. Performance of the Max/Min Bottleneck Node Weight and Link Weight-based DG Trees.

Figure 2. Performance of the Max/Min Bottleneck Node Weight and Link Weight-based DG Trees.

The weights for the edges are uniform-randomly assigned in the range [0...1] and the weights for the nodes are also uniform-randomly assigned in the range [0...1]; the node weights are independent of the link weights. We generate 200 snapshots of the network graphs for each combination of the number of nodes and the transmission range per node and run the algorithms to determine the four DG trees on each of these graph snapshots and average the results (shown in Figure 2). Section 5.4 discusses about the margin of error values for the minimum aggregation delay (confidence interval is 95%).

5.1. Performance Metrics

In this subsection, we introduce the performance metrics that are measured in the simulations. The performance metrics measured are as follows:

(i)

Diameter of the DG Tree—The maximum distance (number of hops) from any leaf node to the root node of the DG tree.

(ii)

Minimum Aggregation Delay—The minimum number of time slots it takes for the data to get aggregated, starting from the leaf nodes and propagating to the root node of the DG tree

(iii)

Hop Count per Path—The average of the number of hops per path from every node (other than the root node) to the root node of the DG tree.

(iv)

Number of Child Nodes per Intermediate Node—The average of the number of immediate child nodes per intermediate node, considered across all the intermediate nodes (including the root node) of the DG tree.

(v)

Fraction of Nodes as Leaf Nodes—The ratio of the total number of leaf nodes (nodes without any child nodes) at all levels divided by the total number of nodes in the network.

5.2. MaxBNW-DG Trees vs. MinBNW-DG Trees and MaxBLW-DG Trees vs. MinBLW-DG Trees

A significant result from the simulations is that the performance of the MaxBNW-DG trees is almost the same as that of the MinBNW-DG trees with respect to all the metrics; and likewise, the performance of the MaxBLW-DG trees is the same as that of the MinBLW-DG trees with respect to all the metrics. This could be observed from the results displayed in Figure 2 for all the metrics. The vertical bars for the MaxBNW-DG trees (■) and MinBNW-DG trees ( ) are almost the same height for each of the performance metrics with respect to any operating condition, and this could be also confirmed on the basis of the magnitude of the average values for the performance metrics listed on the top of the bars. Likewise, the vertical bars for the MaxBLW-DG trees ( ) and MinBLW-DG trees ( ) are almost the same height for each performance metric with respect to any operating condition, and this is further confirmed on the basis of the magnitude of the average values for the performance metrics listed on the top of the bars. We also further confirm our assertion through statistical tests. For any performance metric under a particular operating condition, the ratios for the median and maximum absolute difference in the average values incurred for the MaxBNW-DG trees and MinBNW-DG trees (as well as for the MaxBLW-DG trees and MinBLW-DG trees) to that of the average values incurred for each of these trees is not more than 0.008 and 0.06 respectively. Hence, we hereafter discuss simply on the basis of bottleneck node-weight based DG trees vs. bottleneck link-weight based DG trees.

5.3. Discussion of the Results

In this subsection, we discuss the results for the two categories of data gathering trees with respect to each of the performance metrics and explore the dependence of the aggregation delay on metrics such as the diameter, number of child nodes per intermediate node and the fraction of nodes as leaf nodes. We also discuss the impact of node density on the performance of the two data gathering trees. To begin with, we observe the diameter of the bottleneck node-weight based DG trees to be significantly smaller than the diameter of the bottleneck link-weight based DG trees. The diameter of the bottleneck link-weight based DG trees is about 100–270% larger (for networks of moderate-high node density) and 120%–370% larger (for networks of high–very high node density) compared to that of the bottleneck node-weight based DG trees. With increase in node density, the diameter of the bottleneck link-weight based DG trees increases by about 30–50%, whereas the diameter of the bottleneck node-weight based DG trees increases only by at most 20% with increase in node density. To vindicate the diameters observed for the bottleneck node vs. bottleneck link-weight based DG trees, the average hop count per path for both the categories of DG trees is about half the diameter values observed for the DG trees (for a given node density and transmission range). The smaller diameter and the correspondingly smaller average hop count per path incurred with the bottleneck node weight-based DG trees augurs well for real-time reporting of data by any sensor node to the root node of the DG tree (i.e., one-to-one communication between a sensor node and the root node).

As a consequence of incurring a smaller diameter, the average number of child nodes per intermediate node for the bottleneck node-weight based DG trees is significantly larger (by factors of two to five in networks of moderate-high node density and by factors of 3 to 10 in networks of high–very high node density) than the average number of child nodes per intermediate node incurred with the bottleneck link-weight based DG trees. On the other hand, the fraction of nodes as leaf nodes is more than 0.7 (and could be as large as 0.94 in networks of very high node density) for the bottleneck node-weight based DG trees, whereas the fraction of nodes as leaf nodes is at most 0.42 for the bottleneck link-weight based DG trees.

We observe the minimum aggregation delay for the bottleneck node weight-based DG trees to be lower than that of the bottleneck link weight-based DG trees when the network is operated under moderate transmission range values (of 25 m and 30 m) in networks of moderate-high node density and at 25m transmission range in networks of high–very high node density. As the diameter values are moderate (and not too low) and the average number of child nodes per intermediate node is not too high for the above said conditions, we observe the minimum aggregation delay to be relatively lower for the bottleneck node weight-based DG trees compared to that incurred with the bottleneck link weight-based DG trees (for which the impact of a larger diameter could be felt at these operating conditions). However, as the node density increases with increase in the transmission range and the number of nodes in the network, the minimum aggregation delay for the bottleneck node weight-based DG trees starts increasing significantly and becomes much larger than the minimum aggregation delay incurred with the bottleneck link weight-based DG trees.

With increase in node density, the reduction in the tree diameter and a concave-up pattern of increase (i.e., the rate of increase increases with increase in node density) in the number of child nodes per intermediate node significantly impact the aggregation delay of the bottleneck node weight-based DG trees. The number of time slots required at an intermediate node to sequentially aggregate data from each of its child nodes would get high, especially at intermediate nodes that are closer to the leader node, thereby increasing the aggregation delay at the leader node. On the other hand, the average number of child nodes per intermediate node for the bottleneck link weight-based DG trees remains the same with increase in node density and the tree diameter only marginally reduces; as a result, the aggregation delay for the bottleneck link weight-based DG trees remains about the same with increase in node density (and even marginally reduces with increase in node density). The minimum aggregation delay incurred with the bottleneck node weight-based DG trees could be at most 85% and 160% larger than the aggregation delay incurred with the bottleneck link weight-based DG trees in networks of moderate–high and high–very high node density respectively.

5.4. Margin of Error for Minimum Aggregation Delay

We calculate and display (see Figure 3) the margin of error values (confidence interval: 95%) for the minimum aggregation delay, the primary performance metric of interest in this paper. Since the aggregation delay is directly dependent on the other three key performance metrics (diameter, fraction of leaf nodes and the number of child nodes per intermediate node), the margin of error values for the minimum aggregation delay could be considered as a measure of the statistical accuracy of the simulations. The procedure followed to calculate the margin of error values (using a z-score of 1.96 for a 95% confidence interval) for the minimum aggregation delay is briefly explained below.

Figure 3. Margin of Error Values for Minimum Aggregation Delay.

Figure 3. Margin of Error Values for Minimum Aggregation Delay.

The margin of error for the minimum aggregation delay under a particular operating condition (number of nodes and transmission range per node) is calculated as $z*\sigma /\sqrt{n_s}$, where z is the z-score 1.96, σ is the standard deviation of the samples collected for the minimum aggregation delay under the particular operating condition and n_s is the number of samples collected (200 graph snapshots). If $\overline{x}$ is the average value of the n_s samples collected for the minimum aggregation delay under a particular operating condition, then one could say that the range of values for the minimum aggregation delay is $\left(\overline{x}-z*\sigma /\sqrt{n_s},\mathrm{...},\overline{x}+z*\sigma /\sqrt{n_s}\right)$ with a probability of 0.95 (95% confidence interval; z-score is 1.96).

As the magnitude of the average value for the minimum aggregation delay increases, we observe the margin of error to also increase, especially in the case of the bottleneck node-weight based DG trees. For networks of high to very high density, we observe the margin of error values for the minimum aggregation delay to be relatively low for the bottleneck link weight-based DG trees, partly attributed to the lower values for the average minimum aggregation delay. Only for networks of moderate density, the margin of error values for the bottleneck node-weight base DG trees are slightly lower than that of the bottleneck link-weight based DG trees. We also observe negligible difference in the margin of error values incurred for the MaxBNW-DG trees and MinBNW-DG trees; likewise, there is negligible difference in the margin of error values incurred for the MaxBLW-DG and MinBLW-DG trees. This further vindicates our reason to just base our discussion of the results as bottleneck node-weight based DG trees vs. bottleneck link-weight based DG trees.

5.5. Performance Tradeoffs

In this subsection, we look at each of the performance metrics (listed in Section 5.1) in isolation, independent of the trend of values expected of them to minimize the aggregation delay. This way, we are able to identify the desirable trend of values (low, moderate or high) that would be typically expected of these metrics to optimize network measures other than aggregation delay (such as node lifetime and network lifetime) and thereby also identify any tradeoffs. We define node lifetime [34] as the time of first node failure due to energy exhaustion; whereas, network lifetime [34] is the time the network gets disconnected due to the failure of one or more nodes due to energy exhaustion.

As noticed in Section 5.3 and Figure 2, to obtain a lower aggregation delay (especially with increase in node density), it would be preferable for the data gathering trees to have a moderate-larger diameter, a smaller fraction of nodes as leaf nodes and a low-moderate number of child nodes per intermediate node. However, one or more of these trend in the values for the above metrics may not be desirable for real-time reporting of events from any node to the leader node and/or for optimizing energy consumption-related performance measures such as the node lifetime and network lifetime. To begin with, we typically desire to have lower values for the tree diameter and hop count per path to facilitate faster real-time reporting of events from an individual node to the leader node of the data gathering tree [12]. However, if we were to incur a smaller hop count per path, then the diameter of the data gathering tree would have to be also smaller [23], thereby increasing the aggregation delay (diameter-aggregation delay tradeoff).

With respect to the fraction of nodes as leaf nodes, from a network lifetime standpoint, we would typically desire to have a larger number of leaf nodes. This is because the leaf nodes tend to lose relatively less energy compared to the intermediate nodes [16]. For every data aggregation cycle, the leaf nodes lose energy for transmitting the data only once to their upstream intermediate node and there is no energy lost due to reception. On the other hand, the intermediate nodes lose energy for both transmitting (to an upstream node) as well as for receiving and aggregating data (from the downstream child nodes) [22]. Thus, a larger number of leaf nodes in a data gathering tree is desirable to prolong the lifetime of a majority of the nodes in the network so that the time of network disconnection due to node failures (typically referred to as the network lifetime) could be prolonged as much as possible [16,34]. However, a larger fraction of nodes as leaf nodes would more likely increase the number of child nodes per intermediate node (also confirmed through the simulation results in Figure 2) and thereby increase the aggregation delay (network lifetime-aggregation delay tradeoff).

With respect to the number of child nodes per intermediate node, we notice that a larger value for this metric could increase the aggregation delay as well as trigger premature node failures. As intermediate nodes have to spend energy to aggregate data from their child nodes, a larger number of child nodes per intermediate node could overuse certain nodes (the intermediate nodes) at the cost of the other nodes (the leaf nodes) [24]. A very low value for the number of child nodes per intermediate node would not be desirable either as it would lead to a significantly larger number of nodes functioning as intermediate nodes and aggregating the data (such a scenario could only lower the node lifetime) [6]. Hence, if we are interested in prolonging the lifetime of every node in the network (i.e., maximizing the time of first node failure, typically referred to as the node lifetime [34]), it would be desirable to have a moderate number of child nodes per intermediate node. An open question is how to define the range of moderate values for the number of child nodes per intermediate node. From Figure 2, we also see that a moderate number of child nodes per intermediate node could also lower the aggregation delay, especially if the diameter of the tree is not very high (as observed in the case of bottleneck node-weight based data gathering trees in networks of moderate node density). However, we notice that if each intermediate node can accommodate only moderate number of child nodes, we would need more nodes to serve as intermediate nodes and the fraction of nodes as leaf nodes would only decrease, thereby increasing the energy consumption at several nodes (node lifetime-network lifetime tradeoff).

5.6. Impact of the Algorithm Design Choices on the Structure of the DG Trees and their Performance

The simulation results vindicate the impact of the design choices behind the algorithms for the construction of the two categories of data gathering trees (bottleneck node-weight vs. bottleneck link-weight based trees) on their structure as well as the performance. The smaller diameter of the bottleneck node-weight based data gathering trees is primarily attributed to limiting the Tree-join-weight of a downstream node from not becoming more than the Tree-join-weight of an upstream node (in the case of MaxBNW-DG trees) or from not becoming less than the Tree-join-weight of an upstream node (in the case of MinBNW-DG trees). As a result, a node that is not yet included in a bottleneck node-weight based DG tree simply prefers to join the tree through an upstream node that has the largest Tree-join-weight (for MaxBNW-DG trees) or the smallest Tree-join-weight (for MinBNW-DG trees). Such upstream nodes are more likely to be closer to the root/leader node of the data gathering tree, as the Tree-join-weight for any node cannot be larger than that of the leader node (for MaxBNW-DG trees) or smaller than that of the leader node (for MinBNW-DG trees). In the case of bottleneck link-weight based DG trees, there is no such restriction as seen in the case of bottleneck node-weight based DG trees. A node that is not yet included in a bottleneck link-weight based DG tree could simply join the tree via any upstream node through a link of the largest weight (in case of MaxBLW-DG trees) or the smallest weight (in case of MinBLW-DG trees). Such upstream nodes need not be always closer to the leader node, and this contributes to a relatively larger diameter (and a lower number of child nodes per intermediate node) for the bottleneck link-weight based DG trees vis-a-vis the bottleneck node-weight based DG trees. Thus, the simulation results observed here are only influenced by the structure of the data gathering trees and their construction procedure, and are not influenced by the configuration of the simulation. In other words, the simulation results merely confirm the performance expected of the two categories of DG trees owing to their design choices.

6. Conclusions and Future Work

The high-level contributions of our paper are as follows: We have proposed a benchmarking algorithm to determine the minimum aggregation delay for data gathering trees in wireless sensor networks. We have shown that the performance of the maximum and minimum bottleneck node weight-based DG trees (and likewise for the maximum and minimum bottleneck link weight-based DG trees) to be almost the same with respect to the performance metrics (aggregation delay, diameter/hop count and distribution of child nodes/leaf nodes in the DG tree) evaluated in this paper, indicating that it would be sufficient to compare the performance with respect to just two categories of DG trees (bottleneck node weight vs. bottleneck link weight based; using either the maximum or minimum bottleneck weight-based DG tree from each category would just be sufficient).

The simulation results confirm the diameter-aggregation delay tradeoff that was expected between the bottleneck node and bottleneck link weight-based data gathering trees owing to their design. The bottleneck node weight-based DG trees incur a smaller diameter and a larger number of child nodes per intermediate node (both contributing to the larger aggregation delay, especially in networks of high–very high node density), whereas the bottleneck link weight-based DG trees incur a larger diameter and a much smaller number of child nodes per intermediate node. The larger diameter makes the bottleneck link weight-based DG trees incur a data aggregation delay that is at most 40% larger than that incurred with the bottleneck node weight-based DG trees in networks of moderate node density operated under moderate transmission range values (25m). However, with increase in the node density, the aggregation delay incurred with the bottleneck node weight-based DG trees starts becoming significantly larger than the aggregation delay incurred with the bottleneck link weight-based DG trees (that do not show any significant impact of the increase in node density). We also anticipate observing a similar diameter-aggregation delay tradeoff even for any other complex network of high node density.

The contributions and observations made throughout this paper could be used to focus future research on exploring strategies for maintaining the diameter of the bottleneck node weight-based DG trees at moderate values (and not allowing the number of child nodes per intermediate node to become significantly high) with increase in node density and thereby reducing the network-wide aggregation delay for data gathering. Note that the simulations assume the availability of a sufficient number of unique CDMA codes for the intermediate nodes at the same level or different levels to simultaneously aggregate data from their respective child nodes, if the latter are ready with the data. We will extend our simulation study by running the benchmarking algorithm on a wireless medium with a limited number of CDMA codes and evaluate the impact on the diameter-aggregation delay tradeoff. Likewise, we will also run the benchmarking algorithm under various medium access control protocols for wireless sensor networks [28] and evaluate the impact of collisions (expected to be significant in networks of high–very high node density) on the diameter-aggregation delay tradeoff.