Hyperspectral Estimation Model of Forest Soil Organic Matter in Northwest Yunnan Province, China

Abstract

Soil organic matter (SOM) is an important index to evaluate soil fertility and soil quality, while playing an important role in the terrestrial carbon cycle. The technology of hyperspectral remote sensing is an important method to estimate SOM content efficiently and accurately. This study researched the best hyperspectral estimation model for SOM content in Shangri-La forest soil. The spectral reflectance of soils with sizes of 2 mm, 1 mm, 0.50 mm, and 0.25 mm were measured indoors. After smoothing and de-noising, the reciprocal reflectance (RR), logarithmic reflectance (LR), first-derivative reflectance (FR), reciprocal first-derivative reflectance (RFR), logarithmic first-derivative reflectance (LFR), and mathematical transformations of the original spectral reflectance (REF) were carried out to analyze the relevance of spectral reflectance and SOM content and extract the characteristic bands. Finally the simple linear regression (SLR), multiple stepwise linear regression (SMLR), and partial least squares regression (PLSR) models for SOM content estimation were established. The results showed that: (1) With the decrease of soil particle size, the spectral reflectance increased. The smaller the soil particle sizes, the more obvious was the increase in spectral reflectance. (2) The sensitive bands of SOM were mainly in the 580–690 nm range (correlation coefficient (R) > 0.6, p-value (p) < 0.01), and the spectral information of SOM could be significantly enhanced by first-order differential transformation. (3) Comparing the three models, PLSR had better estimation ability than SMLR and SLR. The precision of the 0.25 mm soil particle size and the LFR index in the PLSR estimation model of SOM content was the best (coefficient of determination of validation (R_v²) = 0.91, root mean square error of validation (RMSE_v) = 13.41, the ratio of percent deviation (RPD) = 3.33). The results provide a basis for monitoring SOM content rapidly in the forests of Northwest Yunnan, and provide a reference for forest SOM estimation in other areas.

1. Introduction

The soil organic matter (SOM) is not only an important basis for measuring soil fertility and quality [1], but also an important part of the terrestrial ecosystem carbon pool [2]. Traditional SOM monitoring from field sampling to indoor chemical analysis has high precision, but it is time-consuming, laborious, has a long cycle and high cost, and is unable to meet the high efficiency, fast and immediate detection requirements [3]. How to quickly and efficiently obtain SOM content information and monitor the soil environment has been an urgent problem in precise management. With the development of technology, non-destructive, fast, accurate and large-scale remote sensing monitoring makes up for the shortcomings of traditional monitoring methods [4,5], while hyperspectral technology is also widely used in soil quality monitoring [6].

Previous studies have shown that soil spectral reflectance is significantly correlated with soil properties, such as soil moisture, iron oxides, clay minerals, and organic matter, while the absorption in the range of 400–1000 nm is mainly caused by iron oxide and organic matter [7]. The reflectance is significantly negatively correlated with organic matter [8,9,10], it has a high correlation with SOM in the visible bands, especially in the red bands [11,12], and the most sensitive bands are mainly in the 550–710 nm range [13,14,15,16,17]. Studies on the spectral estimation of SOM content in different regions by various scholars have shown that the spectral information can be highlighted, the number of characteristic bands can be increased, and the correlation between reflectivity and organic matter can be enhanced by mathematically transforming the original spectrum [18,19,20,21,22]. The researchers also established a variety of SOM content estimation models, including simple linear regression (SLR) [23], Multivariate Linear Regression (MLR) [24,25], stepwise multiple linear regression (SMLR) [9,11,26], partial least squares regression (PLSR) [27,28,29,30], principal component regression (PCR) [31,32,33], boosted regression tree (BRT) [34], support vector machine (SVM) [6], artificial neural network (ANN) [35], etc. There are differences in the best estimation models for different soil types, but the results of SMLR and PLSR are better and more stable [36].

Furthermore, soil particle size is also one of the factors impacting on soil spectral reflectance and the accuracy of SOM content estimation [37,38]. Ma et al. [39] considered that there was a significant negative correlation between soil particle size and soil spectral reflectance that would affect the modeling accuracy [10]. Bao et al. [40] believed that the accuracy of the soil nitrogen content estimation model would be affected when the soil particle size was less than 0.25 mm or more than 5 mm. Si et al. [41] thought that the improvement of the accuracy of the SOM estimation model was not obvious when the soil particle size was less than 0.25 mm, because the soil particles were so fine that they changed the soil physical properties, and the spectral characteristic information of SOM was masked. Li et al. [42] took Huangshui River basin as an example and used soil spectral information to estimate SOM content, which concluded that the SVM model based on 1 mm size had the best estimation accuracy (the coefficient of determination (R²) = 0.96, the ratio of percent deviation (RPD) = 3.3).

Currently, research on estimating SOM content based on hyperspectral technology has made abundant achievements, but there are differences in soil types, causes of formation, soil physical and chemical properties in different regions. There is no unified standard for selecting soil particle size and models in existing studies, furthermore, model estimation accuracy varies greatly. So, it is difficult to apply the estimation model established in one region to other regions, and the results are also not comparable. Most of studies on spectral estimation of SOM focus on areas with low organic matter content (<10%). There are few reports on spectral estimation of SOM content in forests, especially the forests in Northwest Yunnan of China which are rich in organic matter in the topsoil, and where the SOM content is even greater than 20%. However, it is also very difficult to realize remote sensing monitoring of the topsoil under natural conditions, especially in Northwest Yunnan, where the vegetation coverage is high. Because of the noise caused by the vegetation that litters the horizon, the sunlight which is necessary for hyperspectral measurements in the field is blocked by trees, making the spectral information of the topsoil inaccurate. Therefore, this study took the forest soil of Shangri-La, a typical area in Northwest Yunnan of China, as the research object, carried out laboratory experiments, and established hyperspectral estimation models of SOM content in forests of different sizes in order to find a method for rapidly estimating SOM on the large numbers of field-collected samples in the laboratory. The results would allow the changes in SOM in larger areas to be frequently monitored and analyzed.

2. Materials and Methods

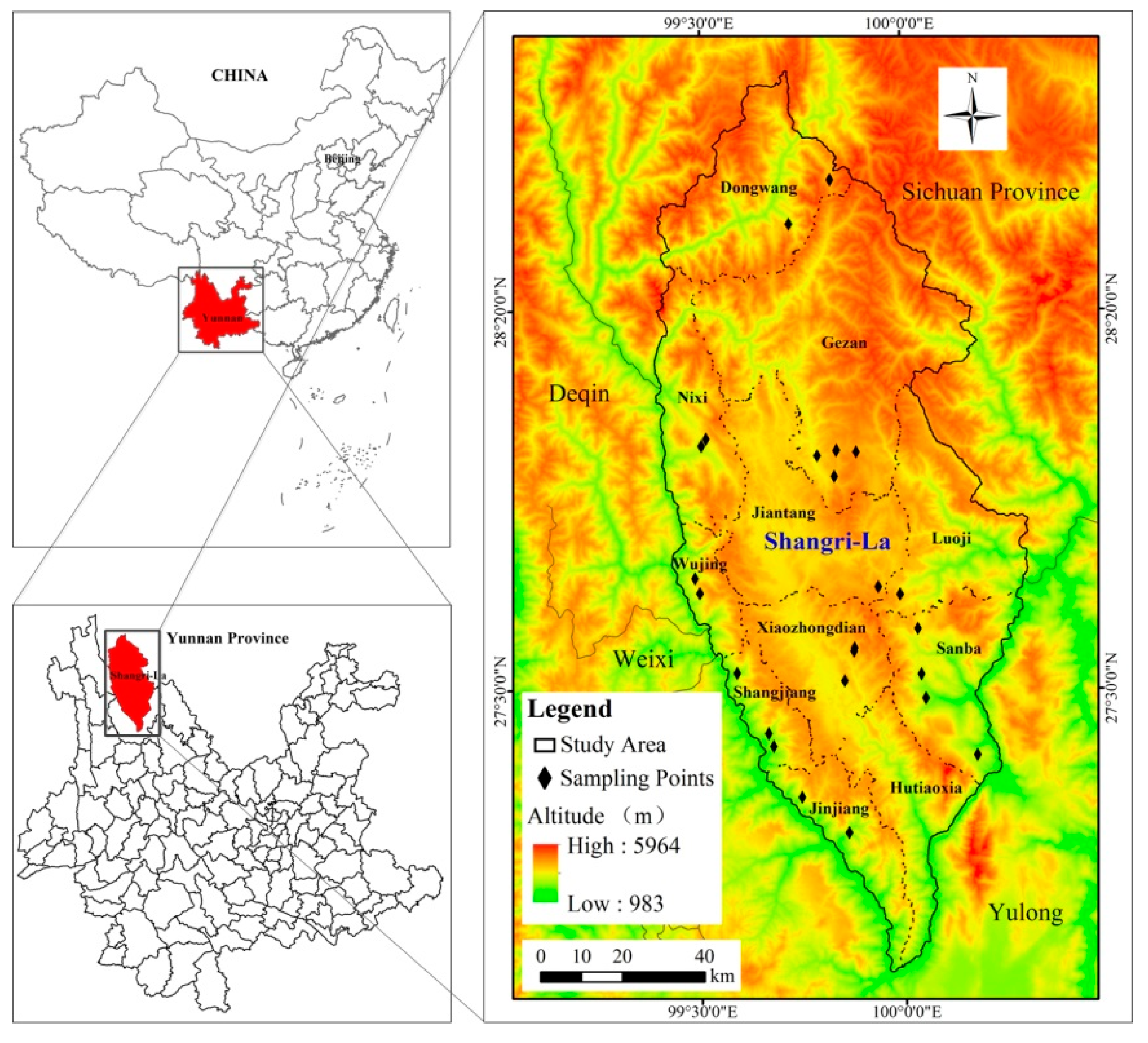
2.1. Study Area

Shangri-La city is the capital of the Diqing Tibetan Autonomous Prefecture, Yunnan Province, China. It is located in the northwest of Yunnan Province, the eastern part of Diqing, between latitudes 26°52′ N–28°52′ N and longitudes 99°20′ E–100°19′ E (Figure 1). The study area, the average elevation is 3280 m and mountain area accounts for over 90%, is an important area for biodiversity conservation and water conservation for ecological protection in the alpine valleys of northwest Yunnan. The climate is alternately controlled by the southwest monsoon and the south branch of the westerly jet. The vertical zoning of the climate is obvious, the dry season (June to October) and wet season (November to next May) are distinct. The annual average precipitation is about 620 mm, the annual average temperature is about 6 °C. According to research by the Soil and Fertility Station of Yunnan Province (SFSY) and the Office of Soil Survey of Yunnan Province (OSSY), the soil parent materials in Shangri-La include plateau lake sediments, river sediments, flood deposits residual, etc., and the soil types include alpine frost desert soil, alpine shrubby meadow soil, brown coniferous forest soil, dark brown soil, subalpine meadow soil, brown soil, red soil, etc. [43]. The city’s forest coverage rate is more than 70% and the total area of four constructive species, Quercus aquifolioides (Quercus aquifolioides Rehd. et Wils.), Abies georgei (Abies georgei Orr), Alpine pine (Pinus densata Mast.), and Yunnan pine (Pinus yunnanensis Franch.), accounts for over 80% of the city’s arbor forests [44,45]. So, the above four kinds of forest soils were selected for research.

2.2. Soil Sample Collection and Experiment

Soil samples of forests were collected in the study area from 17 to 26 July and 24 September to 1 October, in 2017 (Figure 1). Sampling was based on the soil genetic layer, and soil profiles were made at the relatively primitive sites which were less affected by human activities. Soil samples of each occurrence layer were collected from bottom to top. Samples were prepared after indoor air-drying and after roots and stones were removed. The content of SOM was estimated by multiplying 1.724 with the soil organic carbon (SOC) content that was measured by potassium dichromate oxidation with external heating [46]. The remaining dichromate was measured by volumetric titration [46].

Considering the influence of particle size on the accuracy of the SOM content estimation model [40,41], and the difficulty of making soil samples, the air-dried soil samples were prepared into four groups of particle sizes, <2 mm, <1 mm, <0.50 mm, and <0.25 mm, which were named 2 mm, 1 mm, 0.50 mm, and 0.25 mm in turn. Spectral reflectance was measured by an SVC HR-1024i ground object spectrometer (Spectra Vista, Co., Poughkeepsie, NY, USA) with a spectral range of 350–2500 nm and a field-of-view angle of 25 degrees. Spectrum measurement experiments were carried out in a dark room. A light source, with 45 degrees of zenith angle and 65 cm of vertical height, was the standard light source matched with the spectrometer. The spectrometer probe was 10 cm away from the center of the surface of the soil samples which were filled into a black container of 10 cm in diameter and 1 cm in height. The surface was scraped flat, the working table was covered with black paper and the white board was referenced before each spectral measurement. Each soil sample was measured 10 times, the soil sample was rotated 72 degrees every two times, and a total of 10 spectral reflectance curves were obtained for each soil sample. Finally, 64 valid samples were screened with SOM content and spectral data (

Table 1. Statistical characteristics of soil organic matter (SOM) content.

Soil Sample Set	n1	SOM (g/kg)			SD 5	CV 6 (%)
		Min. 2	Max. 3	Mean 4
Whole Set	64	2.58	257.34	63.84	61.70	0.97
Quercus aquifolioides (Quercus aquifolioides Rehd. et Wils.) forest	13	3.28	257.34	75.62	71.09	0.94
Abies georgei (Abies georgei Orr) forest	18	16.56	255.49	106.24	66.13	0.62
Alpine pine (Pinus densata Mast.) forest	12	4.13	84.55	29.23	25.06	0.86
Yunnan pine (Pinus yunnanensis Franch.) forest	21	2.58	186.34	39.97	43.26	1.08

¹ sample numbers; ² minimum value; ³ maximum value; ⁴ average value of SOM content; ⁵ standard deviation; ⁶ coefficient of variation.

).

2.3. Data Pre-processing

In the process of spectral data acquisition, it is unavoidable to be affected by the whiteboard error, instrument error, test environment, sample impurities, etc., resulting in large noise in the spectral data. Therefore, it was necessary to perform whiteboard correction, smooth de-noising, and merging to improve the signal-to-noise ratio. These processes were carried out in software SVC HR-1024i (Spectra Vista Co., Poughkeepsie, NY, USA). In order to enhance the spectral information and highlight the SOM sensitive information, the original spectral reflectance (REF) was transformed into the reciprocal reflectance (RR), logarithmic reflectance (LR), first-derivative reflectance (FR), reciprocal first-derivative reflectance (RFR), and logarithmic first-derivative reflectance (LFR) by Microsoft Office Excel 2010 (Microsoft Corp., Redmond, WA, USA).

2.4. Modeling and Validation

The hyperspectral data contains a large amount of spectral reflection information. It is necessary to establish estimation models to extract the spectral information related to SOM content from the hyperspectral data. Considering the operability, estimation ability, and stability of hyperspectral estimation models, three commonly used Hyperspectral Estimation Models, SLR, SMLR, and PLSR, were established by Matlab R2017a (MathWorks Inc., Natick, MA, USA).

The SLR model only uses the band with the highest correlation between SOM content and reflectance to construct a linear model for SOM content estimation. The model is simple, convenient, and easy to be interpreted physically, but its estimation accuracy is affected in the case of multi-variables [47]. The SMLR model uses multiple bands with high correlation between SOM content and reflectance to construct a linear model [47]. It is developed from the multiple regression model to solve the collinearity problem among independent variables [48]. SMLR usually sets the reliability with 0.05, and adopts a strategy of filtering variables one by one forward or backward, to finally obtain the optimal model [36]. The PLSR model combines principal component analysis, multivariate regression and correlation analysis, it considers the dependent variable while revealing the principal component causing the change of SOM content [49,50]. When the number of samples is small, and the data has strong collinearity and noise, the modeling analysis can still maintain a good effect, and retain all the variable information [36,51].

The whole dataset (n = 64) was split randomly into 54 samples (about 70%) for calibration and 19 samples (about 30%) for validation. Pearson correlation analysis was performed between SOM content and reflectance by using the calibration set and IBM SPSS Statistics 22.0 (IBM Corp., Armonk, NY, USA). The representative bands with significance (p < 0.01) and high correlation coefficient were selected as the characteristic bands of SOM, then SLR, SMLR, and PLSR models were established. The quality of the model was evaluated based on R² (Equation (1)), root mean square error (RMSE; Equation (2)), and RPD (Equation (3)) [36,52]. The bigger the R² and the smaller the RMSE, the better is the fitting effect of the model [35,42]. RPD, the ratio of the standard deviation of the measured value to the RMSE of the validation, was used to test the estimation ability of the model: If RPD >2, the model estimation ability is very good, and if RPD <1.0, the estimation ability is very poor, and cannot be used to estimate organic matter content [52].

$$R^2={\displaystyle \sum _i^n{({\widehat{y}}_i-y_i)}^2}/{\displaystyle \sum _i^n{(y_i-\overline{y})}^2}$$

(1)

$$RMSE=\sqrt{{\displaystyle \sum _i^n{\left({\widehat{y}}_i-y_i\right)}^2}/n}$$

(2)

$$RPD=SD/RMSE$$

(3)

$$SD=\sqrt{{\displaystyle \sum _i^n{\left(y_i-\overline{y}\right)}^2}/n}$$

(4)

where $y$ is the measured value of SOM content, $\overline{y}$ is the average value of SOM content, $\widehat{y}$ is the predicted value of SOM content, n is the total sample number (i = 1, 2, 3…n), SD is the standard deviation.

3. Results

3.1. Spectral Characteristics of Soils with Different Particle Sizes

The average spectral reflectance of the four particle sizes was calculated, and the spectral reflectance curves were obtained (Figure 2). Generally, the spectral reflectance increased rapidly in the 400–800 nm range, while the change at 800–2400 nm was relatively stable. There were absorption valleys around 1400 nm, 1900 nm, and 2200 nm, which are generally considered to be caused by moisture [53]. The effect of particle size on the soil spectral reflectance was obvious, the smaller the soil particle size, the higher the reflectance and the more obvious were the spectral changes. The main reason was that with the decrease of particle size, the void between the soil particles decreased, which made the soil appear smoother, and the spectral reflection was enhanced. The spectral reflectance of the soil sample with 0.25 mm began to change significantly at around 580 nm, however, the spectral reflectance of soil samples with 2 mm, 1 mm, and 0.5 mm changed significantly around 800 nm.

3.2. Feature Band Extraction and Analysis

The correlation coefficient curves (Figure 3, taking the original spectral reflectance as an example) and the characteristic bands (

Table 2. Characteristic bands and correlation coefficients of SOM with different particle sizes.

Particle Sizes	Spectral Pre-processing	Characteristic Bands (nm)	Correlation Coefficient
2 mm	REF	618.5	−0.64
	RR	614.4	0.75
	LR	615.8	−0.71
	FR	566.1, 838.3, 1018.2, 1365.1, 1413.4, 1600.9, 1738.1, 1798.6, 1924.3, 1970.1, 2178.3	−0.72, 0.78, 0.64, 0.58, −0.58, 0.53, 0.61, 0.57, −0.66, 0.61, 0.54
	RFR	791.8, 1048.6, 1424.6, 1520.5, 1738.1, 1798.6, 1924.3, 1956.8, 2168.4	−0.89, −0.78, 0.53, −0.64, −0.59, −0.56, 0.70, −0.63, −0.56
	LFR	757.1, 1044.8, 1413.4, 1600.9, 1738.1, 1921.6, 1956.8, 2168.4	0.89, 0.75, −0.58, 0.60, 0.65, −0.72, 0.70, 0.58
1 mm	REF	619.9	−0.641
	RR	617.1	0.752
	LR	615.8	−0.714
	FR	575.8, 798.1, 1029.6, 1365.1, 1413.4, 1738.1, 1924.3, 1959.4, 2163.5, 2239.3, 2319.6	−0.72, 0.76, 0.61, 0.58, −0.59, 0.67, −0.68, 0.66, 0.67, −0.54, 0.52
	RFR	805.7, 1041, 1428, 1535.2, 1798.6, 1924.3, 1948.7, 2163.5, 2256	−0.89, −0.77, 0.60, 0.65, −0.61, 0.78, −0.60, −0.63, 0.52
	LFR	757.1, 1041, 1413.4, 1619.1, 1738.1, 1924.3, 1959.4, 2163.5, 2239.3, 2319.6	0.88, 0.76, −0.61, 0.64, 0.67, −0.76, 0.68, 0.67, −0.55, 0.55
0.50 mm	REF	619.9	−0.639
	RR	615.8	0.748
	LR	617.1	−0.708
	FR	564.7, 855.5, 1365.1, 1413.4, 1738.1, 1924.3, 1959.4, 2178.3, 2256	−0.71, 0.75, 0.56, −0.55, 0.61, −0.67, 0.61, 0.57, −0.55
	RFR	807, 1044.8, 1424.6, 1619.1, 1738.1, 1921.6, 1967.5, 2178.3, 2312.6	−0.88, −0.76, 0.60, −0.61, −0.55, 0.78, −0.58, −0.60, −0.55
	LFR	754.5, 1044.8, 1365.1, 1413.4, 1619.1, 1738.1, 1924.3, 1959.4, 2178.3, 2256, 2312.6	0.90, 0.72, 0.59, −0.55, 0.58, 0.63, −0.73, 0.67, 0.61, −0.56, 0.54
0.25 mm	REF	626.7	−0.667
	RR	618.5	0.775
	LR	619.9	−0.735
	FR	566.1, 860.4, 1365.1, 1428.3, 1738.1, 1921.6, 1967.5, 2166, 2251.3	−0.75, 0.80, 0.52, −0.51, 0.67, −0.67, 0.58, 0.52, −0.51
	RFR	842, 1048.6, 1428.3, 1553.5, 1738.1, 1921.6, 1956.8, 2190.6, 2248.9	−0.89, −0.76, 0.55, −0.67, −0.62, 0.77, −0.67, −0.57, 0.52
	LFR	755.8, 1048.6, 1428.3, 1600.9, 1738.1, 1921.6, 1956.8, 2190.6, 2251.3, 2319.6	0.89, 0.72, −0.54, 0.59, 0.69, −0.77, 0.70, 0.53, −0.50, 0.50

REF: original spectral reflectance, RR: reciprocal reflectance, LR: logarithmic reflectance, FR: first-derivative reflectance, RFR: reciprocal first-derivative reflectance, LFR: logarithmic first-derivative reflectance.

) were obtained by analyzing the correlation between spectral reflectance information and SOM content. It was shown that REF was highly negatively correlated with the organic matter content (correlation coefficient (R) > 0.6, p-value (p) < 0.01) in the wavelength range of 580–690 nm which meant it was sensitive to the organic matter. The 0.25 mm particle size had the greatest correlation with SOM at 628 nm (R = 0.67, p < 0.01). After the mathematical transformation, the correlation coefficient was improved and the number of characteristic bands of the first-order differential transformation was increased. However, the characteristic bands of the different indicators were contrasting, mainly concentrated in bands of ranges 564–630 nm, 755–861 nm, 1020–1049 nm, 1365–1428 nm, 1520–1554 nm, 1600–1620 nm, 1738 nm, 1798 nm, 1924–1970 nm, 2160–2191 nm, 2239–2256 nm, and 2312–2320 nm (Table 2).

3.3. Simple Linear Regression (SLR)

The SLR models were established by selecting the highest correlation coefficient band from the characteristic bands which was extracted from six spectral transformation indexes of the four particle sizes as the independent variable and the SOM content as the dependent variable (

Table 3. Modeling results of simple linear regression (SLR) for SOM content.

Particle Sizes	Pre-processing	Calibration		Validation
		Rc21	RMSEc 2	Rv23	RMSEv 4	RPD 5
2 mm	REF	0.41	50.05	0.20	39.81	1.12
	RR	0.55	43.41	0.38	35.06	1.27
	LR	0.50	46.14	0.29	37.67	1.18
	FR	0.62	39.91	0.61	27.72	1.61
	RFR	0.68	36.69	0.73	23.09	1.93
	LFR	0.80	28.99	0.70	23.81	1.83
1 mm	REF	0.42	49.67	0.33	36.62	1.22
	RR	0.57	42.88	0.42	34.04	1.31
	LR	0.51	45.56	0.38	35.08	1.27
	FR	0.59	41.56	0.50	31.62	1.41
	RFR	0.72	34.56	0.80	19.82	2.25
	LFR	0.78	30.62	0.72	23.69	1.88
0.5 mm	REF	0.42	49.76	0.36	35.61	1.25
	RR	0.56	43.17	0.43	33.58	1.33
	LR	0.50	45.95	0.42	33.93	1.31
	FR	0.57	42.65	0.39	34.69	1.29
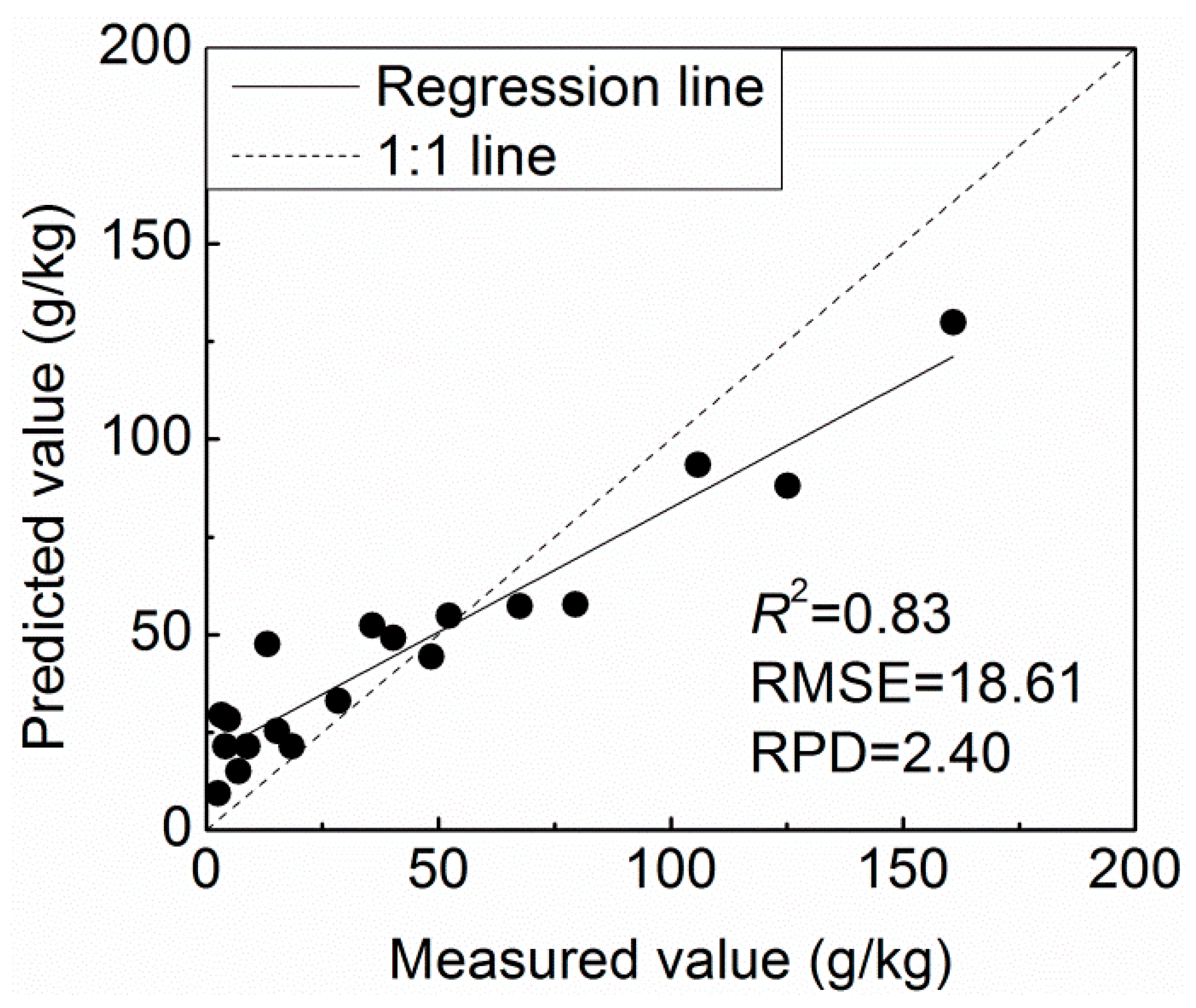
	RFR	0.69	36.39	0.83	18.61	2.40
	LFR	0.80	28.94	0.79	20.21	2.21
0.25 mm	REF	0.46	47.76	0.28	37.83	1.18
	RR	0.60	41.15	0.39	34.86	1.28
	LR	0.54	43.90	0.37	35.39	1.26
	FR	0.65	38.61	0.52	30.77	1.45
	RFR	0.76	31.56	0.70	24.25	1.84
	LFR	0.79	30.03	0.79	20.55	2.17

¹R_c²: coefficient of determination of calibration; ² RMSE_c: root mean square error of calibration; ³ R_v²: coefficient of determination of validation; ⁴ RMSE_v: root mean square error of validation; ⁵ RPD: the ratio of percent deviation.

). The modeling results showed that the coefficients of determination of calibration (R_c²) with indexes of REF, RR, and LR were both less than 0.6, the root mean square error of calibration (RMSE_c) was greater than 41. After the first-order differential transformation, the model fitting effect was improved, the R_c² was increased maximum by 0.39, and the RMSE_c reduced maximum by 21.11. The verification results of different particle sizes and spectral transformations were quite different. The coefficient of determination of validation (R_v²) varied from 0.2 to 0.83 with an average of 0.51, root mean square error of validation (RMSE_v) values ranged from 18.61 to 39.81 with an average of 30.35; RPD varied from 1.12 to 2.40 with an average of 1.55. Generally, the SLR model had poor modeling accuracy and could only roughly estimate SOM content.

Among the four particle sizes, the 2 mm, 1 mm, and 0.50 mm particle sizes with the RFR conversion index were better, the 0.25 mm particle size was better fitted with the LFR transformation index, and R_v² of all of them was greater than 0.7. In the four best models, except for the 2 mm-RFR model, in which the estimation ability is low (RPD < 2), the other models showed good estimation ability (RPD > 2). The best was the 0.50 mm-RFR model (R_v² = 0.83, RMSE_v = 18.61, RPD = 2.40), followed closely by the 1 mm-RFR model (R_v² = 0.80, RMSE_v = 19.82, RPD = 2.25) and the 0.25mm-LFR model (R_v² = 0.79, RMSE_v = 20.55, RPD = 2.17). The worst particle size-transformation combination was 2 mm-RFR, for R_v² = 0.73, RMSE_v = 23.09, RPD = 1.93. Figure 4 shows the comparison of the estimated values by SLR and the measured values of the verification samples with the expression is shown as Equation (5).

$$Y_{SOM}=1\times {10}^6{R}_{807}+21.494$$

(5)

where: Y_SOM = predicted value of SOM, R_j = spectral reflectance of soil at wavelength j in nm.

3.4. Stepwise Multiple Linear Regression (SMLR)

Since REF, RR, and LR indexes only extract one characteristic band, the FR, RFR, and LFR transformation indexes were analyzed in the SMLR and PLSR models. The SMLR models were established by selecting the characteristic bands extracted from three spectral transformation indexes of the four particle sizes as the independent variable and SOM content as the dependent variable (

Table 4. Modeling results of stepwise multiple linear regression (SMLR) for SOM content.

Particle Sizes	Pre-processing	Calibration		Validation
		Rc2	RMSEc	Rv2	RMSEv	RPD
2 mm	FR	0.78	30.47	0.57	32.78	1.53
	RFR	0.85	25.60	0.83	20.47	2.45
	LFR	0.88	22.36	0.74	25.72	1.95
1 mm	FR	0.82	27.37	0.55	33.69	1.49
	RFR	0.85	25.61	0.79	23.21	2.16
	LFR	0.84	26.05	0.75	24.97	2.01
0.50 mm	FR	0.83	26.58	0.55	33.75	1.49
	RFR	0.89	21.46	0.79	23.05	2.18
	LFR	0.87	23.64	0.86	18.86	2.66
0.25 mm	FR	0.83	26.82	0.29	42.38	1.18
	RFR	0.90	20.68	0.78	23.73	2.12
	LFR	0.89	21.34	0.91	13.60	3.28

). R_c² varied from 0.78–0.90 with an average of 0.85, the maximum value of RMSE_c is 30.47 and minimum value is 20.68, average value is 24.83. The best calibration result was the model of 0.25 mm particle size and the RFR transformation index. The validation results showed that R_v² ranged from 0.29 to 0.91 with an average of 0.70, RMSE_v ranged from 42.38 to 13.60 with an average of 26.35, and RPD varied from 1.18 to 3.28 with an average of 2.04. In total, the SMLR model had a good fitting effect and strong SOM content estimation ability, and was superior to the SLR model. Because the average value of R_v² was increased by 0.19, RMSE_v was reduced by 4, and the model estimation ability (RPD) was improved by 0.49.

For the four particle sizes, the models of 2 mm and 1 mm particle sizes with the RFR conversion index were better, while the 0.50 mm and 0.25 mm particle size were better fitted with LFR. The best combination of models was the 0.25 mm-LFR (R_v² = 0.91, RMSE_v = 13.60, RPD = 3.28), followed by the models of 0.50 mm-LFR and 2 mm-RFR, the worst was the 1 mm-RFR (R_v² = 0.79, RMSE_v = 23.21, RPD = 2.16). Figure 5 shows the comparison of the estimated values by SMLR and the measured values of the verification samples, while the expression is shown as Equation (6).

$$Y_{SOM}=102199R_{755.8}+312777R_{1738.1}-41737R_{1921.6}-41.2541$$

(6)

where: Y_SOM = predicted value of SOM, R_j = spectral reflectance of soil at wavelength j in nm.

3.5. Partial Least Squares Regression (PLSR)

The PLSR models were constructed based on reflectance (including its mathematical transformation) and SOM content. The calibration results (

Table 5. Modeling results of partial least squares regression (PLSR) for SOM content.

Particle Sizes	Pre-Processing	Calibration		Validation
		Rc2	RMSEc	Rv2	RMSEv	Rc2
2 mm	FR	0.79	29.93	0.68	25.18	1.77
	RFR	0.85	25.42	0.85	17.45	2.56
	LFR	0.87	23.84	0.75	22.14	2.01
1 mm	FR	0.84	25.73	0.65	26.27	1.70
	RFR	0.84	26.12	0.78	20.91	2.13
	LFR	0.83	26.78	0.76	21.99	2.03
0.50 mm	FR	0.80	29.27	0.74	22.57	1.98
	RFR	0.89	21.36	0.79	20.35	2.19
	LFR	0.86	24.19	0.85	17.31	2.58
0.25 mm	FR	0.82	27.41	0.70	24.46	1.82
	RFR	0.90	21.00	0.81	19.53	2.28
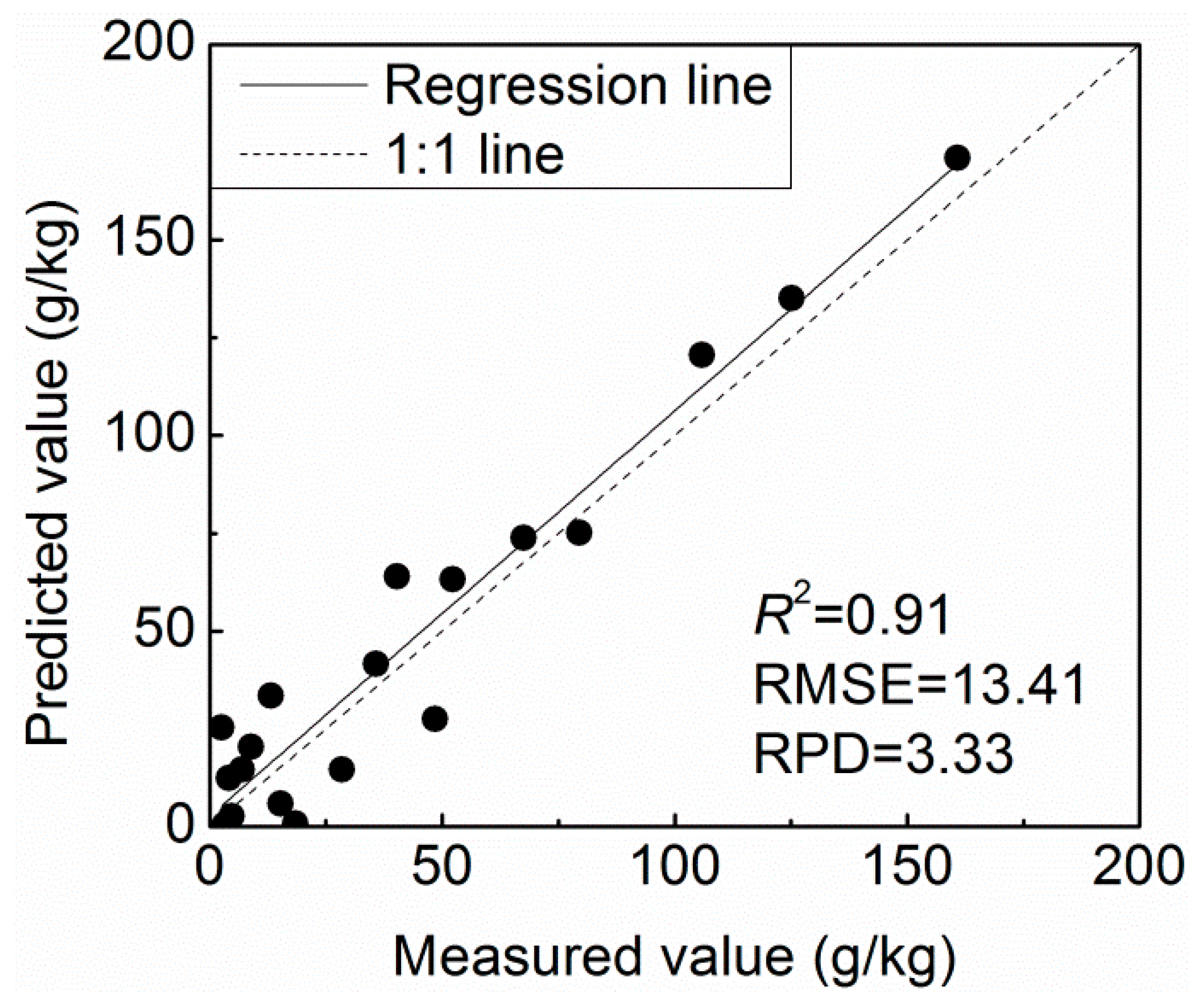
	LFR	0.89	21.69	0.91	13.41	3.33

) showed that the fitting accuracy of the PSLR models was good, R_c² for all was above 0.79 (the maximum was the model of 2 mm-RFR, R_c² = 0.90) and the mean value was 0.85; RMSE_c varied from 21.00 to 29.93, and the average was 25.23. The validation results showed that R_v² ranged from 0.65 to 0.91, with an average of 0.77; RMSE_c ranged from 13.41 to 26.27, with an average of 20.96; and RPD ranged from 3.33 to 1.70, with an average of 2.20. Overall, the PLSR model was better than the models of SLR and SMLR in modeling accuracy. The average of R_v² was 0.9 higher than the SMLR model, the average of RMSE_v was 5.39 lower while RPD was improved by 0.16.

Comparing the best models of the four particle sizes, the results were similar to those of SMLR: the model of 2 mm and 1 mm particle sizes with the RFR conversion index were better, while the 0.50mm and 0.25mm particle sizes were better fitted with LFR. The optimum model was the 0.25 mm-LFR-PLSR model, R_v² = 0.91, RMSE_v = 13.41, RPD = 3.33; followed by the PLSR model of 0.50 mm-LFR (R_v² = 0.85, RMSE_v = 17.31, and RPD = 2.58) and the 2mm-RFR (R_v² = 0.85, RMSE_v = 17.45, and RPD = 2.56). The predicted values obtained by the 0.25 mm-LFR-PLSR model versus observed values are shown in Figure 6, and the expression is shown as Equation (7).

$$Y_{SOM}=100050R_{755.8}+12640R_{1048.6}+309400R_{1738.1}-40760R_{1921.6}-140R_{1956.8}-40$$

(7)

where: Y_SOM = predicted value of SOM, R_j = spectral reflectance of soil at wavelength j in nm.

Summarizing the three models of SLR, SMLR, and PLSR, the estimation ability of the SLR model was the worst. Most SLR models gave R² less than 0.6 and the RMSE was high, while the fitting effect and estimation ability of the PLSR and SMLR models were close and better than the SLR model. However, the accuracy of the PLSR model was higher than that of the SMLR model. Comparing the optimal models of the three modeling methods, the R_v² and RPD of the 0.25 mm-LFR-PLSR model were improved respectively by 0.08 and 0.93 compared to the SLR model, and RMSE_v was reduced by 5.20, in addition, the RPD was 0.05 higher and RMSE was 0.19 less than for the SMLR. Therefore, the hyperspectral estimation model based on 0.25 mm-LFR-PLSR was the best estimation model for forest SOM content in northwest Yunnan.

4. Discussion

The study measured the spectral data of 2 mm, 1 mm, 0.50 mm, and 0.25 mm forest soil samples, and analyzed the relationship between spectral reflectance (mathematical transformation) and SOM content to obtain the characteristic bands. The results showed that with decreased particle size, the spectral reflectance of the soil increased. When the wavelength was greater than 580 nm, the spectral reflectance changed significantly, and the smaller the particle size, the greater was the increase of the reflectivity. This result is in conformity with other study results in that spectral reflectance varies significantly with particle size change when the wavelength is greater than 600 nm [42] and spectral reflectance increases exponentially with decreasing particle size [39]. The response bands of SOM in the original spectral reflectance curve were mainly at wavelength of 580–690 nm (R > 0.6, p < 0.01), this result was basically consistent with those of 620–660 nm proposed by Xu [16], 550–700 nm proposed by Galvão et al. [14,15], 570–630 nm proposed by Peng et al. [13] and 560–710 nm proposed by Fang et al. [17]. Although there is no uniform standard for the pre-processing of spectral reflectance [19], it is undeniable that the first order differential transformation of spectral reflectance can significantly enhance the characteristic spectral information of SOM, reduce the effect of noise, improve the correlation between SOM and reflectance, and increase the number of characteristic bands. In addition, the spectral information of soil is complex, which is affected by the parent material, water, soil nutrients, and texture [22,54,55]. So the focus of SOM content spectrum estimation research is to select the best band according to different research areas and soil types.

SOM spectral reflectance is affected by soil formation factors and soil properties. It is difficult to find a general SOM content estimation model for different soil types [33,56]. Hou et al. [23] established the hyperspectral estimation model of SOM content in the desert, the results showed that the fitting results of the PLSR model were better than the SMLR model and SLR model. Si et al. [41] built SOM estimation models based on PLSR and considered that SOM estimation model with the 0.25 mm particle size was the best, R² and RMSE were 0.816, 4.26, respectively. Zhou et al. [20] and Hu et al. [21] considered that the logarithmic first-order differential model of spectral reflectance was the best for estimating SOM content in soil plowing layers. The 0.25 mm-LFR-PLSR obtained in this study basically conforms with the results of the above studies, and also conforms with the particle size of the SOM chemical analysis. At the same time, the results of estimating SOM content in soil with small particle sizes (0.50 mm, 0.25 mm) were more accurate, and the optimum particle size was 0.25 mm. This was different from research by Li et al. [42] based on particle sizes of 2 mm, 1 mm, 0.25 mm, and 0.15 mm, which concluded the 1mm particle size of soil was best. There are two reasons for this: (1) the modeling accuracy of small samples tends to increase with the decrease of particle size [21]; (2) there may be impurities such as fine grains and root debris, which will affect the spectral information and modeling accuracy of SOM. For the modeling results, R² and RPD of the 0.25 mm-LFR-PLSR are better than the PLSR models in the studies implemented by Fidêncio et al. [27,28], Dunn et al. [29], Kooistra et al. [30], and Hou et al. [23], but the result of RMSE is slightly worse than previous researches [23,27,28,29,30]. The reason is that the variation range of SOM content in soil samples is large (3.28–257.34 g/kg), the difference of SOM content is great, and the coefficient of variation is high (0.95), which have a certain impact on the accuracy of the SOM estimation model. However on the whole, the model has good estimation ability.

5. Conclusions

Overall, with the decrease of soil particle size, the spectral reflectance increases, and the spectral reflectance of different particle sizes changes obviously near the wavelength of 580 nm. The smaller the particle size, the larger the increased range of reflectance. In the original spectral reflectance curve, the sensitive bands of SOM were mainly in the range of 580–690 nm (R > 0.6, p < 0.01), which is negatively correlated with forest SOM, while the spectral information of SOM can be significantly enhanced by first-order differential transformation. The PLSR method outperformed the SLR and SMLR according to R_v², RMSE_v, and RPD. The predictive ability decreased in the following order: PLSR > SMLR > SLR. So the method of PSLR based on the 0.25 mm-LFR is best for estimation of forest soil organic matter by hyperspectral technology in northwest Yunnan.

The results provide a basis for the rapid monitoring of SOM content and ecological environment management in forests in northwest Yunnan, and also provide a reference for hyperspectral estimation of SOM content in other areas. However, with the increasing demand for precise soil management, it is necessary in further studies to collect and analyze more data for estimating the SOM content in other forest areas to improve the applicability of the estimating methods. We hope that, in further study, satellite-borne or airborne hyperspectral remote sensing can be used to estimate the SOM in such areas, and that satisfactory results can be achieved.