Analysis of Economic Feasibility of Ash and Maple Lamella Production for Glued Laminated Timber

Abstract

Background and Objectives: In the near future, in Europe a raised availability of hardwoods is expected. One possible sales market is the building sector, where medium dense European hardwoods could be used as load bearing elements. For the hardwood species beech, oak, and sweet chestnut technical building approvals already allow the production of hardwood glulam. For the species maple and ash this is not possible yet. This paper aims to evaluate the economic feasibility of glulam production from low dimension ash and maple timber from thinnings. Therefore, round wood qualities and the resulting lumber qualities are assessed and final as well as intermediate yields are calculated. Materials and Methods: 81 maple logs and 79 ash logs cut from trees from thinning operations in mixed (beech) forest stands were visually graded, cant sawn, and turned into strength-graded glulam lamellas. The volume yield of each production step was calculated. Results: The highest volume yield losses occur during milling of round wood (around 50%) and “presorting and planning” the dried lumber (56%–60%). Strength grading is another key process in the production process. When grading according to DIN 4074-5 (2008), another 40%–50% volume loss is reported, while combined visual and machine grading only produces 7%–15% rejects. Conclusions: Yield raise potentials were identified especially in the production steps milling, presorting and planning and strength grading.

1. Introduction

The share of hardwoods in the wood stock of Central European forests is steadily increasing [1]. The higher availability of hardwoods requires the development of new markets and new value chains for an overall increase in use. A possible, large sales market is the application in load-bearing structures.

Medium dense hardwoods have preferable mechanical properties compared to softwood. The higher tensile strength of hardwoods leads to either smaller member dimensions or higher load carrying capacities. The high bending strength for hardwood glulam (up to 48 MPa) has been reported by Blaß et al. [2] and Frühwald et al. [3] for beech glulam and by Van de Kuilen and Torno [4] for ash glulam. In recent years, a number of technical approvals for hardwood glulam have been issued:

• Beech glulam [5],
• VIGAM oak glulam [6],
• Schiller oak glulam [7], and
• SIEROLAM glulam of chestnut [8].

Despite the attractive mechanical properties, the use of hardwoods in structural applications remains minor. According to Frühwald et al. [3] and Mack [9], more than 90% of the glulam products in Europe are made of softwood (mainly spruce). The survey by Ohnesorge et al. [10] on glulam producers in Germany, Switzerland, and Austria revealed that in the year 2005 out of 900,000 m³ of glued rod-shaped solid wood products only 1% contained hardwood.

A number of technological reasons as well as historical and silvicultural reasons has led to the fact that mainly softwood is used in wood construction. The use of softwood has been favored over decades because the physical properties are quite predictable and differences between the different softwood species are small. Furthermore, softwood is characterized by long, straight logs with low degrees of taper, homogeneous assortments, and few knots that are usually evenly distributed [11]. There are several further technological constraints for the use of hardwoods in structural applications, such as lack of knowledge of the long-term behavior of hardwood gluing, or the less number of certified grading machines compared to softwood, non-harmonized standardization and production processes not optimized for hardwood species.

One major aspect for the broader use of hardwoods in construction (especially glulam) is the economic feasibility of the production. For hardwoods, at present, no calculated data from a production facility is available. Torno et al. [12] estimated the production cost of ash lamellas to be three times higher as of spruce lamellas. Thus, besides the higher load-bearing capacity of hardwood glulam, the cost-efficient use of the resource hardwood is required, in order to reduce this cost difference. This includes both the optimization of the production process and of the resources used. Processing cheap, particularly small diameter hardwood logs, which are usually used for energy recovery in Europe [12], is one of the frequently discussed issues. Exploiting small diameter hardwoods for material utilization, e.g., sawing, is an important issue in Northern America as well [13].

It is the aim of this paper to contribute to the overall goal of an effective use of the available hardwood resources by minimizing the waste of each production step (of glulam lamellas) separately and for the entire production. The use of small diameter logs from thinnings as a poor-quality resource is the focus of this yield analysis. In the current study, the yield analysis from log sections to planed and graded glulam lamellas is performed using state of the art processing technology. Moreover, the achieved yields are linked to the mechanical properties relevant for glulam lamellas and measured for the investigated samples. Doing so, the economic feasibility of lamella production out of small diameter logs of the rare hardwood species maple and ash can be estimated. The single production steps and technologies of the production of glulam from low-dimension maple and ash logs are analyzed and described.

2. Conversion Efficiency of Hardwoods

In literature, different terms exist to measure the conversion efficiency. In Northern America, the recovery rates with measures like lumber overrun, lumber recovery factor (LRF) and cubic lumber recovery (CLR) are used. In Europe, the term yield is most commonly used. All these definitions have in common that they calculate the volume ratio between the output sawn product and the input logs. The term yield goes even beyond that and can be determined for each production step separately. It can include final, as well as intermediate, products. This allows revealing and analyzing the weakest points of the production process. The use of waste material as side product or for energy production can also be considered. A higher lumber volume does not necessarily lead to higher lumber value. That is why it is important to distinguish between lumber volume recovery and lumber value recovery. For sawmill owners or managers, the latter is decision relevant [14].

Due to the low production volumes of hardwood glulam, yield values are known to only a very small extent. Studies on European hardwoods analyzing the yield from log to planed (dry-dressed) lumber are rare. Torno et al. [12] performed an extensive study on the production of beech lamellas and Van de Kuilen and Torno [15] on beech and ash lamellas. For lamellas sorted according to the German visual grading standard DIN 4074-5 [16], volume yield values as high as 26% for beech and 27.7% for ash were attained. When sorting the lamellas according to the more stringent sorting rules of the German technical approval Z 9.1 679 [5], for the production of glulam the total yield starting at round wood (middle diameter classes 2b–6) ended at only 22% for beech and 26.9% for ash. In this case, however, higher mechanical properties are presumed. As shown by Torno et al. [12], the cutting pattern and the sawing technology affect the final yield. For graded beech lamellas those can drop to 10% or rise to 26%. The highest yield was attained with the grade sawing method, where a vertical bandsaw headrig cuts “around the log” until only a heart plank is left. In these studies, in addition to the cutting pattern and the sawing technology, the quality and the diameter of the round wood had a major influence on the final yield. Frühwald et al. [3] estimate the total yield of the production of high-quality beech glulam from good to medium round wood qualities (B and C) to be around 28.5%.

The reported final yields for hardwood lamellas are below the ones for softwoods. Final yields of the latter range from 24.5%–38.5% [17,18]. Even higher yield values of 40% are stated by Torno et al. [12] for a modern spruce profiling unit. Frühwald et al. [3] mention that the final yield depends greatly on the size (production volume) of the glulam producing company. Only looking at the production of spruce glulam from dried sawn lumber, big producers are able to attain yields between 69% and 75%, while little glulam producers only reach yields of 53%.

Studies like the ones presented by Torno et al. [12] and Van de Kuilen and Torno [15] on the yield from logs to planed and strength graded hardwood lamellas are scarce. A few studies describe the yields of only individual production steps. Their results are summarized below.

2.1. Sawing/Milling

According to Steele [19], the following factors influence the lumber recovery in sawing (milling):

• Log diameter, length, taper, and quality
• Kerf width
• Sawing variation, rough green-lumber size, and size of dry-dressed lumber
• Product mix
• Decision making by sawmill personnel
• Condition and maintenance of mill equipment
• Sawing method

In the study of Lin et al. [14] in small US hardwood sawmills the factors log grade, diameter, sweep, length, species and sawmill specifications had a significant influence on the lumber volume recovery. It is also stressed that interactions between different factors can have a significant influence on the lumber volume recovery. Further influencing factors like board edging and trimming are also introduced. Richards et al. [20] simulate the volume and value yield of sawing hardwood lumber depending on the above mentioned factors. In their simulation the volume yield of live sawing is always higher than that of any four-sided sawing pattern (quadrant, cant, and decision), when sawing the same size logs. When sawing small logs with large core defects the value yield, though, is higher when applying a four-sided sawing pattern. The authors also emphasize the importance of the rotational position on the carriage for the first cut.

Ehlebracht [17] compares volume yield values of four German sawmills for the sawing of square-edged sawn lumber (rough green) from low dimension beech logs. The highest yield value of 57% is attained by a gang saw headrig utilizing the cant sawing method [20]. The lowest yield value of 36% is produced by a circular saw headrig, which produces a comparatively wide kerf. These values are consistent with the values reported by Emhardt and Pfingstag [21] and Fronius [22] that, when combining their findings, present values that range from 42%–47% for the production of square-edged sawn lumber from low dimension beech logs (middle diameter classes 2b and 3a). The lower yield values of Ehlebracht [17] are comparable to the 35% yield reported by Fischer [23] for the production of parquet friezes and pallet boards from low dimension oak logs. For five small US hardwood mills, Lin et al. [14] report cubic recovery percentages (CRP) of 53.2% for red oak (Quercus rubra L.) and 57.5% for yellow polar (Liriodendron tulipifera L.). The CRP expresses the volume of rough green lumber as percentage of cubic log scale volume and is therefore comparable to the yield of the production step “sawing” analyzed by Ehlebracht [17]. The mean small-end diameter (SED) of the input logs in the study of Lin et al. [14] was 33 cm, i.e., also low dimension logs were sawn. All five sawmills used the grade sawing method—two with circular saw headrigs and three with bandsaw headrigs. The simulations of Richards et al. [20] for US hardwood mills result in volume yield values, which range from 54%–76%. The high values, though, are only attainable, when live sawing large logs. According to Fronius [22], a further yield drop of 15%–20% (relative to the original round wood volume) is to be expected when square edging live sawn lumber.

2.2. Drying

Drying losses arise from volumetric shrinkage and the quality of the sawn lumber after drying. For hardwoods such as oak, improper drying results in staining, checking, splitting, and warp, which leads to a reduced sawn wood value [24,25]. Therefore, proper drying schedules are of high importance.

Generally, the higher the specific gravity of the wood is the higher is also the volumetric shrinkage [26]. It varies within a species and even for lumber from the same log. The volumetric shrinkage during technical drying of rough green lumber to a moisture content of 12% ranges from 14%–21% for beech, from 12.8%–13.6% for ash and from 11.5%–11.8% for maple [17,27]. Spruce shrinkage losses are around 12% [27]. The volumetric shrinkage in the production of hardwood lamellas for glulam lies between 11% and 17% for beech and at 9.8% for ash [15].

2.3. Planing

Planing losses depend on the chosen oversize, the final product and the drying quality (i.e., warping and bowing). The resulting losses present a combination of planing away the oversize and sorting out (presorting) boards with intensive bowing. For example, when trimming the lamellas to shorter lengths, the oversize can be reduced and thus the planing losses are also reduced. In similar studies to the presented one [12,15], planing and presorting losses (due to bowing) for the production of hardwood glulam lamellas vary from 18%–46%—a relatively wide range.

2.4. Grading

Grading is an important step within the production, as the quality of sawn wood is assessed in terms of appearance (i.e., cladding, furniture) or mechanical properties predicted. As a consequence, a discrete value is assigned to a lumber specimen. Both the quality of the produced lumber in terms of achieved mechanical properties and the yield are of interest. For grading, the yield is the share of dry-dressed lumber (dried, jointed, and planed), which is assigned to a certain quality class and not rejected.

Data on hardwood grading yield in general, and on strength grading in particular, is scarce, since hardwoods are rarely strength graded. Generally, the yield losses depend on the grading method (machine vs. visual grading), wood quality, growth region, cross-section, and sawing pattern selected. For European hardwoods, the effect the single mentioned factors have on the grading yield, are known to only a small extent. If lamellas are sawn pith free, the grading losses are lower compared to other sawing patterns. This is because the pith is a general rejection criterion for visually graded hardwood lumber after the German visual grading standard for structural timber DIN 4074-5 [16]. Thus, Glos and Torno [28] report for 324 ash boards and 459 maple boards graded according to DIN 4074-5 rules for joists rejection rates of as high as 21% and 37% due to pith and extreme grain deviation. It should be mentioned, though, that for that study the visual assessment of the boards is only being made for that part of each specimen, which is selected as free testing length. In Torno et al. [12] the loss values for beech lamellas range from 37%–62%, if graded visually in accordance with the German visual grading rules for structural lumber DIN 4074-5 [16]. If lamellas are graded in accordance with the German technical building approval for beech glulam Z 9.1 679 [5] the rejection rate increases to 47% and 69%.

3. Test material

The round wood used for this investigation came from thinnings in mixed forest stands (mixed beech forests) of the state forestry offices Leinefelde and Heiligenstadt (Central Germany). The wood was harvested in the winter of 2014/2015 with harvester technology. Until the milling in June 2015, the round wood sections (logs) with a length between 3.20 and 3.40 m remained on the log yard of the department sawmill. According to the transport invoice 14.89 m³ (79 logs) of ash (Fraxinus excelsior L.) and 16.25 m³ (81 logs) of maple (80 logs of Acer platanoides L. and 1 log of Acer pseudoplatanus L.) were delivered (with bark). For the yield analysis, round wood sections (logs) with the following characteristics were ordered:

• Round wood quality C or worse (according to the Framework Agreement on Raw Timber Trade in Germany-RVR [29]);
• Length ≥ 3.20 m; and
• Round wood diameter classes 2–3

4. Production Steps and Determination of Characteristics

4.1. Round Wood Sections (Logs)

On the log yard the round wood sections were trimmed uniformly to a length of 3.15 m in order to be able to determine the heartwood coloring (i.e., brown heart) on both ends. At the top (small) end of each trunk a slice of 1–2 cm thickness was cut off. The final cut was performed at the bottom of each trunk (large end) to a length of 3.15 m. Thus, total log volumes were reduced to 14.3 m³ for ash and 15.8 m³ for maple. For each round wood section the minimum and the maximum diameter was determined in the middle of every 25 cm section. The last section only had a length of 15 cm. Using the mean diameter for each 25 cm section and the one 15 cm section (d_Mn), the section volumes were calculated with Huber’s formula. The single section´s volumes were then added up resulting in Equation (1):

$$V_{\mathrm{Sec}.}=\left({\displaystyle \sum }_1^{12}\frac{\mathsf{\pi }}{4}\times 0.25\mathrm{m}\times {\mathrm{d}}_{Mn}{}^2\right)+\frac{\mathsf{\pi }}{4}\times {0.15\mathrm{m}\times \mathrm{d}}_{Mn}{}^2\left[{\mathrm{m}}^3\right]$$

(1)

The logs were sorted into diameter classes according to their small-end (top-end) diameter (SED) and into quality classes according to the specifications of the RVR [29] and DIN 1316-3 [30]. Both standards allow the assignment to classes from A (highest quality) to D (lowest quality). The quality-determining characteristics of the round wood sections were determined and recorded in accordance with Annex VIII (Measurement of the characteristics) of the RVR [29]. The characteristics shrinkage cracks, insect holes, tree cancer and the so-called moon ring (light discoloration in heartwood) were not recorded and thus were not part of sorting.

The RVR [29] offers no separate quality grading for maple and ash logs. Thus, depending on the particular characteristic, the oak grading rules (e.g., for knots, star shake, twigs, etc.) or those for beech (only for width of brown heart and heart shake) were used.

4.2. Sawing/Milling

The logs were milled with a mobile horizontal bandsaw headrig (Montana ME 90 2.0 from SERRA, Rimsting, Germany) with a kerf width of 2.45 mm. The cant sawing patterns used are shown in Figure 1.

The sawing patterns and the distribution of board dimensions were chosen for each log separately, mainly depending on the small-end log diameter (d_z or SED). Thus, the maximum yield could be attained. The pattern A was used most. If side boards were produced (colored boards in pattern C), they were edged to square edged lumber on a circular saw. For maple, five different lumber dimensions were sawn, for ash three (see

Table 1. Nominal dimensions and quantities (n) of sawn green lumber and the resulting planed lamellas (dry-dressed lumber).

Sawn Green Lumber	Planed Lamellas	Maple	Ash
Width × height	Width × height	n	n
(mm) × (mm)	(mm) × (mm)
115 × 35	100 × 25	88	-
145 × 35	125 × 25	132	-
145 × 40	125 × 30	85	121
115 × 45	100 × 35	92	104
145 × 45	125 × 35	94	162

).

Only the main product glulam lamella was produced for this study. No side products, like trimming or baseboards, etc., were produced. The side products would raise the final yield. The final product—planed glulam lamellas—were subjected to destructive tensile testing after visual and machine strength grading (see sub sample “TH II” in Kovryga et al. [31]).

4.3. Drying

The technical drying took place in the in-house conventional dryer (HB Drying Systems, Almelo, The Netherlands). The drying parameters were chosen in order to ensure gentle drying of the boards. The drying process took 21 days. To determine the volumetric shrinkage, the dry lumber volume (at 12% moisture content) is subtracted from the sawn lumber (rough green) volume. For this purpose, for each dimension and wood species six lamellas were selected randomly. On these lamellas, the lengths (in mm) were determined with a tape measure on the rough green and the dry lumber. Lumber dimensions (in mm) were measured at intervals of 25 cm—starting and ending at the board ends.

4.4. Presorting and Planing

The dried boards were jointed and planed to glulam lamellas (dry-dressed lumber) with the nominal dimensions presented in Table 1. After the planing process, each lamella that could not attain the nominal dimension (cross-section) on the full length was sorted out (due to a combination of bowing and too little oversize). The volume of the remaining glulam lamellas was calculated by determining their lengths with a tape measure and using the nominal lamella dimensions.

4.5. Strength Grading of Planed Boards

4.5.1. Visual Strength Grading

To assess the quality of hardwood lamellas, different grading methods were used. First, each of the lamellas was visually classified according to the German visual strength grading standard DIN 4074-5 [16] over the entire length. The standard uses ten visual criteria to assign hardwood boards to visual strength grading classes. In the current study, the knottiness, presence of pith, bark inclusion, wane, and fiber deviation (grain angle) were considered.

All relevant grading criteria were measured as defined in DIN 4074-5 [16]. To assess the knottiness—one of the major parameters of strength grading—the criteria single knot (SK) and knot cluster (KC) were used. Single knot or DIN Einzelast Brett (DEB) relates the size of the single knot to the lamella width. For grading, the ratio (knot) with the highest value is indicative. Knot cluster (KC) or DIN Astansammlung Brett (DAB) is a multiple knot criterion, which considers all knots appearing in a (moving) window of 150 mm. Therefore, the spread of all knots over the 150 mm window is related to the width of the board. The edge knot criterion (E) or Schmalseitenast is an optional criterion for boards and represents the penetration depth of the knots appearing on the edge side only. A low value of these visual grading criteria stands for either rare occurrence or small size of the strength reducing knots and vice versa.

The only adjustment made concerns the measurement of the fiber deviation (grain angle). Fiber deviation is defined as an angle between the fibers and loading direction over a certain length and is measured in percent. The grain angle has a significant impact on strength [32]. Most grading standards indicate that the fiber deviation can be measured on drying checks or by the scribing method on the wood surface. Both methods are reported to have limited use for medium-dense hardwoods [33,34]. In the present study, the visible fiber deviation was detected on drying checks and, additionally, the surface was assessed qualitatively for fiber deviations exceeding the limits of DIN 4074-5 [16]. The specimens exceeding the limits are rejected.

Hardwood boards are assigned to the visual grades LS13 (highest quality), LS10 (medium quality) and LS7 (lowest quality) based on the boundary values listed in

Table 2. Boundary values for grading of hardwood lamellas to visual grades (LS7 to LS13) after DIN 4074-5 [16].

	LS13	LS10	LS7
DEB (SK)	0.2	0.333	0.5
DAB (KC)	0.333	0.5	0.666
Edge knot (E)	-*	-*	-*
Pith	no	no	no
Fibre deviation	7%	12%	16%

* No requirements set.

. To assign a lamella to a visual grade, all boundary values are to be met. Otherwise, the specimen is assigned to the next lower grade or rejected.

Additionally, to estimate the effect of the grading parameters pith and DAB on the yield, two grading combinations—one without any requirements on pith and one without any requirements on pith and DAB—are applied to the lamellas.

4.5.2. Combined Visual and Machine Strength Grading

Additionally, the boards were graded using a combined visual and machine grading approach. The procedure was suggested by Frese and Blaß [35] and is used for beech glulam produced after the German technical building approval Z-9.1-679 [5]. This grading approach combines visual grading parameters (i.e., SK and KC) with the dynamic Modulus of Elasticity (MOE_dyn), a parameter used in most state of the art grading machines for softwoods. The MOE_dyn was determined using the “eigenfrequency” method (laboratory and grading machine ViSCAN by MiCROTEC, Bressanone/Brixen, Italy). In case of ViSCAN, the natural frequency (f) from longitudinal oscillation was combined with the density (ρ) measured by an X-ray source, and the length (l) of the measured specimen (Equation (2)). In the laboratory, the density was determined using the gravimetric method. Both measurements provide comparable results in terms of R² value (0.972).

$$MO{E}_{dyn}=4\times l^2\times \rho \times f^2\times {10}^6$$

(2)

The combined approach uses separate boundary values for visual grading parameters (i.e., SK, KC) and MOE_dyn. The boundaries presented by Frese and Blaß [35] are fitted to beech lamellas. For the present study, the combined grading is optimized for ash and maple and presented by the paper Kovryga et al. [31].

Table 3. Optimized grading rules for combined visual and machine strength grading of ash and maple (according to Kovryga et al. [31]; maple: “Solution B”, ash: “Solution C”).

	Grade	Boundary Values					Resulting Tensile-Classes
		DEB (SK) (–]	DAB (KC) (–]	Edge knot (E) (–)	Pith (–)	MOEdyn (kN/mm²)
Maple	1	0.1	0.1	-*	Allowed	13.9	DT38
	2	0.2	0.5	-*	Allowed	12.2	DT25
	3	0.3	0.6	-*	Allowed	10.9	T15
	Reject
Ash	1	0.2	0.2	-*	Allowed	16.5	DT38
	2	0.3	0.3	-*	Allowed	15.5	DT34
	3	0.4	0.4	-*	Allowed	11.6	DT22
	Reject

* No requirements set.

shows the combination of boundary values selected for the current study. As example, for maple the “Solution B” and for ash the “Solution C” proposed for combined grading by Kovryga et al. [31] is selected. The presented combination allows grading to three different grades plus reject group. The highest grade shows characteristic tensile strength values (above 38 N/mm²) fitting the tensile strength of finger jointed lamellas stated by Van de Kuilen and Torno [4].

4.6. Yield Calculation

For the determination of the total yield, the yields of each single production step are added up. The yield of each production step is calculated by dividing the output product volume by the input volume. How volumes of each intermediate product are calculated and what assumptions are made for these calculations is described above for each production step separately.

5. Results and Discussion

5.1. Grading of Logs

Table 4. Number of logs per species sorted after small-end diameter (inside bark) class and quality class according to RVR [29].

Diameter Class		2a	2b	3b	4	1b	2a	2b	3a	3b	1b	2a	2b	3a	3b
Quality Class		B				C					D
Quantity	Maple		3	2	1	4	18	11	9	3	5	14	5	2	3
	Ash	1					8	16	5	1	2	23	19	4

shows the sorting of the maple and ash logs into diameter and quality classes. Following the descriptions of Van de Kuilen and Torno [15], the diameter sorting was carried out by considering the small-end diameter (SED) inside bark. The supplied round wood sections mainly cover the diameter classes from 2a to 3b, with individual sections with diameters below 20 cm and over 40 cm. For maple and ash, the bark shows a mean thickness of 0.5 cm. Maple shows a higher number of logs graded to the higher quality classes (B and C) compared to ash.

Table 5. Yields in % for quality sorting of logs according to RVR [29] separated after sorting criteria (log characteristics).

Log Characteristics	Maple				Ash
	A	B	C	D	A	B	C	D
Callused knot (bump)	23	1	76		46		54
Healthy knot	63	29	9		89	10	1
Decayed knot	63	31	5	1	89	6	5
Twigs	76	24			100
Bump on group of broken of twigs	95	1	4		100
Star shake/check	60	29	11		4	14	80	3
Heart shake/check	33	61	5	1	81	15	1	3
Frost crack	98		3		99		1
Ring shake	98	3			99		1
Bow (Sweep and crook)	48	14	6	33	38	1	5	56
Spiral (twisted) grain	98		3		100
Rot	99			1	97			3
Log length	99		1		96		4
Width of brown heart	86	14			25	46	29
Final quality class of logs		8	56	36		1	38	61

and

Table 6. Yields in % for quality sorting of logs according to DIN 1316-3 [30] separated after sorting criteria (log characteristics).

Log characteristics	Maple				Ash
	A	B	C	D	A	B	C	D
Length	99		1		96		4
Mid-diameter	14	11	70	5		4	9 *
Callused knot (bump)	25		34	41	47		42	11
Healthy knot	95		5		91	3	6
Decayed knot	90		8	3	96		4
Eccentricity of pith	88	13			80	20
Star shake/check	60		5	35	4			96
Heart shake/check	40	14	46		87	4	9
Brown heart	66		34		38	25	37
Bow (Sweep and crook)	61	5	1	33	39	5		56
Rot	99			1	97			3
Final quality class of logs	1	1	26	71			4	96

* No requirements set.

show the results of the log quality sorting according to RVR [29] and DIN 1316 3 [30] in detail.

Table 5 and Table 6 present the final assignment of the round wood sections into the quality classes (the last row of both tables) based on the individual class assignment for each sorting criterion. Each single criterion’s influence on the grading can be seen as well as the total distribution of quality classes per species. For example, according to DIN 1316-3 [30], 71% of the maple logs are graded into the lowest quality class D (see Table 6). The final percentage value is a result of all wood characteristics combined. It can be seen that for maple the grading into the D class is mainly due to the characteristics callused knot, star shake, and bow. When sorting according to the RVR [29] specifications, mainly log bowing is decisive for sorting into class D (see Table 5). Especially in the second lowest grade C, it is observable that the two different quality sorting schemes weigh the different characteristics differently, i.e., have different characteristic’s boundary values for the same class. While grading into RVR class C of maple is mainly due to callused knots (76%), DIN 1316-3 [30] sorting into class C is due to a number of characteristics (mid diameter, callused knots, heart shake, and brown heart). Both grading schemes sort the majority of the studied logs into the classes C and D.

In general, the two sorting guidelines for round wood use different lists of characteristics. For example, Table 6 shows that in the case of sorting according to DIN 1316-3 [30] the criterion mid-diameter leads to a classification into quality class C for 70% of the maple logs and for 96% of the ash logs. Compared to that, the diameter of the logs is not relevant, when sorting according to RVR [29]. The possible advantage of the absence of log size criteria is that the actual visible log quality can be assessed and used to qualify the logs for the production in addition to the diameter.

Looking at Table 5 and Table 6, it also becomes obvious that—under the same storage conditions—ash logs tend to form more severe end cracks (star and heart shake) than maple. This cracking results in a serious deterioration of quality and leads to a reduced sawn lumber yield (mainly value yield). Thus, it is recommended to saw (mill) ash logs shortly after logging or adapt storage (e.g., water storage) to ensure the best possible lumber quality and highest yield. Short storage times’ respectively adjusted storage conditions are also advised for maple logs, since fungal discoloration starting from the log ends presents problems [27]. For an end use as construction material, though, these discolorations may be of low significance, since they do not affect the elasto-mechanic properties of the lumber.

5.2. Yields from Logs to Unsorted Glulam Lamellas

Table 7. Yield for each production step from logs to planed lamellas (unsorted).

Product	Production Step (PS)	Maple				Ash
		Yield		Waste/Loss		Yield		Waste/Loss
		in m³	in %	in m³	in % PS	in m³	in %	in m³	in % PS
Logs		15.8				14.3
	Milling/sawing			7.6	48.2			7.1	49.5
Boards (green)		8.2	51.8			7.2	50.5
	Drying			0.7	8.7			0.8	10.7
Boards (dry)		7.5	47.3			6.5	45.1
	Presorting & planing			4.2	56.3			3.8	59.6
Planed lamellas		3.3	20.9			2.6	18.2

summarizes the volume losses and the resulting yields for each production step. It can be seen that the major production losses arise from sawing the logs and presorting the dried boards. Both species do not differ considerably.

5.2.1. Sawing/Milling

The mean volume yield of sawing the 81 maple logs by the cant sawing method to square-edged lumber is 51.8%. The mean volume yield of sawing the 79 ash logs is with 50.5% slightly lower. The log diameter strongly influences the volume yield of this production step. The effect the mid-diameter has on the sawing yield of this study can be observed in Figure 2.

The higher the log diameter gets, the higher the yield gets. The variation in sawing yield values drops with increasing diameters, as the influence of the log grade (quality class) on the yield decreases. Compared to the log diameter, the quality class only has a minor influence. Wade et al. [36] analyzed data from 35 US hardwood mills and also concluded that a positive linear relationship between log diameter and sawing yield (in their case LRF) exists. In the simulation of Richards et al. [20] hardwood sawing yields of sawing low dimension logs (SED = 25 cm) by the cant sawing method start at 56.1%, while from logs with large diameters (SED = 71 cm) up to 67.2% rough green lumber can be produced. In Ehlebracht [17] only one of four hardwood mills attained a sawing yield of 57%, when cant sawing low-dimensional hardwood logs. Two mills achieved yields like this study (50% and 51%), while a mill with a circular saw headrig only reached 36% volume yield. All presented studies show that it is economically advantageous to sort out logs with diameters below a certain value. The boundary value for the diameter has to be determined for each production site and product separately. The results of Wiedenbeck et al. [13] give rise to the assumption that this boundary value also depends on the wood species sawn.

Lin et al. [14] prove that the log grade (quality class) has an effect on the hardwood volume recovery. In this study, this is only observed in the lower log diameter classes. The individual characteristics eccentricity of pith, ovality and taper show no significant influence on the yield of the first production step. The two latter characteristics are not part of the RVR [29] and DIN 1316-3 [30] sorting standards. Nonetheless, their influence on the yield during production is examined. For ash, the degree of bowing (in one direction) has no influence on the yield of milling. For maple, increased bowing (in one direction) leads to a decreased yield of milling. Multiple bows in one log (in one or more directions) decrease the yield of milling significantly. Comparing logs with one bow in only one direction with logs with multiple bows, the yield is reduced from 52.7% to 43.7% for maple and from 51.7% to 46.1% for ash. The same relationship—but less pronounced—can be found in so-called butt-cuts. In these first logs of trees taken above the stump, the milling process removes a high volume of wood from the large end of the log.

5.2.2. Drying

Drying of the green lumber was carried out for all dimensions and species with the same slow drying program, in order to avoid damages due to inadequate (i.e., too fast) drying. For maple, the volumetric shrinkage lies between 8.0% and 8.9% (average 8.7%), while for ash it lies between 9.6% and 11% (average 10.7%). For both species, these values lie in the lower range of the above-mentioned literature values. In some cases, the boards started warping (bowing, crooking, cupping, twisting, etc.) immediately after or even during the milling due to inherent tension in the trunks (eccentric pith, reaction wood, around big knots, etc.). Nonetheless, these boards were stacked and underwent drying.

5.2.3. Presorting and Planing

Before planing the dried boards, they were pre-sorted. Boards with extreme bowing were sorted out. If the infeed and outfeed rollers of the planer were able to press down the bow, resulting in fully planed board surfaces, the lamellas were not sorted out. Nevertheless, the volume loss of this production step is 56.3% for maple and 59.6% for ash. The resulting total yields of planed boards (unsorted glulam lamellas) are, thus, 20.9% for maple and 18.2% for ash. If the presorting was excluded from this calculation, i.e., if the bows were cut out (resulting in shorter lamella lengths) and thus all boards could be planed to the nominal dimensions, total yield values of 33.4% (maple) and 33.2% (ash) could be obtained. For future investigations, it is planned to evaluate the influence round wood quality has on presorting and planning losses. Especially for low-dimension logs of poor quality the question arises, how much of the resulting twisting and bowing in the dried lumber is due to the drying process and how much is already present in the rough green lumber.

5.3. Strength Grading of Glulam Lamellas (Planed Boards)

5.3.1. Grading Results

As explained in Section 4.5, the planed boards were graded visually according to the German visual strength grading standard DIN 4074-5 [16]. Furthermore, the result of two adjusted grading schemes were compared—when the criterion “pith” is excluded from visual strength grading according to DIN 4074-5 [16] and when only single knots (DEB) are evaluated according to DIN 4074-5 [16]. Additionally, the lamellas were graded following the combined visual and machine grading proposed by Kovryga et al. [31] and presented in Table 3.

Figure 3 shows the grading results for ash and maple, respectively. The second box of each diagram gives the results of visual grading according to DIN 4074-5 [16]. For both ash and maple, only few boards are sorted into the classes LS7 and LS10. The majority is either sorted into the highest quality class LS13 or rejected. When excluding the criterion pith from DIN 4074-5 [16] sorting (see third box), no ash lamellas and four maple lamellas were rejected. The majority of the lamellas is graded into LS13 (ash: 195; maple: 238). Only applying the DIN 4074-5 [16] boundary values for the criterion DEB (single knot) gives almost identical sorting results. The combined grading proposed and optimized by Kovryga et al. [31] for the here studied lamellas result in a relatively even distribution of lamellas over the three grades. For ash 6.8% and for maple 15.7% of the lamellas are rejected.

For grading according to DIN 4074-5 [16], a high effect of the pith criterion on the grade class assignment can be stated. Grading with pith as rejection criterion results in a reject rate of 48% for the ash boards and 38% for the maple boards. If the pith criterion is excluded from grading, none of the ash boards and only 1% of the maple boards are rejected. Similar results are reported by Torno et al. [12], who detected pith in 26% and 30% of the graded beech boards. Here the sawing pattern was similar to this study, but logs with larger diameters were sawn. Van de Kuilen and Torno [15] calculated for their study the ratio of pith containing board volume to initial round wood volume (inside bark) to be 0.2% for ash and 0.9% for beech. In this study, this ratio is 9.1% for ash and 8.0% for maple. This much higher appearance of pith can be explained by the fact that lower dimension logs were sawn and the overall log quality was poorer. Furthermore, the study of Van de Kuilen and Torno [15] used a special sawing pattern (“sawing around the log” or “grade sawing”) designed to produce boards without pith. Generally, it can be concluded that the sawing pattern and the low log dimensions chosen for this study resulted in a high amount of pith boards, which have to be sorted out, when sorting according to DIN 4074-5 [16]. Pith is also the main downgrading criterion in the grading of ash and maple lamellas studied by Glos and Torno [28]. The rest of the boards of this study show good quality for both species, resulting in a high proportion in LS13 grading.

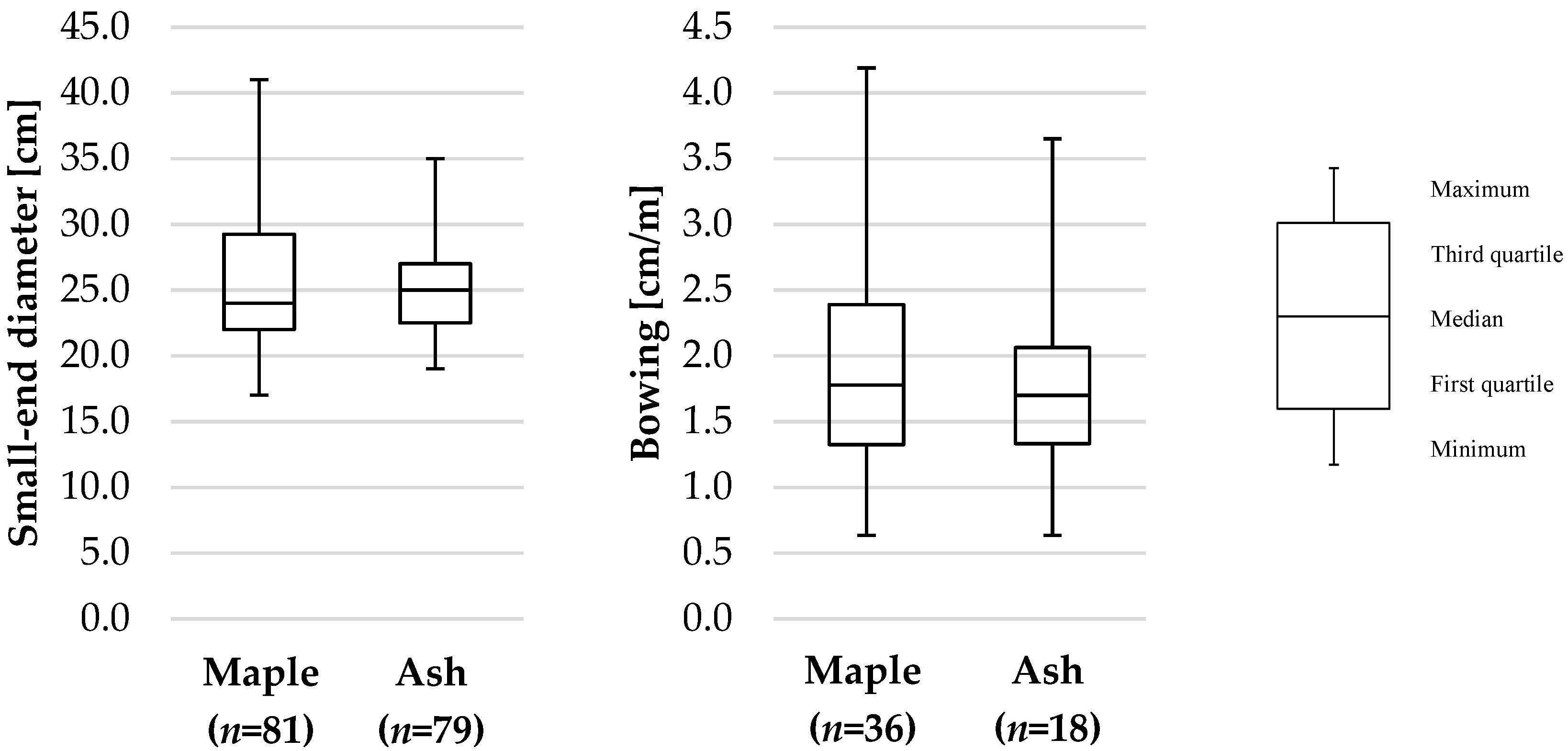
One explanation for the higher amount of pith containing boards in the ash compared to the maple collective can be the fact that in ash trees the pith is typically “wandering”, which is due to crooked growth in early years [17,37]. Other reasons can be more severe bowing of the ash logs or littler log dimensions. Figure 4 proves that the small-end diameters are not severely different for the 81 maple and 79 ash log sections.

The bowing of the raw material was according to RVR [29] specifications only measured for log sections that had one bow over the entire log length. This criterion shows now difference between the species ash and maple as well (see Figure 4). Checking the number of logs with compound bowing (bowing into two or more directions) reveals a different picture, though. While only 55% of the maple log sections are characterized by compound bowing, 77% of the ash log sections have compound bows. This could be an explanation for the higher amount of pith containing boards in the ash collective. Since the collected data does not contain information on the degree of compound bowing, one cannot distinguish between the influence of the “wandering pith” and the log section bowing.

To finalize the discussion of the effect of the grading parameters on the yield, the effect of the knot cluster criterion (DAB) is observed. Comparing both visual grading options—for DIN 4074-5 [16] “without considering pith” and “only DEB (without considering pith and DAB)”—little to no changes can be observed (see Figure 3). The added value (information) of DAB for grading is illustrated in Figure 5, which plots the maximum DEB against maximum DAB values for all ash and maple boards. The paired values (boards) on the bisector show those boards, where the maximum DEB is bigger than or equal to any found DAB. For all other boards a DAB greater then the DEB is reported. The grey area indicates those boards, for which the criterion DAB leads to a sorting class downgrading, when sorting according to for DIN 4074-5 [16]. This is the case for only twelve maple boards (3.7%) and three ash boards (1.4%). Therefore, the criterion knot cluster (DAB) is not decisive for downgrading into a lower sorting class, if graded after DIN 4074-5 [16].

This confirms the findings made by other authors for the hardwood species beech. Frese and Riedler [38] postulate that for flat sawn beech lamellas (with lying annual rings) the sorting criterion DAB is not decisive for downgrading. Glos and Lederer [33] state that out of 219 beech boards only for one board the criterion DAB is sorting class determining. Blaß et al. [2] find similar results for a set of 350 beech boards (for 1.4% DAB decisive) and another set of 1888 beech boards (for 0.4% DAB decisive).

When applying stricter boundary values for the DAB than stated by the DIN 4074-5 [16], the DAB´s influence on the grade rises. In the combined grading proposed by Kovryga et al. [31], the boundary values for DEB and DAB for ash were set to be identical—i.e., the strictest DAB setting possible. Thus, 13.6% of the ash lamellas of this study are downgraded due to the criterion DAB (cluster knot). For maple grading according to the settings proposed by Kovryga et al. [31] only 6.5% of the studied lamellas are downgraded due to the criterion DAB (cluster knot). This is because the proposed DAB boundary values for maple are not as strict as for ash. Regarding knot clusters (DAB), Figure 5 suggests that the investigated maple wood contains proportionally more knot clusters than the ash wood. Further analysis reveals only a difference of 6%, though. A total of 33% of the ash boards and 39% of the maple boards contain knot clusters (greater than the max. DEB). Figure 6 shows that these maximum knot clusters are bigger in the maple collective than in the ash collective. The same holds for single knots. This leads to a higher proportion of LS7 and LS10 boards in the maple collective compared to the ash group (see Figure 3).

In general, special care must be taken when comparing grading results of different publications. The research material can be extremely diverse (i.e., species, origin, quality, sawing pattern, etc.), but also data acquisition for grading can be different. For example, Glos and Torno [28] grade the evaluated lumber only after the sorting criteria occurring within the tension test length, while for this study the entire board length is evaluated. Furthermore, the sorting criterion “grain angle” is a source of confusion, since its visual determination on unbroken boards is problematic [33,34].

5.3.2. Yields of Graded Lumber

The four sorting schemes presented in Figure 3 lead to different rates of so-called “rejects”, i.e., boards that have to be sorted out.

Table 8. Volume yields for the production step grading (from planed board to graded lamella) for four different grading schemes.

Product	Options for Production Step Grading	Maple				Ash
		Yield		Waste/Loss		Yield		Waste/Loss
		in m³	in %	in m³	in % PS	in m³	in %	in m³	in % PS
Boards planed (unsorted lamellas)		3.3	20.9			2.6	18.2
	Grading I (Combined grading according to Kovryga et al. [31])			0.5	15.7			0.2	6.8
Combined grading lamellas		2.8	17.8			2.4	17.0
	Grading II (4074-5)			1.3	39.0			1.3	49.8
4074-5 lamellas		2.0	12.7			1.3	9.1
	Grading III (4074-5 without pith)			0.04	1.3			0	0
4074-5 lamellas without pith		3.3	20.6			2.6	18.2
	Grading IV (4074-5, only DEB)			0.02	0.7			0	0
4074-5 lamellas (only DEB)		3.3	20.8			2.6	18.2

lists the relative and absolute losses for the production step “grading” for each grading scheme and the resulting overall yields (referring to the round wood volume).

When grading the lamellas according to DIN 4074-5 [16], for ash yield values lie around 9%, for maple around 13%. When excluding the sorting criterion “pith”, total yields of ash are doubled (18.2%), those of maple rise to 20.6%. The difference between grading scheme III and IV is very little to none. This is due to the fact that the DAB (KC) has very little influence on the strength grading according to DIN 4074-5 [16].

As Table 8 shows, excluding the sorting criterion pith from the sorting scheme, raises the final yield considerably. Since board tension strength is the key influencing factor on glulam bending strength, tension testing of glulam lamellas has to show the effect the pith has on the board tension strength and stiffness (see [31]). If this influence is neglectable, the yield of grading can be raised extremely. It is important to state, though, that this does not hold equally for other strength properties. Glos and Torno [28], for example, prove for ash and maple that pith has a significant influence on the bending strength of square-edged lumber. They also stress the fact that the appearance of pith is often accompanied by bows, twists, and cracks. Similar results are presented by Glos and Lederer [33] for beech and oak square-edged lumber. Hübner [39] proves the pith’s significant influence on the tension strength perpendicular to grain of ash glulam.

Further research has to work towards a hardwood strength grading system that is based on the mechanical properties of the resulting glulam. Kovryga et al. [31] proposes different optimized grading schemes for ash and maple glulam lamellas. For this study, one optimized combined grading solution from Kovryga et al. [31] was chosen for each species (see Table 3) to show an example of resulting yield. The chosen grading scheme distinguishes between three grades resulting in three board tensile strength classes based on destructive tension testing. For ash, the lowest class is DT22 with a characteristic tensile strength higher than 22 N/mm². For hardwoods, Kovryga et al. [40] proposes no tensile strength class lower than DT18. For lower mechanical properties softwood T-classes can be used. Therefore, for maple the lowest class is T15 (softwood tensile strength class) with a characteristic tensile strength not lower than 15 N/mm² (see Table 3). In this study, the proposed strength grading results in 15.7% rejects for maple and 6.8% rejects for ash. The resulting yields of 17.8% and 17.0% are considerably higher compared to grading according to DIN 4074-5 [16].

The economic feasibility of the production of hardwood glulam is strongly influenced by the final yield of glulam lamellas. Torno et al. [12] calculated that the production of beech glulam lamellas costs at least three times as much as that of spruce lamellas, calculating with beech round wood prices of €53.50–€80.00 per cubic meter. Since final yield figures of this study and Torno et al. [12] lie in a similar range, these costs can also be assumed for the lamellas of this study. This makes raising the yield inevitable, if a competitive hardwood product shall be produced.

When evaluating the competitiveness of a product, not only the production cost, but also the added value should be considered. Following the proposed combined grading of Kovryga et al. [31], for this study strength classes with a characteristic tensile strength as high as 38 N/mm² can be produced. With ash lamellas of this characteristic strength, glulam with bending strength values of as high as 48 N/mm² can be achieved [4]. Via “upgrading”, i.e., cutting out large knots, the characteristic tensile strength of ash lamellas can be raised up to 54 N/mm² [31]. Using the combined grading approach for beech lamellas, Erhardt et al. [41] report tensile strength values of as high as 50 N/mm². This raised strength allows the production of more slender structures, which means material savings but also more construction possibilities for the architect and engineer. The listed benefits would yield obviously in higher reward for the producer. Although the present market situation has not led to a wide spread use of hardwood glulam, future changes in spruce availability, round wood prices (especially hardwood) and wood processing technology (etc.) might make the production lucrative.

6. Conclusions

For this study, the volume yields of the production of glulam lamellas from low quality and low dimension ash and maple log sections are investigated. For this purpose, 16.25 m³ of maple (81 log sections) and 14.89 m³ of ash (79 log sections) were harvested from natural forest stands (mixed beech forests) in central Germany and were turned into dry-dressed lumber (unsorted lamellas) with state of the art technologies. The resulting board volumes amount for only 20.9% (maple) and 18.2% (ash) of the original log volumes. The most waste is produced in the production step “presorting and planing” (maple: 56%; ash: 60%), since here a high percentage of the boards has to be sorted out due to bowing. By trimming these boards to shorter lengths, the waste of this production step could be reduced considerably. In addition, the sawing (milling) of the boards produced in both cases around 50% waste, which is in line with the above-mentioned literature values for sawing low-quality hardwoods. Nonetheless, with an adjusted sawing technology, this waste can be reduced (e.g., through shorter log sections and optimized machine combinations). It is also advisable to define a minimum input log diameter, since the lower the log diameter is, the lower the volume yield of milling becomes. Another approach to a raised final volume and value yield is the diversification of final products. Thus, as an example, glulam lamellas could be produced as a low-quality co-product from the production of high quality lumber for furniture production.

Strength grading of lamellas lowers final volume yields even further. When sorting the lamellas according to DIN 4074-5 [16], final volume yields of 12.7% for maple and 9.1% for ash are attained. One way of raising the final volume and also value yield could be the adjustment of the sorting (grading) scheme. For example, by excluding the criterion “pith” from sorting, final yield values of 20.6% (maple) and 18.2% (ash) can be achieved. Generally, it is advisable to combine visual and machine sorting to an assortment and species adjusted combined grading, which is optimized after the criteria “desired tensile strength and stiffness” but also “yield”. The paper Kovryga et al. [31] is attempting this. Resulting total yields, when applying the selected optimized combined grading of Kovryga et al. [31] to this study´s lumber, lie between 17% and 18%. This yield is considerably lower than that obtained for softwood glulam lamellas. Factors like the higher attainable tensile strength, if compared to 30 N/mm² possible for softwoods [42], and the appealing appearance of hardwood glulam may make up for the yield disadvantages. In general, the economic feasibility of hardwood glulam is influenced by a serious of factors, which have to be analyzed in detail for each final product and production plant separately.