Circumferential and Longitudinal δ13C Variability in a Larix decidua Trunk from the Swiss Alps
Abstract
1. Introduction
2. Materials and Methods
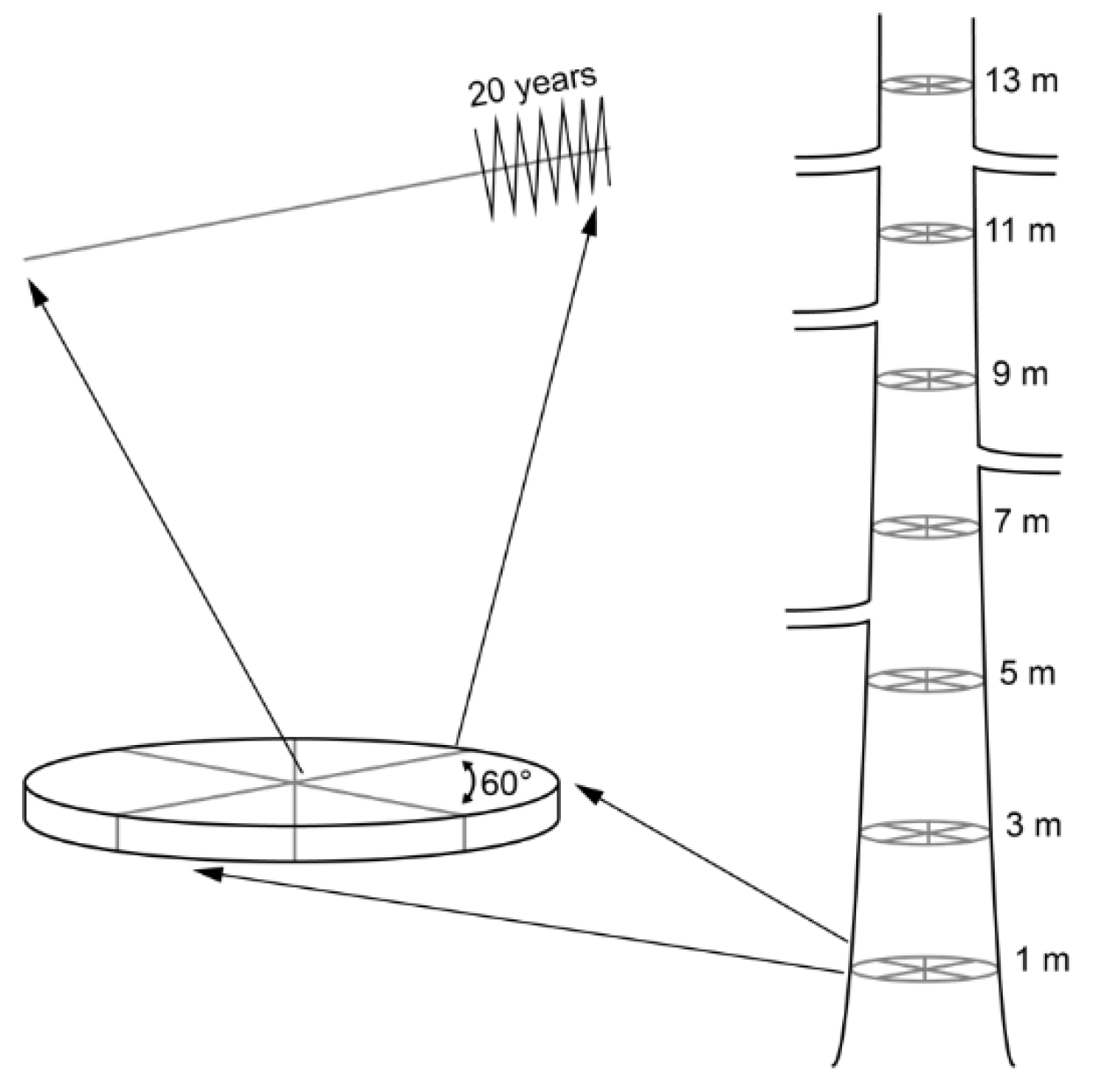
2.1. Site Description and Sample Preparation
2.2. Stable Isotope Measurement and Analysis
3. Results and Discussion
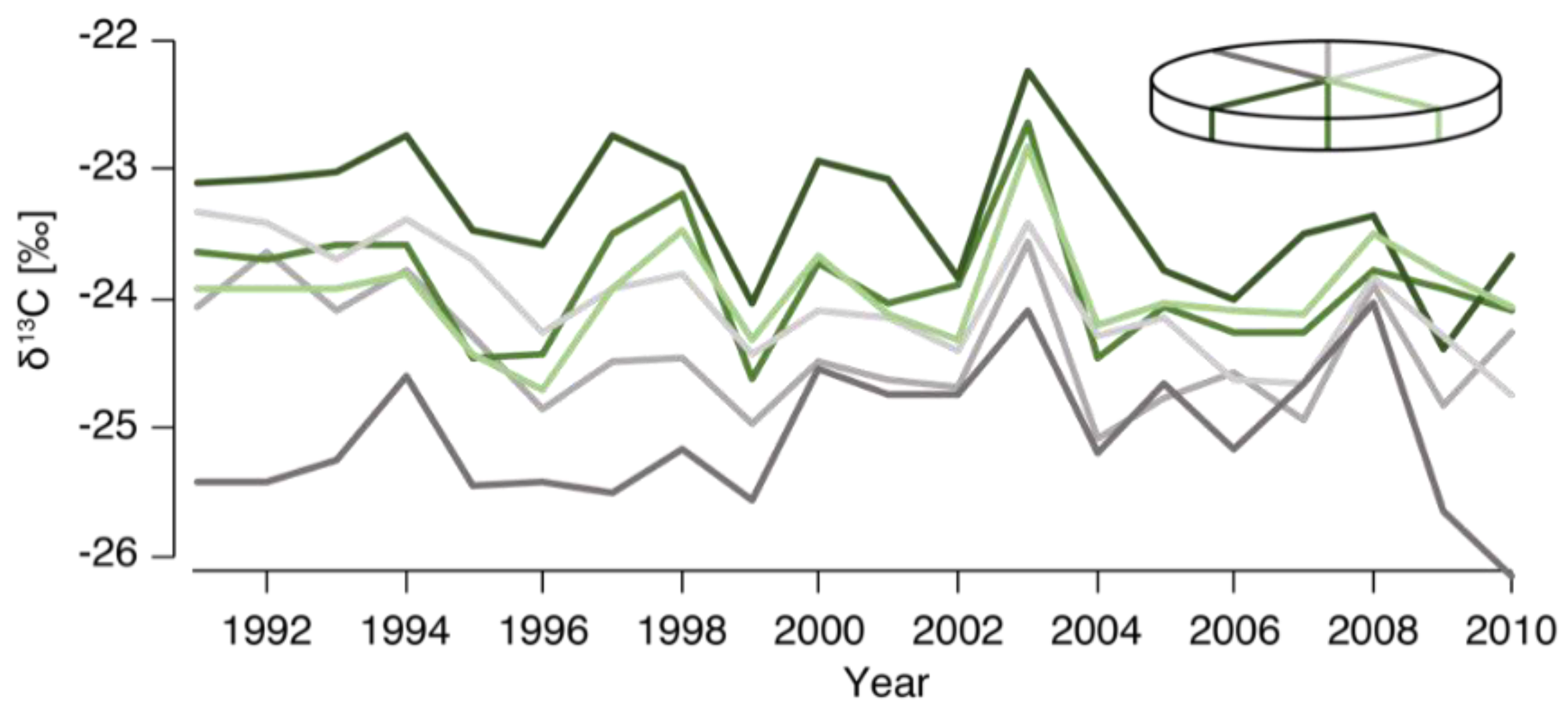
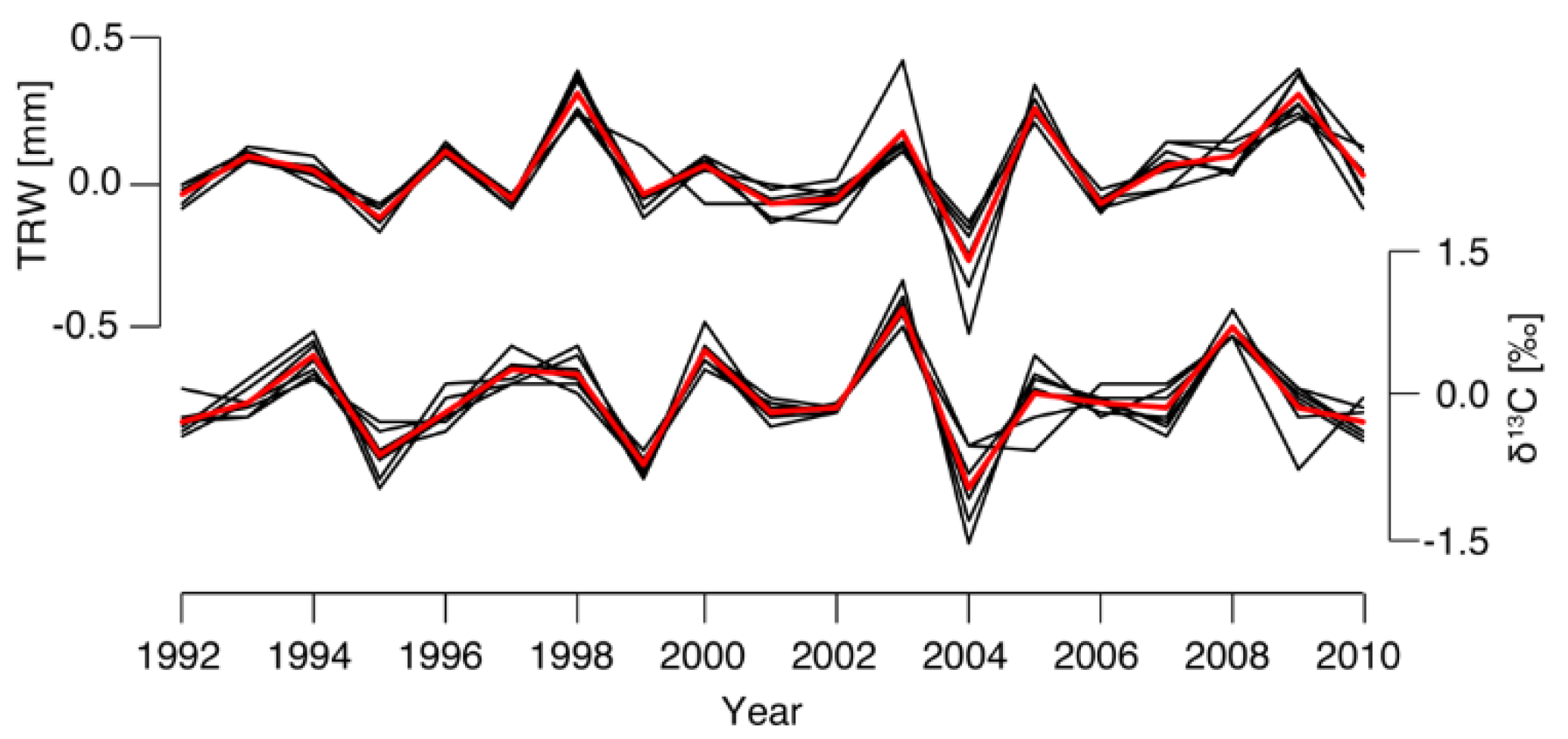
3.1. Circumferential Variability
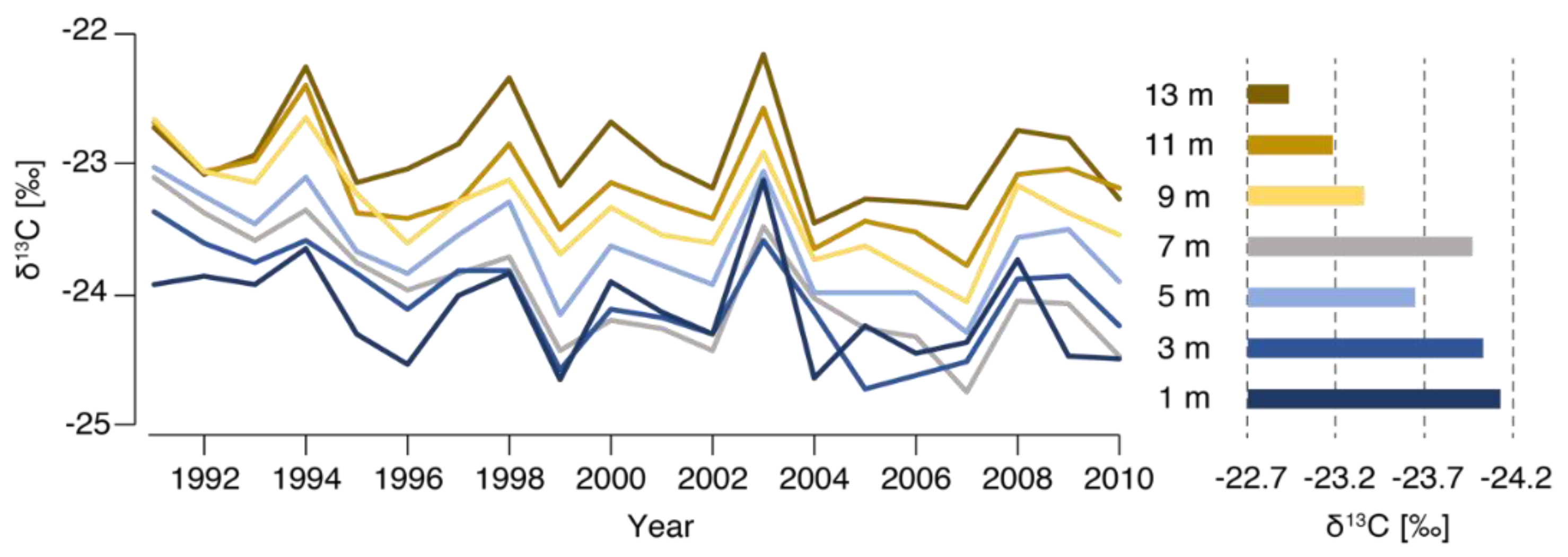
3.2. Longitudinal Variability
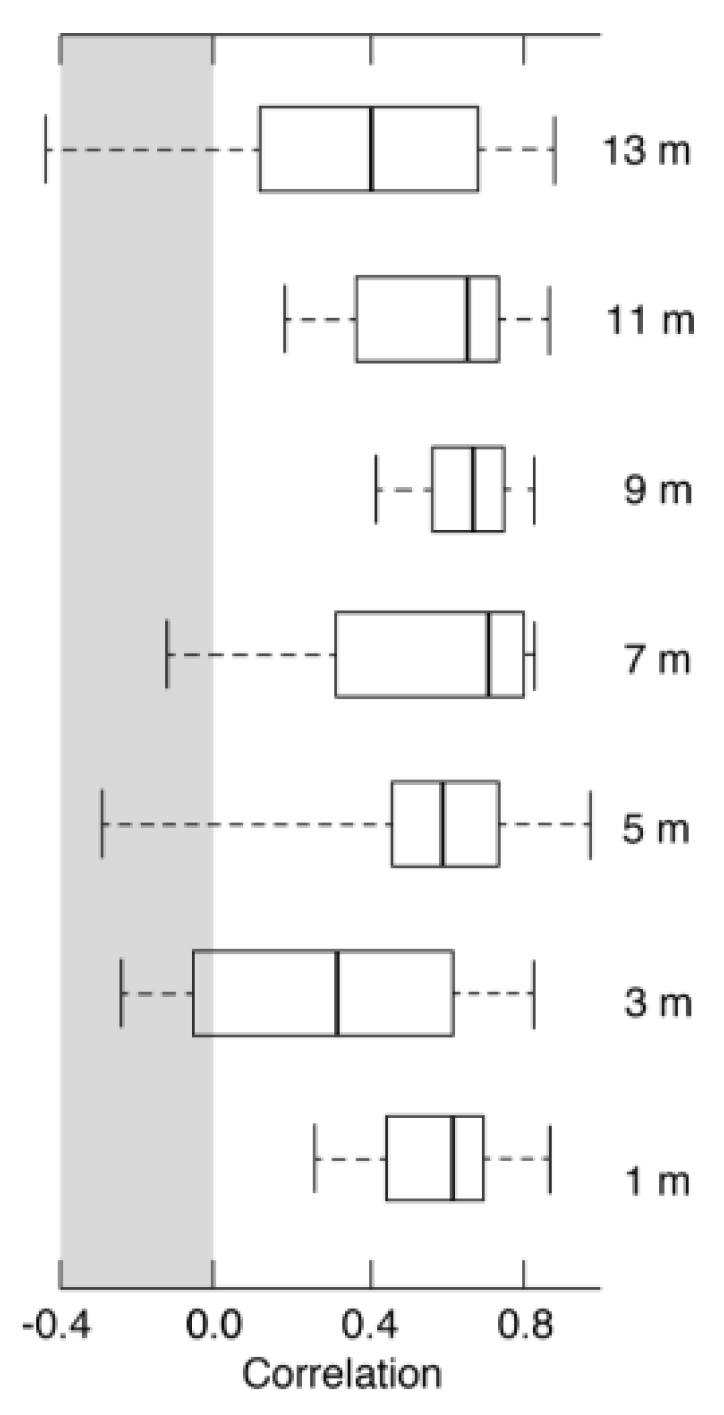
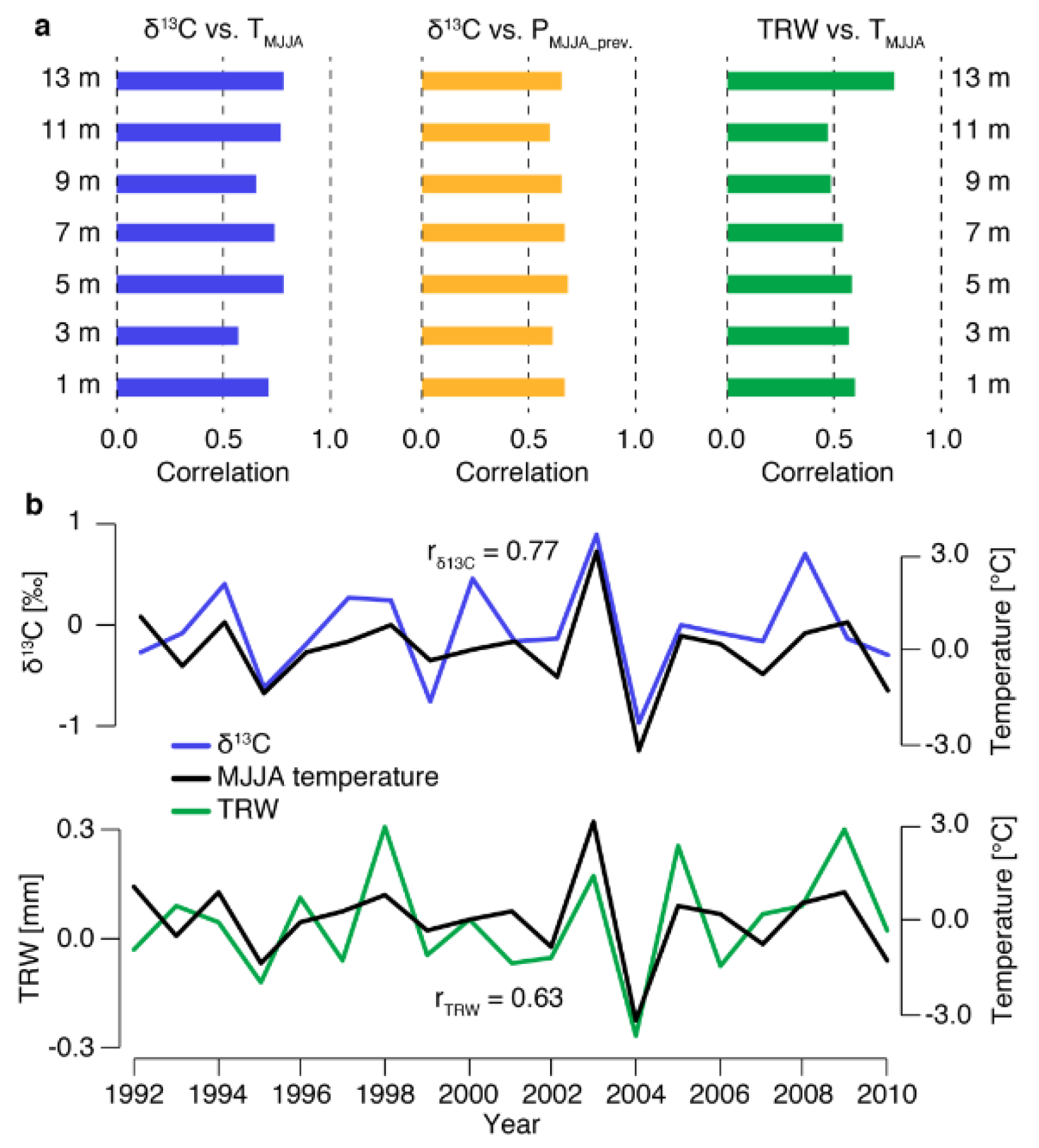
3.3. Climate Signals
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Esper, J.; Konter, O.; Krusic, P.; Saurer, M.; Holzkämper, S.; Büntgen, U. Long-term summer temperature variations in the Pyrenees from detrended stable carbon isotopes. Geochronometria 2015, 42, 53–59. [Google Scholar] [CrossRef]
- Szymczak, S.; Joachimski, M.M.; Bräuning, A.; Hetzer, T.; Kuhlemann, J. A 560yr summer temperature reconstruction for the Western Mediterranean basin based on stable carbon isotopes from Pinus nigra ssp. laricio (Corsica/ France). Clim. Past 2012, 8, 1737–1749. [Google Scholar] [CrossRef]
- Holzkämper, S.; Kuhry, P.; Kultti, S.; Gunnarson, B.E.; Sonninen, E. Stable isotopes in tree rings as proxies for winter precipitation changes in the Russian Arctic over the past 150 years. Geochronometria 2008, 32, 37–46. [Google Scholar] [CrossRef]
- Treydte, K.; Schleser, G.H.; Helle, G.; Frank, D.C.; Winiger, M.; Haug, G.H.; Esper, J. The twentieth century was the wettest period in Northern Pakistan over the past millennium. Nature 2006, 440, 1179–1182. [Google Scholar] [CrossRef] [PubMed]
- Kress, A.; Saurer, M.; Siegwolf, R.T.W.; Frank, D.C.; Esper, J.; Bugmann, H. A 350 year drought reconstruction from Alpine tree ring stable isotopes. Glob. Biogeochem. Cycl. 2010, 24, 2. [Google Scholar] [CrossRef]
- Leavitt, S.W.; Chase, T.N.; Rajagopalan, B.; Lee, E.; Lawrence, P.J.; Woodhouse, C.A. Southwestern US drought maps from pinyon tree-ring carbon isotopes. Eos Trans. 2007, 88, 39–40. [Google Scholar] [CrossRef]
- Helama, S.; Arppe, L.; Timonen, M.; Mielikäinen, K.; Oinonen, M. A 7.5 ka chronology of stable carbon isotopes from tree rings with implications for their use in palaeo-cloud reconstruction. Glob. Planet. Chang. 2018, 170, 20–33. [Google Scholar] [CrossRef]
- Loader, N.J.; Young, G.H.F.; Grudd, H.; McCarroll, D. Stable carbon isotopes from Torneträsk, northern Sweden provide a millennial length reconstruction of summer sunshine and its relationship to Arctic circulation. Quat. Sci. Rev. 2013, 62, 97–113. [Google Scholar] [CrossRef]
- Esper, J.; Holzkämper, S.; Büntgen, U.; Schöne, B.; Keppler, F.; Hartl, C.; St. George, S.; Riechelmann, D.F.C.; Treydte, K. Site-specific climatic signals in stable isotope records from Swedish pine forests. Trees 2018, 32, 855–869. [Google Scholar] [CrossRef]
- Konter, O.; Holzkämper, S.; Helle, G.; Büntgen, U.; Saurer, M.; Esper, J. Climate sensitivity and parameter coherency in annually resolved δ13C and δ18O from Pinus uncinata tree-ring data in the Spanish Pyrenees. Chem. Geol. 2014, 377, 12–19. [Google Scholar] [CrossRef]
- Tardif, J.C.; Conciatori, F.; Leavitt, S.W. Tree rings, δ13C and climate in Picea glauca growing near Churchill, subarctic Manitoba, Canada. Chem. Geol. 2008, 252, 88–101. [Google Scholar] [CrossRef]
- Kłusek, M.; Grabner, M.; Pawełczyk, S.; Pawlyta, J. An 1800-year stable carbon isotope chronology based on sub-fossil wood from Lake Schwarzensee, Austria. Palaeogeogr. Palaeoclimatol. Palaeoecol. 2019, 514, 65–76. [Google Scholar] [CrossRef] [PubMed]
- Sidorova, O.V.; Siegwolf, R.; Saurer, M.; Naurzbaev, M.M.; Vaganov, E.A. Isotopic composition (δ13C, δ18O) in wood and cellulose of Siberian larch trees for early medieval and recent periods. J. Geophys. Res. 2008, 113, G2. [Google Scholar] [CrossRef]
- Sass-Klaassen, U.; Poole, I.; Wils, T.; Helle, G.; Schleser, G.H.; van Bergen, P.F. Carbon and oxygen isotope dendrochronology in sub- fossil bog oak tree rings—A preliminary study. IAWA J. 2005, 26, 121–136. [Google Scholar] [CrossRef]
- Kłusek, M.; Pawełczyk, S. Stable carbon isotope analysis of subfossil wood from Austrian Alps. Geochronometria 2014, 41, 400–408. [Google Scholar] [CrossRef]
- Etien, N.; Daux, V.; Masson-Delmotte, V.; Stievenard, M.; Bernard, V.; Durost, S.; Guillemin, M.T.; Mestre, O.; Pierre, M. A bi-proxy reconstruction of Fontainebleau (France) growing season temperature from A.D. 1596 to 2000. Clim. Past 2008, 4, 1–16. [Google Scholar] [CrossRef]
- Hangartner, S.; Kress, A.; Saurer, M.; Frank, D.; Leuenberger, M. Methods to merge overlapping tree-ring isotope series to generate multi-centennial chronologies. Chem. Geol. 2012, 294, 127–134. [Google Scholar] [CrossRef]
- Haupt, M.; Weigl, M.; Grabner, M.; Boettger, T. A 400-year reconstruction of July relative air humidity for the Vienna region (eastern Austria) based on carbon and oxygen stable isotope ratios in tree-ring latewood cellulose of oaks (Quercus petraea Matt. Liebl.). Clim. Chang. 2011, 105, 243–262. [Google Scholar] [CrossRef]
- Kress, A.; Hangartner, S.; Bugmann, H.; Büntgen, U.; Frank, D.C.; Leuenberger, M.; Siegwolf, R.T.W.; Saurer, M. Swiss tree rings reveal warm and wet summers during medieval times. Geophys. Res. Lett. 2014, 41, 1732–1737. [Google Scholar] [CrossRef]
- Masson-Delmotte, V.; Raffalli-Delerce, G.; Danis, P.A.; Yiou, P.; Stievenard, M.; Guibal, F.; Jouzel, J.; Mestre, O.; Bernard, V.; Goosse, H.; et al. Changes in European precipitation seasonality and in drought frequencies revealed by a four-century-long tree-ring isotopic record from Brittany, western France. Clim. Dyn. 2005, 24, 57–69. [Google Scholar] [CrossRef]
- Büntgen, U.; Bellwald, I.; Kalbermatten, H.; Schmidhalter, M.; Frank, D.C.; Freund, H.; Bellwald, W.; Neuwirth, B.; Nüsser, M.; Esper, J. 700 years of settlement and building history in the Lötschental, Switzerland. Erdkunde 2006, 60, 96–112. [Google Scholar] [CrossRef]
- Fritts, H.C. Tree Rings and Climate; Academic Press: London, UK, 1976. [Google Scholar]
- Tegel, W.; Vanmoerkerke, J.; Büntgen, U. Updating historical tree-ring records for climate reconstruction. Quat. Sci. Rev. 2010, 29, 1957–1959. [Google Scholar] [CrossRef]
- Esper, J.; Frank, D.C.; Battipaglia, G.; Büntgen, U.; Holert, C.; Treydte, K.; Siegwolf, R.; Saurer, M. Low-frequency noise in δ13C and δ18O tree ring data: A case study of Pinus uncinata in the Spanish Pyrenees. Glob. Biogeochem. Cycl. 2010, 24, 4. [Google Scholar] [CrossRef]
- Helama, S.; Arppe, L.; Timonen, M.; Mielikäinen, K.; Oinonen, M. Age-related trends in subfossil tree-ring δ13C data. Chem. Geol. 2015, 416, 28–35. [Google Scholar] [CrossRef]
- Leavitt, S.W. Tree-ring C–H–O isotope variability and sampling. Sci. Total Environ. 2010, 408, 5244–5253. [Google Scholar] [CrossRef] [PubMed]
- Mazany, T.; Lerman, J.C.; Long, A. Carbon-13 in tree-ring cellulose as an indicator of past climates. Nature 1980, 287, 432–435. [Google Scholar] [CrossRef]
- Tans, P.P.; Mook, W.G. Past atmospheric CO2 levels and the 13C/12C ratios in tree rings. Tellus 1980, 32, 268–283. [Google Scholar] [CrossRef][Green Version]
- Hemmann, A.G. Umweltrelevanz von δ13C Korrrelationen an Jahrringen Rezenter Kiefern (Pinus Sylvestris). Ph.D. Thesis, University of Cologne, Cologne, Germany, 1993. [Google Scholar]
- Leavitt, S.W.; Long, A. Sampling strategy for stable carbon isotope analysis of tree rings in pine. Nature 1984, 311, 145–147. [Google Scholar] [CrossRef]
- Francey, R.J. Tasmanian tree rings belie suggested anthropogenic 13C/12C trends. Nature 1981, 290, 232–235. [Google Scholar] [CrossRef]
- Stuiver, M.; Braziunas, T.F. Tree cellulose 13C/12C isotope ratios and climate change. Nature 1987, 328, 58–60. [Google Scholar] [CrossRef]
- Ramesh, R.; Bhattacharya, S.K.; Gopalan, K. Dendrochronological implications of isotope coherence in trees from Kashmir Valley, India. Nature 1985, 317, 802–804. [Google Scholar] [CrossRef]
- Robertson, I.; Field, E.M.; Heaton, T.H.E.; Pilcher, J.R.; Pollard, M.; Switsur, R.; Waterhouse, J.S. Isotope coherence in oak cellulose. In Problems of Stable Isotopes in Tree-Rings, Lake Sediments and Peat-Bogs as Climatic Evidence for the Holocene; Frenzel, B., Stauffer, B., Weib, M.M., Eds.; G. Fischer: Stuttgart, Germany, 1995; pp. 141–155. [Google Scholar]
- Nguyen-Queyrens, A.; Ferhi, A.; Loustau, D.; Guehl, J.M. Within-ring δ13C spatial variability and interannual variations in wood cellulose of two contrasting provenances of Pinus pinaster. Can. J. For. Res. 1998, 28, 766–773. [Google Scholar] [CrossRef]
- Chen, B.; Qian, J.; Pu, P.; Wang, G.; Tu, Q. Azimuthal distribution of stable carbon isotopes in tree rings and its application in climate reconstructions. J. Nanjing Inst. Meteorol. 2002, 25, 463–471. (In Chinese) [Google Scholar]
- De Silva, M.P. δ13C -Variationen in Baumjahresringen als Folge des Anthropogenen CO2-Anstiegs der Atmosphäre: Untersuchung des Einflusses von Klimaparametern. Ph.D. Thesis, Rheinisch-Westfälische Hochschule, Aachen, Germany, 1978. [Google Scholar]
- Leavitt, S.W.; Long, A. Stable-carbon isotope variability in tree foliage and wood. Ecology 1986, 67, 1002–1010. [Google Scholar] [CrossRef]
- Freyer, H.D.; Wiesberg, L. Anthropogenic carbon-13 decrease in atmospheric carbon dioxide as recorded in modem wood. In FAO/IAEA Symposium on Isotope Ratios as Pollutant Source and Behavior Indicators; International Atomic Energy Association: Vienna, Austria, 1975; pp. 49–62. [Google Scholar]
- Schleser, G.H. δ13C pattern in a forest tree as an indicator of carbon transfer in trees. Ecology 1992, 73, 1922–1925. [Google Scholar] [CrossRef]
- Vogel, J.C. Recycling of carbon in a forest environment. Oecologia Plant 1978, 13, 89–94. [Google Scholar]
- Francey, R.J.; Gifford, R.M.; Sharkey, T.D.; Weir, B. Physiological influences on carbon isotope discrimination in huon pine (Lagarostrobos franklinii). Oecologia 1985, 66, 211–218. [Google Scholar] [CrossRef]
- Ehleringer, J.R.; Field, C.B.; Lin, Z.F.; Kuo, C.Y. Leaf carbon isotope and mineral composition in subtropical plants along an irradiance cline. Oecologia 1986, 70, 520–526. [Google Scholar] [CrossRef]
- Duursma, R.A.; Marshall, J.D. Vertical canopy gradients in δ13C correspond with leaf nitrogen content in a mixed-species conifer forest. Trees 2006, 20, 496–506. [Google Scholar] [CrossRef]
- Büntgen, U.; Esper, J.; Frank, D.C.; Nicolussi, K.; Schmidhalter, M. A 1052-year tree-ring proxy for Alpine summer temperatures. Clim. Dyn. 2005, 25, 141–153. [Google Scholar] [CrossRef]
- Büntgen, U.; Frank, D.C.; Nievergelt, D.; Esper, J. Summer temperature variations in the European Alps, A.D. 755-2004. J. Clim. 2006, 19, 5606–5623. [Google Scholar] [CrossRef]
- Badalotti, A.; Anfodillo, T.; Grace, J. Evidence of osmoregulation in Larix decidua at Alpine treeline and comparative responses to water availability of two co-occurring evergreen species. Ann. For. Sci. 2000, 57, 623–633. [Google Scholar] [CrossRef]
- Moser, L.; Fonti, P.; Büntgen, U.; Esper, J.; Luterbacher, J.; Franzen, J.; Frank, D. Timing and duration of European larch growing season along altitudinal gradients in the Swiss Alps. Tree Phys. 2009, 30, 225–233. [Google Scholar] [CrossRef] [PubMed]
- Holmes, R.L. Computer-assisted quality control in tree-ring dating and measurement. Tree Ring Bull. 1983, 43, 69–78. [Google Scholar]
- Rinn, F. TSAP-Win Professional; Rinntech: Heidelberg, Germany, 2007. [Google Scholar]
- Cullen, L.E.; Grierson, P.F. Is cellulose extraction necessary for developing stable carbon and oxygen isotopes chronologies from Callitris glaucophylla? Palaeogeogr. Palaeoclimatol. Palaeoecol. 2006, 236, 206–216. [Google Scholar] [CrossRef]
- Riechelmann, D.F.C.; Maus, M.; Dindorf, W.; Konter, O.; Schöne, B.R.; Esper, J. Comparison of δ13C and δ18O from cellulose, whole wood, and resin-free whole wood from an old high elevation Pinus uncinata in the Spanish central Pyrenees. Isot. Environ. Health Stud. 2016, 52, 694–705. [Google Scholar] [CrossRef]
- Knöller, K.; Boettger, T.; Weise, S.M.; Gehre, M. Carbon isotope analyses of cellulose using two different on-line techniques (elemental analysis and high-temperature pyrolysis)—A comparison. Rap. Commun. Mass Spectrom. 2005, 19, 343–348. [Google Scholar] [CrossRef]
- Treydte, K.S.; Frank, D.C.; Saurer, M.; Helle, G.; Schleser, G.H.; Esper, J. Impact of climate and CO2 on a millennium-long tree-ring carbon isotope record. Geochim. Cosmochim. Acta 2009, 73, 4635–4647. [Google Scholar] [CrossRef]
- Frank, D.C.; Poulter, B.; Saurer, M.; Esper, J.; Huntingford, C.; Helle, G.; Treydte, K.; Zimmermann, N.E.; Schleser, G.H.; Ciais, P.; et al. Water-use efficiency and transpiration across European forests during the Anthropocene. Nature Clim. Chang. 2015, 5, 579–583. [Google Scholar] [CrossRef]
- Schubert, B.A.; Jahren, A.H. The effect of atmospheric CO2 concentration on carbon isotope fractionation in C3 land plants. Geochim. Cosmochim. Acta 2012, 96, 29–43. [Google Scholar] [CrossRef]
- Kürschner, K. Leaf Stomata as Biosensors of Paleoatmospheric CO2 Levels; LPP Contribution Series 5: Utrecht, The Netherlands, 1996. [Google Scholar]
- Francey, R.J. Carbon isotope measurements in baseline air, forest canopy air, and plants. In The Changing Carbon Cycle; Trabalka, J.R., Reichle, D.E., Eds.; Springer: New York, NY, USA, 1986; pp. 160–174. [Google Scholar]
- Freyer, H.D.; Belacy, N. 13C/12C records in northern hemispheric trees during the past 500 years—Anthropogenic impact and climatic superpositions. J. Geophys. Res. Oceans 1986, 88, 6844–6852. [Google Scholar] [CrossRef]
- Helle, G.; Schleser, G.H. Beyond CO2-fixation by Rubisco—An interpretation of 13C/12C variations in tree rings from novel intra-seasonal studies on broad-leaf trees. Plant Cell Environ. 2004, 27, 367–380. [Google Scholar] [CrossRef]
- Switsur, V.R.; Waterhouse, J.S.; Field, E.M.; Carter, A.H.C.; Loader, N.J. Stable isotope studies in tree rings from oak—Techniques and some preliminary results. Paläoklimaforschung 1995, 15, 129–140. [Google Scholar]
- Farquhar, G.D.; Ehleringer, J.R.; Hubick, K.T. Carbon isotope discrimination and photosynthesis. Annu. Rev. Plant Physiol. Plant Mol. Biol. 1989, 40, 503–537. [Google Scholar] [CrossRef]
- Koch, G.W.; Sillett, S.C.; Jennings, G.M.; Davis, S.D. The limits to tree height. Nature 2004, 428, 851–854. [Google Scholar] [CrossRef]
- Palonen, V.; Pumpanen, J.; Kulmala, L.; Levin, I.; Heinonsalo, J.; Vesala, T. Seasonal and diurnal variations in atmospheric and soil air 14CO2 in a boreal scots pine forest. Radiocarbon 2018, 60, 283–297. [Google Scholar] [CrossRef]
- Kagawa, A.; Sugimoto, A.; Maximov, T.C. Seasonal course of translocation, storage and remobilization of 13C pulse-labeled photoassimilate in naturally growing Larix gmelinii saplings. New Phytol. 2006, 171, 793–803. [Google Scholar] [CrossRef]
- Hafner, P.; Robertson, I.; McCarroll, D.; Loader, N.J.; Gagen, M.; Bale, R.J.; Jungner, H.; Sonninen, E.; Hilasvuori, E.; Levanič, T. Climate signals in the ring widths and stable carbon, hydrogen and oxygen isotopic composition of Larix decidua growing at the forest limit in the southeastern European Alps. Trees 2011, 25, 1141–1154. [Google Scholar] [CrossRef]
- Treydte, K.; Frank, D.; Esper, J.; Andreu, L.; Bednarz, Z.; Berninger, F.; Boettger, T.; Filot, M.; Grabner, M.; Grabner, M.; et al. Signal strength and climate calibration of a European tree-ring isotope network. Geophys. Res. Lett. 2007, 34, 24. [Google Scholar] [CrossRef]


| Circum. Variability | Radii | Resolution/Period | Species | Country | Source |
|---|---|---|---|---|---|
| 0.5–1.0‰ | 5 | decadal over 30 years | Pinus ponderosa | USA | [27] |
| 0.1–4.5‰ | 2 | annual over 19 years | Quercus rubra | Netherlands | [28] |
| 0.5–1.0‰ | 4 | pentadal over 130 years | Phyllocladus asplen. | Tasmania | [31] |
| 0.5–2.0‰ | 4 | annual over 100 years | Picea sitchensis | USA | [32] |
| 0.5–2.5‰ | 4 | annual over 100 years | Nothofagus pumillio | Chile | [32] |
| 0.5–1.2‰ | 8 | pentadal over 80 years | Pinus edulis | USA | [30] |
| 0.5–1.3‰ | 3 | annual over 30 years | Abies pindrow | India | [33] |
| 0.1–2.3‰ | 2 | annual over 73 years | Pinus sylvestris | Germany | [29] |
| 0.5–1.0‰ | 3 | annual over 7 years | Quercus petraea | N. Ireland | [34] |
| 0.5‰ | 8 | 1 ring (1991) in 4 trees | Pinus pinaster | France | [35] |
| 0.9–2.1‰ | 8 | annual over 42 years | Cryptomeria fortune | China | [36] |
| 0.4–1.6‰ | 8 | annual over 24 years | Cryptomeria fortune | China | [36] |
| 0.7–2.0‰ | 8 | annual over 20 years | Abies fabri | China | [36] |
| Longitud. Variability | Levels | Resolution | Species | Country | Source |
|---|---|---|---|---|---|
| 0.01‰/m | 7 levels over 14 m | 7-year group | Quercus robur | Germany | [39] |
| 0.05–0.1‰ | 3 levels over 6 m | 25-year group | Pinus sylvestris | Sweden | [37] |
| 1.0–1.5‰ * | 5 levels over 2 m | 1 year (1981) | Juniperus monosp. | USA | [38] |
| 0.5–1.0‰ * | 5 levels over 2.8 m | 7 years (1975–1981) | Pinyon pine | USA | [38] |
| 0.9‰ * | 8 levels over 28 m | 1 year (1983) | Fagus sylvatica | Germany | [40] |
| 1‰ * | 12 levels over 13 m ** | 1 year (1991) | Pinus pinaster | France | [35] |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Esper, J.; Riechelmann, D.F.C.; Holzkämper, S. Circumferential and Longitudinal δ13C Variability in a Larix decidua Trunk from the Swiss Alps. Forests 2020, 11, 117. https://doi.org/10.3390/f11010117
Esper J, Riechelmann DFC, Holzkämper S. Circumferential and Longitudinal δ13C Variability in a Larix decidua Trunk from the Swiss Alps. Forests. 2020; 11(1):117. https://doi.org/10.3390/f11010117
Chicago/Turabian StyleEsper, Jan, Dana F.C. Riechelmann, and Steffen Holzkämper. 2020. "Circumferential and Longitudinal δ13C Variability in a Larix decidua Trunk from the Swiss Alps" Forests 11, no. 1: 117. https://doi.org/10.3390/f11010117
APA StyleEsper, J., Riechelmann, D. F. C., & Holzkämper, S. (2020). Circumferential and Longitudinal δ13C Variability in a Larix decidua Trunk from the Swiss Alps. Forests, 11(1), 117. https://doi.org/10.3390/f11010117






