The Prediction of Stiffness Reduction Non-Linear Phase in Bamboo Reinforced Concrete Beam Using the Finite Element Method (FEM) and Artificial Neural Networks (ANNs)
Abstract
:1. Introduction
2. Materials and Methods
2.1. Treatment of Materials
2.2. Materials
2.3. Experimental Procedure
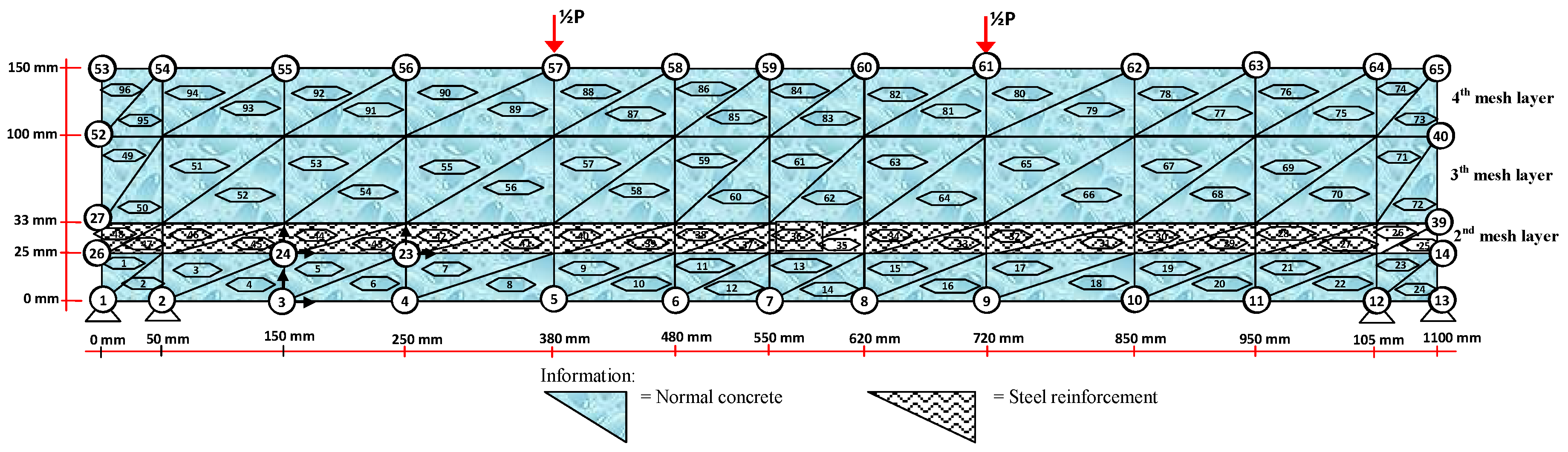
2.4. Validation of Numerical Methods
- Step 1:
- Step 2:
- Calculation and collection of geometry and material data, such as the modulus of elasticity of the material (E), Poisson’s ratio (ν), etc.
- Step 3:
- Writing a programming language for triangular elements using the Fortran PowerStation 4.0 program according to the constitutive relationships and FEM modeling as shown in the following link: http://bit.ly/2F17w8F.
- Step 4:
- Open the Fortran PowerStation 4.0 program. An example is shown at the following link: http://bit.ly/2MTh22j.
- Step 5:
- Write programming language data (Step 3) in the Fortran PowerStation 4.0 program. Examples can be seen at the following link: http://bit.ly/2ZvZWMU.
- Step 6:
- Input DATA.DAT of BRC beam and SRC beam in the Fortran PowerStation 4.0 program. Input data is displayed at the following links: http://bit.ly/351FPqU and http://bit.ly/2MBqas9. An example of displaying input data is shown on the following link: http://bit.ly/2u2K2xR.
- Step 7:
- Analyze the program until there are no warnings and errors. If there are warnings and errors, check and correct program data and input data.
- Step 8:
- Download stress data. The stress data are shown at the following link: http://bit.ly/2rDPeaI for the stress of BRC beam, and http://bit.ly/2Q4Ihc1 for the stress of the SRC beam. An example of displaying stress data from the Fortran PowerStation 4.0 program is shown at the following link: http://bit.ly/2ZybLCd.
- Step 9:
- Download displacement data. An example of displaying data displacement from the Fortran PowerStation 4.0 program is shown on the following link: http://bit.ly/2Q7j2Wp.
- Step 10:
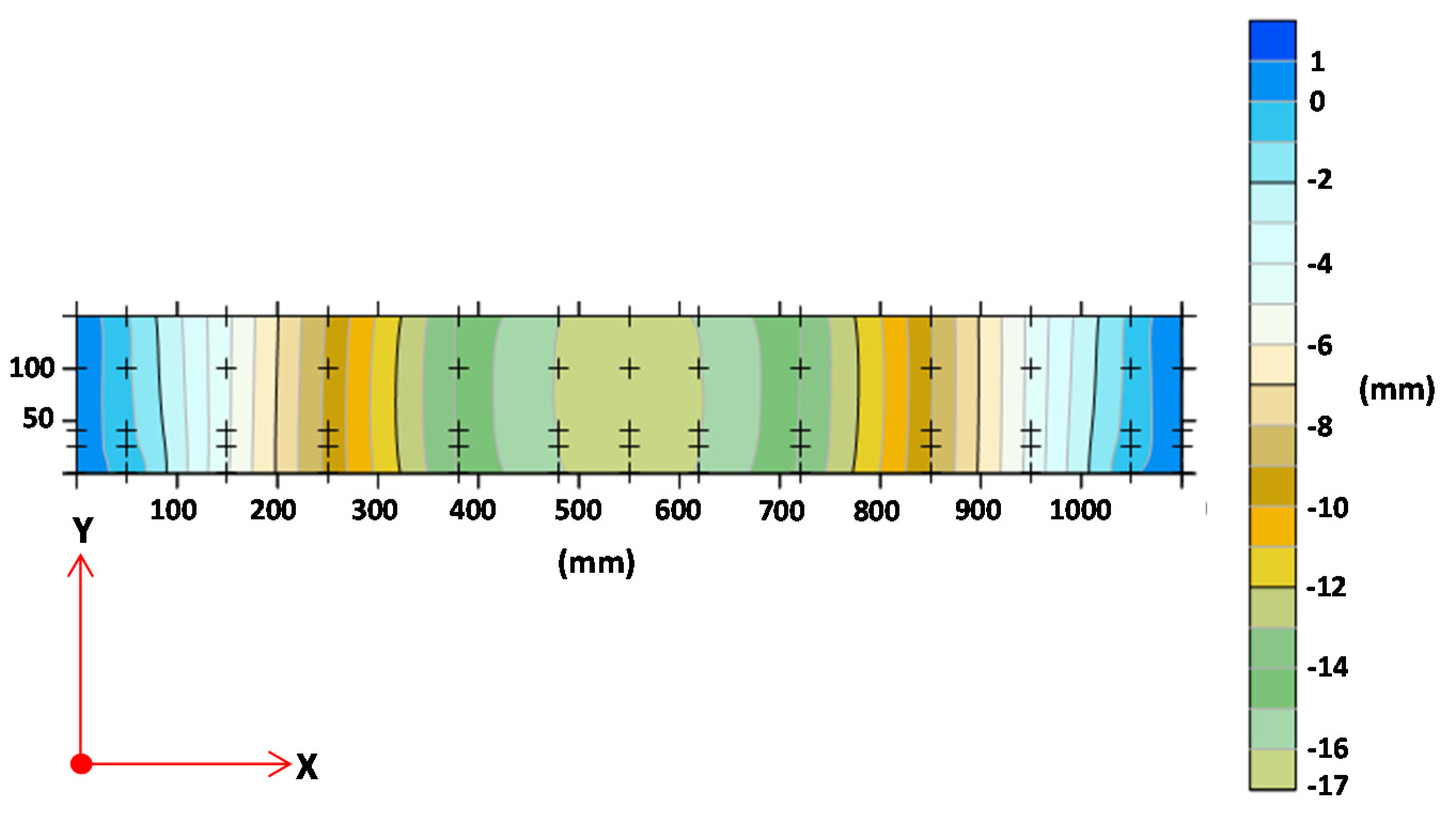
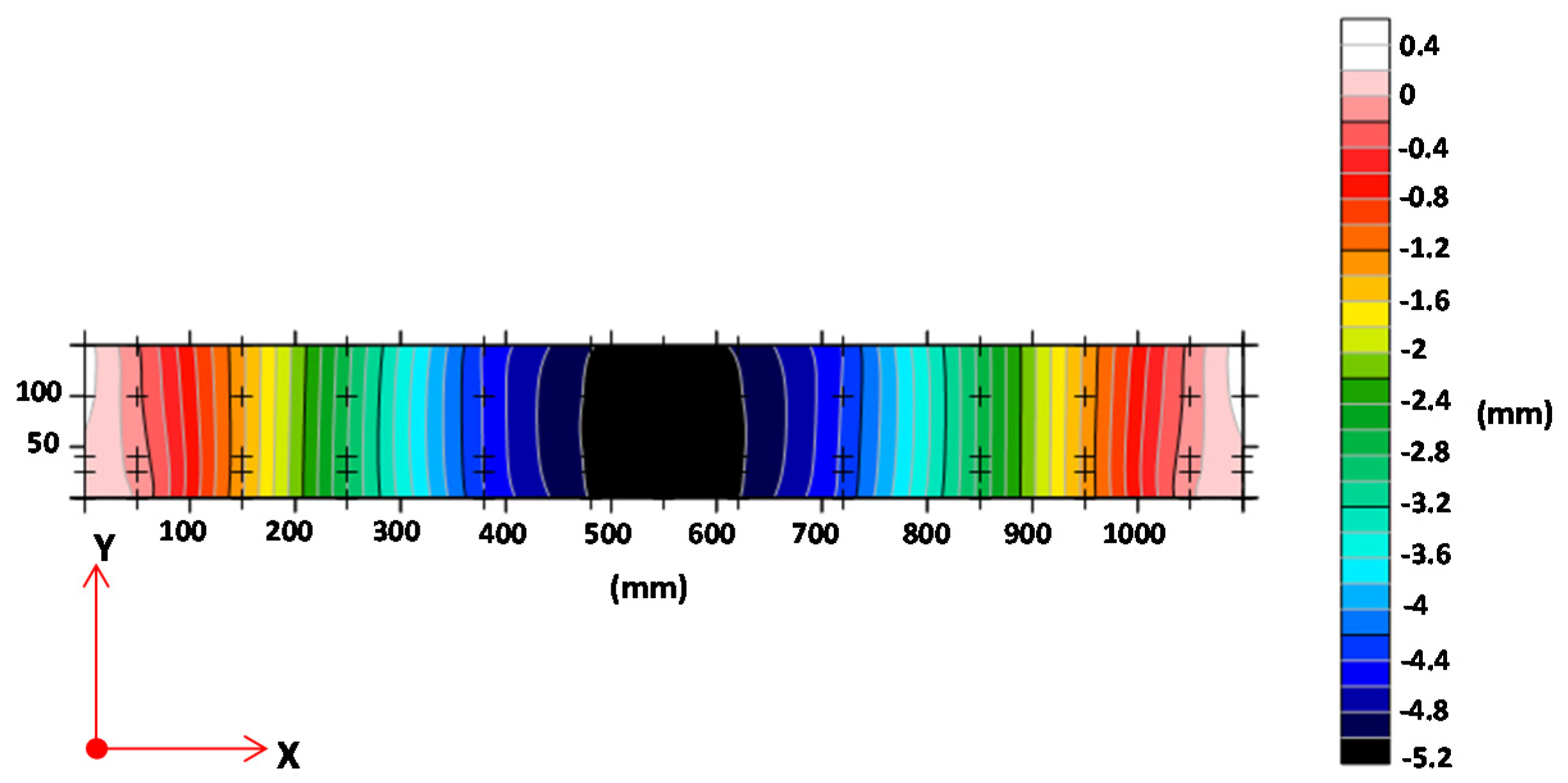
- Enter stress and displacement data into the Surfer program to obtain contour image data of stress and displacement. Stress and displacement contour image data.
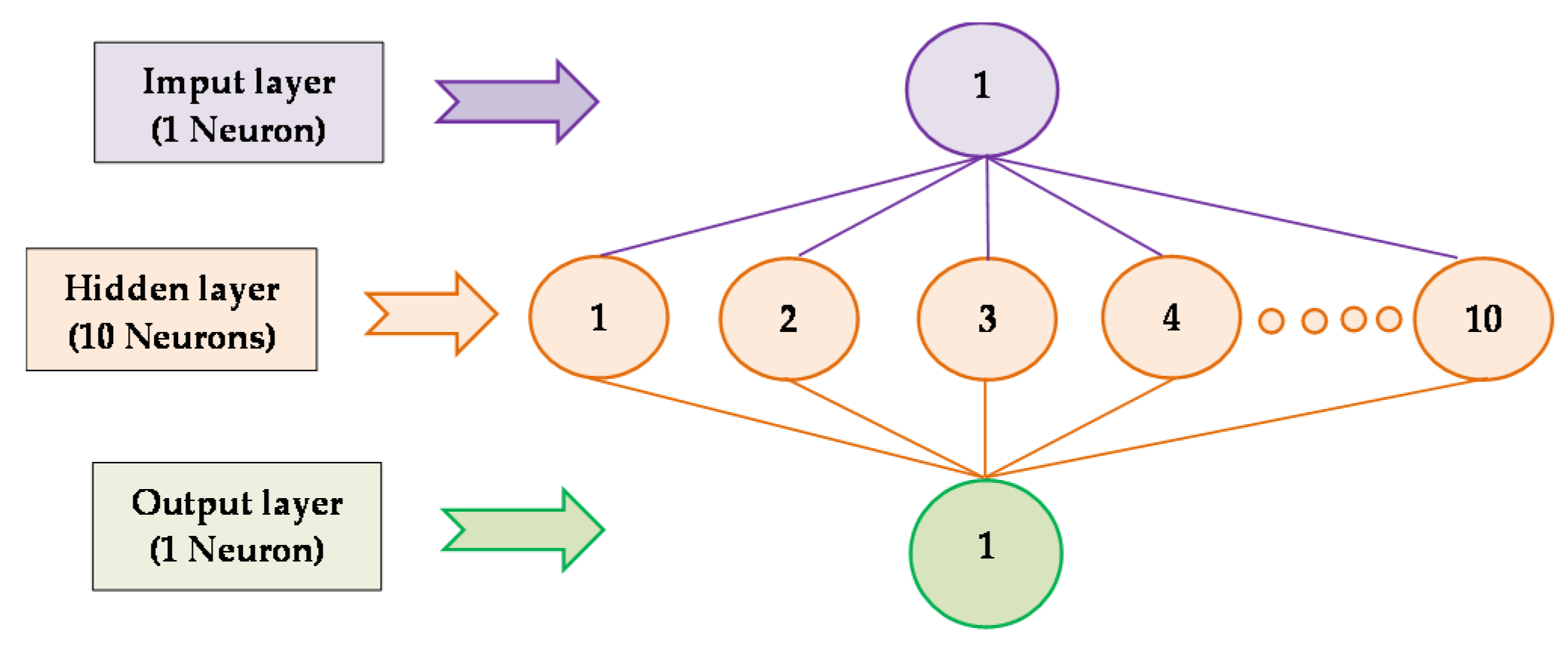
2.5. Validation of Artificial Neural Networks (ANN)
3. Results
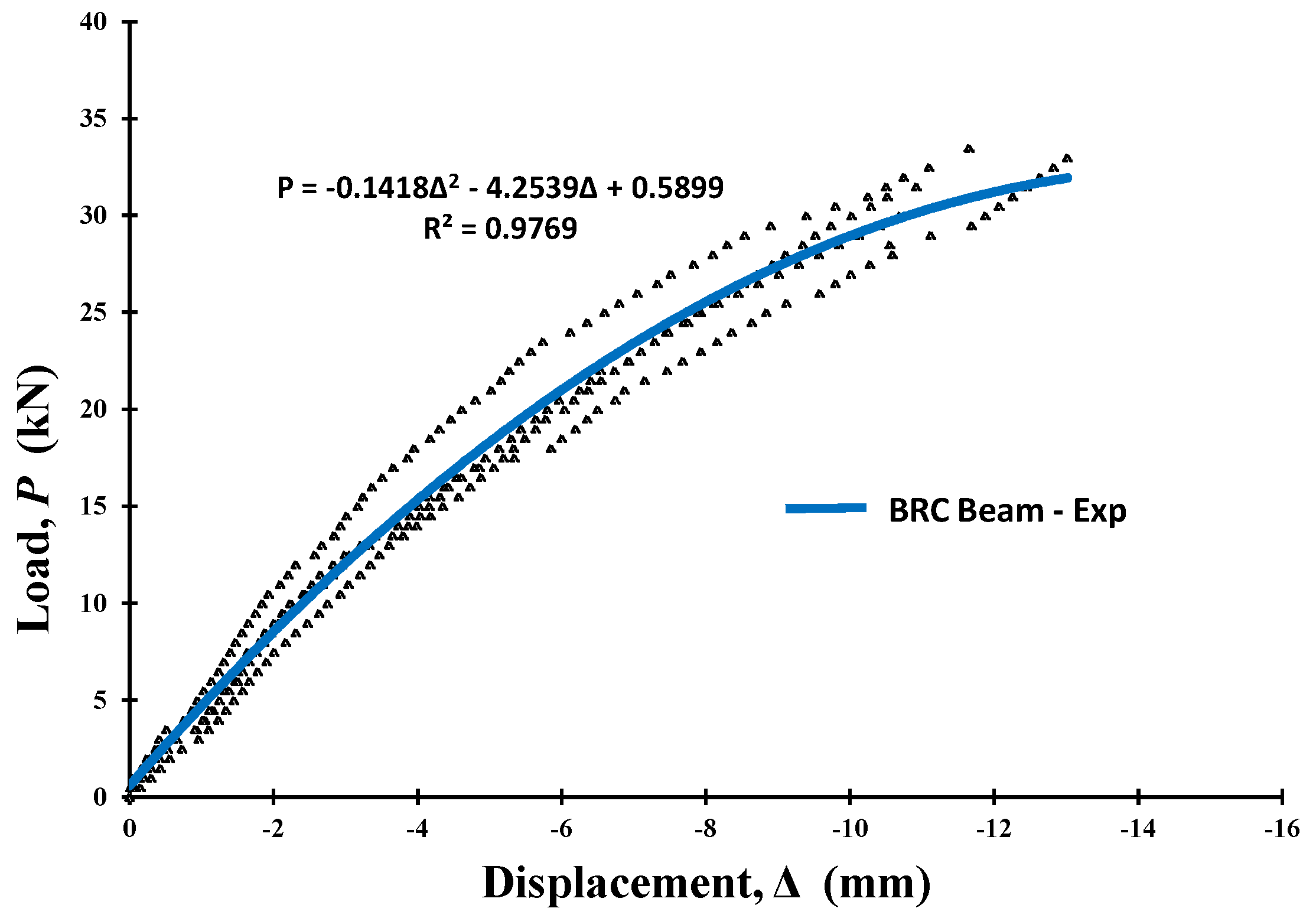
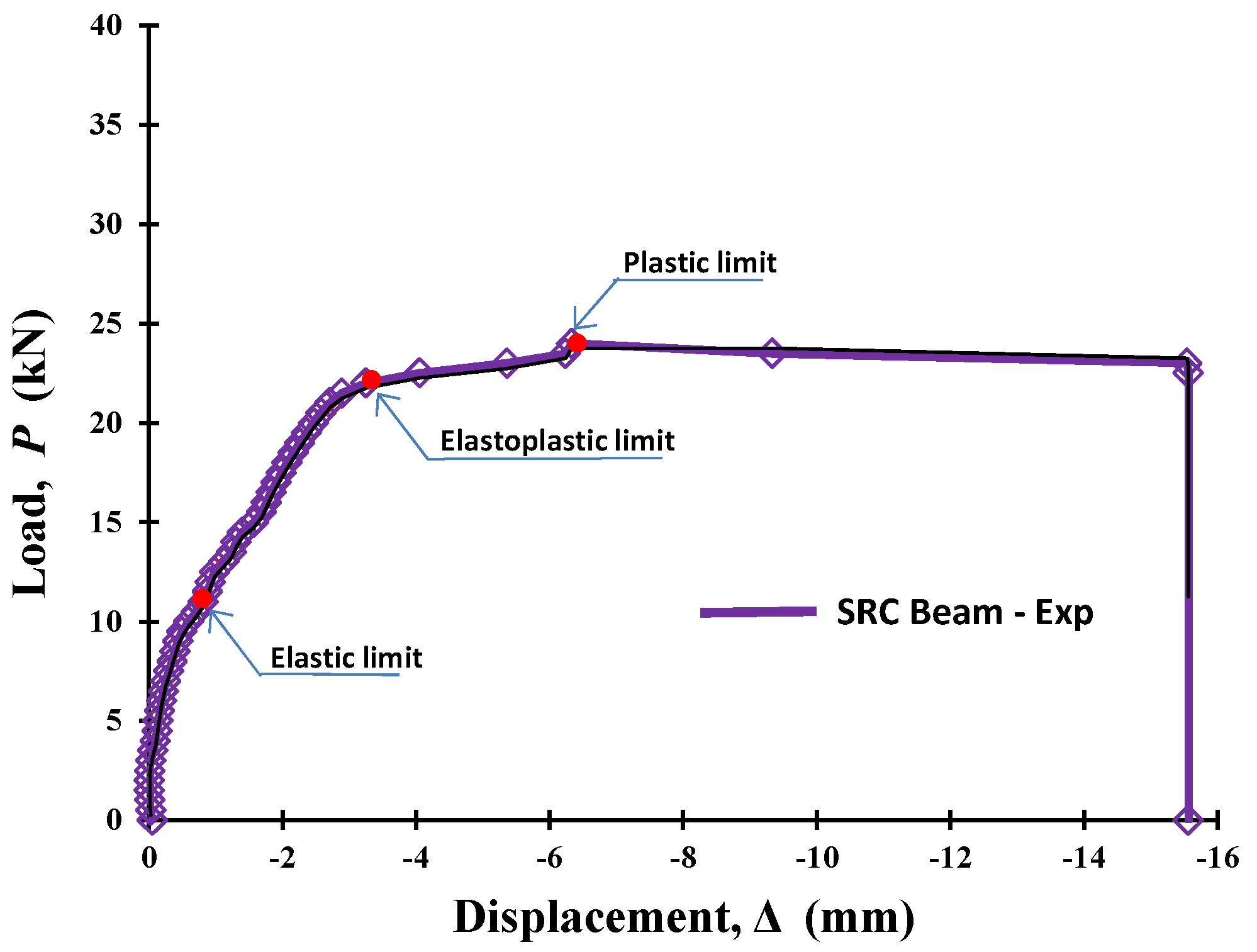
3.1. Experimental
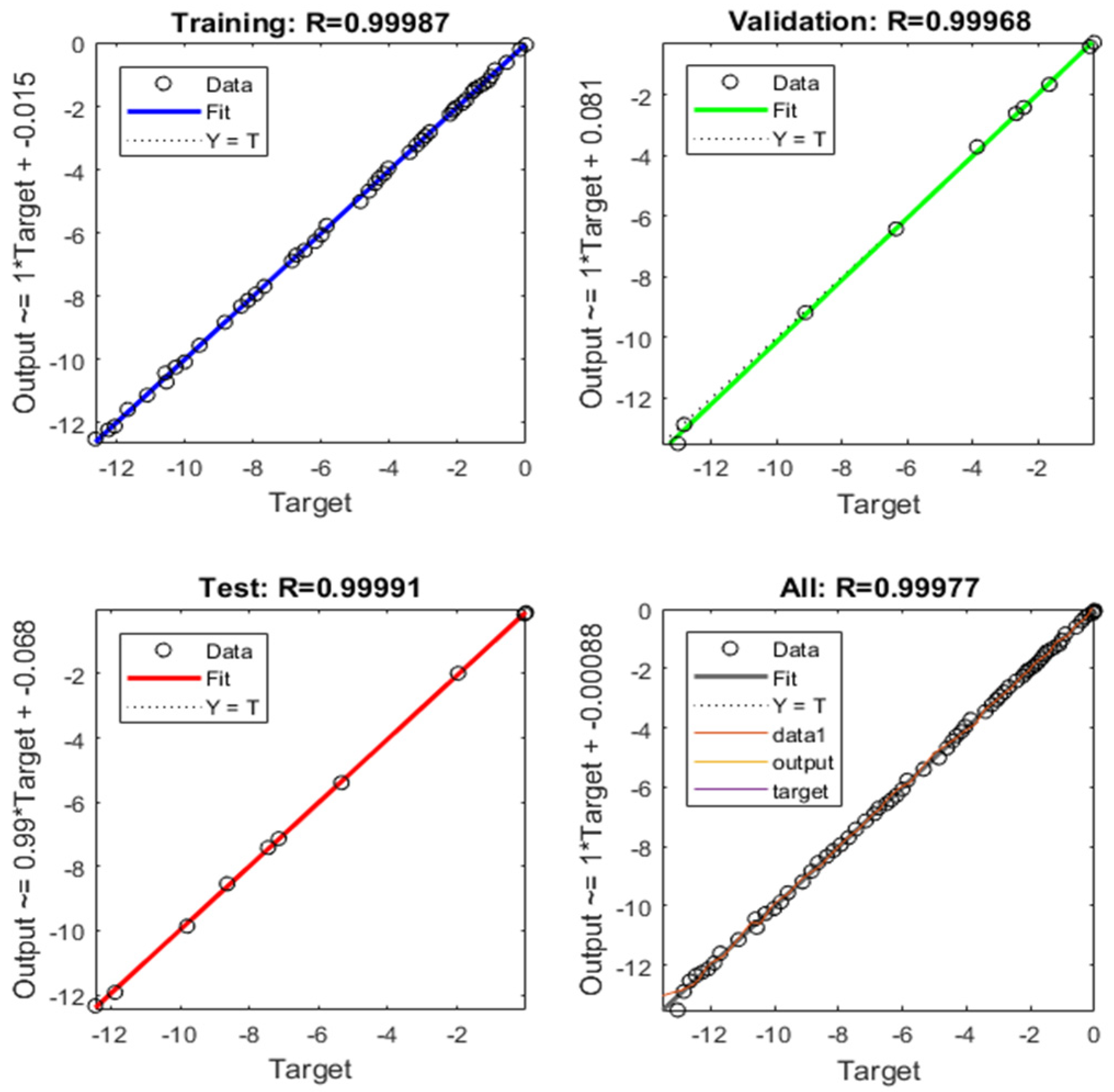
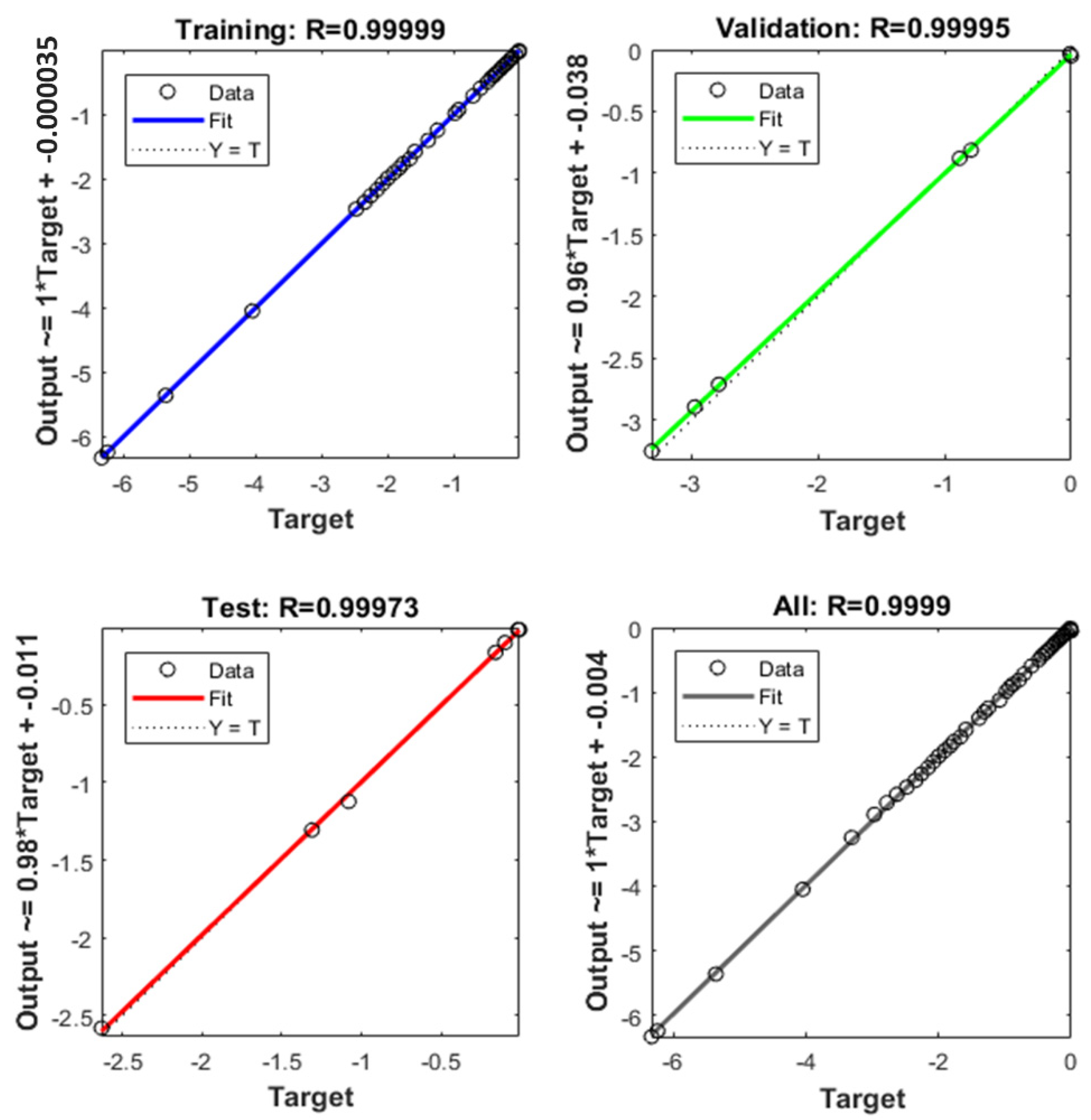
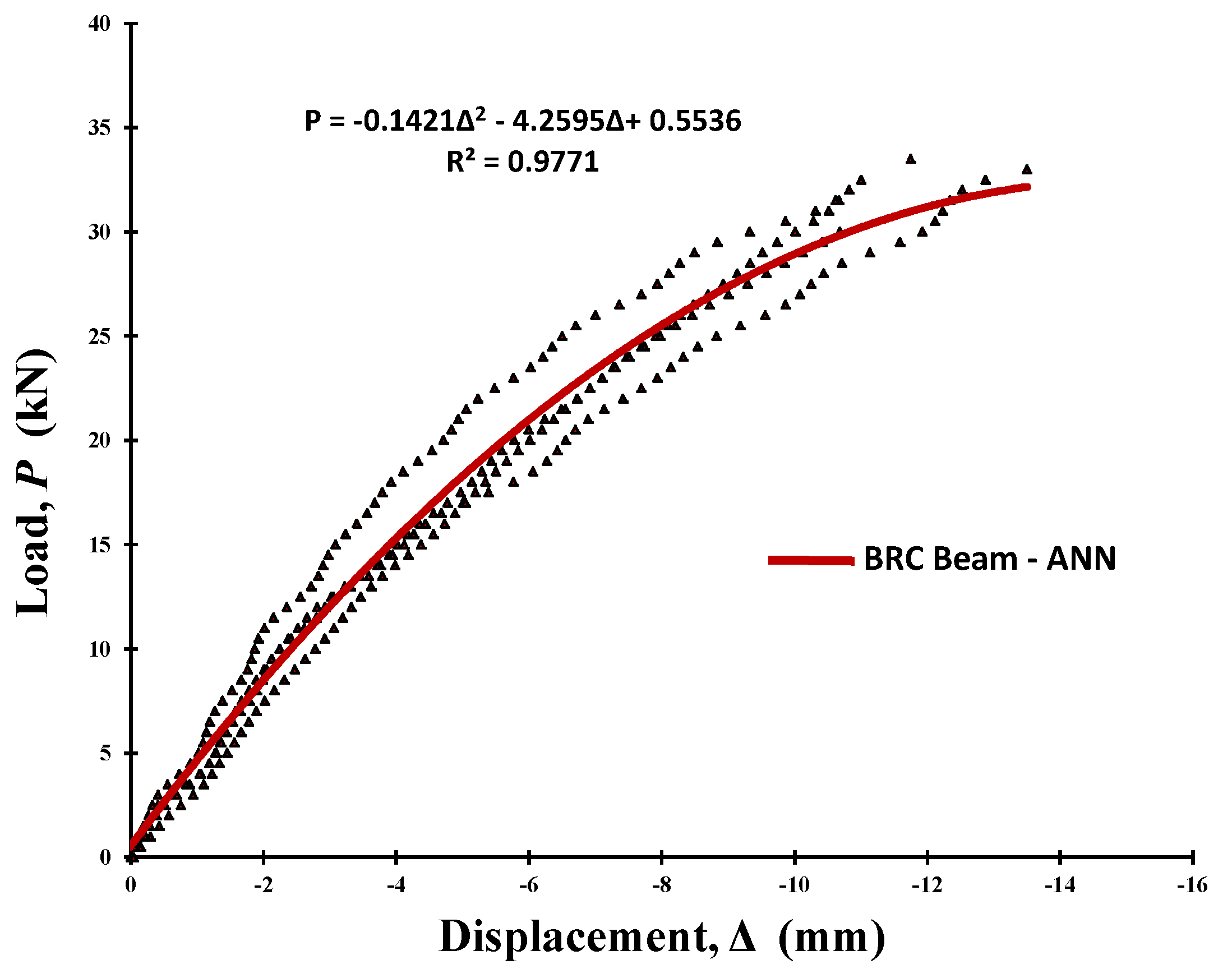
3.2. Validation with the ANN Method
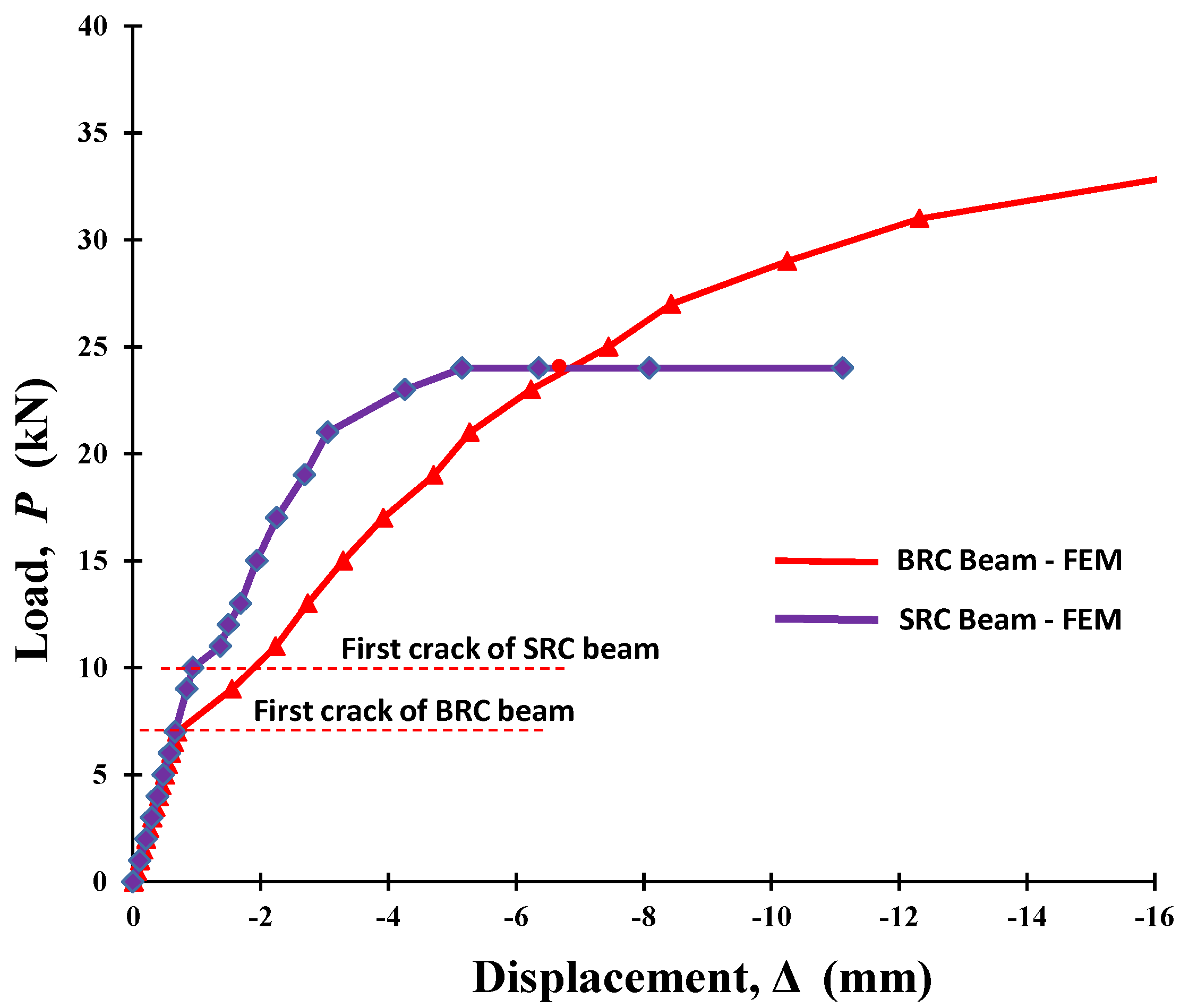
3.3. Validation with the Finite Element Method
4. Discussion
5. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Pandey, K.K.; Ramakantha, V.; Chauhan, S.S.; Kumar, A.A. Wood is Good; Springer: Singapore, 2017. [Google Scholar]
- Mohammadabadi, M.; Jarvis, J.; Yadama, V.; Cofer, W. Predictive Models for Elastic Bending Behavior of a Wood Composite Sandwich Panel. Forests 2020, 11, 624. [Google Scholar] [CrossRef]
- Ministry of Environment and Forestry of the Republic of Indonesia. Memanfaatkan Bambu Sebagai Salah Satu Potensi Hutan Rakyat. 18 October 2018. Available online: https://www.menlhk.go.id/site/single_post/1444 (accessed on 24 October 2020).
- Han, S.W.; Park, Y.M.; Kee, S.H. Stiffness Reduction Factor for Flat Slab Structures under Lateral Loads. J. Struct. Eng. 2009, 135, 743. [Google Scholar] [CrossRef]
- ACI Committee 318 Standard. Building Code Requirements for Structural Concrete; American Concrete Institute: Farmington Hills, MI, USA, 2014. [Google Scholar]
- Gunasti, A.; Dewi, I.C.; Dasuki, M.; Ariyani, S.; Mahmudi, I.; Abadi, T.; Rahman, M.; Hidayatullah, S.; Nilogiri, A.; Galuh, S.D.; et al. The Prediction of Stiffness of Bamboo-Reinforced Concrete Beams Using Experiment Data and Artificial Neural Networks (ANNs). Crystals 2020, 10, 757. [Google Scholar]
- Muhtar; Dewi, S.M.; Wisnumurti; Munawir, A. Enhancing bamboo reinforcement using a hose-clamp to increase bond-stress and slip resistance. J. Build. Eng. 2019, 26, 100896. [Google Scholar] [CrossRef]
- Muhtar; Dewi, S.M.; Wisnumurti; Munawir, A. The flexural behavior model of bamboo reinforced concrete beams using a hose clamp. Proc. Mater. Sci. Eng. Chem. 2019, 276, 1033. [Google Scholar] [CrossRef] [Green Version]
- Zhang, K.; Zhang, J.; Jin, W.; Mao, J.; Long, J. Stiffness degradation for the fatigue of reinforced concrete beams after electrochemical rehabilitation. Constr. Build. Mater. 2020, 260, 120455. [Google Scholar] [CrossRef]
- Salam, A.S.A.; Debra, L.F. Use of negative stiffness in failure analysis of concrete beams. Eng. Struct. 2016, 126, 187–199. [Google Scholar]
- Hu, H.S.; Nie, J.G.; Wang, Y.H. Effective stiffness of rectangular concrete-filled steel tubular members Hong-Song. J. Constr. Steel Res. 2016, 116, 233–246. [Google Scholar] [CrossRef]
- Patel, K.A.; Bhardwaj, A.; Chaudhary, S.; Nagpal, A. Explicit expression for effective moment of inertia of RC beams. Lat. Am. J. Solids Struct. 2015, 12, 542–560. [Google Scholar] [CrossRef] [Green Version]
- Fu, C.; Wang, Y.; Tong, D. Stiffness Estimation of Cracked Beams Based on Nonlinear Stress Distributions Near the Crack. Math. Probl. Eng. 2018, 2018, 5987973. [Google Scholar] [CrossRef] [Green Version]
- Pique, J.R.; Burgos, M. Effective rigidity of reinforced concrete elements in seismic analysis and design. In Proceedings of the 14 World Conference on Earthquake Engineering, Beijing, China, 12–17 October 2008. [Google Scholar]
- Akmaluddin, A.; Pathurahman. Effective Moment of Inertia Approach for Predicting Displacement of Concrete Beams Reinforced with Twisted Bamboo Cables. Int. J. Civ. Environ. Eng. IJCEE-IJENS 2012, 12, 6–13. [Google Scholar]
- Kalkan, İ. Displacement Prediction for Reinforced Concrete Beams through Different Effective Moment of Inertia Expressions. Int. J. Eng. Res. Dev. 2013, 5, 1. [Google Scholar]
- Fu, C.; Tong, D.; Wang, Y. Assessing the Instantaneous Stiffness of Cracked Reinforced Concrete Beams Based on a Gradual Change in Strain Distributions. Adv. Mater. Sci. Eng. 2020, 2020, 7453619. [Google Scholar] [CrossRef] [Green Version]
- Feng, X.; Shen, M.; Sun, C.; Chen, J.; Luo, P. Research on flexural stiffness reduction factor of the reinforced concrete column with equiaxial shaped section. In Proceedings of the 13th COTA International Conference of Transportation Professionals (CICTP 2013), Shenzhen, China, 13–16 August 2013; pp. 168–174. [Google Scholar]
- Muhtar; Dewi, S.M.; Wisnumurti; Munawir, A. The stiffness and cracked pattern of bamboo reinforced concrete beams using a hose clamp. Int. J. Civ. Eng. Technol. 2018, 9, 273–284. [Google Scholar]
- Agarwal, A.; Nanda, B.; Maity, D. Experimental investigation on chemically treated bamboo reinforced concrete beams and columns. Constr. Build. Mater. 2014, 71, 610–617. [Google Scholar] [CrossRef]
- Muhtar. Experimental data from strengthening bamboo reinforcement using adhesives and hose-clamps. Data Brief 2019, 27, 104827. [Google Scholar] [CrossRef]
- Rahman, M.M.; Rashid, M.H.; Hossain, M.A.; Hasan, M.T.; Hasan, M.K. Performance evaluation of bamboo reinforced concrete beam. Int. J. Eng. Technol. IJET-IJENS 2011, 11, 113–118. [Google Scholar]
- Muhtar. Precast Bridges of Bamboo Reinforced Concrete in Disadvantaged Village Areas in Indonesia. Appl. Sci. 2020, 10, 7158. [Google Scholar] [CrossRef]
- Ghavami, K. Bamboo as reinforcement in structural concrete elements. Cem. Concr. Compos. 2005, 27, 637–649. [Google Scholar] [CrossRef]
- Javadian, A.; Wielopolski, M.; Smith, I.F.C.; Hebel, D.E. Bond-behavior study of newly developed bamboo-composite reinforcement in concrete. Constr. Build. Mater. 2016, 122, 110–117. [Google Scholar] [CrossRef]
- Muhtar, M.; Dewi, S.; Wisnumurti; Munawir, A. Bond-slip improvement of bamboo reinforcement in the concrete beam using hose clamps. In Proceedings of the 2nd International Multidisciplinary Conference, Jakarta, Indonesia, 15 November 2016; pp. 385–393. [Google Scholar]
- Gunasti, A.; Manggala, A.S.; Nusant, A.F.P.; Nilogiri, A. Effect of Reinforcement Details on Precast Bridge Frames of Bamboo Reinforced Concrete to Load Capacity and Crack Patterns. Int. J. Eng. Res. Technol. 2020, 13, 631–636. [Google Scholar]
- Muhtar. Cracked Pattern of Bamboo Reinforced Concrete Beams Using Double Reinforcement with the Strengthening on Tensile Reinforcement. Int. J. Eng. Res. Technol. 2020, 13, 608–612. [Google Scholar]
- ASTM C 39 Standard. Standard Test Method for Compressive Strength of Cylindrical Concrete Specimens; ASTM International: West Conshohocken, PA, USA, 2003. [Google Scholar]
- PT SIKA Indonesia. Sikadur®-752. 02, 2-3. 2016. Available online: https://www.scribd.com/document/374071630/Sikadur-752 (accessed on 24 October 2020).
- ASTM C 09 Standard. Standard Test Method for Flexural Strength of Concrete (Using Simple Beam with Third-Point Loading); ASTM International: West Conshohocken, PA, USA, 2002. [Google Scholar]
- Muhtar. Numerical validation data of tensile stress zones and crack zones in bamboo reinforced concrete beams using the Fortran PowerStation 4.0 program. Data Brief 2020, 29, 105332. [Google Scholar] [CrossRef]
- Avram, C.; Facaoaru, I.; Filimon, I.; Mirsu, O.; Tertea, I. Concrete Strength and Strain. In Developments in Civil Engineering 3; Elsvier S.P. Company: New York, NY, USA, 1981. [Google Scholar]
- Naderpour, H.; Kheyroddin, A.; Amiri, G.G. Prediction of FRP-confined compressive strength of concrete using artificial neural networks. Compos. Struct. 2010, 92, 2817–2829. [Google Scholar] [CrossRef]
- Ahmadi, M.; Naderpour, H.; Kheyroddin, A. Utilization of artificial neural networks to prediction of the capacity of CCFT short columns subject to short term axial load. Arch. Civ. Mech. Eng. 2014, 14, 510–517. [Google Scholar] [CrossRef]
- Khademi, F.; Akbari, M.; Nikoo, M. Displacement determination of concrete reinforcement building using data-driven models. Int. J. Sustain. Built Environ. 2017, 6, 400–411. [Google Scholar] [CrossRef]
- Kaczmarek, M.; Szymanska, A. Application of Artificial Neural Networks to Predict the Displacements of Reinforced Concrete Beams. Studia Geotech. Mech. 2016, 38, 37–46. [Google Scholar] [CrossRef] [Green Version]
- Abd, A.M.; Salman, W.D.; Ahmed, Q.W. ANN, and Statistical Modelling to Predict the Displacement of Continuous Reinforced Concrete. Diyala J. Eng. Sci. 2015, 08, 134–143. [Google Scholar]
- Ya Tuan, T.M.Y.S.; Alebrahim, R.; Fitri, N.; Alebrahim, M. Analysis of Cantilever Beam Displacement under Uniformly Distributed Load using Artificial Neural Networks. In Proceedings of the MATEC Web of Conferences, Los Angeles, CA, USA, 3–4 February 2018. [Google Scholar]
- Khademi, F.; Akbari, M.; Mohammadmehdi, S.; Nikoo, M. Multiple linear regression, artificial neural network, and fuzzy logic prediction of 28 days compressive strength of concrete. Front. Struct. Civ. Eng. 2017, 11, 90–99. [Google Scholar] [CrossRef]
- Li, X.; Khademi, F.; Liu, Y.; Akbari, M.; Wang, C.; Bond, P.L.; Keller, J.; Jiang, G. Evaluation of data-driven models for predicting the service life of concrete sewer pipes subjected to corrosion. J. Environ. Manag. 2019, 234, 431–439. [Google Scholar] [CrossRef]
- Dewi, S.M.; Nuralinah, D. The Recent Research on Bamboo Reinforced Concrete. MATEC Web Conf. 2017, 103, 2001. [Google Scholar] [CrossRef] [Green Version]
- Nathan, S. Application of Bamboo for Flexural and Shear Reinforcement in Concrete Beams; Clemson University: Clemson, SC, USA, 2014. [Google Scholar]
- Khare, L. Performance Evaluation of Bamboo Reinforced Concrete Beams; UT Arlington: Arlington, TX, USA, 2005. [Google Scholar]
- Mishra, M.; Agarwal, A.; Maity, D. Neural-network-based approach to predict the displacement of plain, steel-reinforced, and bamboo-reinforced concrete beams from experimental data. SN Appl. Sci. 2019, 1, 584. [Google Scholar] [CrossRef] [Green Version]
- FEMA 356 Standard. Prestandard and Commentary for the Seismic Rehabilitation of Buildings; American Society of Civil Engineers: Reston, VA, USA, 2000. [Google Scholar]
- New Zealand Standard. Code of Practice for the Design of Concrete Structures; Part 1; Standards New Zealand: Wellington, New Zealand, 1995. [Google Scholar]
- Paulay, T.; Priestley, M.J.N. Seismic Design of Reinforced Concrete and Masonry Buildings; Wiley Interscience: New York, NY, USA, 1992. [Google Scholar]
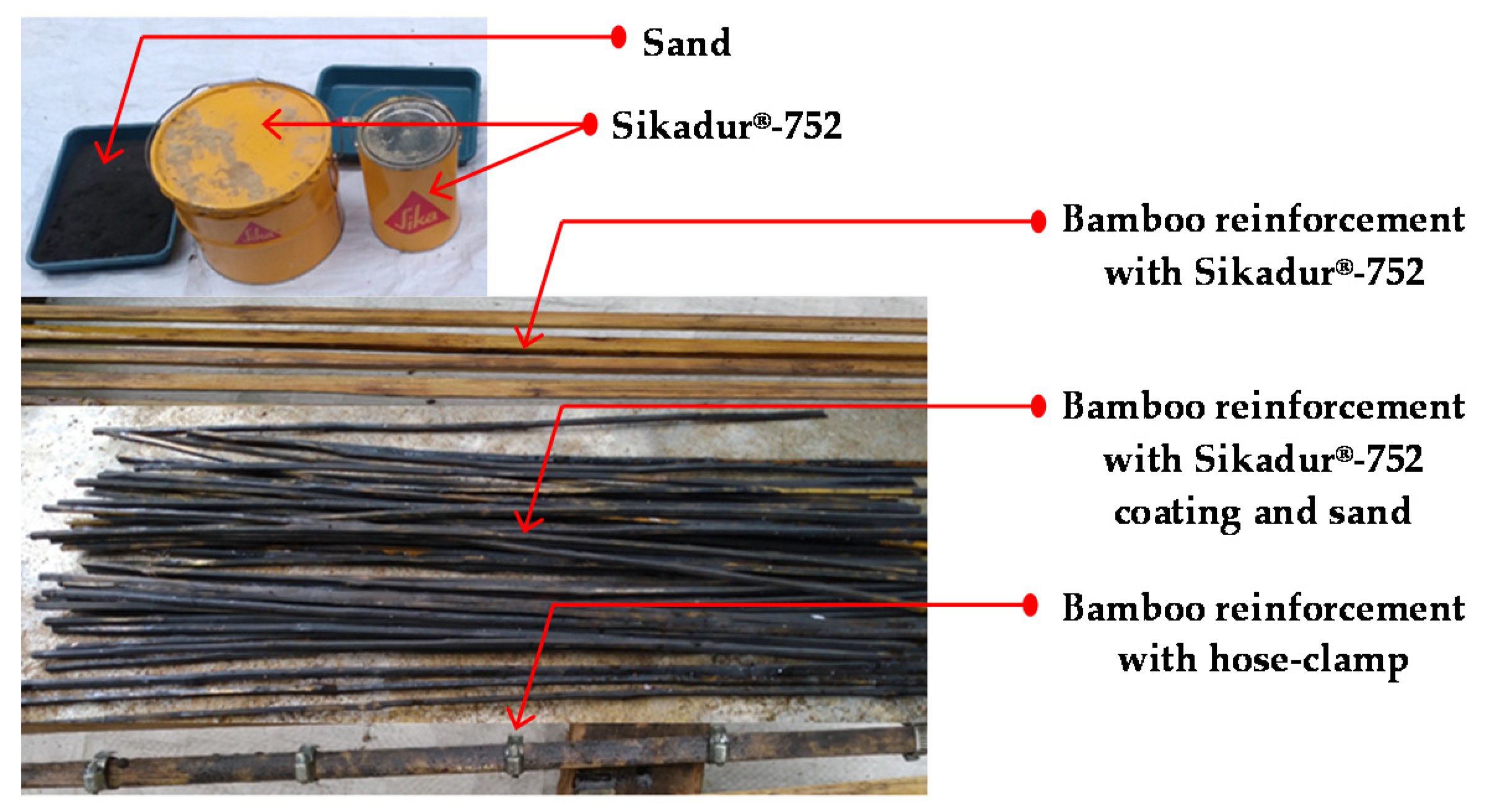
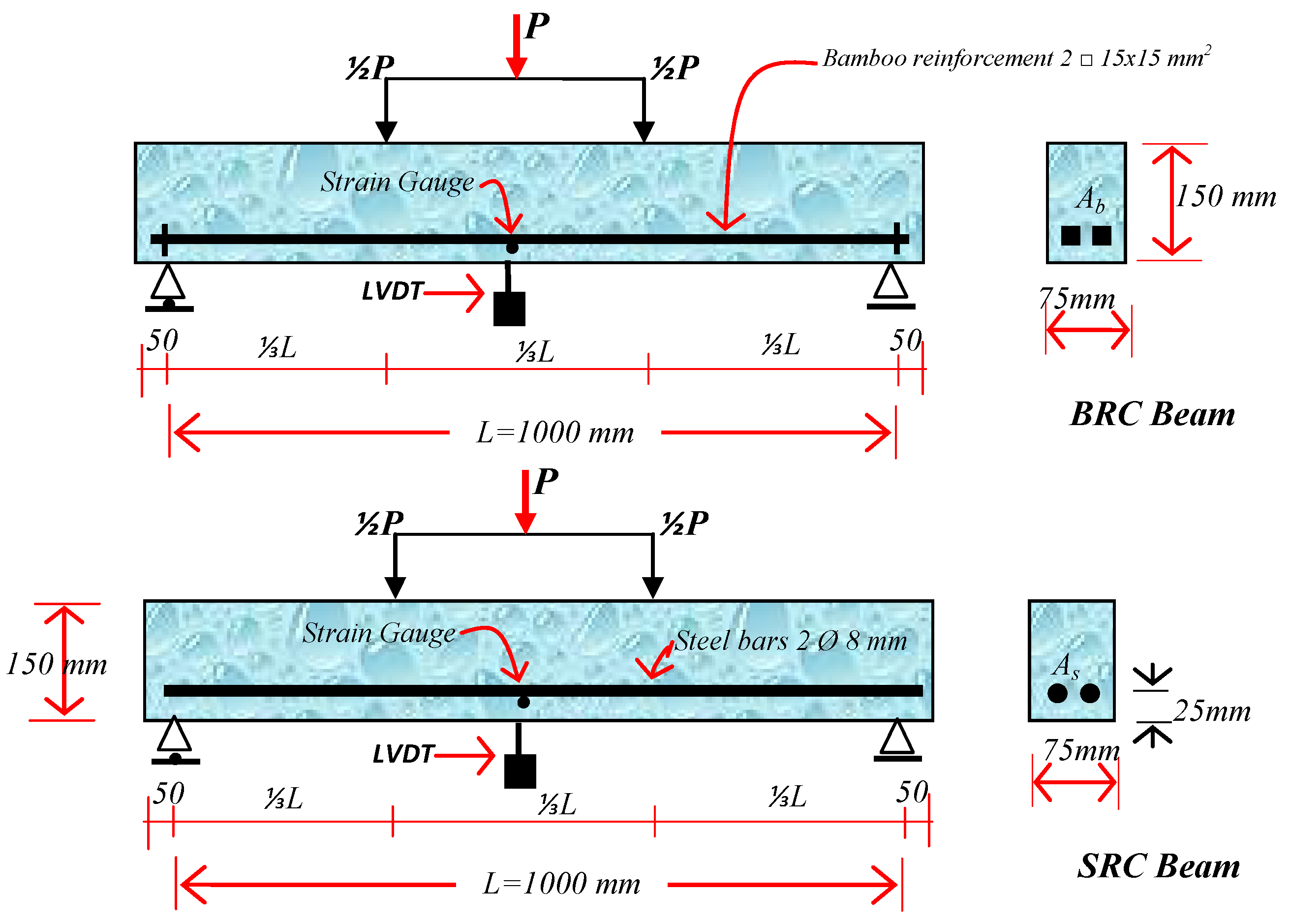




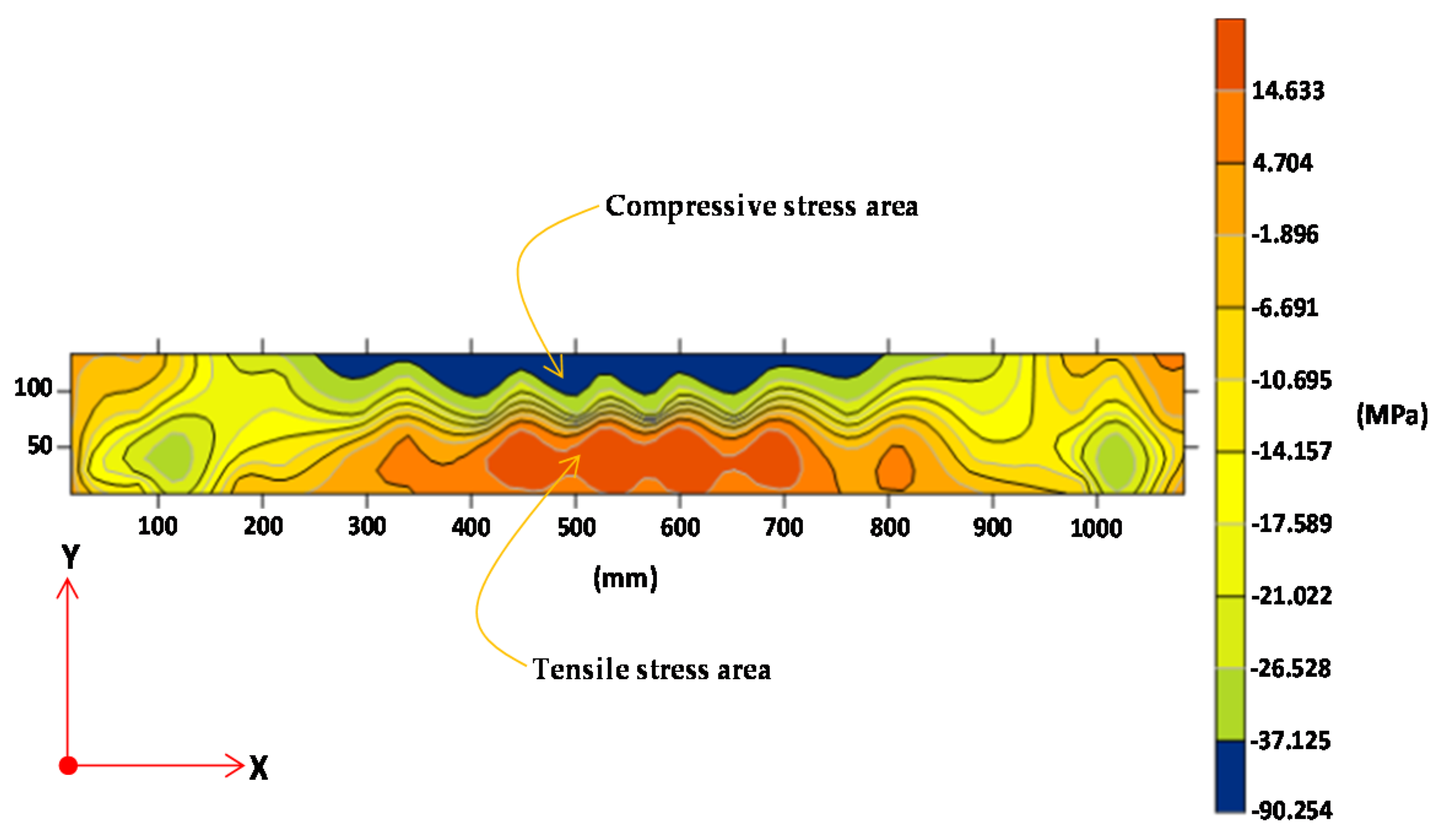

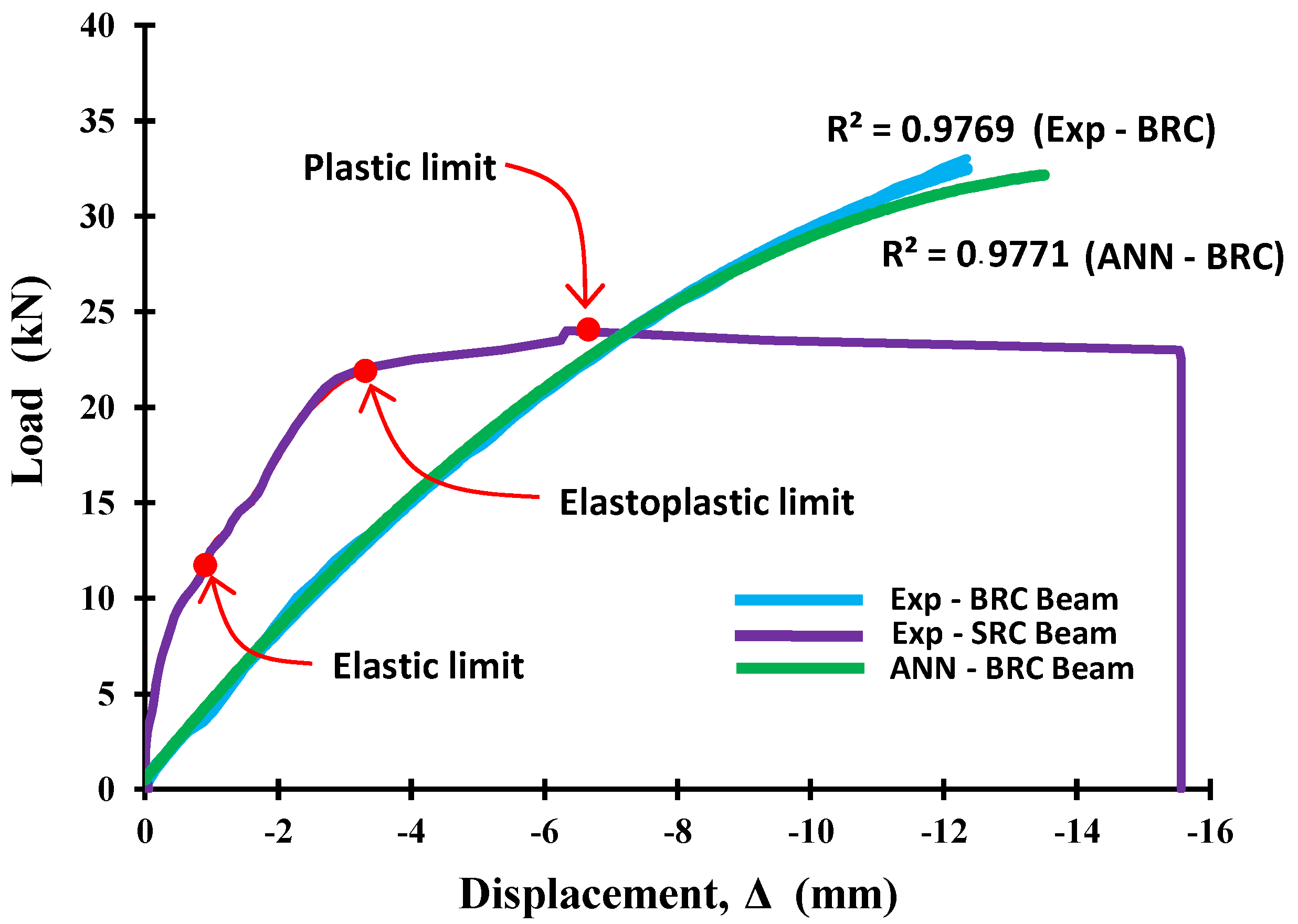

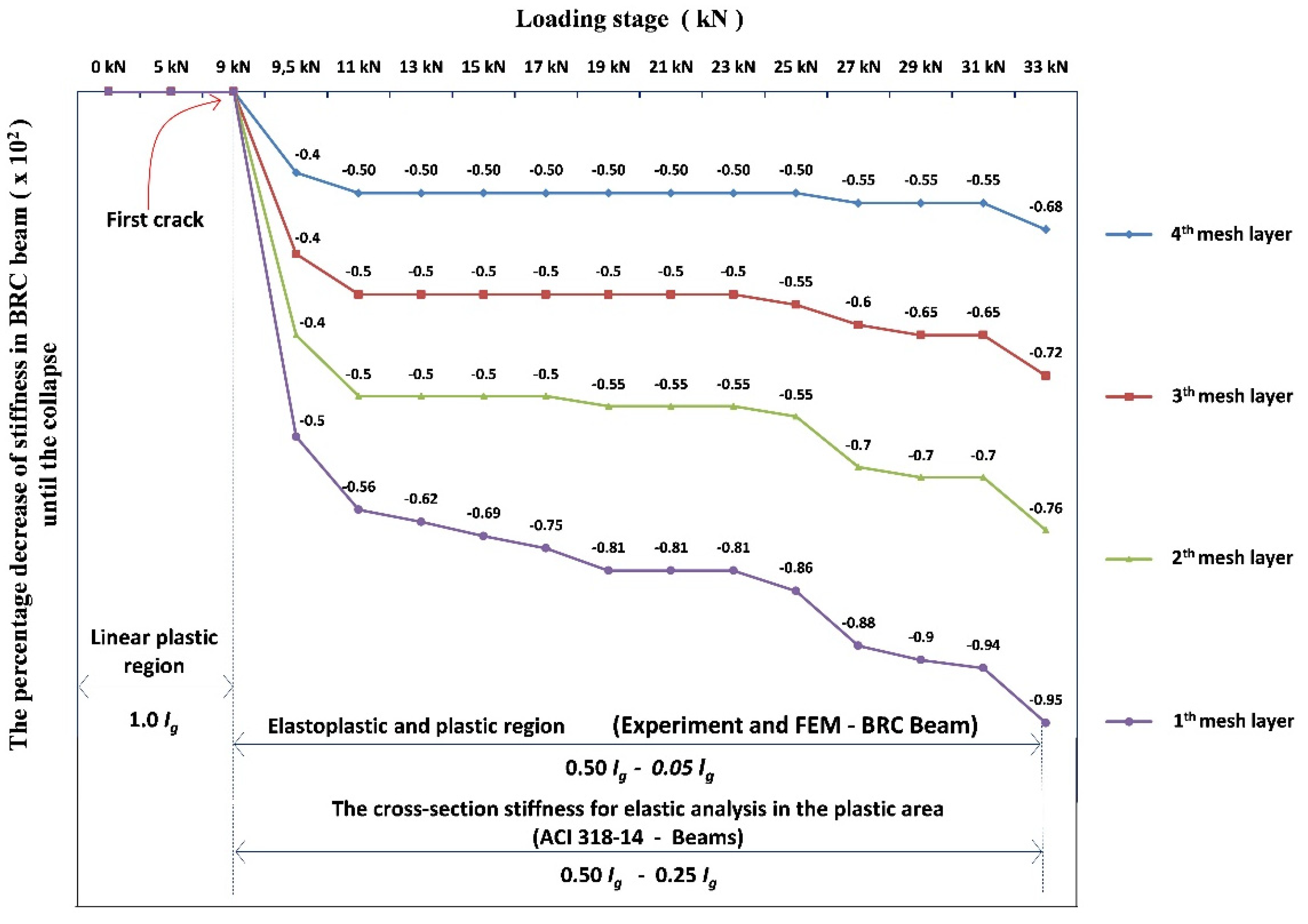
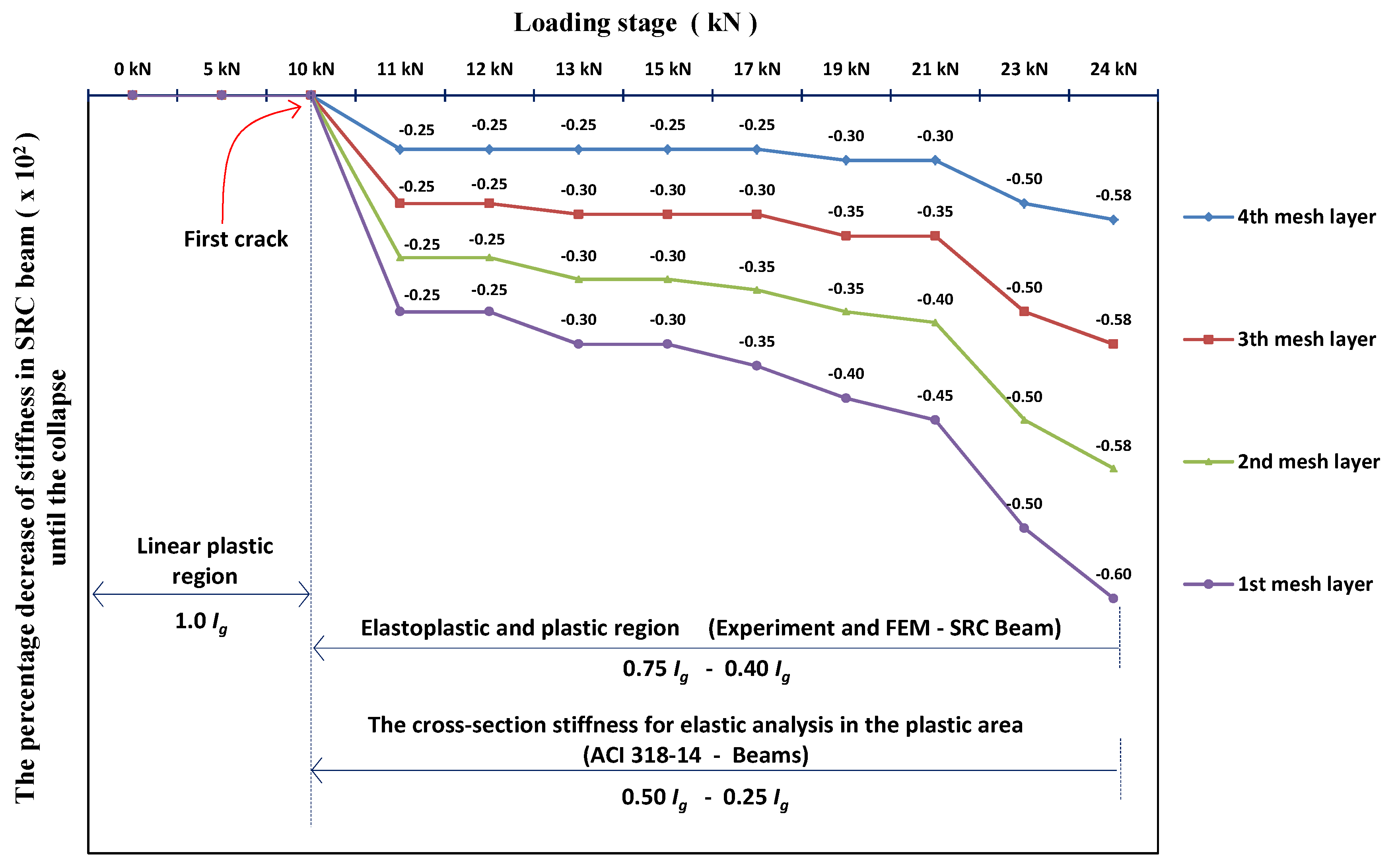


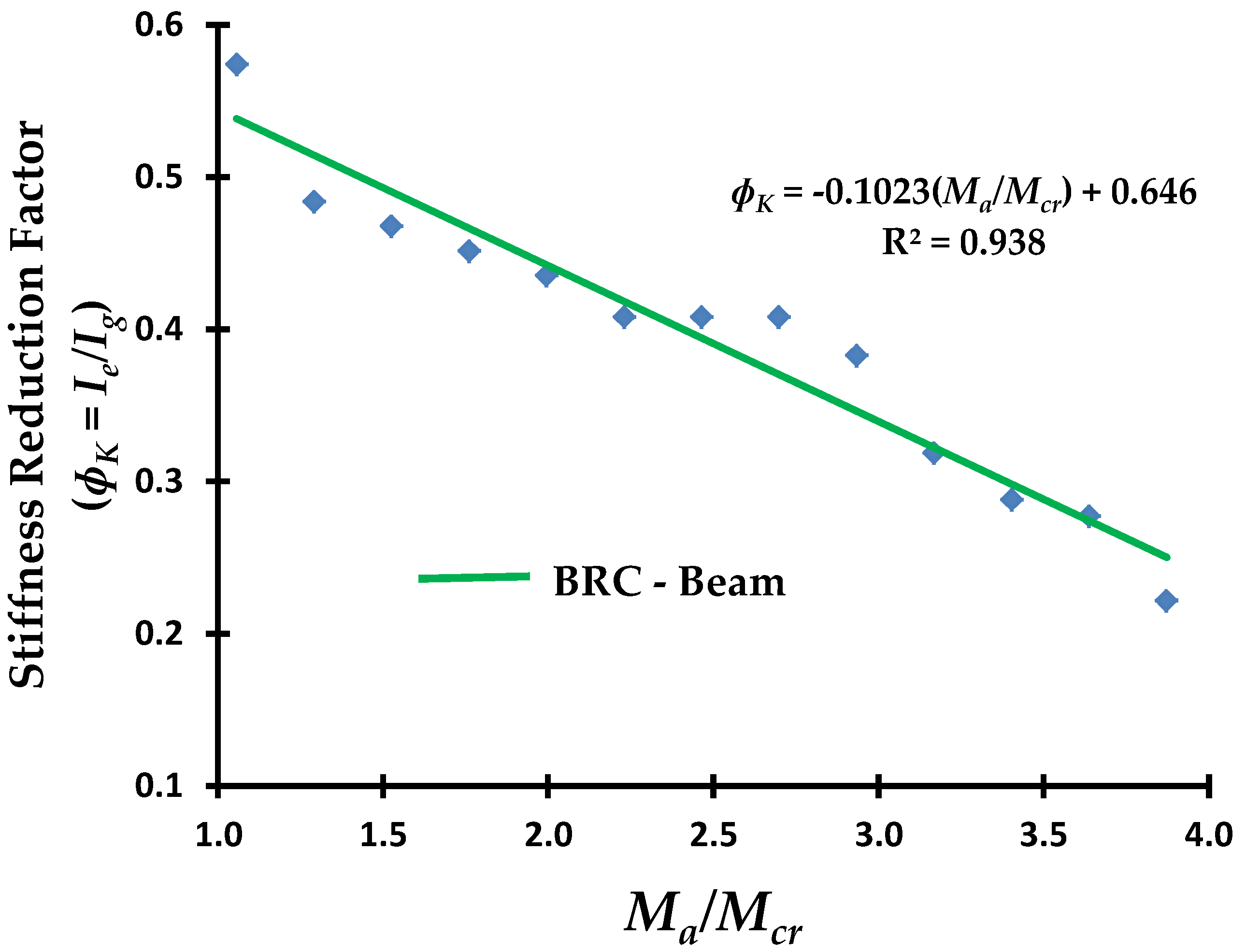
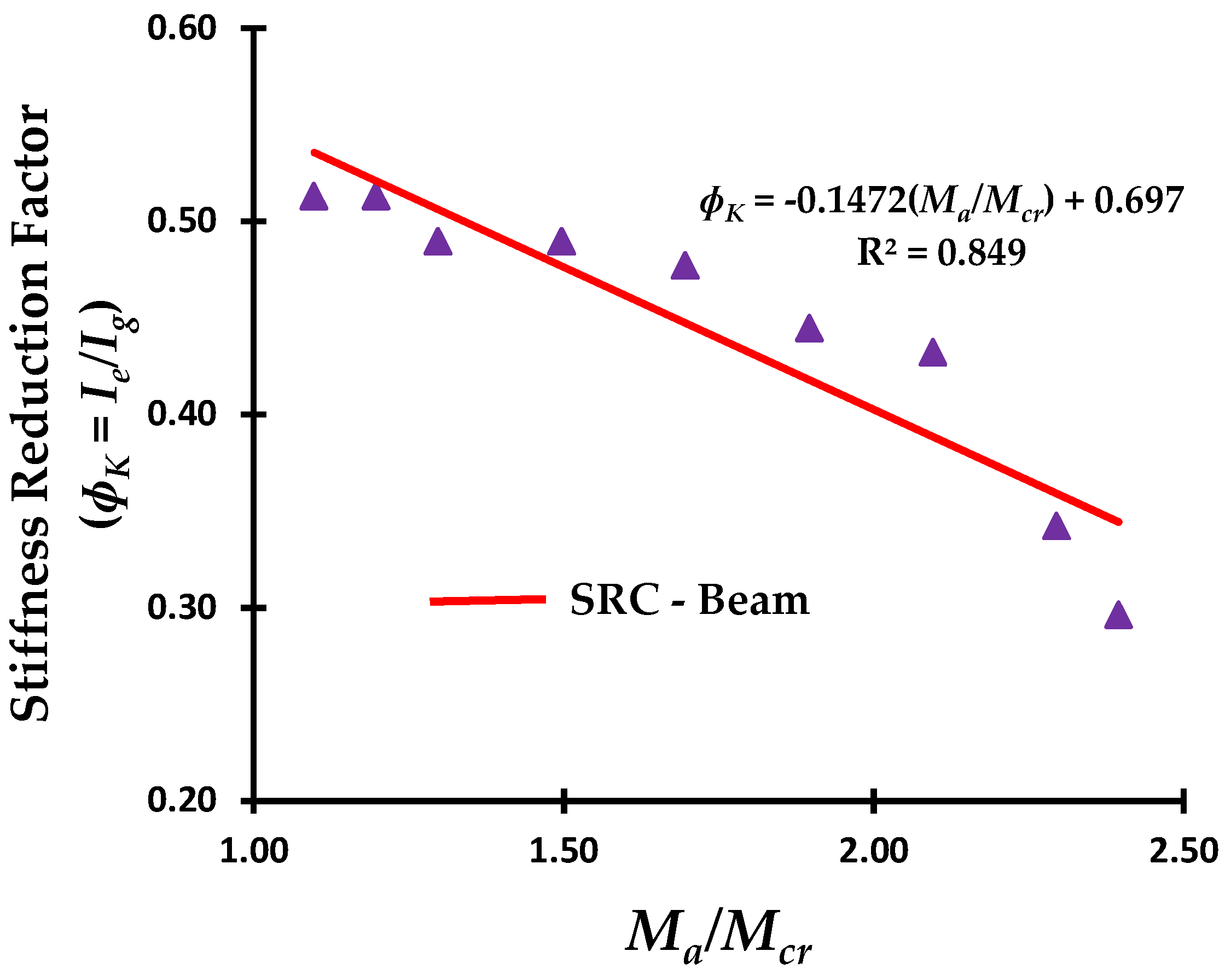

| Bar Type and Concrete | Diameter, d (mm) | Modulus of Elasticity (E), (MPa) | Poisson’s Ratio (ν) | Tensile Strength, fy (MPa) | Compressive Strength, f′c (MPa) |
|---|---|---|---|---|---|
| Bamboo | □ 15 × 15 | 17,235.74 | 0.20 | 126.68 | - |
| Steel | ϕ 8 | 207,735.92 | 0.25 | 392.28 | - |
| Concrete | - | 26,324.79 | 0.30 | - | 31.31 |
| Components | Properties |
|---|---|
| Color | Yellowish |
| Density | Approx. 1.08 kg/L |
| Mix comparison (weight/volume) | 2:1 |
| Pot life at +30 °C | 35 min |
| Compressive strength | 62 MPa at 7 days (ASTM D-695) 64 MPa at 28 days |
| Tensile strength | 40 MPa at 28 days (ASTM D-790) |
| Tensile Adhesion Strength | 2 MPa (Concrete failure, over mechanically prepared concrete surface) |
| Coefficient of Thermal Expansion | −20 °C to + 40 °C 89 × 10−6 per °C |
| Modulus of elasticity | 1060 MPa |
| Layer Number | Compressive Strength of Concrete, f′c | Dimensions of per Layer | Modulus of Elasticity of the Material (E) | Elasticity Modulus of Composite (Ecomp) | ||
|---|---|---|---|---|---|---|
| Mpa | b (mm) | h (mm) | Concrete, Ec (MPa) | Bamboo, Eb (MPa) | MPa | |
| 4th mesh layer | 31.31 | 75 | 50 | 26,851.29 | 0 | 26,851.29 |
| 3rd mesh layer | 31.31 | 75 | 60 | 26,851.29 | 0 | 26,851.29 |
| 2nd mesh layer | 31.31 | 75 | 15 | 26,851.29 | 1723.57 | 23,140.89 |
| 1st mesh layer | 31.31 | 75 | 25 | 26,851.29 | 0 | 26,851.29 |
| Layer Number | Compressive Strength of Concrete, f′c | Dimensions of per Layer | Modulus of Elasticity of the Material (E) | Elasticity Modulus of Composite (Ecomp) | ||
|---|---|---|---|---|---|---|
| Mpa | b (mm) | h (mm) | Concrete, Ec (MPa) | Steel, Es (MPa) | MPa | |
| 4th mesh layer | 31.31 | 5 | 50 | 26,851.29 | 0 | 26,851.29 |
| 3rd mesh layer | 31.31 | 75 | 67 | 26,851.29 | 0 | 26,851.29 |
| 2nd mesh layer | 31.31 | 75 | 8 | 26,851.29 | 207,735.92 | 43,209.32 |
| 1st mesh layer | 31.31 | 75 | 25 | 26,851.29 | 0 | 26,851.29 |
| Specimens | Sample No | Theoretical Calculations | Flexural Test Results | ||||
|---|---|---|---|---|---|---|---|
| First Crack Load (kN) | Ultimate Load (kN) | First Crack Load, Pcr (kN) | Failure Load, Pult (kN) | Displacement at Failure (mm) | Pcr/Pult (%) | ||
| (a) BRC-1 | 1 | 6.90 | 32.20 | 8.50 | 31.50 | 10.92 | 26.98 |
| 2 | 8.00 | 29.00 | 11.90 | 27.59 | |||
| (b) BRC-2 | 3 | 7.00 | 31.00 | 13.02 | 22.58 | ||
| 4 | 7.50 | 33.00 | 12.18 | 22.73 | |||
| (c) BRC-3 | 5 | 8.00 | 33.50 | 14.69 | 23.88 | ||
| 6 | 7.50 | 33.00 | 9.32 | 22.73 | |||
| (d) BRC-4 | 7 | 7.50 | 29.50 | 7.61 | 25.42 | ||
| 8 | 7.50 | 30.00 | 10.69 | 25.00 | |||
| Average: | 7.69 | 31.31 | 24.61 | ||||
| (e) SRC | 9 | 6.50 | 24.20 | 10.00 | 24.00 | 6.33 | 41.57 |
| Specimens | The Correlation Coefficient (R) | Mean Square Error (MSE) | ||||
|---|---|---|---|---|---|---|
| Training | Validation | Testing | Training | Validation | Testing | |
| BRC-1 | 1.0000 | 0.9999 | 0.9997 | 0.0004 | 0.0011 | 0.0110 |
| BRC-2 | 0.9999 | 0.9997 | 0.9999 | 0.0038 | 0.0276 | 0.0048 |
| BRC-3 | 0.9998 | 0.9999 | 0.9993 | 0.0034 | 0.0075 | 0.0152 |
| BRC-4 | 1.0000 | 1.0000 | 1.0000 | 0.0001 | 0.0009 | 0.0010 |
| SRC | 1.0000 | 1.0000 | 0.9997 | 0.0001 | 0.0027 | 0.0006 |
| Layer Number | Modulus of Elasticity (E) of the BRC Beam | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Elastic Condition | Plastic Conditions with Gradual Loads | |||||||||||||
| 0–8.5 kN | 9 kN | 11 kN | 13 kN | 15 kN | 17 kN | 19 kN | 21 kN | 23 kN | 25 kN | 27 kN | 29 kN | 31 kN | 33 kN | |
| 4th mesh layer | 26,851.29 | 16,110.77 | 16,110.77 | 16,110.77 | 16,110.77 | 16,110.77 | 16,110.77 | 16,110.77 | 16,110.77 | 16,110.77 | 12,083.08 | 11,277.54 | 11,277.54 | 8592.41 |
| 3th mesh layer | 26,851.29 | 16,110.77 | 16,110.77 | 16,110.77 | 16,110.77 | 16,110.77 | 16,110.77 | 16,110.77 | 16,110.77 | 1208.31 | 10,740.52 | 9397.95 | 9397.95 | 7518.36 |
| 2nd mesh layer | 23,140.89 | 13,884.53 | 11,570.44 | 11,570.44 | 11,570.44 | 11,570.44 | 10,413.40 | 10,413.40 | 10,413.40 | 10,413.40 | 6942.27 | 6942.27 | 6942.27 | 5553.81 |
| 1st mesh layer | 26,851.29 | 13,425.65 | 11,814.57 | 10,203.49 | 8323.90 | 6712.82 | 5101.75 | 5101.75 | 5101.75 | 3759.18 | 3222.16 | 2685.13 | 1611.08 | 1329.14 |
| Layer Number | Modulus of Elasticity (E) of the SRC Beam | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Elastic Condition | Plastic Conditions with Gradual Loads | ||||||||||
| 0–9 kN | 10 kN | 11 kN | 12 kN | 13 kN | 15 kN | 17 kN | 19 KN | 21 KN | 23 kN | 24 kN | |
| 4th mesh layer | 26,851.29 | 26,851.29 | 20,138.47 | 20,138.47 | 20,138.47 | 20,138.47 | 20,138.47 | 18,795.90 | 18,795.90 | 13,425.65 | 11,411.80 |
| 3th mesh layer | 26,851.29 | 26,851.29 | 20,138.47 | 20,138.47 | 18,795.90 | 18,795.90 | 18,795.90 | 17,453.34 | 17,453.34 | 13,425.65 | 11,411.80 |
| 2nd mesh layer | 43,209.32 | 43,209.32 | 30,586.93 | 30,586.93 | 28,547.80 | 28,547.80 | 26,508.67 | 26,508.67 | 24,469.54 | 20,391,29 | 17,332.60 |
| 1st mesh layer | 26,851.29 | 26,851.29 | 20,138.47 | 20,138.47 | 18,795.90 | 18,795.90 | 17,453.34 | 16,110.77 | 14,768.21 | 13,425.65 | 12,083.08 |
| Source and Information | Alternative Value of I for Elastic Analysis |
|---|---|
| ACI-318M-14 [5] | 0.25Ig–0.5Ig |
| FEMA 356-2000 [46] | 0.5 EIg–0.8EIg |
| New Zealand Code [47] | 0.35Ig |
| Paulay and Priestley, 1992 [48] | 0.30Ig–0.50Ig |
| In this research (singly reinforced beam) | |
| -BRC Beam | 0.05Ig–0.5Ig |
| -SRC Beam | 0.4Ig–0.75Ig |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Muhtar. The Prediction of Stiffness Reduction Non-Linear Phase in Bamboo Reinforced Concrete Beam Using the Finite Element Method (FEM) and Artificial Neural Networks (ANNs). Forests 2020, 11, 1313. https://doi.org/10.3390/f11121313
Muhtar. The Prediction of Stiffness Reduction Non-Linear Phase in Bamboo Reinforced Concrete Beam Using the Finite Element Method (FEM) and Artificial Neural Networks (ANNs). Forests. 2020; 11(12):1313. https://doi.org/10.3390/f11121313
Chicago/Turabian StyleMuhtar. 2020. "The Prediction of Stiffness Reduction Non-Linear Phase in Bamboo Reinforced Concrete Beam Using the Finite Element Method (FEM) and Artificial Neural Networks (ANNs)" Forests 11, no. 12: 1313. https://doi.org/10.3390/f11121313
APA StyleMuhtar. (2020). The Prediction of Stiffness Reduction Non-Linear Phase in Bamboo Reinforced Concrete Beam Using the Finite Element Method (FEM) and Artificial Neural Networks (ANNs). Forests, 11(12), 1313. https://doi.org/10.3390/f11121313





