Abstract
Urban vegetation biomass is a key indicator of the carbon storage and sequestration capacity and ecological effect of an urban ecosystem. Rapid and effective monitoring and measurement of urban vegetation biomass provide not only an understanding of urban carbon circulation and energy flow but also a basis for assessing the ecological function of urban forest and ecology. In this study, field observations and Sentinel-2A image data were used to construct models for estimating urban vegetation biomass in the case study of the east Chinese city of Xuzhou. Results show that (1) Sentinel-2A data can be used for urban vegetation biomass estimation; (2) compared with the Boruta based multiple linear regression models, the stepwise regression models—also multiple linear regression models—achieve better estimations (RMSE = 7.99 t/hm2 for low vegetation, 45.66 t/hm2 for broadleaved forest, and 6.89 t/hm2 for coniferous forest); (3) the models for specific vegetation types are superior to the models for all-type vegetation; and (4) vegetation biomass is generally lowest in September and highest in January and December. Our study demonstrates the potential of the free Sentinel-2A images for urban ecosystem studies and provides useful insights on urban vegetation biomass estimation with such satellite remote sensing data.
1. Introduction
According to the World Urbanized Prospects, urban residents are expected to compose 68% of the global population by 2050 [1], and this would bring increasingly intensive urban heat island (UHI) effects, environmental degradation, and ecological damage. As an important carrier of urban ecosystems, urban vegetation—which refers to all naturally growing and human-planted vegetation within an urban area [2,3]—brings considerable ecological, economic, and social benefits [4]. These include improving urban microclimates, mitigating UHI effects, increasing surface runoffs, maintaining the urban carbon–oxygen balance, and equally importantly, enhancing the quality of urban life by providing spaces for relaxation and recreation [5,6,7,8]. As such, the focus of urban eco-environmental studies has been long on urban vegetation, particularly the biomass of urban vegetation [9]. Urban vegetation biomass is an effective indicator of the capacity of carbon storage and sequestration, and ecological effect of an urban ecosystem [10,11]; it is, therefore, important to estimate urban vegetation biomass in urban eco-environmental management.
Traditional biomass measurement is simply to remove and weigh all the biomass occurring in quadrats, which is a labor-intensive and time-consuming practice [12,13]. This method does not allow quick monitoring and, more importantly, to some extent, might be destructive to the phenomenon being investigated. Remote sensing, however, provides an alternative to biomass measurement largely because it makes objective and mostly non-destructive observations of vegetated areas at various spatial and temporal resolutions. While vegetation biomass cannot be directly derived from remote sensing image data, remote sensing based estimation requires the use of sample plots to acquire field measurements for allometric growth equations based modeling and image interpretation for estimation (e.g., [14]). Vegetation biomass estimation with remote sensing has been summarized and reviewed in previous studies [15,16,17]. While optical sensor, radar, and lidar data can be used for biomass estimation separately or jointly [18,19,20,21,22], multispectral data is the most frequently used data type [15]. Although it has been widely recognized for its advantages, remote sensing has been mostly used to measure the biomass of individual vegetation types in natural forest [23,24], grassland [25,26,27], wetlands [28,29], and deserts [30] but rarely the biomass of urban vegetation [14,31].
Sentinel satellites are an Earth observation satellite constellation developed by the European Space Agency (ESA) as part of the Copernicus Program. Sentinel-2 is a wide-swath, high-resolution, multispectral imaging mission with two twin satellites (Sentinel-2A and Sentinel-2B), supporting land and climate-change monitoring [32]. Sentinel-2A was launched in June 2015 and has offered free image data at the ESA’s website as of December 2015. The Sentinel-2 MSI (multispectral imager) samples 13 different spectral bands ranging from the visible to shortwave infrared of electromagnetic spectrum, four bands at 10 m, six bands at 20 m, and three bands at 60 m spatial resolution [32]. It has now been used for a variety of forestry applications such as fire damage monitoring [33,34], forest storage estimation [35,36], and canopy cover calculation [37]. While some researchers have combined Sentinel-2A with radar data for biomass estimation [24], using such free optical sensor data alone has not been assessed. Testing the capability of Sentinel-2A data to estimate urban vegetation biomass would be interesting as Sentinel-2A data is being increasingly important for land monitoring, particularly for forestry.
In this study, we therefore focus on the modeling of urban vegetation biomass estimation from Sentinel-2A image data. Quadrat biomass was calculated using the allometric biomass equations with field measurements, and then vegetation biomass models were constructed with remote sensing derived variables. Specific objectives are testing the capability of Sentinel-2A data to estimate urban vegetation biomass and examining whether vegetation type-specific modeling can improve estimation accuracy.
2. Study Area
Bordering the provinces of Shandong, Henan, and Anhui, Xuzhou (33°43’~34°58’ N, 116°22’~118°40’ E) (Figure 1) is a national key railway hub located in the northwestern part of Jiangsu province, east China [38]. It has a monsoon-influenced humid subtropical climate with an annual mean daily temperature of 14.5 °C and an annual total precipitation of 832 mm [39]. As a typical forested city, Xuzhou has received multiple titles and awards such as the National Forest City in 2012, the National Ecological Gardening City in 2015, and particularly the UN-Habitat Scroll of Honor Award in 2018 [40], which is attributed largely to the implementation of several greening and ecological restoration programs in recent decades. Although the importance of urban vegetation to cities is generally acknowledged here, no research has been conducted to estimate and assess the urban vegetation biomass for Xuzhou.
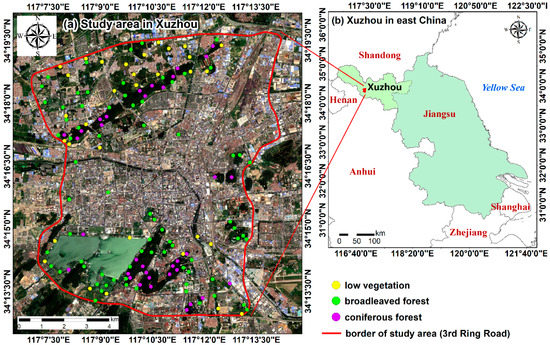
Figure 1.
The location of the study area: (a) the border of the study area (i.e., the third ring road of Xuzhou) and the sites for field investigations (yellow for low vegetation, green for broadleaved forest, and purple for coniferous forest); (b) Xuzhou in east China.
The area within the third ring road of Xuzhou (indicated by the red line in Figure 1a) was selected for this research, covering a geographical area of ~108.51 km2. The area within the third ring road is traditionally considered as the urbanized part of Xuzhou and home to the majority of Xuzhou’s urban residents. Its urban green areas have expanded remarkably in recent years and would be an ideal area for this research. The study area is flat in the central area with thick soil and hilly in the north, east, and south parts with thin humus-poor soil. The soil type is leached cinnamon soil, weak alkaline with pH ranging from 7.63 to 8.07 [41].
According to our fieldwork, most of the trees in the study area are coniferous, consisting largely of arborvitae trees (Platycladus orientalis). These evergreen trees were mainly planted during the 1950s and 1960s with 700–3000 trees per hectare [41]. They are usually 5–12 m high (avg. 8.36 m) with diameters at breast height (DBH) ranging from 5 to 15 cm (avg. 12.47 cm) [41]. Broadleaved forest is dominated by poplar (Populus euramevicana), black locust (Robinia pseudoacacia), and paper mulberry (Broussonetia papyrifera) trees. While the poplar trees are usually large (avg. DBH = 21.40 cm) and high (avg. height = 20 m) and concentrated along rivers and roads, the black locust and paper mulberry trees are scattered in parks and small hills. Shrubs are mostly found in parks, including colorful and decorative species such as Buxus megistophylla, and Berberis thunbergii. Grassland is relatively small in urban Xuzhou, usually in parks and residential/institutional properties. Typical grass includes Setaria viridis, Ophiopogon bodinieri, Iris tectorum, and Allium macrostemon.
3. Materials and Methods
3.1. Remote Sensing Data
In this study, we used Sentinel-2A image data—freely obtained from ESA’s website—for urban vegetation biomass estimation. These L1C-level data, which have already been radiometrically calibrated, were acquired in six different months of 2017 (Table 1). The image quality is generally good with a mean cloudiness of less than 10%. Although the January and May images were more cloud-contaminated, the study area remains cloud-free in the images—the images are therefore still usable. For data preprocessing, they were first atmospherically corrected and then re-sampled to 10-m, both using SNAP (SentiNel Application Platform), an image processing package developed by ESA for processing Sentinel data [42]. Lastly, the study area was extracted from the image data in ENVI 5.1 software for further processing.

Table 1.
Remote sensing image data used for urban vegetation estimation.
3.2. Urban Vegetation Classification
Based on our preliminary field investigations, we decided to classify the vegetation of the study area into three coarse categories, namely low vegetation (mostly shrubs and grass), broadleaved forest (mostly poplar, black locust, and paper mulberry), and coniferous forest (mostly arborvitae trees). While many areas are characterized by a single vegetation type, there are some areas with mixed vegetation, which justifies the use of linear spectral mixture analysis (LSMA) [38,43]—where the spectrum of a pixel is considered a linear combination of spectra of pure endmembers within the pixel weighted by their fractional abundance. To this end, a wide variety of features, such as spectral features (spectral reflectance and spectral indices), textural features (calculated by the gray level co-occurrence matrix), and vegetation abundances (the abundances of coniferous forest, broad-leaved forest, and low vegetation, obtained by LSMA) were derived from the Sentinel-2A image data and combined with topographical features (DEM—digital elevation model, and slope and aspect derived from DEM) to classify urban vegetation classification using the support vector machine (SVM) method. SVM is a machine learning algorithm used for image classification [44,45] and can achieve high accuracy. We compared SVM with other classifiers, namely random forest (RF), artificial neural network (ANN), and quick unbiased efficient statistical tree (QUEST), and found that the SVM produced the best result when vegetation abundances were added for classification. For a detailed description of the classification procedure, please refer to our previous research [2]. The produced classification map helps to identify the dominant vegetation type of each pixel so the biomass of each vegetated pixel can be estimated with the models constructed later.
3.3. Candidate Variables for Modeling
A total of 116 variables (features) on spectral reflectance, vegetation indices, topographical features, and vegetation abundances were selected as candidate variables (features) for biomass estimation. They are given in Table 2 (see Table A1 for their description and calculation formulas).

Table 2.
Candidate variables for biomass estimation.
3.4. Field Measurements
Biomass sampling is necessary for vegetation biomass modeling. Usually, quadrat biomass is the sum of the dry weight of every single plant in the quadrat [12,13]. Despite high accuracy, this method requires the vegetation being investigated to be cut. As such, it is applicable to primeval forest or experimental plots but not desirable for urban green land. As a frequently used indirect biomass estimation method [46], the allometric biomass equations, where the quantitative relationships between the biomass and the growth variables of a plant are established [11], however, provide an alternative biomass sampling approach in an urban context. As they are reliable for determining tree biomass, a growing number of biomass equations have been proposed for various vegetation species across the world [47,48,49,50,51,52,53,54]. In this study, the allometric biomass equations were considered for calculating the biomass of each quadrat.
From extensive literature, the allometric biomass equations for various types of trees and shrubs in Xuzhou were summarized (Table A2 and Table A3). For grass, a different estimation approach was adopted in this study: the average unit grassland biomass of Xuzhou is the spatially weighted biomass of Jiangsu, Anhui, Henan, and Shandong provinces [55] since Xuzhou is located at the junction of these four provinces (Table 3). Through the calculation, the average unit biomass of Xuzhou’s grassland is 61.89 g/m2.

Table 3.
The calculation of the average unit (aboveground) biomass of grassland of Xuzhou [55].
The growth variables of plants required in the allometric biomass equations were measured in the field investigations conducted from October to December 2017. The general investigation procedure is as follows: (1) a total of 192 urban vegetation quadrats were randomly pre-selected over the false-color Sentinel-2A imagery of the study area and their central coordinates were retrieved; (2) 10 m × 10 m quadrats were determined (matching the spatial resolution of Sentinel-2A imagery) by navigation in the field with hand-held GPS (Global Positioning System) devices to these coordinates; (3) the growth variables of each single plant (shrubs and trees only) in each quadrat were recorded and the biomass of each single plant using the plant-specific allometric biomass equations was calculated; and (4) the biomass of the all the plants in a quadrat were summed to obtain the total biomass of that quadrat and this was repeated for each quadrat.
Note that our records varied with vegetation type. Within each quadrat, we documented the name, tree height (from the base to the crown), and DBH (diameter at breast height, i.e., ~1.3 m) for trees, the name, basal diameter, height, and crown width for shrubs, and the name, height, and coverage area for grass. Different measuring tools were used in accordance with the plants to be investigated and the parameters to be recorded. The DBHs and basal diameters were measured by a 2-m tape measure with a minimum scale of 1 mm while shrub heights were measured by a 5-m tape measure with a minimum scale of 1 mm. For tree heights, we used a telescopic height measuring rod with a maximum range of 20 m and a minimal scale of 1 mm. Photos illustrating the fieldwork are shown in Figure 2.

Figure 2.
Photos taken in the field illustrating the measurements.
Although 192 vegetation quadrats were initially selected, only 140 quadrats of them (shown in Figure 1) were visited and investigated in practice—because some of the pre-selected quadrats were not accessible for various reasons (e.g., physical barriers and refusal to access). Among the 140 quadrats were 35 dominated by coniferous forest, 73 by broadleaved forest, and 32 by low vegetation. The results of quadrat biomass calculated mainly by using the allometric biomass equations are detailed in Table A4.
3.5. Modeling
3.5.1. Correlation Analysis
Prior to modeling, the relationship between the candidate variables (Table 2) and the vegetation biomass was examined through correlation analysis. The biomass of the quadrats dominated by low vegetation, broadleaved forest, and coniferous forest is hereinafter referred to as low vegetation biomass, broadleaved forest biomass, and coniferous forest biomass, respectively. The correlation coefficients were computed with and without vegetation types discriminated.
3.5.2. Stepwise Regression Modeling
Stepwise regression (SR) is essentially a multiple linear regression method, but it is different from the general multiple linear regression in the selection of variables. In a stepwise regression analysis, the most significant or least significant variable is added to or removed with iteration from the multiple linear regression model based on its statistical significance [56,57]. At each iteration of adding or removing a potential independent variable, resultant models are assessed by means of the p-value of an F-statistic (p-value < 0.05 for statistical significance) [56,57]. Stepwise regression has proved effective in selecting variables for modeling and has been widely used in different fields [58,59], including forest biomass estimation [60]. As such, it was considered more suitable for constructing the urban vegetation biomass estimation models in this study.
As it is likely that collinearity exists in the predictive variables, the variance inflation factor (VIF) [57,61] is used to examine it in this study:
where Ri is the correlation coefficient between the ith predictive variable and the remaining predictive variables. There is no multicollinearity if VIF ranges between 0 and 10. If VIF ≥ 10, high multicollinearity exists between variables and some of them should be removed from the model [62].
3.5.3. Boruta Based Multiple Linear Regression Modeling
In addition to the SR modeling, the general multiple linear regression (MLR) is also considered in this study for comparative analysis. It is too complicated to include all the 116 candidate variables (Table 2) in the MLR modeling as it would decrease accuracy, cause overfitting, and slow computation. It is advisable to reduce the dimensionality of data when there are a large number of variables [63]. To this end, a group of important variables is then selected, which is done in this study by using the Boruta algorithm. Boruta is a feature selection wrapper built around the random forest classification algorithm and helps to determine important variables [64,65]. A detailed description of this feature selection technique can be found in [65,66]. The Boruta algorithm can be performed in the statistical software of , where important variables are confirmed for modeling and unimportant one are rejected, and some artificial variables called shadow variables are generated from the original variables [65]).
Despite the capability to locate important variables, the Boruta algorithm does not consider the collinearity among these variables. Like the SR modeling, closely correlated variables are removed if VIF ≥ 10. The final MLR biomass estimation models are finally determined until the VIF of each remaining variable is less than 10.
3.5.4. Accuracy Assessment
While 70% of the calculated quadrat biomass were used for modeling, the remaining 30% were reserved for assessing the models using two measures, namely the coefficient of determination (Ryz2) and the root-mean-square-error (RMSEyz):
where is the calculated quadrat biomass, is the modeled quadrat biomass, is the average of calculated biomass of all quadrats, and is the number of quadrats.
3.6. Seasonal Variation of Urban Vegetation Biomass
After the accuracy assessment, the superior models can be determined and used for exploring the seasonal vegetation biomass variation of the study area. With the variables required by the determined models derived from the Sentinel-2A image data (Table 1), the biomass of low vegetation, broadleaved forest, and coniferous forest can be estimated for January, March, May, July, September, and December of 2017, respectively. The total urban vegetation biomass of the study area is then calculated by summing the estimated type-specific biomass. The change rate (CR) is defined by the following equation:
where and are the maximum and minimum biomass of the year 2017.
4. Results and Analysis
4.1. Urban Vegetation Classification
By the SVM classifier, the urban vegetation of the study area was classified into three types, namely low vegetation, broadleaved forest, and coniferous forest (Figure 3) in the 24-July-2107 image; the overall accuracy of this classification was 89.86% with a Kappa coefficient of 0.83. While the central part of the study area had limited vegetation, vegetated areas were mostly covered by low vegetation, followed by coniferous forest.
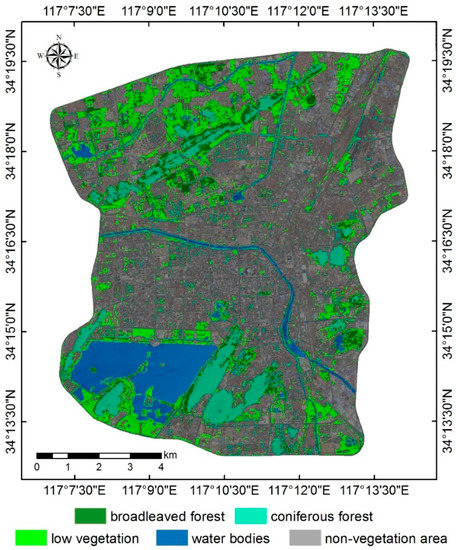
Figure 3.
Urban vegetation classification by support vector machine.
4.2. Correlations between Candidate Variables and Urban Vegetation Biomass
4.2.1. For Low Vegetation
There were 14 candidate variables significantly correlated with low vegetation biomass (Table 4). Eight spectral reflectance variables had negative correlations with all-vegetation biomass, coefficients ranging from −0.364 to −0.553. It was negatively associated with low vegetation abundance and positively with coniferous forest abundance. Low vegetation biomass is generally lower than the biomass of broadleaved and coniferous forests, and more low vegetation in the quadrat means lower quadrat biomass. The correlation of low vegetation biomass with topographic features was not significant because low vegetation is usually scattered in the study area. Low vegetation biomass was negatively correlated with two vegetation indices and two textural features.

Table 4.
Variables significantly correlated with low vegetation biomass.
4.2.2. For Broadleaved Forest
A total of 54 variables were significantly correlated with broadleaved forest biomass (Table 5). Four spectral reflectance variables were negatively correlated with broadleaved forest biomass. Regarding vegetation abundance variables, only low vegetation abundance was negatively correlated with broadleaved forest biomass, but the coefficient was low. As for topographic features, broadleaved forest grows in relatively flat areas (e.g., parks and residential land) and low-elevated hills in the study area and, therefore, no significant correlation exists between topography and broadleaved forest biomass. The biomass was also correlated with seven vegetation indices, higher correlation coefficients with DVI and SR4. Textural features had close, mostly positive, correlations with broadleaved forest biomass, although the highest correlation (−0.72), with Cor (VRE2), was negative.

Table 5.
Variables significantly correlated with broadleaved forest biomass.
4.2.3. For Coniferous Forest
Among the 116 candidate variables, 16 were significantly correlated with coniferous forest biomass (Table 6). Seven spectral reflectance variables were all negatively correlated with coniferous forest biomass, with correlation coefficients mostly higher than 0.5. Not surprisingly, only coniferous forest abundance (CLF) was highly positively correlated with coniferous forest biomass. DEM was the only topographic feature significantly correlated with coniferous forest biomass, and the negative correlation is probably linked to the fact that coniferous forest grows in hills and its biomass decreases with elevation. Coniferous forest biomass was highly significantly correlated with several vegetation indices but, interestingly, no correlation was found with textural features. The Var (variance), Cont (contrast), Diss (difference), Entr (entropy) values were all zero while Mean (mean), Homo (homogeneity), Sec_M (second moment), and Cor (correlation) values were all one—coniferous forest is densely distributed in the study area, thus no clear textural characteristics.

Table 6.
Variables significantly correlated with coniferous forest biomass.
4.2.4. For All-Type Vegetation
Results show that 39 variables were significantly correlated with all-type vegetation biomass (Table 7). In total, ten spectral reflectance variables had negative correlations with all-type vegetation biomass, coefficients ranging from −0.308 (Red) to −0.496 (Green). It was negatively associated with low vegetation abundance but positively with broadleaved and coniferous forest abundances. Low vegetation has lower biomass than coniferous and broadleaved forest and, in a given area (e.g., a pixel size), the all-type vegetation biomass would be lower if low vegetation abundance is larger than the other two vegetation abundances. While it had no significant correlation with topographic features, all-type vegetation biomass was correlated with half of the vegetation indices. The highest positive correlation coefficient was found with SR4 (0.390) while the highest negative with DVI (−0.396) (Table A1). In addition, only 14 (17.50% of the total) textural features were significantly correlated with all-type vegetation biomass and coefficients were generally low.

Table 7.
Variables significantly correlated with all-type vegetation biomass.
4.3. Urban Vegetation Biomass Estimation Models
4.3.1. Stepwise Regression Models
The results of performing SR for constructing vegetation biomass estimation models are presented in Table A5. All the (adjusted) coefficients of determination (Rnh2 and adj-Rnh2) were higher than 0.70, and the fitting was generally good. The variables in the models were less than those (highly) significantly correlated with vegetation biomass (Table 4, Table 5, Table 6 and Table 7). The type-specific and all-vegetation biomass estimation models are given below.
The SR biomass estimation model for low vegetation:
The SR biomass estimation model for broadleaved forest:
The SR biomass estimation model for coniferous forest:
The SR biomass estimation model for all-type vegetation:
4.3.2. Multiple Linear Regression Models
The results of performing the Boruta algorithm in the statistical software of are shown in Figure 4. Important variables were labeled as Confirmed in blue, unimportant ones as Rejected in red, and shadow ones as Shadow in grey.
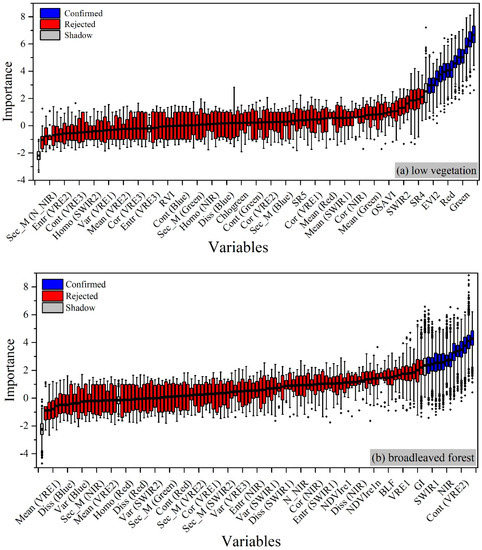
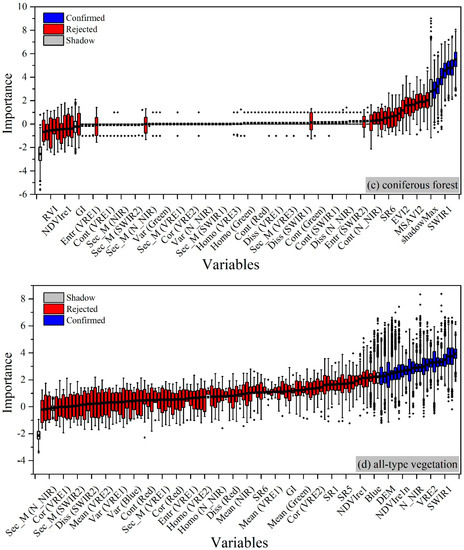
Figure 4.
Importance of candidate variables: (a) low vegetation; (b) broadleaved forest; (c) coniferous forest; and (d) all-type vegetation. Important variables are labeled as Confirmed in blue, unimportant ones as Rejected in red, and shadow ones as Shadow in grey.
Using the same biomass data as the SR modeling, the MLR biomass estimation models for low vegetation, broadleaved forest, coniferous forest, and all-type vegetation were built with the important variables identified through the Boruta algorithm and the use of VIF.
The MLR biomass estimation model for low vegetation biomass:
The MLR biomass estimation model for broadleaved forest:
The MLR biomass estimation model for coniferous forest:
The MLR biomass estimation model for all-type vegetation:
4.3.3. Accuracy Assessment
Figure 5 illustrates the results of assessing the SR biomass estimation models for low vegetation, broadleaved forest, coniferous forest, and all-type vegetation. It shows that Ryz2 values of the models for specific vegetation types (viz. the models for low vegetation, broadleaved forest, and coniferous forest) were all higher than 0.7. The coniferous model had the highest Ryz2 (0.786) and the lowest RMSEyz (6.89 t/hm2). The all-type model had a larger RMSE than the type-specific models.
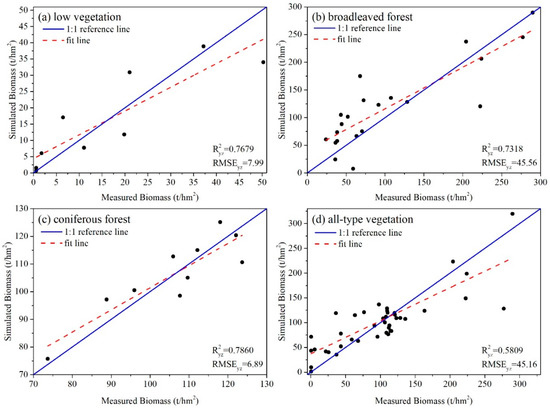
Figure 5.
Accuracy assessment of the SR biomass estimation models: (a) low vegetation; (b) broadleaved forest; (c) coniferous forest; and (d) all-type vegetation.
Similarly, the remaining 30% of field observation data are used to assess the accuracy of the MLR biomass estimation models. After this, the two types of models are compared in terms of accuracy measured by the coefficient of determination (Ryz2) and root-mean-square-error (RMSEyz) (Table 8).

Table 8.
Comparing the accuracies of the SR and MLR biomass estimation models (unit for RMSE: t/hm2).
4.4. Seasonal Variation
As the SR models produced better estimates, they were used to calculate the biomass of each urban vegetation type in January, March, May, July, September, and December of 2017. The type-specific vegetation biomass and total vegetation biomass are shown in Figure 6.
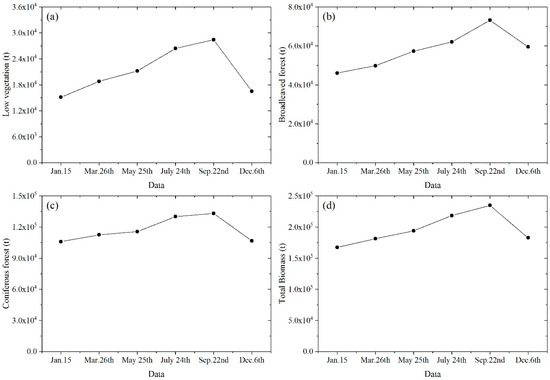
Figure 6.
Type-specific biomass and the total vegetation biomass in the selected months of 2017: (a) low vegetation; (b) broadleaved forest; (c) coniferous forest; and (d) all vegetation.
Overall, vegetation biomass increased over time and decreased after peaking in autumn. The highest biomass of low vegetation was in September (28,423 t) and lowest in January and December (~15,000 t) with a maximal change rate of 87.60%. Despite an increase of 27,150 t biomass from January to September, the change rate of broadleaved forest was 58.93%, much lower than low vegetation (Figure 7). The biomass change rate of coniferous forest (25.58%) was the lowest in the three vegetation types. The total vegetation biomass change was 67,524 t with a change rate of 40.39%.
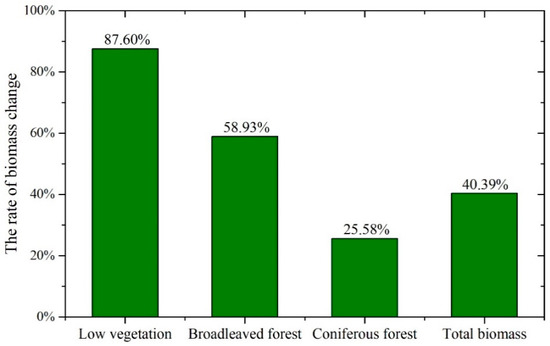
Figure 7.
The seasonal change rate of vegetation biomass of the study area.
5. Discussion
Correlation analysis is useful to identify what variables are related to the dependent variable [59]. While the biomass of low vegetation and broadleaved forest is correlated mostly with spectral reflectance, broadleaved biomass is correlated mostly with textural features. Although there might be close correlations among some of the candidate variables (e.g., NDVI and RVI in the category of vegetation indices), we here did not provide a full correlation matrix for this because the number of variables was so large and would take substantial space of the publication. In addition, the use of stepwise regression and variance inflation factor can avoid the models with correlated variables [57].
Our modeling results show that for both individual vegetation types and all-type vegetation, the SR models have higher coefficients of determination and lower root-mean-square-errors than the MLR models. This clearly suggests that the SR modeling outperforms the MLR modeling in the estimation of urban vegetation biomass. The superiority of SR modeling is also noted in the study of Xu et al., where degraded grassland biomass was estimated using machine learning methods from terrestrial laser scanning data [27]. By comparing SR, random forest, and artificial neural network, they claimed that SR produced the highest accuracy (R2 = 0.84, RMSE = 48.89g/m2). However, it might be controversial to conclude that SR is best for vegetation biomass modeling as some researchers favor machine learning algorithms. For example, Lu et al. report that RF (R2 = 0.78, RMSE = 1.34 t/ha) performs better than SR (R2 = 0.75, RMSE = 1.46 t/ha) in wheat biomass estimation with unmanned aerial vehicle data [67]. We here do not attempt to compare the results of our models with those of others because the data for modeling and the contexts (various vegetation types in an urban area vs. a single type of vegetation in (semi-) environments) were different.
Although some researchers estimated vegetation biomass from remote sensing without discriminating types [29], our study revealed that vegetation biomass should be modeled for specific vegetation types for higher modeling accuracy. This is often done for different contexts by other researchers, e.g., Gao et al. who discriminated broadleaved, coniferous, mixed, and bamboo forest in China’s Zhejiang province [68], and González-Jaramillo et al. who divided vegetation of the San Francisco watershed (south Ecuador) into tropical mountain forest, subpáramo, and pastures [23]. In fact, the finding of correlation analysis that variables significantly correlated with vegetation biomass varies largely with vegetation type implies that type-specific biomass estimations models should be constructed. Similarly, non-species-specific allometric growth models yielded larger errors than species-specific ones [69]. Urban vegetation cannot be regarded as a single vegetation type as it varies largely in biophysical characteristics and thus biomass. Such variations, which might be minimized in plantations, should be considered for urban green areas. As such, it is important to discriminate urban vegetation types through image classification before modeling urban vegetation biomass from remote sensing image data.
Regarding the seasonal variation of vegetation biomass, coniferous forest has much lower biomass loss than low vegetation and broadleaved forest, which is because coniferous forest consists mainly of evergreen arborvitae trees that do not lose their leaves through the year. This suggests that more coniferous trees should be planted if the biomass loss of low vegetation and broadleaved forest needs to be compensated. In this multi-season analysis, the same type-specific estimation models were used for estimating vegetation biomass from remote sensing data imaged in different months. For a plant species in an area, there is only one allometric growth equation, which is often built with measurements acquired, e.g., when plants are luxuriant with maximal biomass in a year. The biomass estimation models constructed with quadrat biomass calculated using these equations should best reflect that time. If these models are used for other dates, estimation biomass would be less accurate (e.g., due to less leaves in winter). Remote sensing variables derived from remote sensing images can however characterize the vegetative status of the plants and compensate the impact.
In addition, there are some other limitations that might undermine the results. Firstly, the allometric biomass equations for a variety of plant species with high reported accuracies were borrowed from previous studies, but we were not able to individually verify these equations as this work is out of the scope of the present study. Secondly, tree biomass could be, to some extent, underestimated from remote sensing image data. While it is likely that under large coniferous and broadleaved and coniferous trees grow some low vegetation like grass and bushes, this cannot be recognized in pixels, notwithstanding the application of linear spectral mixture analysis. Despite these limitations, our study proves the capability of free optical sensor data like Sentinel-2A to estimate urban vegetation biomass. It would be interesting if urban vegetation biomass could be regularly monitored; however, this seems currently challenging as Sentinel-2A data now remains scarce and does not allow a retrospective assessment.
6. Conclusions
This study demonstrates how Sentinel-2A image data can be used for vegetation biomass in an urban context. The main findings and conclusions of this study are as follows:
- Freely available multispectral Sentinel-2A satellite data has proven its capability in urban vegetation biomass estimation. The measured biomass of each vegetation type is closely correlated with different remote sensing derived variables, mostly spectral reflectance for low vegetation and coniferous forest and mostly textural features for broadleaved forest.
- The vegetation biomass estimation models built by the stepwise regression (SR) outperform those with the multiple linear regression. It is necessary to discriminate vegetation types in biomass modeling and the highest accuracy is obtained by the SR model for coniferous forest.
- Highest vegetation biomass occurs in autumn (September) while lowest in winter (January and December). Low vegetation and broadleaved forest have larger seasonal change rates than coniferous forest that consists mostly of evergreen trees.
Urban green areas are a key component of urban eco-environment and make a vital contribution to improving the quality of life and moderating climate. In general, trees have a stronger carbon sequestration capability and produce more biomass than low vegetation. More coniferous trees can maintain less biomass loss in winter. However, tree species should be diversified to reduce ecological vulnerability and guarantee a more robust urban ecosystem and more sustainable urban development.
Author Contributions
Conceptualization, X.Z. and L.L.; methodology, X.Z., L.L., and L.C. (Longqian Chen); software, X.Z., Y.L., and Y.Z.; validation, Y.L. and Y.Z.; formal analysis, L.L., and X.Z; investigation, X.Z., Y.L., and L.L.; resources, L.C (Longqian Chen). and L.C. (Longgao Chen); data curation, X.Z. and L.L.; writing—original draft preparation, L.L. and X.Z.; writing—review and editing, L.L., L.C. (Longqian Chen), and L.C. (Longgao Chen); visualization, Y.Z. and Y.L.; supervision, L.C. (Longqian Chen); project administration, L.L. and L.C. (Longqian Chen); funding acquisition, L.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by “the Fundamental Research Funds for the Central Universities” (Grant No.: 2018QNB06).
Acknowledgments
The authors would like to thank the United States Geological Survey (USGS) for freely providing satellite remote sensing image data required in this study, Guanghui Hong for his assistance in the fieldwork, and Jinyu Zang, Ruiyang Liu, Zhiqiang Wang, and Ziqi Yu for their help in preparing an early version of this manuscript. Comments and suggestions from three anonymous reviewers are greatly appreciated for improving the study.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Table A1.
Formulas used for calculating spectral indices [70].
Table A1.
Formulas used for calculating spectral indices [70].
| Spectral Index | Formula |
|---|---|
| Green index (GI) | |
| Green normalized different vegetation index (gNDVI) | |
| Normalized difference vegetation index (NDVI) | |
| Ratio vegetation index (RVI) | |
| Difference vegetation index (DVI) | |
| Enhanced vegetation index 2 (EVI2) | |
| Chlorophyll green index (Chlogreen) | |
| Normalized difference vegetation index (NDVIre1) | |
| Normalized difference vegetation index (NDVIre1n) | |
| Simple ratio 1 (SR1) | |
| Simple ratio 2 (SR2) | |
| Simple ratio 3 (SR3) | |
| Simple ratio 4 (SR4) | |
| Simple ratio 5 (SR5) | |
| Simple ratio 6 (SR6) | |
| Simple ratio 7 (SR7) | |
| Normalized difference infrared index (NDII) | |
| Soil-adjusted vegetation index (SAVI) | |
| Modified soil-adjusted vegetation index 2 (MSAVI2) | |
| Optimized soil-adjusted vegetation index (OSAVI) |
Note: VRE1–VRE3 represent the three red-edge bands; N_NIR represents the narrow near-infrared bands.

Table A2.
Allometric biomass equations for trees, used for calculating quadrat biomass.
Table A2.
Allometric biomass equations for trees, used for calculating quadrat biomass.
| Tree species | Model | R2 | Reference |
|---|---|---|---|
| Platycladus orientalis | WS = 0.0573 (D2H) 0.8657 | 0.97 | [71] |
| WB = 0.0043 (D2H) 1.1085 | 0.89 | ||
| WL = 0.0038 (D2H) 1.0385 | 0.84 | ||
| WR = 0.0485 (D2H) 0.6886 | 0.80 | ||
| Robinia pseudoacacia | WS = 0.0681 (D2H) 0.9865 | 0.9545 | [72] |
| WB = 12020 + 0.009 (D2H) | 0.8862 | ||
| WL = −0.549 + 0.007 (D2H) | 0.9174 | ||
| WR = 0.0087 (D2H) 1.0513 | 0.9472 | ||
| Metasequoia glyptostroboides | WS = 0.0146 (D2H) 0.9835 | 0.993 | [73] |
| WB = 0.0243 (D2H) 0.7359 | 0.993 | ||
| WL = 0.0949 (D2H) 0.4795 | 0.982 | ||
| WR = 0.0102 (D2H) 0.8745 | 0.975 | ||
| Populus euramevicana | WS = 0.006 (D2H) 1.098 | 0.995 | [74] |
| WB =0.001 (D2H) 1.157 | 0.984 | ||
| WL = 0.012 (D2H) 0.685 | 0.955 | ||
| WR = 0.083 (D2H) 0.636 | 0.915 | ||
| Cinnamomum camphora | WS = 0.0914 (D2H) 0.7755 | 0.944 | [73] |
| WB = 0.0099 (D2H) 1.0256 | 0.946 | ||
| WL = 0.0011 (D2H) 1.1713 | 0.941 | ||
| WR = 0.0298 (D2H) 0.8740 | 0.935 | ||
| Ginkgo biloba | lnWS = −3.84 + 0.95ln (D2H) | 0.98 | [75] |
| lnWB = −9.38 + 1.46ln (D2H) | 0.852 | ||
| lnWL = −6.95 + 1.03ln (D2H) | 0.853 | ||
| lnWR = −5.60 + 1.07ln (D2H) | 0.967 | ||
| Platanus acerifolia | WT = 0.0690(D2H) 0.9133 | / | [76] |
| Larix gmelinii | lnWS = −2.8319 + 0.8379ln (D2H) | 0.9996 | [77] |
| lnWB = −3.9021 + 0.8822ln (D2H) | 0.9015 | ||
| lnWL = −4.0174 + 0.7659ln (D2H) | 0.9007 | ||
| lnWR = −3.6497 + 0.8247ln (D2H) | 0.9994 | ||
| Broussonetia papyrifera | WT = 0.07112 (D2H) 0.910358078 | / | [78] |
| Ligustrum lucidum | WS = 0.03939 (D2H) 0.95679 | 0.97 | [79] |
| WB = 0.03357 (D2H) 0.77809 | 0.84 | ||
| WL = 0.11613 (D2H) 0.45871 | 0.61 | ||
| WT = 0.11394 (D2H) 0.84957 | 0.97 | ||
| Koelreuteria bipinnata | WS = 0.08259 (D2H) 0.80831 | 0.97 | [79] |
| WB = 0.00053 (D2H) 1.29104 | 0.94 | ||
| WL = 0.01286 (D2H) 0.69408 | 0.81 | ||
| WT = 0.12238 (D2H) 0.84468 | 0.98 | ||
| Magnolia grandiflora | WS = 0.0649 (D2H) 0.8131 | 0.969 | [73] |
| WB = 0.0431 (D2H) 0.6697 | 0.904 | ||
| WL = 0.0254 (D2H) 0.8701 | 0.837 | ||
| WR = 0.0885 (D2H) 0.6713 | 0.883 | ||
| Liriodendron chinense | WS = 0.02426 (D2H) 0.942303 | 0.99537 | [80] |
| WB = 0.000349 (D2H) 1.268207 | 0.962865 | ||
| WL = 0.000419 (D2H) 1.048786 | 0.834806 | ||
| WR = 0.023475 (D2H) 0.770233 | 0.918072 | ||
| Paulownia fortunei | WS = 0.021158D 2.43244 | 0.9978 | [81] |
| WB = 0.057869D 2.06599 | 0.9959 | ||
| WL = 0.060045D 1.54688 | 0.9891 | ||
| WR = 0.030740D 2.10612 | 0.8387 |
Note: D is DBH (diameter at breast height); H is tree height; WS, WB, WL, refer to the biomass of stem, branch, and leaves; and WT and WR to the total aboveground biomass and root biomass.

Table A3.
Allometric biomass equation of shrubs, used for calculating quadrat biomass [82,83].
Table A3.
Allometric biomass equation of shrubs, used for calculating quadrat biomass [82,83].
| Species | Model | R2 | Species | Model | R2 |
|---|---|---|---|---|---|
| Ligustrum quihoui | WB = 26.332 (CH) 0.666 | 0.950 | Buxus bodinieri | WB = 262.879 (CH) 1.546 | 0.895 |
| WL = 14.646C 1.164 | 0.972 | WL = 224.662 (CH) 1.364 | 0.890 | ||
| WR = 18.721 (VC) 0.421 | 0.965 | WR = 294.262 (CH) 1.639 | 0.889 | ||
| WT = 52.388 (CH) 0.654 | 0.959 | WT = 756.343 (CH) 1.497 | 0.913 | ||
| Berberis thunbergii | WB = 73.468 (AC) 0.766 | 0.927 | Buxus megistophylla | WB = 15.572D 1.325 | 0.979 |
| WL = 3.340 (AC) 0.465 | 0.601 | WL = 20.649 + 9.047ln (CH) | 0.902 | ||
| WR = 29.029 (AC) 0.721 | 0.785 | WR = 9.654D 1.308 | 0.975 | ||
| WT = 104.637 (AC) 0.734 | 0.903 | WT = 35.982D 1.212 | 0.980 | ||
| Photinia serrulata | WB = 0.310 (D2H) 1.097 | 0.985 | Pittosporum tobira | WB = 765.073 (VC) 0.824 | 0.991 |
| WL = 0.264 (D2H) 0.916 | 0.986 | WL = 2.958 (D2H) 0.607 | 0.911 | ||
| WR = 0.259 (D2H) 1.053 | 0.988 | WR = 445.103 (VC) 0.742 | 0.972 | ||
| WT = 0.805 (D2H) 1.051 | 0.988 | WT = 1411.387 (VC) 0.742 | 0.979 | ||
| Hibiscus syriacus | WB = 108.688 (VC) 1.693 | 0.984 | Nandina domestica | WB = 75.700 (CH) 1.110 | 0.980 |
| WL = 18.925 (CH) 1.565 | 0.969 | WL = 11.109 + 17.911lnH | 0.971 | ||
| WR = 69.564 (VC) 1.563 | 0.985 | WR = 57.553 (CH) 1.187 | 0.939 | ||
| WT = 206.627 (VC) 1.589 | 0.986 | WT = 167.114 (CH) 1.174 | 0.960 | ||
| Lagerstroemia indica | WB = 30.213H 6.318 | 0.987 | Syringa oblata | WB = 0.876 (D2H) 0.894 | 0.988 |
| WL = 6.656H 5.065 | 0.994 | WL = 0.683 (D2H) 0.715 | 0.988 | ||
| WR = 20.934H 5.905 | 0.989 | WR = 0.603 (D2H) 0.877 | 0.991 | ||
| WT = 58.305H 6.065 | 0.989 | WT = 2.011 (D2H) 0.863 | 0.991 | ||
| Forsythia suspensa | WB = 0.385 (D2H) 1.025 | 0.997 | |||
| WL = 0.187 (D2H) 0.868 | 0.985 | ||||
| WR = 0.176 (D2H) 0.954 | 0.990 | ||||
| WT = 0.716 (D2H) 0.989 | 0.996 | ||||
Note: D is basal diameter; H is height; C is crown width (which is the average of south-north crown diameter C1 and east-west crown diameter C2; C = (C1 + C2)/2); AC is the area of crown (AC = π × C1 × C2); VC is the volume of crown (VC = AC × H); WS, WB, WL, refer to the biomass of stem, branch, and leaves; and WT and WR to the total biomass and root biomass.

Table A4.
The calculated biomass for each quadrat. As only 140 of the 192 pre-selected quadrats were visited and investigated, the quadrat ID ranges from 1 to 192.
Table A4.
The calculated biomass for each quadrat. As only 140 of the 192 pre-selected quadrats were visited and investigated, the quadrat ID ranges from 1 to 192.
| ID | Biomass (kg) | ID | Biomass (kg) | ID | Biomass (kg) | ID | Biomass (kg) |
|---|---|---|---|---|---|---|---|
| 1 | 1005.74 | 2 | 654.00 | 3 | 1192.37 | 5 | 1372.71 |
| 6 | 1711.81 | 7 | 11,250.00 | 8 | 972.12 | 9 | 1286.95 |
| 10 | 2118.96 | 11 | 1043.43 | 13 | 1258.78 | 14 | 1114.78 |
| 15 | 502.87 | 16 | 431.85 | 17 | 638.50 | 21 | 985.40 |
| 22 | 918.67 | 23 | 989.10 | 24 | 1212.90 | 25 | 349.37 |
| 26 | 732.72 | 27 | 838.38 | 28 | 1580.27 | 29 | 383.54 |
| 30 | 110.76 | 31 | 100.03 | 33 | 766.57 | 34 | 1556.81 |
| 35 | 917.00 | 36 | 56.07 | 37 | 383.64 | 38 | 1171.94 |
| 39 | 759.66 | 40 | 519.31 | 41 | 1383.84 | 42 | 1300.94 |
| 43 | 711.91 | 45 | 1158.74 | 46 | 831.58 | 47 | 447.30 |
| 48 | 906.36 | 50 | 607.56 | 51 | 362.14 | 52 | 325.44 |
| 53 | 734.24 | 54 | 634.06 | 55 | 2152.83 | 56 | 965.29 |
| 59 | 240.68 | 60 | 777.64 | 63 | 2042.87 | 65 | 1237.21 |
| 66 | 1573.60 | 67 | 901.01 | 68 | 1641.06 | 69 | 805.89 |
| 70 | 612.32 | 71 | 1658.79 | 72 | 433.56 | 74 | 2225.07 |
| 75 | 257.17 | 76 | 893.24 | 77 | 1209.58 | 80 | 8.23 |
| 82 | 706.14 | 83 | 989.41 | 84 | 1105.56 | 86 | 551.12 |
| 87 | 38.43 | 88 | 222.73 | 90 | 879.47 | 91 | 1285.60 |
| 92 | 17.95 | 94 | 442.08 | 95 | 822.52 | 96 | 680.24 |
| 97 | 1085.41 | 99 | 1153.80 | 100 | 188.35 | 101 | 11,085.08 |
| 106 | 2771.95 | 107 | 590.58 | 110 | 884.22 | 111 | 1531.30 |
| 116 | 984.55 | 117 | 3452.27 | 118 | 525.76 | 119 | 120.16 |
| 121 | 371.84 | 123 | 663.12 | 124 | 559.32 | 126 | 1610.53 |
| 127 | 866.05 | 129 | 3437.13 | 132 | 384.20 | 134 | 2179.22 |
| 135 | 216.23 | 137 | 2915.05 | 139 | 610.32 | 140 | 6.19 |
| 142 | 1100.06 | 143 | 1634.99 | 145 | 973.77 | 146 | 364.50 |
| 147 | 1421.20 | 148 | 1841.15 | 149 | 2707.82 | 151 | 969.84 |
| 152 | 2899.26 | 153 | 6.19 | 154 | 1176.14 | 156 | 1100.67 |
| 157 | 3279.12 | 158 | 6.19 | 159 | 1265.47 | 162 | 1007.43 |
| 163 | 2240.88 | 164 | 1189.30 | 166 | 6.19 | 168 | 6.19 |
| 169 | 6.19 | 170 | 698.32 | 172 | 198.72 | 173 | 6.19 |
| 174 | 1772.22 | 175 | 2304.31 | 176 | 6.19 | 177 | 6.19 |
| 178 | 1045.89 | 179 | 131.80 | 180 | 78.79 | 181 | 888.34 |
| 182 | 64.71 | 183 | 320.74 | 185 | 210.05 | 187 | 724.18 |
| 188 | 308.44 | 189 | 1002.98 | 190 | 6.19 | 192 | 623.21 |

Table A5.
The results of the SR modeling.
Table A5.
The results of the SR modeling.
| Vegetation Type | Rnh2 | Adj-Rnh2 | Variable | Coefficient | VIF |
|---|---|---|---|---|---|
| Low vegetation | 0.853 | 0.818 | Constant | −171.896 | |
| Low | −49.335 | 1.382 | |||
| CLF | 76.406 | 3.254 | |||
| gNDVI | 316.404 | 3.181 | |||
| SR2 | −13.710 | 4.274 | |||
| Cor (VRE2) | −0.365 | 1.311 | |||
| DEM | 1.087 | 1.207 | |||
| Broadleaved forest | 0.821 | 0.805 | Constant | 660.327 | |
| Cor (VRE2) | −16.739 | 2.095 | |||
| Green | −3601.606 | 1.066 | |||
| Cor (SWIR1) | 9.944 | 2.317 | |||
| OSAVI | −695.210 | 1.375 | |||
| Var (VRE2) | −196.861 | 5.043 | |||
| Cont (SWIR1) | 98.126 | 5.674 | |||
| Coniferous forest | 0.838 | 0.810 | Constant | 183.909 | |
| SWIR1 | −473.034 | 1.151 | |||
| SR3 | −0.016 | 1.346 | |||
| DEM | −0.232 | 1.109 | |||
| GI | 0.299 | 1.461 | |||
| Cor (VRE2) | 14.747 | 1.079 | |||
| All vegetation | 0.754 | 0.721 | Constant | 213.811 | |
| Green | −4566.311 | 4.279 | |||
| Cor (VRE2) | −5.370 | 1.889 | |||
| Red | 2655.001 | 4.530 | |||
| Cont (SWIR2) | 237.815 | 9.833 | |||
| Cont (VRE1) | −108.805 | 6.695 | |||
| Cor (N_NIR) | 0.366 | 1.905 | |||
| Var (SWIR1) | −273.149 | 3.947 | |||
| Var (Blue) | −395.915 | 3.295 | |||
| Var (VRE1) | 157.094 | 4.905 | |||
| Cont (Red) | −49.701 | 3.396 | |||
| Entr (Green) | 163.695 | 9.353 | |||
| Sec_M (VRE2) | −203.368 | 4.150 |
References
- United Nations. World Urbanization Prospects: The 2080 Revision; United Nations: New York, NY, USA, 2018. [Google Scholar]
- Zhou, X.; Li, L.; Chen, L.; Liu, Y.; Cui, Y.; Zhang, Y.; Zhang, T. Discriminating urban forest types from Sentinel-2A image data through linear spectral mixture analysis: A case study of Xuzhou, East China. Forests 2019, 10, 478. [Google Scholar] [CrossRef]
- Miller, R.W.; Hauer, R.J.; Werner, L.P. Urban Forestry: Planning and Managing Urban Greenspaces, 3rd ed.; Waveland Press, Inc.: Long Grove, IL, USA, 2015; ISBN 9781478606376. [Google Scholar]
- Zhao, S.; Tang, Y.; Chen, A. Carbon storage and sequestration of urban street trees in Beijing, China. Front. Ecol. Evol. 2016, 4, 53. [Google Scholar] [CrossRef]
- Cohen-Cline, H.; Turkheimer, E.; Duncan, G.E. Access to green space, physical activity and mental health: A twin study. J. Epidemiol. Community Health 2015, 69, 523–529. [Google Scholar] [CrossRef] [PubMed]
- White, M.P.; Alcock, I.; Wheeler, B.W.; Depledge, M.H. Would you be happier living in a greener urban area? A fixed-effects analysis of Panel Data. Psychol. Sci. 2013, 24, 920–928. [Google Scholar] [CrossRef] [PubMed]
- Wilkes, P.; Disney, M.; Vicari, M.B.; Calders, K.; Burt, A. Estimating urban above ground biomass with multi-scale LiDAR. Carbon Balance Manag. 2018, 13, 10. [Google Scholar] [CrossRef]
- Reis, C.; Lopes, A. Evaluating the cooling potential of urban green spaces to tackle urban climate change in Lisbon. Sustainability 2019, 11, 2480. [Google Scholar] [CrossRef]
- Pérez, G.; Perini, K. (Eds.) Nature Based Strategies for Urban and Building Sustainability; Elsevier: Oxford, UK, 2018; ISBN 9780128121504. [Google Scholar]
- He, M.; Zhao, B.; Ouyang, Z.; Yan, Y.; Li, B. Linear spectral mixture analysis of Landsat TM data for monitoring invasive exotic plants in estuarine wetlands. Int. J. Remote Sens. 2010, 31, 4319–4333. [Google Scholar] [CrossRef]
- He, H.; Zhang, C.; Zhao, X.; Fousseni, F.; Wang, J.; Dai, H.; Yang, S.; Zuo, Q. Allometric biomass equations for 12 tree species in coniferous and broadleaved mixed forests, Northeastern China. PLoS ONE 2018, 13, e0186226. [Google Scholar] [CrossRef]
- Weaver, T.; Collins, D. Measuring vegetation biomass and production. Am. Biol. Teach. 1988, 50, 164–166. [Google Scholar] [CrossRef]
- Launchbaugh, K. Direct Measures of Biomass. Available online: https://www.webpages.uidaho.edu/veg_measure/Modules/Lessons/Module7(Biomass&Utilization)/7_3_DirectMethods.htm (accessed on 1 October 2019).
- Wu, J. Developing general equations for urban tree biomass estimation with high-resolution satellite imagery. Sustainability 2019, 11, 4347. [Google Scholar] [CrossRef]
- Galidaki, G.; Zianis, D.; Gitas, I.; Radoglou, K.; Karathanassi, V.; Tsakiri-Strati, M.; Woodhouse, I.; Mallinis, G. Vegetation biomass estimation with remote sensing: Focus on forest and other wooded land over the Mediterranean ecosystem. Int. J. Remote Sens. 2017, 38, 1940–1966. [Google Scholar] [CrossRef]
- Lu, D. The potential and challenge of remote sensing-based biomass estimation. Int. J. Remote Sens. 2006, 27, 1297–1328. [Google Scholar] [CrossRef]
- Kumar, L.; Mutanga, O. Remote sensing of above-ground biomass. Remote Sens. 2017, 9, 935. [Google Scholar] [CrossRef]
- Sousa, A.M.O.; Gonçalves, A.C.; Mesquita, P.; Marques da Silva, J.R. Biomass estimation with high resolution satellite images: A case study of Quercus rotundifolia. ISPRS J. Photogramm. Remote Sens. 2015, 101, 69–79. [Google Scholar] [CrossRef]
- Simonson, W.; Ruiz-Benito, P.; Valladares, F.; Coomes, D. Modelling above-ground carbon dynamics using multi-temporal airborne lidar: Insights from a Mediterranean woodland. Biogeosciences 2016, 13, 961–973. [Google Scholar] [CrossRef]
- Gonzalez, P.; Asner, G.P.; Battles, J.J.; Lefsky, M.A.; Waring, K.M.; Palace, M. Forest carbon densities and uncertainties from Lidar, QuickBird, and field measurements in California. Remote Sens. Environ. 2010, 114, 1561–1575. [Google Scholar] [CrossRef]
- Nijland, W.; Addink, E.A.; De Jong, S.M.; Van der Meer, F.D. Optimizing spatial image support for quantitative mapping of natural vegetation. Remote Sens. Environ. 2009, 113, 771–780. [Google Scholar] [CrossRef]
- Vaglio Laurin, G.; Chen, Q.; Lindsell, J.A.; Coomes, D.A.; Del Frate, F.; Guerriero, L.; Pirotti, F.; Valentini, R. Above ground biomass estimation in an African tropical forest with lidar and hyperspectral data. ISPRS J. Photogramm. Remote Sens. 2014, 89, 49–58. [Google Scholar] [CrossRef]
- González-Jaramillo, V.; Fries, A.; Zeilinger, J.; Homeier, J.; Paladines-Benitez, J.; Bendix, J. Estimation of above ground biomass in a tropical mountain forest in Southern Ecuador using airborne LiDAR data. Remote Sens. 2018, 10, 660. [Google Scholar] [CrossRef]
- Vafaei, S.; Soosani, J.; Adeli, K.; Fadaei, H.; Naghavi, H.; Pham, T.; Tien Bui, D. Improving accuracy estimation of forest aboveground biomass based on incorporation of ALOS-2 PALSAR-2 and Sentinel-2A imagery and machine learning: A case study of the Hyrcanian forest area (Iran). Remote Sens. 2018, 10, 172. [Google Scholar] [CrossRef]
- Ren, H.; Zhou, G. Estimating green biomass ratio with remote sensing in arid grasslands. Ecol. Indic. 2019, 98, 568–574. [Google Scholar] [CrossRef]
- Jia, W.; Liu, M.; Yang, Y.; He, H.; Zhu, X.; Yang, F.; Yin, C.; Xiang, W. Estimation and uncertainty analyses of grassland biomass in Northern China: Comparison of multiple remote sensing data sources and modeling approaches. Ecol. Indic. 2016, 60, 1031–1040. [Google Scholar] [CrossRef]
- Xu, K.; Su, Y.; Liu, J.; Hu, T.; Jin, S.; Ma, Q.; Zhai, Q.; Wang, R.; Zhang, J.; Li, Y.; et al. Estimation of degraded grassland aboveground biomass using machine learning methods from terrestrial laser scanning data. Ecol. Indic. 2020, 108, 105747. [Google Scholar] [CrossRef]
- Klemas, V. Remote Sensing of Coastal Wetland Biomass: An Overview. J. Coast. Res. 2013, 290, 1016–1028. [Google Scholar] [CrossRef]
- Han, M.; Pan, B.; Liu, Y.B.; Yu, H.Z.; Liu, Y.R. Wetland biomass inversion and space differentiation: A case study of the Yellow River Delta Nature Reserve. PLoS ONE 2019, 14, e0210774. [Google Scholar] [CrossRef]
- Zhang, C.; Lu, D.; Chen, X.; Zhang, Y.; Maisupova, B.; Tao, Y. The spatiotemporal patterns of vegetation coverage and biomass of the temperate deserts in Central Asia and their relationships with climate controls. Remote Sens. Environ. 2016, 175, 271–281. [Google Scholar] [CrossRef]
- Mueed Choudhury, M.A.; Costanzini, S.; Despini, F.; Rossi, P.; Galli, A.; Marcheggiani, E.; Teggi, S. Photogrammetry and remote sensing for the identification and characterization of trees in urban areas. J. Phys. Conf. Ser. 2019, 1249, 12008. [Google Scholar] [CrossRef]
- SUHET Sentinel-2 User Handbook. Available online: https://sentinel.esa.int/documents/247904/685211/Sentinel-2_User_Handbook (accessed on 1 July 2016).
- Fernández-Manso, A.; Fernández-Manso, O.; Quintano, C. SENTINEL-2A red-edge spectral indices suitability for discriminating burn severity. Int. J. Appl. Earth Obs. Geoinf. 2016, 50, 170–175. [Google Scholar] [CrossRef]
- Navarro, G.; Caballero, I.; Silva, G.; Parra, P.C.; Vázquez, Á.; Caldeira, R. Evaluation of forest fire on Madeira Island using Sentinel-2A MSI imagery. Int. J. Appl. Earth Obs. Geoinf. 2017, 58, 97–106. [Google Scholar] [CrossRef]
- Chrysafis, I.; Mallinis, G.; Siachalou, S.; Patias, P. Assessing the relationships between growing stock volume and Sentinel-2 imagery in a Mediterranean forest ecosystem. Remote Sens. Lett. 2017, 8, 508–517. [Google Scholar] [CrossRef]
- Puliti, S.; Saarela, S.; Gobakken, T.; Ståhl, G.; Næsset, E. Combining UAV and Sentinel-2 auxiliary data for forest growing stock volume estimation through hierarchical model-based inference. Remote Sens. Environ. 2018, 204, 485–497. [Google Scholar] [CrossRef]
- Korhonen, L.; Packalen, P.; Rautiainen, M. Comparison of Sentinel-2 and Landsat 8 in the estimation of boreal forest canopy cover and leaf area index. Remote Sens. Environ. 2017, 195, 259–274. [Google Scholar] [CrossRef]
- Li, H.; Li, L.; Chen, L.; Zhou, X.; Cui, Y.; Liu, Y.; Liu, W. Mapping and characterizing spatiotemporal dynamics of impervious surfaces using Landsat images: A case study of Xuzhou, East China from 1995 to 2018. Sustainability 2019, 11, 1224. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, L.; Qin, K.; Wang, Y.; Chen, L.; Yang, X. Remote sensing estimation of urban surface evapotranspiration based on a modified Penman–Monteith model. J. Appl. Remote Sens. 2018, 12, 046006. [Google Scholar] [CrossRef]
- Xinhua China’s Xuzhou City Wins UN-Habitat Scroll of Honor for Promoting Urban Renewal. Available online: http://www.xinhuanet.com/english/2018-10/01/c_137506123.htm (accessed on 1 July 2019).
- Zhou, W. Study on Carbon Stock of Vegetation and Its Affecting Factors in Xuzhou. Ph.D. Thesis, Nanjing Forestry University, Nanjing, China, 2012. [Google Scholar]
- ESA SNAP. Available online: http://step.esa.int/main/toolboxes/snap/ (accessed on 1 October 2019).
- Li, L.; Canters, F.; Solana, C.; Ma, W.; Chen, L.; Kervyn, M. Discriminating lava flows of different age within Nyamuragira’s volcanic field using spectral mixture analysis. Int. J. Appl. Earth Obs. Geoinf. 2015, 40, 1–10. [Google Scholar] [CrossRef]
- Ahmad, M.; Khan, A.; Mazzara, M.; Distefano, S. Multi-layer extreme learning machine-based autoencoder for hyperspectral image classification. In Proceedings of the 14th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications, Prague, Czech Republic, 25–27 February 2019; SCITEPRESS—Science and Technology Publications: Setúbal, Portugal, 2019; pp. 75–82. [Google Scholar]
- Ahmad, M.; Khan, A.; Khan, A.M.; Mazzara, M.; Distefano, S.; Sohaib, A.; Nibouche, O. Spatial prior fuzziness pool-based interactive classification of hyperspectral images. Remote Sens. 2019, 11, 1136. [Google Scholar] [CrossRef]
- Somogyi, Z.; Cienciala, E.; Mäkipää, R.; Muukkonen, P.; Lehtonen, A.; Weiss, P. Indirect methods of large-scale forest biomass estimation. Eur. J. For. Res. 2007, 126, 197–207. [Google Scholar] [CrossRef]
- Chave, J.; Andalo, C.; Brown, S.; Cairns, M.A.; Chambers, J.Q.; Eamus, D.; Fölster, H.; Fromard, F.; Higuchi, N.; Kira, T.; et al. Tree allometry and improved estimation of carbon stocks and balance in tropical forests. Oecologia 2005, 145, 87–99. [Google Scholar] [CrossRef]
- Pastor, J.; Aber, J.D.; Melillo, J.M. Biomass prediction using generalized allometric regressions for some northeast tree species. For. Ecol. Manag. 1984, 7, 265–274. [Google Scholar] [CrossRef]
- Haase, R.; Haase, P. Above-ground biomass estimates for invasive trees and shrubs in the Pantanal of Mato Grosso, Brazil. For. Ecol. Manag. 1995, 73, 29–35. [Google Scholar] [CrossRef]
- Kuyah, S.; Dietz, J.; Muthuri, C.; van Noordwijk, M.; Neufeldt, H. Allometry and partitioning of above- and below-ground biomass in farmed eucalyptus species dominant in Western Kenyan agricultural landscapes. Biomass Bioenergy 2013, 55, 276–284. [Google Scholar] [CrossRef]
- Cushman, K.C.; Muller-Landau, H.C.; Condit, R.S.; Hubbell, S.P. Improving estimates of biomass change in buttressed trees using tree taper models. Methods Ecol. Evol. 2014, 5, 573–582. [Google Scholar] [CrossRef]
- Mosseler, A.; Major, J.E.; Labrecque, M.; Larocque, G.R. Allometric relationships in coppice biomass production for two North American willows (Salix spp.) across three different sites. For. Ecol. Manag. 2014, 20, 190–196. [Google Scholar] [CrossRef]
- Zhao, H.; Li, Z.; Zhou, G.; Qiu, Z.; Wu, Z. Site-specific allometric models for prediction of above-and belowground biomass of subtropical forests in Guangzhou, southern China. Forests 2019, 10, 862. [Google Scholar] [CrossRef]
- Zianis, D.; Muukkonen, P.; Mäkipää, R.; Mencuccini, M. Biomass and Stem Volume Equations for Tree Species in Europe; Tammer-Paino Oy: Tampere, Finland, 2005. [Google Scholar]
- Piao, S.; Fang, J.; He, J.; Xiao, Y. Spatial distribution of grassland biomass in China. Acta Phytocol. Sin. 2004, 28, 491–498. [Google Scholar]
- Draper, N.R.; Smith, H. Applied Regression Analysis, 3rd ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1998; ISBN 9781118625590. [Google Scholar]
- Li, L.; Bakelants, L.; Solana, C.; Canters, F.; Kervyn, M. Dating lava flows of tropical volcanoes by means of spatial modeling of vegetation recovery. Earth Surf. Process. Landf. 2018, 43, 840–856. [Google Scholar] [CrossRef]
- Whittingham, M.J.; Stephens, P.A.; Bradbury, R.B.; Freckleton, R.P. Why do we still use stepwise modelling in ecology and behaviour? J. Anim. Ecol. 2006, 75, 1182–1189. [Google Scholar] [CrossRef]
- Yang, X.; Li, L.; Chen, L.; Chen, L.; Shen, Z. Improving ASTER GDEM accuracy using land use-based linear regression methods: A case study of Lianyungang, East China. ISPRS Int. J. Geo-Inf. 2018, 7, 145. [Google Scholar] [CrossRef]
- Li, Y.; Li, C.; Li, M.; Liu, Z. Influence of variable selection and forest type on forest aboveground biomass estimation using machine learning algorithms. Forests 2019, 10, 1073. [Google Scholar] [CrossRef]
- Cheng, L.; Li, L.; Chen, L.; Hu, S.; Yuan, L.; Liu, Y.; Cui, Y.; Zhang, T. Spatiotemporal variability and influencing factors of aerosol optical depth over the Pan Yangtze River Delta during the 2014–2017 period. Int. J. Environ. Res. Public Health 2019, 16, 3522. [Google Scholar] [CrossRef]
- Hair, J.F.; Black, W.C.; Babin, B.J.; Anderson, R.E. Multivariate Data Analysis, 7th ed.; Pearson: New Jersey, NJ, USA, 2009; ISBN 9780138132637. [Google Scholar]
- Sauerbrei, W.; Royston, P.; Binder, H. Selection of important variables and determination of functional form for continuous predictors in multivariable model building. Stat. Med. 2007, 26, 5512–5528. [Google Scholar] [CrossRef] [PubMed]
- Shaheen, A.; Iqbal, J. Spatial distribution and mobility assessment of carcinogenic heavy metals in soil profiles using geostatistics and random forest, Boruta algorithm. Sustainability 2018, 10, 799. [Google Scholar] [CrossRef]
- Kursa, M.B.; Rudnicki, W.R. Feature selection with the Boruta package. J. Stat. Softw. 2010, 36, 1–13. [Google Scholar] [CrossRef]
- Liaw, A.; Wiener, M. Classification and Regression by randomForest. R News 2002, 2, 18–22. [Google Scholar]
- Lu, N.; Zhou, J.; Han, Z.; Li, D.; Cao, Q.; Yao, X.; Tian, Y.; Zhu, Y.; Cao, W.; Cheng, T. Improved estimation of aboveground biomass in wheat from RGB imagery and point cloud data acquired with a low-cost unmanned aerial vehicle system. Plant Methods 2019, 15, 17. [Google Scholar] [CrossRef]
- Gao, Y.; Lu, D.; Li, G.; Wang, G.; Chen, Q.; Liu, L.; Li, D. Comparative analysis of modeling algorithms for forest aboveground biomass estimation in a subtropical region. Remote Sens. 2018, 10, 627. [Google Scholar] [CrossRef]
- Rocha de Souza Pereira, F.; Kampel, M.; Gomes Soares, M.; Estrada, G.; Bentz, C.; Vincent, G. Reducing uncertainty in mapping of mangrove aboveground biomass using airborne discrete return Lidar data. Remote Sens. 2018, 10, 637. [Google Scholar] [CrossRef]
- Huete, A. Vegetation indices. In Encyclopedia of Remote Sensing; Njoku, E.G., Ed.; Springer: New York, NY, USA, 2014; pp. 883–886. [Google Scholar]
- Li, C.; Zhou, W.; Guan, Q.; Wei, W.; Dong, P.; Zhang, H. Biomass and its influencing factors of Platyclatdus orientalis plantation in the limestone mountains. J. Anhui Agric. Univ. 2010, 37, 669–674. [Google Scholar]
- Lu, Y.; Liang, Z.; Wu, Z.; Cai, Y.; Zhou, K.; Yang, G.; Yin, Z. Biomass and productivity of main afforestation tree species on the seawall in Northern Jiangsu. J. Jiangsu For. Sci. Technol. 2000, 27, 12–15. [Google Scholar]
- Zhu, Y. Characteristics of Structure and Carbon Storage of Greening on the Campus of Anhui Agricultural University. Master’s Thesis, Anhui Agricultural University, Hefei, China, 2016. [Google Scholar]
- Li, J.; Li, C.; Peng, S. Study on the biomass expansion factor of poplar plantation. J. Nanjing For. Univ. 2007, 31, 37–40. [Google Scholar]
- Kun, L.; Cao, L.; Wang, G.; Cao, F. Biomass allocation patterns and allometric models of Ginkgo biloba. J. Beijing For. Univ. 2017, 39, 12–20. [Google Scholar]
- Wen, J. Effects of Urbanization on Carbon Storage and Sequestration in the Built-Up Area. Master’s Thesis, Zhejiang University, Hangzhou, China, 2010. [Google Scholar]
- Che, R. Study on single tree biomass model for Larix Principis-rupprechtii. Shanxi For. Sci. Technol. 2017, 46, 35–36. [Google Scholar]
- State Forestry Administration of China. Carbon Accounting and Monitoring Guide for Afforestation Projects; China Forestry Press: Beijing, China, 2014; ISBN 9787503873676. [Google Scholar]
- Zhang, X.; Leng, H.; Zhao, G.; Jing, J.; Tu, A.; Song, K.; Da, L. Allometric models for estimating aboveground biomass for four common greening tree species in Shanghai City, China. J. Nanjing For. Univ. (Nat. Sci. Ed.) 2018, 42, 141–146. [Google Scholar]
- Huang, T.; Zhong, Q.; Peng, X. Sutdy on biomass and productivity of Liriodendron chinense plantation. For. Sci. Technol. 2000, 9, 12–15. [Google Scholar]
- Yang, X.; Wu, G.; Huang, D.; Yang, C. Quantitative study on biomass accumulation of Paulownia. Chin. J. Appl. Ecol. 1999, 10, 143–146. [Google Scholar]
- Yao, Z.; Liu, J.; Zhao, X.; Long, D.; Wang, L. Spatial dynamics of aboveground carbon stock in urban green space: A case study of Xi’an, China. J. Arid Land 2015, 7, 350–360. [Google Scholar] [CrossRef]
- Yao, Z.; Liu, J. Models for biomass estimation of four shrub species planted in urban area of Xi’an City, Northwest China. Chin. J. Appl. Ecol. 2014, 25, 111–116. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).