Predicting Tree Height-Diameter Relationship from Relative Competition Levels Using Quantile Regression Models for Chinese Fir (Cunninghamia lanceolata) in Fujian Province, China
Abstract
:1. Introduction
2. Materials and Methods
2.1. Data Collection
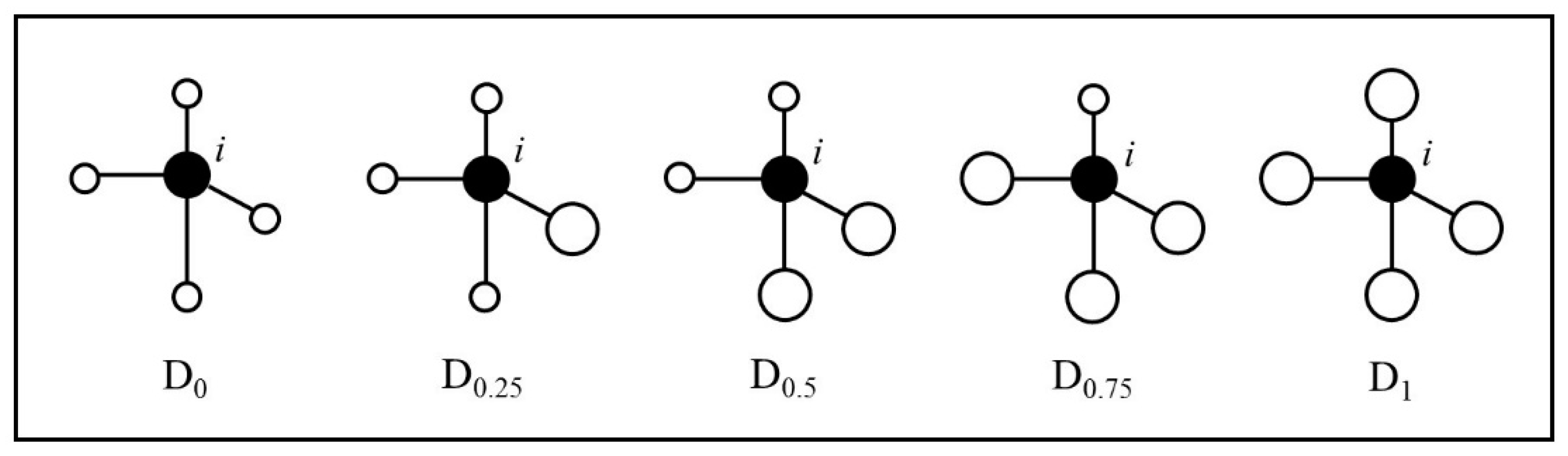
2.2. Relative Competition Quantification
2.3. Base Model
2.4. Quantile Regression Model
2.5. Evaluation and Testing
3. Results
3.1. The Quantification of Five Relative Competition Levels
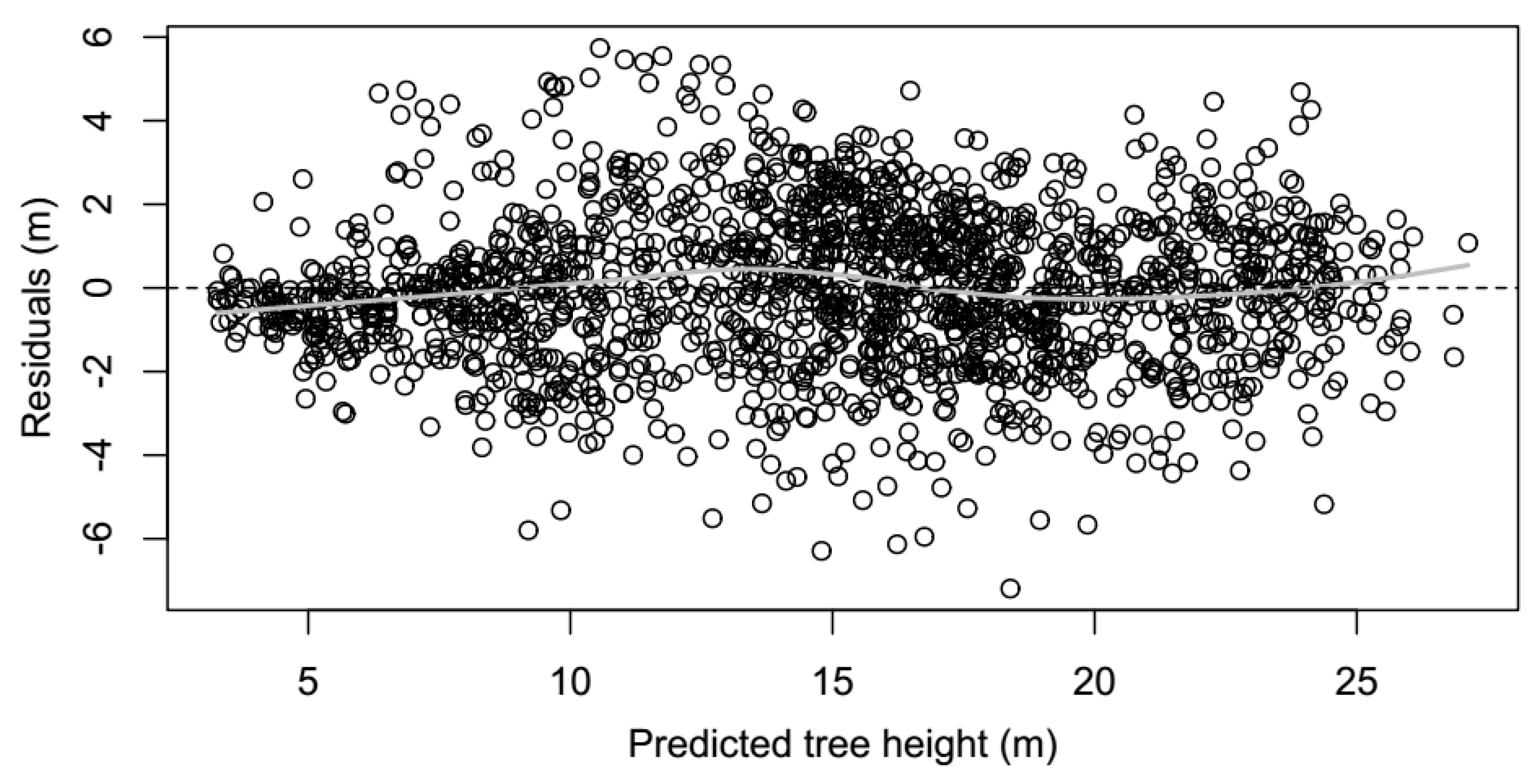
3.2. Base H-D Model Validation
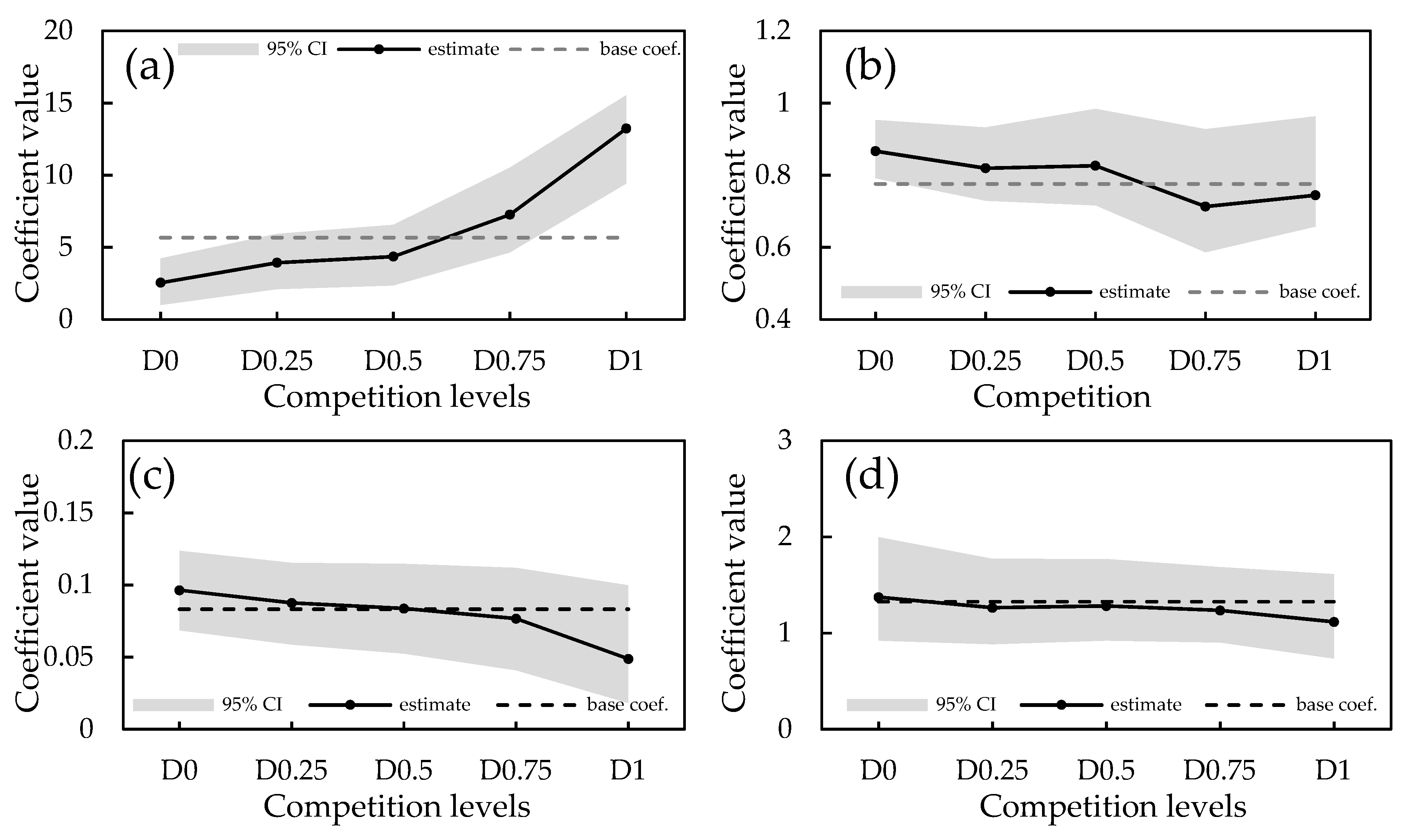
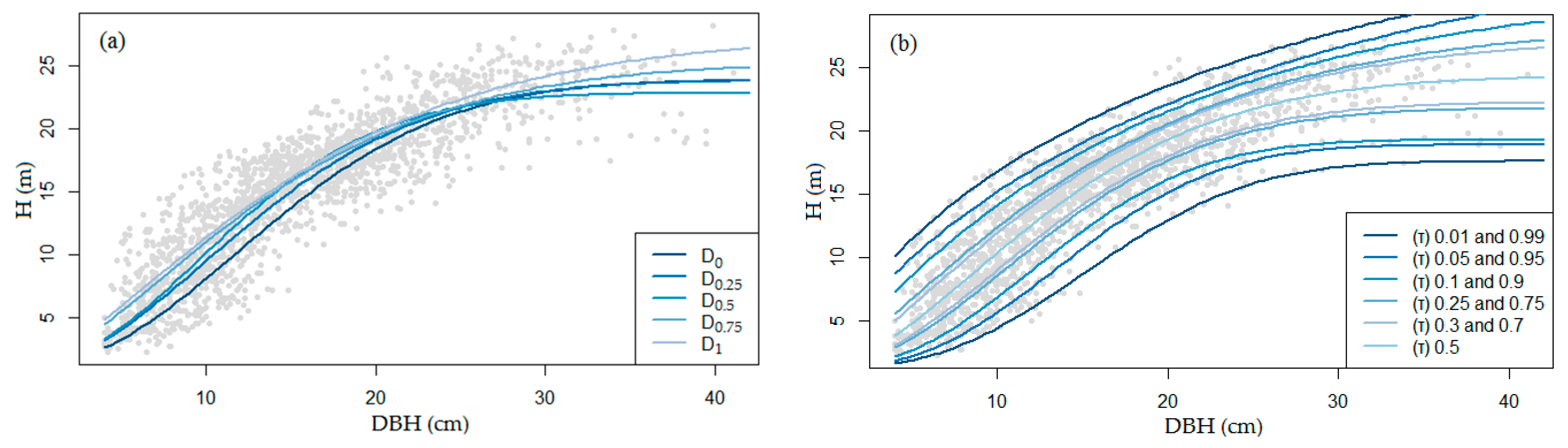
3.3. Mean Regression Models for Five Competition Levels
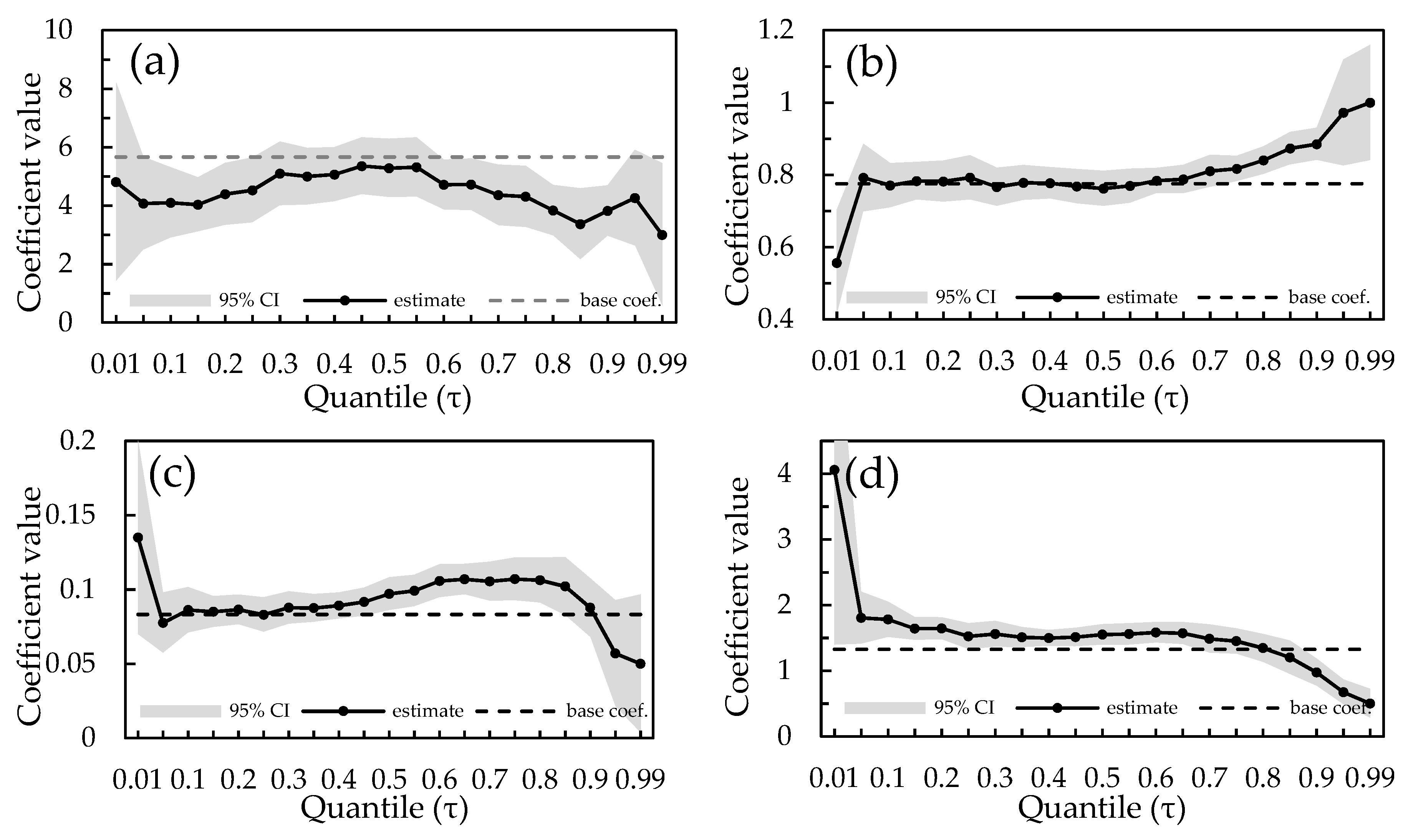
3.4. Quantile Regression Models
3.5. Comparison of Modeling Approaches
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. The Core Code in R
| # library the request packages |
| library(xlsx, stats, spatstat, forestSAS, quantreg, broom, caret) |
| data<-read.xlsx(mydata,1) # input the data |
| head(data) |
| > ID Age.G plot S.plot No. species x y DBHcm CWm Hm Remark DH |
| > 1 1 Young YN1 YN1-1 C046 Chinese fir 9.5 2.55 6.8 4.1 6.2 Live 12.86 |
| > 2 2 Young YN1 YN1-1 B033 Chinese fir 8.2 0.79 7.1 2.2 6.3 Live 12.86 |
| …… |
| plot.1<-subset(data,plot==“YN1”) |
| ppp.1<-ppp(x=plot.1$x,y=plot.1$y,window=owin(c(0,30),c(0,30)),marks=plot.1[,c(1:13)]) |
| nnindices<-nnIndex(ppp.1),N=4,smark=c(“ID”,”species”,”DBHcm”,”Hm”,”DH”,”CWm”,”x”,”y”), |
| buffer=FALSE,buf.xwid=2,buf.ywid=2) |
| Dindex <-fsasN4( nnindices$nnDBHcm,match.fun=dominance) |
| Dindex |
| …… |
| mod1<-function(DBHcm,DH,a,b,c,d){1.3+(a+b*DH)*(1-exp(-c*DBHcm))^d} |
| head(mod.data) |
| > ID Age.G plot species DBHcm Hm Dindex DH |
| > 4 5 Young YN1 Chinese fir 14.5 11.8 0.00 12.86 |
| > 6 7 Young YN1 Chinese fir 6.3 6.8 0.75 12.86 |
| # fit models with 10-fold cross-validation |
| set.seed(65536) |
| sumtable<-data.frame(Stat.=c(“AIC”,”BIC”,”logLik”,”RMSE”,”MAE”,”R2”,”RMSE2”,”MAE2”,”R22”)) |
| coftable<-c() |
| folds <- createFolds(y=mod.data$Hm,k=10) |
| for(i in 1:10){ |
| fold_test <- mod.data[folds[[i]],] # set folds[[i]] as test data |
| fold_train <- mod.data[-folds[[i]],] # others as train data |
| fold_fit <- nls(Hm~mod1(DBHcm,DH,a,b,c,d),start = list(a=5,b=1,c=0.05,d=1.5),data=fold_train) |
| fold_AIC <- AIC(fold_fit) |
| fold_BIC <- BIC(fold_fit) |
| fold_logLik <- logLik(fold_fit) |
| fold_predict1 <- predict(fold_fit,type=‘response’,newdata=fold_train) |
| fold_RMSE = sqrt(mean((fold_predict1-fold_train$Hm)^2)) |
| fold_MAE = mean(abs(fold_predict1-fold_train$Hm)) |
| fold_R2 = 1-(sum((fold_predict1-fold_train$Hm)^2)/sum((fold_train$Hm-mean(fold_train$Hm))^2)) |
| fold_predict2 <- predict(fold_fit,type=‘response’,newdata=fold_test) |
| fold_RMSE2 = sqrt(mean((fold_predict2-fold_test$Hm)^2)) |
| fold_MAE2 = mean(abs(fold_predict2-fold_test$Hm)) |
| fold_R22 = 1-(sum((fold_predict2-fold_test$Hm)^2)/sum((fold_test$Hm-mean(fold_test$Hm))^2)) |
| Fold<-c(fold_AIC,fold_BIC,fold_logLik,fold_RMSE,fold_MAE,fold_R2,fold_RMSE2,fold_MAE2,fold_R22) |
| cofnew<-tidy(fold_fit,conf.level=0.95,conf.int = TRUE) |
| coftable<-rbind(coftable,cofnew) |
| sumtable<-data.frame(sumtable,Fold) |
| } |
| coftable |
| sumtable |
| #quantile regression model fitting |
| tuslist <- c(0.01, 0.05, 0.1, 0.25, 0.3, 0.5, 0.7, 0.75, 0.9, 0.95, 0.99) |
| coftable<-c() |
| cfMat <- matrix(0, 11, 5) |
| for(i in 1:length(tuslist)) { |
| tau <- tuslist[i] |
| cat(“tau = “, format(tau), “.. “) |
| fit <- nlrq(Hm~mod1(DBHcm,DH,a,b,c,d), |
| start = list(a=3,b=1,c=0.1,d=1), |
| data = mod.data, tau = tau, |
| trace = F) |
| cfMat[i,1] <- tau |
| cfMat[i,2:5] <- coef(fit) |
| cat(“\n”) |
| cofnew<- tidy(fit,conf.level=0.95,conf.int = TRUE) |
| coftable<-rbind(coftable,cofnew) |
| } |
| colnames(cfMat) <- c(“Quantile”,names(coef(fit))) |
| cfMat |
| coftable |
References
- Fu, L.; Lei, X.; Sharma, R.P.; Li, H.; Zhu, G.; Hong, L.; You, L.; Duan, G.; Guo, H.; Lei, Y.; et al. Comparing height–age and height–diameter modelling approaches for estimating site productivity of natural uneven-aged forests. For. Int. J. For. Res. 2018, 91, 419–433. [Google Scholar] [CrossRef]
- Trorey, L.G. A Mathematical Method for the Construction of Diameter Height Curves Based on Site. For. Chron. 1932, 8, 121–132. [Google Scholar] [CrossRef]
- Stout, B.B.; Shumway, D.L. Site Quality Estimation Using Height and Diameter. Forest Sci. 1982, 28, 639–645. [Google Scholar]
- Crecente-Campo, F.; Tomé, M.; Soares, P.; Diéguez-Aranda, U. A generalized nonlinear mixed-effects height–diameter model for Eucalyptus globulus L. in northwestern Spain. For. Ecol. Manag. 2010, 259, 943–952. [Google Scholar] [CrossRef] [Green Version]
- Özçelik, R.; Cao, Q.V.; Trincado, G.; Göçer, N. Predicting tree height from tree diameter and dominant height using mixed-effects and quantile regression models for two species in Turkey. Forest Ecol. Manag. 2018, 419–420, 240–248. [Google Scholar] [CrossRef]
- Kang, H.; Seely, B.; Wang, G.; Cai, Y.; Innes, J.; Zheng, D.; Chen, P.; Wang, T. Simulating the impact of climate change on the growth of Chinese fir plantations in Fujian province, China. Nz. J. For. Sci. 2017, 47, 20. [Google Scholar] [CrossRef]
- Huang, S.; Wiens, D.P.; Yang, Y.; Meng, S.X.; Vanderschaaf, C.L. Assessing the impacts of species composition, top height and density on individual tree height prediction of quaking aspen in boreal mixedwoods. Forest Ecol. Manag. 2009, 258, 1235–1247. [Google Scholar] [CrossRef]
- Arney, J.D. A modeling strategy for the growth projection of managed stands. Can. J. Forest Res. 1985, 15, 511–518. [Google Scholar] [CrossRef]
- Parresol, B.R. Baldcypress height–diameter equations and their prediction confidence intervals. Can. J. Forest Res. 1992, 22, 1429–1434. [Google Scholar] [CrossRef]
- Larsen, D.R.; Hann, D.W. Height-Diameter Equations for Seventeen Tree Species in Southwest Oregon; Oregon State University, College of Forestry, Forest Research Laboratory: Corvallis, OR, USA, 1987; Volume 49. [Google Scholar]
- Vanclay, J.K. Tree diameter, height and stocking in even-aged forests. Ann. Forest Sci. 2009, 66, 702. [Google Scholar] [CrossRef] [Green Version]
- Huang, S.; Price, D.J.; Titus, S. Development of ecoregion-based height–diameter models for white spruce in boreal forests. Forest Ecol. Manag. 2000, 129, 125–141. [Google Scholar] [CrossRef]
- Lei, X.; Peng, C.; Wang, H.; Zhou, X. Individual height–diameter models for young black spruce (Picea mariana) and jack pine (Pinus banksiana) plantations in New Brunswick, Canada. For. Chron. 2009, 85, 43–56. [Google Scholar] [CrossRef] [Green Version]
- Sánchez-González, M.; Cañellas, I.; Montero, G. Generalized height-diameter and crown diameter prediction models for cork oak forests in Spain. Investig. Agrar. Sist. Recur. For. 2007, 16. [Google Scholar] [CrossRef] [Green Version]
- Newton, P.F.; Amponsah, I.G. Comparative evaluation of five height–diameter models developed for black spruce and jack pine stand-types in terms of goodness-of-fit, lack-of-fit and predictive ability. Forest Ecol. Manag. 2007, 247, 149–166. [Google Scholar] [CrossRef]
- Schumacher, F.X.; Day, B.B. The Influence of Precipitation upon the Width of Annual Rings of Certain Timber Trees. Ecol. Monogr. 1939, 9, 387–429. [Google Scholar] [CrossRef]
- Meyer, H.A. A Mathematical Expression for Height Curves. J. For. 1940, 38, 415–420. [Google Scholar] [CrossRef]
- Huang, S.; Titus, S.J. An index of site productivity for uneven-aged or mixed-species stands. Can. J. Forest Res. 1993, 23, 558–562. [Google Scholar] [CrossRef]
- Kearsley, E.; Moonen, P.C.J.; Hufkens, K.; Doetterl, S.; Lisingo, J.; Boyemba Bosela, F.; Boeckx, P.; Beeckman, H.; Verbeeck, H. Model performance of tree height-diameter relationships in the central Congo Basin. Ann. For. Sci. 2017, 74. [Google Scholar] [CrossRef] [Green Version]
- Paulo, J.A.; Tomé, J.; Tomé, M. Nonlinear fixed and random generalized height–diameter models for Portuguese cork oak stands. Ann. For. Sci. 2011, 68, 295–309. [Google Scholar] [CrossRef] [Green Version]
- Koenker, R.; Bassett, G. Regression Quantiles. Econometrica 1978, 46. [Google Scholar] [CrossRef]
- Furno, M.; Vistocco, D. Quantile Regression: Estimation and Simulation; John Wiley & Sons: Hoboken, NJ, USA, 2018. [Google Scholar]
- Kocherginsky, M.; He, X.; Mu, Y. Practical Confidence Intervals for Regression Quantiles. J. Comput. Graph. Stat. 2005, 14, 41–55. [Google Scholar] [CrossRef]
- Mäkinen, A.; Kangas, A.; Kalliovirta, J.; Rasinmäki, J.; Välimäki, E. Comparison of treewise and standwise forest simulators by means of quantile regression. Forest Ecol. Manag. 2008, 255, 2709–2717. [Google Scholar] [CrossRef]
- Ducey, M.J.; Knapp, R.A. A stand density index for complex mixed species forests in the northeastern United States. Forest Ecol. Manag. 2010, 260, 1613–1622. [Google Scholar] [CrossRef]
- Mehtätalo, L.; Gregoire, T.G.; Burkhart, H.E. Comparing strategies for modeling tree diameter percentiles from remeasured plots. Environmetrics 2008, 19, 529–548. [Google Scholar] [CrossRef]
- Bohora, S.B.; Cao, Q.V. Prediction of tree diameter growth using quantile regression and mixed-effects models. Forest Ecol. Manag. 2014, 319, 62–66. [Google Scholar] [CrossRef]
- Cao, Q.V.; Wang, J. Calibrating fixed- and mixed-effects taper equations. Forest Ecol. Manag. 2011, 262, 671–673. [Google Scholar] [CrossRef]
- Lim, K.S.; Treitz, P.M. Estimation of above ground forest biomass from airborne discrete return laser scanner data using canopy-based quantile estimators. Scand. J. Forest Res. 2006, 19, 558–570. [Google Scholar] [CrossRef] [Green Version]
- Zang, H.; Lei, X.; Zeng, W. Height–diameter equations for larch plantations in northern and northeastern China: A comparison of the mixed-effects, quantile regression and generalized additive models. Forestry 2016, 89, 434–445. [Google Scholar] [CrossRef]
- Cade, B.S.; Noon, B.R. A gentle introduction to quantile regression for ecologists. Front. Ecol. Environ. 2003, 1, 412–420. [Google Scholar] [CrossRef]
- Lingxin Hao, D.Q.N. Quantile regression; SAGE Publications, Inc: Southend Oaks, CA, USA, 2007. [Google Scholar]
- Shen, Y.; Wang, F.; Zhang, Y.; Zhu, Z.; Wang, X.; Amp, Z.A.; University, F.J.S.S.S. Economic Analysis of Chinese Fir Forest Carbon Sequestration Supply in South China. Sci. Silvae Sin. 2013, 49, 140–147. [Google Scholar] [CrossRef]
- Liang, W.; Yang, Y.; Fan, D.; Guan, H.; Zhang, T.; Long, D.; Zhou, Y.; Bai, D. Analysis of spatial and temporal patterns of net primary production and their climate controls in China from 1982 to 2010. Agr. Forest Meteorol. 2015, 204, 22–36. [Google Scholar] [CrossRef]
- Yunfei, D.; Yujun, S.; Yifu, W.; Xiaoyu, G. Generalized Height-diameter Model for Chinese Fir Based on BP Neural Network. J. Northeast For. Univ. 2014, 42, 154–165. [Google Scholar] [CrossRef]
- Guangyi, M.; Yujun, S.; Saeed, S. Models for Predicting the Biomass of Cunninghamialanceolata Trees and Stands in Southeastern China. PLoS ONE 2017, 12, e0169747. [Google Scholar] [CrossRef] [Green Version]
- Sumida, A.; Miyaura, T.; Torii, H. Relationships of tree height and diameter at breast height revisited: Analyses of stem growth using 20-year data of an even-aged Chamaecyparis obtusa stand. Tree Physiol. 2013, 33, 106–118. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Hui, G.; Zhao, Z.; Hu, Y.; Ye, S. Spatial structural characteristics of three hardwood species in Korean pine broad-leaved forest—Validating the bivariate distribution of structural parameters from the point of tree population. Forest Ecol. Manag. 2014, 314, 17–25. [Google Scholar] [CrossRef]
- Fortin, M.J.; Dale, M.R.T. Spatial Analysis: A Guide for Ecologist; Cambridge University Press: New York, NY, USA, 2005. [Google Scholar]
- Hui, G.; Wang, Y.; Zhang, G.; Zhao, Z.; Bai, C.; Liu, W. A novel approach for assessing the neighborhood competition in two different aged forests. Forest Ecol. Manag. 2018, 422, 49–58. [Google Scholar] [CrossRef]
- Mori, A.S. Ecosystem management based on natural disturbances: Hierarchical context and non-equilibrium paradigm. J. Appl. Ecol. 2011, 48, 280–292. [Google Scholar] [CrossRef]
- Chai, Z. Quantitative Evaluation and R Programming of Forest Spatial Structure Based on the Relationship of Neighborhood Trees: A Case Study of Typical Secondary Forests in the Midaltitude Zone of the Qinling Mountins, China; Northwest Agriculture and Forestry University: Shanxi, China, 2016. [Google Scholar]
- Hui, G.Y.; Albert, M.; Gadow, K.V. Das Umgebungsmaß als Parameter zur Nachbildung von Bestandesstrukturen. Forstwiss. Cent. 1998, 117, 258–266. [Google Scholar] [CrossRef]
- Hui, G. Studies on the application of stand spatial structure parameters based on the relationship of neighborhood trees. J. Beijing For. Univ. 2013, 35, 1–8. [Google Scholar]
- Chai, Z. forestSAS:An R package for forest spatial structure analysis systems. Available online: https://github.com/Zongzheng/forestSAS (accessed on 19 December 2019).
- Fang, Z.; Bailey, R.L. Height–diameter models for tropical forests on Hainan Island in southern China. Forest Ecol. Manag. 1998, 110, 315–327. [Google Scholar] [CrossRef]
- Yang, R.C.; Kozak, A.; Smith, J.H.G. The potential of Weibull-type functions as flexible growth curves. Can. J. For. Res. 1978, 8, 424–431. [Google Scholar] [CrossRef]
- Koenker, R. Quantile Regression; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Koenker, R.; Machado, J.A.F. Goodness of Fit and Related Inference Processes for Quantile Regression. J. Am. Stat. Assoc. 1999, 94. [Google Scholar] [CrossRef]
- Fushiki, T. Estimation of prediction error by using K-fold cross-validation. Stat. Comput. 2011, 21, 137–146. [Google Scholar] [CrossRef]
- Jun-Hui, Z.; Xin-Gang, K.; Hui-Dong, Z.; Yan, L. Relationships between coefficient of variation of diameter and height and competition index of main coniferous trees in Changbai Mountains. Chin. J. Appl. Ecol. 2009, 20, 1832–1837. [Google Scholar] [CrossRef]
- Buechling, A.; Martin, P.H.; Canham, C.D.; Piper, F. Climate and competition effects on tree growth in Rocky Mountain forests. J. Ecol. 2017, 105, 1636–1647. [Google Scholar] [CrossRef] [Green Version]
- Muggeo, V.M.R.; Sciandra, M.; Tomasello, A.; Calvo, S. Estimating growth charts via nonparametric quantile regression: A practical framework with application in ecology. Environ. Ecol. Stat. 2013, 20, 519–531. [Google Scholar] [CrossRef]
- Wei, Y.; Pere, A.; Koenker, R.; He, X. Quantile regression methods for reference growth charts. Stat. Med. 2006, 25, 1369–1382. [Google Scholar] [CrossRef]
- Wei, Y.; He, X. Conditional growth charts. Ann. Stat. 2006, 34, 2069–2097. [Google Scholar] [CrossRef] [Green Version]
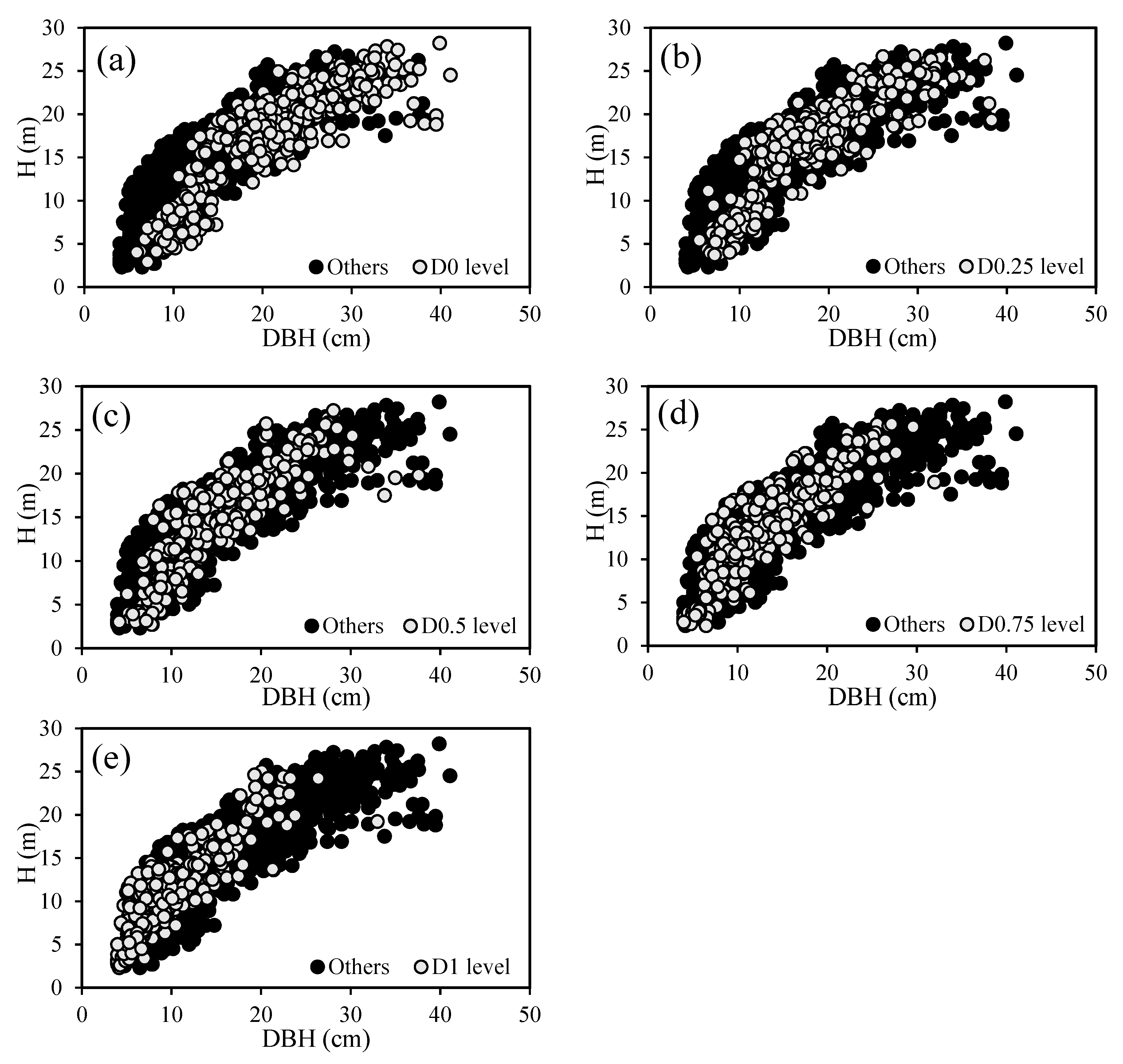
| Age groups | Measurement | Mean | S.D. | Min. | Max. |
|---|---|---|---|---|---|
| Young (575 trees in three plots) | DBH (cm) | 8.47 | 2.47 | 4.00 | 18.90 |
| H (m) | 6.34 | 2.23 | 2.30 | 14.40 | |
| CW (m) | 2.25 | 0.75 | 0.50 | 5.50 | |
| N (trees/ha) | 3255 | 456 | 2625 | 3689 | |
| DH (m) | 10.49 | 2.92 | 6.24 | 12.86 | |
| Middle-aged (866 trees in eight plots) | DBH (cm) | 15.64 | 4.52 | 5.00 | 31.00 |
| H (m) | 14.82 | 3.17 | 5.80 | 23.90 | |
| CW (m) | 3.05 | 1.24 | 0.50 | 9.30 | |
| N (trees/ha) | 2208 | 391 | 1367 | 2644 | |
| DH (m) | 19.38 | 1.51 | 17.40 | 23.24 | |
| Nearly mature (645 trees in six plots) | DBH (cm) | 15.46 | 6.23 | 4.40 | 36.50 |
| H (m) | 16.24 | 4.50 | 3.40 | 26.50 | |
| CW (m) | 3.29 | 1.55 | 0.20 | 6.90 | |
| N (trees/ha) | 2247 | 553 | 1000 | 3083 | |
| DH (m) | 22.48 | 1.55 | 20.56 | 26.18 | |
| Mature (755 trees in seven plots) | DBH (cm) | 18.21 | 7.71 | 4.70 | 53.50 |
| H (m) | 17.32 | 5.00 | 6.00 | 31.99 | |
| CW (m) | 3.59 | 1.68 | 0.40 | 10.20 | |
| N (trees/ha) | 1846 | 685 | 1025 | 3000 | |
| DH (m) | 24.29 | 1.15 | 22.74 | 27.66 | |
| Over-mature (292 trees in four plots) | DBH (cm) | 23.77 | 6.87 | 4.00 | 41.10 |
| H (m) | 21.01 | 4.31 | 4.50 | 27.40 | |
| CW (m) | 3.77 | 1.67 | 0.50 | 8.10 | |
| N (trees/ha) | 1217 | 395 | 700 | 1767 | |
| DH (m) | 25.99 | 0.43 | 25.54 | 26.62 |
| Relative Competition Levels | No. of Trees | DBH | H | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Mean | S.D. | Min. | Max. | Mean | S.D. | Min. | Max. | ||
| D0 | 425 | 20.6 | 7.3 | 5.9 | 41.1 | 17.3 | 5.8 | 2.9 | 28.2 |
| D0.25 | 382 | 17.8 | 6.5 | 5.5 | 38.3 | 16.3 | 5.5 | 3.7 | 26.7 |
| D0.5 | 352 | 15.0 | 6.0 | 4.2 | 37.6 | 14.7 | 5.7 | 2.7 | 27.2 |
| D0.75 | 361 | 13.3 | 5.3 | 4.0 | 32.0 | 13.6 | 5.1 | 2.3 | 25.6 |
| D1 | 350 | 10.2 | 4.8 | 4.0 | 33.0 | 11.2 | 4.9 | 2.3 | 25.0 |
| Total | 1870 | 15.6 | 7.1 | 4.0 | 41.1 | 14.8 | 5.8 | 2.3 | 28.2 |
| Fold | AIC | BIC | logLik | Training Group | Testing Group | ||||
|---|---|---|---|---|---|---|---|---|---|
| RMSE | MAE | R2 | RMSE | MAE | R2 | ||||
| 1 | 6881.5 | 6908.6 | −3435.7 | 1.8636 | 1.449 | 0.901 | 1.8707 | 1.4747 | 0.8931 |
| 2 | 6888.2 | 6915.3 | −3439.1 | 1.865 | 1.4545 | 0.9003 | 1.8555 | 1.4217 | 0.8999 |
| 3 | 6926.6 | 6953.8 | −3458.3 | 1.8864 | 1.4703 | 0.8982 | 1.6479 | 1.296 | 0.9193 |
| 4 | 6863.7 | 6890.8 | −3426.8 | 1.856 | 1.4494 | 0.9006 | 1.9349 | 1.4941 | 0.8974 |
| 5 | 6895.0 | 6922.1 | −3442.5 | 1.8734 | 1.4595 | 0.8993 | 1.7779 | 1.389 | 0.9087 |
| 6 | 6833.8 | 6861.0 | −3411.9 | 1.8374 | 1.4357 | 0.9027 | 2.0886 | 1.6167 | 0.8791 |
| 7 | 6885.5 | 6912.6 | −3437.7 | 1.8658 | 1.4475 | 0.8997 | 1.8493 | 1.5116 | 0.9053 |
| 8 | 6869.7 | 6896.9 | −3429.9 | 1.8571 | 1.4459 | 0.9014 | 1.9263 | 1.5266 | 0.8898 |
| 9 | 6853.3 | 6880.4 | −3421.6 | 1.848 | 1.4419 | 0.9014 | 2.0025 | 1.5416 | 0.8908 |
| 10 | 6919.8 | 6946.9 | −3454.9 | 1.8849 | 1.4723 | 0.8983 | 1.6660 | 1.2747 | 0.9180 |
| D0 | D0.25 | D0.5 | D0.75 | D1 | |
|---|---|---|---|---|---|
| AIC | 1463.3 | 1338.3 | 1271.8 | 1364.1 | 1326.2 |
| BIC | 1483.1 | 1357.5 | 1290.6 | 1383.0 | 1344.9 |
| logLik | −726.7 | −664.2 | −630.9 | −677.1 | −658.1 |
| RMSE (Training) | 1.6135 | 1.6683 | 1.7817 | 1.9432 | 1.9677 |
| MAE (Training) | 1.2978 | 1.3250 | 1.3699 | 1.5277 | 1.5641 |
| R2 (Training) | 0.9256 | 0.9086 | 0.9069 | 0.8537 | 0.8440 |
| RMSE (Testing) | 2.0513 | 1.9273 | 2.3651 | 2.2568 | 2.4648 |
| MAE (Testing) | 1.5157 | 1.5042 | 1.8294 | 1.7752 | 1.8375 |
| R2 (Testing) | 0.8724 | 0.8844 | 0.7998 | 0.8334 | 0.7431 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, B.; Sajjad, S.; Chen, K.; Zhou, L.; Zhang, Y.; Yong, K.K.; Sun, Y. Predicting Tree Height-Diameter Relationship from Relative Competition Levels Using Quantile Regression Models for Chinese Fir (Cunninghamia lanceolata) in Fujian Province, China. Forests 2020, 11, 183. https://doi.org/10.3390/f11020183
Zhang B, Sajjad S, Chen K, Zhou L, Zhang Y, Yong KK, Sun Y. Predicting Tree Height-Diameter Relationship from Relative Competition Levels Using Quantile Regression Models for Chinese Fir (Cunninghamia lanceolata) in Fujian Province, China. Forests. 2020; 11(2):183. https://doi.org/10.3390/f11020183
Chicago/Turabian StyleZhang, Bo, Saeed Sajjad, Keyi Chen, Lai Zhou, Yaxin Zhang, Kok Kian Yong, and Yujun Sun. 2020. "Predicting Tree Height-Diameter Relationship from Relative Competition Levels Using Quantile Regression Models for Chinese Fir (Cunninghamia lanceolata) in Fujian Province, China" Forests 11, no. 2: 183. https://doi.org/10.3390/f11020183





