Impacts of Global Warming on the Radial Growth and Long-Term Intrinsic Water-Use Efficiency (iWUE) of Schrenk Spruce (Picea schrenkiana Fisch. et Mey) in the Sayram Lake Basin, Northwest China

Abstract

Global warming and the sharp rise in atmospheric CO₂ concentrations have a profound impact on forest ecosystems. To better manage these changes, a comprehensive understanding of forest ecosystem responses to global change is essential. There is a lack of knowledge about the growth response of Schrenk spruce (Picea schrenkiana Fisch. et Mey)—an endemic tree species found in the arid Central Asian region—to climate change and rising atmospheric CO₂ concentrations. In this study, core samples of Schrenk spruce were collected in the Sayram Lake Basin, Xinjiang. Tree-ring radial growth and long-term intrinsic water-use efficiency (iWUE) chronologies were established based on standard tree-ring width and stable carbon isotope methods. The relationships between atmospheric CO₂ concentrations, climate, radial growth, and iWUE were analyzed. Our results indicate that the iWUE of trees in this region has continued to rise rapidly but that radial growth has not increased over the past 160 years. The main factor affecting iWUE is atmospheric CO₂ concentrations (C_a), whereas the radial growth is much more sensitive to water availability. This may explain why the increase C_a has not had a fertilizer effect on the radial growth of trees.

1. Introduction

Over the past century, the global temperature has increased by 0.85 °C (0.65–1.06 °C) from 1880 to 2012 [1] and the atmosphere CO₂ concentrations (C_a) has increased from 303 μmol/mol to 412 μmol/mol [2,3]. Global warming and increased C_a have profound effects on forest ecosystems, directly regulate their physiological processes, such as photosynthesis, and indirectly alter forest structure [4]. Meanwhile, forests are the most active carbon sinks in response to the current warming [5]. Theoretically, increasing C_a could have a fertilizing effect on trees, leading to an increase in plant growth rates and an (indirect) reduction in transpiration [6,7,8]. However, the magnitude of the fertilization effect in natural forests is one of the biggest uncertainties in the global carbon cycle [9]. At present, the long-term effects of increasing C_a on the growth of trees in natural forests are not fully understood. Studies have shown that C_a and intrinsic water-use efficiency (iWUE) have increased more than expected over the past century, causing trees to grow faster [10,11,12,13]; others have shown stable or even declined tree growth [14,15,16,17,18]. It is thought that trees may adapt to elevated C_a and become less sensitive to increases in carbon dioxide [14].

Tree rings provide an opportunity to test the CO₂ fertilization hypothesis [9,16]. The stable carbon isotope ratio (δ¹³C) of tree rings can be used to infer iWUE changes [11] and to track the long-term, combined effects of rising CO₂ on water use efficiency and tree growth [17]. Tree-ring δ¹³C has been widely used to study iWUE changes and their relationship to tree growth and environmental factors [10,19]. Elevated CO₂ levels in the atmosphere are expected to improve tree growth rates and iWUE [7]. However, an analysis of tree growth, iWUE, and climate over the past 150 years in the tropical region of southeast China by Li et al. [20] suggests that the radial growth of trees is not significantly affected by water use efficiency. Huang et al. [21] suggest that an increase in iWUE contributes to tree growth, but that temperature controls inter-annual changes in tree growth at the timberline on the southeastern Qinghai–Tibetan Plateau. The fertilizing effects of CO₂ have been observed under drought conditions in northwestern China. Huang et al. [14] suggest that increased C_a levels can alleviate drought stress for trees. Similarly, Liu et al. [22] show that higher C_a levels stimulate the radial growth of trees on the banks of Heihe River, making up for the negative effects of reduced river flow and an arid climate.

The Tianshan Mountains are located in the inland region of western China at the center of Eurasia. Their total length is 2500 km and they span about one million square kilometers. There are a large number of Schrenk spruce (Picea schrenkiana Fisch. et Mey) virgin forests in this region and this species has been shown to be suitable for dendrochronological study [23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38]. However, few studies have discussed the relationship between C_a, climate, radial growth, and iWUE in the Tianshan Mountains [39,40]. Sayram Lake is located in this arid region, and its climate is affected by the westerlies. Many Schrenk spruce forests are distributed on the shady slopes of the sub-alpine belt in the mountains around Sayram Lake. In this study, tree-ring width and δ¹³C chronologies were established for the Sayram Lake Basin, and the relationships between C_a, climate, radial growth, and iWUE were analyzed. Using this information, we explore the effects of global change on the radial growth and water use efficiency of Schrenk spruce.

2. Data and Methods

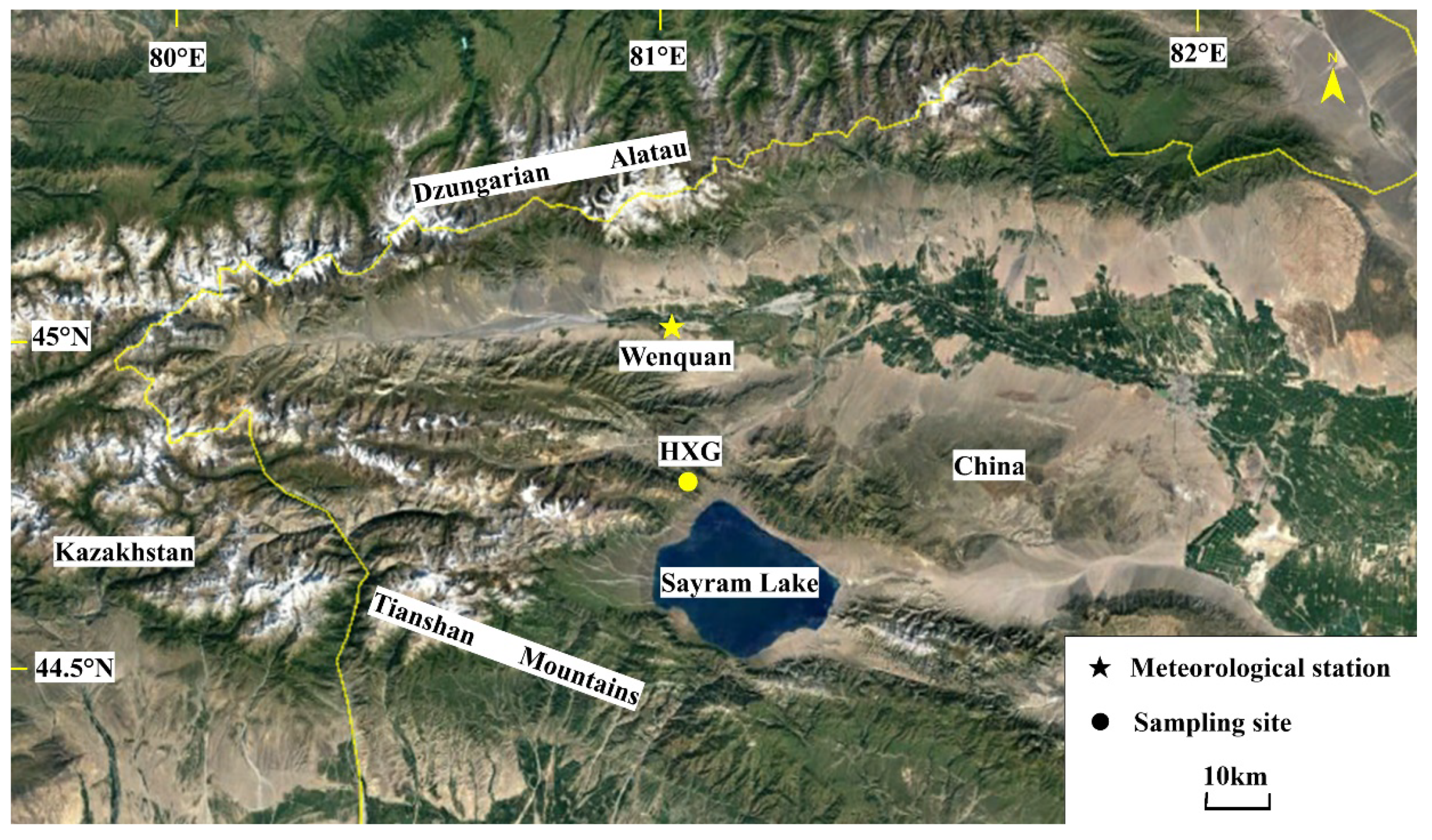
2.1. Study Area and Tree-Ring Sampling Site

The study area is located in the Sayram Lake Basin in western Tianshan, China (80°59′–81°22′ E, 44°29′–44°32′ N). The catchment area of the lake is 1408 km², and there are 39 small rivers in the lake area. Sayram Lake is fed primarily by precipitation that falls in the surrounding mountains. Water vapor brought by the westerly circulation is the main source of moisture for the area. Schrenk spruce covers the shady slopes of the sub-alpine zone (2150–2600 m) around the lake, forming a dark, primitive coniferous forest. Schrenk spruce forest is the most dominant and widespread boreal forest type in the Tianshan Mountains. It is also one of the most important zonal vegetation types in the region.

Tree-ring samples were collected in 2010 at Haixigou, which is located in the northern part of the Sayram Lake Basin (81°11′ E, 44°43′ N; designated “HXG” group; elevation is 2240–2280 m a.s.l.) (Figure 1). To minimize non-climatic effects, we identified representative trees with minimal bole and crown damage for sampling. Two cores were extracted at breast height from each tree at cross-slope positions using a 10-mm diameter Swedish increment borer. Trees grow on the north or northwest slopes of the study area, typically on slopes of 20–40 degrees. In total, 60 increment cores were collected from 30 healthy trees.

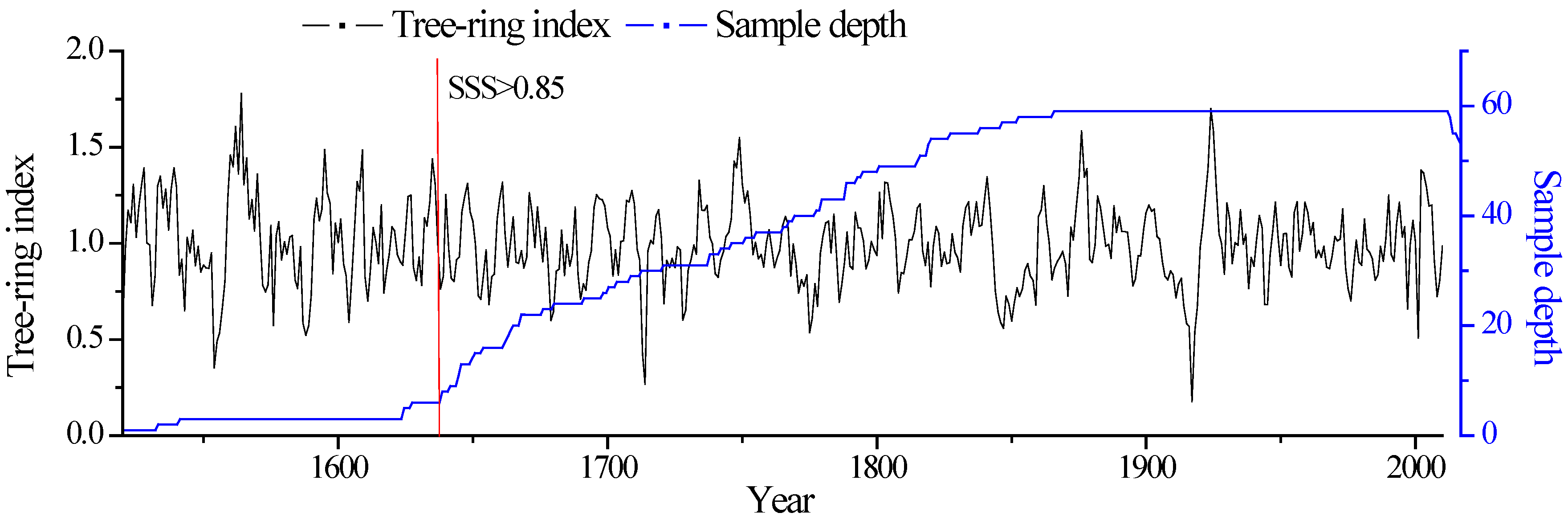
2.2. Establishing the Tree-Ring-Width Chronology

All tree-ring samples were dried naturally, mounted, and sanded until the ring structures were clear following standard dendrochronological methods. A preliminary dating of the cores was done under a binocular microscope, and rings were measured with 0.001 mm precision using a Velmex measuring system [41]. All cores were cross-dated with comparison samples, TT, and the COFECHA program [42] to ensure exact dating for each annual ring. The program ARSTAN [43] was used to develop the tree-ring width chronology. Finally, we established a standard (STD) chronology using the spline curve method (step length of 110) (Figure 2) in order to de-trend the natural trend of radial tree growth [44].

2.3. Stable Carbon Isotopic Extraction

For stable carbon isotope analysis, we selected 10 cores from five trees without missing rings or growth abnormalities that are highly correlated with the main sequence. We used a scalpel to separate each annual ring under a binocular microscope, then mixed the woody material from all samples in a given year to produce a single composite sample. The chronology covers the period from 1850 to 2008; there was too little radial growth of trees in 2009 and 2010 for cellulose extraction. All pooled samples were grounded into powder in a ball mill (MM 400, Retsch GmbH, Germany), and the α cellulose was extracted using the method of Brendel et al. [45]. This method has been widely used in dendroclimatology studies [34,35,46].

The α cellulose δ¹³C values of the tree-ring were measured using a stable isotope ratio mass spectrometer (MAT253, Thermo Fisher Scientific Bremen GmbH, Germany) coupled with an element analyzer (Flash EA 1112; Thermo Fisher Scientific, Waltham, MA, USA).

We measured the laboratory standard after every seven samples in order to calibrate the error of the instruments. The Glycine, Graphite, and Soil standards were used interchangeably. The analytical errors (standard deviations) of all the isotope standards were less than 0.056‰. δ¹³C was expressed relative to the Vienna Pee Dee Belemnite (VPDB) standard [47,48]:

$${\delta }^{13}C=\left[\frac{{\left({}^{13}C{/}^{12}C\right)}_{sample}}{{\left({}^{13}C{/}^{12}C\right)}_{VPDB}}-1\right]\times {10}^3‰$$

(1)

From this, a tree-ring δ¹³C chronology from 1850 to 2008 was obtained.

2.4. Long-Term Intrinsic Water-Use Efficiency (iWUE) Calculations

The majority of trees has C₃ photosynthesis and thus is more directly dependent on variations of the CO₂ atmospheric concentration [2]. The carbon isotope discrimination (Δ¹³C) in C₃ plants can be expressed as:

$${\Delta }^{13}C=\frac{{\delta }^{13}{C}_a-{\delta }^{13}{C}_p}{1+{\delta }^{13}{C}_p/1000}$$

(2)

where δ¹³C_a and δ¹³C_p represent the stable carbon isotopic values of ambient air and plant cellulose, respectively [49]. Discrimination against ¹³C during carbon fixation by trees (and other C3 plants) can be expressed as

$${\Delta }^{13}C=a+(b-a)\times (C_i/C_a)$$

(3)

where a (≈4.4‰) is the discrimination against ¹³CO₂ during diffusion through the stomata, b (≈27‰) is the net discrimination due to carboxylation and C_i and C_a are the CO₂ concentrations in the intercellular space of leaves and in the atmosphere, respectively [2].

The ratio of the CO₂ assimilation rate (A) to stomatal conductance (g_s) for water vapor is defined as the intrinsic water-use efficiency (iWUE), which is calculated as

$$iWUE=A/g_s=C_a\times \left[\left(1-C_i/C_a\right)/1.6\right]$$

(4)

where A (mol·m⁻² s⁻¹) is the rate of CO₂ assimilation by the tree’s leaves, g_s (μmol·m⁻² s⁻¹) is the rate of leaf stomatal conductance, C_a is the ambient CO₂ concentration, and C_i is the intercellular leaf CO₂ concentration [50,51].

2.5. Climate Data

We obtained climatological information from the Wenquan meteorological station (44°58′ N, 81°01′ E, elevation 1353.9 m) for the period 1959–2010 (China Meteorological Science Data Center, https://data.cma.cn). This is the closest station to the sampling site, with a straight line distance of less than 30 km. Analysis of monthly changes in observation data from the Wenquan meteorological station reveals that both average monthly temperature and precipitation are unimodal in the study area, and that peaking occurs in July (Figure 3a). This means that the region has a typical continental climate. The average annual precipitation in the study area is 231.8 mm, and the mean temperature is 3.93 °C. Both mean temperature and precipitation have increased significantly over the past 52 years, with amplitudes of 0.24 °C/decade and 15.6 mm/decade, respectively. The warming and wetting process has been most obvious since the 1980s (Figure 3b). These changes are in line with the warming and wetting trend observed in areas with similar climatic conditions in arid northwest China [52]. The monthly vapor pressure deficit (VPD) is calculated using the following equation:

VPD = (1 − RH) × 0.6108 × e ^{(17.27T / (T + 273.3))}

(5)

where VPD is monthly mean vapor pressure deficit, RH is the monthly mean relative humidity, and T is the monthly mean temperature [53].

The self-calibrated Palmer Drought Severity Index (scPDSI) was obtained from the gridded datasets of the Climate Research Unit (CRU) TS 3.22 (Harris et al., 2014) for the period 1901–2014 using the KNMI Climate Explorer (http://climexp.knmi.nl/start.cgi). We chose the monthly scPDSI of the CRU grid (81°20′ E, 44°40′ N) nearest the sampling site for further analysis. We also used the standardized precipitation-evapotranspiration index (SPEI) data (1901–2015) of the nearest grid (81°20′ E, 44°40′ N). The data were obtained from the global SPEI database, with a 0.5-degree spatial resolution (http://sac.csic.es/spei/database.html).

2.6. Statistical Methodology

We used conventional mathematical statistical methods to analyze the data [41]. Climate-growth response analyses were performed over the length of a biological year (i.e., previous October to current September) because tree growth can be affected by the climatic conditions of both the previous and current growing seasons. The relationships between climatic factors and tree-ring parameters were analyzed using Pearson correlation analysis with the Statistical Product and Service Solutions (SPSS Statistics 21) program.

3. Results and Discussion

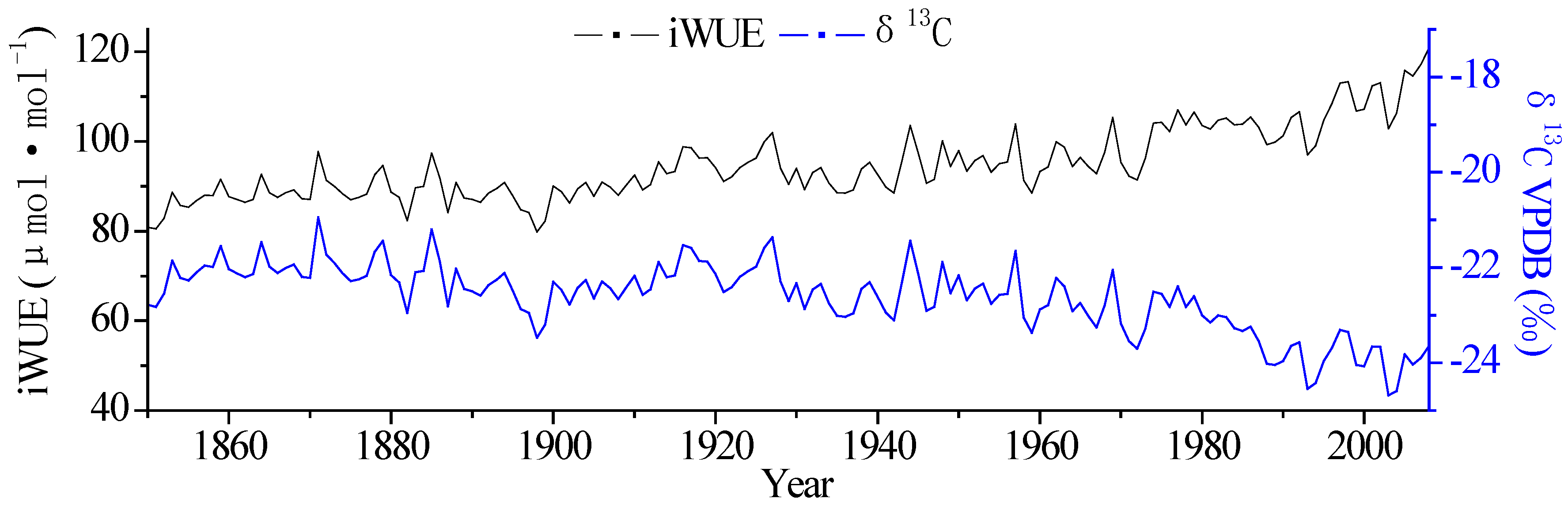
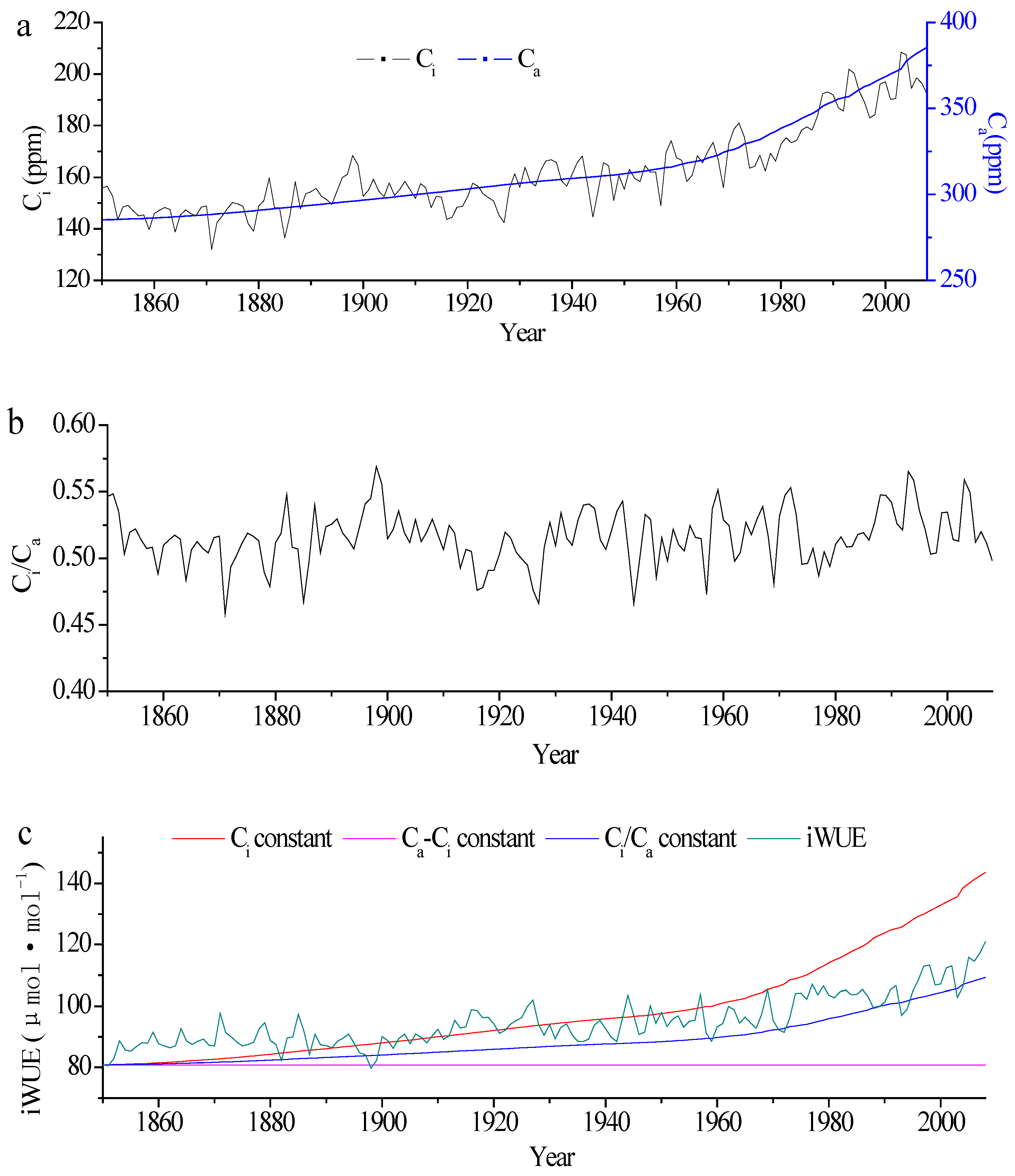
3.1. Changes in Tree-Ring δ¹³C and iWUE

For the period 1850 to 2008, Schrenk spruce tree-ring δ¹³C values ranged from −24.68‰ to −20.95‰, with an average value of −22.62 ‰ (

Table 1. The statistical characteristics of tree-ring δ¹³C and iWUE (1850–2008).

	Maximum	Minimum	Mean	Standard Deviation	Variance	Skewness	Kurtosis
δ13C (‰)	−20.95	−24.68‰	−22.62‰	0.717	0.514	−0.616	0.256
iWUE (μmol/mol)	120.93	79.78	94.73	7.98	63.736	0.849	0.457

). Over the past 158 years, δ¹³C in tree rings exhibits a decreasing trend, with an average annual decline of 0.011‰. Prior to the 1970s, the decline in δ¹³C was slow, with a slope of 0.005‰. Starting in the 1980s, the decline became steeper, with a slope of 0.035 ‰. The δ¹³C value of plant tissues is significantly lower than that of the atmosphere. In C₃ plants, it is generally between −20‰ and −35‰, with the majority of C₃ plants having values between −25‰ and −28‰. In arid regions, the δ¹³C value of C₃ plants is relatively higher. The δ¹³C values obtained in this study (−24.68‰ to −20.95‰) are within the expected range for C₃ plants (Table 1, Figure 4).

The iWUE of Schrenk spruce in the Sayram Lake Basin increased significantly and non-linearly from 1850 to 2008 and is negatively correlated with tree ring δ¹³C. The iWUE of trees in this region ranges from 79.78 to 120.93 μmol mol⁻¹ and exhibits an average annual increase of 0.141 μmol·mol⁻¹ (Table 1). The maximum iWUE value occurred in 2008; the minimum occurred in 1898 (Figure 4). Prior to the 1980s, iWUE increased slowly, with an average value of 91.35 μmol·mol⁻¹ and a rate of increase of 0.09 μmol·mol⁻¹. Accompanied by the warming and humidification process in Xinjiang after the 1980s, the iWUE increased rapidly, with an average value of 105.15 μmol·mol⁻¹ and a rate of increase of 0.416 μmol mol⁻¹.

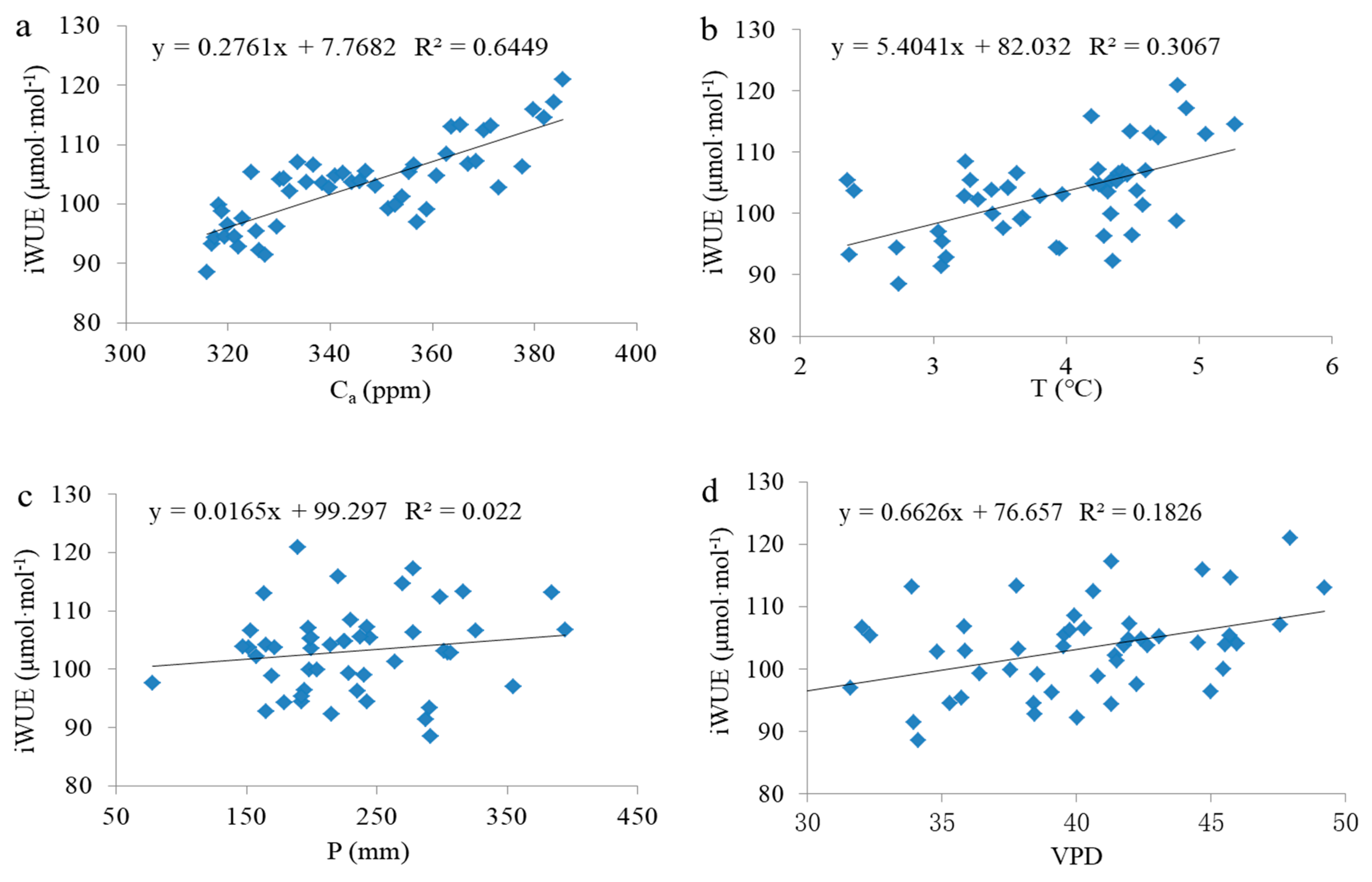
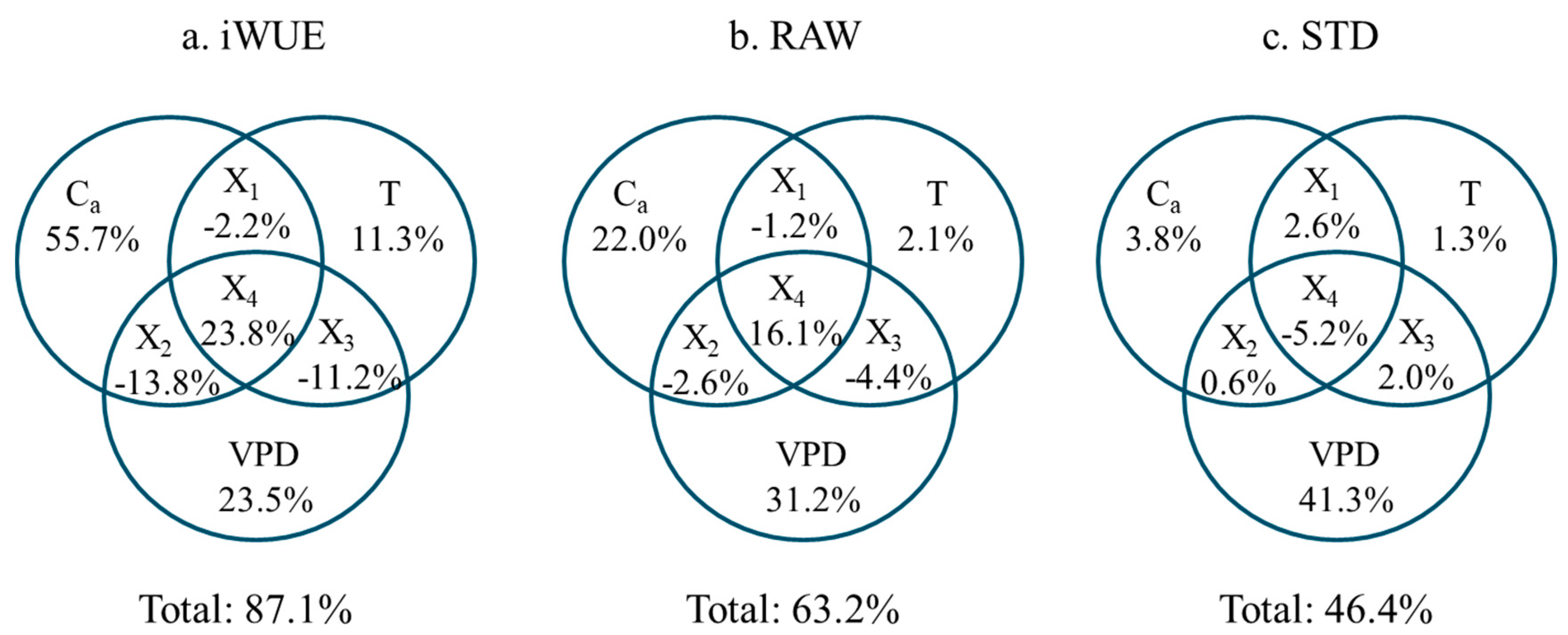
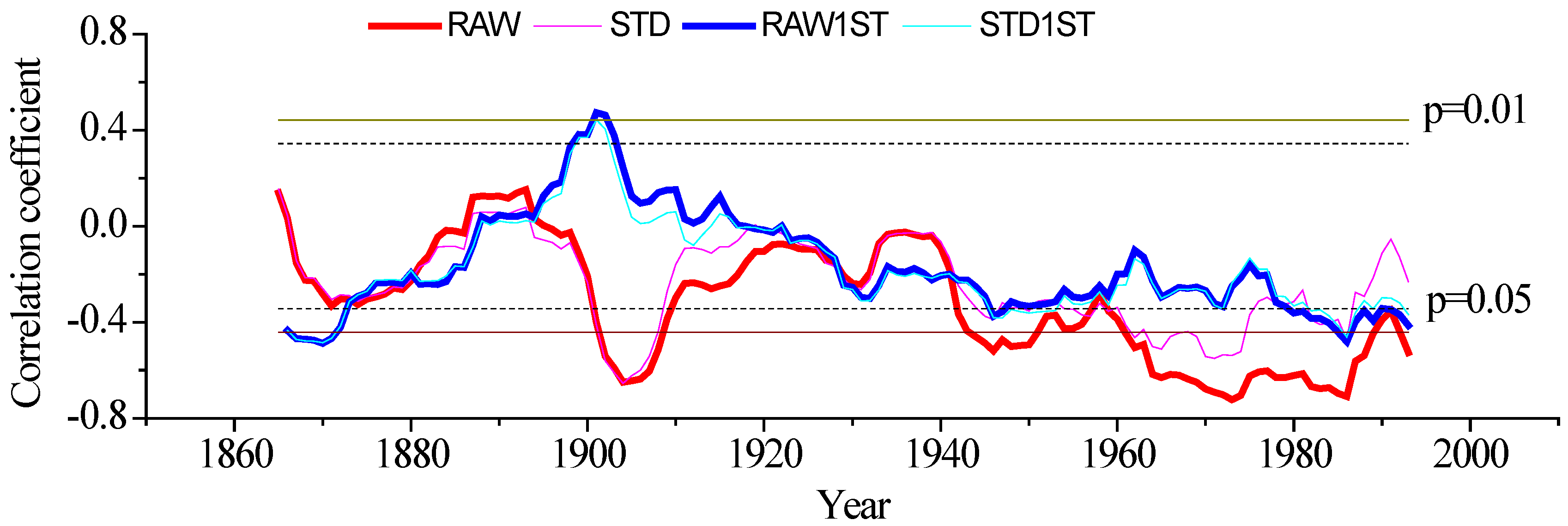
3.2. Response of Tree Radial Growth and iWUE to Environmental Factors

Pearson correlation analysis shows that there is no significant correlation between radial growth and increasing atmospheric CO₂ concentration. Radial growth is significantly negatively correlated with May–July temperature and VPD, and its correlation coefficient with VPD in May is as high as −0.448 (p < 0.01, n = 51; Figure 5). At the same time, the radial growth of trees is significantly and positively correlated with precipitation, relative humidity, SPEI, and scPDSI in the growing season (Figure 5). Whether radial growth is negatively related to temperature and VPD or positively related to relative humidity and precipitation, these results indicate that the main environmental factor affecting the radial growth of trees is water stress, especially during the growing season. Many other studies have confirmed that the radial growth of Schrenk spruce is limited by water stress during the main growing season [26,27,28,29,30,31,32,33,34,35]. Yuan et al. [26] found that tree-ring width chronologies are most closely correlated with the number of precipitation days between 20 May and 8 June in the Urumqi River Basin. Zhang et al. [54] analyzed intra-annual radial growth of Schrenk spruce based on data from continuously monitored dendrometers and found that radial growth is positively correlated with precipitation and relative humidity (RH), and negatively correlated with evaporation and vapor pressure deficit (VPD). The authors suggest that tree growth on the northern slopes of the Tianshan Mountains is moisture-limited. Our results are consistent with the results from the continuously monitored dendrometers. The increasing trend in VPD magnifies evaporation and plant transpiration [55]. The combination of elevated temperatures and VPD may therefore lead to more severe droughts and may have a fundamental impact on plant and forest ecosystems [56].

The correlation coefficient between iWUE and atmospheric CO₂ concentration (C_a) is as high as 0.803 (n = 50, p < 0.01) (Figure 6). Meanwhile, iWUE correlates significantly with temperature and VPD, with correlation coefficients of 0.554 (p < 0.01, n = 50) and 0.427 (p < 0.01, n = 50), respectively (Figure 6). However, there is no significant correlation between iWUE and precipitation changes (Figure 6). This suggests that changes in iWUE may be related to photosynthesis and transpiration. The high correlation between iWUE and atmospheric CO₂ concentration (C_a) may be due to increased C_a, which can increase the photosynthesis rate and reduce stomatal conductance, leading to improved iWUE [14,39,49]. Numerous studies have attributed the increase in plant iWUE to the continued increase in C_a [6,16,51].

In this study, we find that intercellular CO₂ concentration (C_i) increases with increasing C_a and that trees are not showing any signs of adaptations that would allow them to maintain constant C_i (Figure 7a). However, the C_i/C_a ratio has barely changed over the past 160 years (Figure 7b). This ratio reflects the balance between the net assimilation of CO₂ (A) and stomatal conductance (g_s) according to Fick’s law: A = g_s (C_a − C_i). The stability of the C_i/C_a ratio indicates that changes in C_i and C_a are consistent in both timing and magnitude, and that there is no physiological response to higher C_a levels. Previous studies have also found that C_i/C_a has remained constant over the past century [10,57,58]. The constant C_i/C_a ratio means that C_i increases synchronously with increasing C_a. According to the theory of Saurer et al. [10], this is an active response of the iWUE to the increasing C_a (Figure 7c). Similar results have been revealed by many previous studies [21,52,59]. Before the 1980s, the trend in iWUE strongly reflected the trend that would exist under a scenario of constant C_i (which assumes a strong response to C_a). However, iWUE values after the 1980s are more consistent with the values predicted under a scenario with constant C_i/C_a. This phenomenon may be related to changes in physiological mechanisms caused by the rapid warming that began in the 1980s.

Collinearity analysis shows that atmospheric CO₂ concentration (C_a), temperature (T), and vapor pressure deficit (VPD) can explain 87.1% of the variance in iWUE. C_a explains the largest portion (64.5%) of iWUE changes based on a commonality analysis for the period for which there are meteorological observation data (Figure 8). The factors affecting the radial growth of trees are more complicated. The contribution of the three environmental factors to the radial growth of trees is 63.2%. VPD has the strongest influence, whereas C_a promotes radial growth mainly by affecting tree physiological processes. If this physiological effect is not considered, the three environmental factors only explain 46.4% of the variance in the radial growth of trees, and C_a appears to have almost no direct influence. Hence, the main factor driving iWUE is C_a, whereas the main factor limiting the radial growth of trees is water stress (VPD). The VPD has not increased in the past few decades, so the radial growth of trees has not shown a significant increase. This may be the reason why the increase in C_a has not resulted in a fertilizer effect on tree radial growth. Giguere-Croteau et al. [60] have also shown that trees have not benefitted from increased iWUE due to increased C_a since 1850.

Further analysis reveals that C_a explains the majority of iWUE changes during the period for which there are meteorological observations; climate change explains the others (Figure 8). The increase in C_a is expected to affect the relationship between plant carbon and water utilization by reducing stomatal conductance [61,62]. However, although higher C_a concentrations cannot directly promote tree radial growth, they may promote tree growth by increasing the photosynthetic rate. This then reduces the stomatal conductance for the physiological adaptability of trees to the increasing C_a [63]. Meanwhile, a warming environment enhances plant evapo-transpiration and soil transpiration, which further reduces stomatal conductance.

The leaf stomata of Schrenk spruce in the Sayram Lake Basin reduce or close their aperture in response to increasing global atmospheric CO₂ concentrations. This reduces the rate of photosynthesis and enhances the water use efficiency. Increasing temperatures cause a decrease in soil moisture, which results in drought stress, which further reduces the radial growth of trees [6,51]. This pattern of differentiation between iWUE and tree growth is considered evidence of water stress caused by warming [16,17,51]. In summary, climatic factors, especially changes in water stress, are the main factors affecting the growth of Schrenk spruce in the Sayram Lake Basin.

3.3. The Relationship between Radial Growth and iWUE

The iWUE exhibits a clear increasing trend, but radial growth of Schrenk spruce growing in the Sayram Lake Basin hasn’t increased over the past 160 years (Figure 2). An analysis of the relationship between iWUE and radial growth shows that the correlation coefficient is as high as −0.711 (p < 0.01, n = 50). The sliding correlation indicates that there is significant correlation during the 1910s and over the last 51 years, but the correlation is not significant during other periods. The correlation has been weakening since the late 1980s, in synch with increasing precipitation. Thus, when the climate is generally dry, iWUE is more strongly correlated with the radial growth of trees. The correlation weaken as precipitation increases. However, the first-order difference correlation analysis shows that there is no significant correlation between iWUE and radial growth in high-frequency changes, a finding that is corroborated by the first-order difference sliding correlation (Figure 9). There is therefore no direct relationship between iWUE and radial growth with respect to long-term changes.

4. Conclusions

In this study, we established tree-ring width and iWUE chronologies in order to explore the effects of rising atmospheric CO₂ concentrations (C_a) and global warming on the radial growth and iWUE of Schrenk spruce growing in the Sayram Lake Basin. This study shows that while iWUE has continued to rise rapidly and radial growth has not increased over the past 160 years. Radial growth in this region is mainly limited by moisture conditions from May to July. The iWUE has increased significantly since the 1850s in response to increasing C_a and decreasing stomatal conductance. Stomatal closure is further enhanced by warming-induced drought and is responsible for a sharp increase in iWUE since the 1980s. However, the increased iWUE has not been able to compensate for the negative effects of warming-induced water stress. Hence, the main factor affecting iWUE is atmospheric CO₂ concentration (C_a), whereas radial growth is more sensitive to water availability. Although increasing C_a is driving a rapid increase in iWUE, it is not having a fertilizer effect on the radial growth of Schrenk spruce in the Sayram Lake Basin. It is expected that the radial growth of Schrenk spruce will decrease further, perhaps even leading to tree mortality as global warming intensifies. This study is helpful for understanding long-term dynamic changes in forest ecosystems in response to global changes and provides a reference for forest resource management in arid regions.