Aggregated Biomass Model Systems and Carbon Concentration Variations for Tree Carbon Quantification of Natural Mongolian Oak in Northeast China
Abstract
:1. Introduction
2. Data and Methods
2.1. Data Collection
2.2. Additive Biomass Models
2.2.1. Base Model
2.2.2. Aggregated Model Systems
- Aggregated model systems with no parameter restriction
- Aggregated model systems with one parameter restriction
- Aggregated model systems with three parameter restrictions
2.3. Weighting Function for Heteroscedasticity
2.4. Model Assessment and Validation
2.5. Effects of Tree Size, Region, and Component
2.6. Tree Carbon Quantifications
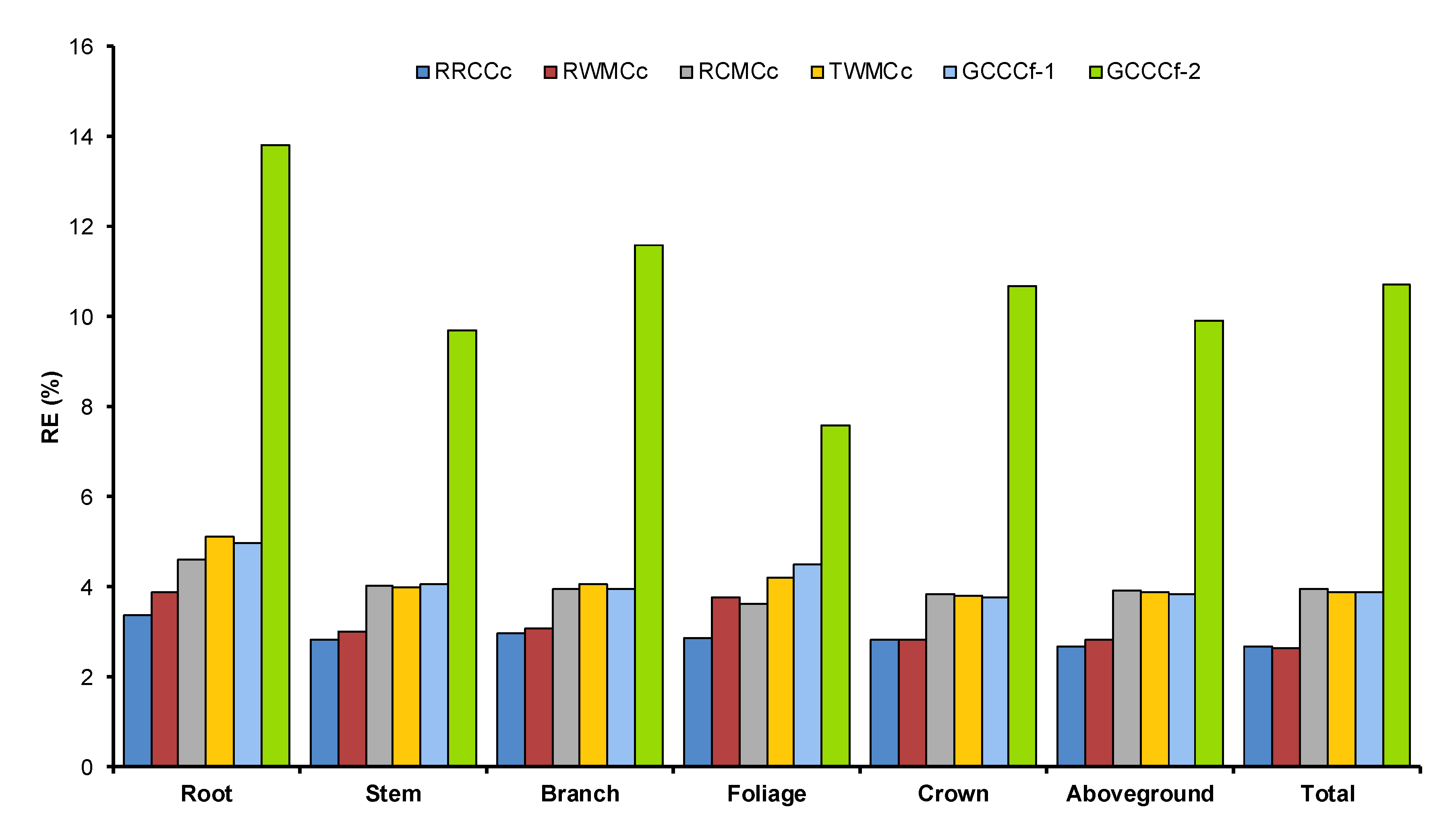
- Regional respective component carbon concentration (RRCCc): This procedure multiplied the observed biomass value () of each component by the respective component carbon concentration for each region. Further, the carbon stock of an individual tree was obtained by summing the component estimates.
- Regional weighted mean carbon concentration (RWMCc): In this procedure, each of the observed component biomass values () were multiplied by the weighted mean carbon concentration for each region. The weighted mean carbon concentration was measured as follows:where WC is the weighted mean carbon concentration for the jth region, and and are the measured carbon concentration and the relative proportion to total biomass partitioning for the component within the region, respectively.
- Respective component mean carbon concentration (RCMCc): This procedure multiplied the observed biomass value () of each component by the respective component mean carbon concentration regardless of the region for all sampled trees and subtotaling and totaling carbon stocks by summing respective components.
- Total weighted mean carbon concentration (TWMCc): This procedure multiplied each component observed biomass value () by the total weighted mean carbon concentration of all sample data. The weighted calculation was similar with the RWMCc procedure but disregarded region. Hence, the carbon stock of the subtotal and total individual tree was acquired by the summation of each component’s carbon stock.
- Generic carbon concentration conversion factor 1 (GCCCf-1): This procedure multiplied the observed biomass value () of each component by a generic carbon concentration conversion factor of 0.45.
- Generic carbon concentration conversion factor 2 (GCCCf-2): This procedure resembles GCCCf-1 instead employing the generic carbon concentration conversion factor of 0.50 for tree components to quantify the carbon stock of an individual tree.
3. Results
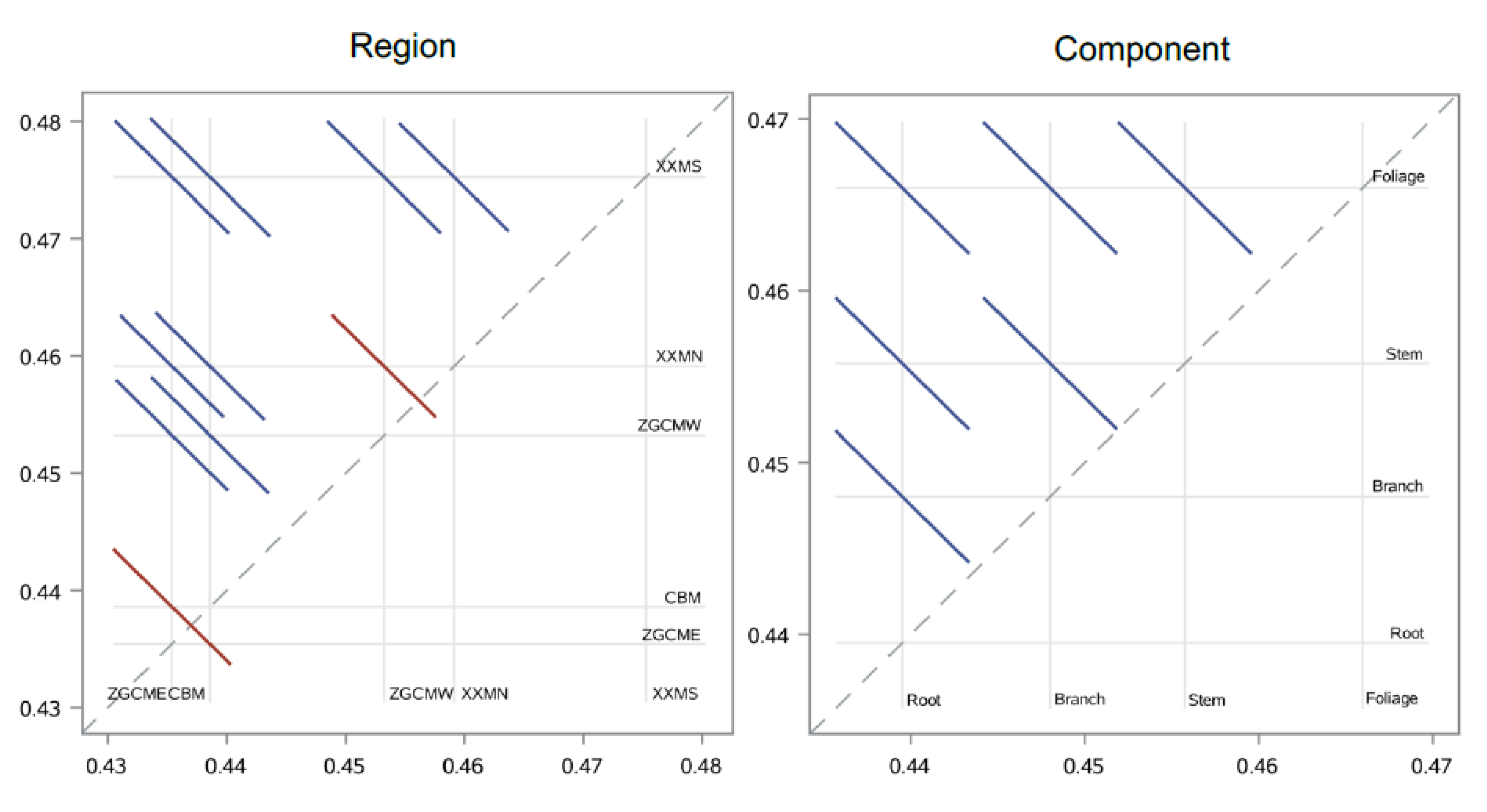
3.1. Variation of Carbon Concentration
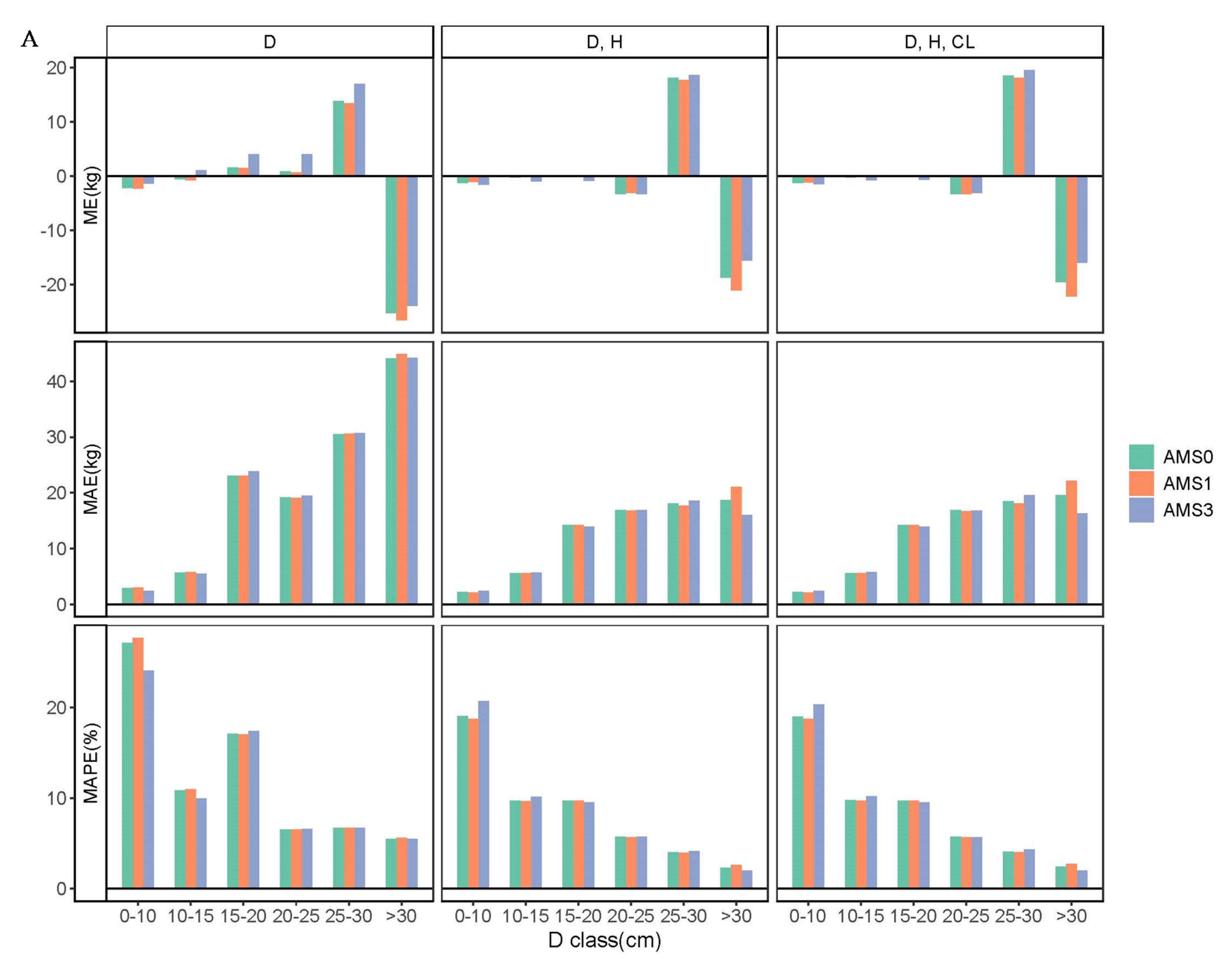
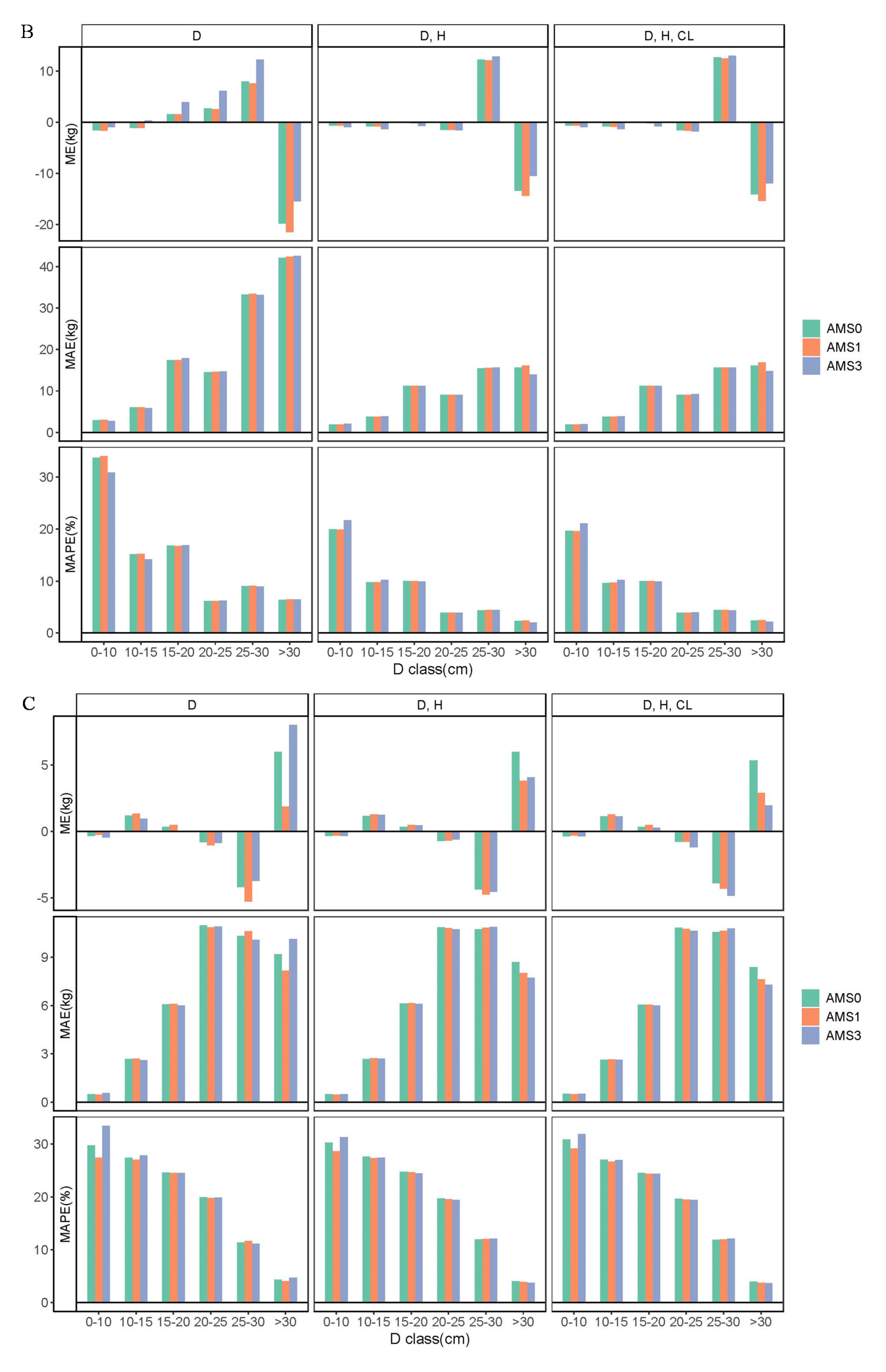
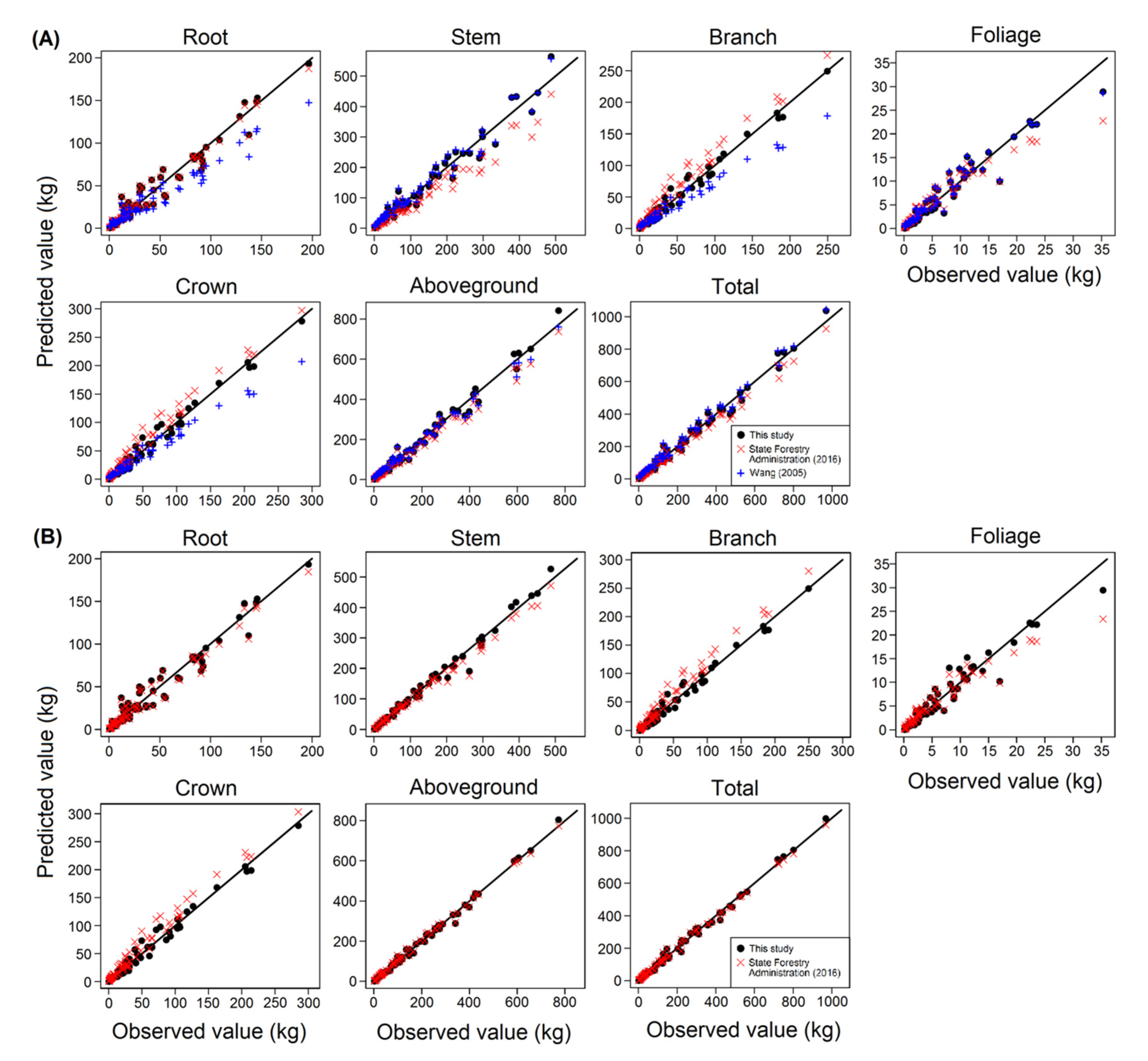
3.2. Aggregated Model Systems and Validation of Models
3.3. Comparison of Biomass Models
3.4. Comparison of Tree Carbon Quantification Methods
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- FAO (Food and Agriculture Organization of United Nations). Global Forest Resources Assessment 2015; FAO: Rome, Italy, 2016; ISBN 9789251088265. [Google Scholar]
- Wang, X.; Fang, J.; Zhu, B. Forest biomass and root-shoot allocation in northeast China. For. Ecol. Manag. 2008, 255, 4007–4020. [Google Scholar] [CrossRef]
- González-García, M.; Hevia, A.; Majada, J.; Barrio-Anta, M. Above-ground biomass estimation at tree and stand level forshort rotation plantations of Eucalyptus nitens (Deane & Maiden) Maiden in Northwest Spain. Biomass Bioenergy 2013, 54, 147–157. [Google Scholar]
- Clark, D.A.; Brown, S.; Kicklighter, D.W.; Chambers, J.Q.; Thomlinson, J.R.; Ni, J. Measuring net primary production in forests: Concepts and field methods. Ecol. Appl. 2001, 11, 356–370. [Google Scholar] [CrossRef]
- Zeng, W.S.; Duo, H.R.; Lei, X.D.; Chen, X.Y.; Wang, X.J.; Pu, Y.; Zou, W.T. Individual tree biomass equations and growth models sensitive to climate variables for Larix spp. in China. Eur. J. For. Res. 2017, 136, 233–249. [Google Scholar] [CrossRef]
- Bi, H.; Turner, J.; Lambert, M.J. Additive biomass equations for native eucalypt forest tress of temperate Australia. Trees 2004, 18, 467–479. [Google Scholar] [CrossRef]
- Dong, L.; Zhang, L.; Li, F. Developing additive systems of biomass equations for nine hardwood species in Northeast China. Trees 2015, 29, 1149–1163. [Google Scholar] [CrossRef]
- Dong, L.; Zhang, L.; Li, F. A compatible system of biomass equations for three conifer species in Northeast, China. For. Ecol. Manag. 2014, 329, 306–317. [Google Scholar] [CrossRef]
- Fayolle, A.; Doucet, J.L.; Gillet, J.F.; Bourland, N.; Lejeune, P. Tree allometry in Central Africa: Testing the validity of pantropical multi-species allometric equations for estimating biomass and carbon stocks. For. Ecol. Manag. 2013, 305, 29–37. [Google Scholar] [CrossRef]
- Sileshi, G.W. A critical review of forest biomass estimation models, common mistakes and corrective measures. For. Ecol. Manag. 2014, 329, 237–254. [Google Scholar] [CrossRef]
- Zeng, W.S. Using nonlinear mixed model and dummy variable model approaches to develop origin-based individual tree biomass equations. Trees Struct. Funct. 2015, 29, 275–283. [Google Scholar] [CrossRef]
- Radtke, P.; Walker, D.; Frank, J.; Weiskittel, A.; DeYoung, C.; MacFarlane, D.; Domke, G.; Woodall, C.; Coulston, J.; Westfall, J. Improved accuracy of aboveground biomass and carbon estimates for live trees in forests of the eastern United States. For. Int. J. For. Res. 2017, 90, 32–46. [Google Scholar] [CrossRef] [Green Version]
- Luo, Y.; Wang, X.; Ouyang, Z.; Lu, F.; Feng, L.; Tao, J. A review of biomass equations for China’s tree species. Earth Syst. Sci. Data 2020, 12, 21–40. [Google Scholar] [CrossRef] [Green Version]
- Dong, L.; Zhang, L.; Li, F. Developing two additive biomass equations for three coniferous plantation species in northeast China. Forests 2016, 7, 136. [Google Scholar] [CrossRef] [Green Version]
- Zhao, D.; Kane, M.; Markewitz, D.; Teskey, R.; Clutter, M. Additive tree biomass equations for midrotation loblolly pine plantations. For. Sci. 2015, 61, 613–623. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.; Zhao, D.; Liu, G.; Yang, C.; Teskey, R.O. Additive tree biomass equations for Betula platyphylla Suk. plantations in Northeast China. Ann. For. Sci. 2018, 75. [Google Scholar] [CrossRef] [Green Version]
- Parresol, B.R. Additivity of nonlinear biomass equations. Can. J. For. Res. 2001, 31, 865–878. [Google Scholar] [CrossRef]
- Tang, S.; Wang, Y. A parameter estimation program for the error-in-variable model. Ecol. Modell. 2002, 156, 225–236. [Google Scholar] [CrossRef]
- Dong, L.; Zhang, L.; Li, F. A three-step proportional weighting system of nonlinear biomass equations. For. Sci. 2015, 61, 35–45. [Google Scholar] [CrossRef]
- Reed, D.D.; Green, E.J. A method of forcing additivity of biomass tables when using nonlinear models. Can. J. For. Res. 1985, 15, 1184–1187. [Google Scholar] [CrossRef]
- Zhao, D.; Westfall, J.; Coulston, J.W.; Lynch, T.B.; Bullock, B.P.; Montes, C.R. Additive biomass equations for slash pine trees: Comparing three modeling approaches. Can. J. For. Res. 2019, 49, 27–40. [Google Scholar] [CrossRef]
- Russell, M.B.; Burkhart, H.E.; Amateis, R.L. Biomass partitioning in a miniature-scale loblolly pine spacing trial. Can. J. For. Res. 2009, 39, 320–329. [Google Scholar] [CrossRef]
- Menéndez-Miguélez, M.; Canga, E.; Barrio-Anta, M.; Majada, J.; Álvarez-Álvarez, P. A three level system for estimating the biomass of Castanea sativa Mill. coppice stands in north-west Spain. For. Ecol. Manag. 2013, 291, 417–426. [Google Scholar] [CrossRef]
- Dong, L.; Zhang, Y.; Zhang, Z.; Xie, L.; Li, F. Comparison of Tree Biomass Modeling Approaches for Larch (Larix olgensis Henry) Trees in Northeast China. Forests 2020, 11, 202. [Google Scholar] [CrossRef] [Green Version]
- Affleck, D.L.R.; Diéguez-Aranda, U. Additive nonlinear biomass equations: A likelihood-based approach. For. Sci. 2016, 62, 129–140. [Google Scholar] [CrossRef]
- Thomas, S.C.; Malczewski, G. Wood carbon content of tree species in Eastern China: Interspecific variability and the importance of the volatile fraction. J. Environ. Manag. 2007, 85, 659–662. [Google Scholar] [CrossRef] [PubMed]
- Tashi, S.; Keitel, C.; Singh, B.; Adams, M. Allometric equations for biomass and carbon stocks of forests along an altitudinal gradient in the eastern Himalayas. For. Int. J. For. Res. 2017, 90, 445–454. [Google Scholar] [CrossRef]
- Losi, C.J.; Siccama, T.G.; Condit, R.; Morales, J.E. Analysis of alternative methods for estimating carbon stock in young tropical plantations. For. Ecol. Manag. 2003, 184, 355–368. [Google Scholar] [CrossRef]
- Houghton, R.A. Converting Terrestrial Ecosystems from Sources to Sinks of Carbon. Ambio 1996, 25, 267–272. [Google Scholar]
- Kraenzel, M.; Castillo, A.; Moore, T.; Potvin, C. Carbon storage of harvest-age teak (Tectona grandis) plantations, Panama. For. Ecol. Manag. 2003, 173, 213–225. [Google Scholar] [CrossRef]
- Laiho, R.; Laine, J. Tree stand biomass and carbon content in an age sequence of drained pine mires in southern Finland. For. Ecol. Manag. 1997, 93, 161–169. [Google Scholar] [CrossRef]
- Lamlom, S.H.; Savidge, R.A. A reassessment of carbon content in wood: Variation within and between 41 North American species. Biomass Bioenergy 2003, 25, 381–388. [Google Scholar] [CrossRef]
- Bert, D.; Danjon, F. Carbon concentration variations in the roots, stem and crown of mature Pinus pinaster (Ait.). For. Ecol. Manag. 2006, 222, 279–295. [Google Scholar] [CrossRef]
- Rodríguez-Soalleiro, R.; Eimil-Fraga, C.; Gómez-García, E.; García-Villabrille, J.D.; Rojo-Alboreca, A.; Muñoz, F.; Oliveira, N.; Sixto, H.; Pérez-Cruzado, C. Exploring the factors affecting carbon and nutrient concentrations in tree biomass components in natural forests, forest plantations and short rotation forestry. For. Ecosyst. 2018, 5, 35. [Google Scholar]
- Wang, C.; Sang, Y. STUDIES ON STRUCTURE AND FUNCTIONS OF MONGOLIAN OAK FORESTS. J. Northeast Univ. 1995, 6, 65–70. [Google Scholar]
- Wang, C. Biomass allometric equations for 10 co-occurring tree species in Chinese temperate forests. For. Ecol. Manag. 2006, 222, 9–16. [Google Scholar] [CrossRef]
- Zhang, Q.; Wang, C.; Wang, X.; Quan, X. Carbon concentration variability of 10 Chinese temperate tree species. For. Ecol. Manag. 2009, 258, 722–727. [Google Scholar] [CrossRef]
- Beck, H.E.; Zimmermann, N.E.; McVicar, T.R.; Vergopolan, N.; Berg, A.; Wood, E.F. Present and future köppen-geiger climate classification maps at 1-km resolution. Sci. Data 2018, 5, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Dong, L.; Zhang, L.; Li, F. Allometry and partitioning of individual tree biomass and carbon of Abies nephrolepis Maxim in northeast China. Scand. J. For. Res. 2016, 31, 399–411. [Google Scholar] [CrossRef]
- SAS Institute Inc. SAS/ETS 9.3 User’s Guide; SAS Institute Inc.: Cary, NC, USA, 2011. [Google Scholar]
- Balboa-Murias, M.Á.; Rodríguez-Soalleiro, R.; Merino, A.; Álvarez-González, J.G. Temporal variations and distribution of carbon stocks in aboveground biomass of radiata pine and maritime pine pure stands under different silvicultural alternatives. For. Ecol. Manag. 2006, 237, 29–38. [Google Scholar] [CrossRef]
- State Forestry Administration. Tree Biomas Models and Related Parameters to Carbon Accounting for Quercus; China Forestry Press: Beijing, China, 2016.
- Xing, Z.; Bourque, C.P.A.; Swift, D.E.; Clowater, C.W.; Krasowski, M.; Meng, F.R. Carbon and biomass partitioning in balsam fir (Abies balsamea). Tree Physiol. 2005, 25, 1207–1217. [Google Scholar] [CrossRef] [Green Version]
- Wu, H.; Xiang, W.; Fang, X.; Lei, P.; Ouyang, S.; Deng, X. Tree functional types simplify forest carbon stock estimates induced by carbon concentration variations among species in a subtropical area. Sci. Rep. 2017, 7, 1–11. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ngo, K.M.; Turner, B.L.; Muller-Landau, H.C.; Davies, S.J.; Larjavaara, M.; bin Nik Hassan, N.F.; Lum, S. Carbon stocks in primary and secondary tropical forests in Singapore. For. Ecol. Manag. 2013, 296, 81–89. [Google Scholar] [CrossRef]
- Singh, V.; Tewari, A.; Kushwaha, S.P.S.; Dadhwal, V.K. Formulating allometric equations for estimating biomass and carbon stock in small diameter trees. For. Ecol. Manag. 2011, 261, 1945–1949. [Google Scholar] [CrossRef]
- Arif, M.; Shahzad, M.K.; Elzaki, E.E.A.; Hussain, A.; Zhang, B.; Yukun, C. Biomass and carbon stocks estimation in Chichawatni irrigated plantation in Pakistan. Int. J. Agric. Biol. 2017, 19, 1339–1349. [Google Scholar]
- Roy, J.; Saugier, B.; Mooney, H.A. Terrestrial Primary Productivity: Definitions and Milestones; Academic Press: New York, NY, USA, 2001; ISBN 0125052901. [Google Scholar]
- Wenzl, H.F.J. The Chemical Technology of Wood; Academic Press: New York, NY, USA, 1970; ISBN 8645182191751. [Google Scholar]
- de Mello, A.A.; Nutto, L.; Weber, K.S.; Sanquetta, C.E.; Monteiro de Matos, J.L.; Becker, G. Individual biomass and carbon equations for Mimosa scabrella Benth. (Bracatinga) in Southern Brazil. Silva Fenn. 2012, 46, 333–343. [Google Scholar] [CrossRef] [Green Version]
- Van Vinh, T.; Marchand, C.; Linh, T.V.K.; Vinh, D.D.; Allenbach, M. Allometric models to estimate above-ground biomass and carbon stocks in Rhizophora apiculata tropical managed mangrove forests (Southern Viet Nam). For. Ecol. Manag. 2019, 434, 131–141. [Google Scholar] [CrossRef]
- Chauhan, S.K.; Singh, S.; Sharma, S.; Sharma, R.; Saralch, H.S. Tree biomass and carbon sequestration in four short rotation tree plantations. Range Manag. Agrofor. 2019, 40, 77–82. [Google Scholar]
- Dong, L.; Liu, Y.; Zhang, L.; Xie, L.; Li, F. Variation in carbon concentration and allometric equations for estimating tree carbon contents of 10 broadleaf species in natural forests in Northeast China. Forests 2019, 10, 928. [Google Scholar] [CrossRef] [Green Version]
- Gschwantner, T.; Schadauer, K.; Vidal, C.; Lanz, A.; Tomppo, E.; Di Cosmo, L.; Robert, N.; Duursma, D.E.; Lawrence, M. Common tree definitions for national forest inventories in Europe. Silva Fenn. 2009, 43, 303–321. [Google Scholar] [CrossRef] [Green Version]
- Zianis, D.; Muukkonen, P.; Mäkipää, R.; Mencuccini, M. Biomass and stem volume equations for tree species in Europe. Silva Fenn. Monogr. 2005, 4, 1–63. [Google Scholar]
- Basuki, T.M.; van Laake, P.E.; Skidmore, A.K.; Hussin, Y.A. Allometric equations for estimating the above-ground biomass in tropical lowland Dipterocarp forests. For. Ecol. Manag. 2009, 257, 1684–1694. [Google Scholar] [CrossRef]
- Jenkins, J.C.; Chojnacky, D.C.; Heath, L.S.; Birdsey, R.A. National-scale biomass estimators for United States tree species. For. Sci. 2003, 49, 12–35. [Google Scholar]
- Zou, W.T.; Zeng, W.S.; Zhang, L.J.; Zeng, M. Modeling crown biomass for four pine species in China. Forests 2015, 6, 433–449. [Google Scholar] [CrossRef] [Green Version]
- Dong, L.; Zhang, L.; Li, F. Additive biomass equations based on different dendrometric variables for two dominant species (Larix gmelini Rupr. and Betula platyphylla Suk.) in natural forests in the Eastern Daxing’an Mountains, Northeast China. Forests 2018, 9, 261. [Google Scholar] [CrossRef] [Green Version]
- Ma, W.; Lei, X. Nonlinear Simultaneous Equations for Individual-Tree Diameter Growth and Mortality Model of Natural Mongolian Oak Forests in Northeast China. Forests 2015, 6, 2261–2280. [Google Scholar] [CrossRef] [Green Version]
- Nicoll, B.C.; Ray, D. Adaptive growth of tree root systems in response to wind action and site conditions. Tree Physiol. 1996, 16, 891–898. [Google Scholar] [CrossRef] [Green Version]
- Satoo, T.; Madgwick, H.A.I. Forest Biomass; DR W. Junk Publishers: The Hague, The Netherlands, 1982; ISBN 9781510817173. [Google Scholar]

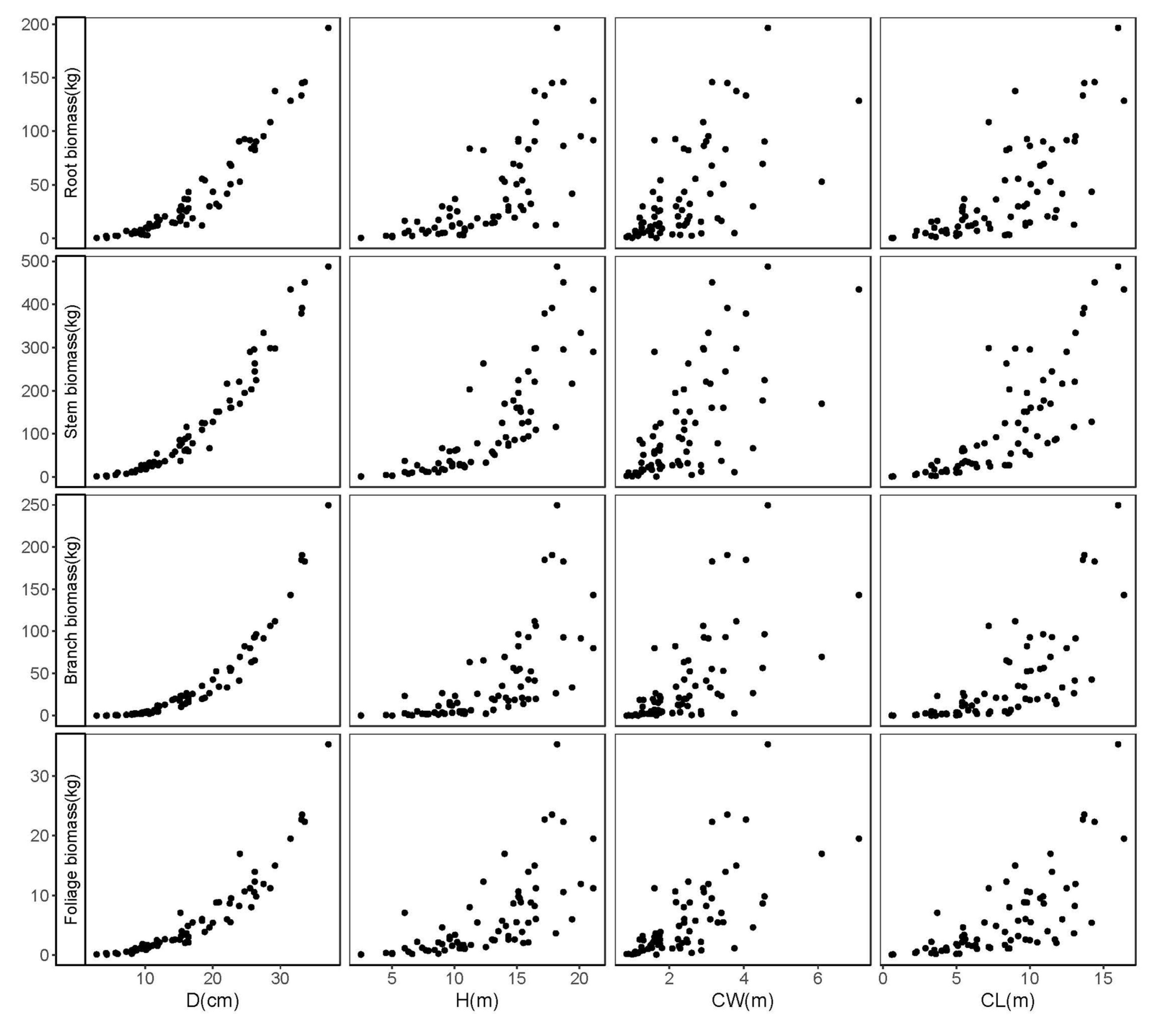
| Statistics | N | Mean | Min | Max | SD |
|---|---|---|---|---|---|
| D (cm) | 72 | 16.7 | 2.8 | 37.1 | 8.2 |
| H (m) | 72 | 12.3 | 2.5 | 21.1 | 4.5 |
| CW (m) | 72 | 2.4 | 0.9 | 7.1 | 1.2 |
| CL (m) | 72 | 8.1 | 0.6 | 16.4 | 3.7 |
| Total biomass (kg) | 72 | 202.14 | 1.74 | 969.13 | 222.94 |
| Root biomass (kg) | 72 | 40.67 | 0.48 | 196.50 | 44.06 |
| Stem biomass (kg) | 72 | 117.21 | 0.87 | 487.70 | 123.23 |
| Branch biomass (kg) | 72 | 38.41 | 0.13 | 249.64 | 52.01 |
| Foliage biomass (kg) | 72 | 5.84 | 0.09 | 35.29 | 6.73 |
| Region | Sites | Components | N | Mean | Min | Max | SD |
|---|---|---|---|---|---|---|---|
| XXMN | Heihe, Luobei and Sunwu | Root | 18 | 0.4461 | 0.4137 | 0.4744 | 0.0202 |
| Stem | 0.4638 | 0.4372 | 0.4917 | 0.0156 | |||
| Branch | 0.4506 | 0.4082 | 0.4735 | 0.0159 | |||
| Foliage | 0.4755 | 0.4392 | 0.5085 | 0.0201 | |||
| RWMCC | 0.4578 | 0.4313 | 0.4842 | 0.0147 | |||
| XXMS | Qingan | Root | 12 | 0.4662 | 0.4463 | 0.4863 | 0.0127 |
| Stem | 0.4786 | 0.4640 | 0.4962 | 0.0113 | |||
| Branch | 0.4710 | 0.4426 | 0.5043 | 0.0165 | |||
| Foliage | 0.4858 | 0.4639 | 0.5207 | 0.0177 | |||
| RWMCC | 0.4747 | 0.4607 | 0.4885 | 0.0102 | |||
| ZGCME | Hulin and Ningan | Root | 12 | 0.4194 | 0.3949 | 0.4423 | 0.0171 |
| Stem | 0.4396 | 0.4200 | 0.4538 | 0.0109 | |||
| Branch | 0.4324 | 0.4166 | 0.4465 | 0.0097 | |||
| Foliage | 0.4502 | 0.4305 | 0.4766 | 0.0133 | |||
| RWMCC | 0.4349 | 0.4143 | 0.4430 | 0.0095 | |||
| ZGCMW | Acheng and Wuchang | Root | 12 | 0.4408 | 0.4029 | 0.4773 | 0.0220 |
| Stem | 0.4571 | 0.4230 | 0.4835 | 0.0228 | |||
| Branch | 0.4527 | 0.4256 | 0.4859 | 0.0233 | |||
| Foliage | 0.4624 | 0.4293 | 0.4846 | 0.0161 | |||
| RWMCC | 0.4537 | 0.4225 | 0.4806 | 0.0215 | |||
| CBM | Fusong and Baishan | Root | 10 | 0.4250 | 0.4049 | 0.4475 | 0.0133 |
| Stem | 0.4385 | 0.4110 | 0.4623 | 0.0166 | |||
| Branch | 0.4356 | 0.4139 | 0.4613 | 0.0162 | |||
| Foliage | 0.4551 | 0.4379 | 0.4858 | 0.0168 | |||
| RWMCC | 0.4361 | 0.4110 | 0.4595 | 0.0148 | |||
| Total | All sites | Root | 64 | 0.4406 | 0.3949 | 0.4863 | 0.0234 |
| Stem | 0.4568 | 0.4110 | 0.4962 | 0.0211 | |||
| Branch | 0.4491 | 0.4082 | 0.5043 | 0.0208 | |||
| Foliage | 0.4670 | 0.4293 | 0.5207 | 0.0210 | |||
| TWMCC | 0.4525 | 0.4110 | 0.4885 | 0.0201 |
| Source | DF | Type III SS | Mean Square | F-Values | p-Values |
|---|---|---|---|---|---|
| Tree size (D) | 1 | 0.00001407 | 0.00001407 | 0.05 | 0.8326 |
| Region | 4 | 0.04853293 | 0.01213323 | 42.93 | <0.0001 |
| Component | 3 | 0.02437421 | 0.00812474 | 28.75 | <0.0001 |
| Model Type | Biomass Component | βi0 | βi1 | Weight Function | R2 | RMSE | MPE | MAE | MAPE | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Estimate | SE | Estimate | SE | ||||||||
| AMS0 | Root | −3.295 | 0.217 | 2.369 | 0.072 | D3.4640 | 0.956 | 9.13 | 0.08 | 6.39 | 30.82 |
| Stem | −2.303 | 0.173 | 2.391 | 0.055 | D2.6952 | 0.964 | 23.33 | −0.26 | 16.11 | 22.89 | |
| Branch | −5.725 | 0.214 | 3.112 | 0.067 | D3.6937 | 0.983 | 6.74 | 0.01 | 4.77 | 28.23 | |
| Foliage | −5.492 | 0.274 | 2.451 | 0.085 | D2.2455 | 0.937 | 1.67 | 0.02 | 1.03 | 24.78 | |
| Crown | 0.983 | 7.50 | 0.03 | 5.46 | 22.75 | ||||||
| Aboveground | 0.984 | 22.56 | −0.23 | 15.15 | 17.47 | ||||||
| Total | 0.988 | 24.63 | −0.16 | 16.83 | 14.82 | ||||||
| AMS1 | Root | −3.260 | 0.169 | 2.358 | 0.056 | D3.4640 | 0.956 | 9.13 | 0.02 | 6.38 | 31.07 |
| Stem | −2.272 | 0.162 | 2.380 | 0.051 | D2.6952 | 0.964 | 23.16 | −0.11 | 16.03 | 23.10 | |
| Branch | −5.843 | 0.206 | 3.151 | 0.064 | D3.6937 | 0.983 | 6.77 | −0.35 | 4.85 | 27.26 | |
| Foliage | −5.529 | 0.273 | 2.463 | 0.085 | D2.2455 | 0.938 | 1.67 | 0.01 | 1.03 | 24.70 | |
| Crown | 0.984 | 7.47 | −0.34 | 5.41 | 22.12 | ||||||
| Aboveground | 0.984 | 22.71 | −0.44 | 15.19 | 17.55 | ||||||
| Total | D2.8621 | 0.988 | 24.73 | −0.43 | 16.90 | 14.97 | |||||
| AMS3 | Root | −3.397 | 0.174 | 2.403 | 0.057 | D3.4640 | 0.956 | 9.17 | −0.21 | 6.44 | 30.43 |
| Stem | −2.441 | 0.117 | 2.428 | 0.037 | D2.6952 | 0.963 | 23.63 | 1.97 | 16.27 | 21.53 | |
| Branch | −5.641 | 0.187 | 3.084 | 0.057 | D3.6937 | 0.983 | 6.82 | 0.16 | 4.80 | 29.05 | |
| Foliage | −5.268 | 0.139 | 2.385 | 0.044 | D2.2455 | 0.935 | 1.71 | −0.09 | 1.06 | 26.32 | |
| Crown | D4.7602 | 0.983 | 7.62 | 0.07 | 5.47 | 23.68 | |||||
| Aboveground | D3.1438 | 0.984 | 22.65 | 2.04 | 15.20 | 16.63 | |||||
| Total | D2.8621 | 0.987 | 24.88 | 1.83 | 16.94 | 14.01 | |||||
| Model Type | Biomass Component | βi0 | βi1 | βi2 | Weight Function | R2 | RMSE | MPE | MAE | MAPE | |||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Estimate | SE | Estimate | SE | Estimate | SE | ||||||||
| AMS0 | Root | −3.2901 | 0.2168 | 2.3671 | 0.0718 | D3.4640 | 0.956 | 9.14 | 0.09 | 6.39 | 30.83 | ||
| Stem | −3.2510 | 0.1289 | 1.9183 | 0.0454 | 0.8907 | 0.0688 | D2.6952 | 0.988 | 13.17 | 0.06 | 7.96 | 10.79 | |
| Branch | −5.7238 | 0.2136 | 3.1111 | 0.0669 | D3.6937 | 0.983 | 6.74 | 0.00 | 4.77 | 28.25 | |||
| Foliage | −5.1835 | 0.3017 | 2.6080 | 0.1172 | −0.2958 | 0.1482 | D2.2455 | 0.938 | 1.66 | 0.01 | 1.07 | 25.50 | |
| Crown | 0.983 | 7.52 | 0.01 | 5.48 | 22.97 | ||||||||
| Aboveground | 0.996 | 11.77 | 0.08 | 8.16 | 10.32 | ||||||||
| Total | 0.995 | 15.40 | 0.17 | 10.82 | 10.22 | ||||||||
| AMS1 | Root | −3.3745 | 0.1565 | 2.3935 | 0.0518 | D3.4640 | 0.956 | 9.14 | 0.13 | 6.38 | 30.39 | ||
| Stem | −3.2397 | 0.1250 | 1.9091 | 0.0438 | 0.8971 | 0.0663 | D2.6952 | 0.989 | 13.10 | 0.07 | 7.94 | 10.91 | |
| Branch | −5.8051 | 0.1867 | 3.1370 | 0.0580 | D3.6937 | 0.983 | 6.73 | −0.12 | 4.80 | 27.50 | |||
| Foliage | −5.1801 | 0.2958 | 2.6091 | 0.1159 | −0.2980 | 0.1469 | D2.2455 | 0.938 | 1.66 | 0.01 | 1.07 | 25.42 | |
| Crown | 0.983 | 7.48 | −0.11 | 5.44 | 22.49 | ||||||||
| Aboveground | 0.996 | 11.86 | −0.04 | 8.21 | 10.33 | ||||||||
| Total | D2.8621 | 0.995 | 15.56 | 0.09 | 10.89 | 10.13 | |||||||
| AMS3 | Root | −3.2692 | 0.1115 | 2.3609 | 0.0356 | D3.4640 | 0.956 | 9.13 | 0.04 | 6.37 | 30.96 | ||
| Stem | −3.1704 | 0.0887 | 1.8928 | 0.0358 | 0.8905 | 0.0546 | D2.6952 | 0.989 | 12.91 | 0.10 | 7.83 | 11.44 | |
| Branch | −5.8247 | 0.1338 | 3.1426 | 0.0409 | D3.6937 | 0.983 | 6.72 | −0.06 | 4.80 | 27.22 | |||
| Foliage | −4.8658 | 0.1606 | 2.6140 | 0.0901 | −0.4180 | 0.1158 | D2.2455 | 0.935 | 1.71 | −0.02 | 1.08 | 27.04 | |
| Crown | D4.7602 | 0.983 | 7.49 | −0.08 | 5.40 | 23.06 | |||||||
| Aboveground | D3.1438 | 0.996 | 11.63 | 0.02 | 8.10 | 10.81 | |||||||
| Total | D2.8621 | 0.995 | 15.30 | 0.06 | 10.72 | 10.63 | |||||||
| Model Type | Biomass Component | βi0 | βi1 | βi2 | βi3 | Weight Function | R2 | RMSE | MPE | MAE | MAPE | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Estimate | SE | Estimate | SE | Estimate | SE | Estimate | SE | ||||||||
| AMS0 | Root | −3.2968 | 0.2173 | 2.3693 | 0.0719 | D3.4640 | 0.956 | 9.13 | 0.08 | 6.39 | 30.80 | ||||
| Stem | −3.2523 | 0.1289 | 1.9182 | 0.0454 | 0.8912 | 0.0688 | D2.6952 | 0.988 | 13.17 | 0.06 | 7.96 | 10.78 | |||
| Branch | −5.7253 | 0.2137 | 3.1116 | 0.0669 | D3.6937 | 0.983 | 6.74 | −0.00 | 4.77 | 28.23 | |||||
| Foliage | −4.8127 | 0.3444 | 2.5364 | 0.1179 | −0.6352 | 0.2194 | 0.3333 | 0.1634 | D2.2455 | 0.949 | 1.51 | 0.00 | 1.01 | 25.02 | |
| Crown | 0.984 | 7.45 | 0.00 | 5.41 | 22.91 | ||||||||||
| Aboveground | 0.996 | 11.86 | 0.07 | 8.19 | 10.24 | ||||||||||
| Total | 0.995 | 15.53 | 0.15 | 10.94 | 10.21 | ||||||||||
| AMS1 | Root | −3.3749 | 0.1560 | 2.3939 | 0.0517 | D3.4640 | 0.956 | 9.14 | 0.11 | 6.38 | 30.41 | ||||
| Stem | −3.2393 | 0.1249 | 1.9096 | 0.0437 | 0.8965 | 0.0662 | D2.6952 | 0.989 | 13.10 | 0.06 | 7.95 | 10.91 | |||
| Branch | −5.8117 | 0.1866 | 3.1392 | 0.0580 | D3.6937 | 0.983 | 6.73 | −0.14 | 4.80 | 27.44 | |||||
| Foliage | −4.7837 | 0.3382 | 2.5326 | 0.1161 | −0.6634 | 0.2162 | 0.3593 | 0.1607 | D2.2455 | 0.949 | 1.51 | 0.00 | 1.00 | 24.92 | |
| Crown | 0.984 | 7.41 | −0.14 | 5.35 | 22.40 | ||||||||||
| Aboveground | 0.996 | 11.96 | −0.08 | 8.24 | 10.24 | ||||||||||
| Total | D2.8621 | 0.995 | 15.71 | 0.03 | 11.02 | 10.14 | |||||||||
| AMS3 | Root | −3.2855 | 0.1225 | 2.3634 | 0.0397 | D3.4640 | 0.956 | 9.16 | 0.38 | 6.36 | 30.68 | ||||
| Stem | −3.1905 | 0.0903 | 1.8852 | 0.0368 | 0.9059 | 0.0562 | D2.6952 | 0.989 | 12.93 | 0.30 | 7.79 | 11.32 | |||
| Branch | −5.8156 | 0.1626 | 3.1419 | 0.0502 | D3.6937 | 0.983 | 6.76 | −0.31 | 4.82 | 27.46 | |||||
| Foliage | −4.5376 | 0.1803 | 2.5288 | 0.0741 | −0.7336 | 0.1580 | 0.3484 | 0.1029 | D2.2455 | 0.947 | 1.54 | −0.10 | 1.00 | 26.45 | |
| Crown | D4.7602 | 0.984 | 7.45 | −0.41 | 5.32 | 23.10 | |||||||||
| Aboveground | D3.1438 | 0.996 | 11.75 | −0.12 | 8.16 | 10.66 | |||||||||
| Total | D2.8621 | 0.995 | 15.45 | 0.27 | 10.85 | 10.56 | |||||||||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Widagdo, F.R.A.; Li, F.; Zhang, L.; Dong, L. Aggregated Biomass Model Systems and Carbon Concentration Variations for Tree Carbon Quantification of Natural Mongolian Oak in Northeast China. Forests 2020, 11, 397. https://doi.org/10.3390/f11040397
Widagdo FRA, Li F, Zhang L, Dong L. Aggregated Biomass Model Systems and Carbon Concentration Variations for Tree Carbon Quantification of Natural Mongolian Oak in Northeast China. Forests. 2020; 11(4):397. https://doi.org/10.3390/f11040397
Chicago/Turabian StyleWidagdo, Faris Rafi Almay, Fengri Li, Lianjun Zhang, and Lihu Dong. 2020. "Aggregated Biomass Model Systems and Carbon Concentration Variations for Tree Carbon Quantification of Natural Mongolian Oak in Northeast China" Forests 11, no. 4: 397. https://doi.org/10.3390/f11040397
APA StyleWidagdo, F. R. A., Li, F., Zhang, L., & Dong, L. (2020). Aggregated Biomass Model Systems and Carbon Concentration Variations for Tree Carbon Quantification of Natural Mongolian Oak in Northeast China. Forests, 11(4), 397. https://doi.org/10.3390/f11040397







