Wind Loading on Scaled Down Fractal Tree Models of Major Urban Tree Species in Singapore
Abstract
:1. Introduction
2. Materials and Methods
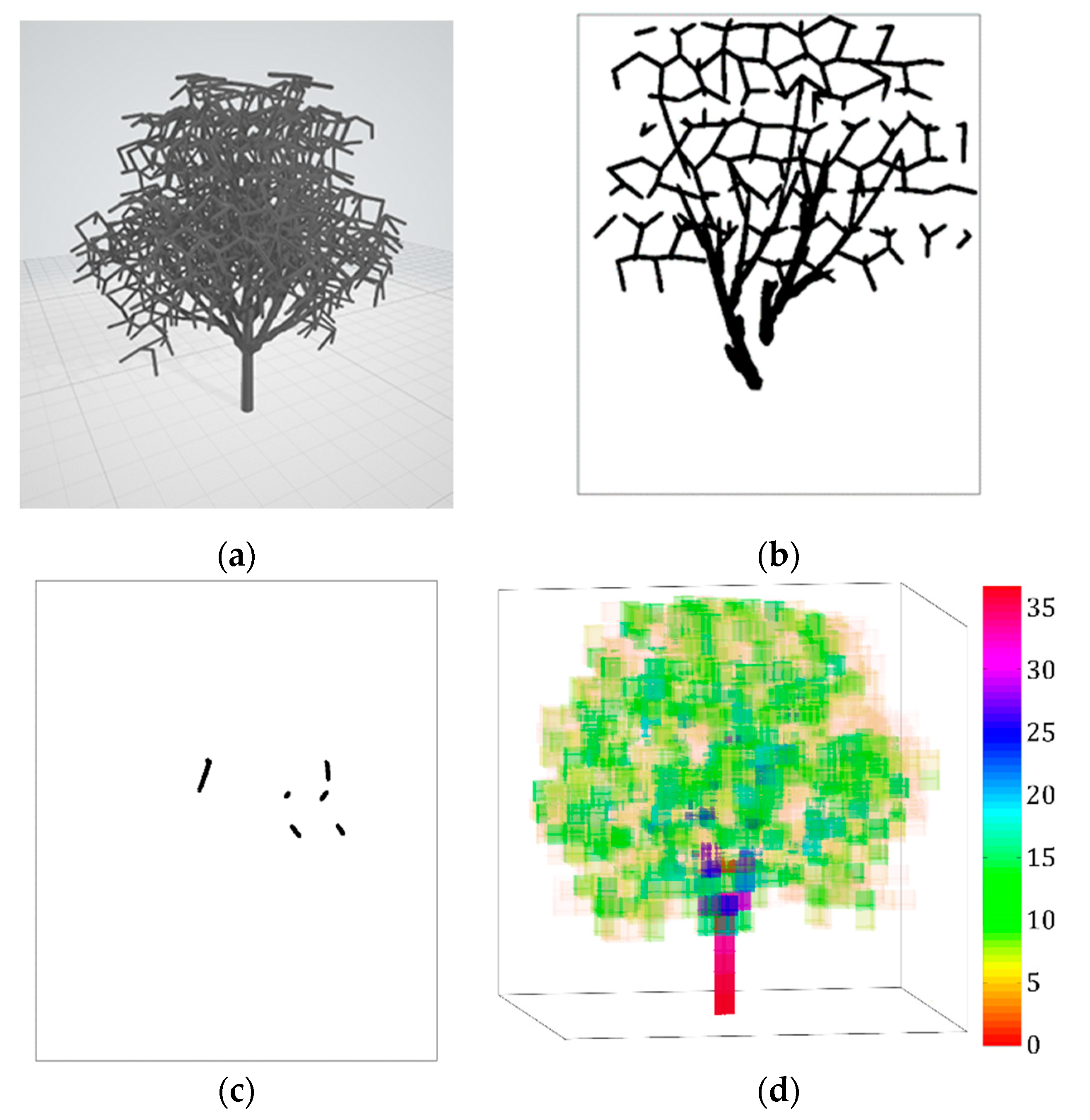
2.1. Tree Models
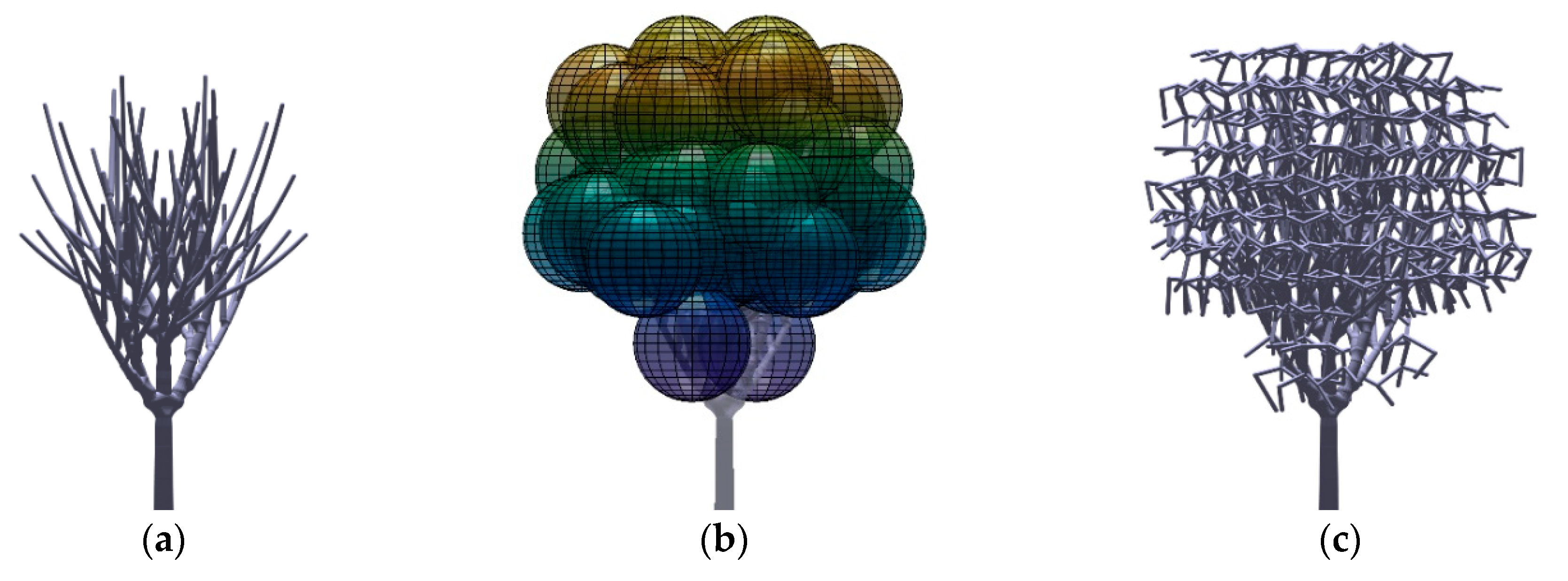
2.1.1. Development of the Fractal Tree Models
2.1.2. Development of the Tree Crown Models
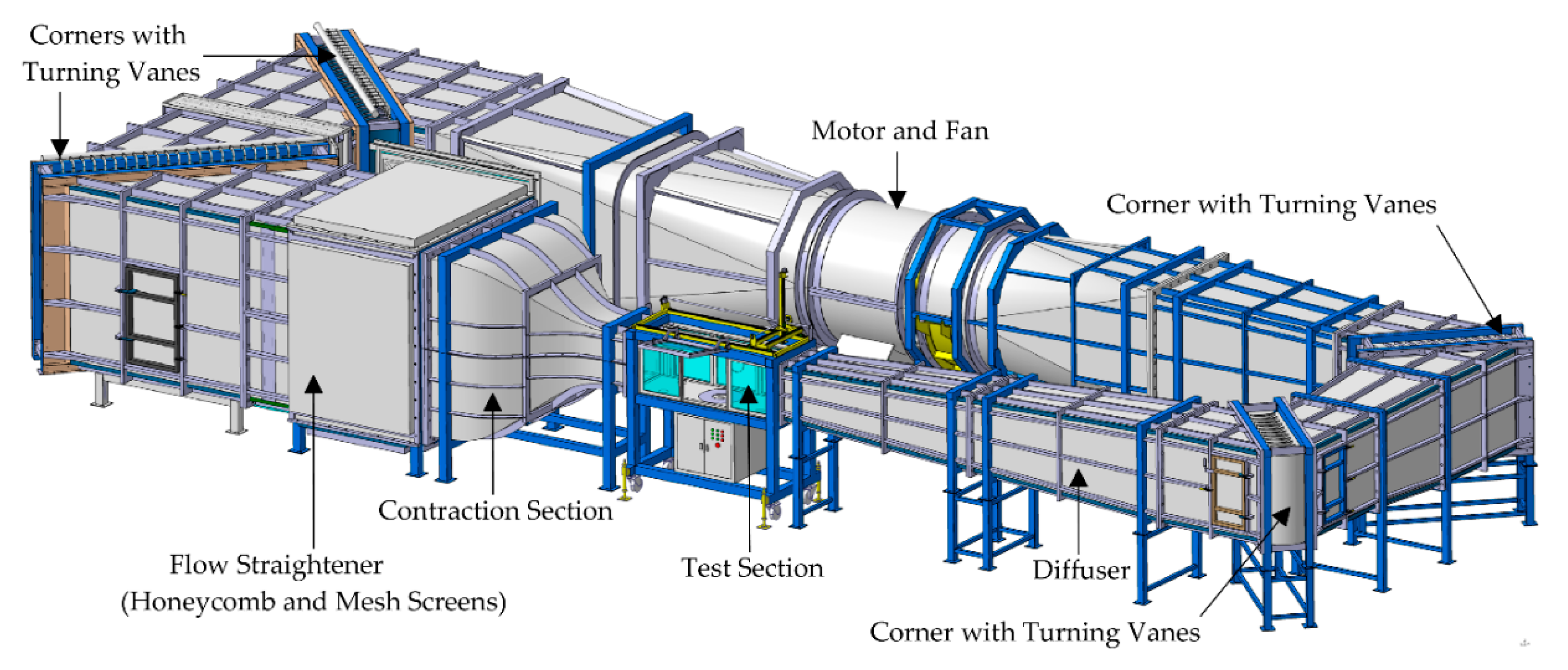
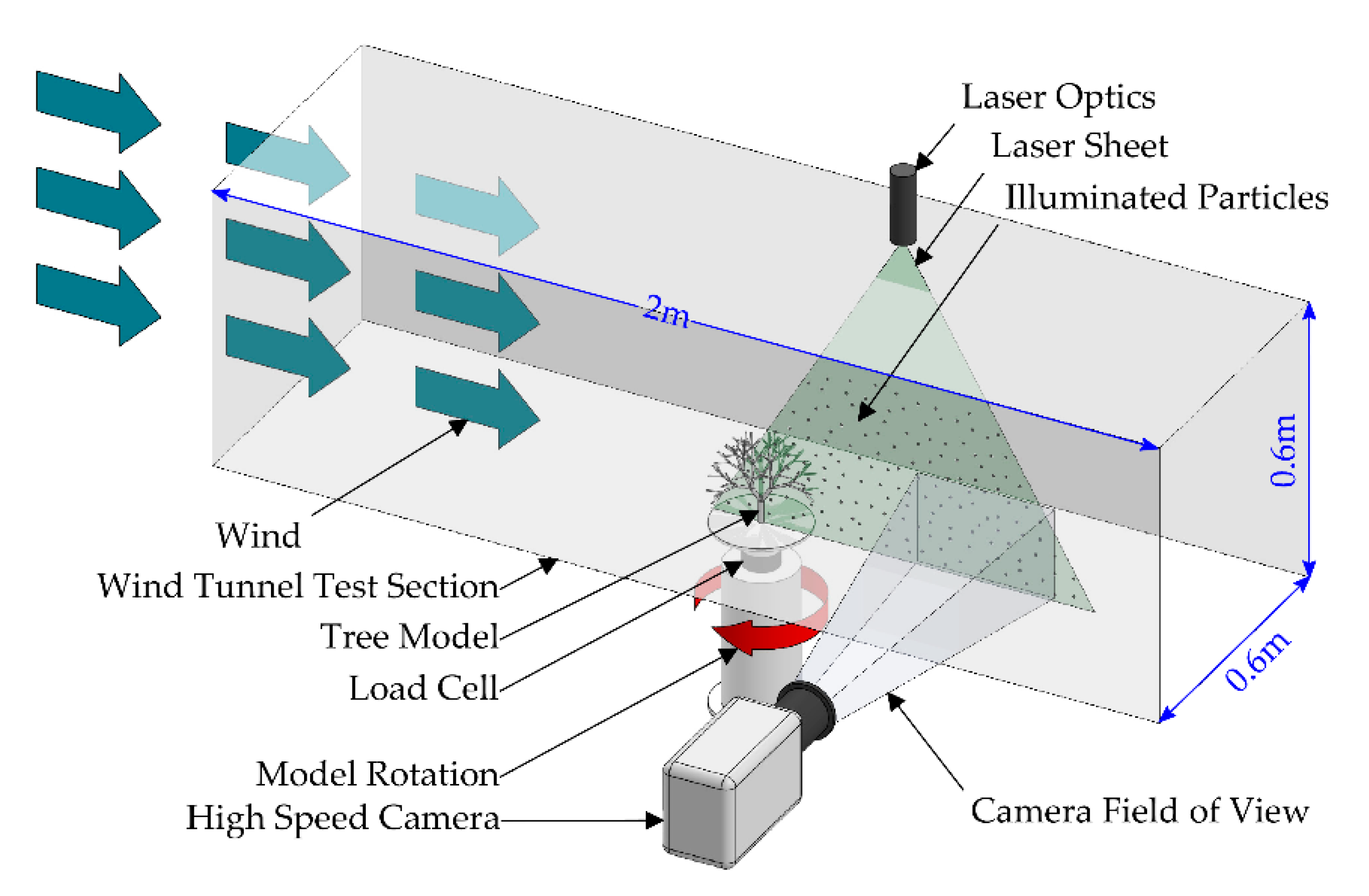
2.2. Wind Tunnel Tests
2.2.1. Wake Profile Measurement
2.2.2. Bulk Drag Measurement
- = Reference area;
- = Bulk drag coefficient;
- = Bulk drag measurement in wind tunnel;
- = Reference wind speed;
- = Air density.
2.3. Numerical Simulations
2.3.1. Solver and Numerical Models
- = Frontal silhouette area density, frontal silhouette area divided by tree crown volume;
- = Momentum sink;
- = Drag coefficient;
- = Velocity magnitude = (using the Einstein summation convention);
- = Velocity component.
2.3.2. Grid and Boundary Conditions
2.3.3. Tree Modelling
- = Total frontal optical silhouette area;
- = Frontal optical silhouette area;
- = Local drag coefficient;
- = Drag force measurement in wind tunnel;
- = Total number of discretized elements;
- = Volume of element.
3. Results and Discussion
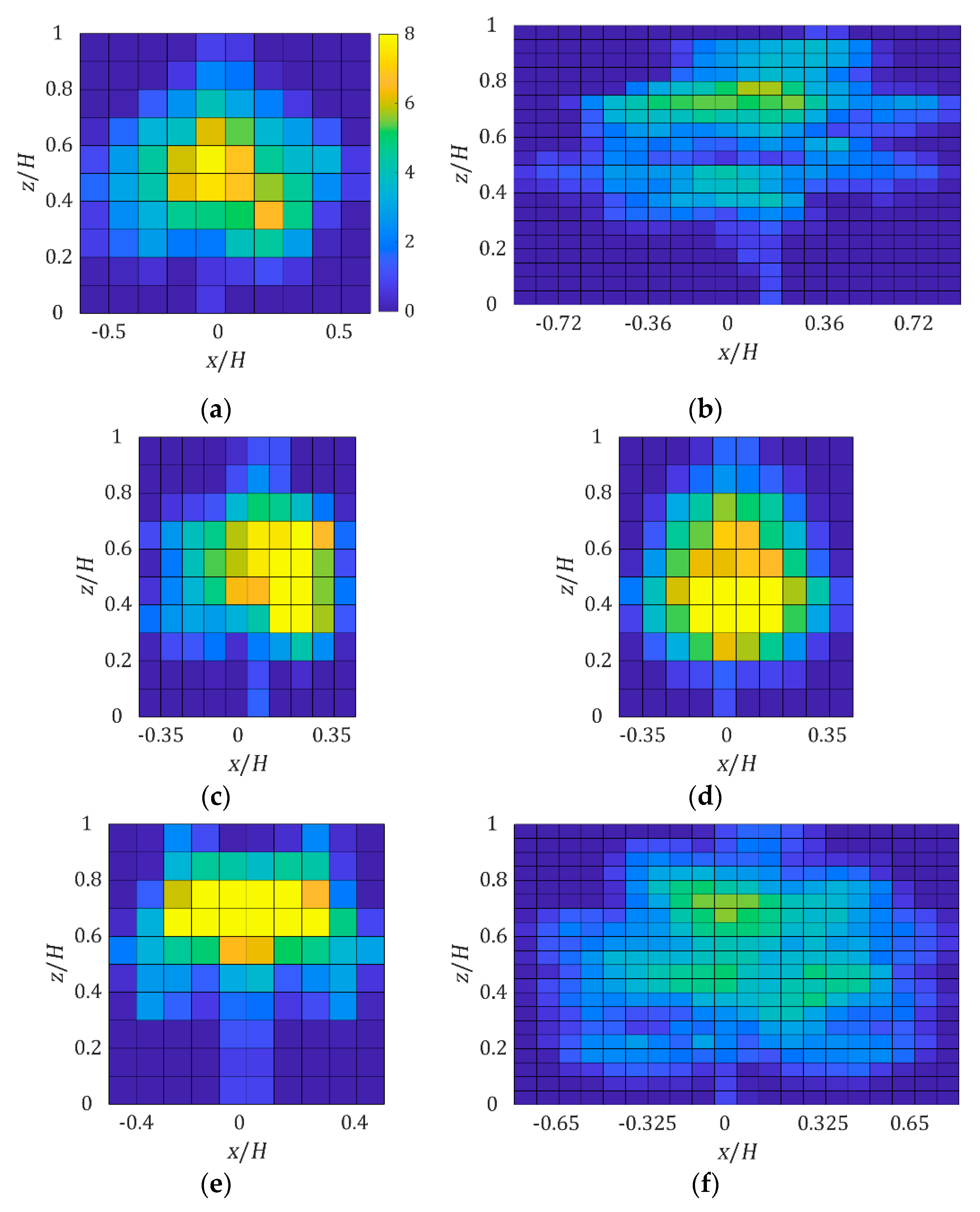
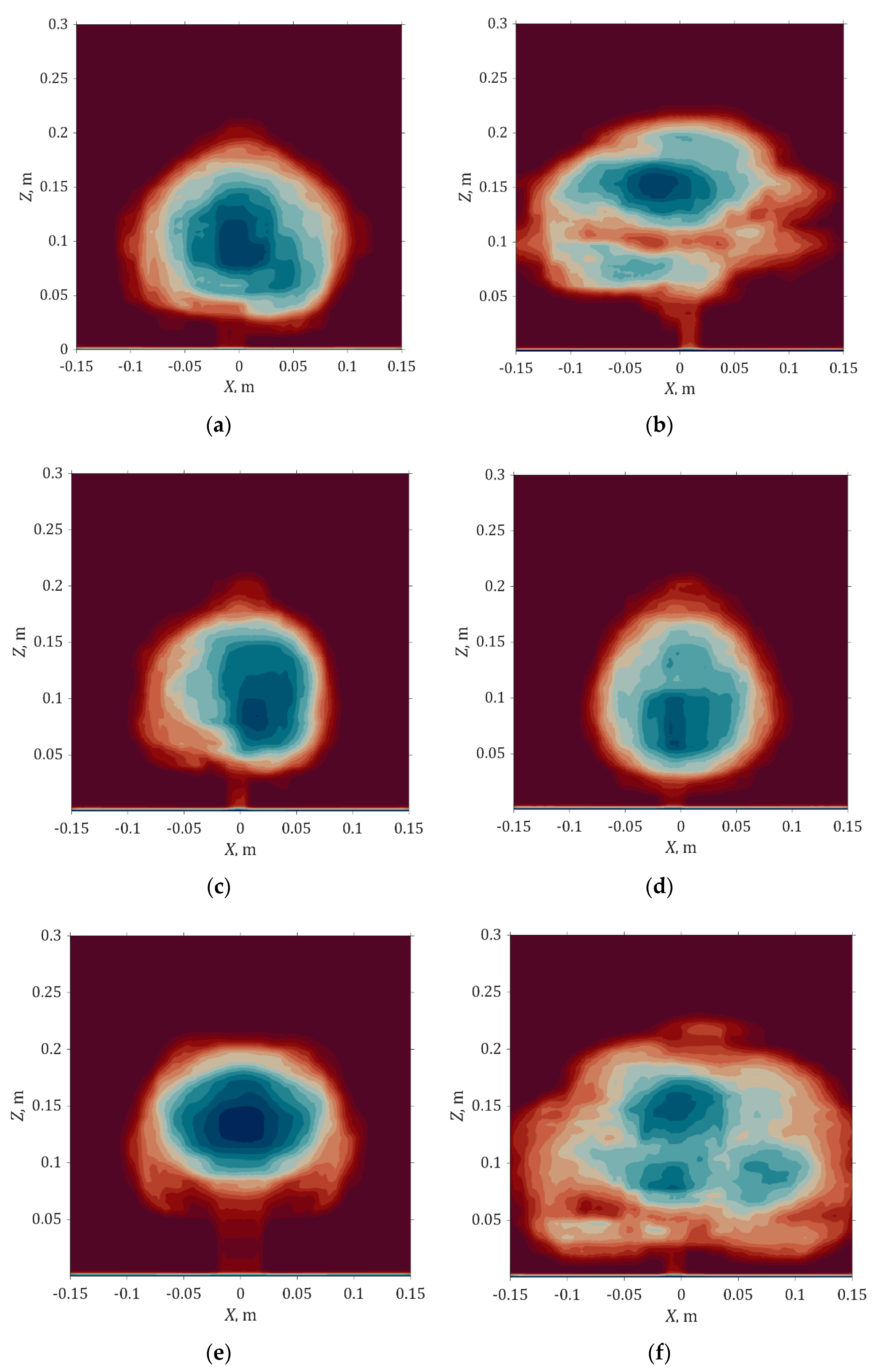
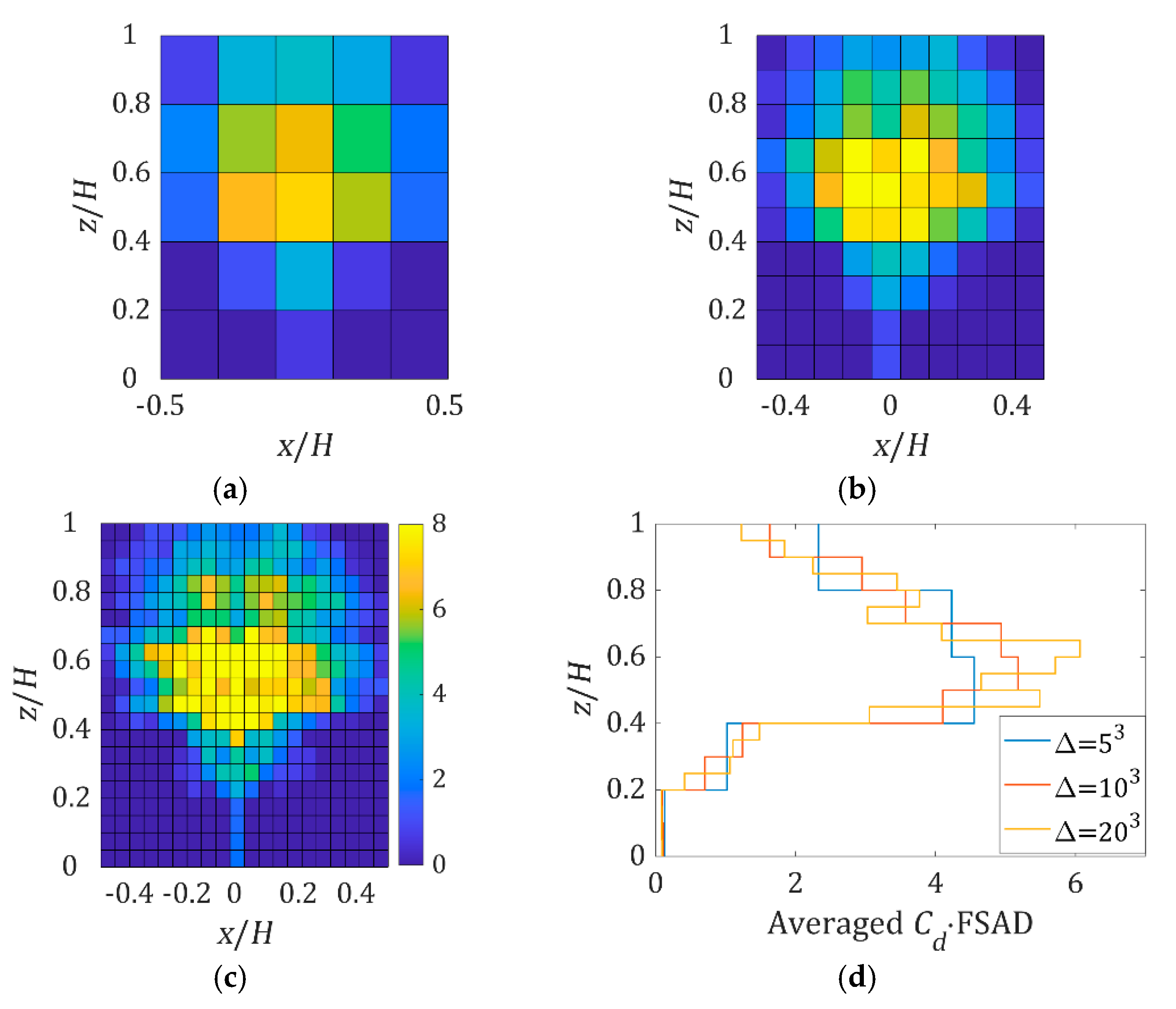
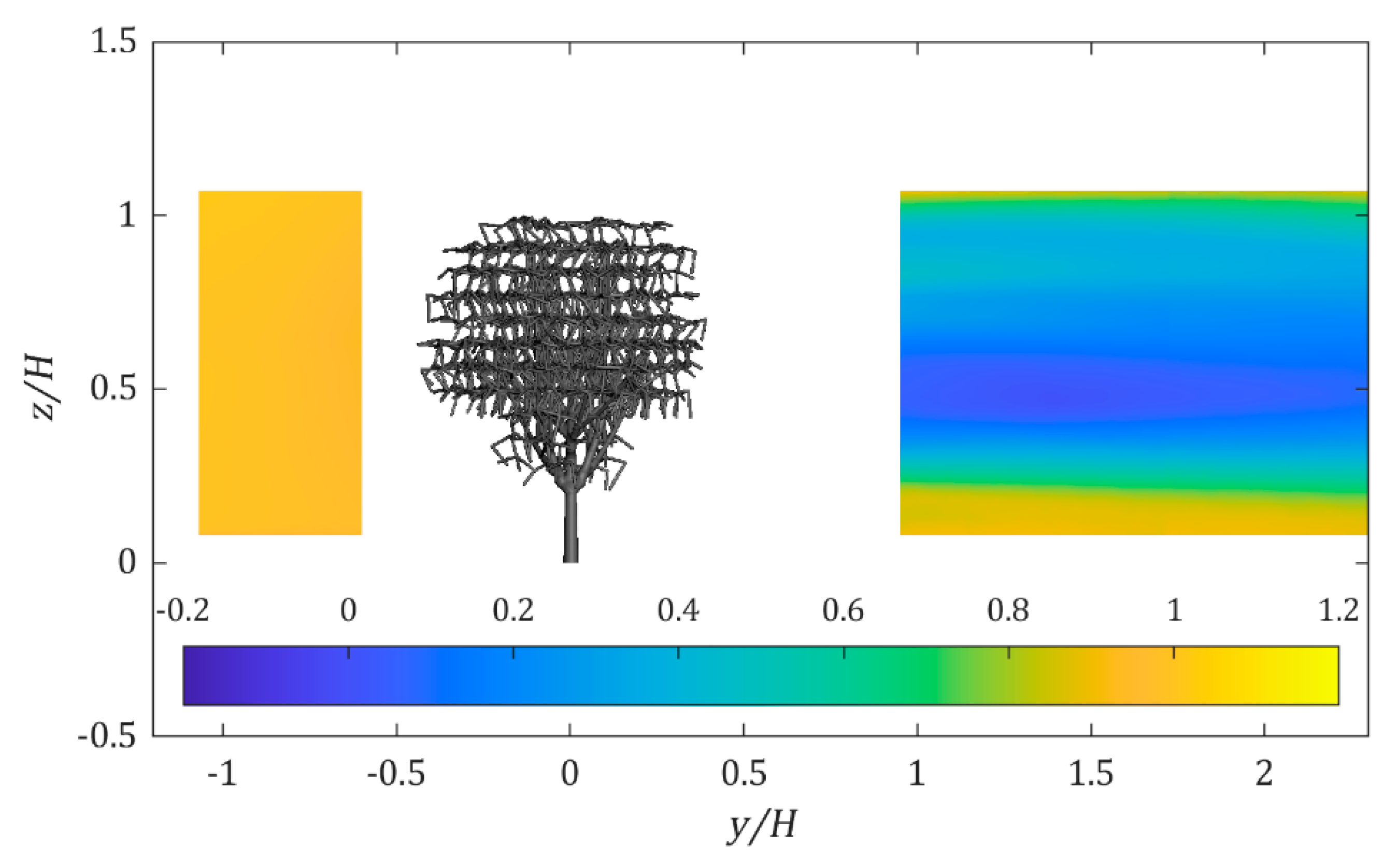
3.1. Velocity Profile
3.2. Drag Force
3.3. Bulk Drag Coefficients
- = Aerodynamic porosity;
- = Frontal optical porosity.
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
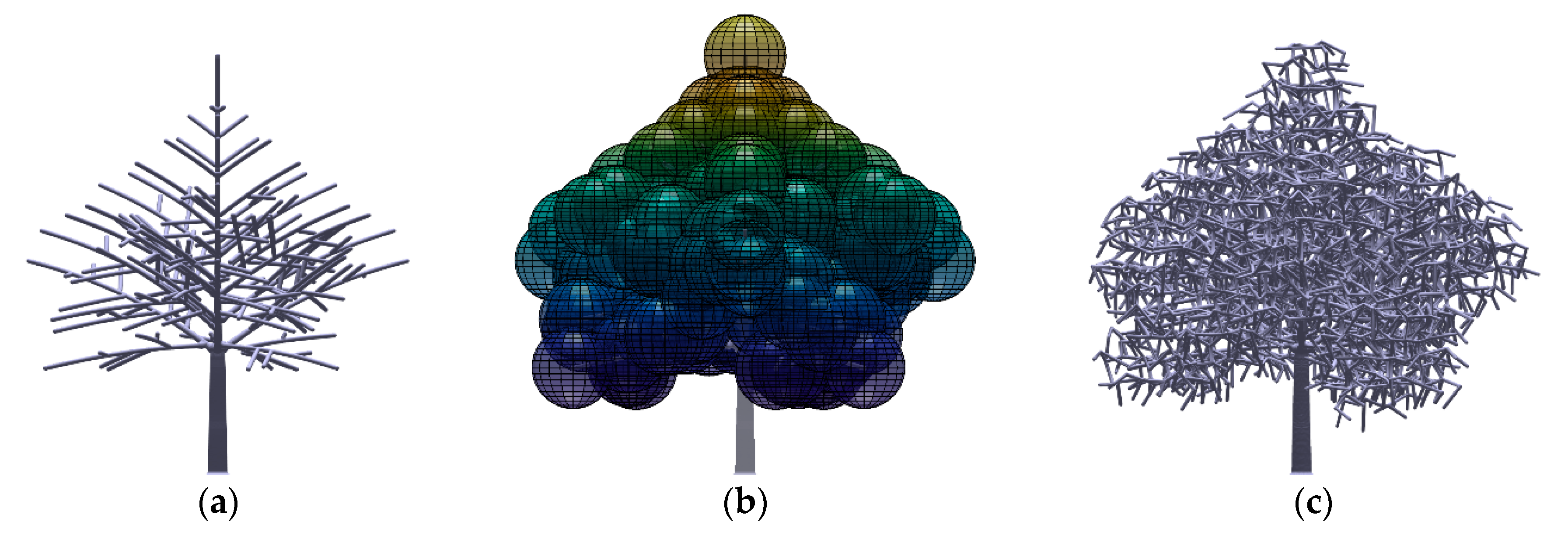
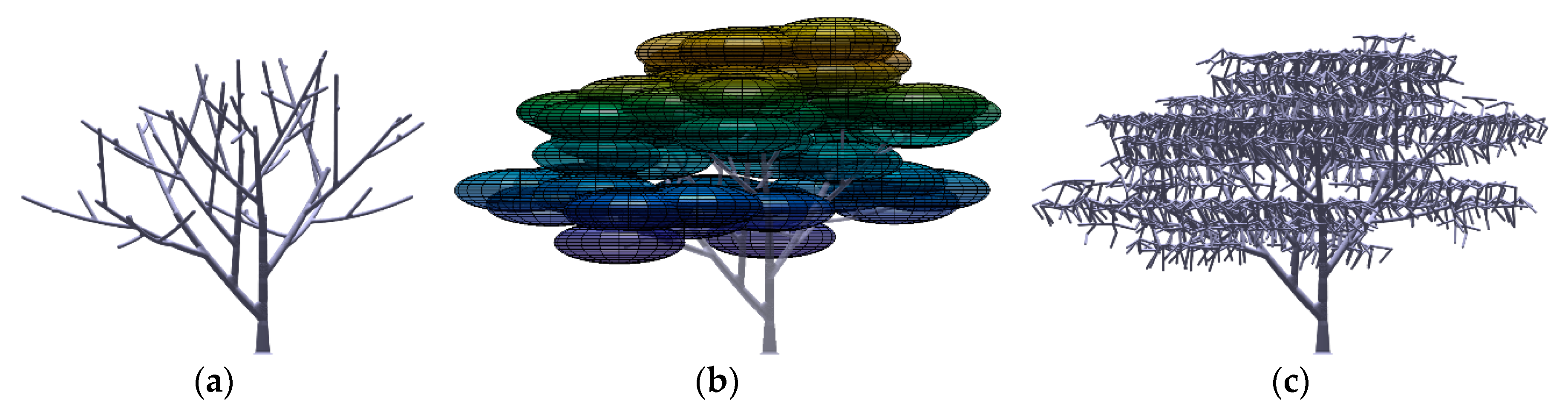

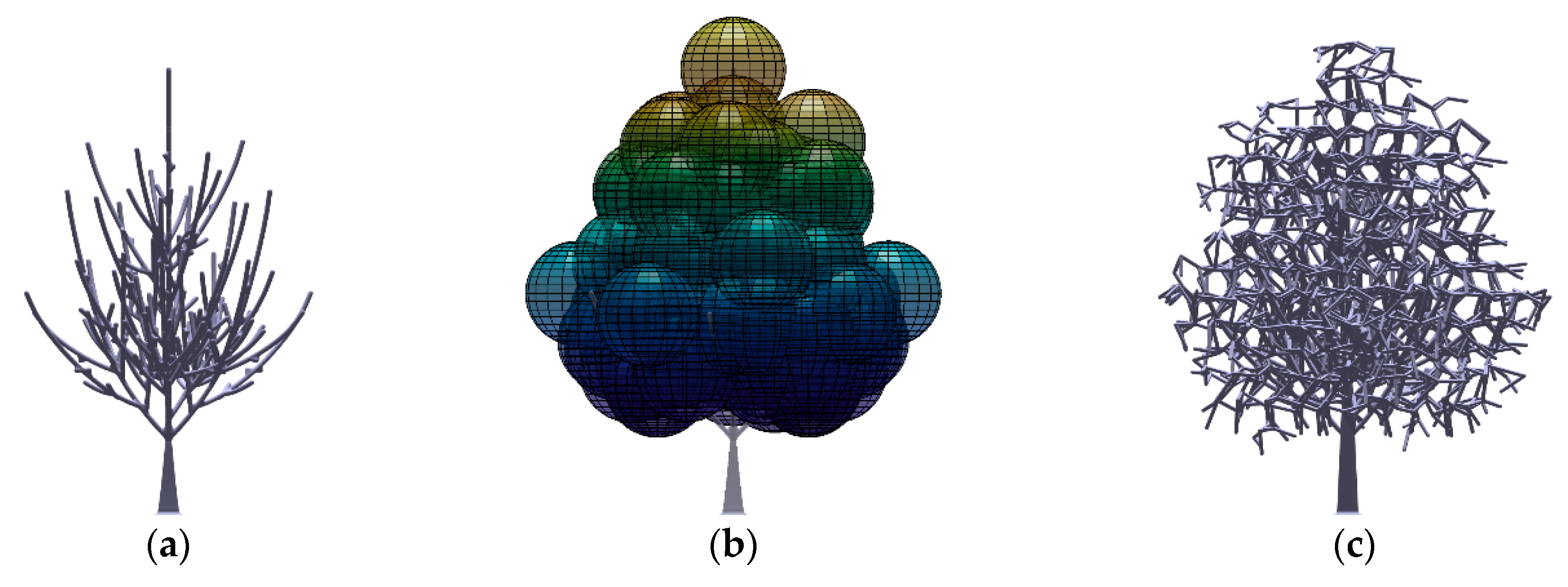
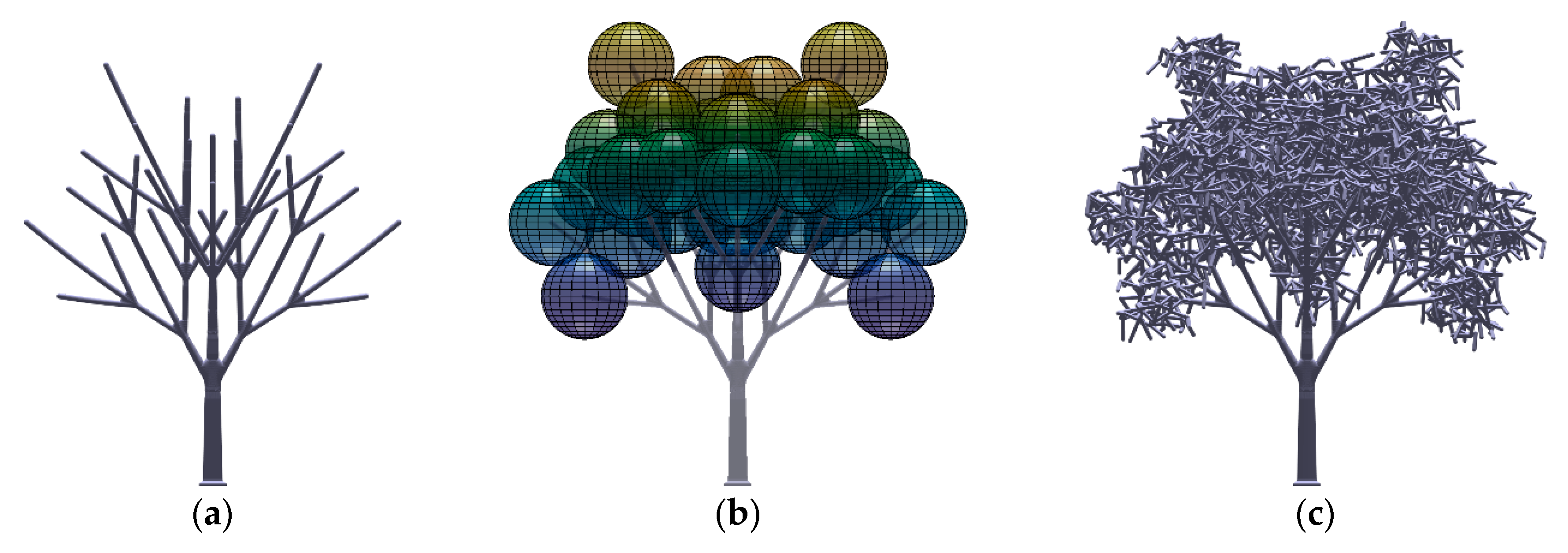

Appendix B
Appendix C
References
- Thom, A.S. Momentum absorption by vegetation. Q. J. R. Meteorol. Soc. 1971, 97, 414–428. [Google Scholar] [CrossRef]
- Wilson, N.R.; Shaw, R.H. A higher order closure model for canopy flow. J. Appl. Meteorol. 1977, 16, 1197–1205. [Google Scholar] [CrossRef] [Green Version]
- Wilson, J.D. Numerical studies of flow through a windbreak. J. Wind. Eng. Ind. Aerodyn. 1985, 21, 119–154. [Google Scholar] [CrossRef]
- Li, Z.; Lin, J.D.; Miller, D.R. Air flow over and through a forest edge: A steady-state numerical simulation. Bound.-Layer Meteorol. 1990, 51, 179–197. [Google Scholar] [CrossRef]
- Brunet, Y.; Finnigan, J.J.; Raupach, M.R. A wind tunnel study of air flow in waving wheat: Single-point velocity statistics. Bound.-Layer Meteorol. 1994, 70, 95–132. [Google Scholar] [CrossRef]
- Liu, J.; Chen, J.M.; Black, T.A.; Novak, M.D. E-modelling of turbulent air flow downwind of a model forest edge. Bound.-Layer Meteorol. 1996, 77, 21–44. [Google Scholar] [CrossRef]
- Ayotte, K.W.; Finnigan, J.J.; Raupach, M.R. A second-order closure for neutrally stratified vegetative canopy flows. Bound.-Layer Meteorol. 1999, 90, 189–216. [Google Scholar] [CrossRef]
- Pinard, J.D.J.P.; Wilson, J.D. First- and second-order closure models for wind in a plant canopy. J. Appl. Meteorol. 2001, 40, 1762–1768. [Google Scholar] [CrossRef]
- Sanz, C. A note on k-modelling of vegetation canopy air-flows. Bound.-Layer Meteorol. 2003, 108, 191–197. [Google Scholar] [CrossRef]
- Endalew, A.M.; Hertog, M.; Gebrehiwot, M.G.; Baelmans, M.; Ramon, H.; Nicolaï, B.; Verboven, P. Modelling airflow within model plant canopies using an integrated approach. Comput. Elec tron. Agric. 2009, 66, 9–24. [Google Scholar] [CrossRef]
- Dellwik, E.; Laan, M.V.D.; Angelou, N.; Mann, J.; Sogachev, A. Observed and modeled near-wake flow behind a solitary tree. Agric. For. Meteorol. 2019, 265, 78–87. [Google Scholar] [CrossRef]
- Poh, H.J.; Chan, W.L.; Wise, D.J.; Lim, C.W.; Khoo, B.C.; Gobeawan, L.; Ge, Z.; Eng, Y.; Peng, J.X.; Raghavan, V.S.G.; et al. Wind load prediction on single tree with integrated approach of L-system fractal model, wind tunnel and tree aerodynamic simulation. AIP Adv. 2020, 10, 075202. [Google Scholar] [CrossRef]
- Kanda, M.; Hino, M. Organized structures in developing turbulent flow within and above a plant canopy, using a Large Eddy Simulation. Bound.-Layer Meteorol. 1994, 68, 237–257. [Google Scholar] [CrossRef]
- Shaw, R.H.; Schumann, U. Large-eddy simulation of turbulent flow above and within a forest. Bound. Layer Meteorol. 1992, 61, 47–64. [Google Scholar] [CrossRef] [Green Version]
- Vasaturo, R.; Kalkman, I.; Blocken, B.; Wesemael, P.V. Large eddy simulation of the neutral atmospheric boundary layer: Performance evaluation of three inflow methods for terrains with different roughness. J. Wind. Eng. Ind. Aerodyn. 2018, 173, 241–261. [Google Scholar] [CrossRef]
- Li, Q.; Wang, Z.H. Large-eddy simulation of the impact of urban trees on momentum and heat fluxes. Agric. For. Meteorol. 2018, 255, 44–56. [Google Scholar] [CrossRef]
- Mayhead, G. Some drag coefficients for British forest trees derived from wind tunnel studies. Agric. Meteorol. 1973, 12, 123–130. [Google Scholar] [CrossRef]
- Rudnicki, M.; Mitchell, S.J.; Novak, M.D. Wind tunnel measurements of crown streamlining and drag relationships for three conifer species. Can. J. For. Res. 2004, 34, 666–676. [Google Scholar] [CrossRef]
- Vollsinger, S.; Mitchell, S.J.; Byrne, K.E.; Novak, M.D.; Rudnicki, M. Wind tunnel measurements of crown streamlining and drag relationships for several hardwood species. Can. J. For. Res. 2005, 35, 1238–1249. [Google Scholar] [CrossRef]
- Gromke, C.; Ruck, B. Aerodynamic modelling of trees for small-scale wind tunnel studies. Forestry 2008, 81, 243–258. [Google Scholar] [CrossRef] [Green Version]
- Cao, J.; Tamura, Y.; Yoshida, A. Wind tunnel study on aerodynamic characteristics of shrubby specimens of three tree species. Urban. For. Urban. Green. 2012, 11, 465–476. [Google Scholar] [CrossRef]
- Manickathan, L.; Defraeye, T.; Allegrini, J.; Derome, D.; Carmeliet, J. Comparative study of flow field and drag coefficient of model and small natural trees in a wind tunnel. Urban. For. Urban. Green. 2018, 35, 230–239. [Google Scholar] [CrossRef]
- Bai, K.; Meneveau, C.; Katz, J. Experimental study of spectral energy fluxes in turbulence generated by a fractal, tree-like object. Phys. Fluids 2013, 25, 110810. [Google Scholar] [CrossRef]
- Bai, K.; Katz, J.; Meneveau, C. Turbulent flow structure inside a canopy with complex multi-scale elements. Bound.-Layer Meteorol. 2015, 155, 435–457. [Google Scholar] [CrossRef]
- Chan, W.L.; Cui, Y.; Jadhav, S.S.; Khoo, B.C.; Lee, H.P.; Lim, C.W.C.; Gobeawan, L.; Wise, D.J.; Ge, Z.; Poh, H.J.; et al. Experimental study of wind load on tree using scaled fractal tree model. Int. J. Mod. Phys. B 2020, 2040087. [Google Scholar] [CrossRef]
- Lindenmayer, A. Mathematical models for cellular interactions in development I. Filaments with one-sided inputs. J. Theor. Biol. 1968, 18, 280–299. [Google Scholar] [CrossRef]
- Prusinkiewicz, P.; Lindenmayer, A. The Algorithmic Beauty of Plants, 1st ed.; Springer: Berlin/Heidelberg, Germany, 1990. [Google Scholar] [CrossRef] [Green Version]
- Gobeawan, L.; Wise, D.; Alex Thiam Koon, Y.; Wong, S.; Lim, C.; Lin, E.; Su, Y. Convenient tree species modeling for virtual cities. In Lecture Notes in Computer Science; Gavrilova, M., Chang, J., Thalmann, N., Hitzer, E., Ishikawa, H., Eds.; Springer: Cham, Switzerland, 2019; Volume 11542, pp. 304–315. [Google Scholar] [CrossRef]
- Nobis, M.; Hunziker, U. Automatic thresholding for hemispherical canopy-photographs based on edge detection. Agric. For. Meteorol. 2005, 128, 243–250. [Google Scholar] [CrossRef]
- Korhonen, L.; Heikkinen, J. Automated analysis of in situ canopy images for the estimation of forest canopy cover. For. Sci. 2009, 55, 323–334. [Google Scholar] [CrossRef]
- DaVis. Software for Intelligent Imaging. 2016. Available online: https://www.lavision.de/en/download.php?id=3 (accessed on 12 July 2020).
- Weller, H.G.; Tabor, G.; Jasak, H.; Fureby, C. A tensorial approach to computational continuum mechanics using object-oriented techniques. Comput. Phys. 1998, 12, 620. [Google Scholar] [CrossRef]
- Nicoud, F.; Ducros, F. Subgrid-scale stress modelling based on the square of the velocity gradient tensor. Flow Turbul. Combust. 1999, 62, 183–200. [Google Scholar] [CrossRef]
- Selle, L. Compressible large eddy simulation of turbulent combustion in complex geometry on unstructured meshes. Combust. Flame 2004, 137, 489–505. [Google Scholar] [CrossRef]
- Roux, S.; Lartigue, G.; Poinsot, T.; Meier, U.; Bérat, C. Studies of mean and unsteady flow in a swirled combustor using experiments, acoustic analysis, and large eddy simulations. Combust. Flame 2005, 141, 40–54. [Google Scholar] [CrossRef] [Green Version]
- Menter, F.R.; Egorov, Y. The scale-adaptive simulation method for unsteady turbulent flow predictions. Part 1: Theory and model description. Flow Turbul. Combust. 2010, 85, 113–138. [Google Scholar] [CrossRef]
- Li, Y.; Rahardjo, H.; Irvine, K.N.; Law, A.W.K. CFD analyses of the wind drags on Khaya Senegalensis and Eugenia Grandis. Urban. For. Urban. Green. 2018, 34, 29–43. [Google Scholar] [CrossRef]
- Hagen, L.J.; Skidmore, E.L. Windbreak drag as influenced by porosity. Trans. ASAE 1971, 14, 464–465. [Google Scholar] [CrossRef]
- Guan, D.; Zhang, Y.; Zhu, T. A wind-tunnel study of windbreak drag. Agric. For. Meteorol. 2003, 118, 75–84. [Google Scholar] [CrossRef]
- Dong, Z.; Luo, W.; Qian, G.; Wang, H. A wind tunnel simulation of the mean velocity fields behind upright porous fences. Agric. For. Meteorol. 2007, 146, 82–93. [Google Scholar] [CrossRef]
- Dong, Z.; Luo, W.; Qian, G.; Lu, P.; Wang, H. A wind tunnel simulation of the turbulence fields behind upright porous wind fences. J. Arid. Environ. 2010, 74, 193–207. [Google Scholar] [CrossRef]
- Schindler, D.; Schönborn, J.; Fugmann, H.; Mayer, H. Responses of an individual deciduous broadleaved tree to wind excitation. Agric. For. Meteorol. 2013, 177, 69–82. [Google Scholar] [CrossRef]



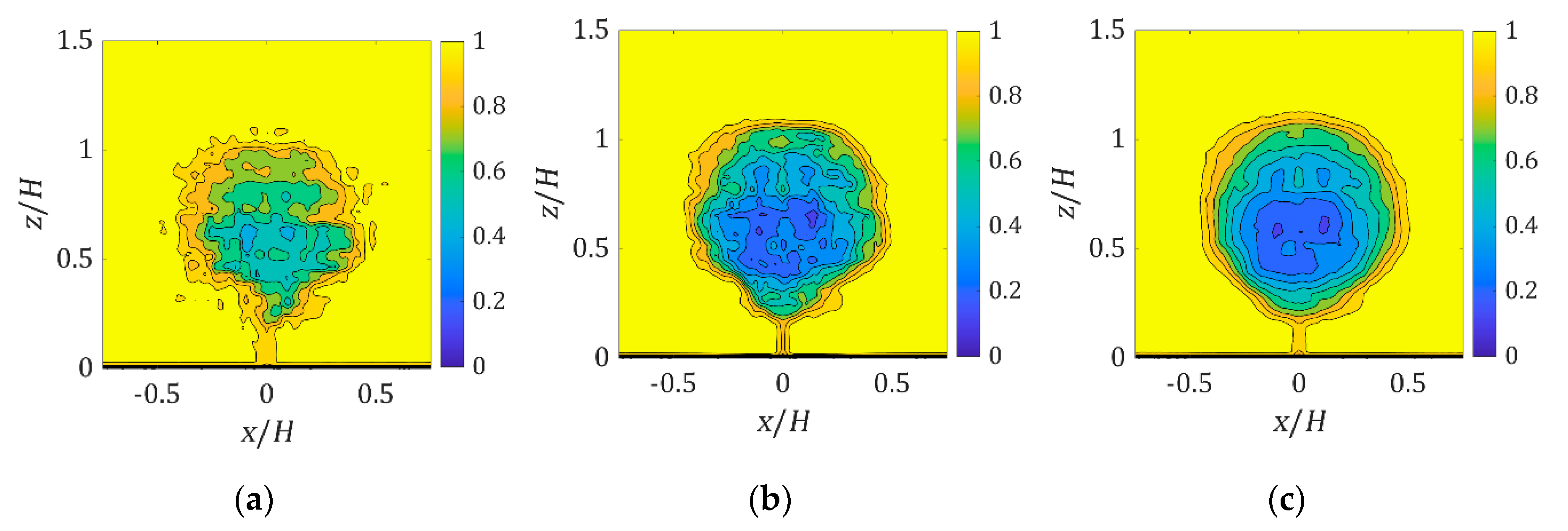

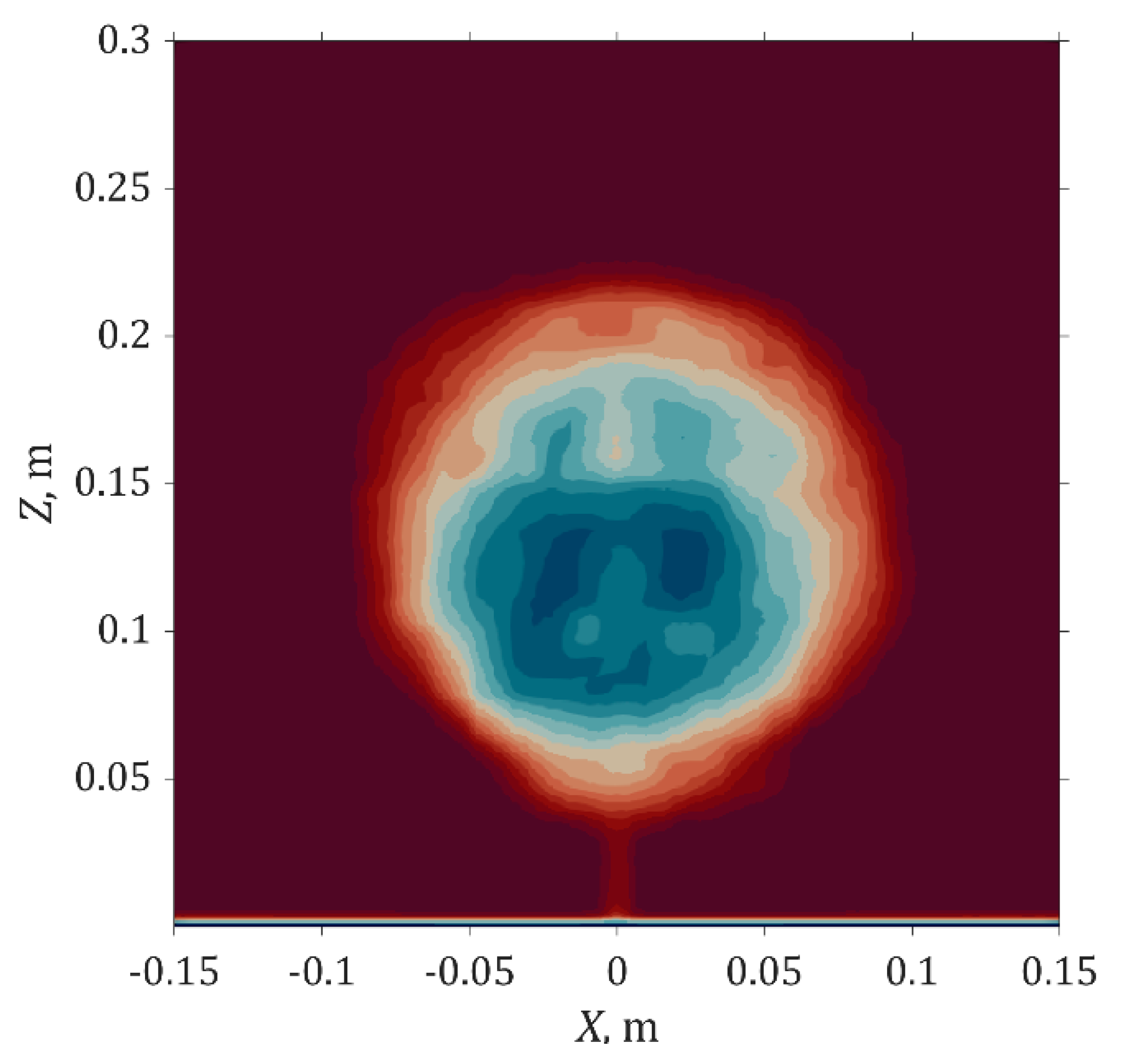

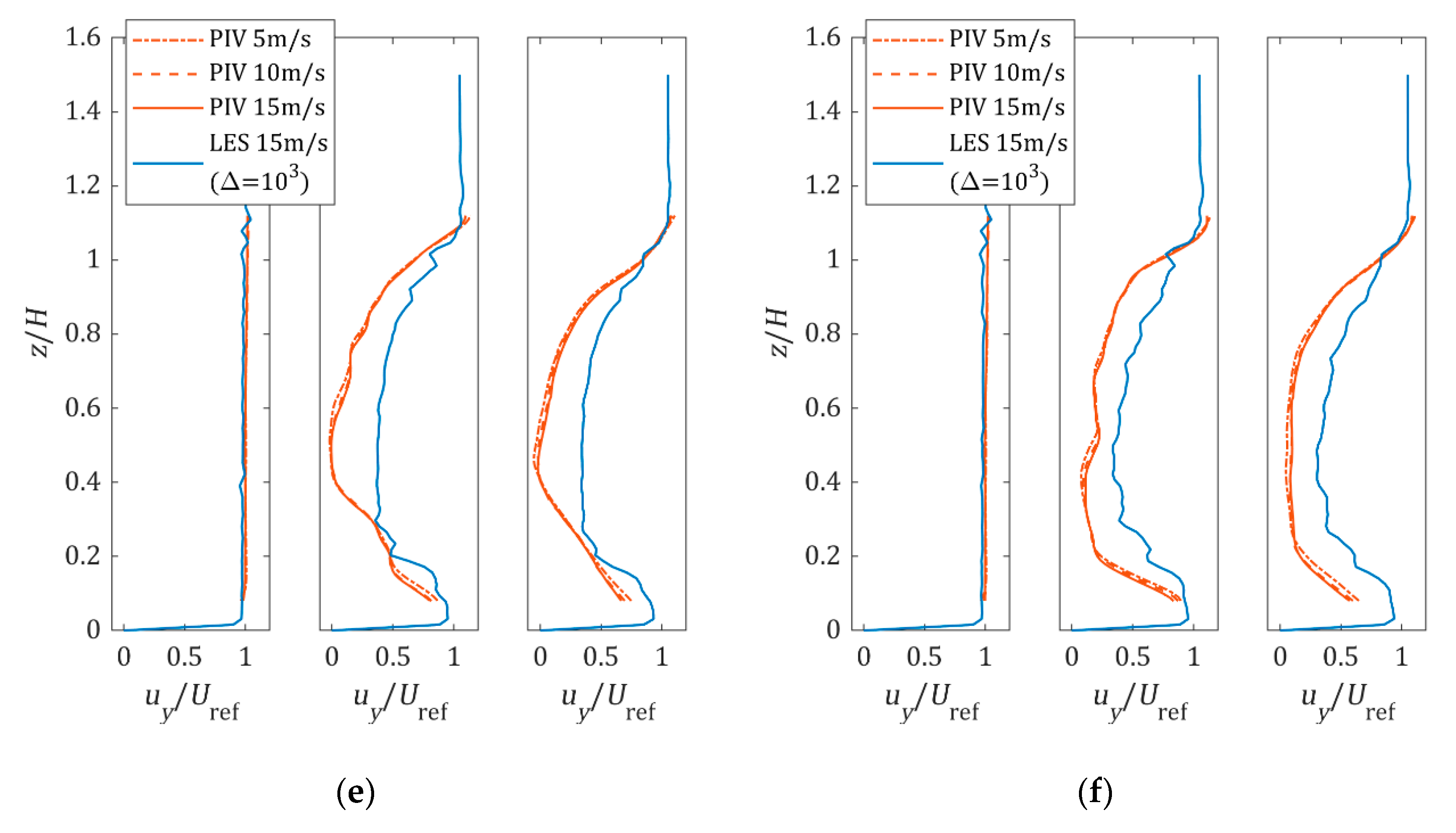
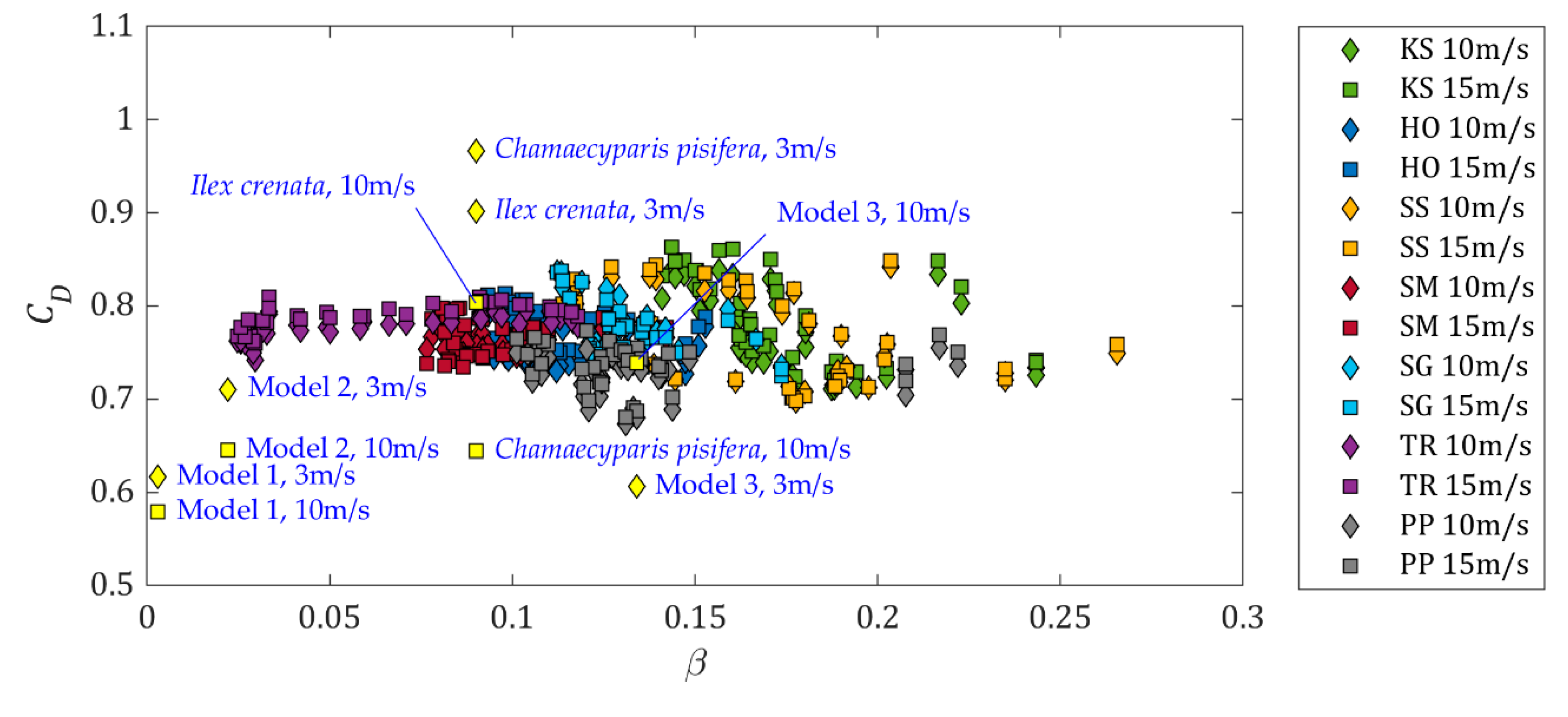

| Tree Species | Sample Size | Optical Porosity | |
|---|---|---|---|
| Average | Standard Deviation | ||
| K. senegalensis | 5 | 0.1237 | 0.0711 |
| H. odorata | 5 | 0.1005 | 0.0732 |
| S. saman | 7 | 0.1864 | 0.0743 |
| S. macrophylla | 11 | 0.1424 | 0.0506 |
| S. grande | 7 | 0.1157 | 0.0573 |
| T. rosea | 12 | 0.1172 | 0.0421 |
| P. pterocarpum | 7 | 0.1583 | 0.0499 |
| K. senegalensis at 0° Rotation | ||||
|---|---|---|---|---|
| Experiment | Simulations | |||
| Δ = 53 | Δ = 103 | Δ = 203 | ||
| Drag, N | 2.040 ± 0.016 | 1.90 | 2.00 | 2.02 |
| Difference, % | −6.75 | −2.03 | −0.86 | |
| Tree Species | Rotation Angle, ° | Drag, N | Difference, % | |
|---|---|---|---|---|
| Experiment | Simulations | |||
| K. senegalensis | 0 | 2.040 ± 0.016 | 2.00 | −2.03 |
| 45 | 2.022 ± 0.007 | 2.11 | 4.18 | |
| 90 | 1.896 ± 0.007 | 2.00 | 5.41 | |
| H. odorata | 0 | 2.402 ± 0.011 | 2.35 | −2.00 |
| 45 | 2.286 ± 0.016 | 2.28 | −0.08 | |
| 90 | 2.262 ± 0.013 | 2.27 | 0.23 | |
| S. saman1 | 0 | 3.116 ± 0.039 | 3.13 | 0.34 |
| 45 | 3.080 ± 0.041 | 3.27 | 6.01 | |
| 90 | 2.745 ± 0.012 | 2.88 | 4.96 | |
| S. macrophylla | 0 | 1.842 ± 0.025 | 1.87 | 1.43 |
| 45 | 1.700 ± 0.011 | 1.79 | 5.17 | |
| 90 | 1.526 ± 0.009 | 1.54 | 1.12 | |
| S. grande | 0 | 1.749 ± 0.016 | 1.72 | −1.56 |
| 45 | 1.608 ± 0.013 | 1.64 | 1.77 | |
| 90 | 1.658 ± 0.014 | 1.72 | 3.94 | |
| T. rosea | 0 | 1.969 ± 0.012 | 1.92 | −2.49 |
| 45 | 1.584 ± 0.017 | 1.57 | −1.14 | |
| 90 | 1.056 ± 0.007 | 1.04 | −1.14 | |
| P. pterocarpum1 | 0 | 4.288 ± 0.022 | 4.65 | 8.33 |
| 45 | 3.814 ± 0.044 | 4.09 | 7.20 | |
| 90 | 3.355 ± 0.016 | 3.74 | 3.93 | |
| Tree Species | Wind Speed, m/s | Tree Species | Wind Speed, m/s | ||
|---|---|---|---|---|---|
| Populus trichocarpa1 | 5 | 0.780 | Thuja plicata2 | 5 | 0.886 |
| 10 | 0.642 | 10 | 0.696 | ||
| 15 | 0.574 | 15 | 0.596 | ||
| Populus tremuloides1 | 5 | 0.817 | Hibiscus syriacus3 | 5 | 0.607 |
| 10 | 0.688 | 10 | 0.531 | ||
| 15 | 0.647 | 15 | 0.491 | ||
| Alnus rubra1 | 5 | 0.738 | Thuja occidentalis3 | 5 | 0.856 |
| 10 | 0.595 | 10 | 0.791 | ||
| 15 | 0.551 | 15 | 0.753 | ||
| Betula papyrifera1 | 5 | 0.765 | Ilex crenata3 | 5 | 0.807 |
| 10 | 0.660 | 10 | 0.780 | ||
| 15 | 0.640 | 15 | 0.765 | ||
| Acer macrophyllum1 | 5 | 0.813 | S. grande4 | 1 | 1.521 |
| 10 | 0.635 | 2 | 0.509 | ||
| 15 | 0.599 | 3 | 0.319 | ||
| Tsuga heterophylla2 | 5 | 1.117 | K. senegalensis4 | 1 | 1.565 |
| 10 | 1.030 | 2 | 0.506 | ||
| 15 | 0.941 | 3 | 0.390 | ||
| Pinus contorta2 | 5 | 1.037 | |||
| 10 | 0.940 | ||||
| 15 | 0.836 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chan, W.-L.; Eng, Y.; Ge, Z.; Lim, C.W.C.; Gobeawan, L.; Poh, H.J.; Wise, D.J.; Burcham, D.C.; Lee, D.; Cui, Y.; et al. Wind Loading on Scaled Down Fractal Tree Models of Major Urban Tree Species in Singapore. Forests 2020, 11, 803. https://doi.org/10.3390/f11080803
Chan W-L, Eng Y, Ge Z, Lim CWC, Gobeawan L, Poh HJ, Wise DJ, Burcham DC, Lee D, Cui Y, et al. Wind Loading on Scaled Down Fractal Tree Models of Major Urban Tree Species in Singapore. Forests. 2020; 11(8):803. https://doi.org/10.3390/f11080803
Chicago/Turabian StyleChan, Woei-Leong, Yong Eng, Zhengwei Ge, Chi Wan Calvin Lim, Like Gobeawan, Hee Joo Poh, Daniel Joseph Wise, Daniel C. Burcham, Daryl Lee, Yongdong Cui, and et al. 2020. "Wind Loading on Scaled Down Fractal Tree Models of Major Urban Tree Species in Singapore" Forests 11, no. 8: 803. https://doi.org/10.3390/f11080803
APA StyleChan, W.-L., Eng, Y., Ge, Z., Lim, C. W. C., Gobeawan, L., Poh, H. J., Wise, D. J., Burcham, D. C., Lee, D., Cui, Y., & Khoo, B. C. (2020). Wind Loading on Scaled Down Fractal Tree Models of Major Urban Tree Species in Singapore. Forests, 11(8), 803. https://doi.org/10.3390/f11080803






