Direct Versus Indirect Tree Ring Reconstruction of Annual Discharge of Chemora River, Algeria
Abstract
1. Introduction
2. Study Basin
3. Materials and Methods
3.1. Hydrologic, Climatic, and Tree Ring Data
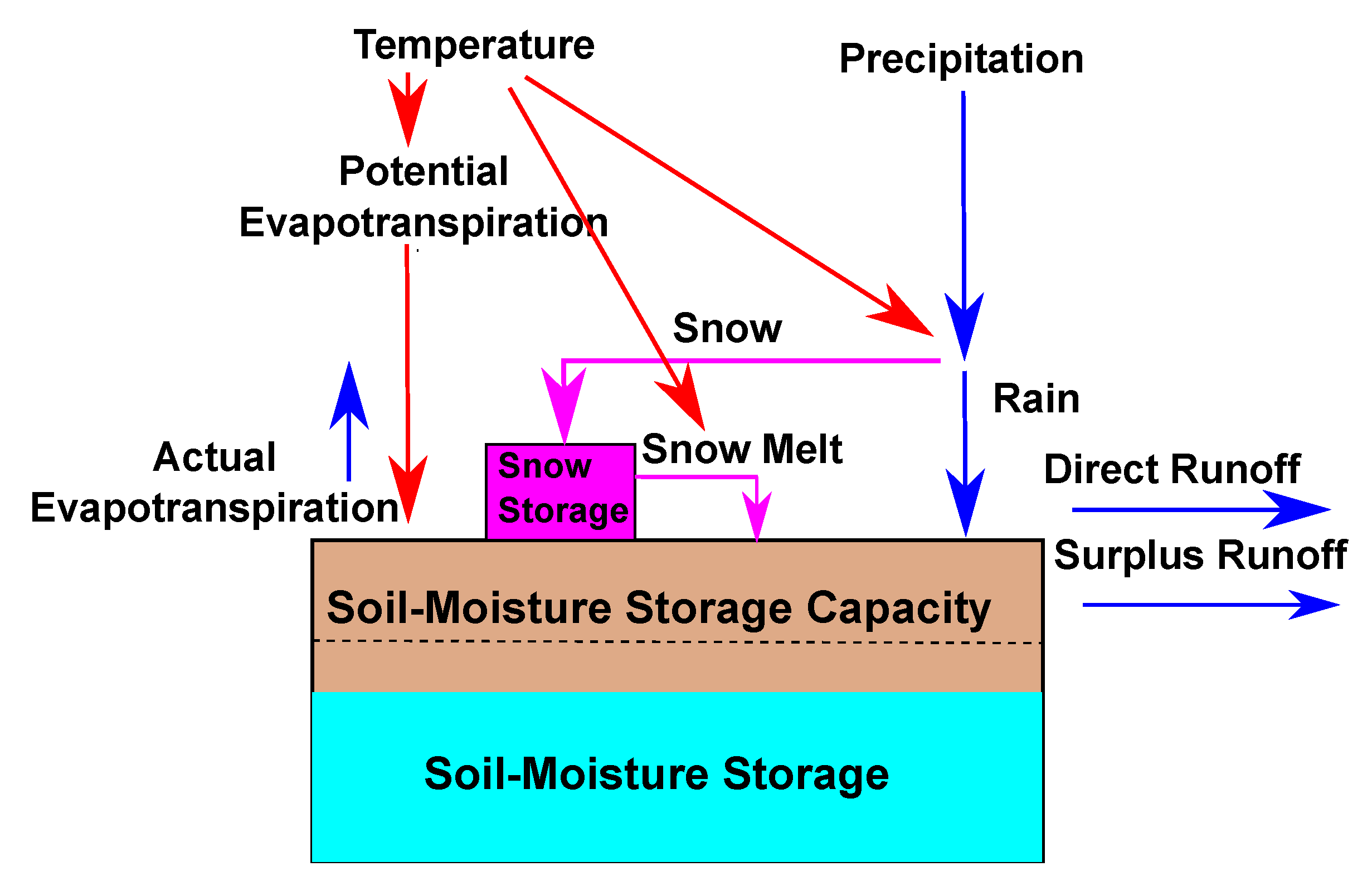
3.2. Water-Balance Model
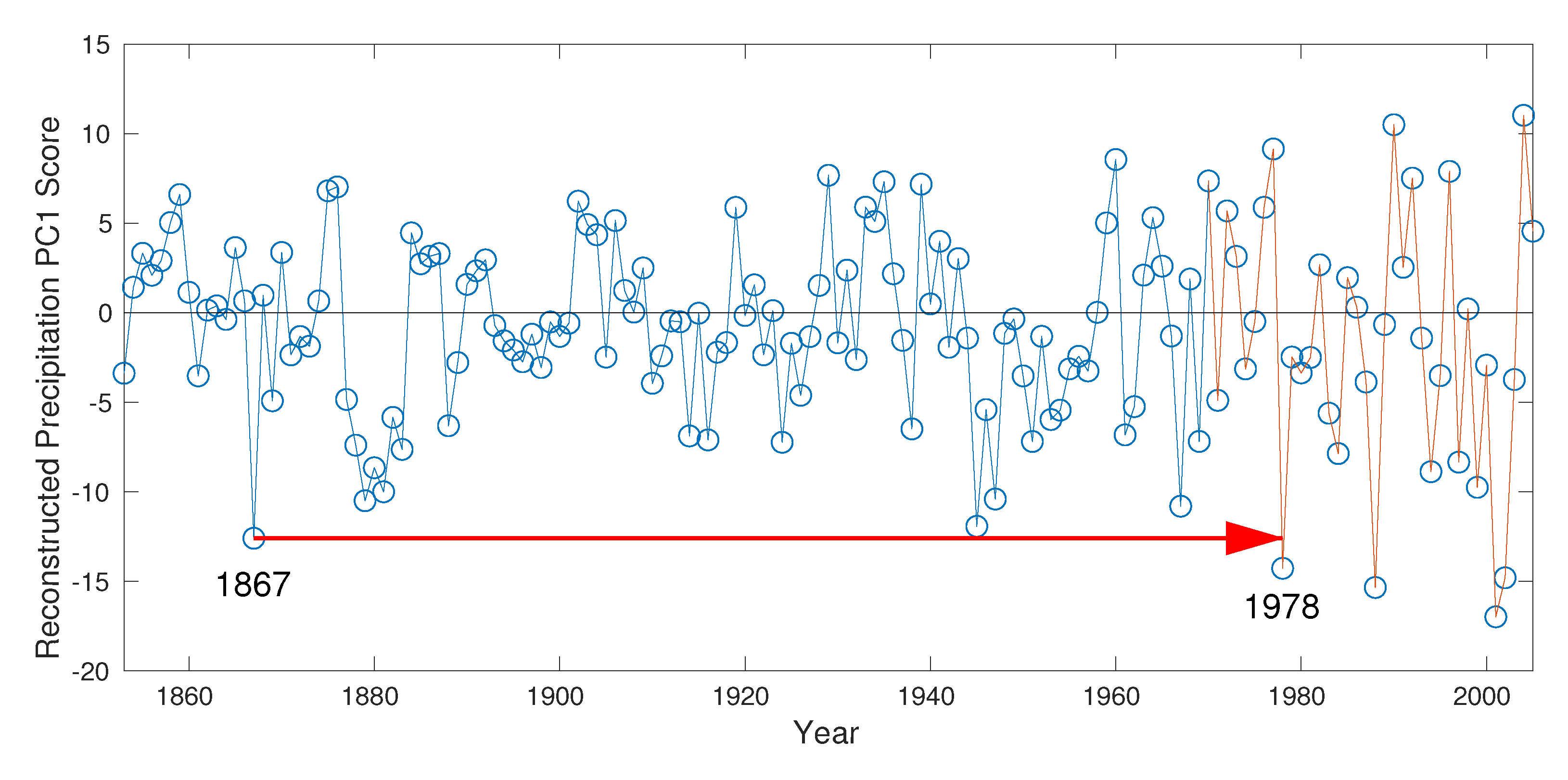
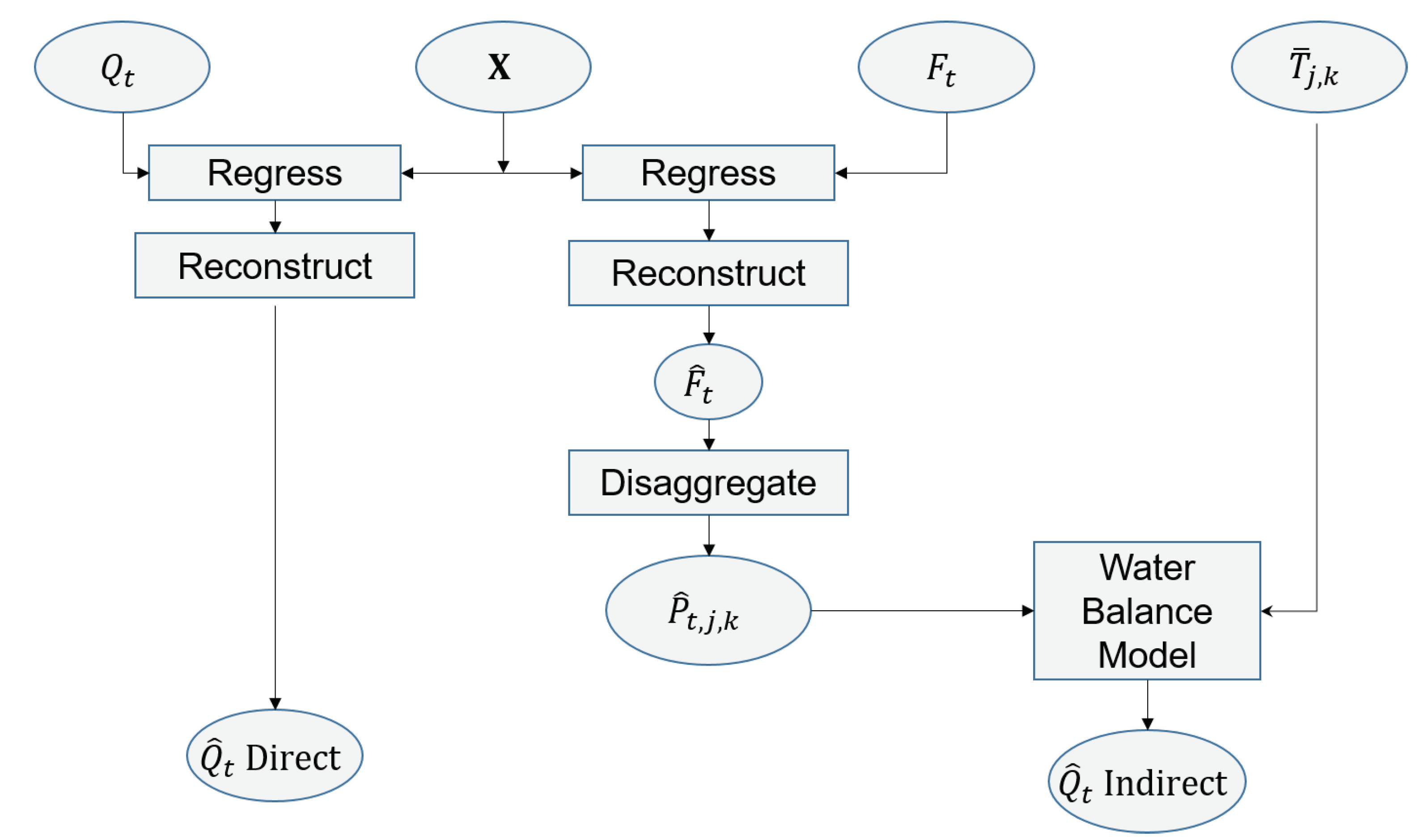
3.3. Reconstruction
3.3.1. Indirect Reconstruction
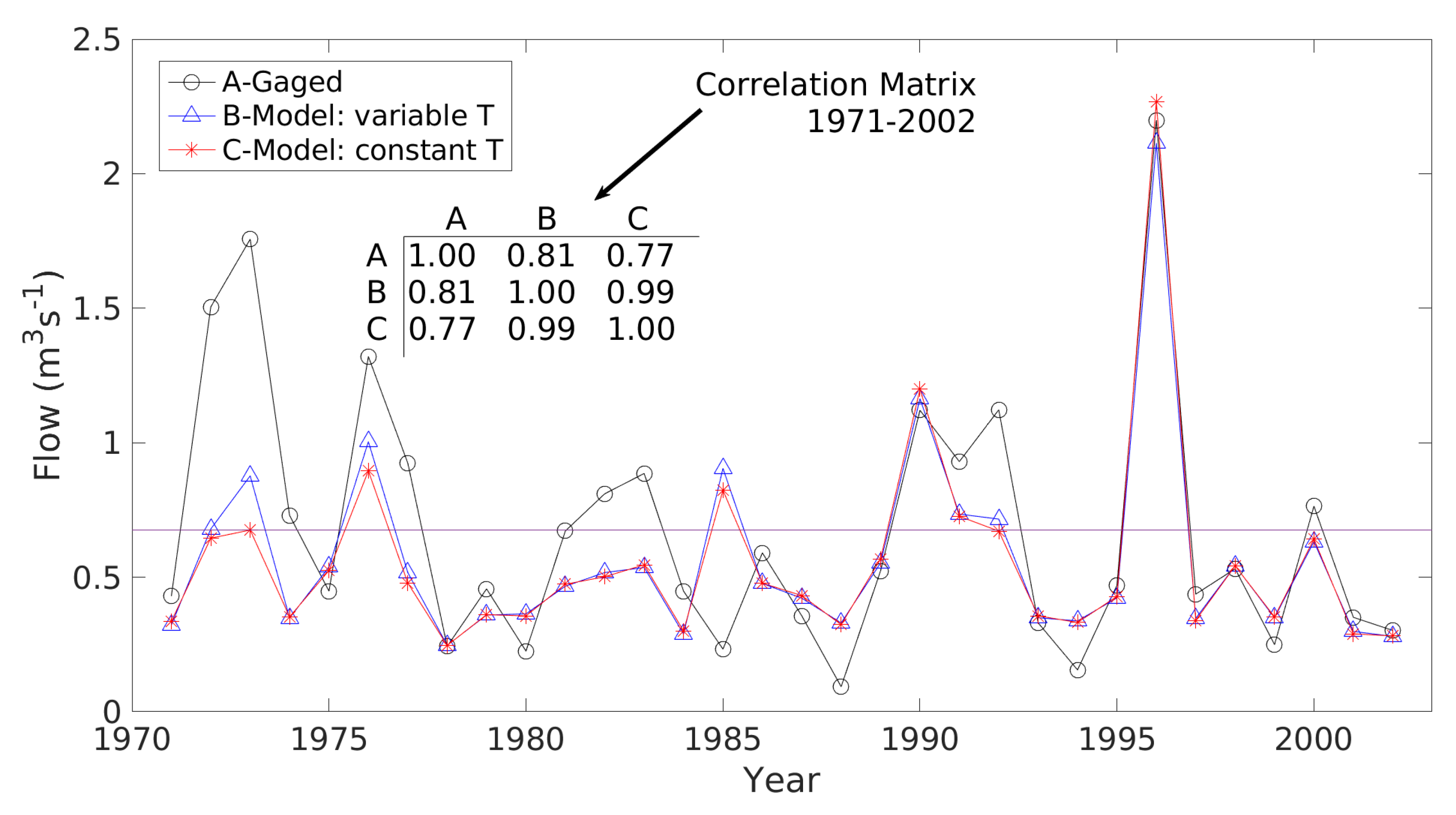
3.4. Model Comparisons
4. Results and Discussion
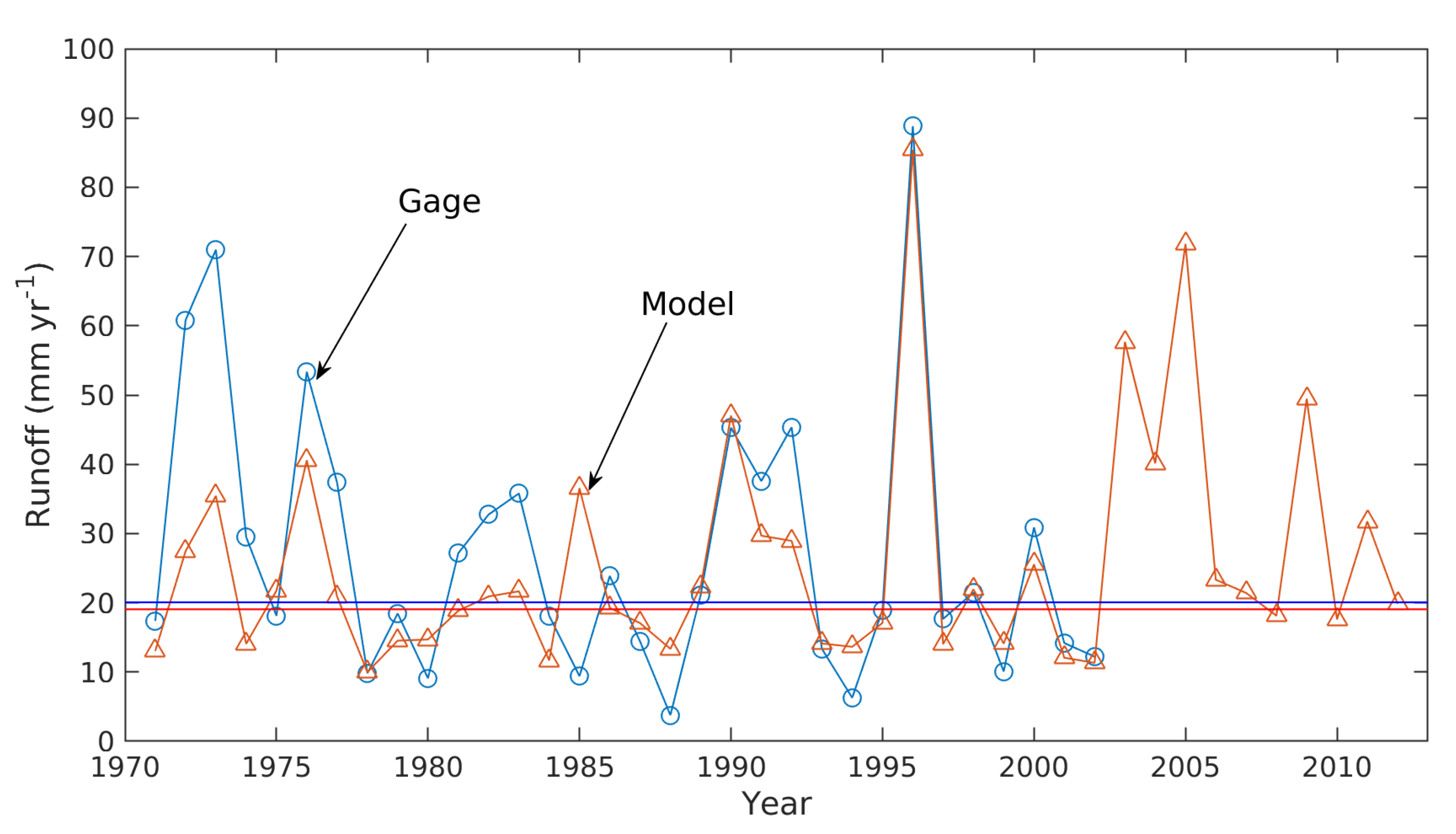
4.1. Water-Balance Modeling
- “Snowfall is extremely variable and irregular from one year to another such that high mountain tops are quite often free of snow during almost all of the winter season—as in the winter of 1989–1990, which did not record any days of snow. Quézel [46] reported that the snow season starts by the end of November and continues, depending on the year, until March or April, whenever polar and tropical masses meet during cold periods.”
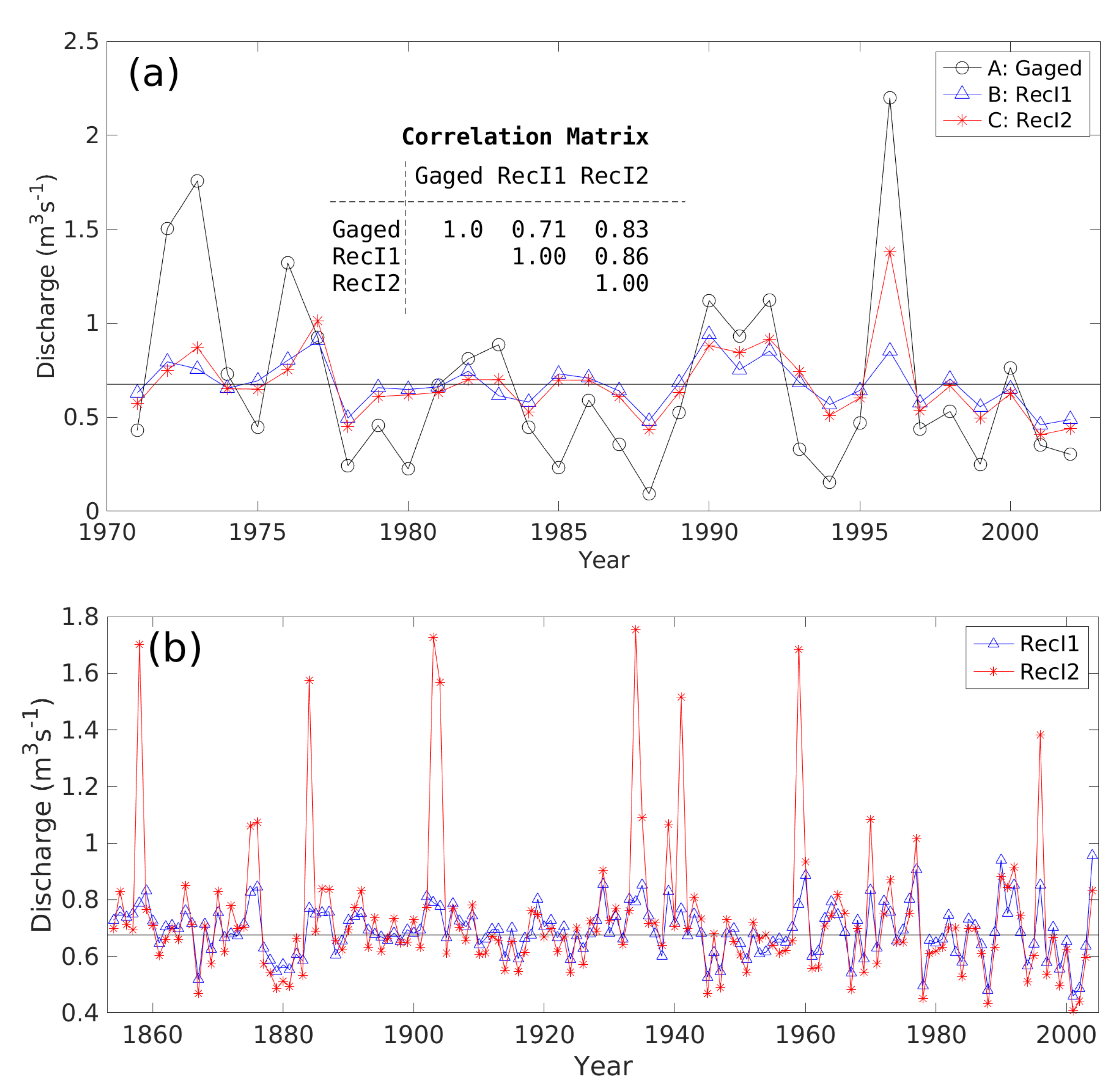
4.2. Reconstruction Modeling
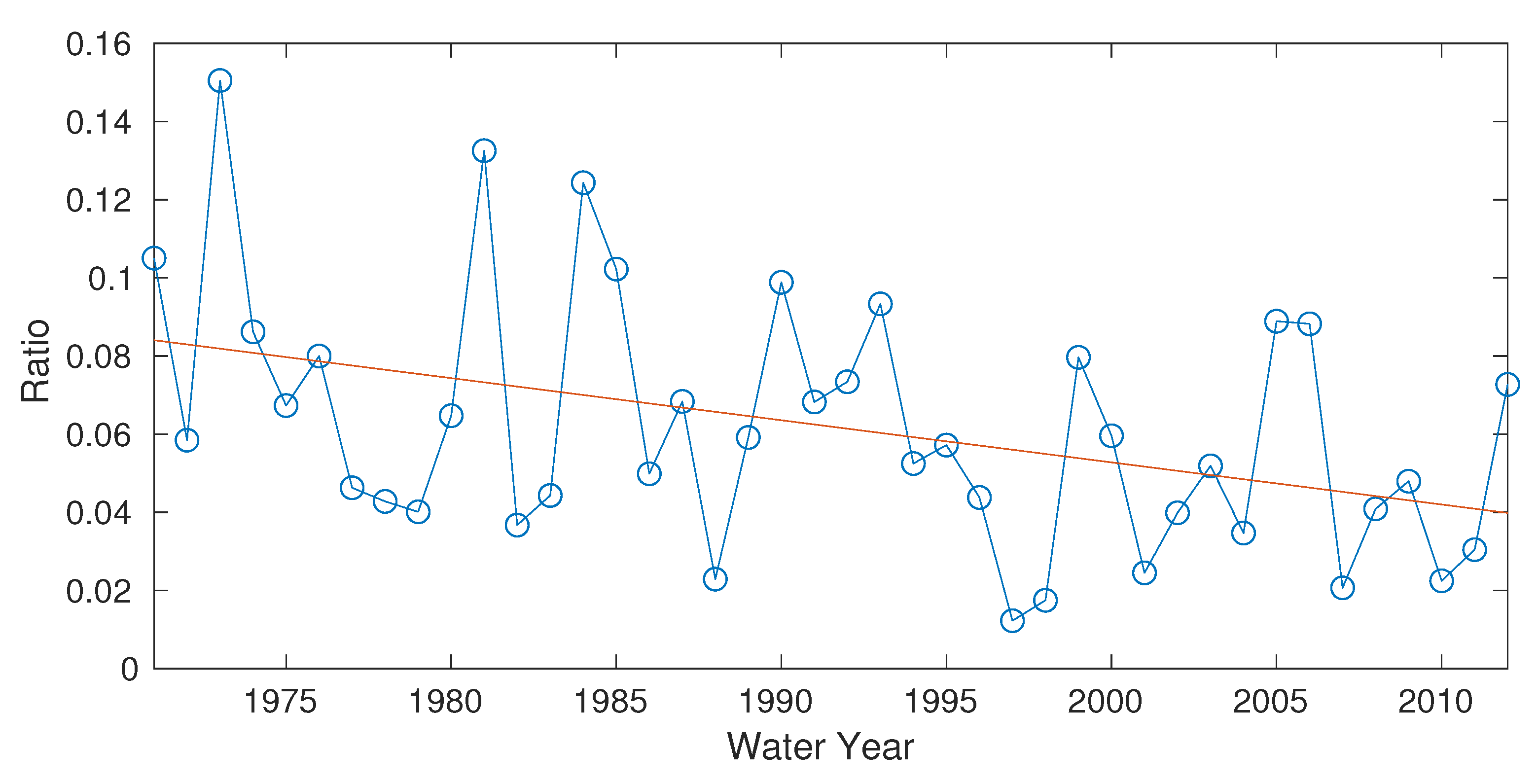
4.3. Comparative Statistics of RecD and RecI1
4.4. Sensitivity of Reconstruction to Temporal Disaggregation of Annual P
4.5. Temporally Variable T
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| Actual evapotranspiration | |
| CDF | Cumulative distribution function |
| GHCN | Global Historical Climate Network |
| P | Precipitation |
| Principal component | |
| Principal component analysis | |
| Potential evapotranspiration | |
| Q | River discharge (e.g., in ) |
| RecD | Direct reconstruction |
| RecI | Indirect reconstruction ( in general) |
| RecI1 | Indirect reconstruction with constant (year-to-year) monthly proportion of annual P |
| RecI2 | Indirect reconstruction with variable (year-to-year) monthly proportion of annual P |
| Runoff | |
| S | Soil water storage |
| Change in soil water storage | |
| T | Air temperature |
| WB model | Water-balance model |
Appendix A
Appendix A.1. Statistics of Tree Ring Site Chronologies
- A uniform and systematic procedure was applied in chronology development. Each series of tree ring width measurements was fit with a cubic smoothing spline with a 50% frequency response at 67% of the series length to remove non-climatic trends due to age, size, and the effects of stand dynamics [62]. The detrended series were then prewhitened with low-order autoregressive models to remove persistence not related to climatic variations. The individual indices were combined into a single master chronology for each combination of site and species using a bi-weight robust estimate of the mean [63]. The adequacy of sample replication was judged by the expressed population signal (EPS), computed from pooled interseries correlations and the time-varying sample size [23].
| N | ID | Species | Lat | Long | Elev (m) | Years | PC1 | PC2 | PC3 |
|---|---|---|---|---|---|---|---|---|---|
| 1 | AEH | CEAT | 35.33 | 6.90 | 1756 | 1607–2012 (1607) | 0.2185 | 0.0007 | 0.3258 |
| 2 | BOR | CEAT | 35.59 | 6.04 | 1876 | 1148–2011 (1733) | 0.2308 | 0.0204 | −0.0185 |
| 3 | DJT | CEAT | 36.45 | 4.10 | 1460 | 1534–2011 (1725) | 0.1206 | 0.3934 | 0.0031 |
| 4 | FER | CEAT | 35.38 | 6.96 | 1522 | 1384–2011 (1672) | 0.2554 | 0.0107 | 0.2045 |
| 5 | IGI | CEAT | 36.47 | 4.00 | 1443 | 1621–2005 (1845) | 0.1893 | 0.3090 | −0.0959 |
| 6 | KER | CEAT | 36.42 | 2.89 | 1398 | 1849–2011 (1913) | 0.0851 | 0.2862 | −0.0257 |
| 7 | KES | CEAT | 35.85 | 2.00 | 1560 | 1717–2006 (1819) | 0.1641 | 0.1698 | −0.2941 |
| 8 | LMO | CEAT | 36.45 | 4.11 | 1518 | 1697–2005 (1894) | 0.1242 | 0.3974 | 0.0564 |
| 9 | OUT | CEAT | 35.31 | 6.63 | 2073 | 1002–2011 (1480) | 0.2157 | 0.0142 | 0.2283 |
| 10 | PIP | CEAT | 35.85 | 1.98 | 1452 | 1533–2012 (1854) | 0.1817 | 0.0376 | −0.3265 |
| 11 | TAG | CEAT | 35.17 | 6.15 | 1704 | 1814–2012 (1821) | 0.2340 | −0.1280 | 0.0799 |
| 12 | THT | CEAT | 36.47 | 4.02 | 1550 | 1747–2005 (1878) | 0.1192 | 0.3801 | 0.0024 |
| 13 | TIG | CEAT | 36.45 | 4.10 | 1697 | 1552–2011 (1741) | 0.0974 | 0.4037 | −0.0157 |
| 14 | TIZ | CEAT | 35.30 | 6.63 | 1970 | 1344–2011 (1445) | 0.2111 | −0.0503 | 0.2809 |
| 15 | TUG | CEAT | 35.57 | 6.04 | 1674 | 1732–2009 (1737) | 0.2722 | −0.0731 | 0.1346 |
| 16 | AKS | PIHA | 35.28 | 6.66 | 1413 | 1851–2011 (1857) | 0.2337 | −0.1282 | 0.2514 |
| 17 | ALK | PIHA | 34.55 | 2.80 | 1357 | 1853–2011 (1866) | 0.2464 | −0.1007 | −0.2572 |
| 18 | BOC | PIHA | 35.13 | 6.62 | 1273 | 1695–2011 (1756) | 0.2196 | −0.0799 | 0.2016 |
| 19 | DJE | PIHA | 35.21 | 6.47 | 1303 | 1834–2011 (1850) | 0.2183 | −0.1102 | 0.2404 |
| 20 | FEB | PIHA | 34.56 | 2.78 | 1334 | 1794–2011 (1833) | 0.2419 | −0.1561 | −0.2601 |
| 21 | THN | PIHA | 34.61 | 3.09 | 1386 | 1830–2011 (1861) | 0.2542 | −0.1100 | −0.2613 |
| 22 | TOB | PIHA | 34.62 | 3.13 | 1331 | 1851–2011 (1855) | 0.2365 | −0.2144 | −0.2583 |
| 23 | ZEB | PIHA | 34.53 | 3.01 | 1415 | 1835–2011 (1848) | 0.2586 | −0.1403 | −0.2435 |

Appendix A.2. Water-Balance Modeling
- = 150 mm; water holding capacity of the soil (soil moisture storage capacity).Any excess of soil moisture storage, S, above in the monthly accounting is allocated to runoff (). In running the model, it is necessary to assume an S at the beginning of the first month of available P and T. Because this initial value is unknown, the WB output for some time can be distorted by incorrect specification of initial S. This is typically handled by disregarding the first year or two of model outputs. Our modeling, for example, on observed data, begins with January of 1969. We assume initial saturation ( mm), and we do not start interpreting the WB-model outputs until water year 1971 (defined as October 1970 to September 1971). If is exceeded, the excess is “surplus.”
- ; T threshold for snow. Below this threshold of monthly mean T all P is snow, or .
- T threshold for rain. Above this threshold of monthly mean T all P is rain, or . Between a monthly mean T of and , the fraction of P as varies linearly in proportion to the fraction .
- ; decimal fraction of to direct runoff. This small fraction of total is assumed to immediately (same month) contribute to direct rather than to enter into the water balance of the soil column, no matter how dry that soil is.
- ; runoff factor. The decimal fraction of surplus assigned to . This surplus, as defined above, is not all assigned to in the same month, but is gradually released according to this rule.
- ; daily melt coefficient. This coefficient along with the difference determines what fracton of the snow water storage is assigned to snowmelt runoff in the month. (Notation here is taken from the Fortran program rather than [35].) The snowmelt is computed as , where N is the number of days in the month. This equation can yield an greater than the actual snow water storage, and in that case the entire snowpack is assumed to melt (i.e., cannot exceed the existing snow water storage).
Appendix A.3. Grid-Cell Monthly P and T from Station Data
Appendix A.4. Indirect Reconstruction Modeling
- Convert to standardized anomalies, , using the 1970–2012 column means and standard deviations, and store the column-wise statistics in column vectors and .
- PCA on to get: , a matrix of principal component (PC) loadings and , a time series matrix of PC scores.
- Regress first column of (scores of first precipitation PC) on tree ring variables in stepwise regression using a calibration period of years, 1971–2002; this calibration period was selected to match the calibration period for direct reconstruction, and so is limited by the usable part of the discharge record at Tkabaout.
- Apply the estimated regression equation to get reconstructed for the years 1853–2005, where the refers to “predicted”, and the subscript “1” refers to the first component.
- Spatially disaggregate to get reconstruction annual z-scores of P at the 91 grid cells: , where denotes transpose and is the first column of the principal components matrix, .
- Restore grid-cell means and standard deviations to convert to annual (water year) reconstructed grid-cell P in units of mm: , where is a diagonal matrix with elements of along the diagonal, and is a column vector of ones of length .
- Temporally disaggregate the time series matrix , as described in the main paper, to derive the reconstructed monthly grid-cell P needed as input to the WB model.
- Route the resulting monthly P, and assumed monthly time series of grid-cell T through the WB model to come up with estimated monthly grid-cell runoff (), 1854–2004. For the indirect reconstructions in this study we used long-term monthly mean observed T, invariable from year to year. Water balance modeling was applied to roughly assess how sensitive discharge in this basin is to the interannual variability of T (see main paper, and Figure A5). The different spans, 1853–2005 vs 1854–2004, of the tree ring coverage and the WB-model output water year totals (e.g., ) are due to (1) loss of leading year to allow spin-up of WB model from initial conditions and (2) loss of trailing year in reorganizing water-year (October-September) monthly data from the temporal disaggregation into water-year monthly input required by the WB model.
- Convert grid-cell estimated to monthly, seasonal or annual discharge at the Tkabaout gage by multiplying (a depth of water) by grid-cell area, and integrating over cells and months.
- Choose one of the 91 grid cells.
- Drop 1970 (first year) from the vector of annual values and matrix of monthly values.
- Assign as the analog year the year in the interval 1971–2012 with closest annual P to that in 1970.
- Compute Spearman correlation coefficient between the 12-element vector of monthly P proportions in 1970 and in the analog year.
- Compute Spearman correlation coefficient between the 12-element vector of monthly P proportions in 1970 and the vector of long-term-mean proportions for 1971–2012.
- The method giving the highest correlation is judged “best” for that year (1970).
- Repeat steps 2–6 for all years 1970–2012, each time leaving out one year and using the remaining 42 years for getting the “predicted” proportions. This process results in two sets of 43 Spearman correlations—one set with the monthly proportions in the analog-year as the predictor, the other set with the long-term-mean monthly proportions as the predictor.
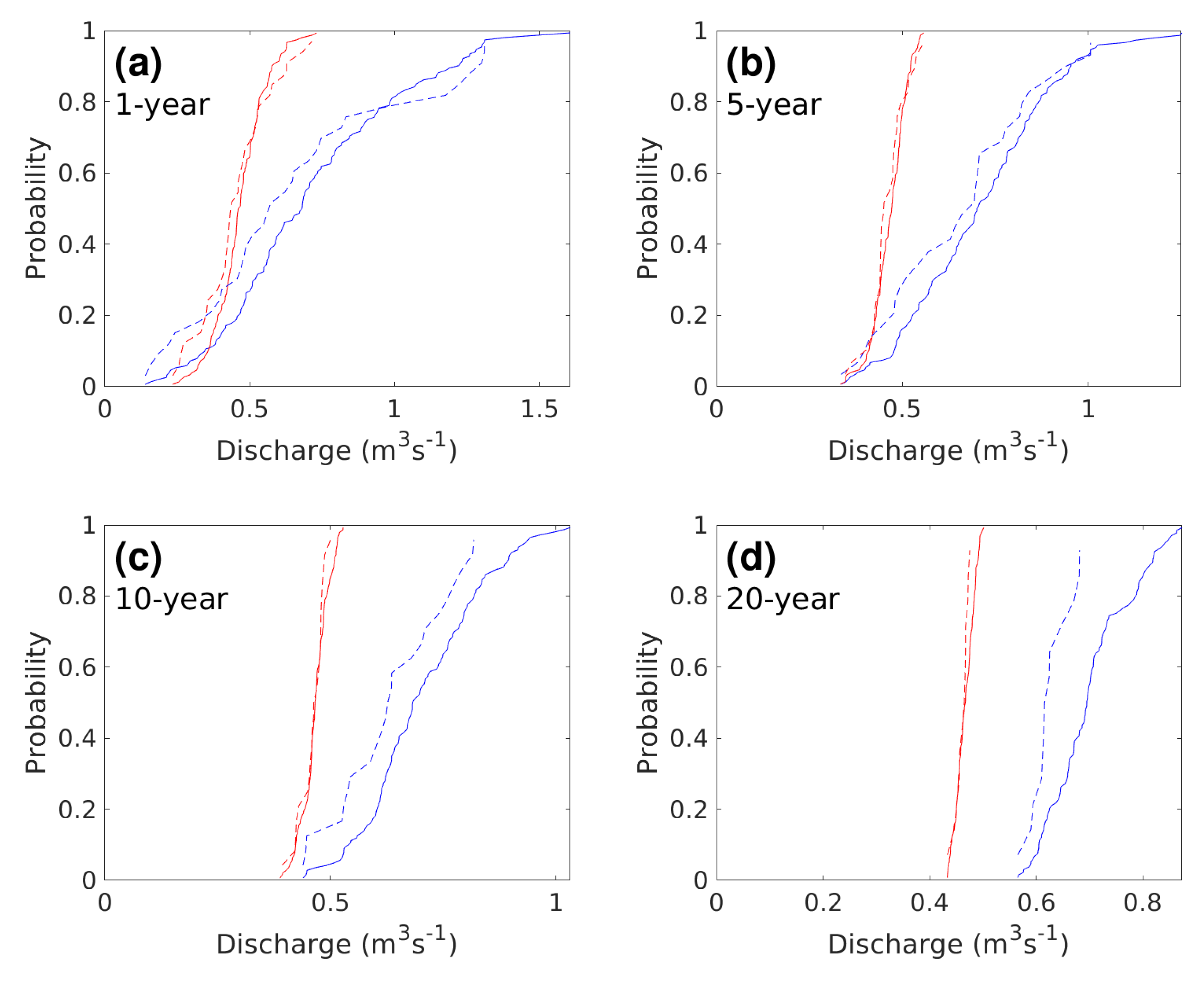
- Plot the histograms of the correlations for this grid cell (e.g., Figure A4, for grid cell #84—a representative higher-elevation gridpoint).
- Repeat 1–8 for all gridpoints. This gives 91 pairs of distributions of correlation cofficients for each of the two disaggregation methods being compared. Results are summarized in the caption to Figure A4.

References
- Loaiciga, H.A.; Haston, L.; Michaelsen, J. Dendrohydrology and long-term hydrologic phenomena. Rev. Geophys. 1993, 31, 151–171. [Google Scholar] [CrossRef]
- Meko, D.M.; Woodhouse, C.A. Application of Streamflow Reconstruction to Water Resources Management. In Dendroclimatology, Progress and Prospects; Hughes, M.K., Swetnam, T.W., Diaz, H.F., Eds.; Developments in Paleoenvironmental Research; Springer: Dordrecht, The Netherlands, 2011; Volume 11, pp. 231–261. [Google Scholar]
- Graham, N.E.; Hughes, M.K. Reconstructing the Mediaeval low stands of Mono Lake, Sierra Nevada, California, USA. Holocene 2007, 17, 1197–1210. [Google Scholar] [CrossRef]
- Saito, L.; Biondi, F.; Salas, J.D.; Panorska, A.K.; Kozubowski, T.J. A watershed modeling approach to streamflow reconstruction from tree ring records. Environ. Res. Lett. 2008, 3. [Google Scholar] [CrossRef]
- Saito, L.; Biondi, F.; Devkota, R.; Vittori, J.; Salas, J.D. A water balance approach for reconstructing streamflow using tree ring proxy records. J. Hydrol. 2015, 529, 535–547. [Google Scholar] [CrossRef]
- Gray, S.T.; McCabe, G.J. A combined water balance and tree ring approach to understanding the potential hydrologic effects of climate change in the central Rocky Mountain region. Water Resour. Res. 2014, 46, W05513. [Google Scholar] [CrossRef]
- Gangopadhyay, S.; McCabe, G.J.; Woodhouse, C.A. Beyond annual streamflow reconstructions for the Upper Colorado River Basin: A paleo-water-balance approach. Water Resour. Res. 2015, 51, 9763–9774. [Google Scholar] [CrossRef]
- Cleaveland, M.K. A 963-year reconstruction of summer (JJA) stream flow in the White River, Arkansas, USA, from tree rings. Holocene 2000, 10, 33–41. [Google Scholar] [CrossRef]
- Meko, D.M.; Woodhouse, C.A.; Baisan, C.H.; Knight, T.; Lukas, J.J.; Hughes, M.K.; Salzer, M.W. Medieval drought in the Upper Colorado River Basin. Geophys. Res. Lett. 2007, 34. [Google Scholar] [CrossRef]
- Cook, E.R.; Palmer, J.G.; Ahmed, M.; Woodhouse, C.A.; Fenwick, P.; Zafar, M.U.; Wahab, M.; Khan, N. Five centuries of Upper Indus River flow from tree rings. J. Hydrol. 2013, 486, 365–375. [Google Scholar] [CrossRef]
- Biondi, F.; Meko, D.M. Long-term hydroclimatic patterns in the Truckee-Carson Basin of the eastern Sierra Nevada, USA. Water Resour. Res. 2019, 55, 5559–5574. [Google Scholar] [CrossRef]
- McCabe, G.J.; Wolock, D.M. Joint variability of global runoff and global sea-surface temperatures. J. Hydrometeorol. 2008, 9, 816–824. [Google Scholar] [CrossRef]
- Touchan, R.; Anchukaitis, K.J.; Meko, D.M.; Kerchouche, D.; Slimani, S.; Ilmen, R.; Hasnaoui, F.; Guibal, F.; Camarero, J.J.; Sánchez-Salguero, R.; et al. Climate controls on tree growth in the Western Mediterranean. Holocene 2017, 27, 1429–1442. [Google Scholar] [CrossRef]
- Guidoum, A.; Nemouchi, A.; Hamlat, A. Modeling and mapping of water erosion in northeastern Algeria using a seasonal multicriteria approach. Arab. J. Geosci. 2014, 7, 3925–3943. [Google Scholar] [CrossRef]
- Tiri, A.; Lahbari, N.; Boudoukha, A. Assessment of the quality of water by hierarchical cluster and variance analyses of the Koudiat Medouar Watershed, East Algeria. Appl. Water Sci. 2017, 7, 4197–4206. [Google Scholar] [CrossRef]
- Berghout, A.; Meddi, M. Sediment transport modeling in Wadi chemora during flood flow events. J. Water Land Dev. 2016, 31, 23–31. [Google Scholar] [CrossRef]
- Trouet, V.; van Oldenborgh, G. KNMI Climate Explorer: A web-based research tool for high-resolution paleoclimatology. Tree Ring Res. 2013, 69, 3–13. [Google Scholar] [CrossRef]
- Sharples, J.J.; Hutchinson, M.F.; Jellett, D.R. On the horizontal scale of elevation dependence of Australian monthly precipitation. J. Appl. Meteorol. 2007, 44, 1850–1865. [Google Scholar] [CrossRef]
- NCEI. 2-Minute Gridded Global Relief Data (ETOPO2v2). 2020. Available online: https://www.ngdc.noaa.gov/mgg/global/etopo2.html (accessed on 13 August 2015).
- Fritts, H.C. Tree Rings and Climate; Academic Press: London, UK, 1976; 567p. [Google Scholar]
- Cook, E.R.; Krusic, P.J.; Holmes, R.H.; Peters, K. Program ARSTAN, Version 41d. 2007. Available online: www.ldeo.columbia.edu/tree-ring-laboratory (accessed on 10 August 2020).
- Cook, E.R.; Kairiukstis, L.A. (Eds.) Methods of Dendrochronology: Applications in the Environmental Sciences; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1990; 394p. [Google Scholar]
- Wigley, T.M.L.; Briffa, K.R.; Jones, P.D. On the average value of correlated time series, with applications in dendroclimatology and hydrometeorology. J. Clim. Appl. Meteor. 1984, 23, 201–213. [Google Scholar] [CrossRef]
- Touchan, R.; Anchukaitis, K.J.; Meko, D.M.; Attalah, S.; Baisan, C.; Aloui, A. Long term context for recent drought in northwestern Africa. Geophys. Res. Lett. 2008, 35, L13705. [Google Scholar] [CrossRef]
- Touchan, R.; Anchukaitis, K.; Meko, D.M.; Sabir, M.; Attalah, S. Spatiotemporal drought variability in northwestern Africa over the last nine centuries. Clim. Dynam. 2011, 37, 237–252. [Google Scholar] [CrossRef]
- Mardia, K.; Kent, J.; Bibby, J. Multivariate Analysis; Academic Press: London, UK, 1979; 518p. [Google Scholar]
- Thornthwaite, C.W. An approach toward a rational classification of climate. Geog. Rev. 1948, 38, 55–94. [Google Scholar] [CrossRef]
- Thornthwaite, C.W.; Mather, J.R. The Water Balance: Publications in Climatology; Technical Report; Drexel Institute of Technology: Philadelphia, PA, USA, 1955; Volume 1, 144p. [Google Scholar]
- McCabe, G.J.; Wolock, D.M. Warming may create substantial water supply shortages in the Colorado River basin. Geophys. Res. Lett. 2007, 34. [Google Scholar] [CrossRef]
- McCabe, G.J.; Wolock, D.M. Century–scale variability in global annual runoff examined using a water balance model. Int. J. Climatol. 2011, 31, 1739–1748. [Google Scholar] [CrossRef]
- Palmer, W.C. Meteorological Drought, Research Paper No. 54; Technical Report; NOAA: Washington, DC, USA, 1965; 58p. Available online: https://www.ncdc.noaa.gov/temp-and-precip/drought/historical-palmers/overview (accessed on 18 July 2020).
- Stockton, C.W.; Meko, D.M. A long-term history of drought occurrence in western United States as inferred from tree rings. Weatherwise 1975, 28, 244–249. [Google Scholar] [CrossRef]
- Cook, E.R.; Meko, D.M.; Stahle, D.W.; Cleaveland, M.K. Drought reconstructions for the continental United States. J. Climate 1999, 12, 1145–1162. [Google Scholar] [CrossRef]
- Hamon, W.R. Estimating potential evapotranspiration. J. Hydraul. Div. 1961, 87, 107–120. [Google Scholar]
- McCabe, G.J.; Markstrom, S.L. A Monthly Water-Balance Model Driven by a Graphical User Interface; Open-File Report 2007-1088; U.S. Geological Survey: Reston, VA, USA, 2007; 6p.
- Jones, P.D.; Hulme, M. Calculating regional climate time series for temperature and precipitation: Methods and illustrations. Int. J. Climatol. 1996, 16, 3. [Google Scholar] [CrossRef]
- Haan, C.T. Statistical Methods in Hydrology, 2nd ed.; Iowa State University Press: Iowa City, IA, USA, 2002; 496p. [Google Scholar]
- Barry, R.G. (Ed.) Mountain Weather and Climate, 3rd ed.; Cambridge University Press: London, UK, 2008; 506p. [Google Scholar]
- Weisberg, S. Applied Linear Regression, 2nd ed.; John Wiley: New York, NY, USA, 1985; 324p. [Google Scholar]
- Michaelsen, J. Cross-validation in statistical climate forecast models. J. Clim. Appl. Meteor. 1987, 26, 1589–1600. [Google Scholar] [CrossRef]
- Fritts, H.C.; Guiot, J.; Gordon, G.A. Verification. In Methods of Dendrochronology: Applications in the Environmental Sciences; Cook, E.R., Kairiukstis, L.A., Eds.; Kluwer Academic Publishers: New York, NY, USA, 1990; pp. 178–185. [Google Scholar]
- Woodhouse, C.A.; Gray, S.T.; Meko, D.M. Updated streamflow reconstructions for the Upper Colorado River Basin. Water Resour. Res. 2006, 42. [Google Scholar] [CrossRef]
- Hidalgo, H.G.; Piechota, T.C.; Dracup, J.A. Alternative principal components regression procedures for dendrohydrologic reconstructions. Water Resour. Res. 2000, 36, 3241–3249. [Google Scholar] [CrossRef]
- Snedecor, G.W.; Cochran, W.G. Statistical Methods, 8th ed.; Iowa State University Press: Ames, IA, USA, 1989; 503p. [Google Scholar]
- Meharzi, M.K.E. Forêts, Géosystèmes et Dynamique du Milieu: Le cas de l’Aurès. Ph.D. Thesis, Université des frères Mentouri Constantine, Constantine, Algeria, 2010. [Google Scholar]
- Quézel, P. Peuplement Végétal des Hautes Montagnes de l’Afrique du Nord. Essai de Synthèse Biogéographique et Phytosociologique; Lahure, A., Ed.; Éditions Paul Lechevalier: Paris, France, 1957; 463p. [Google Scholar]
- Belloula, N. Etude expérimentale de l’Influence de la typologie des Cédraies sur la distribution des formes d’Azote dans certains sols du massif forestier du Chélia (W. de Khenchela). In Mémoire de Magister; Université Hadj Lakhdar Batna: Batna, Algeria, 2011; 136p. [Google Scholar]
- Slimani, S.; Touchan, R.; Derridj, A.; Kherchouche, D.; Gutiérrez, E. Fire history of Atlas cedar (Cedrus atlantica Manetti) in Mount Chélia, Northern Algeria. J. Arid Environ. 2014, 104, 116–124. [Google Scholar] [CrossRef]
- Seager, R.; Liu, H.; Henderson, N.; Simpson, I.; Kelley, C.; Shaw, T.; Kushnir, Y.; Ting, M. Causes of increasing aridification of the Mediterranean region in response to rising greenhouse gases. J. Clim. 2014, 27, 4655–4676. [Google Scholar] [CrossRef]
- Abdessemed, K. Le cèdre de l’Atlas (Cedrus atlantica Man.) dans les Massifs de l’Aurès et du Belezma: Etude Phytosociologique, Problèmes de Conservation D’aménagement. Ph.D. Thesis, Université de Droit d’Economie et des Sciences d’Aix-Marseille, Aix-en-Provence, France, 1981. [Google Scholar]
- Bentouati, A.; Bariteau, M. Réflexions sur le dépérissement du cèdre de l’Atlas des Aurés (Algérie). Forêt Méditerranéenne 2006, XXVII, 317–322. [Google Scholar]
- Kherchouche, D.; Kalla, M.; Gutierrez, E.; Attallah, S.; Bouzghaia, M. Impacts of droughts on Cedrus atlantica forests dieback in the Aurés (Algeria). J. Life Sci. 2012, 6, 1262–1269. [Google Scholar]
- Kherchouche, D.; Kalla, M.; Gutierrez, E.; Briki, A.; Hamchi, A. La sécheresse et le dépérissement du cèdre de l’Atlas (Cedrus atlantica Manetti) dans le massif du Belezma (Algérie). J. Life Sci. 2013, 24, 129–137. [Google Scholar]
- Moon, H.; Solomon, T. Forest decline in Africa: Trends and impacts of foreign direct investment: A review. Int. J. Curr. Adv. Res. 2018, 7. [Google Scholar] [CrossRef]
- Meharzi, M.K. Le rôle de l’orographie dans la répartition spatiale des précipitations dans le massif de l’Aurès. Méditerranée 1994, 3, 73–78. [Google Scholar] [CrossRef]
- Björklund, J.; Gunnarson, B.E.; Seftigen, K.; Zhang, P.; Linderholm, H.W. Using adjusted Blue Intensity data to attain high-quality summer temperature information: A case study from Central Scandinavian. Holocene 2015, 25, 547–556. [Google Scholar] [CrossRef]
- Robeson, S.M.; Maxwell, J.T.; Ficklin, D.L. Bias correction of paleoclimatic reconstructions: A new look at 1200+ years of Upper Colorado River flow. Geophys. Res. Lett. 2020, 47, e2019GL086689. [Google Scholar] [CrossRef]
- Griffin, D.; Woodhouse, C.A.; Meko, D.M.; Stahe, D.W.; Faulstich, H.L.; Carillo, C.; Touchan, R.; Castro, C.; Leavitt, S. North American monsoon precipitation reconstructed from tree ring latewood. Geophys. Res. Lett. 2013, 40, 1–5. [Google Scholar] [CrossRef]
- Woodhouse, C.A.; Meko, D.M.; Griffin, D.; Castro, C.L. Tree rings reveal multi-season drought variability in the lower Rio Grande basin, USA. Water Resour. Res. 2013, 49, 844–850. [Google Scholar] [CrossRef]
- Camarero, J.; Fernández-Pérez, L.; Kirdyanov, A.V.; Shestakova, T.A.; Knorre, A.A.; Kukarskih, V.V.; Voltas, J. Minimum wood density of conifers portrays changes in early season precipitation at dry and cold Eurasian regions. Trees 2017, 31, 1423–1437. [Google Scholar] [CrossRef]
- Lionello, P.; Scarascia, L. The relation between climate change in the Mediterranean region and global warming. Reg. Environ. Chang. 2018, 18, 1481–1493. [Google Scholar] [CrossRef]
- Cook, E.R.; Briffa, K.; Shiyatov, S.; Mazepa, V. Tree ring standardization and growth-trend estimation. In Methods of Dendrochronology: Applications in the Environmental Sciences; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1990; pp. 104–123. 394p. [Google Scholar]
- Cook, E.R. A Time Series Approach to Tree Ring Standardization. Ph.D. Thesis, The University of Arizona, Tucson, AZ, USA, 1985. [Google Scholar]




| PC | Pctg | Interpretation | |
|---|---|---|---|
| 1 | 9.337 | 40.6 | Common growth signal; all loadings positive |
| 2 | 3.303 | 14.4 | Species contrast or north-south contrast |
| 3 | 2.321 | 10.1 | East-west contrast |
| 4 | 1.691 | 7.4 | Remaining components have no clear interpretation |
| 5 | 1.005 | 4.4 | — |
| 6 | 0.879 | 3.8 | — |
| Predictand | Steps | PCs Entered | RE | |
|---|---|---|---|---|
| Discharge | 2 | 1, 2 | 0.65 | 0.59 |
| Precipitation | 3 | 1, 3, 2 | 0.68 | 0.63 |
| Years | Statistics | |||||||
|---|---|---|---|---|---|---|---|---|
| Segment | Series | First | Last | Mean | Median | Std | Skew | r1 |
| Calib. Period | Gaged | 1971 | 2002 | 0.676 | 0.497 | 0.488 | 1.39 * | 0.14 |
| RecD | 1971 | 2002 | 0.651 | 0.566 | 0.360 | 0.58 | 0.33 * | |
| RecI1 | 1971 | 2002 | 0.450 | 0.434 | 0.120 | 0.23 | 0.13 | |
| Earlier | RecD | 1854 | 1970 | 0.726 | 0.685 | 0.290 | 0.59 * | 0.44 * |
| RecI1 | 1854 | 1970 | 0.470 | 0.468 | 0.077 | 0.01 | 0.29 * | |
| Full | RecD | 1854 | 2004 | 0.712 | 0.680 | 0.309 | 0.53 * | 0.39 * |
| RecI1 | 1854 | 2004 | 0.467 | 0.460 | 0.090 | 0.13 | 0.20 * | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meko, D.M.; Touchan, R.; Kherchouche, D.; Slimani, S. Direct Versus Indirect Tree Ring Reconstruction of Annual Discharge of Chemora River, Algeria. Forests 2020, 11, 986. https://doi.org/10.3390/f11090986
Meko DM, Touchan R, Kherchouche D, Slimani S. Direct Versus Indirect Tree Ring Reconstruction of Annual Discharge of Chemora River, Algeria. Forests. 2020; 11(9):986. https://doi.org/10.3390/f11090986
Chicago/Turabian StyleMeko, David M., Ramzi Touchan, Dalila Kherchouche, and Said Slimani. 2020. "Direct Versus Indirect Tree Ring Reconstruction of Annual Discharge of Chemora River, Algeria" Forests 11, no. 9: 986. https://doi.org/10.3390/f11090986
APA StyleMeko, D. M., Touchan, R., Kherchouche, D., & Slimani, S. (2020). Direct Versus Indirect Tree Ring Reconstruction of Annual Discharge of Chemora River, Algeria. Forests, 11(9), 986. https://doi.org/10.3390/f11090986





