Effects of Slope Gradient on Runoff and Sediment Yield on Machine-Induced Compacted Soil in Temperate Forests
Abstract
:1. Introduction
2. Materials and Methods
2.1. Site Description
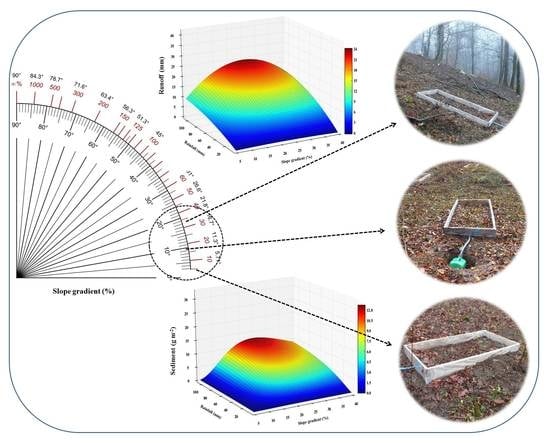
2.2. Experimental Design and Measurements
2.3. Statistical Analyses
3. Results
3.1. Rainfall and Plot Characteristics
3.2. Runoff, Runoff Coefficient, and Sediment Yield
3.3. Runoff and Sediment Yield Model
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Giadrossich, F.; Cohen, D.; Schwarz, M.; Seddaiu, G.; Contran, N.; Lubino, M.; Valdés-Rodrŕguez, O.A.; Niedda, M. Modeling bio-engineering traits of Jatropha curcas L. Ecol. Eng 2016, 89, 40–48. [Google Scholar] [CrossRef]
- Vergani, C.; Giadrossich, F.; Buckley, P.; Conedera, M.; Pividori, M.; Salbitano, F.; Rauch, H.S.; Lovreglio, R.; Schwarz, M. Root reinforcement dynamics of European coppice woodlands and their effect on shallow landslides: A review. Earth-Sci. Rev. 2017, 167, 88–102. [Google Scholar] [CrossRef]
- Jourgholami, M.; Khajavi, S.; Labelle, E.R. Recovery of forest soil chemical properties following soil rehabilitation treatments: An assessment six years after machine impact. Croat. J. For. Eng. 2020, 41, 163–175. [Google Scholar] [CrossRef] [Green Version]
- Giadrossich, F.; Cohen, D.; Schwarz, M.; Ganga, A.; Marrosu, R.; Pirastru, M.; Capra, G.F. Large roots dominate the contribution of trees to slope stability. Earth Surf. Process. Landf. 2019, 44, 1602–1609. [Google Scholar] [CrossRef]
- Giadrossich, F.; Schwarz, M.; Cohen, D.; Cislaghi, A.; Vergani, C.; Hubble, T.; Phillips, C.; Stokes, A. Methods to measure the mechanical behaviour of tree roots: A re-view. Ecol. Eng. 2017, 109, 256–271. [Google Scholar] [CrossRef]
- Vergani, C.; Schwarz, M.; Soldati, M.; Corda, A.; Giadrossich, F.; Chiaradia, E.A.; Morando, P.; Bassanelli, C. Root reinforcement dynamics in subalpine spruce forests following timber harvest: A case study in Canton Schwyz, Switzerland. Catena 2016, 143, 257–288. [Google Scholar] [CrossRef] [Green Version]
- Jourgholami, M.; Labelle, E.R.; Feghhi, J. Efficacy of leaf litter mulch to mitigate runoff and sediment yield following mechanized operations in the Hyrcanian mixed forests. J. Soils Sediments 2019, 19, 2076–2088. [Google Scholar] [CrossRef]
- Cambi, M.; Certini, G.; Neri, F.; Marchi, E. The impact of heavy traffic on forest soils: A review. For. Ecol. Manag. 2015, 338, 124–138. [Google Scholar] [CrossRef]
- Marchi, E.; Picchio, R.; Mederski, P.S.; Vusić, D.; Perugini, M.; Venanzi, R. Impact of silvicultural treatment and forest operation on soil and regeneration in Mediterranean Turkey oak (Quercus cerris L.) coppice with standards. Ecol. Eng. 2016, 95, 475–484. [Google Scholar] [CrossRef]
- Picchio, R.; Mercurio, R.; Venanzi, R.; Gratani, L.; Giallonardo, T.; Lo Monaco, A.; Frattaroli, A.R. Strip clear-cutting application and logging typologies for renaturalization of pine afforestation—A case study. Forests 2018, 9, 366. [Google Scholar] [CrossRef] [Green Version]
- Jourgholami, M.; Ghassemi, T.; Labelle, E.R. Soil physio-chemical and biological indicators to evaluate the restoration of compacted soil following reforestation. Ecol. Indic. 2019, 101, 102–110. [Google Scholar] [CrossRef]
- Picchio, R.; Mederski, P.S.; Tavankar, F. How and how much, do harvesting activities affect forest soil, regeneration and stands? Curr. For. Rep. 2020, 6, 115–118. [Google Scholar] [CrossRef] [Green Version]
- Marchi, E.; Chung, W.; Visser, R.; Abbas, D.; Nordfjell, T.; Mederski, P.S.; McEwan, A.; Brink, M.; Laschi, A. Sustainable Forest Operations (SFO): A new paradigm in a changing world and climate. Sci. Total Environ. 2018, 634, 1385–1397. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sohrabi, H.; Jourgholami, M.; Tavankar, F.; Venanzi, R.; Picchio, R. Post-Harvest Evaluation of Soil Physical Properties and Natural Regeneration Growth in Steep-Slope Terrains. Forests 2019, 10, 1034. [Google Scholar] [CrossRef] [Green Version]
- Picchio, R.; Neri, F.; Petrini, E.; Verani, S.; Marchi, E.; Certini, G. Machinery-induced soil compaction in thinning two pine stands in central Italy. For. Ecol. Manag. 2012, 285, 38–43. [Google Scholar] [CrossRef]
- Sohrabi, H.; Jourgholami, M.; Jafari, M.; Shabanian, N.; Venanzi, R.; Tavankar, F.; Picchio, R. Soil recovery assessment after timber harvesting based on the Sustainable Forest Operation (SFO) perspective in Iranian temperate forests. Sustainability 2020, 12, 2874. [Google Scholar] [CrossRef] [Green Version]
- Picchio, R.; Tavankar, F.; Nikooy, M.; Pignatti, G.; Venanzi, R.; Lo Monaco, A. Morphology, growth and architecture response of Beech (Fagus orientalis Lipsky) and Maple tree (Acer velutinum Boiss.) seedlings to soil compaction stress caused by mechanized logging operations. Forests 2019, 10, 771. [Google Scholar] [CrossRef] [Green Version]
- Jourgholami, M.; Fathi, K.; Labelle, E.R. Effects of litter and straw mulch amendments on compacted soil properties and Caucasian alder (Alnus subcordata) growth. New. For. 2020, 51, 349–365. [Google Scholar] [CrossRef]
- Jourgholami, M.; Labelle, E.R.; Feghhi, J. Response of runoff and sediment on skid trails of varying gradient and traffic intensity over a two-year period. Forests 2017, 8, 472. [Google Scholar] [CrossRef] [Green Version]
- Bracken, L.J.; Kirkby, M.J. Differences in hillslope runoff and sediment transport rates within two semi-arid catchments in southeast Spain. Geomorphology 2005, 68, 183–200. [Google Scholar] [CrossRef]
- Moreno de las Heras, M.; Nicolau, J.M.; Merino-Martin, L.; Wilcox, B.P. Plot-scale effects on runoff and erosion along a slope degradation gradient. Water Resour. Res. 2010, 46, 4503. [Google Scholar] [CrossRef] [Green Version]
- Fu, S.; Liu, B.; Liu, H.; Xu, L. The effect of slope on interrill erosion at short slopes. Catena 2011, 84, 29–34. [Google Scholar] [CrossRef]
- Liu, D.; She, D.; Yu, S.; Shao, G.; Chen, D. Rainfall intensity and slope gradient effects on sediment losses and splash from a saline–sodic soil under coastal reclamation. Catena 2015, 128, 54–62. [Google Scholar] [CrossRef]
- Kinnell, P.I.A. Slope length factor for applying the USLE-M to erosion in grid cells. Soil Tillage Res. 2001, 58, 11–17. [Google Scholar] [CrossRef]
- Kinnell, P.I.A. A review of the design and operation of runoff and soil loss plots. Catena 2016, 145, 257–265. [Google Scholar] [CrossRef]
- Fox, D.M.; Bryan, R.B.; Price, A.G. The influence of slope angle on final infiltration rate for interrill conditions. Geoderma 1997, 80, 181–194. [Google Scholar] [CrossRef]
- Khan, M.N.; Gong, Y.; Hu, T.; Lal, R.; Zheng, J.; Justine, M.F.; Azhar, M.; Che, M.; Zhang, H. Effect of slope, rainfall intensity and mulch on erosion and infiltration under simulated rain on purple soil of south-western Sichuan province, China. Water 2016, 8, 528. [Google Scholar] [CrossRef]
- Nord, G.; Esteves, M. The effect of soil type, meteorological forcing and slope gradient on the simulation of internal erosion processes at the local scale. Hydrol. Process. 2010, 24, 1766–1780. [Google Scholar] [CrossRef]
- El Kateb, H.; Zhang, H.; Zhang, P.; Mosandl, R. Soil erosion and surface runoff on different vegetation covers and slope gradients: A field experiment in Southern Shaanxi Province, China. Catena 2013, 105, 1–10. [Google Scholar] [CrossRef]
- Zhang, X.; Hu, M.; Guo, X.; Yang, H.; Zhang, Z.; Zhang, K. Effects of topographic factors on runoff and soil loss in Southwest China. Catena 2018, 16, 394–402. [Google Scholar] [CrossRef]
- Liu, Q.; Singh, V.P. Effect of microtopography, slope length and gradient, and vegetative cover on overland flow through simulation. J. Hydrol. Eng. 2004, 9, 375–382. [Google Scholar] [CrossRef] [Green Version]
- Jourgholami, M.; Fathi, K.; Labelle, E.R. Effects of foliage and traffic intensity on runoff and sediment in skid trails after trafficking in a deciduous forest. Eur. J. For. Res. 2018, 137, 223–235. [Google Scholar] [CrossRef]
- Jourgholami, M.; Labelle, E.R. Effects of plot length and soil texture on runoff and sediment yield occurring on machine-trafficked soils in a mixed deciduous forest. Ann. For. Sci. 2020, 77, 19. [Google Scholar] [CrossRef]
- Morbidelli, R.; Saltalippi, C.; Flammini, A.; Cifrodelli, M.; Picciafuoco, T.; Corradini, C.; Govindaraju, R.S. Laboratory investigation on the role of slope on infiltration over grassy soils. J. Hydrol. 2016, 543, 542–547. [Google Scholar] [CrossRef]
- Morbidelli, R.; Corradini, C.; Saltalippi, C.; Flammini, A.; Dari, J.; Govindaraju, R.S. A New Conceptual Model for Slope-Infiltration. Water 2019, 11, 678. [Google Scholar] [CrossRef] [Green Version]
- Morbidelli, R.; Saltalippi, C.; Flammini, A.; Govindaraju, R.S. Role of slope on infiltration: A review. J. Hydrol. 2018, 557, 878–886. [Google Scholar] [CrossRef]
- Sagheb-Talebi, K.; Sajedi, T.; Pourhashemi, M. Forests of Iran: A Treasure from the Past, a Hope for the Future. Plant Veg. 2014, 10, 1–152. [Google Scholar]
- Li, X.; Niu, J.; Xie, B. The effect of leaf litter cover on surface runoff and soil erosion in northern China. PLoS ONE 2014, 9, e107789. [Google Scholar] [CrossRef] [Green Version]
- Kemper, W.D.; Rosenau, R.C. Aggregate Stability and Size Distribution. In Methods of Soil Analysis. Physical and Mineralogical Properties. Part I, 2nd ed.; Klute, A., Ed.; ASA-SSSA: Madison, WI, USA, 1986; pp. 425–442. [Google Scholar]
- Thien, S.J.; Graveel, J.G. Laboratory Manual for Soil Science: Agriculture & Environmental Principles; McGraw-Hill Companies, Inc.: Boston, MA, USA, 2008; p. 218. [Google Scholar]
- Gee, G.W.; Bauder, J.W. Particle-size Analysis. In Methods of Soil Analysis, Part 1. Physical and Mineralogical Methods; Klute, A., Ed.; Soil Science Society of America: Madison, WI, USA, 1983; pp. 383–411. [Google Scholar]
- Walkley, A.; Black, I.A. An examination of the Degtjareff method for determining soil organic matter and a proposed modification of chromic acid titration method. Soil Sci. 1934, 37, 29–38. [Google Scholar] [CrossRef]
- Prats, S.A.; Wagenbrenner, J.; Malvar, M.C.; Martins, M.A.S.; Keizer, J.J. Mid-term and scaling effects of forest residue mulching on post-fire runoff and soil erosion. Sci. Total Environ. 2016, 573, 1242–1254. [Google Scholar] [CrossRef]
- Xing, W.; Yang, P.; Ren, S.; Ao, C.; Li, X.; Gao, W. Slope length effects on processes of total nitrogen loss under simulated rainfall. Catena 2016, 139, 73–81. [Google Scholar] [CrossRef]
- Etehadi Abari, M.; Majnounian, B.; Malekian, A.; Jourgholami, M. Effects of forest harvesting on runoff and sediment characteristics in the Hyrcanian forests, northern Iran. Eur. J. For. Res. 2017, 136, 375–386. [Google Scholar] [CrossRef]
- Jourgholami, M.; Etehadi Abari, M. Effectiveness of sawdust and straw mulching on postharvest runoff and soil erosion of a skid trail in a mixed forest. Ecol. Eng. 2017, 109, 1–9. [Google Scholar] [CrossRef]
- Tsiko, C.T.; Makurira, H.; Gerrits, A.M.J.; Savenije, H.H.G. Measuring forest floor and canopy interception in a savannah ecosystem. Phys. Chem. Earth 2012, 47–48, 122–127. [Google Scholar] [CrossRef]
- Kim, J.K.; Onda, Y.; Kim, M.S.; Yang, D.Y. Plot-scale study of surface runoff on well-covered forest floors under different canopy species. Quat. Int. 2014, 344, 75–85. [Google Scholar] [CrossRef]
- Du, J.; Niu, J.; Gao, Z.; Chen, X.; Zhang, L.; Li, X.; Zhu, Z. Effects of rainfall intensity and slope on interception and precipitation partitioning by forest litter layer. Catena 2019, 172, 711–718. [Google Scholar] [CrossRef]
- Zagyvainé, K.K.A.; Kalicz, P.; Szilágyi, J.; Gribovszki, Z. On the specific water holding capacity of litter for three forest ecosystems in the eastern foothills of the Alps. Agric. For. Meteorol. 2019, 278, 107656. [Google Scholar] [CrossRef]
- Zhao, L.; Hou, R.; Fang, Q. Differences in interception storage capacities of undecomposed broad-leaf and needle-leaf litter under simulated rainfall conditions. For. Ecol. Manag. 2019, 446, 135–142. [Google Scholar] [CrossRef]
- Koulouri, M.; Giourga, C. Land abandonment and slope gradient as key factors of soil erosion in Mediterranean terraced lands. Catena 2007, 69, 274–281. [Google Scholar] [CrossRef]
- Han, Z.; Zhong, S.; Ni, J.; Shi, Z.; Wei, C. Estimation of soil erosion to define the slope length of newly reconstructed gentle-slope lands in hilly mountainous regions. Sci. Rep. 2019, 9, 46–76. [Google Scholar] [CrossRef]
- Wu, S.; Yu, M.; Chen, L. Nonmonotonic and spatial-temporal dynamic slope effects on soil erosion during rainfall-runoff processes. Water Resour. Res. 2017, 53, 1369–1389. [Google Scholar]
- Puntenney-Desmond, K.C.; Bladon, K.D.; Silins, U. Runoff and sediment production from harvested hillslopes and the riparian area during high intensity rainfall events. J. Hydrol. 2020, 582, 124452. [Google Scholar] [CrossRef]
- Chen, B.; Krajewski, W.F.; Helmers, M.J.; Zhang, Z. Spatial variability and temporal persistence of event runoff coefficients for cropland hillslopes. Water Resour. Res. 2019, 55, 1583–1597. [Google Scholar] [CrossRef]
- Guastini, E.; Zuecco, G.; Errico, A.; Castelli, G.; Bresci, E.; Preti, F.; Penna, D. How does streamflow response vary with spatial scale? Analysis of controls in three nested Alpine catchments. J. Hydrol. 2019, 570, 705–718. [Google Scholar] [CrossRef]
- Defersha, M.B.; Quraishi, S.; Mellese, A.M. The effect of slope steepness and antecedent moisture content on interrill erosion, runoff and sediment size distribution in the highlands of Ethiopia. Hydrol. Earth Syst. Sci. 2011, 15, 2367–2375. [Google Scholar] [CrossRef] [Green Version]
- Arjmand Sajjadi, S.; Mahmoodabadi, M. Aggregate breakdown and surface seal development influenced by rain intensity, slope gradient and soil particle size. Solid Earth 2015, 6, 311–321. [Google Scholar] [CrossRef] [Green Version]
- Parsons, A.J.; Brazier, R.E.; Wainwright, J.; Powell, D.M. Scale relationships in hillslope runoff and erosion. Earth Surf. Process. Landf. 2006, 31, 1381–1393. [Google Scholar] [CrossRef]
- Jourgholami, M.; Nasirian, A.; Labelle, E. Ecological restoration of compacted soil following the application of different leaf litter mulches on the skid trail over a five-year period. Sustainability 2018, 10, 2148. [Google Scholar] [CrossRef] [Green Version]
- Picchio, R.; Proto, A.R.; Civitarese, V.; Di Marzio, N.; Latterini, F. Recent contributions of some fields of the electronics in development of forest operations technologies. Electronics 2019, 8, 1465. [Google Scholar] [CrossRef] [Green Version]
- Jourgholami, M.; Ramineh, A.; Zahedi Amiri, G.; Labelle, E.R. The Influence of slope positions on the recovery response of compacted soil properties and enzyme activity in an Oriental beech stand in the Hyrcanian forests, Iran. Sustainability 2019, 11, 1940. [Google Scholar] [CrossRef] [Green Version]
- Venanzi, R.; Picchio, R.; Spinelli, R.; Grigolato, S. Soil disturbance and recovery after coppicing a Mediterranean Oak stand: The effects of silviculture and technology. Sustainability 2020, 12, 4074. [Google Scholar] [CrossRef]
- Jourgholami, M.; Feghhi, J.; Picchio, R.; Tavankar, F.; Venanzi, R. Efficiency of leaf litter mulch in the restoration of soil physiochemical properties and enzyme activities in temporary skid roads in mixed high forests. Catena 2020, 105012. [Google Scholar] [CrossRef]
- Wang, C.; Chen, M.; Qi, H.; Intasen, W.; Kanchanapant, A. Grain-Size Distribution of Surface Sediments in the Chanthaburi Coast, Thailand and Implications for the Sedimentary Dynamic Environment. J. Mar. Sci. Eng. 2020, 8, 242. [Google Scholar] [CrossRef] [Green Version]
- Ekwue, E.I.; Harrilal, A. Effect of soil type, peat, slope, compaction effort and their interactions on infiltration, runoff and raindrop erosion of some Trinidadian soils. Biosyst. Eng. 2010, 105, 112–118. [Google Scholar] [CrossRef]
- Mohr, C.H.; Coppus, R.; Iroume, A.; Huber, A.; Bronstert, A. Runoff generation and soil erosion processes after clear cutting. J. Geophys. Res. Earth Surf. 2013, 118, 814–831. [Google Scholar] [CrossRef]





| Soil Properties | Unit | Method | Reference for Method |
|---|---|---|---|
| Soil bulk density | g cm−3 | Clod method | Kemper and Rosenau (1986) [39] |
| Water content | % | By drying soil samples at 105 °C for 24 h | Thien and Graveel (2008) [40] |
| Soil particle size distribution | % | Hydrometer method | Gee and Bauder (1986) [41] |
| Soil particle density | g cm−3 | ASTM D854-00 2000 standard | Thien and Graveel (2008) [40] |
| Soil organic C | % | Walkley-Black technique | Walkley and Black (1934) [42] |
| Slope Gradient (%) | Bulk Density (Mg m−3) | Total Porosity (%) | Organic Matter Content (%) | Canopy Cover (%) | Sand (%) | Clay (%) | Silt (%) |
|---|---|---|---|---|---|---|---|
| 5 | 1.33 ± 0.05a | 47.83 ± 1.98a | 2.77 ± 0.51a | 85 ± 3.5a | 38.0 ± 1.7a | 20.3 ± 3.2a | 41.7 ± 1.5a |
| 10 | 1.35 ± 0.02a | 46.97 ± 0.78a | 3.00 ± 0.46a | 85 ± 3.0a | 36.7 ± 1.5a | 22.3 ± 1.2a | 41.0 ± 1.7a |
| 15 | 1.33 ± 0.06a | 47.50 ± 2.15a | 2.61 ± 0.58a | 84 ± 2.5a | 36.3 ± 1.5a | 24.0 ± 1.7a | 39.7 ± 1.2a |
| 20 | 1.34 ± 0.04a | 47.90 ± 2.25a | 3.04 ± 0.29a | 86 ± 2.0a | 37. 7 ± 2.5a | 21.0 ± 1.0a | 41.3 ± 3.2a |
| 25 | 1.35 ± 0.05a | 47.37 ± 1.79a | 2.68 ± 0.60a | 83 ± 2.0a | 36.7 ± 2.5a | 24.0 ± 2.0a | 39.3 ± 2.1a |
| 30 | 1.33 ± 0.05a | 47.63 ± 2.10a | 2.73 ± 0.51a | 83 ± 5.0a | 39.0 ± 2.0a | 24.0 ± 1.7a | 37.0 ± 3.6a |
| 35 | 1.36 ± 0.04a | 46.60 ± 1.92a | 2.61 ± 0.62a | 84 ± 3.0a | 36.4 ± 1.5a | 24.3 ± 1.2a | 39.3 ± 0.6a |
| 40 | 1.34 ± 0.04a | 47.50 ± 1.75a | 2.85 ± 0.43a | 82 ± 3.1a | 39.3 ± 2.5a | 22.7 ± 1.5a | 38.0 ± 4.0a |
| Variable | Runoff (mm) | Runoff Coefficient | Sediment Yield (g m−2) | Bulk Density (Mg m−3) | Total Porosity (%) | Organic Matter Content (%) | Canopy Cover (%) | Sand (%) | Clay (%) | Silt (%) |
|---|---|---|---|---|---|---|---|---|---|---|
| Slope gradient | 0.51 * | 0.55 ** | 0.51 * | 0.06 ns | −0.07 ns | −0.08 ns | −0.28 ns | 0.20 ns | 0.38 ns | −0.47 * |
| Runoff (mm) | 1 | 0.93 ** | 0.78 ** | 0.06 ns | −0.18 ns | −0.09 ns | −0.28 ns | 0.08 ns | 0.49 * | −0.46 * |
| Runoff Coefficient | 1 | 0.83 ** | 0.01 ns | −0.01 ns | −0.04 ns | −0.29 ns | 0.08 ns | 0.46 * | −0.43 * | |
| Sediment Yield (g m−2) | 1 | 0.21 ns | 0.01 ns | −0.08 ns | −0.10 ns | 0.04 ns | 0.37 ns | −0.33 ns | ||
| Bulk Density (Mg m−3) | 1 | −0.28 ns | 0.01 ns | −0.04 ns | −0.06 ns | 0.2 ns | −0.18 ns | |||
| Total Porosity (%) | 1 | −0.32 ns | 0.25 ns | −0.01 ns | −0.42 * | 0.34 ns | ||||
| Organic Matter Content (%) | 1 | 0.01 ns | 0.01 ns | 0.12 ns | −0.09 ns | |||||
| Canopy Cover (%) | 1 | −0.38 ns | −0.19 ns | 0.45 * | ||||||
| Sand (%) | 1 | −0.20 ns | −0.62 ** | |||||||
| Clay (%) | 1 | −0.64 ** | ||||||||
| Silt (%) | 1 |
| Source | Sum of Squares | d.f. | Mean Square | F | P Value |
|---|---|---|---|---|---|
| Runoff | 1582.97 | 7 | 226.14 | 4.76 | ≤0.01 ** |
| Runoff coefficient | 2.56 | 7 | 0.37 | 12.83 | ≤0.01 ** |
| Sediment | 1027.84 | 7 | 146.84 | 8.72 | ≤0.01 ** |
| Slope (%) | Runoff (mm) | Runoff Coefficient | Sediment Yield (g m−2) |
|---|---|---|---|
| 5 | 2.45 ± 0.59c | 0.102 ± 0.027e | 1.36 ± 0.35d |
| 10 | 3.78 ± 0.27bc | 0.157 ± 0.034d | 1.56 ± 0.29d |
| 15 | 5.14 ± 0.31b | 0.205 ± 0.047bc | 1.95 ± 0.27cd |
| 20 | 5.51 ± 0.51b | 0.222 ± 0.082bc | 3.15 ± 0.31b |
| 25 | 6.43 ± 0.35a | 0.265 ± 0.071a | 3.91 ± 0.18a |
| 30 | 6.07 ± 0.28a | 0.244 ± 0.069b | 4.08 ± 0.45a |
| 35 | 4.96 ± 0.37b | 0.210 ± 0.058bc | 2.76 ± 0.21bc |
| 40 | 4.62 ± 0.46b | 0.188 ± 0.063cd | 2.18 ± 0.18cd |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jourgholami, M.; Karami, S.; Tavankar, F.; Lo Monaco, A.; Picchio, R. Effects of Slope Gradient on Runoff and Sediment Yield on Machine-Induced Compacted Soil in Temperate Forests. Forests 2021, 12, 49. https://doi.org/10.3390/f12010049
Jourgholami M, Karami S, Tavankar F, Lo Monaco A, Picchio R. Effects of Slope Gradient on Runoff and Sediment Yield on Machine-Induced Compacted Soil in Temperate Forests. Forests. 2021; 12(1):49. https://doi.org/10.3390/f12010049
Chicago/Turabian StyleJourgholami, Meghdad, Sara Karami, Farzam Tavankar, Angela Lo Monaco, and Rodolfo Picchio. 2021. "Effects of Slope Gradient on Runoff and Sediment Yield on Machine-Induced Compacted Soil in Temperate Forests" Forests 12, no. 1: 49. https://doi.org/10.3390/f12010049
APA StyleJourgholami, M., Karami, S., Tavankar, F., Lo Monaco, A., & Picchio, R. (2021). Effects of Slope Gradient on Runoff and Sediment Yield on Machine-Induced Compacted Soil in Temperate Forests. Forests, 12(1), 49. https://doi.org/10.3390/f12010049