Simulation of Vegetation Cover Based on the Theory of Ecohydrological Optimality in the Yongding River Watershed, China
Abstract
:1. Introduction
2. Materials and Methods
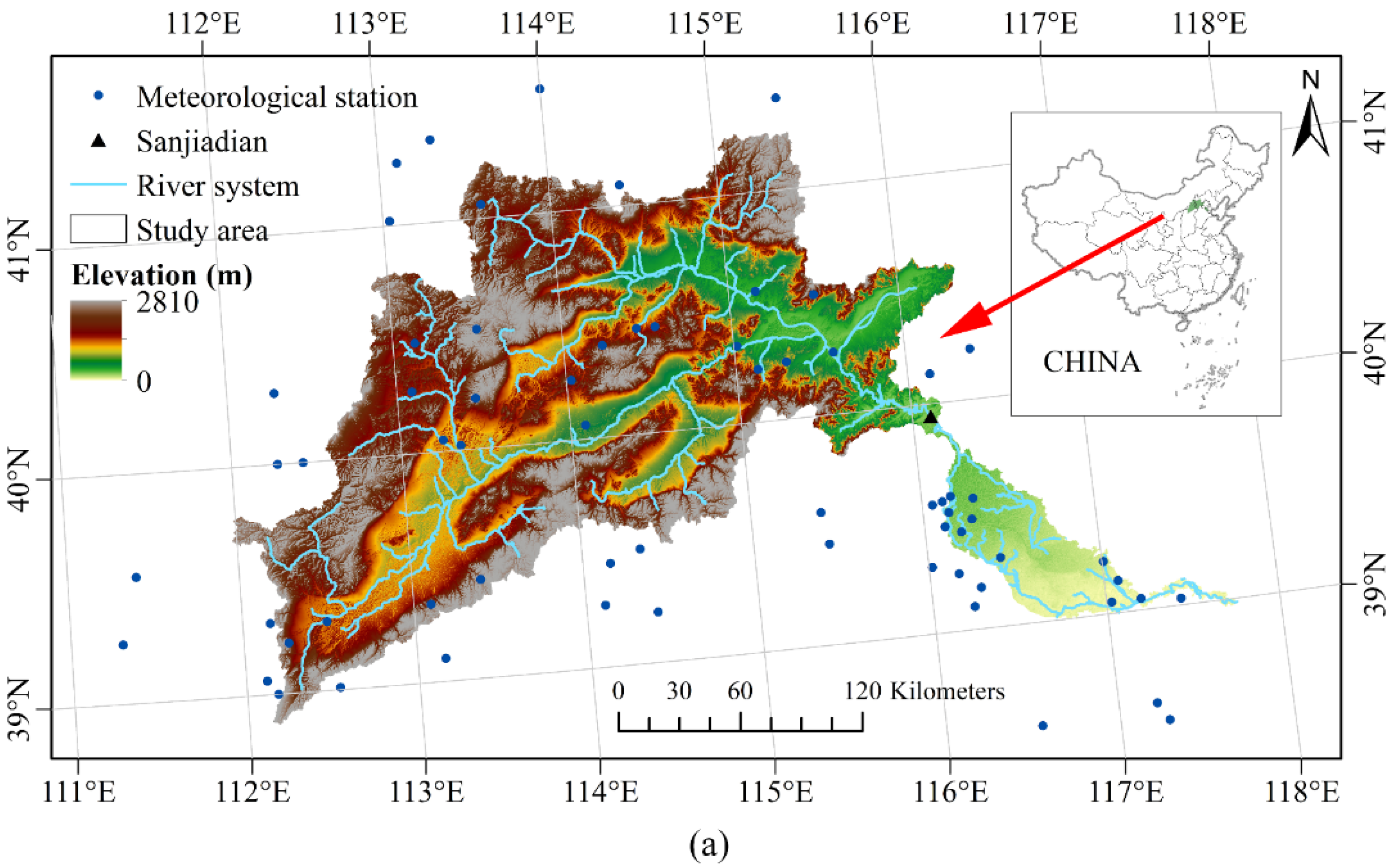
2.1. Study Area
2.2. Data Preparation
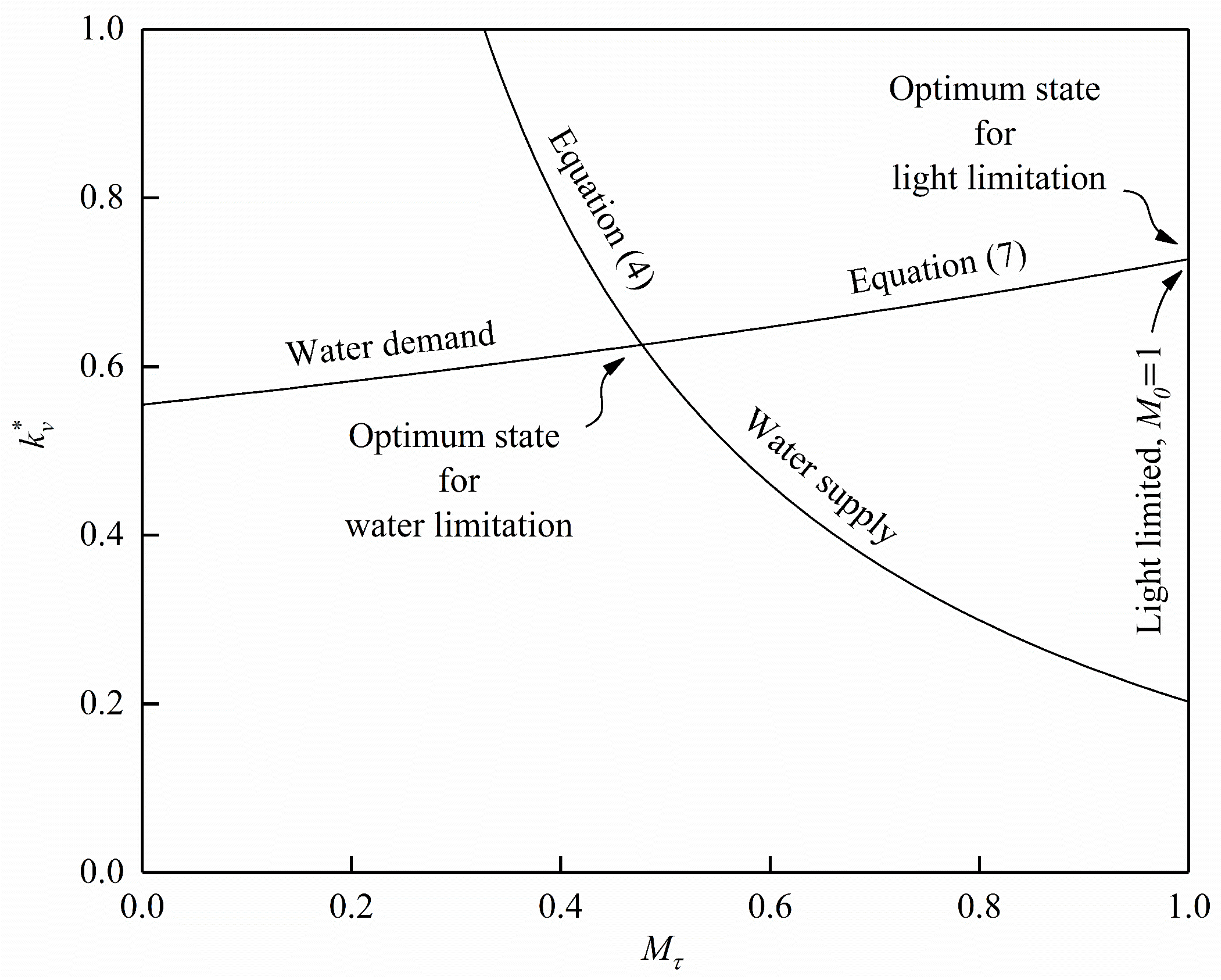
2.3. The Ecohydrological Optimality Model
2.3.1. Water Balance Equation
2.3.2. Potential Canopy Conductance Equation
2.3.3. Ideal Vegetation Coverage
2.4. Multiple Linear Stepwise Regression Analysis
2.5. Sensitivity Analysis
3. Results
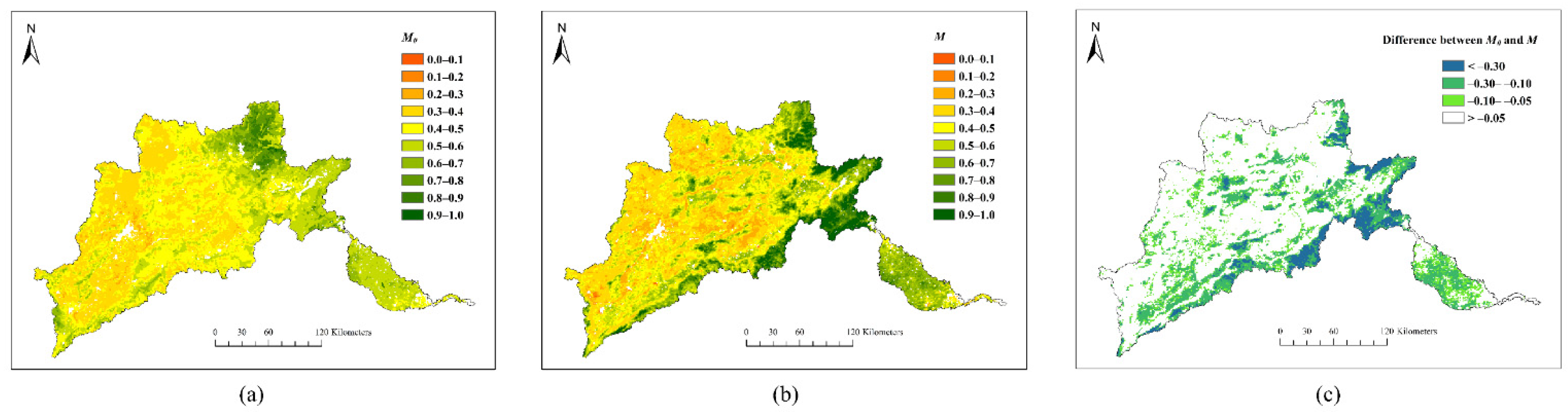
3.1. Spatial Distribution and Impact Factors of Observed Vegetation Coverage
3.2. Verification of Ecohydrological Optimality Theory
3.3. Simulated Vegetation Coverage Based on the Ecohydrological Optimality Model
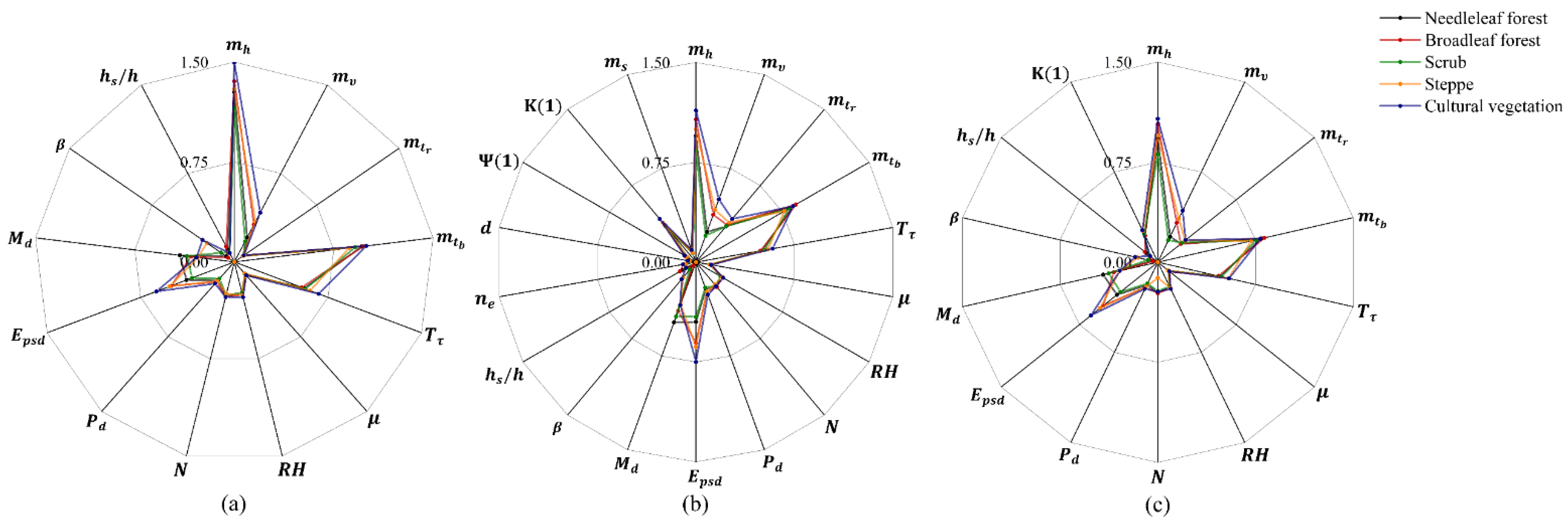
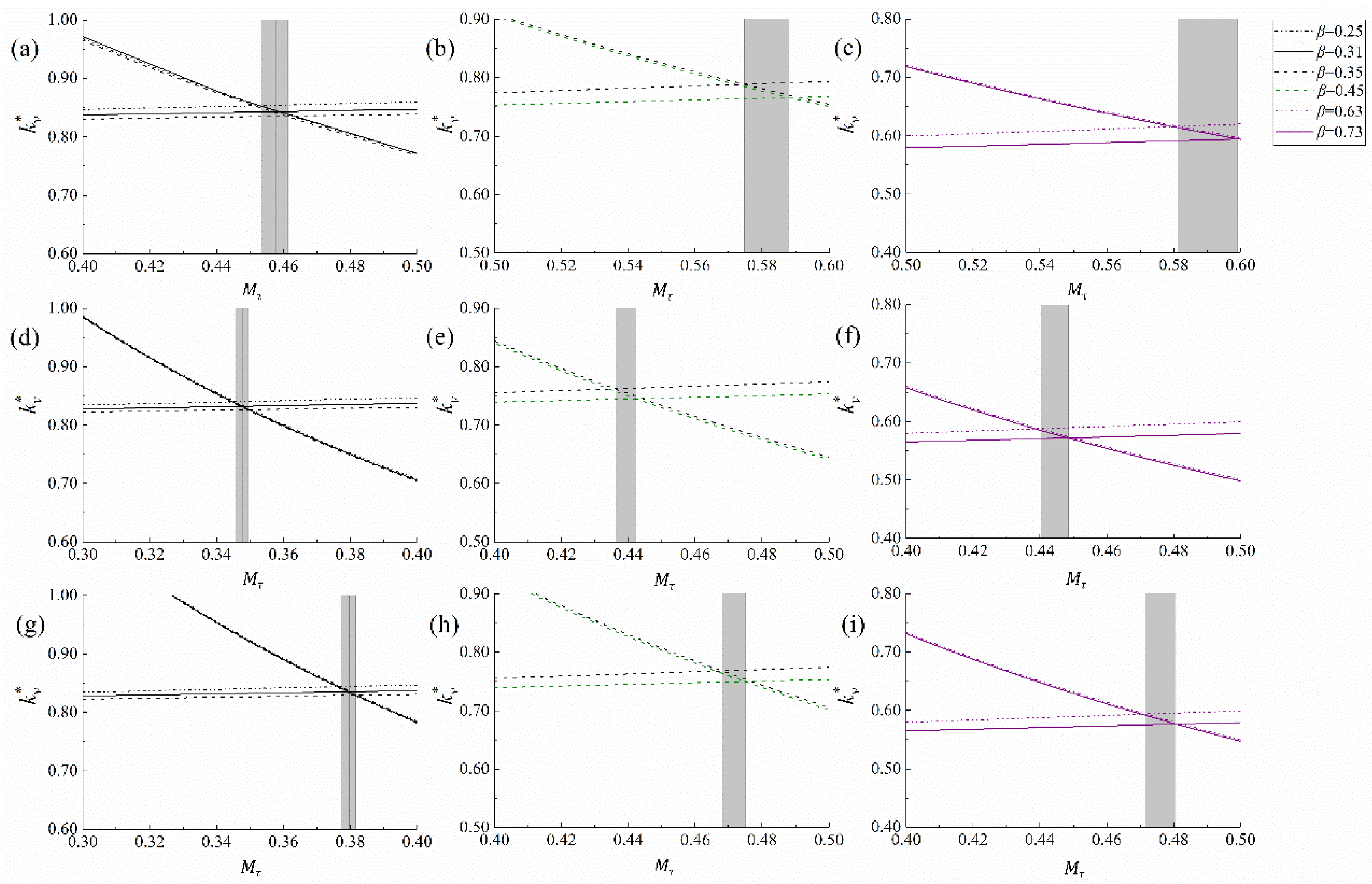
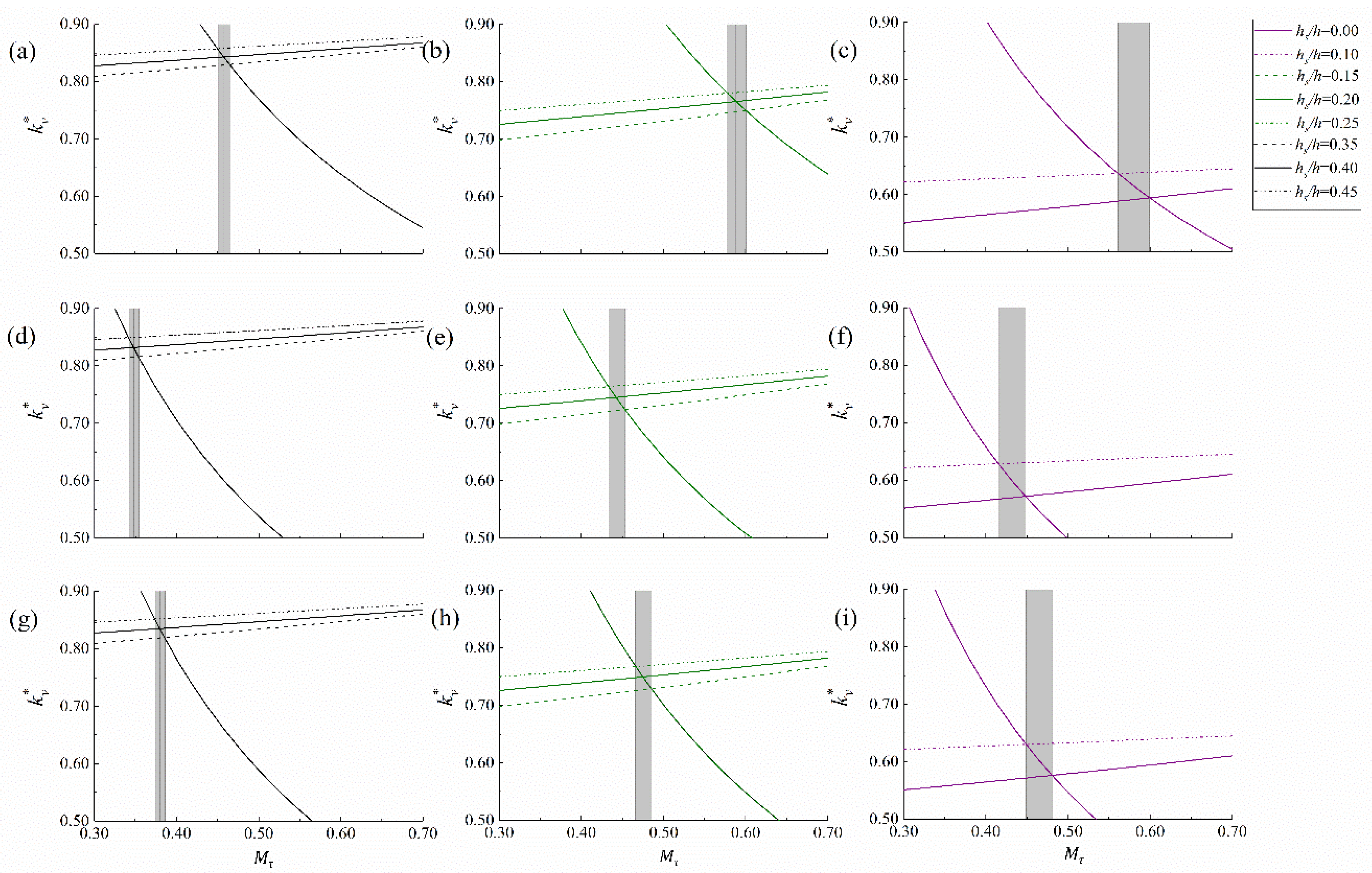
3.4. Sensitivity of the Ideal Vegetation Coverage to the Input Data of the Model
4. Discussion
4.1. Causes for the Distribution Pattern of Vegetation
4.2. Applicability of the Ecohydrological Optimality Theory
4.3. Comparison between Simulated and Observed Vegetation Coverage
4.4. Sensitivity of the Ideal Vegetation Coverage to Meteorological, Soil, and Vegetation Factors
5. Conclusions
- From the spatial point of view, the holistic exhibits horizontal zonal changes that basically correspond to topographic factors, which gradually decrease from the eastern edge of the mountainous area to the central section. Temperature increases limited the water needed by the steppe. The , , and values had the highest correlation with the value, as they controlled the spatial and temporal distribution of the water available for vegetation.
- The ecohydrological optimality model simulates a kind of vegetation coverage that maximizes the productivity of biomass in the absence of water stress rather than the maximum vegetation coverage, as this model cannot completely simulate the adaptive strategies of vegetation to water stress. The vegetation coverage proposed by ecohydrological optimality theory can reduce the risk of embolism in the xylem or roots or vegetation death in the years following drought events, which is significant for maintaining the stability of ecosystems.
- The should be used as the limit of vegetation restoration, regardless of whether the vegetation evolves drought resistance measures. For forests that have reached , we should strengthen the management and improve the quality of existing vegetation. For cultural vegetation that has not reached the value, we should use water-saving irrigation technologies and adjust the structure of agricultural planting. For the steppe, we should use fencing and strengthen management measures to ensure natural growth.
- In this model, the accuracy of meteorological data is essential. The value was the most sensitive to the meteorological factors and when the soil texture of the study area was simulated as sandy loam instead of the other types. The of the steppe is most sensitive to , , and .
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Assumptions of the Theory of Ecohydrological Optimality
Appendix B. Supplementary Formula
References
- Rodriguez-Iturbe, I.; Porporato, A. Ecohydrology of Water-Controlled Ecosystems: Soil Moisture and Plant Dynamics; Cambridge University Press: New York, NY, USA, 2004. [Google Scholar]
- Wang, X.J.; Zhang, B.Q.; Xu, X.F.; Tian, J.; He, C.S. Regional water-energy cycle response to land use/cover change in the agropastoral ecotone, northwest China. J. Hydrol. 2020, 580, 124246. [Google Scholar] [CrossRef]
- Tian, S.Y.; Renzullo, L.J.; van Dijk, A.I.J.M.; Tregoning, P.; Walker, J.P. Global joint assimilation of GRACE and SMOS for improved estimation of root-zone soil moisture and vegetation response. Hydrol. Earth Syst. Sci. 2019, 23, 1067–1081. [Google Scholar] [CrossRef] [Green Version]
- Xu, X.Y.; Yang, D.W.; Sivapalan, M. Assessing the impact of climate variability on catchment water balance and vegetation cover. Hydrol. Earth Syst. Sci. 2012, 16, 43–58. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.Y.; Zhang, B.Q. The responses of natural vegetation dynamics to drought during the growing season across China. J. Hydrol. 2019, 574, 706–714. [Google Scholar] [CrossRef]
- Weltzin, J.F.; Loik, M.E.; Susanne, S.; Williams, D.G.; Fay, P.A.; Haddad, B.M.; John, H.; Huxman, T.E.; Knapp, A.K.; Guanghui, L. Assessing the response of terrestrial ecosystems to potential changes in precipitation. Bioscience 2003, 53, 941–952. [Google Scholar] [CrossRef]
- Noy-Meir, I. Desert ecosystems: Environment and producers. Annu. Rev. Ecol. Syst. 1973, 4, 25–51. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Gouveia, C.; Camarero, J.J.; Begueria, S.; Trigo, R.; Lopez-Moreno, J.I.; Azorin-Molina, C.; Pasho, E.; Lorenzo-Lacruz, J.; Revuelto, J.; et al. Response of vegetation to drought time-scales across global land biomes. Proc. Natl. Acad. Sci. USA 2013, 110, 52–57. [Google Scholar] [CrossRef] [Green Version]
- Brady, N.C.; Weil, R.R. The Nature and Properties of Soils, 8th ed.; Macmillan Publishers: New York, NY, USA, 1974. [Google Scholar]
- Osman, K.T. Physical properties of forest soils. In Forest Soils: Properties and Management; Springer International Publishing: Heidelberg, Germany, 2013; pp. 19–44. [Google Scholar]
- Eagleson, P.S. Ecological optimality in water-limited natural soil-vegetation systems: 1. Theory and hypothesis. Water Resour. Res. 1982, 18, 325–340. [Google Scholar] [CrossRef] [Green Version]
- Chaves, M.M.; Maroco, J.P.; Pereira, J.S. Understanding plant responses to drought—From genes to the whole plant. Funct. Plant Biol. 2003, 30, 239–264. [Google Scholar] [CrossRef]
- Ding, Y.B.; Xu, J.T.; Wang, X.W.; Peng, X.B.; Cai, H.J. Spatial and temporal effects of drought on Chinese vegetation under different coverage levels. Sci. Total Environ. 2020, 716, 137166. [Google Scholar] [CrossRef]
- Volaire, F. A unified framework of plant adaptive strategies to drought: Crossing scales and disciplines. Global Chang. Biol. 2018, 24, 2929–2938. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z.; Huang, M.; Zhao, X.; Wu, L. Adjustments of leaf traits and whole plant leaf area for balancing water supply and demand in Robinia pseudoacacia under different precipitation conditions on the Loess Plateau. Agric. For. Meteorol. 2019, 279, 107733. [Google Scholar] [CrossRef]
- Xu, H.J.; Wang, X.P.; Zhao, C.Y.; Yang, X.M. Diverse responses of vegetation growth to meteorological drought across climate zones and land biomes in northern China from 1981 to 2014. Agric. For. Meteorol. 2018, 262, 1–13. [Google Scholar] [CrossRef]
- Anderegg, L.; Hillerislambers, J. Drought stress limits the geographic ranges of two tree species via different physiological mechanisms. Glob. Chang. Biol. 2016, 22, 1029–1045. [Google Scholar] [CrossRef] [PubMed]
- Kijowska-Oberc, J.; Staszak, A.M.; Kamiński, J.; Ratajczak, E. Adaptation of forest trees to rapidly changing climate. Forests 2020, 11, 123. [Google Scholar] [CrossRef] [Green Version]
- Givnish, T.J. Adaptation to sun and shade: A whole-plant perspective. Aust. J. Plant Physiol. 1988, 15, 63–92. [Google Scholar] [CrossRef] [Green Version]
- Caylor, K.K.; Scanlon, T.M.; Rodriguez-Iturbe, I. Feasible optimality of vegetation patterns in river basins. Geophys. Res. Lett. 2004, 31, 1–4. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.J.; Sperry, J.S.; Anderegg, W.R.L.; Venturas, M.D.; Trugman, A.T. A theoretical and empirical assessment of stomatal optimization modeling. New Phytol. 2020, 227, 311–325. [Google Scholar] [CrossRef] [Green Version]
- Eagleson, P.S.; Tellers, T.E. Ecological optimality in water-limited natural soil-vegetation systems: 2. Tests and applications. Water Resour. Res. 1982, 18, 341–354. [Google Scholar] [CrossRef] [Green Version]
- Eagleson, P.S. Ecohydrology: Darwinian Expression of Vegetation Form and Function; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Eagleson, P.S. Dynamics of flood frequency. Water Resour. Res. 1972, 8, 878–898. [Google Scholar] [CrossRef]
- Eagleson, P.S. Climate, soil, and vegetation: 1. Introduction to water balance dynamics. Water Resour. Res. 1978, 14, 705–712. [Google Scholar] [CrossRef] [Green Version]
- Eagleson, P.S. Climate, soil, and vegetation: 2. The distribution of annual precipitation derived from observed storm sequences. Water Resour. Res. 1978, 14, 713–721. [Google Scholar] [CrossRef] [Green Version]
- Eagleson, P.S. Climate, soil, and vegetation: 3. A simplified model of soil moisture movement in the liquid phase. Water Resour. Res. 1978, 14, 722–730. [Google Scholar] [CrossRef] [Green Version]
- Eagleson, P.S. Climate, soil, and vegetation: 4. The expected value of annual evapotranspiration. Water Resour. Res. 1978, 14, 731–739. [Google Scholar] [CrossRef] [Green Version]
- Eagleson, P.S. Climate, soil, and vegetation: 5. A derived distribution of storm surface runoff. Water Resour. Res. 1978, 14, 741–748. [Google Scholar] [CrossRef] [Green Version]
- Eagleson, P.S. Climate, soil, and vegetation: 6. Dynamics of the annual water balance. Water Resour. Res. 1978, 14, 749–764. [Google Scholar] [CrossRef] [Green Version]
- Eagleson, P.S. Climate, soil, and vegetation: 7. A derived distribution of annual water yield. Water Resour. Res. 1978, 14, 765–776. [Google Scholar] [CrossRef] [Green Version]
- Restrepo-Posada, P.J.; Eagleson, P.S. Identification of independent rainstorms. J. Hydrol. 1982, 55, 303–319. [Google Scholar] [CrossRef]
- Entekhabi, D.; Rodriguez-Iturbe, I.; Eagleson, P.S. Probabilistic representation of the temporal rainfall process by a modified Neyman-Scott rectangular pulses model: Parameter estimation and validation. Water Resour. Res. 1989, 25, 295–302. [Google Scholar] [CrossRef] [Green Version]
- Guo, Y.P.; Adams, B.J. Hydrologic analysis of urban catchments with event-based probabilistic models: 1. Runoff volume. Water Resour. Res. 1998, 34, 3421–3431. [Google Scholar] [CrossRef]
- Guo, Y.P.; Adams, B.J. Hydrologic analysis of urban catchments with event-based probabilistic models: 2. Peak discharge rate. Water Resour. Res. 1998, 34, 3433–3443. [Google Scholar] [CrossRef]
- Guo, Y.P.; Liu, S.G.; Baetz, B.W. Probabilistic rainfall-runoff transformation considering both infiltration and saturation excess runoff generation processes. Water Resour. Res. 2012, 48, 1–17. [Google Scholar] [CrossRef] [Green Version]
- Kochendorfer, J.P.; Ramirez, J.A. Modeling the monthly mean soil-water balance with a statistical-dynamical ecohydrology model as coupled to a two-component canopy model. Hydrol. Earth Syst. Sci. 2010, 14, 2099–2120. [Google Scholar] [CrossRef]
- Salvucci, G.D.; Entekhabi, D. Comparison of the Eagleson statistical-dynamical water balance model with numerical simulations. Water Resour. Res. 1994, 30, 2751–2757. [Google Scholar] [CrossRef]
- Rodriguez-Iturbe, I. Ecohydrology: A hydrologic perspective of climate-soil-vegetation dynamies. Water Resour. Res. 2000, 36, 3–9. [Google Scholar] [CrossRef] [Green Version]
- Mo, K.L.; Cong, Z.T.; Lei, H.M. Optimal vegetation cover in the Horqin Sands, China. Ecohydrology 2016, 9, 700–711. [Google Scholar] [CrossRef]
- Cong, Z.T.; Li, Q.S.; Mo, K.L.; Zhang, L.X.; Shen, H. Ecohydrological optimality in the Northeast China Transect. Hydrol. Earth Syst. Sci. 2017, 21, 2449–2462. [Google Scholar] [CrossRef] [Green Version]
- Zhang, S.L.; Yang, D.W.; Yang, Y.T.; Piao, S.L.; Yang, H.B.; Lei, H.M.; Fu, B.J. Excessive afforestation and aoil drying on China’s Loess Plateau. J. Geophys. Res. Biogeosci. 2018, 123, 923–935. [Google Scholar] [CrossRef]
- Kerkhoff, A.J.; Martens, S.N.; Milne, B.T. An ecological evaluation of Eagleson’s optimality hypotheses. Funct. Ecol. 2004, 18, 404–413. [Google Scholar] [CrossRef]
- Li, M.M.; Wu, B.F.; Yan, C.Z.; Zhou, W.F. Estimation of vegetation fraction in the upper basin of Miyun reservoir by remote sensing. Resour. Sci. 2004, 26, 153–159. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. FAO Irrigation and Drainage Paper; Food and Agriculture Organization of the United Nations: Rome, Italy, 1998. [Google Scholar]
- Rauner, J.L. Deciduous forests. In Vegetation and the Atmosphere; Academic Press: New York, NY, USA, 1976; Volume 2, pp. 241–264. [Google Scholar]
- Ripley, E.A.; Redmann, R.E. Grassland. In Vegetation and the Atmosphere; Academic Press: New York, NY, USA, 1976; Volume 2. [Google Scholar]
- Waring, R.H. Estimating forest growth and efficiency in relation to canopy leaf area. Adv. Ecol. Res. 1983, 13, 327–354. [Google Scholar] [CrossRef]
- Amiro, B.D. Drag coefficients and turbulence spectra within three boreal forest anopies. Bound.-Lay Meteorol. 1990, 52, 227–246. [Google Scholar] [CrossRef]
- Horn, H.S. The Adaptive Geometry of Trees; Princeton University Press: Princeton, NJ, USA, 1971. [Google Scholar]
- Afantitis, A.; Melagraki, G.; Sarimveis, H.; Koutentis, P.A.; Markopoulos, J.; Igglessi-Markopoulou, O. A novel simple QSAR model for the prediction of anti-HIV activity using multiple linear regression analysis. Mol. Divers. 2006, 10, 405–414. [Google Scholar] [CrossRef]
- Francos, A.; Elorza, F.J.; Bouraoui, F.; Bidoglio, G.; Galbiati, L. Sensitivity analysis of distributed environmental simulation models: Understanding the model behaviour in hydrological studies at the catchment scale. Reliab. Eng. Syst. Saf. 2003, 79, 205–218. [Google Scholar] [CrossRef]
- Gao, Y.H.; Sha, X.J.; Xu, X.Y. Sensitivity analysis of SWMM model parameters based on Morris method. J. Water Res. Water Eng. 2016, 27, 87–90. [Google Scholar] [CrossRef]
- Al Balasmeh, O.I.; Karmaker, T. Effect of temperature and precipitation on the vegetation dynamics of high and moderate altitude natural forests in India. J. Indian Soc. Remote 2020, 48, 121–144. [Google Scholar] [CrossRef]
- Liu, S.Y.; Huang, S.Z.; Xie, Y.Y.; Wang, H.; Huang, Q.; Leng, G.Y.; Li, P.; Wang, L. Spatial-temporal changes in vegetation cover in a typical semi-humid and semi-arid region in China: Changing patterns, causes and implications. Ecol. Indic. 2019, 98, 462–475. [Google Scholar] [CrossRef]
- Yu, X.; Yang, H.B.; Li, S.E.; Yang, D.W. An improved conceptual model quantifying the effect of climate change and anthropogenic activities on vegetation change in arid regions. Remote Sens. 2019, 11, 2110. [Google Scholar] [CrossRef] [Green Version]
- Shen, Q.; Gao, G.Y.; Han, F.; Xiao, F.Y.; Ma, Y.; Wang, S.; Fu, B.J. Quantifying the effects of human activities and climate variability on vegetation cover change in a hyper-arid endorheic basin. Land Degrad. Dev. 2018, 29, 3294–3304. [Google Scholar] [CrossRef]
- Shaver, G.R.; Canadell, J.; Chapin, F.S.; Gurevitch, J.; Harte, J.; Henry, G.; Ineson, P.; Jonasson, S.; Melillo, J.; Pitelka, L. Global warming and terrestrial ecosystems: A conceptual framework for analysis. Bioscience 2000, 50, 871–882. [Google Scholar] [CrossRef]
- Illman, S. Hilbert’s fifth problem: Review. J. Math. Sci. 2001, 105, 1843–1847. [Google Scholar] [CrossRef]
- Bao, G.; Bao, Y.H.; Sanjjava, A.; Qin, Z.H.; Zhou, Y.; Xu, G. NDVI-indicated long-term vegetation dynamics in Mongolia and their response to climate change at biome scale. Int. J. Climatol. 2015, 35, 4293–4306. [Google Scholar] [CrossRef]
- Chen, Z.F.; Wang, W.G.; Fu, J.Y. Vegetation response to precipitation anomalies under different climatic and biogeographical conditions in China. Sci. Rep. 2020, 10, 830. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sun, W.Y.; Song, X.Y.; Mu, X.M.; Gao, P.; Wang, F.; Zhao, G.G. Spatiotemporal vegetation cover variations associated with climate change and ecological restoration in the Loess Plateau. Agric. For. Meteorol. 2015, 209, 87–99. [Google Scholar] [CrossRef]
- Bhusal, N.; Lee, M.; Han, A.R.; Han, A.; Kim, H.S. Responses to drought stress in Prunus sargentii and Larix kaempferi seedlings using morphological and physiological parameters. For. Ecol. Manag. 2020, 465, 1–12. [Google Scholar] [CrossRef]
- Verbruggen, W.; Schurgers, G.; Horion, S.; Ardo, J.; Bernardino, P.N.; Cappelaere, B.; Demarty, J.; Fensholt, R.; Kergoat, L.; Sibret, T.; et al. Contrasting responses of woody and herbaceous vegetation to altered rainfall characteristics in the Sahel. Biogeosciences 2021, 18, 77–93. [Google Scholar] [CrossRef]
- Zhang, W.M.; Brandt, M.; Tong, X.Y.; Tian, Q.J.; Fensholt, R. Impacts of the seasonal distribution of rainfall on vegetation productivity across the Sahel. Biogeosciences 2018, 15, 319–330. [Google Scholar] [CrossRef] [Green Version]
- Deng, S.F.; Yang, T.B.; Zeng, B.; Zhu, X.F.; Xu, H.J. Vegetation cover variation in the Qilian Mountains and its response to climate change in 2000–2011. J. Mt. Sci. 2013, 10, 1050–1062. [Google Scholar] [CrossRef]
- Riihimäki, H.; Heiskanen, J.; Luoto, M. The effect of topography on arctic-alpine aboveground biomass and NDVI patterns. Int. J. Appl. Earth Obs. 2017, 56, 44–53. [Google Scholar] [CrossRef] [Green Version]
- Shavrukov, Y.; Kurishbayev, A.; Jatayev, S.; Shvidchenko, V.; Zotova, L.; Koekemoer, F.; De Groot, S.; Soole, K.; Langridge, P. Early flowering as a drought escape mechanism in plants: How can it aid wheat production? Front. Plant Sci. 2017, 8, 1950. [Google Scholar] [CrossRef]
- Craine, J.M.; Ocheltree, T.W.; Nippert, J.B.; Towne, E.G.; Skibbe, A.M.; Kembel, S.W.; Fargione, J.E. Global diversity of drought tolerance and grassland climate-change resilience. Nat. Clim. Chang. 2013, 3, 63–67. [Google Scholar] [CrossRef]
- Piao, S.L.; Friedlingstein, P.; Ciais, P.; Viovy, N.; Demarty, J. Growing season extension and its impact on terrestrial carbon cycle in the Northern Hemisphere over the past 2 decades. Glob. Biogeochem. Cycles 2007, 21, 3018. [Google Scholar] [CrossRef]
- Butterfield, Z.; Buermann, W.; Keppel-Aleks, G. Satellite observations reveal seasonal redistribution of northern ecosystem productivity in response to interannual climate variability. Remote Sens. Environ. 2020, 242, 111755. [Google Scholar] [CrossRef]
- Running, S.W.; Mu, Q.Z.; Zhao, M.S.; Moreno, A. MODIS Global Terrestrial Evapotranspiration (ET) Product (MOD16A2/A3 and Year-End Gap-Filled MOD16A2GF/A3GF) NASA Earth Observing System MODIS Land Algorithm (For Collection 6). 2019. Available online: https://modis-land.gsfc.nasa.gov/pdf/MOD16UsersGuideV2.022019.pdf (accessed on 29 January 2019).
- Levitt, J. Water, radiation, salt, and other stresses. In Responses of Plants to Environmental Stresses, 2nd ed.; Academic Press: New York, NY, USA, 1980; Volume 2. [Google Scholar]
- McDowell, N.; Pockman, W.T.; Allen, C.D.; Breshears, D.D.; Cobb, N.; Kolb, T.; Plaut, J.; Sperry, J.; West, A.; Williams, D.G. Mechanisms of plant survival and mortality during drought: Why do some plants survive while others succumb to drought? New Phytol. 2008, 178, 719–739. [Google Scholar] [CrossRef] [PubMed]
- Lu, Y.J.; Duursma, R.A.; Farrior, C.E.; Medlyn, B.E.; Feng, X. Optimal stomatal drought response shaped by competition for water and hydraulic risk can explain plant trait covariation. New Phytol. 2020, 225, 1206–1217. [Google Scholar] [CrossRef]
- Moran, E.; Lauder, J.; Musser, C.; Stathos, A.; Shu, M. The genetics of drought tolerance in conifers. New Phytol. 2017, 216, 1034–1048. [Google Scholar] [CrossRef] [Green Version]
- Schwarz, J.; Skiadaresis, G.; Kohler, M.; Kunz, J.; Schnabel, F.; Vitali, V.; Bauhus, J. Quantifying growth responses of trees to drought—A critique of commonly used resilience indices and recommendations for future studies. Curr. For. Rep. 2020, 6, 185–200. [Google Scholar] [CrossRef]
- Samuelson, L.J.; Stokes, T.A.; Ramirez, M.R.; Mendonca, C.C. Drought tolerance of a Pinus palustris plantation. For. Ecol. Manag. 2019, 451, 117557. [Google Scholar] [CrossRef]
- Anderegg, W.R.L.; Plavcova, L.; Anderegg, L.D.L.; Hacke, U.G.; Berry, J.A.; Field, C.B. Drought’s legacy: Multiyear hydraulic deterioration underlies widespread aspen forest die-off and portends increased future risk. Glob. Chang. Biol. 2013, 19, 1188–1196. [Google Scholar] [CrossRef] [PubMed]
- Berdanier, A.B.; Clark, J.S. Multiyear drought-induced morbidity preceding tree death in southeastern US forests. Ecol. Appl. 2016, 26, 17–23. [Google Scholar] [CrossRef] [Green Version]
- McDowell, N.G.; Williams, A.P.; Xu, C.; Pockman, W.T.; Dickman, L.T.; Sevanto, S.; Pangle, R.; Limousin, J.; Plaut, J.; Mackay, D.S.; et al. Multi-scale predictions of massive conifer mortality due to chronic temperature rise. Nat. Clim. Chang. 2016, 6, 295–300. [Google Scholar] [CrossRef]
- Li, Y.R.; Cao, Z.; Long, H.L.; Liu, Y.S.; Li, W.J. Dynamic analysis of ecological environment combined with land cover and NDVI changes and implications for sustainable urban–rural development: The case of Mu Us Sandy Land, China. J. Clean. Prod. 2017, 142, 697–715. [Google Scholar] [CrossRef]
- Horton, R.E. The role of infiltration in the hydrologic cycle. Eos Trans. Am. Geophys. Union 1933, 14, 446–460. [Google Scholar] [CrossRef]



| Symbols | Description | Units | Values | |||||
|---|---|---|---|---|---|---|---|---|
| Needleleaf Forest | Broadleaf Forest | Scrub | Steppe | Cultural Vegetation | ||||
| Meteorological data | mean storm depth during growing season | mm | 13.90 | 13.41 | 14.25 | 12.93 | 13.63 | |
| number of independent storms per growing season | time−1 | 28.41 | 28.87 | 28.49 | 29.30 | 28.73 | ||
| mean storm duration during growing season | days | 0.54 | 0.53 | 0.54 | 0.53 | 0.53 | ||
| mean time between storms during growing season | days | 5.91 | 5.81 | 5.89 | 5.72 | 5.85 | ||
| mean daily air temperature during growing season | °C | 19.64 | 18.17 | 19.30 | 16.37 | 18.29 | ||
| mean daily wind speed at 2 m height during growing season | m/s | 2.14 | 2.20 | 2.13 | 2.36 | 2.29 | ||
| mean daily relative humidity during growing season | % | 56.38 | 55.21 | 56.75 | 55.41 | 55.78 | ||
| mean sunshine duration per day during growing season | h | 7.79 | 7.94 | 7.73 | 8.03 | 7.87 | ||
| precipitation during nongrowing season | mm | 57.09 | 56.81 | 58.92 | 55.95 | 56.44 | ||
| mean potential rate evaporation during growing season | mm/day | 4.14 | 4.14 | 4.12 | 4.12 | 4.14 | ||
| mean potential rate evaporation during nongrowing season | mm/day | 1.35 | 1.30 | 1.34 | 1.27 | 1.30 | ||
| slope of saturation vapor pressure curve | kPa/°C | 0.15 | 0.14 | 0.14 | 0.13 | 0.14 | ||
| surface psychrometric constant | kPa/°C | 0.06 | 0.06 | 0.06 | 0.06 | 0.06 | ||
| length of the growing season | days | 183 | 183 | 183 | 183 | 183 | ||
| length of the nongrowing season | days | 182 | 182 | 182 | 182 | 182 | ||
| Vegetation data | mean vegetation coverage during growing season | dimensionless | 0.78 | 0.59 | 0.69 | 0.50 | 0.46 | |
| mean vegetation coverage during nongrowing season | dimensionless | 0.52 | 0.39 | 0.51 | 0.35 | 0.31 | ||
| mean foliage area index during growing season | dimensionless | 1.82 | 1.29 | 1.47 | 0.92 | 0.86 | ||
| cosine of leaf angle | dimensionless | 0.45 a | 0.31 a | 0.45 a | 0.73 a | 0.73 a | ||
| stem fraction, stem height/tree height | dimensionless | 0.40 b | 0.40 b | 0.20 b | 0.00 b | 0.15 b | ||
| stomatal leaf area/illuminated leaf area | dimensionless | 2.50 c | 1.00 c | 1.00 c | 1.00 c | 1.00 c | ||
| exponent relating shear stress on foliage to horizontal wind velocity | dimensionless | 0.50 d | 0.50 d | 0.50 d | 0.59 d | 0.59 d | ||
| number of sides of each foliage element producing surface resistance to wind | dimensionless | 2.00 d | 2.00 d | 2.00 d | 2.00 d | 2.00 d | ||
| Symbols | Description | Units | Values | ||||
|---|---|---|---|---|---|---|---|
| Loamy Clay | Clay Loam | Sandy Clay Loam | Loam | Sandy Loam | |||
| effective soil porosity | dimensionless | 0.45 | 0.45 | 0.45 | 0.35 | 0.25 | |
| diffusivity index of soil | dimensionless | 4.30 | 4.30 | 4.30 | 2.90 | 2.30 | |
| saturated matrix potential of soil | mm | 900 | 900 | 900 | 450 | 250 | |
| effective saturated hydraulic conductivity of soil | mm/day | 29.40 | 29.40 | 29.40 | 29.40 | 2940 | |
| soil pore-size distribution index | dimensionless | 0.44 | 0.44 | 0.44 | 1.20 | 3.30 | |
| Meteorological Variables | Vegetation Types | ||||
|---|---|---|---|---|---|
| Needleleaf Forest | Broadleaf Forest | Scrub | Steppe | Cultural Vegetation | |
| 0.5515 | 0.5256 | 0.2060 | 0.1305 | 0.7294 | |
| - | - | - | - | - | |
| 0.1907 | 0.2778 | 0.02631 | 0.05210 | 0.04273 | |
| −0.1144 | −0.1214 | −0.05810 | −0.1769 | −0.2335 | |
| - | - | - | −0.2071 | - | |
| - | −0.1674 | −0.1687 | −0.2834 | −0.06677 | |
| - | - | 0.3956 | 0.5016 | - | |
| - | −0.08726 | - | - | - | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Zhao, T.; Shi, C.; Ma, Q. Simulation of Vegetation Cover Based on the Theory of Ecohydrological Optimality in the Yongding River Watershed, China. Forests 2021, 12, 1377. https://doi.org/10.3390/f12101377
Zhang Y, Zhao T, Shi C, Ma Q. Simulation of Vegetation Cover Based on the Theory of Ecohydrological Optimality in the Yongding River Watershed, China. Forests. 2021; 12(10):1377. https://doi.org/10.3390/f12101377
Chicago/Turabian StyleZhang, Yixuan, Tingning Zhao, Changqing Shi, and Qiang Ma. 2021. "Simulation of Vegetation Cover Based on the Theory of Ecohydrological Optimality in the Yongding River Watershed, China" Forests 12, no. 10: 1377. https://doi.org/10.3390/f12101377
APA StyleZhang, Y., Zhao, T., Shi, C., & Ma, Q. (2021). Simulation of Vegetation Cover Based on the Theory of Ecohydrological Optimality in the Yongding River Watershed, China. Forests, 12(10), 1377. https://doi.org/10.3390/f12101377






