Testing the Performance of Some Competition Indices against Experimental Data and Outputs of Spatially Explicit Simulation Models
Abstract
:1. Introduction
2. Materials and Methods
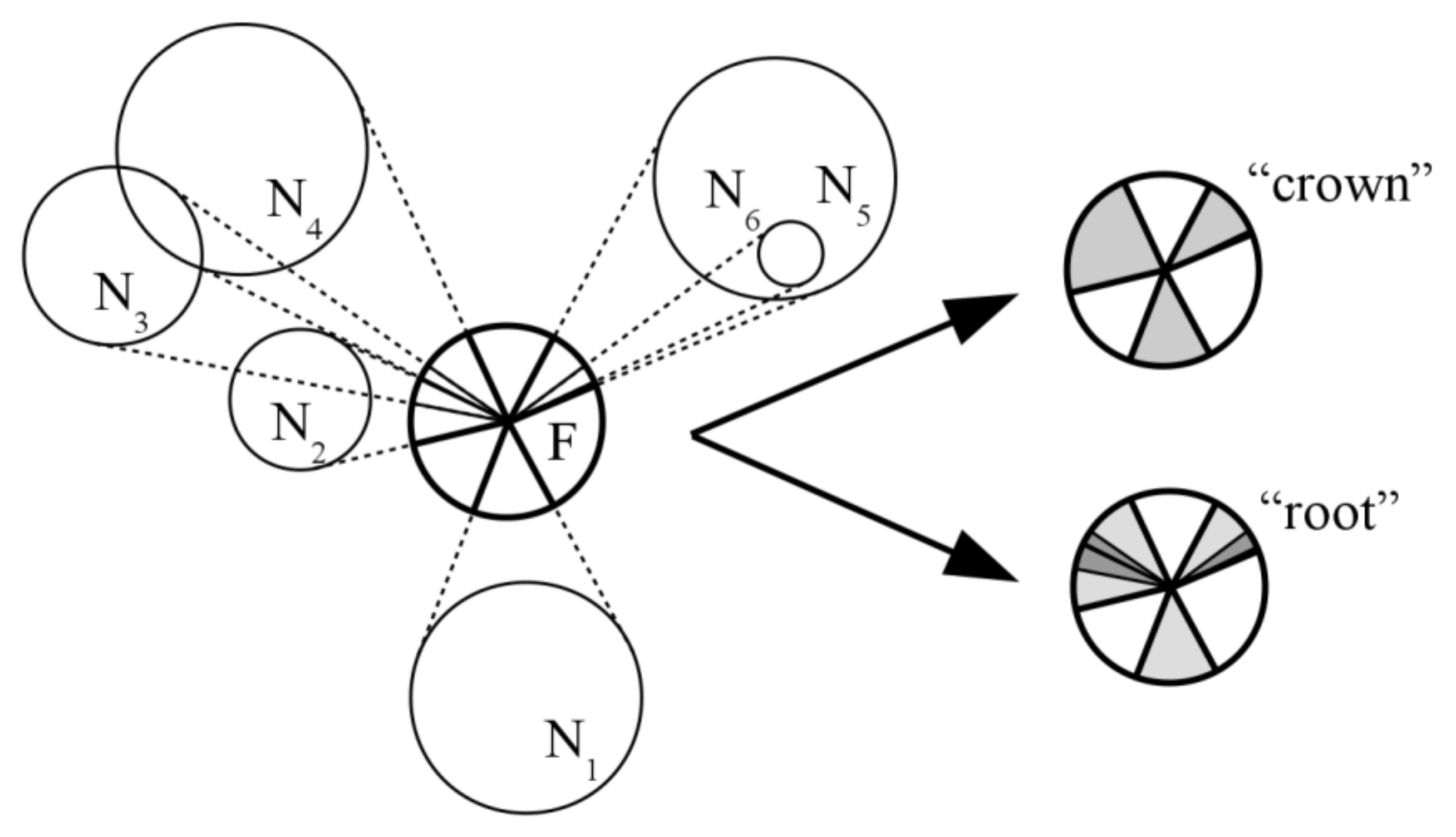
2.1. Description of Competition Indices
2.2. Brief Description of Spatially Explicit Mechanistic Models of Competition
2.3. Design of the Simulation Experiment
2.4. Description of Experimental Data Used for Comparison of the Competition Indices
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Uria-Diez, J.; Pommerening, A. Crown plasticity in Scots pine (Pinus sylvestris L.) as a strategy of adaptation to competition and environmental factors. Ecol. Model. 2017, 356, 117–126. [Google Scholar] [CrossRef]
- Cabal, C.; Martínez-García, R.; Valladares, F. The ecology of plant interactions: A giant with feet of clay. Preprints 2020, unpublished work. [Google Scholar]
- Trinder, C.J.; Brooker, R.W.; Davidson, H.; Robinson, D. Directly quantifying multiple interacting influences on plant competition. Plant Cell Environ. 2021, 44, 1268–1277. [Google Scholar] [CrossRef] [PubMed]
- Pretzsch, H. Canopy space filling and tree crown morphology in mixed-species stands. For. Ecol. Manag. 2014, 327, 251–264. [Google Scholar] [CrossRef] [Green Version]
- Perttunen, J. The LIGNUM Functional-Structural Tree Model [Dissertation]; Systems Analysis Laboratory, Helsinki University of Technology: Helsinki, Finland, 2009; ISBN 978-951-22-9709-2. [Google Scholar]
- Olchev, A.; Radler, K.; Sogachev, A.; Panferov, O.; Gravenhorst, G. Application of a three-dimensional model for assessing effects of small clear-cuttings on radiation and soil temperature. Ecol. Model. 2009, 220, 3046–3056. [Google Scholar] [CrossRef]
- Mao, Z.; Saint-André, L.; Bourrier, F.; Stokes, A.; Cordonnier, T. Modelling and predicting the spatial distribution of tree root density in heterogeneous forest ecosystems. Ann. Bot. 2015, 116, 261–277. [Google Scholar] [CrossRef] [Green Version]
- Daniels, R.F.; Burkhart, H.E.; Clason, T.R. A comparison of competition measures for predicting growth of loblolly pine trees. Can. J. For. Res. 1986, 16, 1230–1237. [Google Scholar] [CrossRef]
- Rouvinen, S.; Kuuluvainen, T. Structure and asymmetry of tree crowns in relation to local competition in a natural mature Scot pine forest. Can. J. For. Res. 1997, 27, 890–902. [Google Scholar] [CrossRef]
- Corral Rivas, J.J.; Álvarez González, J.G.; Aguirre, O.; Hernández, F.J. The effect of competition on individual tree basal area growth in mature stands of Pinus cooperi Blanco in Durango (Mexico). Eur. J. For. Res. 2005, 124, 133–142. [Google Scholar] [CrossRef]
- Shanin, V.; Mäkipää, R.; Shashkov, M.; Ivanova, N.; Shestibratov, K.; Moskalenko, S.; Rocheva, L.; Grabarnik, P.; Bobkova, K.; Manov, A.; et al. New procedure for the simulation of belowground competition can improve the performance of forest simulation models. Eur. J. For. Res. 2015, 134, 1055–1074. [Google Scholar] [CrossRef]
- Shanin, V.N.; Grabarnik, P.Y.; Shashkov, M.P.; Ivanova, N.V.; Bykhovets, S.S.; Frolov, P.V.; Stamenov, M.N. Crown asymmetry and niche segregation as an adaptation of trees to competition for light: Conclusions from simulation experiments in mixed boreal stands. MCFNS 2020, 12, 26–49. [Google Scholar] [CrossRef]
- Hegyi, F. A simulation model for managing jack-pine stands. In Growth Models for Tree and Stand Simulation. Proceedings IUFRO Meeting S4.01.04; Fries, J., Ed.; Royal College of Forestry: Stockholm, Sweden, 1974; pp. 74–90. [Google Scholar]
- Sizov, I.; Grabarnik, P. The comparison of competition indices with simulation model of the light regime of forest canopy [Sravnenie indeksov konkurentsii s pomoshch’yu imitatsionnoi modeli svetovogo rezhima drevostoya]. In Principles and Ways to the Biodiversity Conservation: Proceedings of III All-Russian Scientific Conference; Zhukova, L., Ed.; Mari State University: Yoshkar-Ola, Russia, 2008; pp. 488–489. [Google Scholar]
- Arney, J.D. Tables for Quantifying Competitive Stress on Individual Trees; Inf. Rep. BC-X-7; Canadian Forestry Service, Pacific Forest Research Center: Victoria, BC, Canada, 1973. [Google Scholar]
- Schneider, M.K.; Law, R.; Illian, J.B. Quantification of neighborhood-dependent plant growth by Bayesian hierarchical modelling. J. Ecol. 2006, 94, 310–321. [Google Scholar] [CrossRef]
- Pommerening, A.; LeMay, V.; Stoyan, D. Model-based analysis of the influence of ecological processes on forest point pattern formation—A case study. Ecol. Model. 2011, 222, 666–678. [Google Scholar] [CrossRef]
- Pommerening, A.; Maleki, K. Differences between competition kernels and traditional size-ratio based competition indices used in forest ecology. For. Ecol. Manag. 2014, 331, 135–143. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing. Available online: http://www.R-project.org/ (accessed on 26 August 2021).
- Shanin, V.N.; Shashkov, M.P.; Ivanova, N.V.; Grabarnik, P.Y. The effect of aboveground competition on spatial structure and crown shape of the dominating canopy species of forest stands of European Russia [Vliyanie konkurentsii v pologe lesa na prostranstvennuyu strukturu drevostoev i formu kron dominantov drevesnogo yarusa na primere lesov evropeiskoi chasti Rossii]. RJEE 2016, 1. (In Russian) [Google Scholar] [CrossRef]
- Shashkov, M.; Ivanova, N.; Shanin, V.; Grabarnik, P. Ground surveys versus UAV photography: The comparison of two tree crown mapping techniques. In Information Technologies in the Research of Biodiversity; Springer Proceedings in Earth and Environmental Sciences; Bychkov, I., Voronin, V., Eds.; Springer: Cham, Switzerland, 2019; pp. 48–56. [Google Scholar] [CrossRef]
- Shvidenko, A.Z.; Schepaschenko, D.G.; Nilsson, S.; Buluy, Y.I. Tables and Models of Growth and Productivity of Forests of Major Forest Forming Species of Northern Eurasia (Standard and Reference Materials), Second Edition, Supplemented; Federal Agency of Forest Management, International Institute For Applied Systems Analysis: Moscow, Russia, 2008. [Google Scholar]
- Usoltsev, V.A. Biological Productivity of Forest-Forming Species in Eurasia’s Climatic Gradients (as Related to Supporting Decision-Making Processes in Forest Management) [Biologicheskaya Produktivnost’ Lesoobrazuyushchikh Porod v Klimaticheskikh Gradientakh Evrazii (k Menedzhmentu Biosfernykh Funktsiy Lesov)]; Ural State Forest Engineering University: Ekaterinburg, Russia, 2016. (In Russian) [Google Scholar]
- Collalti, A.; Perugini, L.; Santini, M.; Chiti, T.; Nolèc, A.; Matteucci, G.; Valentini, R. A process-based model to simulate growth in forests with complex structure: Evaluation and use of 3D-CMCC Forest Ecosystem Modeling a deciduous forest in Central Italy. Ecol. Model. 2014, 272, 362–378. [Google Scholar] [CrossRef]
- Haefner, J.W.; Poole, G.C.; Dunn, P.V.; Decker, R.T. Edge effects in computer models of spatial competition. Ecol. Model. 1991, 56, 221–244. [Google Scholar] [CrossRef]
- Illian, J.; Penttinen, A.; Stoyan, H.; Stoyan, D. Statistical Analysis and Modelling of Spatial Point Patterns; John Wiley & Sons: New York, NY, USA, 2008. [Google Scholar]
- Vasander, H.; Laine, J. Site type classification on drained peatlands. In Finland—Fenland: Research and Sustainable Utilisation of Mires and Peat; Korhonen, R., Korpela, L., Sarkkola, S., Eds.; Finnish Peatland Society, Maahenki Ltd.: Helsinki, Finland, 2008; pp. 146–151. ISBN 978-952-5652-47-5. [Google Scholar]
- Pedersen, R.Ø.; Næsset, E.; Gobakken, T.; Bollandsås, O.M. On the evaluation of competition indices—The problem of overlapping samples. For. Ecol. Manag. 2013, 310, 120–133. [Google Scholar] [CrossRef]
- Maleki, K.; Kiviste, A.; Korjus, H. Analysis of individual tree competition effect on diameter growth of silver birch in Estonia. For. Syst. 2015, 24, e23. [Google Scholar] [CrossRef] [Green Version]
- Shanin, V.N.; Rocheva, L.K.; Shashkov, M.P.; Ivanova, N.V.; Moskalenko, S.V.; Burnasheva, E.R. Spatial distribution features of the root biomass of some tree species (Picea abies, Pinus sylvestris, Betula sp.). Biol. Bull. 2015, 42, 260–268. [Google Scholar] [CrossRef]
- Pretzsch, H.; Schütze, G. Effect of tree species mixing on the size structure, density, and yield of forest stands. Eur. J. For. Res. 2016, 135, 1–22. [Google Scholar] [CrossRef]
- Morin, X.; Fahse, L.; Scherer-Lorenzen, M.; Bugmann, H. Tree species richness promotes productivity in temperate forests through strong complementarity between species. Ecol. Lett. 2011, 14, 1211–1219. [Google Scholar] [CrossRef]


| Species | A | γl | x | y | z | W | α | β |
|---|---|---|---|---|---|---|---|---|
| pine | 4.5 | 5.0 | 5 | 4 | 3 | 18 | 3.64 | 0.95 |
| spruce | 3.0 | 16.0 | 4 | 1 | 17 | 15 | 4.07 | 0.29 |
| birch | 5.5 | 11.5 | 3 | 5 | 7 | 19 | 3.82 | 1.22 |
| aspen | 5.0 | 10.9 | 3 | 5 | 5 | 21 | 3.78 | 1.25 |
| Stand Type | Age, Years | Density, ha−1 | Height, m | DBH, cm | |
|---|---|---|---|---|---|
| Young | 5 | 10,000 | 1.8 ± 0.45 | 1 ± 0.25 | |
| Pole | 30 | 1600 | 5 ± 1.25 | 5 ± 1.25 | |
| Mature | 70 | 448 | 22 ± 3.3 | 25 ± 3.75 | |
| 2-layered | Canopy | 70 | 224 | 22 ± 3.3 | 25 ± 3.75 |
| Undergrowth | 30 | 800 | 5 ± 1.25 | 5 ± 1.25 | |
| Uneven aged | 20–230 | 768 | 1.9–19.2 | 4.1–38.9 | |
| Subplot | Hegyi Index | Angular Index | Competition Kernel |
|---|---|---|---|
| 1 | 0.544 | 0.657 | 0.493 |
| 2 | 0.590 | 0.662 | 0.515 |
| 3 | 0.567 | 0.669 | 0.509 |
| 4 | 0.556 | 0.680 | 0.499 |
| 5 | 0.545 | 0.677 | 0.516 |
| 6 | 0.567 | 0.671 | 0.520 |
| 7 | 0.571 | 0.663 | 0.516 |
| 8 | 0.559 | 0.672 | 0.515 |
| 9 | 0.584 | 0.665 | 0.507 |
| 10 | 0.539 | 0.652 | 0.489 |
| 11 | 0.590 | 0.679 | 0.520 |
| 12 | 0.548 | 0.674 | 0.509 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shanin, V.; Hökkä, H.; Grabarnik, P. Testing the Performance of Some Competition Indices against Experimental Data and Outputs of Spatially Explicit Simulation Models. Forests 2021, 12, 1415. https://doi.org/10.3390/f12101415
Shanin V, Hökkä H, Grabarnik P. Testing the Performance of Some Competition Indices against Experimental Data and Outputs of Spatially Explicit Simulation Models. Forests. 2021; 12(10):1415. https://doi.org/10.3390/f12101415
Chicago/Turabian StyleShanin, Vladimir, Hannu Hökkä, and Pavel Grabarnik. 2021. "Testing the Performance of Some Competition Indices against Experimental Data and Outputs of Spatially Explicit Simulation Models" Forests 12, no. 10: 1415. https://doi.org/10.3390/f12101415
APA StyleShanin, V., Hökkä, H., & Grabarnik, P. (2021). Testing the Performance of Some Competition Indices against Experimental Data and Outputs of Spatially Explicit Simulation Models. Forests, 12(10), 1415. https://doi.org/10.3390/f12101415






