Prediction of Regional Forest Soil Nutrients Based on Gaofen-1 Remote Sensing Data
Abstract
:1. Introduction
2. Materials and Methods
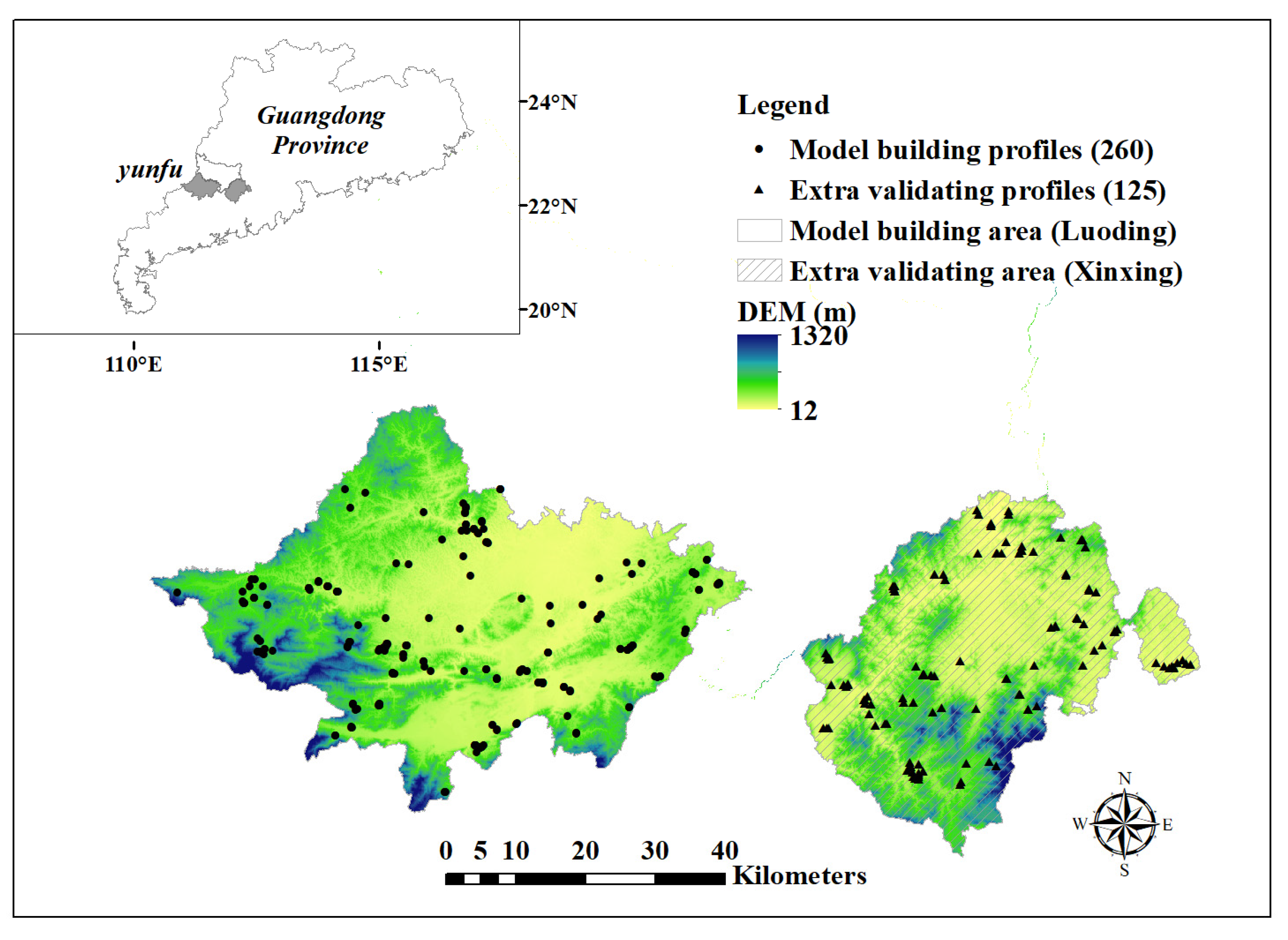
2.1. Study Area
2.2. Data Sources
2.2.1. Coarse-Resolution Soil Map and Soil Sampling
2.2.2. Terrain-Hydrology Variables
2.2.3. Remote Sensing Variables
2.3. Artificial Neural Network Model
Screening and Assessing ANN Models
3. Results
3.1. Exploratory Data Analysis
3.2. Optimal Variables Combination of Each Soil Depths
3.3. Performance of ANN Model Outside of the Model-Building Area
3.4. Spatial Prediction of Soil Nutrients
4. Discussion
4.1. Assessment of Prediction Models
4.2. Effect of Remote Sensing Data on Predicting Soil Nutrients
4.3. Effect of Terrain-Hydrology Data on Predicting Soil Nutrients
4.4. Spatial Distribution of Soil Properties
4.5. Uncertainty and Insufficiency in Current Research
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Grinand, C.; Maire, G.L.; Vieilledent, G.; Razakamanarivo, H.; Razafimbelo, T.; Bernoux, M. Estimating Temporal Changes in Soil Carbon Stocks at Ecoregional Scale in Madagascar Using Remote-Sensing. Int. J. Appl. Earth Obs. Geoinf. 2017, 54, 1–14. [Google Scholar] [CrossRef]
- Tian, L.; Zhao, L.; Wu, X.; Hu, G.; Fang, H.; Zhao, Y.; Sheng, Y.; Chen, J.; Wu, J.; Li, W.; et al. Variations in Soil Nutrient Availability across Tibetan Grassland from the 1980s to 2010s. Geoderma 2019, 338, 197–205. [Google Scholar] [CrossRef]
- Yang, W.; Zhong, Z.; Tang, J.; Heng, W. Study on temporal and spatial characteristics of available soil nitrogen, phosphorus, and potassium among the forest ecosystem of Mt Jinyun. Acta Ecol. Sin. 2001, 21, 1285–1289. (In Chinese) [Google Scholar]
- Heuck, C.; Weig, A.; Spohn, M. Soil Microbial Biomass C:N:P Stoichiometry and Microbial Use of Organic Phosphorus. Soil Biol. Biochem. 2015, 85, 119–129. [Google Scholar] [CrossRef]
- Kindler, R.; Miltner, A.; Richnow, H.; Kastner, M. Fate of Gram-Negative Bacterial Biomass in Soil—Mineralization and Contribution to SOM. Soil Biol. Biochem. 2006, 38, 2860–2870. [Google Scholar] [CrossRef]
- Schloeder, C.A.; Zimmerman, N.E.; Jacobs, M.J. Comparison of Methods for Interpolating Soil Properties Using Limited Data. Soil Sci. Soc. Am. J. 2001, 65, 470–479. [Google Scholar] [CrossRef]
- Martin, M.P.; Wattenbach, M.; Smith, P.; Meersmans, J.; Jolivet, C.; Boulonne, L.; Arrouays, D. Spatial Distribution of Soil Organic Carbon Stocks in France. Biogeosciences 2011, 8, 1053–1065. [Google Scholar] [CrossRef] [Green Version]
- Wu, C.; Wu, J.; Luo, Y.; Zhang, L.; DeGloria, S.D. Spatial Prediction of Soil Organic Matter Content Using Cokriging with Remotely Sensed Data. Soil Sci. Soc. Am. J. 2009, 73, 1202–1208. [Google Scholar] [CrossRef]
- Yigini, Y.; Panagos, P. Assessment of Soil Organic Carbon Stocks under Future Climate and Land Cover Changes in Europe. Sci. Total. Environ. 2016, 557–558, 838–850. [Google Scholar] [CrossRef]
- Behrens, T.; Scholten, T. Digital Soil Mapping in Germany—A Review. J. Plant Nutr. Soil Sci. 2007, 170, 181. [Google Scholar] [CrossRef]
- McBratney, A.B.; Odeh, I.O.A.; Bishop, T.F.A.; Dunbar, M.S.; Shatar, T.M. An Overview of Pedometric Techniques for Use in Soil Survey. Geoderma 2000, 97, 293–327. [Google Scholar] [CrossRef]
- Minasny, B.; McBratney, A.B.; Malone, B.P.; Wheeler, I. Digital Mapping of Soil Carbon. In Advances in Agronomy; Elsevier: Amsterdam, The Netherlands, 2013; Volume 118, pp. 1–47. ISBN 978-0-12-405942-9. [Google Scholar]
- Mulder, V.L.; Lacoste, M.; Richer-de-Forges, A.C.; Martin, M.P.; Arrouays, D. National versus Global Modelling the 3D Distribution of Soil Organic Carbon in Mainland France. Geoderma 2016, 263, 16–34. [Google Scholar] [CrossRef]
- McBratney, A.B.; Mendonça Santos, M.L.; Minasny, B. On Digital Soil Mapping. Geoderma 2003, 117, 3–52. [Google Scholar] [CrossRef]
- Taghizadeh-Mehrjardi, R.; Nabiollahi, K.; Kerry, R. Digital Mapping of Soil Organic Carbon at Multiple Depths Using Different Data Mining Techniques in Baneh Region, Iran. Geoderma 2016, 266, 98–110. [Google Scholar] [CrossRef]
- Zhao, Z.; Chow, T.L.; Yang, Q.; Rees, H.W.; Benoy, G.; Xing, Z.; Meng, F.-R. Model Prediction of Soil Drainage Classes Based on Digital Elevation Model Parameters and Soil Attributes from Coarse Resolution Soil Maps. Can. J. Soil. Sci. 2008, 88, 787–799. [Google Scholar] [CrossRef]
- Zhao, Z.; Yang, Q.; Sun, D.; Ding, X.; Meng, F. Extended Model Prediction of High-Resolution Soil Organic Matter over a Large Area Using Limited Number of Field Samples. Comput. Electron. Agric. 2020, 169, 105172. [Google Scholar] [CrossRef]
- Wang, S.; Jin, X.; Adhikari, K.; Li, W.; Yu, M.; Bian, Z.; Wang, Q. Mapping Total Soil Nitrogen from a Site in Northeastern China. Catena 2018, 166, 134–146. [Google Scholar] [CrossRef]
- Zhao, Z.; Ashraf, M.I.; Meng, F.-R. Model Prediction of Soil Drainage Classes over a Large Area Using a Limited Number of Field Samples: A Case Study in the Province of Nova Scotia, Canada. Can. J. Soil. Sci. 2013, 93, 73–83. [Google Scholar] [CrossRef]
- Zhao, Z.; Yang, Q.; Ding, X.; Xing, Z. Impacts of Coarse-Resolution Soil Maps and High-Resolution Digital-Elevation-Model-Generated Attributes on Modelling Forest Soil Zinc and Copper. Can. J. Soil. Sci. 2021, 101, 261–276. [Google Scholar] [CrossRef]
- Ding, X.; Zhao, Z.; Yang, Q.; Chen, L.; Tian, Q.; Li, X.; Meng, F.-R. Model Prediction of Depth-Specific Soil Texture Distributions with Artificial Neural Network: A Case Study in Yunfu, a Typical Area of Udults Zone, South China. Comput. Electron. Agric. 2020, 169, 105217. [Google Scholar] [CrossRef]
- Ballabio, C.; Fava, F.; Rosenmund, A. A Plant Ecology Approach to Digital Soil Mapping, Improving the Prediction of Soil Organic Carbon Content in Alpine Grasslands. Geoderma 2012, 187–188, 102–116. [Google Scholar] [CrossRef]
- Ben-Dor, E.; Taylor, R.G.; Hill, J.; Demattê, J.A.M.; Whiting, M.L.; Chabrillat, S.; Sommer, S. Imaging Spectrometry for Soil Applications. In Advances in Agronomy; Elsevier: Amsterdam, The Netherlands, 2008; Volume 97, pp. 321–392. ISBN 978-0-12-374352-7. [Google Scholar]
- Yang, R.-M.; Guo, W.-W.; Zheng, J.-B. Soil Prediction for Coastal Wetlands Following Spartina Alterniflora Invasion Using Sentinel-1 Imagery and Structural Equation Modeling. Catena 2019, 173, 465–470. [Google Scholar] [CrossRef]
- Mulder, V.L.; de Bruin, S.; Schaepman, M.E.; Mayr, T.R. The Use of Remote Sensing in Soil and Terrain Mapping—A Review. Geoderma 2011, 162, 1–19. [Google Scholar] [CrossRef]
- Zhou, T.; Geng, Y.; Chen, J.; Liu, M.; Haase, D.; Lausch, A. Mapping Soil Organic Carbon Content Using Multi-Source Remote Sensing Variables in the Heihe River Basin in China. Ecol. Indic. 2020, 114, 106288. [Google Scholar] [CrossRef]
- Odebiri, O.; Mutanga, O.; Odindi, J.; Peerbhay, K.; Dovey, S. Predicting Soil Organic Carbon Stocks under Commercial Forest Plantations in KwaZulu-Natal Province, South Africa Using Remotely Sensed Data. GIScience Remote. Sens. 2020, 57, 450–463. [Google Scholar] [CrossRef]
- Yang, D.; Yan, S.; Yang, Y.; Tian, M. Soil Moisture Retrieval Based on Multi-temporal GF-1 Images. Sci. Technol. Eng. 2021, 21, 4540–4549. (In Chinese) [Google Scholar]
- Li, X.; Ding, X.; Ceng, S.; Zhang, C.; Yang, H. Forest Soil Survey of Yunfu, Guangdong Province; China Forestry Publishing House: Beijing, China, 2018; pp. 112–124. (In Chinese) [Google Scholar]
- Moore, I.D.; Grayson, R.B.; Ladson, A.R. Digital Terrain Modelling: A Review of Hydrological, Geomorphological, and Biological Applications. Hydrol. Process. 1991, 5, 3–30. [Google Scholar] [CrossRef]
- Scull, P.; Franklin, J.; Chadwick, O.A.; McArthur, D. Predictive Soil Mapping: A Review. Prog. Phys. Geogr. Earth Environ. 2003, 27, 171–197. [Google Scholar] [CrossRef] [Green Version]
- Meng, F.R.; Castonguay, M.; Ogilvie, J.; Murphy, P.N.C.; Arp, P.A. Developing a GIS-Based flow-channel and wet areas mapping framework for precision forestry planning. In Proceedings of the IUFRO Precision Forestry Symposium, Stellenbosch, South Africa, 5–10 March 2006. [Google Scholar]
- Yang, R.; Rossiter, D.G.; Liu, F.; Lu, Y.; Yang, F.; Yang, F.; Zhao, Y.; Li, D.; Zhang, G. Predictive Mapping of Topsoil Organic Carbon in an Alpine Environment Aided by Landsat TM. PLoS ONE 2015, 10, e0139042. [Google Scholar] [CrossRef] [PubMed]
- Goward, S.N.; Markham, B.; Dye, D.G.; Dulaney, W.; Yang, J. Normalized Difference Vegetation Index Measurements from the Advanced Very High Resolution Radiometer. Remote Sens. Environ. 1991, 35, 257–277. [Google Scholar] [CrossRef]
- Powell, S.L.; Cohen, W.B.; Healey, S.P.; Kennedy, R.E.; Moisen, G.G.; Pierce, K.B.; Ohmann, J.L. Quantification of Live Aboveground Forest Biomass Dynamics with Landsat Time-Series and Field Inventory Data: A Comparison of Empirical Modeling Approaches. Remote Sens. Environ. 2010, 114, 1053–1068. [Google Scholar] [CrossRef]
- Major, D.J.; Baret, F.; Guyot, G. A Ratio Vegetation Index Adjusted for Soil Brightness. Int. J. Remote Sens. 1990, 11, 727–740. [Google Scholar] [CrossRef]
- McGillem, C.; Svedlow, M. Short Papers Optimum Filter for Minimization of Image Registration Error Variance. IEEE Trans. Geosci. Electron. 1977, 15, 257–259. [Google Scholar] [CrossRef]
- Xue, J.; Su, B. Significant Remote Sensing Vegetation Indices: A Review of Developments and Applications. J. Sens. 2017, 2017, 1353691. [Google Scholar] [CrossRef] [Green Version]
- Sun, Q. Study on Classification Method of Main Forest Types in Badaling Forest Farm Based on GF-2. Master Thesis, Beijing Forestry University, Beijing, China, 2017. (In Chinese). [Google Scholar]
- Zhao, Z.; Chow, T.L.; Rees, H.W.; Yang, Q.; Xing, Z.; Meng, F.-R. Predict Soil Texture Distributions Using an Artificial Neural Network Model. Comput. Electron. Agric. 2009, 65, 36–48. [Google Scholar] [CrossRef]
- Zhao, Z.; Yang, Q.; Benoy, G.; Chow, T.L.; Xing, Z.; Rees, H.W.; Meng, F.-R. Using Artificial Neural Network Models to Produce Soil Organic Carbon Content Distribution Maps across Landscapes. Can. J. Soil. Sci. 2010, 90, 75–87. [Google Scholar] [CrossRef]
- Schillaci, C.; Lombardo, L.; Saia, S.; Fantappiè, M.; Märker, M.; Acutis, M. Modelling the Topsoil Carbon Stock of Agricultural Lands with the Stochastic Gradient Treeboost in a Semi-Arid Mediterranean Region. Geoderma 2017, 286, 35–45. [Google Scholar] [CrossRef]
- Sigillito, V.G.; Hutton, L.V. Case Study II: Radar Signal Processing. In Neural Network PC Tools; Elsevier: Amsterdam, The Netherlands, 1990; pp. 235–250. ISBN 978-0-12-228640-7. [Google Scholar]
- Vaysse, K.; Lagacherie, P. Evaluating Digital Soil Mapping Approaches for Mapping GlobalSoilMap Soil Properties from Legacy Data in Languedoc-Roussillon (France). Geoderma Reg. 2015, 4, 20–30. [Google Scholar] [CrossRef]
- Akpa, S.I.C.; Odeh, I.O.A.; Bishop, T.F.A.; Hartemink, A.E. Digital Mapping of Soil Particle-Size Fractions for Nigeria. Soil Sci. Soc. Am. J. 2014, 78, 1953–1966. [Google Scholar] [CrossRef] [Green Version]
- Wang, S.; Gao, J.; Zhuang, Q.; Lu, Y.; Gu, H.; Jin, X. Multispectral Remote Sensing Data Are Effective and Robust in Mapping Regional Forest Soil Organic Carbon Stocks in a Northeast Forest Region in China. Remote Sens. 2020, 12, 393. [Google Scholar] [CrossRef] [Green Version]
- Mahmoudabadi, E.; Karimi, A.; Haghnia, G.H.; Sepehr, A. Digital Soil Mapping Using Remote Sensing Indices, Terrain Attributes, and Vegetation Features in the Rangelands of Northeastern Iran. Environ. Monit. Assess. 2017, 189, 500. [Google Scholar] [CrossRef]
- Yang, R.-M.; Zhang, G.-L.; Liu, F.; Lu, Y.-Y.; Yang, F.; Yang, F.; Yang, M.; Zhao, Y.-G.; Li, D.-C. Comparison of Boosted Regression Tree and Random Forest Models for Mapping Topsoil Organic Carbon Concentration in an Alpine Ecosystem. Ecol. Indic. 2016, 60, 870–878. [Google Scholar] [CrossRef]
- Kempen, B.; Brus, D.J.; Stoorvogel, J.J. Three-Dimensional Mapping of Soil Organic Matter Content Using Soil Type–Specific Depth Functions. Geoderma 2011, 162, 107–123. [Google Scholar] [CrossRef] [Green Version]
- Liu, F.; Zhang, G.-L.; Sun, Y.-J.; Zhao, Y.-G.; Li, D.-C. Mapping the Three-Dimensional Distribution of Soil Organic Matter across a Subtropical Hilly Landscape. Soil Sci. Soc. Am. J. 2013, 77, 1241–1253. [Google Scholar] [CrossRef]
- Nyssen, J.; Temesgen, H.; Lemenih, M.; Zenebe, A.; Haregeweyn, N.; Haile, M. Spatial and Temporal Variation of Soil Organic Carbon Stocks in a Lake Retreat Area of the Ethiopian Rift Valley. Geoderma 2008, 146, 261–268. [Google Scholar] [CrossRef]
- Kim, J.; Grunwald, S. Assessment of Carbon Stocks in the Topsoil Using Random Forest and Remote Sensing Images. J. Environ. Qual. 2016, 45, 1910–1918. [Google Scholar] [CrossRef]
- Yimer, F.; Ledin, S.; Abdelkadir, A. Soil Organic Carbon and Total Nitrogen Stocks as Affected by Topographic Aspect and Vegetation in the Bale Mountains, Ethiopia. Geoderma 2006, 135, 335–344. [Google Scholar] [CrossRef]
- Demattê, J.A.M.; Sayão, V.M.; Rizzo, R.; Fongaro, C.T. Soil Class and Attribute Dynamics and Their Relationship with Natural Vegetation Based on Satellite Remote Sensing. Geoderma 2017, 302, 39–51. [Google Scholar] [CrossRef]
- Mirzaee, S.; Ghorbani-Dashtaki, S.; Mohammadi, J.; Asadi, H.; Asadzadeh, F. Spatial Variability of Soil Organic Matter Using Remote Sensing Data. Catena 2016, 145, 118–127. [Google Scholar] [CrossRef]
- Wang, S.; Zhuang, Q.; Yang, Z.; Yu, N.; Jin, X. Temporal and Spatial Changes of Soil Organic Carbon Stocks in the Forest Area of Northeastern China. Forests 2019, 10, 1023. [Google Scholar] [CrossRef] [Green Version]
- Liu, X.; Li, H.; Cao, L.; Zhang, Y. Analysis on the heterogeneity of forest soil nutrients in Guangdong Province of southern China. J. Beijing For. Univ. 2021, 43, 90–101. [Google Scholar]
- Rivero, R.G.; Grunwald, S.; Binford, M.W.; Osborne, T.Z. Integrating Spectral Indices into Prediction Models of Soil Phosphorus in a Subtropical Wetland. Remote Sens. Environ. 2009, 113, 2389–2402. [Google Scholar] [CrossRef]
- Taghizadeh-Mehrjardi, R.; Minasny, B.; Sarmadian, F.; Malone, B.P. Digital Mapping of Soil Salinity in Ardakan Region, Central Iran. Geoderma 2014, 213, 15–28. [Google Scholar] [CrossRef]
- Pouladi, N.; Møller, A.B.; Tabatabai, S.; Greve, M.H. Mapping Soil Organic Matter Contents at Field Level with Cubist, Random Forest and Kriging. Geoderma 2019, 342, 85–92. [Google Scholar] [CrossRef]
- Mosleh, Z.; Salehi, M.H.; Jafari, A.; Borujeni, I.E.; Mehnatkesh, A. The Effectiveness of Digital Soil Mapping to Predict Soil Properties over Low-Relief Areas. Environ. Monit. Assess. 2016, 188, 195. [Google Scholar] [CrossRef]
- Adhikari, K.; Hartemink, A.E.; Minasny, B.; Bou Kheir, R.; Greve, M.B.; Greve, M.H. Digital Mapping of Soil Organic Carbon Contents and Stocks in Denmark. PLoS ONE 2014, 9, e105519. [Google Scholar] [CrossRef]
- Li, X.; Ding, J.; Liu, J.; Ge, X.; Zhang, J. Digital Mapping of Soil Organic Carbon Using Sentinel Series Data: A Case Study of the Ebinur Lake Watershed in Xinjiang. Remote Sens. 2021, 13, 769. [Google Scholar] [CrossRef]
- Deng, X.; Cao, J.; Song, X.; Tang, J.; Chen, F. Vertical Distribution Characteristics of Three Forest Types’ Soil Properties on Mao’er Mountain Biosphere Reserve. Ecol. Sci. 2014, 33, 1129–1134. (In Chinese) [Google Scholar] [CrossRef]
- Wang, B.; Waters, C.; Orgill, S.; Gray, J.; Cowie, A.; Clark, A.; Liu, D.L. High Resolution Mapping of Soil Organic Carbon Stocks Using Remote Sensing Variables in the Semi-Arid Rangelands of Eastern Australia. Sci. Total Environ. 2018, 630, 367–378. [Google Scholar] [CrossRef]
- Wang, S.; Zhuang, Q.; Jin, X.; Yang, Z.; Liu, H. Predicting Soil Organic Carbon and Soil Nitrogen Stocks in Topsoil of Forest Ecosystems in Northeastern China Using Remote Sensing Data. Remote Sens. 2020, 12, 1115. [Google Scholar] [CrossRef] [Green Version]
- Eckert, S. Improved Forest Biomass and Carbon Estimations Using Texture Measures from WorldView-2 Satellite Data. Remote Sens. 2012, 4, 810–829. [Google Scholar] [CrossRef] [Green Version]
- Meng, J.; Li, S.; Wang, W.; Liu, Q.; Xie, S.; Ma, W. Estimation of Forest Structural Diversity Using the Spectral and Textural Information Derived from SPOT-5 Satellite Images. Remote Sens. 2016, 8, 125. [Google Scholar] [CrossRef] [Green Version]



| Variable | Abbr. | Description | Resolution |
|---|---|---|---|
| Coarse-resolution soil maps | |||
| Coarse resolution alkali hydro nitrogen | CAN | The content of AN in a coarse-resolution soil map | 1000 m |
| Coarse resolution available phosphorus | CAP | The content of AP in a coarse-resolution soil map | 1000 m |
| Coarse resolution available potassium map | CAK | The content of AK in a coarse-resolution soil map | 1000 m |
| Coarse resolution organic matter map | COM | The content of OM in a coarse-resolution soil map | 1000 m |
| DEM-derived terrain-hydrology | |||
| Slope | Slope | Slope gradient (degrees) | 12.5 m |
| Aspect | Aspect | Direction of the steepest slope from the north | 12.5 m |
| Topographical position index | TPI | The relative terrain position of the central pixel | 12.5 m |
| Potential solar radiation | PSR | Total solar radiation reaching the earth surface based on location for a single year | 12.5 m |
| Depth to water | DTW | The elevation differences between the pixel and the nearest water surfaces (m) | 12.5 m |
| Sediment delivery ratio | SDR | The ratio of the sediment transported to the outlet and total erosion in watershed area (%) | 12.5 m |
| Flow length | FL | The length of the maximum ground distance along the flow direction projected to the horizon (m) | 12.5 m |
| Soil terrain factor | STF | A modified version of the hydrological similarity index | 12.5 m |
| Flow direction | FD | The steepest descent direction of each pixel along the water flow | 12.5 m |
| GF-1 derived remote sensing variables | |||
| Blue band | B | Wavelength of 450–520 nm | 8 m |
| Green band | G | Wavelength of 520–590 nm | 8 m |
| Red band | R | Wavelength of 630–690 nm | 8 m |
| Near infrared band | NIR | Wavelength of 770–890 nm | 8 m |
| Normalized difference vegetation index | NDVI | (NIR−R)/(NIR+ R) | 8 m |
| Difference vegetation index | DVI | NIR–R | 8 m |
| Ratio vegetation index | RVI | NIR/R | 8 m |
| Renormalized difference vegetation index | RDVI | 8 m | |
| Forest types | Forest | Broad leaved forest, coniferous forest, mixed forest, bamboo, bush, and other | 8 m |
| Nutrient | Depth | Number * | RMSE | R² | ROA ± 5% (%) | Optimal Candidate Variables Combination |
|---|---|---|---|---|---|---|
| AN | D1 | 1 | 1536.42 | 0.23 | 55 | SDR |
| 2 | 863.56 | 0.55 | 59 | SDR, Slope | ||
| 3 | 823.64 | 0.58 | 66 | SDR, Slope, Aspect | ||
| 4 | 580.53 | 0.71 | 70 | SDR, Slope, Aspect, DTW | ||
| 5 | 528.38 | 0.74 | 71 | SDR, Slope, Aspect, DTW, TPI | ||
| 6 | 495.68 | 0.76 | 74 | SDR, Slope, Aspect, DTW, TPI, FD | ||
| 7 | 593.21 | 0.72 | 72 | SDR, Slope, Aspect, DTW, TPI, FD, FL | ||
| 8 | 638.11 | 0.69 | 69 | SDR, Aspect, Slope, FL, TPI, STF, PSR, FD | ||
| 9 | 748.31 | 0.67 | 68 | SDR, Aspect, Slope, FL, TPI, STF, PSR, FD, DTW | ||
| D2 | 5 | 476.36 | 0.76 | 74 | SDR, Slope, Aspect, DTW, FL | |
| D3 | 7 | 630.51 | 0.79 | 77 | SDR, Slope, Aspect, STF, DTW, FL, FD | |
| D4 | 5 | 554.46 | 0.76 | 78 | SDR, Aspect, Slope, STF, FL | |
| D5 | 6 | 668.18 | 0.79 | 77 | SDR, Slope, Aspect, TPI, STF, FD | |
| AP | D1 | 6 | 0.88 | 0.74 | 53 | PSR, Slope, Aspect, SDR, TPI, FD |
| D2 | 6 | 0.34 | 0.74 | 48 | PSR, Slope, Aspect, TPI, DTW, FD | |
| D3 | 6 | 0.17 | 0.68 | 45 | PSR, Aspect, Slope, SDR, TPI, FD | |
| D4 | 7 | 0.15 | 0.66 | 43 | PSR, Slope, Aspect, SDR, TPI, STF, FD | |
| D5 | 7 | 0.12 | 0.69 | 45 | PSR, Slope, Aspect, TPI, DTW, FL, FD | |
| AK | D1 | 6 | 253.96 | 0.75 | 62 | Slope, SDR, Aspect, FL, TPI, STF |
| D2 | 6 | 208.53 | 0.76 | 59 | Slope, Aspect, FL, SDR, TPI, DTW | |
| D3 | 7 | 156.68 | 0.77 | 61 | Slope, Aspect, FL, SDR, FD, TPI, PSR | |
| D4 | 7 | 141.35 | 0.78 | 61 | Slope, Aspect, FL, SDR, STF, DTW, PSR | |
| D5 | 6 | 143.60 | 0.76 | 59 | Slope, Aspect, FL, SDR, STF, FD | |
| OM | D1 | 6 | 45.26 | 0.75 | 56 | Slope, Aspect, SDR, TPI, STF, DTW |
| D2 | 6 | 15.23 | 0.76 | 60 | Slope, Aspect, SDR, TPI, DTW, PSR | |
| D3 | 7 | 10.68 | 0.79 | 63 | Slope, Aspect, SDR, TPI, STF, FD, PSR | |
| D4 | 5 | 14.82 | 0.76 | 60 | Slope, Aspect, SDR, STF, FL | |
| D5 | 6 | 11.40 | 0.77 | 62 | Slope, Aspect, TPI, STF, DTW, FD |
| Nutrient | Depth | Number * | RMSE | R² | ROA ± 5% (%) | Optimal Candidate Variables Combination |
|---|---|---|---|---|---|---|
| AN | D1 | 1 | 447.67 | 0.79 | 84 | A1 + NDVI |
| 2 | 400.34 | 0.80 | 85 | A1 + NDVI, Forest | ||
| 3 | 361.25 | 0.84 | 87 | A1 + NDVI, Forest, G | ||
| 4 | 232.80 | 0.86 | 88 | A1 + NDVI, Forest, G, R | ||
| 5 | 214.25 | 0.89 | 90 | A1 + NDVI, Forest, G, R, NIR | ||
| 6 | 307.44 | 0.85 | 88 | A1 + NDVI, Forest, G, RVI, R, NIR | ||
| 7 | 391.30 | 0.81 | 85 | A1 + NDVI, Forest, G, RDVI, RVI, B, NIR | ||
| 8 | 448.61 | 0.79 | 82 | A1 + NDVI, Forest, G, RVI, RDVI, B, DVI, NIR | ||
| 9 | 491.35 | 0.78 | 80 | A1 + NDVI, Forest, G, RVI, RDVI, B, DVI, NIR, R | ||
| D2 | 5 | 263.60 | 0.88 | 88 | A2 + NDVI, Forest, G, RVI, NIR | |
| D3 | 5 | 419.03 | 0.85 | 87 | A3 + NDVI, Forest, G, B, NIR | |
| D4 | 6 | 544.59 | 0.81 | 85 | A4 + NDVI, Forest, G, RDVI, RVI, NIR | |
| D5 | 5 | 423.17 | 0.84 | 84 | A5 + NDVI, Forest, G, R, DVI | |
| AP | D1 | 5 | 0.45 | 0.87 | 82 | A1 + G, NDVI, Forest, RDVI, NIR |
| D2 | 4 | 0.19 | 0.86 | 80 | A2 + G, NDVI, Forest, RDVI | |
| D3 | 7 | 0.14 | 0.73 | 75 | A3 + G, NDVI, Forest, DVI, RDVI, RVI, NIR | |
| D4 | 7 | 0.12 | 0.71 | 74 | A4 + G, NDVI, Forest, RVI, DVI, B, R | |
| D5 | 6 | 0.10 | 0.75 | 77 | A5+G, NDVI, Forest, RDVI, DVI, B | |
| AK | D1 | 6 | 144.70 | 0.83 | 81 | A1 + NDVI, G, Forest, DVI, RDVI, NIR |
| D2 | 6 | 126.83 | 0.82 | 79 | A2 + NDVI, Forest, DVI, B, R, NIR | |
| D3 | 5 | 127.90 | 0.81 | 76 | A3 + Forest, G, RVI, DVI, B | |
| D4 | 7 | 116.43 | 0.83 | 77 | A4 + NDVI, G, Forest, DVI, RDVI, B, NIR | |
| D5 | 7 | 120.30 | 0.81 | 75 | A5 + NDVI, G, Forest, RDVI, DVI, B, R | |
| OM | D1 | 6 | 21.98 | 0.89 | 82 | A1 + Forest, NDVI, RDVI, G, B, R |
| D2 | 4 | 10.20 | 0.86 | 82 | A2 + Forest, NDVI, RVI, DVI | |
| D3 | 5 | 9.67 | 0.84 | 75 | A3 + Forest, RDVI, G, B, RVI | |
| D4 | 6 | 10.31 | 0.80 | 72 | A4 + Forest, NDVI, RDVI, DVI, G, NIR | |
| D5 | 7 | 9.60 | 0.80 | 74 | A5 + Forest, NDVI, RDVI, RVI, DVI, R, NIR |
| Nutrient | Depth | RMSE | R² | ROA ± 5% (%) |
|---|---|---|---|---|
| AN | D1 | 552.37 | 0.77 | 71 |
| D2 | 575.99 | 0.71 | 63 | |
| D3 | 753.97 | 0.61 | 58 | |
| D4 | 785.83 | 0.56 | 55 | |
| D5 | 806.17 | 0.51 | 47 | |
| AP | D1 | 0.83 | 0.75 | 63 |
| D2 | 0.21 | 0.68 | 49 | |
| D3 | 0.29 | 0.56 | 43 | |
| D4 | 0.34 | 0.50 | 40 | |
| D5 | 0.42 | 0.46 | 37 | |
| AK | D1 | 289.90 | 0.66 | 52 |
| D2 | 326.76 | 0.60 | 47 | |
| D3 | 569.44 | 0.51 | 42 | |
| D4 | 597.39 | 0.44 | 38 | |
| D5 | 620.77 | 0.38 | 35 | |
| OM | D1 | 35.41 | 0.78 | 75 |
| D2 | 13.56 | 0.72 | 67 | |
| D3 | 15.67 | 0.60 | 58 | |
| D4 | 18.45 | 0.54 | 52 | |
| D5 | 20.08 | 0.50 | 48 |
| Validation Accuracy | Extra Validation Accuracy–Building Accuracy * | ||||||
|---|---|---|---|---|---|---|---|
| Soil Depths | GF-1 Variables | RMSE | R2 | ROA ± 5% (%) | RMSE | R2 | ROA ± 5% (%) |
| AN_D1 | 5 | 280.02 | 0.64 | 64 | 65.77 | −0.25 | −26 |
| AN_D2 | 5 | 334.51 | 0.61 | 55 | 70.91 | −0.27 | −33 |
| AN_D3 | 6 | 508.60 | 0.51 | 47 | 89.57 | −0.34 | −40 |
| AN_D4 | 5 | 649.67 | 0.53 | 58 | 105.08 | −0.28 | −27 |
| AN_D5 | 5 | 515.43 | 0.57 | 46 | 92.26 | −0.27 | −38 |
| AP_D1 | 4 | 0.60 | 0.60 | 62 | 0.15 | −0.27 | −20 |
| AP_D2 | 7 | 0.33 | 0.53 | 51 | 0.14 | −0.33 | −29 |
| AP_D3 | 7 | 0.25 | 0.36 | 44 | 0.11 | −0.37 | −31 |
| AP_D4 | 6 | 0.20 | 0.32 | 36 | 0.08 | −0.39 | −38 |
| AP_D5 | 6 | 0.24 | 0.37 | 38 | 0.14 | −0.38 | −39 |
| AK_D1 | 6 | 180.20 | 0.51 | 50 | 35.50 | −0.32 | −31 |
| AK_D2 | 5 | 171.32 | 0.44 | 35 | 44.49 | −0.38 | −44 |
| AK_D3 | 7 | 185.40 | 0.38 | 44 | 57.50 | −0.43 | −32 |
| AK_D4 | 7 | 163.67 | 0.46 | 53 | 47.24 | −0.37 | −24 |
| AK_D5 | 7 | 170.92 | 0.37 | 38 | 50.62 | −0.44 | −37 |
| OM_D1 | 6 | 26.33 | 0.57 | 52 | 4.35 | −0.32 | −30 |
| OM_D2 | 6 | 12.93 | 0.63 | 48 | 2.73 | −0.23 | −34 |
| OM_D3 | 6 | 10.69 | 0.55 | 51 | 1.02 | −0.29 | −24 |
| OM_D4 | 4 | 12.84 | 0.38 | 34 | 2.53 | −0.42 | −38 |
| OM_D5 | 5 | 11.30 | 0.43 | 47 | 1.70 | −0.37 | −27 |
| Predicted Value | Predicted Value–Measured Value | |||
|---|---|---|---|---|
| Soil Depths | Mean | SD | Mean | SD |
| AN_D1 | 159.93 | 10.93 | −2.93 | −21.87 |
| AN_D2 | 153.46 | 8.20 | 1.06 | −24.21 |
| AN_D3 | 150.15 | 14.59 | −1.35 | −23.38 |
| AN_D4 | 139.54 | 14.34 | 4.91 | −20.47 |
| AN_D5 | 133.91 | 18.18 | 2.10 | −12.12 |
| AP_D1 | 0.96 | 0.92 | −0.19 | −0.73 |
| AP_D2 | 0.64 | 0.65 | −0.09 | −0.34 |
| AP_D3 | 0.65 | 0.73 | 0.03 | −0.02 |
| AP_D4 | 0.57 | 0.58 | 0.01 | −0.04 |
| AP_D5 | 0.53 | 0.56 | 0.02 | 0.02 |
| AK_D1 | 49.94 | 27.09 | −1.20 | −1.22 |
| AK_D2 | 43.07 | 27.06 | 0.53 | −1.05 |
| AK_D3 | 39.68 | 24.74 | 0.84 | −0.53 |
| AK_D4 | 39.18 | 24.39 | 1.43 | 0.76 |
| AK_D5 | 37.78 | 22.2 | 1.37 | 0.38 |
| OM_D1 | 23.17 | 11.69 | −1.00 | −1.75 |
| OM_D2 | 16.25 | 8.21 | −0.54 | −0.19 |
| OM_D3 | 13.05 | 7.00 | −0.66 | −0.33 |
| OM_D4 | 11.7 | 7.56 | −0.36 | 0.37 |
| OM_D5 | 10.05 | 6.16 | −0.35 | −0.44 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Zhao, Z.; Wei, S.; Sun, D.; Yang, Q.; Ding, X. Prediction of Regional Forest Soil Nutrients Based on Gaofen-1 Remote Sensing Data. Forests 2021, 12, 1430. https://doi.org/10.3390/f12111430
Li Y, Zhao Z, Wei S, Sun D, Yang Q, Ding X. Prediction of Regional Forest Soil Nutrients Based on Gaofen-1 Remote Sensing Data. Forests. 2021; 12(11):1430. https://doi.org/10.3390/f12111430
Chicago/Turabian StyleLi, Yingying, Zhengyong Zhao, Sunwei Wei, Dongxiao Sun, Qi Yang, and Xiaogang Ding. 2021. "Prediction of Regional Forest Soil Nutrients Based on Gaofen-1 Remote Sensing Data" Forests 12, no. 11: 1430. https://doi.org/10.3390/f12111430
APA StyleLi, Y., Zhao, Z., Wei, S., Sun, D., Yang, Q., & Ding, X. (2021). Prediction of Regional Forest Soil Nutrients Based on Gaofen-1 Remote Sensing Data. Forests, 12(11), 1430. https://doi.org/10.3390/f12111430






