Experimental Investigations and Numerical Simulations of the Vibrational Performance of Wood Truss Joist Floors with Strongbacks
Abstract
:1. Introduction
2. Configurations of Wood Truss Joist Floor
3. Experimental Floor Test Method
3.1. Vibration Mode and Frequency Testing
3.2. Point Load Deflection Testing
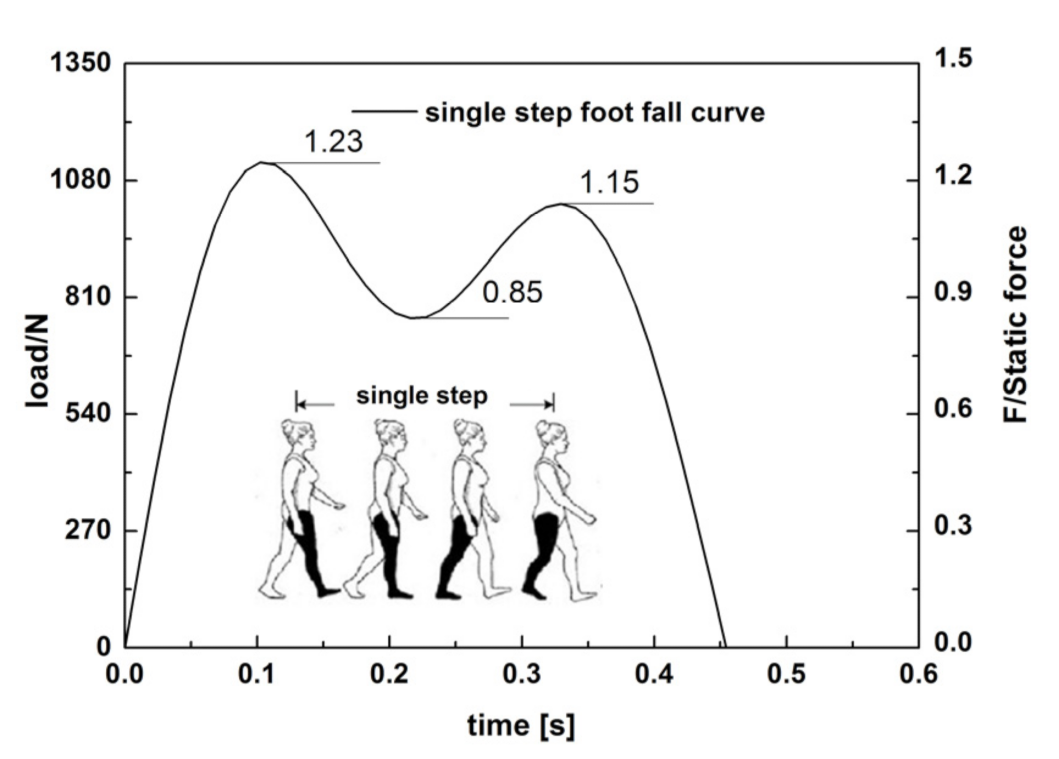
3.3. Human Induced Vibration Tests under Single Person Loading
4. Numerical Simulation Method
5. Results and Discussion
5.1. Vibration Frequencies and Modes
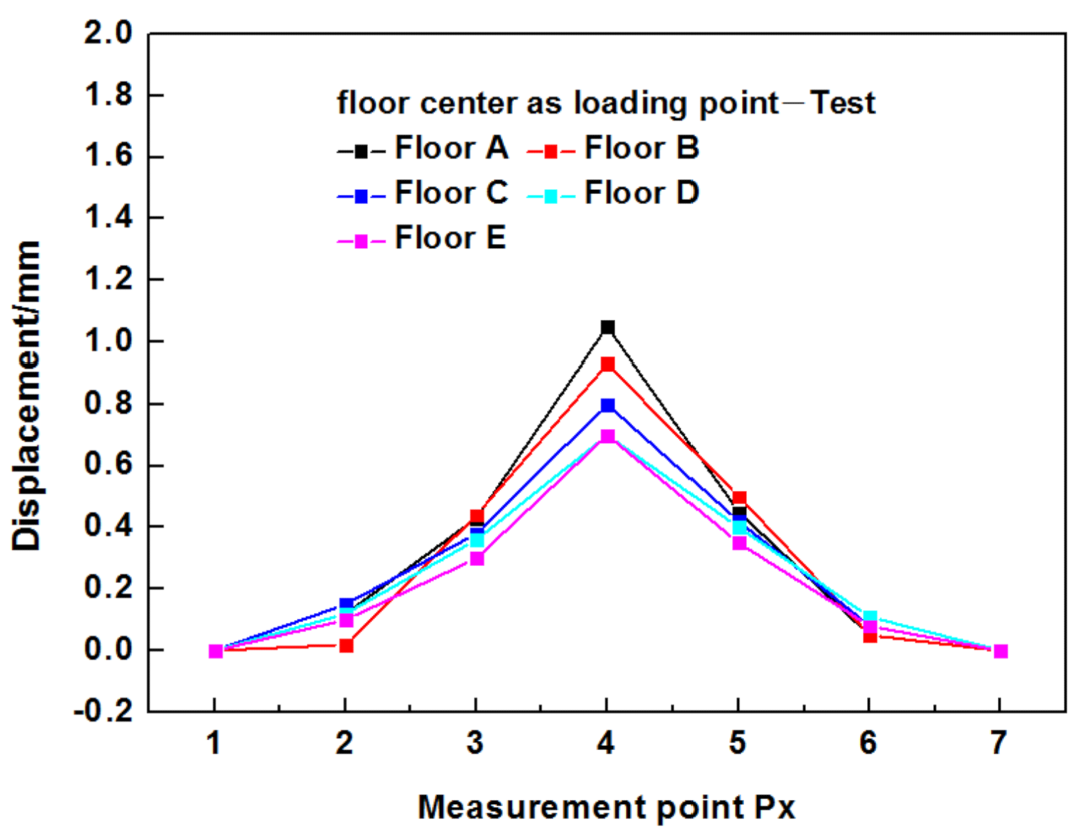
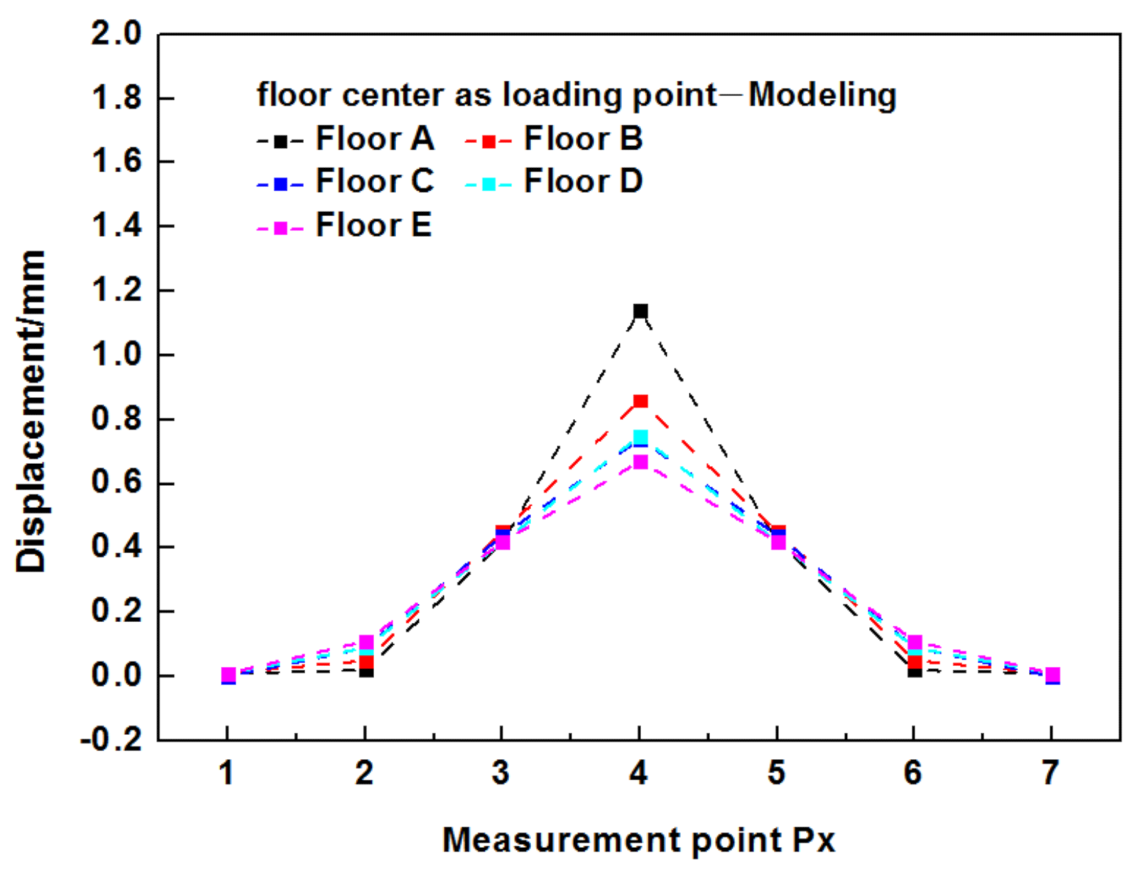
5.2. Point Load Deflections
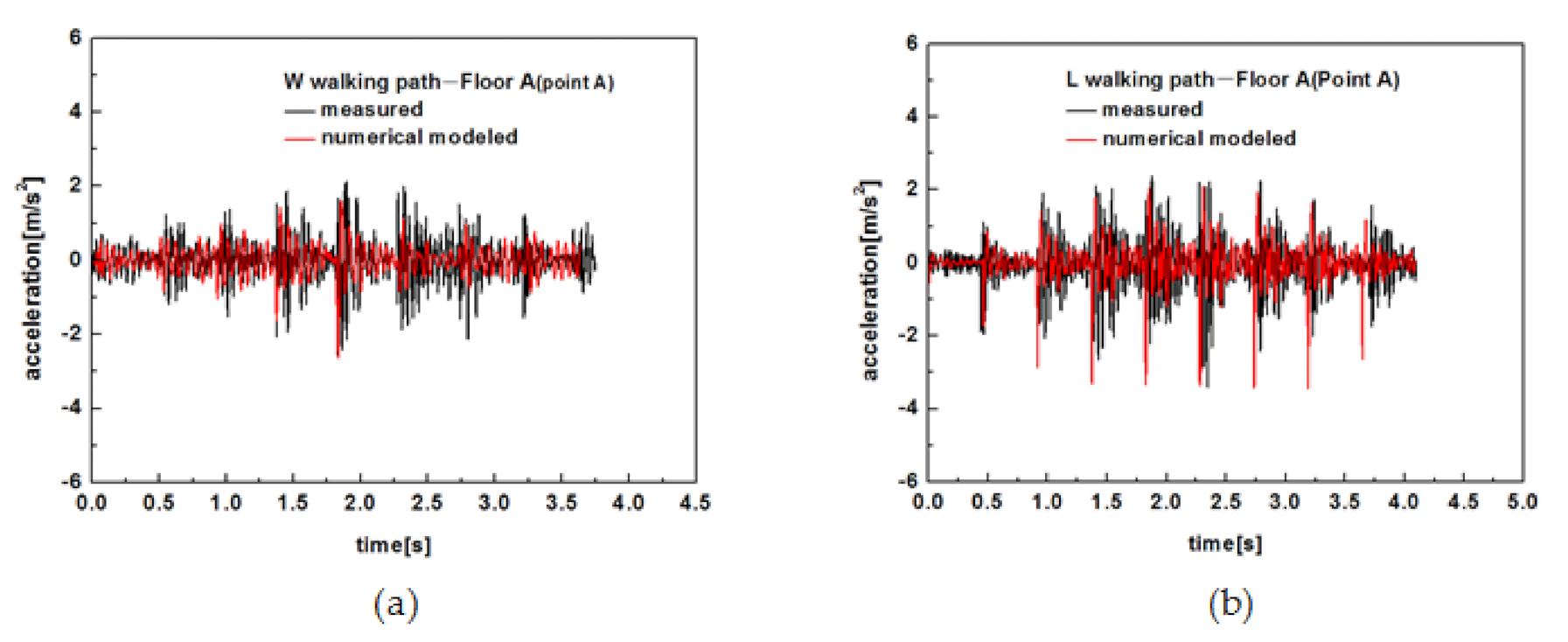
5.3. Floor Vibration under Single Person Walking Loading
6. Conclusions
- (1)
- The use of strongbacks significantly can improve the floor stiffness and lower the peak deformation of the sheathing. The use of one strongback rows at mid-span and the use of two strongback rows at mid-span effectively decreased the maximum deformation of point loading at floor center by 11% and 24%, respectively. The effect of adding strongbacks at one-third of each span on decreasing the maximum deformation at the floor center was minimal. In addition, strongbacks does not improve greatly the integrity of the floor, and the deflection influence under point loading on other joists that are three joists spaces away is minimal.
- (2)
- The strongbacks do not significantly affect the fundamental natural frequency of wood truss joist floors. The increase in the stiffness of the floors due to addition of strongbacks compensated for the increased mass of the floors. All the tested wood truss joist floors have similar fundamental frequencies of about 15 Hz. However, strongbacks with the increase of the number from zero to four influenced the higher-order mode frequencies of the wood truss joist floors.
- (3)
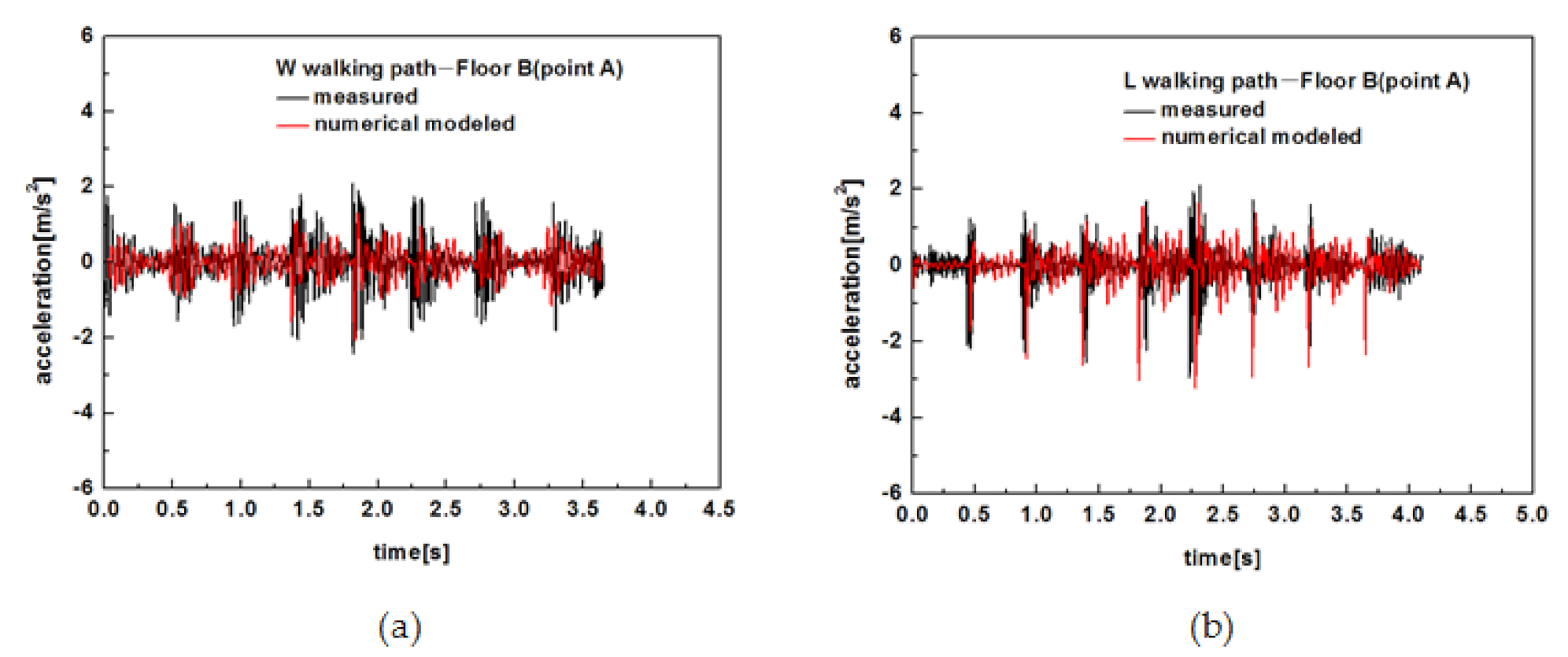
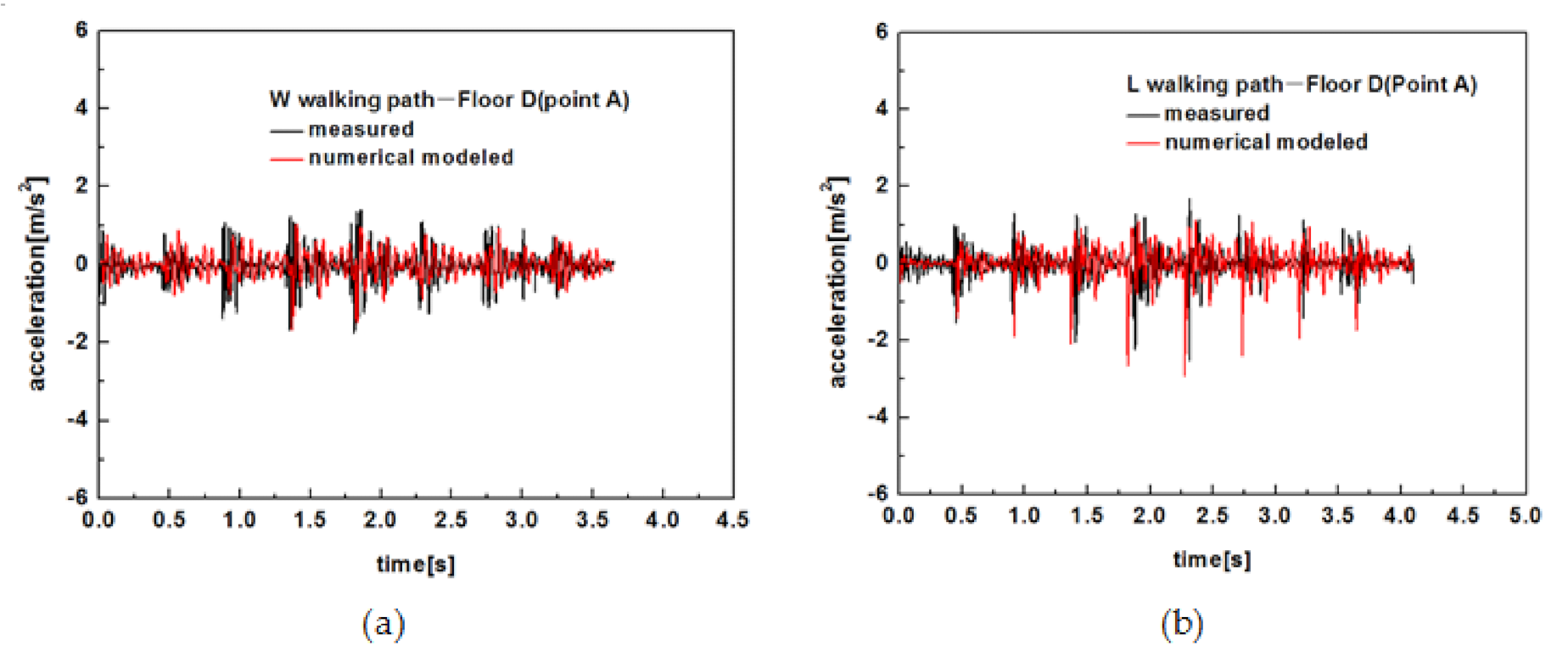
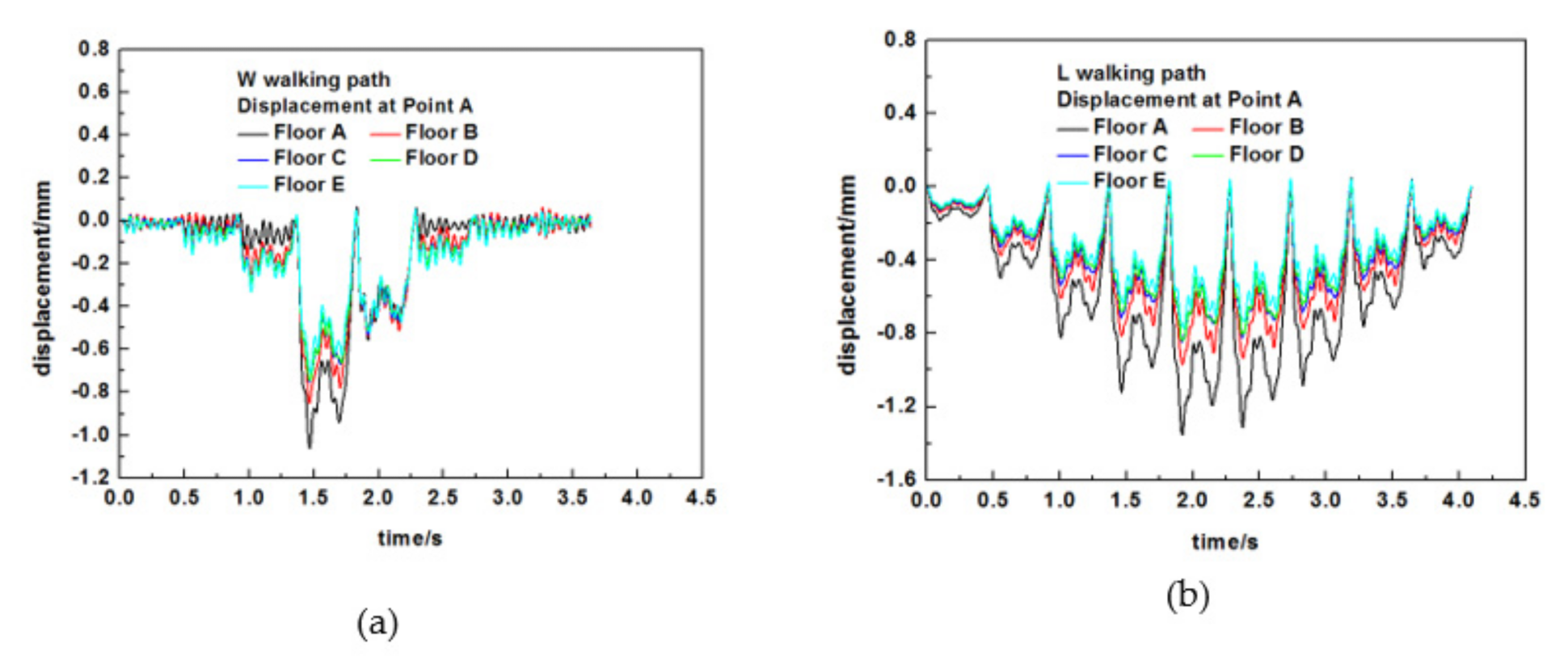
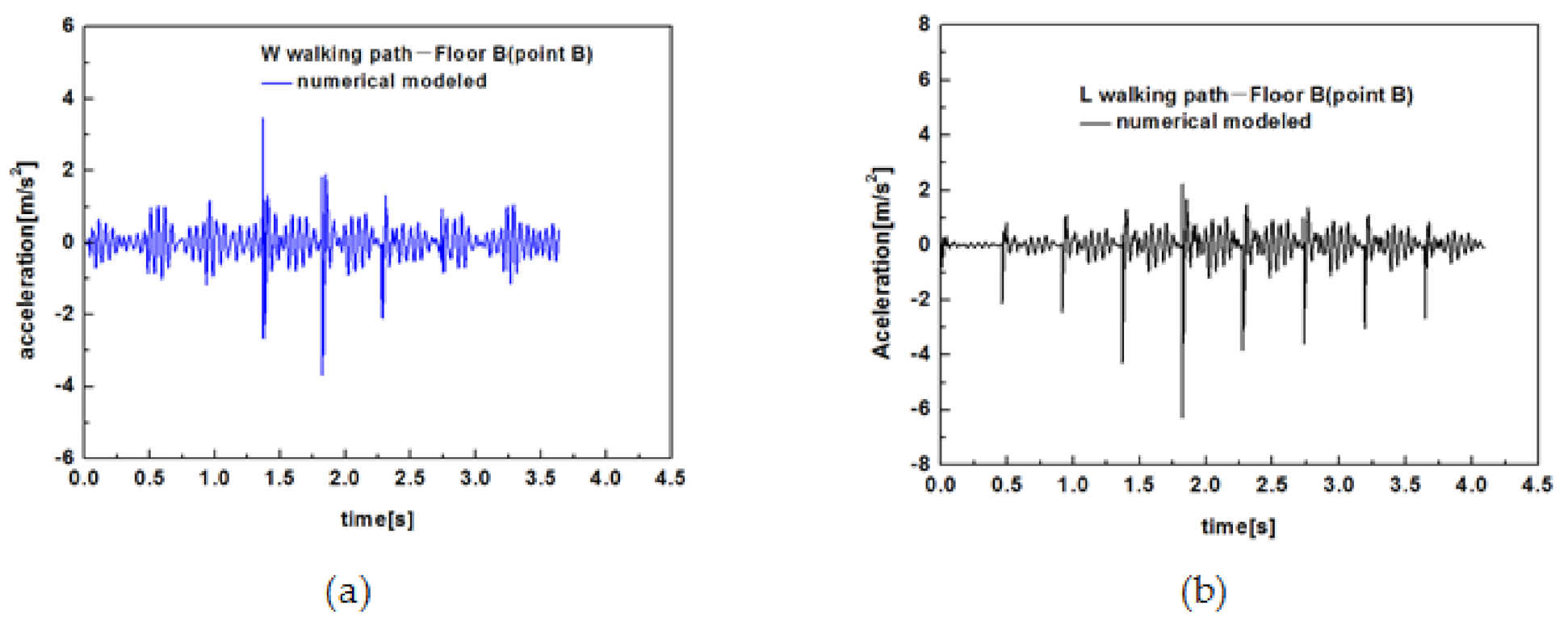
- Each footstep on wood truss joist floors resulted in each clear transient vibration including a stiff initial peak and quickly decays. Walking along L path (parallel to the joist) produced higher vibration response at the floor center of wood truss joist floors than that of walking along W path (perpendicular to the joist).
- (4)
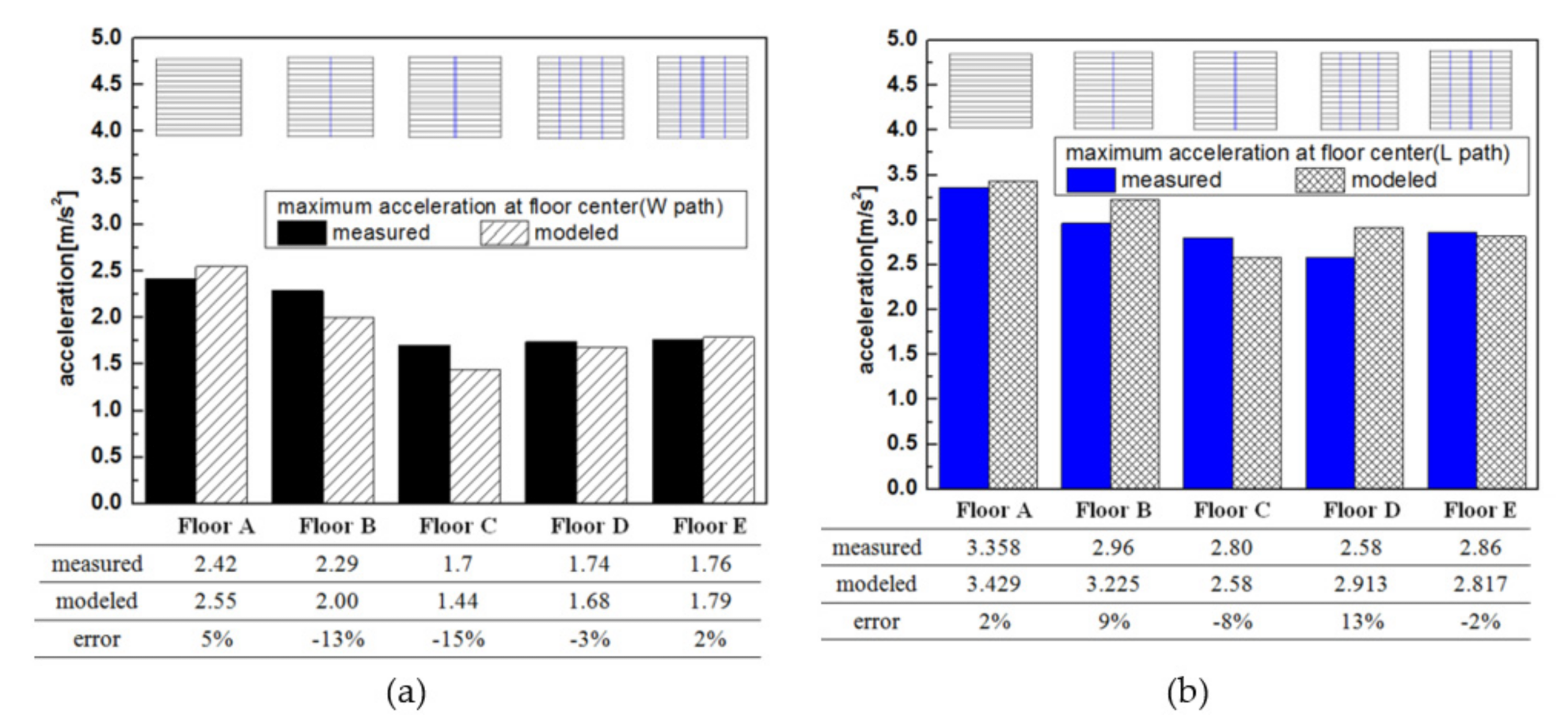
- The strongbacks substantially reduced the peak acceleration of the sheathing at the joists. The closer placements of strongbacks were to the mid-span, the more significant reduction of vibration was. The use of a strongback row at mid-span effectively decreased the peak acceleration of vibration at floor center on the joists by a decrease of 22% for W path and 6% for L path. The use of two strongback rows at mid-span has further decreased the peak acceleration at floor center on the joists by 43% for W path and 25% for L path. The addition of strongbacks at one-third of each span had negligible influence on reducing the peak accelerations at floor center. Two strongback rows at mid-span perform best effect on reduction of vibration response at floor center.
- (5)
- However, the strongbacks have limits of reduction peak acceleration of the sheathing between the joists. It was found that the addition of strongbacks had a negligible influence on reducing the peak accelerations at point B on the sheathing between the joists.
Author Contributions
Funding
Conflicts of Interest
References
- Ohlsson, S. Serviceability criteria-especially floor vibration criteria. In Proceeding of the International Timber Engineering Conference, London, UK, 2–5 September 1991; pp. I.58–I.65. [Google Scholar]
- European Committee for Standardization. Eurocode 5: Design of Timber Structures. General Common Rules and Rules for Buildings. BS EN 1995-1-1-2004+A1-2008; CEN: Brussels, Brussels, 2001; p. 53. [Google Scholar]
- Smith, I.; Chui, Y.H. Design of lightweight wooden floors to avoid human discomfort. Can. J. Civil. Eng. 1987, 5, 254–261. [Google Scholar] [CrossRef]
- Chui, Y.H. Vibrational Performance of Wooden Floors in Domestic Dwellings. Ph.D. Thesis, Brighton Polytechnic, Brighton, UK, 1987. [Google Scholar]
- Khokhar, A.M. Influence of Lateral Element Stiffness on Performance of Wooden Floors. Master’s Thesis, University of New Brunswick, Fredericton, NB, Canada, 2006. [Google Scholar]
- Weckendorf, J. Dynamic Response of Structural Timber Flooring Systems. Ph.D. Thesis, Edinburgh Napier University, Edinburgh, UK, 2009. [Google Scholar]
- Weckendorf, J.; Toratti, T.; Smith, I.; Tannert, T. Vibration serviceability performance of timber floors. Eur. J. Wood Prod. 2016, 74, 353–367. [Google Scholar] [CrossRef]
- Zhang, B.S. Parametric Study on the Design of Timber Floor Joists to Eurocode 5 and National Annex; Technical Document for BSI Technical Committee, B/525/5; BSI: London, UK, 2004. [Google Scholar]
- Zhang, B.S.; Bahadori, A.; Kermani, A. Influence of EC5 and the UK National Annex on the Design of Timber Flooring Systems Built with Multi-Webbed Engineered Joists and Solid Timber Joists; Technical Document for BSI Technical Committee B/525/5; BSI: London, UK, 2005. [Google Scholar]
- Zhang, B.S.; Kermani, A.; Fillingham, T. Vibrational performance of timber floors constructed with metal web joists. Eng. Struct. 2013, 56, 1321–1334. [Google Scholar] [CrossRef]
- Zhang, B.S.; Kermani, A.; Fillingham, T. Vibrations of metal web joist timber floors with strongbacks. Proc. Inst. Civ. Eng. (ICE)-Struct. Build. 2016, 169, 549–562. [Google Scholar] [CrossRef] [Green Version]
- Jarnero, K. Vibrations in Timber Floors: Dynamic Properties and Human Perception. Ph.D. Thesis, Linnaeus University, Växjö, Sweden, 2014. [Google Scholar]
- Jarnero, K.; Brandt, A.; Olsson, A. Vibration properties of a timber floor assessed in laboratory and during construction. Eng. Struct. 2015, 82, 44–54. [Google Scholar] [CrossRef]
- Bernard, E.S. Dynamic Serviceability in Lightweight Engineered Timber Floors. J. Struct. Eng. 2008, 134, 258–268. [Google Scholar] [CrossRef]
- Huang, H.Y.; Gao, Y.; Chang, W.S. Human-induced vibration of cross-laminated timber (CLT) floor under different boundary conditions. Eng. Struct. 2020, 204, 1–11. [Google Scholar] [CrossRef]
- Wang, C.; Chang, W.S.; Yan, W.M.; Huang, H.Y. Predicting the human-induced vibration of cross laminated timber floor under multi-person loadings. Structures 2021, 29, 65–78. [Google Scholar] [CrossRef]
- Norhayati, A.G.; Deam, B.; Fragiacomo, M. Dynamic Measurements of LVL Concrete Composite Floors. In Proceedings of the 13th Asia Pacific Vibration Conference, Christchurch, New Zealand, 22–25 November 2009. [Google Scholar]
- Skinner, J.; Martins, C.; Bregulla, J.; Harris, R.; Paine, K.; Walker, P.; Dias, A.M. Concrete upgrade to improve the vibration response of timber floors. Proc. Inst. Civ. Eng.-Struct. Build. 2014, 167, 559–568. [Google Scholar] [CrossRef] [Green Version]
- Santos, P.G.G.D.; Martins, C.E.D.J.; Skinner, J.; Harris, R.; Dias, A.M.P.G.; Godinho, L.M.C. Modal Frequencies of a Reinforced Timber-Concrete Composite Floor: Testing and Modeling. J. Struct. Eng. 2015, 141, 04015029. [Google Scholar] [CrossRef]
- Xie, Z.; Hu, X.M.; Du, H.; Zhang, X.Y. Vibration behavior of timber-concrete composite floors under human-induced excitation. J. Build. Eng. 2020, 32, 101744. [Google Scholar] [CrossRef]
- Basaglia, B.M.; Li, J.; Shrestha, R.; Crews, K. Response Prediction to Walking-Induced Vibrations of a Long-Span Timber Floor. J. Struct. Eng. 2021, 147, 04020326. [Google Scholar] [CrossRef]
- Hu, L.J. Prediction of Vibration Responses of Ribbed Plates by Modal Synthesis. Ph.D. Thesis, University of New Brunswick, Fredericton, NB, Canada, 1992. [Google Scholar]
- Eriksson, P.E. Vibration of Low-Frequency Floors-Dynamic Forces and Response Prediction. Ph.D. Thesis, Chalmers University of Technology, Gothenburg, Sweden, 1994. [Google Scholar]
- Weckendorf, J.; Zhang, B.; Kermani, A.; Reid, D. Finite element modeling of I-joist timber flooring systems to predict modal frequencies, modal shapes and static point load deflections. In Proceedings of the 11th World Conference on Timber Engineering (WCTE), Trentino, Italy, 20–24 June 2010. [Google Scholar]
- Glisovic, I.; Stevanovic, B. Vibrational behavior of timber floors. In Proceedings of the 11th World Conference on Timber Engineering (WCTE), Trentino, Italy, 20–24 June 2010. [Google Scholar]
- Shen, Y.L.; Zhou, H.B.; Xue, S.; Zhang, J.C. A Comparison on Numerical Simulation Models for Vibrational Performances of the Wood Truss Joist Floor System. Shock Vib. 2021, 2021, 5560554. [Google Scholar]
- International Organization for Standardization. Timber Structures-Test Methods-Floor Vibration Performance; ISO18324; ISO: Geneva, Switzerland, 2016. [Google Scholar]
- ASTM. ASTM2126. Standard Test Methods for Cyclic (Reversed) Load Test for Shear Resistance of Walls for Buildings; ASTM: West Conshohocken, PA, USA, 2011. [Google Scholar]
- CEN. EN12512 Timber Structures-Test Methods-Cyclic Testing of Joints Made with Mechanical Fasteners; CEN: Brussels, Brussels, 2001. [Google Scholar]
- Yasumura, M.; Kawai, N. Estimating seismic performance of wood-framed structures. In Proceedings of the World Conference on Timber Engineering (WCTE), Montreux, Switzerland, 17–20 August 1998; pp. 564–571. [Google Scholar]
- Commonwealth Scientific and Industrial Research Organization (CSIRO). Timber Evaluation of Mechanical Joint Systems-Part 3, Earthquake Loading; CSIRO: Melbourne, Australia, 1996. [Google Scholar]
- Karacabeyli, E.; Ceccotti, A. Quasi-static reversed cyclic testing of nailed joints. In Proceedings of the International Council for Building and Research Studies and Documentation Working Commission W18-Timber Structure, Vancouver, BC, Canada, 26–29 August 2013. [Google Scholar]
- Shen, Y.; Schneider, J.; Tesfamariam, S.; Stiemer, S.F.; Chen, Z. Cyclic behavior of bracket connections for cross-laminated timber (CLT): Assessment and comparison of experimental and numerical models studies. J. Build. Eng. 2021, 39, 102197. [Google Scholar] [CrossRef]
- The Engineered Wood Association. Minimizing Floor Vibrations by Design and Retrofit; Technical Note 70; APA: Tacoma, WA, USA, 2004. [Google Scholar]
- Ellingwood, B.; Tallin, A. Structural serviceability-floor vibrations. J. Struct. Eng. 1984, 110, 401–418. [Google Scholar] [CrossRef]


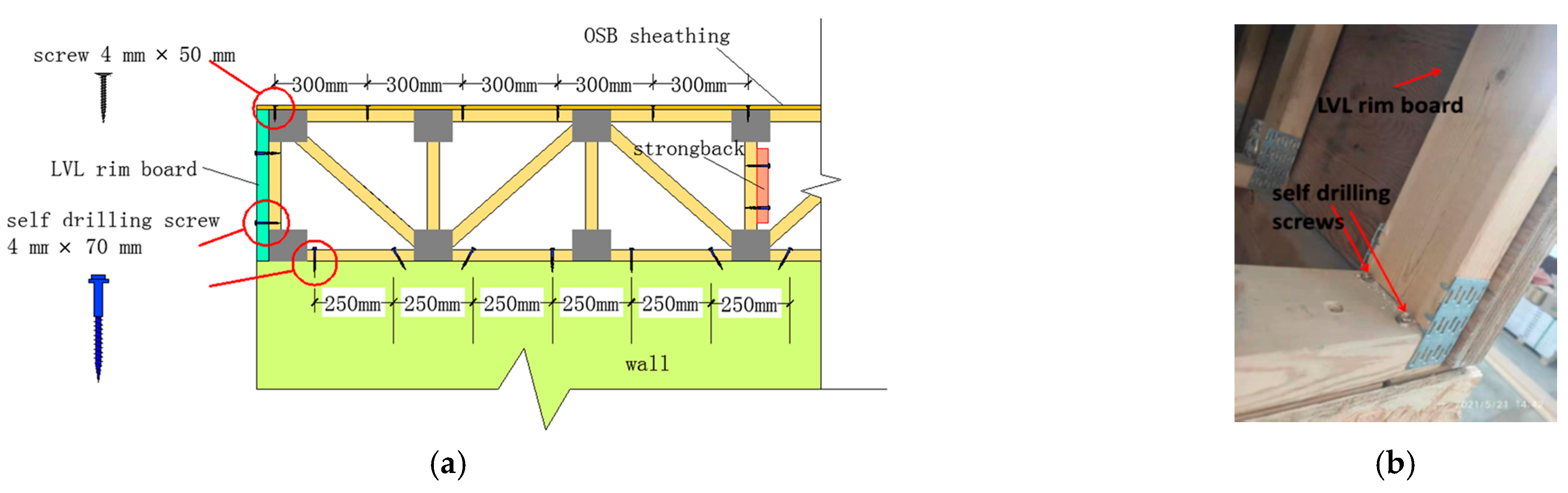
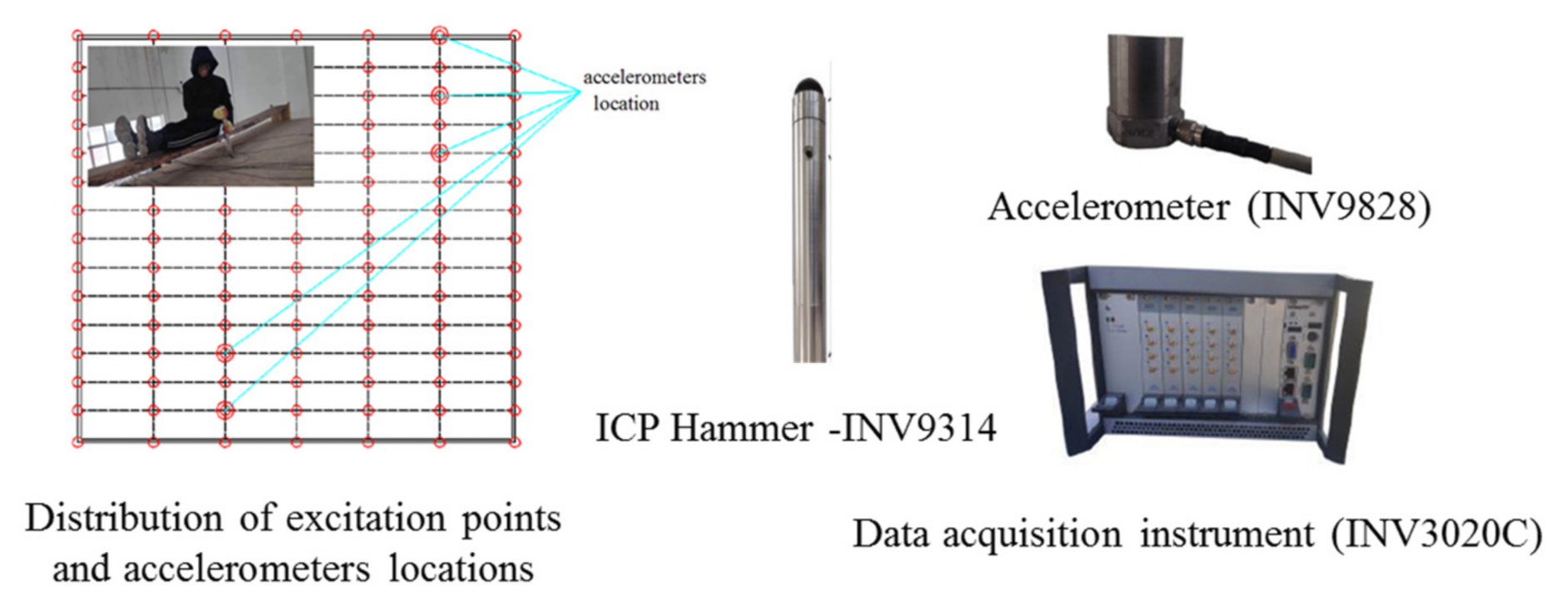

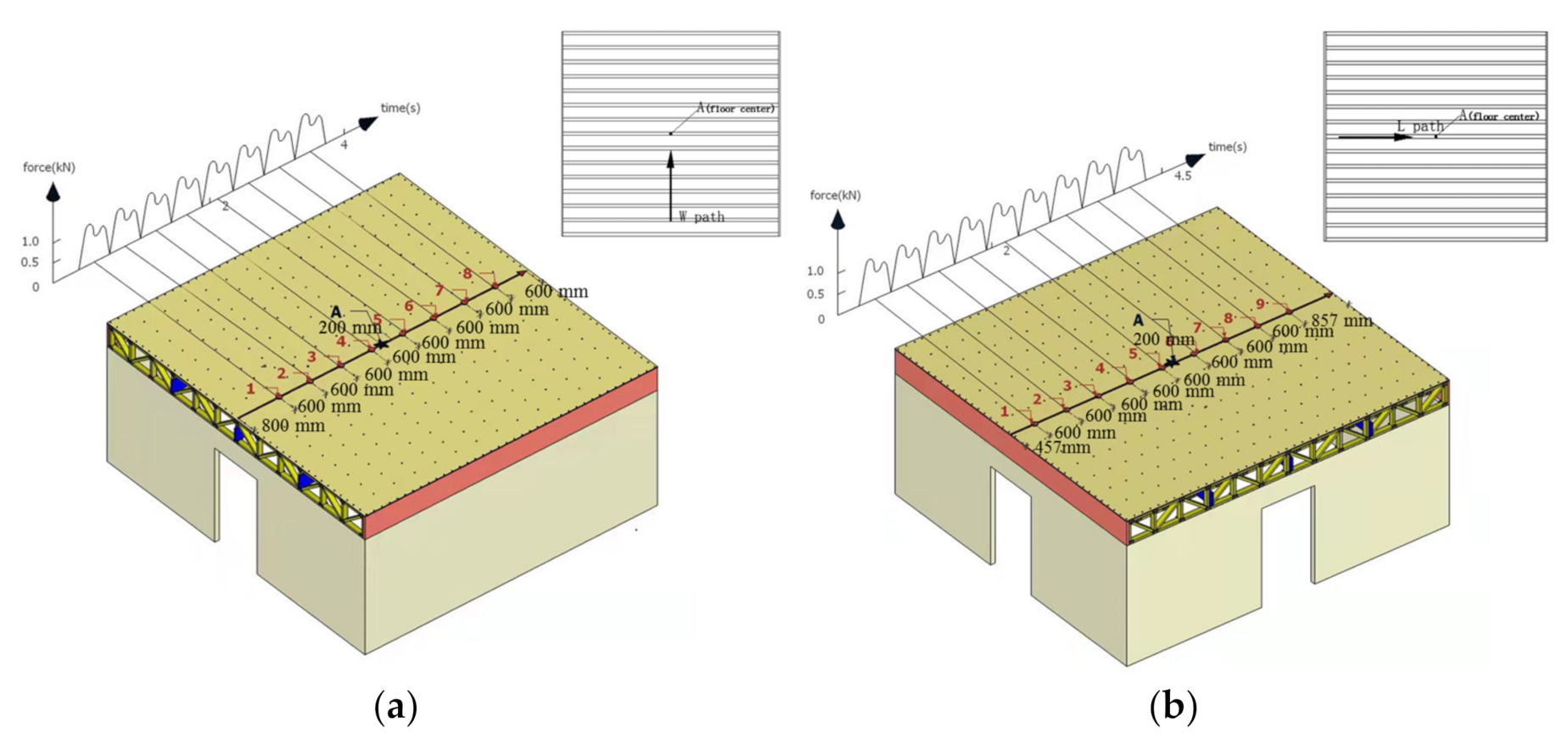
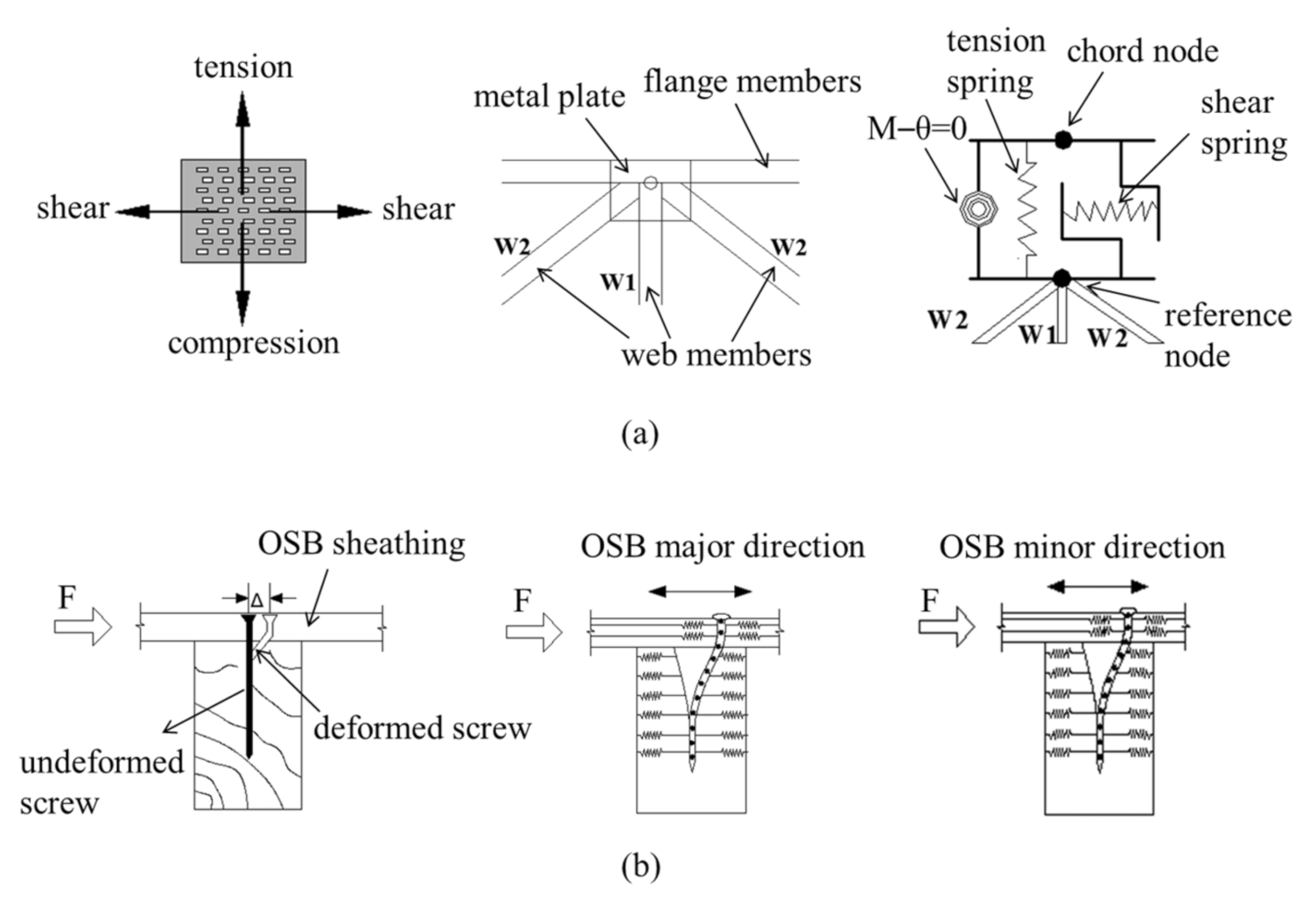
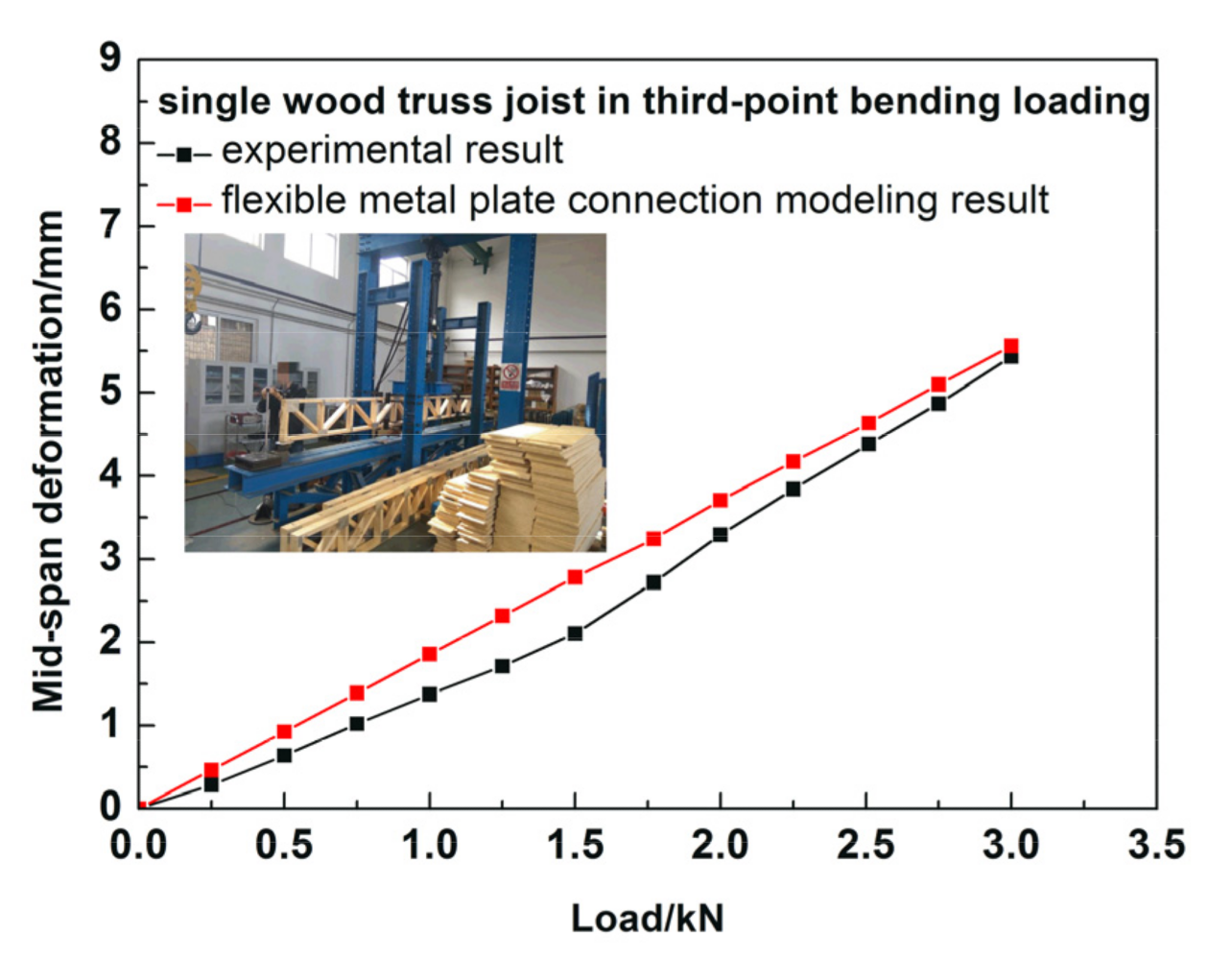
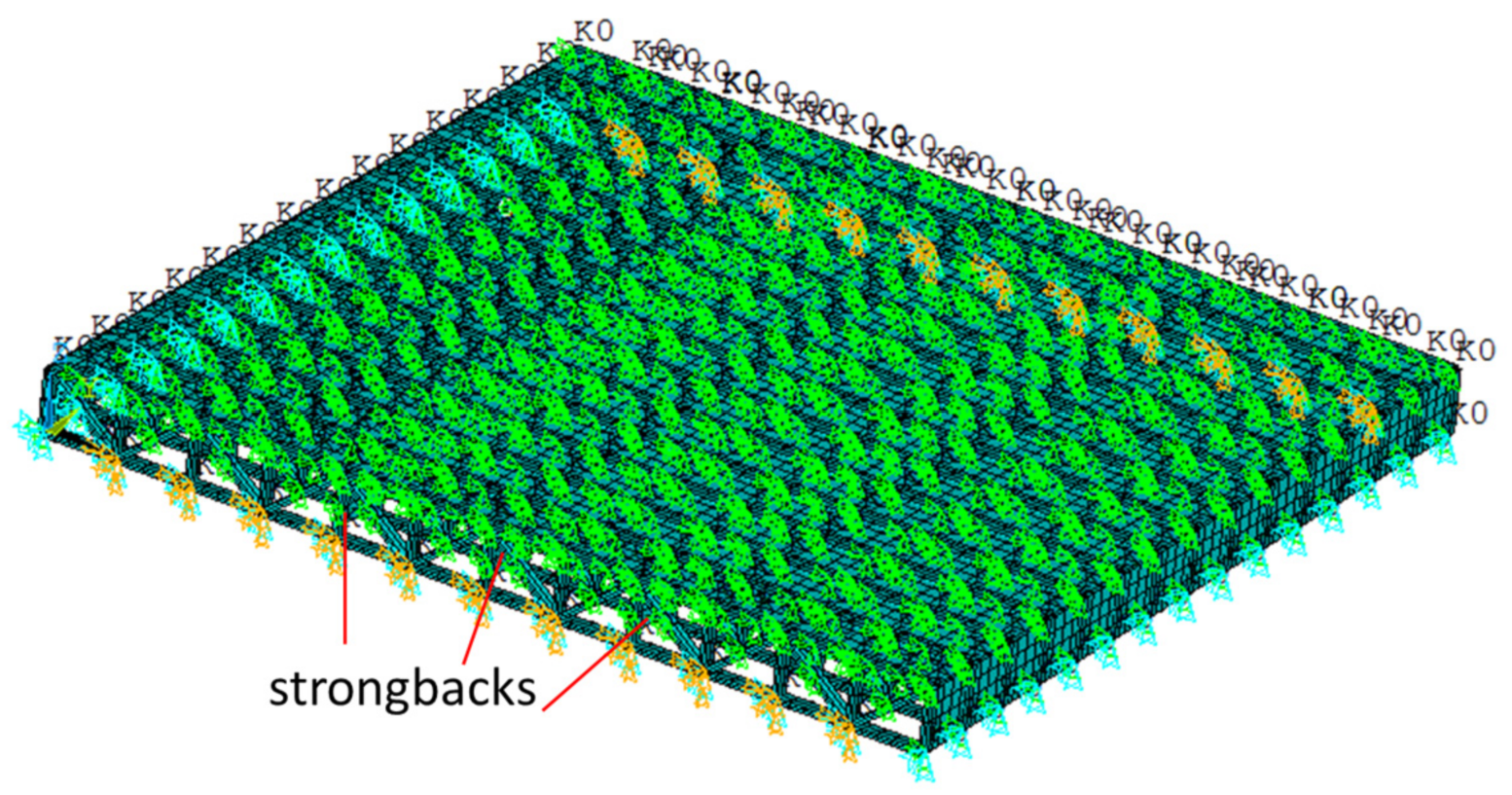

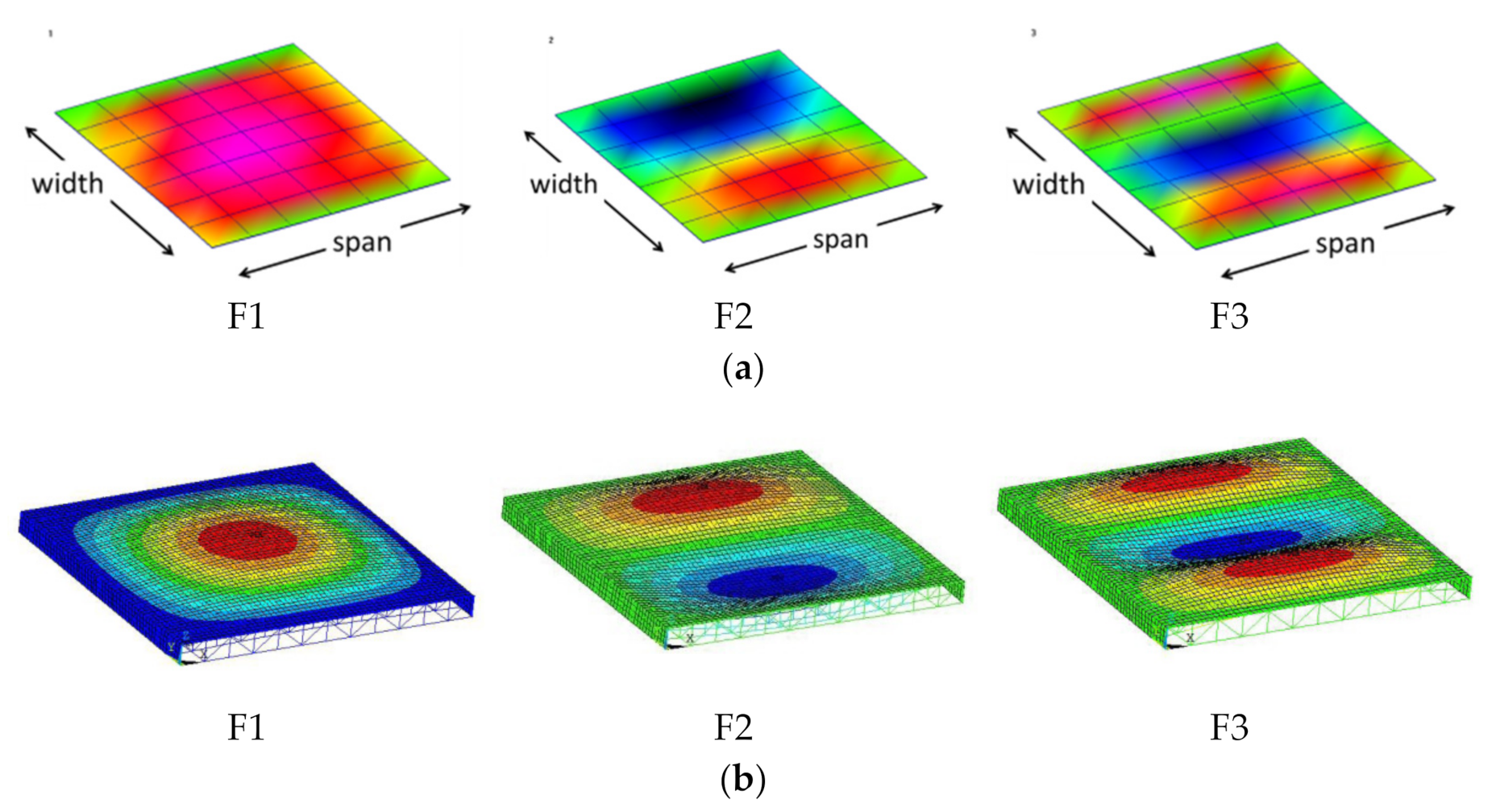
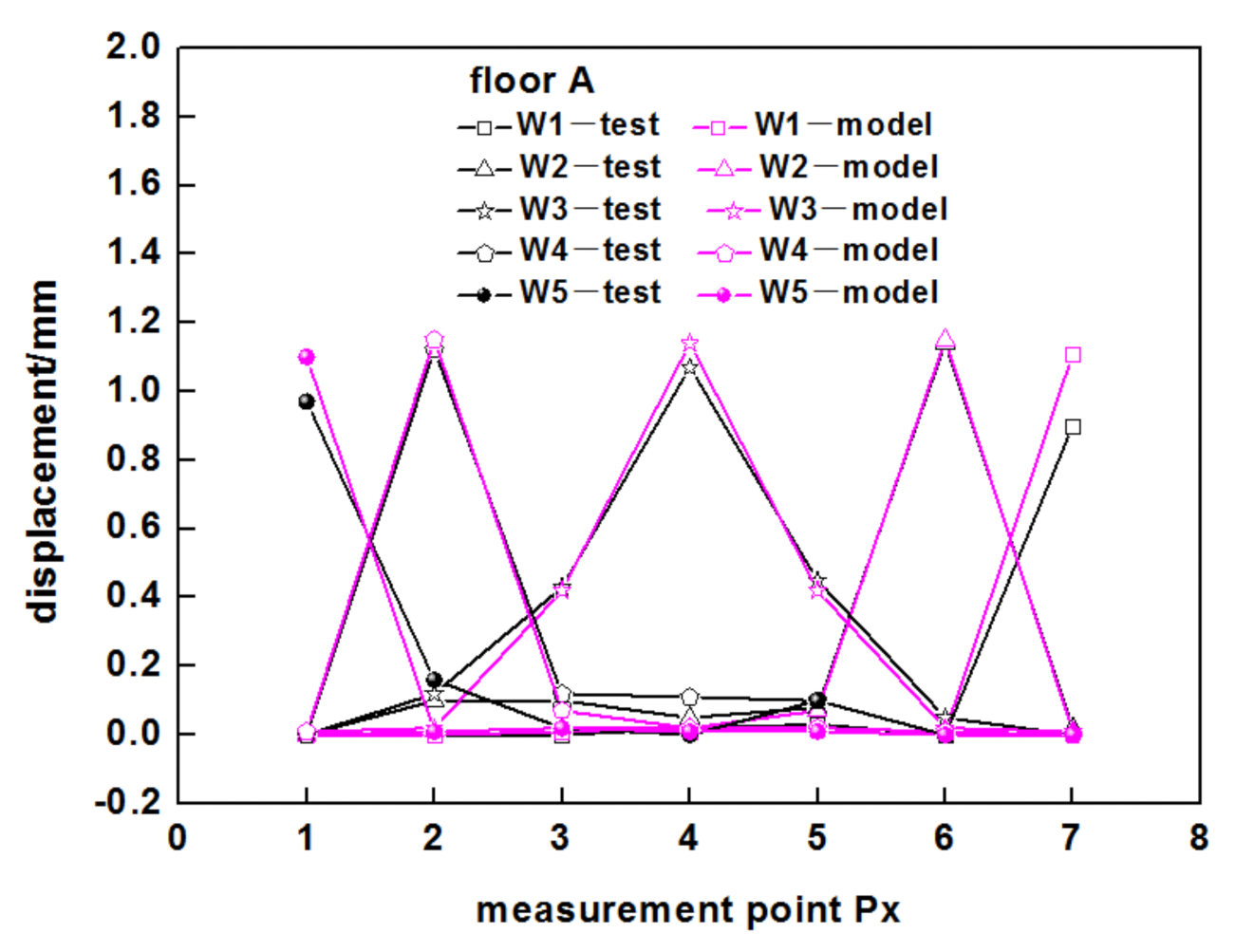







| Floor | Joist Spacing | Sheathing Thickness | Strongback Configuration | Test | Modeling |
|---|---|---|---|---|---|
| A | 400 mm | 15 mm | None | √ | √ |
| B | 400 mm | 15 mm | One strongback row at mid-span | √ | √ |
| C | 400 mm | 15 mm | Two strongback rows at mid-span | √ | √ |
| D | 400 mm | 15 mm | One strongback row at mid-span and one strongback row at one-third of the span | √ | √ |
| E | 400 mm | 15 mm | Two strongback rows at mid-span and one strongback row at one-third of the span | √ | √ |
| Type of Connections | Directions | Disp1 (m) | Load 1 (N) | Stiffness (kN/m) |
|---|---|---|---|---|
| Single-shear screwed OSB panel connections | OSB minor axis (shear) | 0.001 | 807 | 807 |
| OSB major axis (shear) | 0.001 | 863 | 863 |
| Type of Connections | Directions | Disp1 (m) | Load 1 (N) | Stiffness (kN/mm) |
|---|---|---|---|---|
| Metal plate connections | Major axis (shear) | 0.000158 | 5500 | 34.80 |
| Minor axis (tension) | 0.000158 | 9000 | 56.96 |
| Items | SPF Truss | SPF Strongback | OSB Sheathing | LVL Rim Board |
|---|---|---|---|---|
| EL [MPa] | 8700 | 9000 | 4280 | 13000 |
| ER [MPa] | 660 | 870 | 2080 | 1000 |
| ET [MPa] | 400 | 710 | 2080 | 1000 |
| GLR [MPa] | 500 | 600 | 1000 | 700 |
| GLT [MPa] | 500 | 600 | 50 | 700 |
| GRT [MPa] | 53 | 30 | 57 | 60 |
| μLR | 0.43 | 0.03 | 0.15 | 0.335 |
| μLT | 0.47 | 0.2 | 0.3 | 0.03 |
| μRT | 0.2 | 0.43 | 0.15 | 0.466 |
| ρ [kg/m3] | 560 | 540 | 650 | 600 |
| Floor | F1 (Hz) | F2 (Hz) | F3 (Hz) |
|---|---|---|---|
| A | 15 | 17.8 | 21 |
| B | 14.8 | 18.8 | 23.4 |
| C | 15 | 18.8 | 25.3 |
| D | 15 | 20.1 | 25.4 |
| E | 15 | 20.6 | 27.4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, Y.; Zhou, H.; Xue, S.; Yan, X.; Si, J.; Guan, C. Experimental Investigations and Numerical Simulations of the Vibrational Performance of Wood Truss Joist Floors with Strongbacks. Forests 2021, 12, 1493. https://doi.org/10.3390/f12111493
Shen Y, Zhou H, Xue S, Yan X, Si J, Guan C. Experimental Investigations and Numerical Simulations of the Vibrational Performance of Wood Truss Joist Floors with Strongbacks. Forests. 2021; 12(11):1493. https://doi.org/10.3390/f12111493
Chicago/Turabian StyleShen, Yinlan, Haibin Zhou, Shuo Xue, Xingchen Yan, Jiahao Si, and Cheng Guan. 2021. "Experimental Investigations and Numerical Simulations of the Vibrational Performance of Wood Truss Joist Floors with Strongbacks" Forests 12, no. 11: 1493. https://doi.org/10.3390/f12111493
APA StyleShen, Y., Zhou, H., Xue, S., Yan, X., Si, J., & Guan, C. (2021). Experimental Investigations and Numerical Simulations of the Vibrational Performance of Wood Truss Joist Floors with Strongbacks. Forests, 12(11), 1493. https://doi.org/10.3390/f12111493






