Using TLS-Measured Tree Attributes to Estimate Aboveground Biomass in Small Black Spruce Trees
Abstract
:1. Introduction
2. Materials and Methods
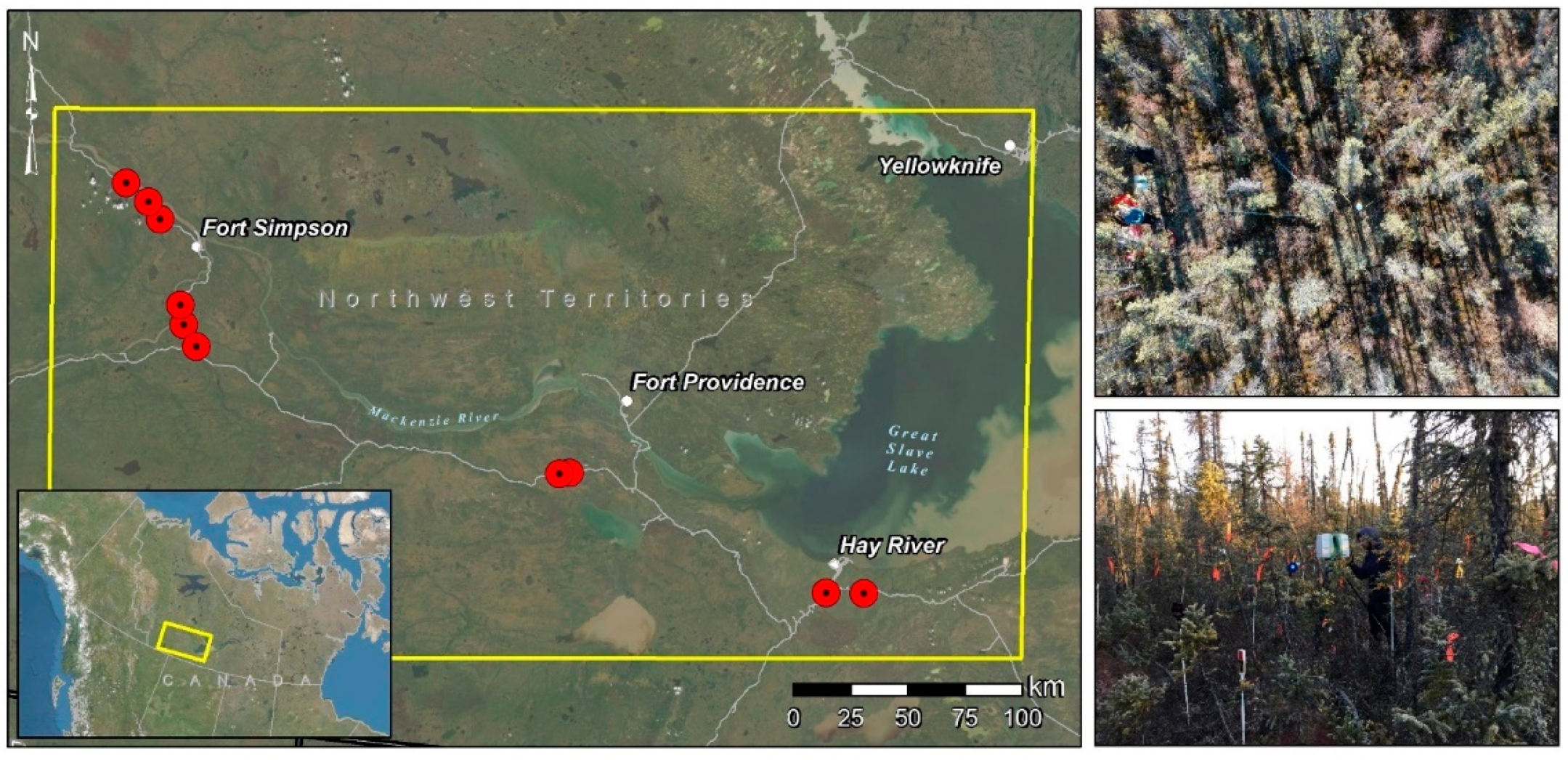
2.1. Study Area
2.2. Plot Characteristics
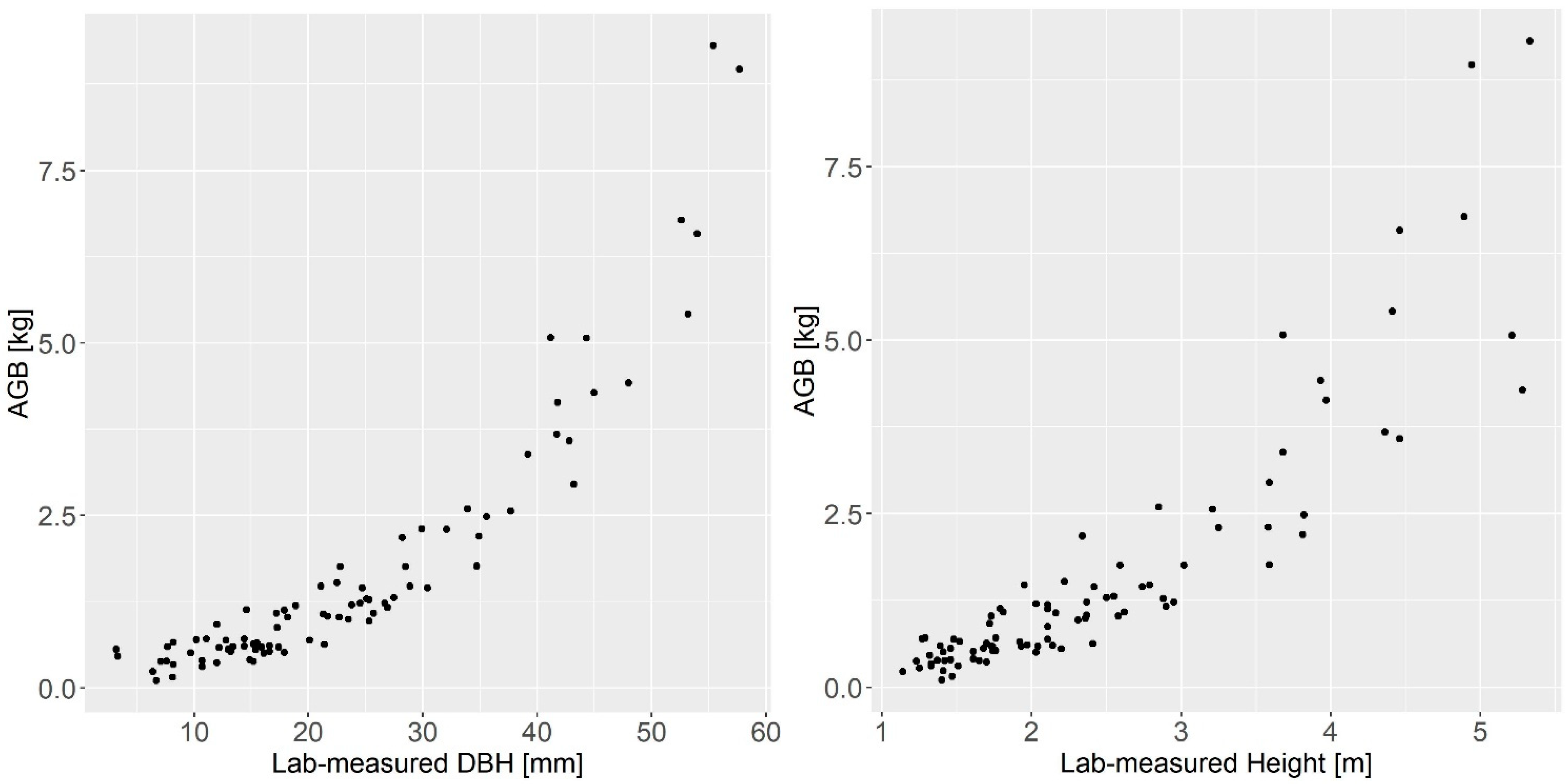
2.3. Destructive Sampling and Biomass Measurements
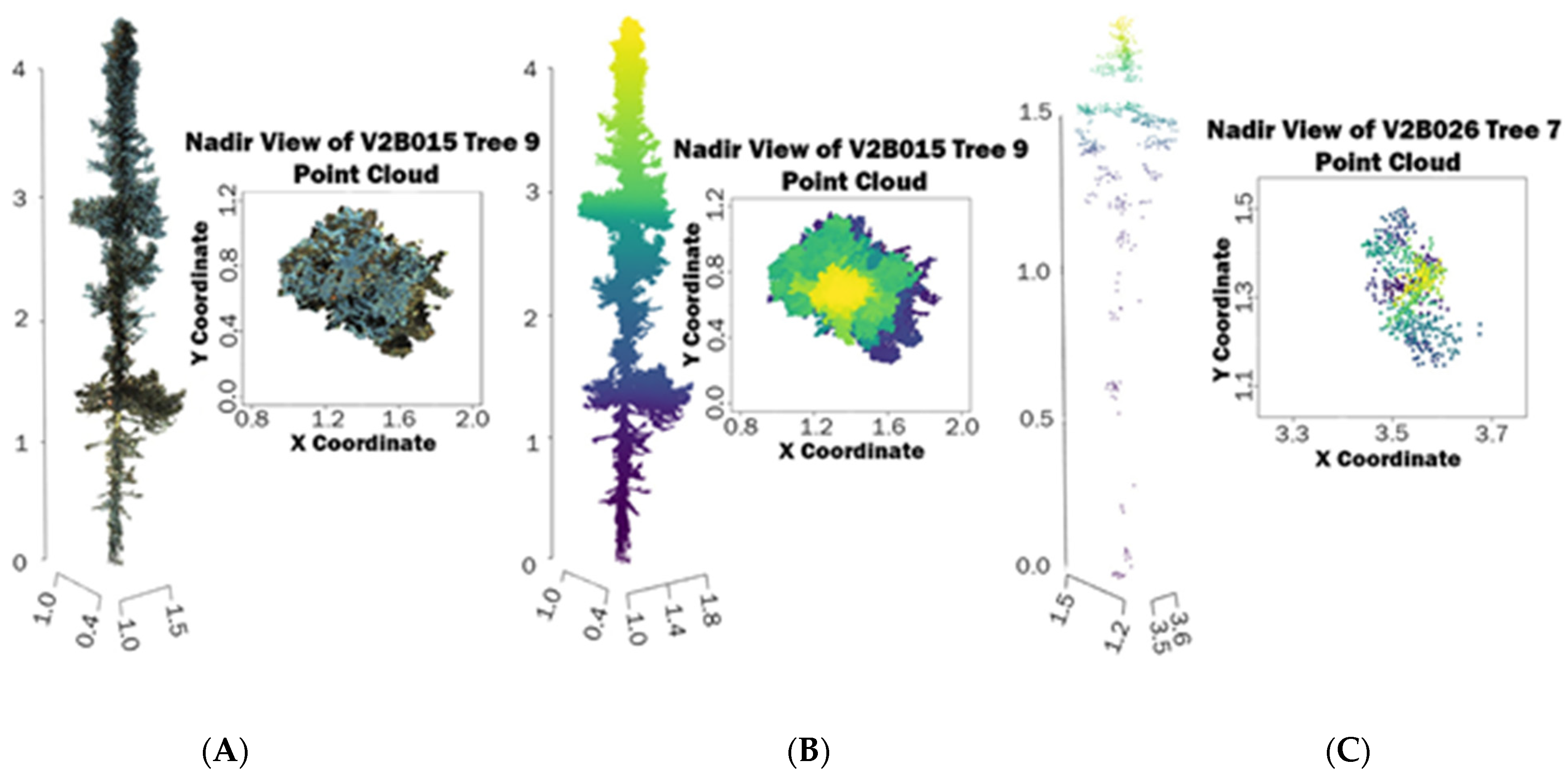
2.4. Point Cloud Processing, Tree Extraction, and Height Measurements
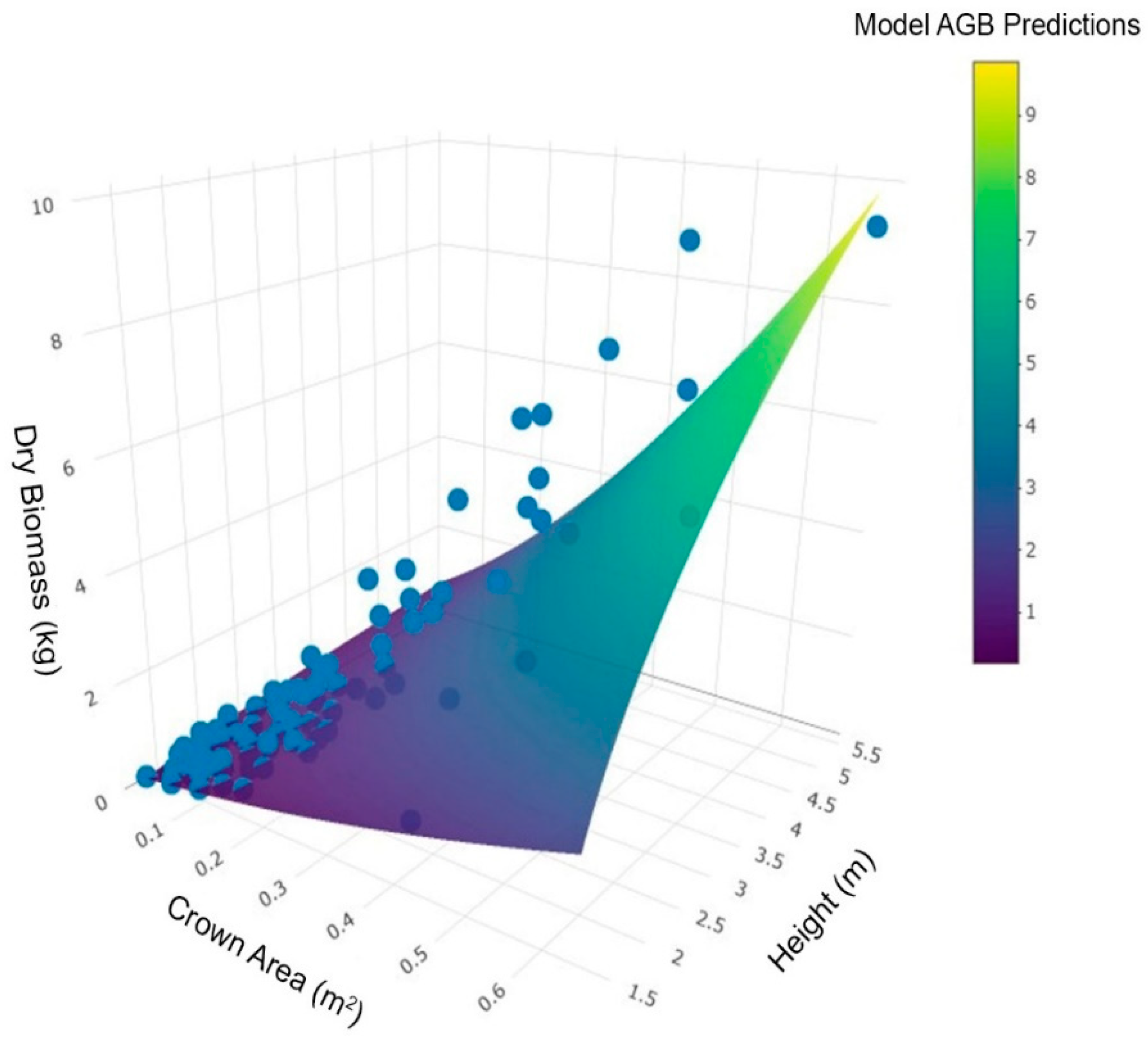
2.5. Crown Diameter and Crown Area Measurements
2.6. TreeQSM Estimates of Height, DBH, and Volume
2.7. Bounding Box Volume
2.8. Fitting and Testing the Models
2.9. Surrogate Point Density Sensitivity Analysis
3. Results
3.1. Effect of Weights on Final Models
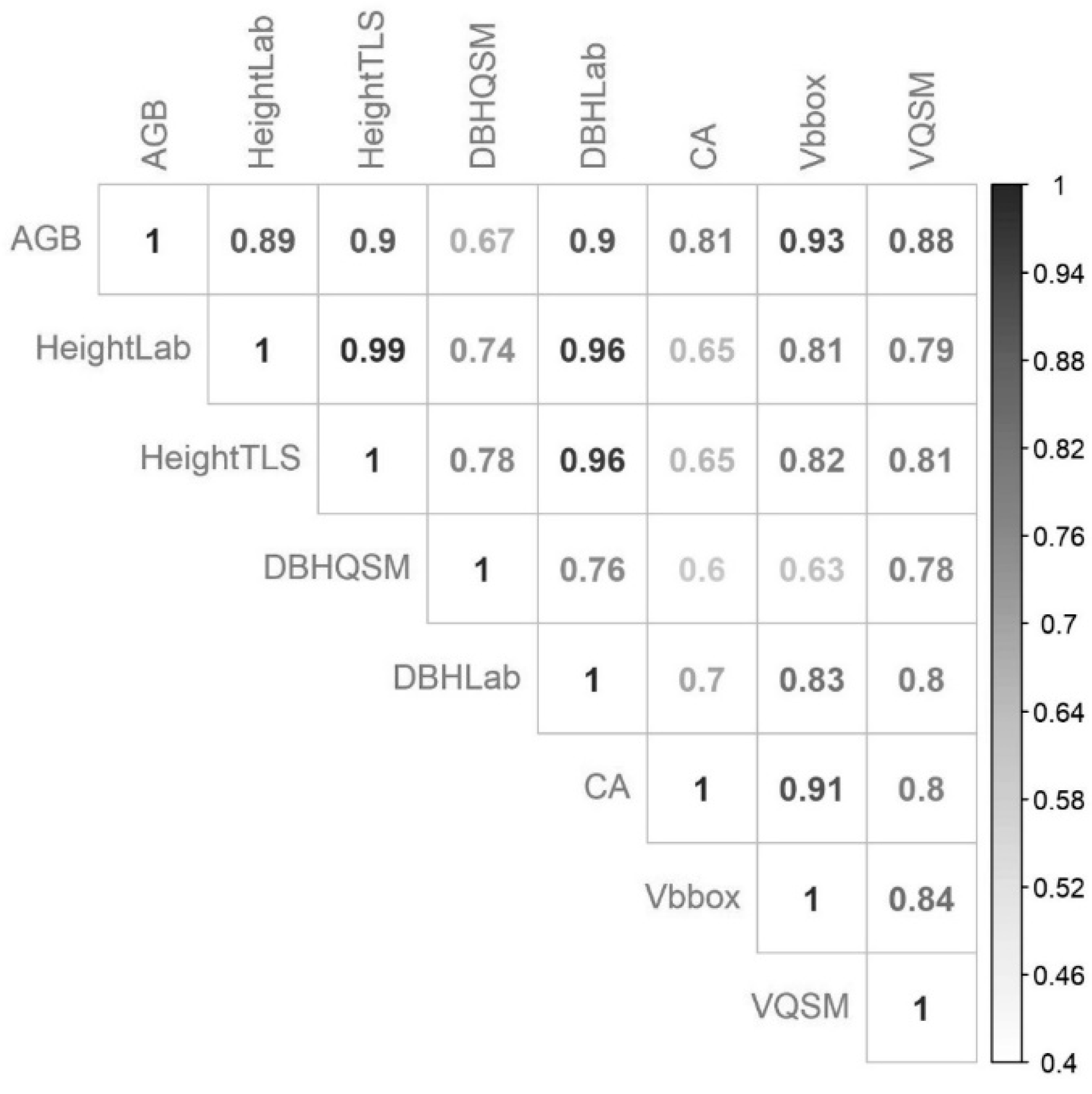
3.2. QSM Effectiveness
3.3. Model Rankings
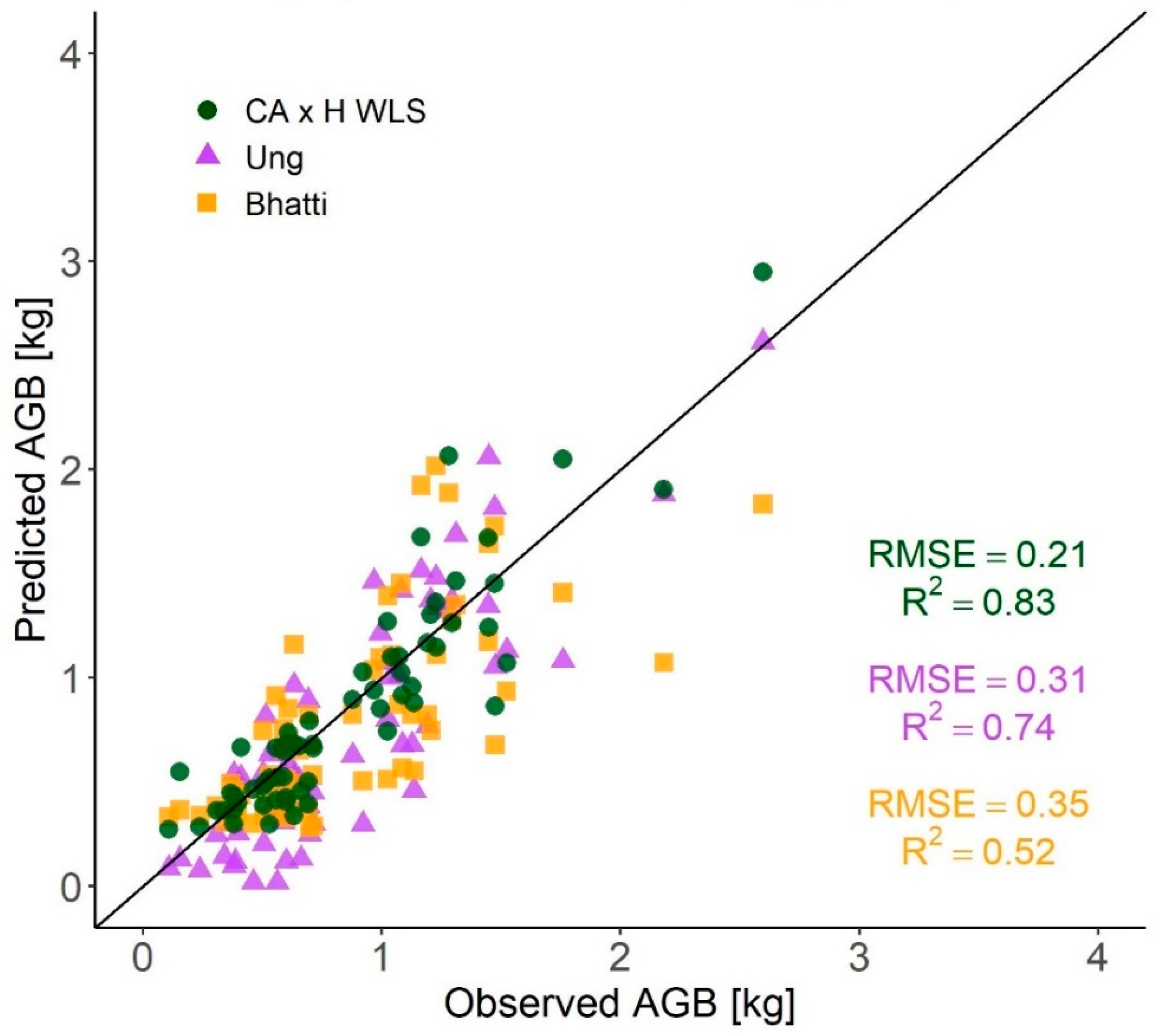
3.4. Comparisons with Published AGB Equations for Black Spruce
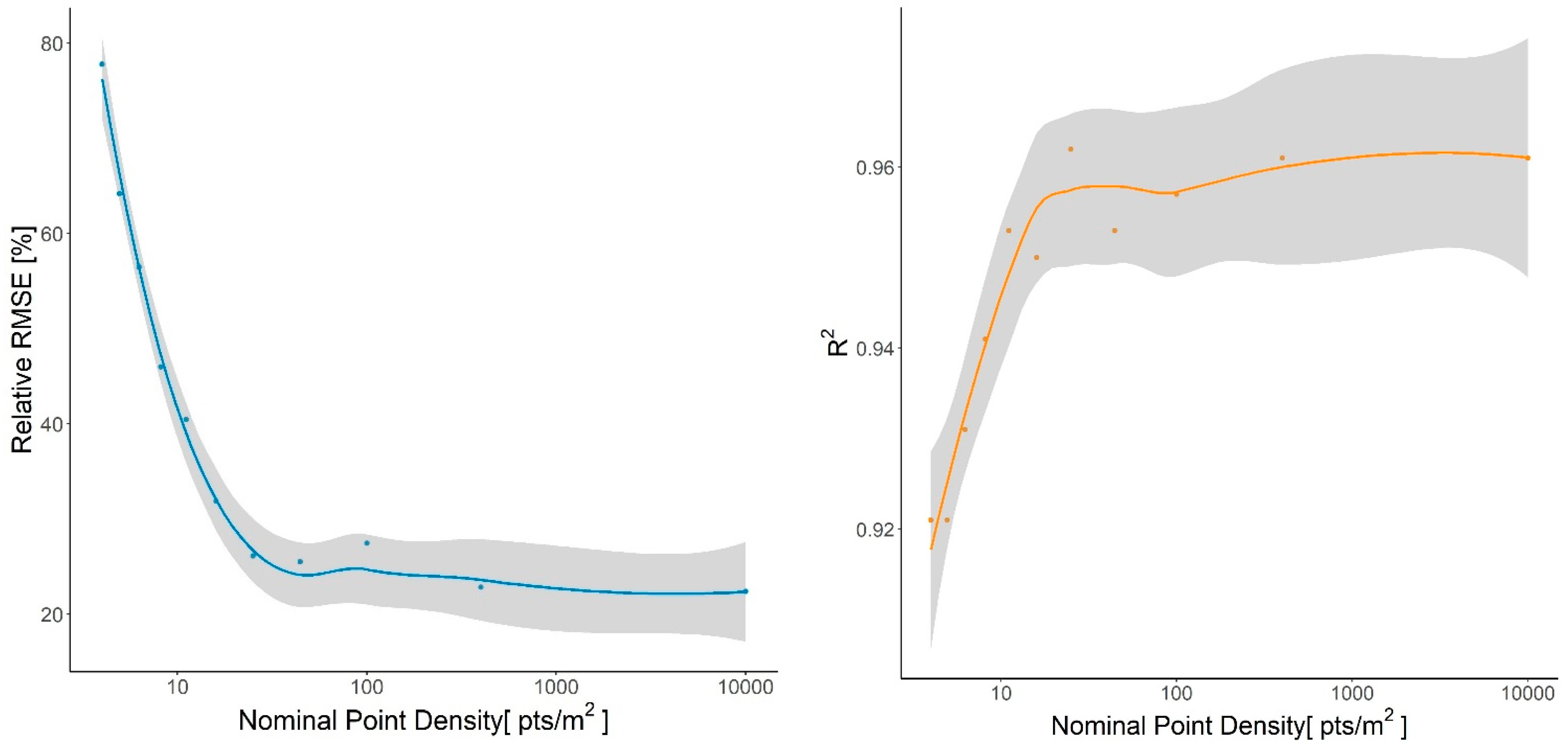
3.5. Crown Area Sensitivity Analysis
4. Discussion
4.1. Effect of Weights on Final Models
4.2. QSM Effectiveness
4.3. Model Rankings
4.4. Comparisons with Other AGB Estimation Methods
4.5. Crown Area Sensitivity Analysis
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Uncertainty Propagation
References
- Novotný, J.; Navrátilová, B.; Janoutová, R.; Oulehle, F.; Homolová, L. Influence of site-specific conditions on estimation of forest above ground biomass from airborne laser scanning. Forests 2020, 11, 268. [Google Scholar] [CrossRef] [Green Version]
- Gibbs, M.; Latzko, E. (Eds.) Photosynthesis II; Springer: Berlin/Heidelberg, Germany, 1979; ISBN 978-3-642-67244-6. [Google Scholar]
- Lorenz, K.; Lal, R. The natural dynamic of carbon in forest ecosystems. In Carbon Sequestration in Forest Ecosystems; Lorenz, K., Lal, R., Eds.; Springer: Dordrecht, The Netherlands, 2010; pp. 23–101. ISBN 978-90-481-3266-9. [Google Scholar]
- Ciais, P.; Sabine, C.; Bala, G.; Bopp, L.; Brovkin, V.; Canadell, J.; Chhabra, A.; DeFries, R.; Galloway, J.; Heimann, M.; et al. Carbon and other biogeochemical cycles. In Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Stocker, T.F., Qin, D., Plattner, G.-K., Tignor, M., Allen, S.K., Boschung, J., Nauels, A., Xia, Y., Bex, V., Midgley, P.M., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013. [Google Scholar]
- Vashum, K. Methods to estimate above-ground biomass and carbon stock in natural forests—A review. J. Ecosyst. Ecography 2012, 2, 1–7. [Google Scholar] [CrossRef]
- Chen, X.; YE, C.; Li, J.; Chapman, M.A. Quantifying the carbon storage in urban trees using multispectral ALS data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 3358–3365. [Google Scholar] [CrossRef]
- Houghton, R.A. Biomass. In Encyclopedia of Ecology; Jørgensen, S.E., Fath, B.D., Eds.; Academic Press: Oxford, UK, 2008; pp. 448–453. ISBN 978-0-08-045405-4. [Google Scholar]
- Natural Resources Canada. Boreal Forest. Available online: https://www.nrcan.gc.ca/our-natural-resources/forests/sustainable-forest-management/boreal-forest/13071 (accessed on 6 July 2021).
- Wells, J.V.; Dawson, N.; Culver, N.; Reid, F.A.; Morgan Siegers, S. The state of conservation in North America’s boreal forest: Issues and opportunities. Front. For. Glob. Chang. 2020, 3, 90. [Google Scholar] [CrossRef]
- Carlson, M.; Roberts, D.; Wells, J. The Carbon the World Forgot: Conserving the Capacity of Canada’s Boreal Forest Region to Mitigate and Adapt to Climate Change; Boreal Songbird Initiative: Seattle, WA, USA, 2009; ISBN 978-0-9842238-1-7. [Google Scholar]
- Disney, M.; Burt, A.; Calders, K.; Schaaf, C.; Stovall, A. Innovations in ground and airborne technologies as reference and for training and validation: Terrestrial laser scanning (TLS). Surv. Geophys. 2019, 40, 937–958. [Google Scholar] [CrossRef] [Green Version]
- Alemdag, I.S. Mass Equations and Merchantability Factors for Ontario Softwoods; Information Report PI-X-23; Canadian Forest Service: Ottawa, ON, Canada, 1983; pp. 1–24.
- Lau, A.; Calders, K.; Bartholomeus, H.; Martius, C.; Raumonen, P.; Herold, M.; Vicari, M.; Sukhdeo, H.; Singh, J.; Goodman, R. Tree Biomass Equations from Terrestrial LiDAR: A Case Study in Guyana. Forests 2019, 10, 527. [Google Scholar] [CrossRef] [Green Version]
- Lambert, M.-C.; Ung, C.-H.; Raulier, F. Canadian national tree aboveground biomass equations. Can. J. For. Res. 2005, 35, 1996–2018. [Google Scholar] [CrossRef]
- Ung, C.-H.; Bernier, P.; Guo, X.-J. Canadian national biomass equations: New parameter estimates that include British Columbia data. Can. J. For. Res. 2008, 38, 1123–1132. [Google Scholar] [CrossRef]
- Calders, K.; Wilkes, P.; Disney, M.; Armston, J.; Schaefer, M.; Woodgate, W. Chapter 19. Terrestrial LiDAR for measuring above-ground biomass and forest structure. In Effective Field Calibration and Validation Practices; TERN: Indooroopilly, QLD, Australia, 2018; ISBN 978-0-646-94137-0. [Google Scholar]
- Kalwar, O.P.P.; Hussin, Y.A.; Weir, M.J.C.; de Bie, C.A.J.M.; Karna, Y. Deriving forest plot inventory parameters using terrestrial laser scanning in the tropical rainforest of Malaysia. Int. J. Remote Sens. 2021, 42, 884–901. [Google Scholar] [CrossRef]
- Hopkinson, C.; Chasmer, L.; Colville, D.; Fournier, R.A.; Hall, R.J.; Luther, J.E.; Milne, T.; Petrone, R.M.; St-Onge, B. Moving Toward Consistent ALS Monitoring of Forest Attributes across Canada. Photogramm. Eng. Remote Sens. 2013, 79, 159–173. [Google Scholar] [CrossRef] [Green Version]
- Vauhkonen, J.; Maltamo, M.; McRoberts, R.E.; Næsset, E. Introduction to forestry applications of airborne laser scanning. In Forestry Applications of Airborne Laser Scanning: Concepts and Case Studies; Maltamo, M., Næsset, E., Vauhkonen, J., Eds.; Managing Forest Ecosystems; Springer: Dordrecht, The Netherlands, 2014; pp. 1–16. ISBN 978-94-017-8663-8. [Google Scholar]
- Brede, B.; Calders, K.; Lau, A.; Raumonen, P.; Bartholomeus, H.M.; Herold, M.; Kooistra, L. Non-destructive tree volume estimation through quantitative structure modelling: Comparing UAV laser scanning with terrestrial LIDAR. Remote Sens. Environ. 2019, 233, 111355. [Google Scholar] [CrossRef]
- Liang, X.; Kankare, V.; Hyyppä, J.; Wang, Y.; Kukko, A.; Haggrén, H.; Yu, X.; Kaartinen, H.; Jaakkola, A.; Guan, F.; et al. Terrestrial laser scanning in forest inventories. ISPRS J. Photogramm. Remote Sens. 2016, 115, 63–77. [Google Scholar] [CrossRef]
- Watt, P.J.; Donoghue, D.N.M. Measuring forest structure with terrestrial laser scanning. Int. J. Remote Sens. 2005, 26, 1437–1446. [Google Scholar] [CrossRef]
- Tansey, K.; Selmes, N.; Anstee, A.; Tate, N.J.; Denniss, A. Estimating tree and stand variables in a Corsican Pine woodland from terrestrial laser scanner data. Int. J. Remote Sens. 2009, 30, 5195–5209. [Google Scholar] [CrossRef]
- Srinivasan, S.; Popescu, S.C.; Eriksson, M.; Sheridan, R.D.; Ku, N.-W. Terrestrial laser scanning as an effective tool to retrieve tree level height, crown width, and stem diameter. Remote Sens. 2015, 7, 1877–1896. [Google Scholar] [CrossRef] [Green Version]
- White, J.C.; Coops, N.C.; Wulder, M.A.; Vastaranta, M.; Hilker, T.; Tompalski, P. Remote sensing technologies for enhancing forest inventories: A review. Can. J. Remote Sens. 2016, 42, 619–641. [Google Scholar] [CrossRef] [Green Version]
- Abegg, M.; Kükenbrink, D.; Zell, J.; Schaepman, M.E.; Morsdorf, F. Terrestrial laser scanning for forest inventories--tree diameter distribution and scanner location impact on occlusion. Forests 2017, 8, 184. [Google Scholar] [CrossRef] [Green Version]
- Soma, M.; Pimont, F.; Allard, D.; Fournier, R.; Dupuy, J.-L. Mitigating occlusion effects in leaf area density estimates from Terrestrial LiDAR through a specific kriging method. Remote Sens. Environ. 2020, 245, 111836. [Google Scholar] [CrossRef]
- Ghimire, S.; Xystrakis, F.; Koutsias, N. Using terrestrial laser scanning to measure forest inventory parameters in a mediterranean coniferous stand of Western Greece. PFG–J. Photogramm. Remote Sens. Geoinf. Sci. 2017, 85, 213–225. [Google Scholar] [CrossRef]
- Heinzel, J.; Huber, M.O. Tree stem diameter estimation from volumetric TLS image data. Remote Sens. 2017, 9, 614. [Google Scholar] [CrossRef] [Green Version]
- Liu, G.; Wang, J.; Dong, P.; Chen, Y.; Liu, Z. Estimating individual tree height and diameter at breast height (DBH) from terrestrial laser scanning (TLS) data at plot level. Forests 2018, 9, 398. [Google Scholar] [CrossRef] [Green Version]
- Moskal, L.M.; Zheng, G. Retrieving forest inventory variables with terrestrial laser scanning (TLS) in urban heterogeneous forest. Remote Sens. 2011, 4, 1–20. [Google Scholar] [CrossRef] [Green Version]
- Clough, B.F.; Scott, K. Allometric relationships for estimating above-ground biomass in six mangrove species. For. Ecol. Manag. 1989, 27, 117–127. [Google Scholar] [CrossRef]
- Nelson, B.W.; Mesquita, R.; Pereira, J.L.G.; Garcia Aquino de Souza, S.; Teixeira Batista, G.; Bovino Couto, L. Allometric regressions for improved estimate of secondary forest biomass in the central Amazon. For. Ecol. Manag. 1999, 117, 149–167. [Google Scholar] [CrossRef]
- Yamakura, T.; Hagihara, A.; Sukardjo, S.; Ogawa, H. Aboveground biomass of tropical rain forest stands in Indonesian Borneo. Vegetatio 1986, 68, 71–82. [Google Scholar] [CrossRef]
- Kadeba, O. Biomass equations for evenaged stands of Caribbean Pine (Pinus Caribaea) planted as an exotic in Nigeria. J. Trop. For. Sci. 1989, 1, 346–355. [Google Scholar]
- Jucker, T.; Caspersen, J.; Chave, J.; Antin, C.; Barbier, N.; Bongers, F.; Dalponte, M.; van Ewijk, K.Y.; Forrester, D.I.; Haeni, M.; et al. Allometric equations for integrating remote sensing imagery into forest monitoring programmes. Glob. Chang. Biol. 2017, 23, 177–190. [Google Scholar] [CrossRef]
- Harikumar, A.; Bovolo, F.; Bruzzone, L. An approach to conifer stem localization and modeling in high density airborne LiDAR data. In Proceedings of the Image and Signal Processing for Remote Sensing XXIII, Warsaw, Poland, 4 October 2017; International Society for Optics and Photonics: Bellingham, WA, USA, 2017; Volume 10427, p. 104270Q. [Google Scholar]
- Malek, S.; Miglietta, F.; Gobakken, T.; Næsset, E.; Gianelle, D.; Dalponte, M. Prediction of stem diameter and biomass at individual tree crown level with advanced machine learning techniques. IForest-Biogeosci. For. 2019, 12, 323–329. [Google Scholar] [CrossRef] [Green Version]
- Markus, T.; Neumann, T.; Martino, A.; Abdalati, W.; Brunt, K.; Csatho, B.; Farrell, S.; Fricker, H.; Gardner, A.; Harding, D.; et al. The Ice, Cloud, and land Elevation Satellite-2 (ICESat-2): Science requirements, concept, and implementation. Remote Sens. Environ. 2017, 190, 260–273. [Google Scholar] [CrossRef]
- Dubayah, R.; Blair, J.B.; Goetz, S.; Fatoyinbo, L.; Hansen, M.; Healey, S.; Hofton, M.; Hurtt, G.; Kellner, J.; Luthcke, S.; et al. The Global Ecosystem Dynamics Investigation: High-resolution laser ranging of the Earth’s forests and topography. Sci. Remote Sens. 2020, 1, 100002. [Google Scholar] [CrossRef]
- Dorado-Roda, I.; Pascual, A.; Godinho, S.; Silva, C.A.; Botequim, B.; Rodriguez-Gonzalvez, P.; Gonzalez-Ferreiro, E.; Guerra-Hernandez, J. Assessing the accuracy of GEDI data for canopy height and aboveground biomass estimates in Mediterranean forests. Remote Sens. 2021, 13, 2279. [Google Scholar] [CrossRef]
- Ni, W.; Zhang, Z.; Sun, G. Assessment of Slope-Adaptive Metrics of GEDI Waveforms for Estimations of Forest Aboveground Biomass over Mountainous Areas. J. Remote Sens. 2021, 2021. [Google Scholar] [CrossRef]
- Wieder, R.K.; Vitt, D.H.; Jackson, R.B. Boreal Peatland Ecosystems; Springer: Berlin/Heidelberg, Germany, 2006; ISBN 978-3-540-31913-9. [Google Scholar]
- Zhang, J. Boreal forests and taiga. In Encyclopedia of Science; Salem Press: Pasadena, CA, USA, 2019. [Google Scholar]
- Tarnocai, C.; Kettles, I.M.; Lacelle, B. Peatlands of Canada database. Geol. Surv. Can. 2011, 10, 6561. [Google Scholar]
- Warner, B.G.; Asada, T. Biological diversity of peatlands in Canada. Aquat. Sci. 2006, 68, 240–253. [Google Scholar] [CrossRef]
- Rencz, A.N.; Auclair, A.N.D. Biomass distribution in a subarctic picea mariana – cladonia alpestris woodland. Can. J. For. Res. 1978, 8, 168–176. [Google Scholar] [CrossRef]
- Lieffers, V.J. Stand structure, variability in growth and intraspecific competition in a peatland stand of black spruce picea mariana. Holarct. Ecol. 1986, 9, 58–64. [Google Scholar] [CrossRef]
- Bona, K.A.; Hilger, A.; Burgess, M.; Wozney, N.; Shaw, C. A peatland productivity and decomposition parameter database. Ecology 2018, 99, 2406. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bona, K.A.; Shaw, C.; Thompson, D.K.; Hararuk, O.; Webster, K.; Zhang, G.; Voicu, M.; Kurz, W.A. The Canadian model for peatlands (CaMP): A peatland carbon model for national greenhouse gas reporting. Ecol. Model. 2020, 431, 109164. [Google Scholar] [CrossRef]
- Thompson, D.K.; Simpson, B.N.; Beaudoin, A. Using forest structure to predict the distribution of treed boreal peatlands in Canada. For. Ecol. Manag. 2016, 372, 19–27. [Google Scholar] [CrossRef]
- Kurz, W.A.; Shaw, C.H.; Boisvenue, C.; Stinson, G.; Metsaranta, J.; Leckie, D.; Dyk, A.; Smyth, C.; Neilson, E.T. Carbon in Canada’s boreal forest—A synthesis. Environ. Rev. 2013, 21, 260–292. [Google Scholar] [CrossRef]
- Thompson, D.K.; Schroeder, D.; Wilkinson, S.L.; Barber, Q.; Baxter, G.; Cameron, H.; Hsieh, R.; Marshall, G.; Moore, B.; Refai, R.; et al. Recent crown thinning in a boreal black spruce forest does not reduce spread rate nor total fuel consumption: Results from an experimental crown fire in Alberta, Canada. Fire 2020, 3, 28. [Google Scholar] [CrossRef]
- Calders, K.; Newnham, G.; Burt, A.; Murphy, S.; Raumonen, P.; Herold, M.; Culvenor, D.; Avitabile, V.; Disney, M.; Armston, J.; et al. Nondestructive estimates of above-ground biomass using terrestrial laser scanning. Methods Ecol. Evol. 2015, 6, 198–208. [Google Scholar] [CrossRef]
- Lau, A.; Bentley, L.P.; Martius, C.; Shenkin, A.; Bartholomeus, H.; Raumonen, P.; Malhi, Y.; Jackson, T.; Herold, M. Quantifying branch architecture of tropical trees using terrestrial LiDAR and 3D modelling. Trees 2018, 32, 1219–1231. [Google Scholar] [CrossRef] [Green Version]
- Bhatti, J.S.; Errington, R.C.; Bauer, I.E.; Hurdle, P.A. Carbon stock trends along forested peatland margins in central Saskatchewan. Can. J. Soil Sci. 2006, 86, 321–333. [Google Scholar] [CrossRef]
- Environment and Natural Resources. Ecosystem Classification. Available online: https://www.enr.gov.nt.ca/en/node/351 (accessed on 9 February 2021).
- Ecosystem Classification Group; Northwest Territories; Department of Environment and Natural Resources. Ecological Regions of the Northwest Territories: Taiga Plains; Dept. of Environment and Natural Resources, Govt. of the Northwest Territories: Yellowknife, NT, Canada, 2009; ISBN 978-0-7708-0161-8.
- Leica Cyclone 3D Point Cloud Processing Software. Available online: https://leica-geosystems.com/products/laser-scanners/software/leica-cyclone (accessed on 13 June 2021).
- CloudCompare (v2.11.1). Available online: https://www.danielgm.net/cc/ (accessed on 28 March 2021).
- Raumonen, P.; Kaasalainen, M.; Åkerblom, M.; Kaasalainen, S.; Kaartinen, H.; Vastaranta, M.; Holopainen, M.; Disney, M.; Lewis, P. Fast automatic precision tree models from terrestrial laser scanner data. Remote Sens. 2013, 5, 491–520. [Google Scholar] [CrossRef] [Green Version]
- Disney, M.; Boni Vicari, M.; Burt, A.; Calders, K.; Lewis, S.L.; Raumonen, P.; Wilkes, P. Weighing trees with lasers: Advances, challenges and opportunities. Interface Focus 2018, 8, 20170048. [Google Scholar] [CrossRef] [Green Version]
- Gonzalez de Tanago, J.; Lau, A.; Bartholomeus, H.; Herold, M.; Avitabile, V.; Raumonen, P.; Martius, C.; Goodman, R.C.; Disney, M.; Manuri, S.; et al. Estimation of above-ground biomass of large tropical trees with terrestrial LiDAR. Methods Ecol. Evol. 2017, 9, 223–234. [Google Scholar] [CrossRef] [Green Version]
- Flade, L.; Hopkinson, C.; Chasmer, L. Allometric equations for shrub and short-stature tree aboveground biomass within boreal ecosystems of northwestern Canada. Forests 2020, 11, 1207. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2020. [Google Scholar]
- Mascaro, J.; Litton, C.M.; Hughes, R.F.; Uowolo, A.; Schnitzer, S.A. Is logarithmic transformation necessary in allometry? Ten, one-hundred, one-thousand-times yes: Yes, we need the logarithm in allometry. Biol. J. Linn. Soc. 2014, 111, 230–233. [Google Scholar] [CrossRef] [Green Version]
- Baskerville, G.L. Use of logarithmic regression in the estimation of plant biomass. Can. J. For. Res. 1972, 2, 49–53. [Google Scholar] [CrossRef]
- Breusch, T.S.; Pagan, A.R. A simple test for heteroscedasticity and random coefficient variation. Econometrica 1979, 47, 1287–1294. [Google Scholar] [CrossRef]
- Zeileis, A.; Hothorn, T. Diagnostic checking in regression relationships. R News 2002, 2, 7–10. [Google Scholar]
- Nwanganga, F.; Chapple, M. Practical Machine Learning in R; John Wiley & Sons: Hoboken, NJ, USA, 2020; ISBN 978-1-119-59153-5. [Google Scholar]
- Wenger, S.J.; Olden, J.D. Assessing transferability of ecological models: An underappreciated aspect of statistical validation. Methods Ecol. Evol. 2012, 3, 260–267. [Google Scholar] [CrossRef]
- Singh, T. Biomass Equations for Six Major Tree Species of the Northwest Territories; Environment Canada, Canadian Forestry Service: Ottawa, ON, Canada; Northern Forestry Research Centre: Edmonton, AB, USA, 1984; pp. 1–30.
- Peng, X.; Zhao, A.; Chen, Y.; Chen, Q.; Liu, H. Tree height measurements in degraded tropical forests based on UAV-LiDAR data of different point cloud densities: A case study on dacrydium pierrei in China. Forests 2021, 12, 328. [Google Scholar] [CrossRef]
- Martin-Ducup, O.; Mofack, G., II; Wang, D.; Raumonen, P.; Ploton, P.; Sonké, B.; Barbier, N.; Couteron, P.; Pélissier, R. Evaluation of automated pipelines for tree and plot metric estimation from TLS data in tropical forest areas. Ann. Bot. 2021. [Google Scholar] [CrossRef]
- Burt, A.; Disney, M.I.; Raumonen, P.; Armston, J.; Calders, K.; Lewis, P. Rapid characterisation of forest structure from TLS and 3D modelling. In Proceedings of the 2013 IEEE International Geoscience and Remote Sensing Symposium-IGARSS, Melbourne, VIC, Australia, 21–26 July 2013; pp. 3387–3390. [Google Scholar]
- Xi, Z.; Hopkinson, C.; Chasmer, L. Filtering stems and branches from terrestrial laser scanning point clouds using deep 3-D fully convolutional networks. Remote Sens. 2018, 10, 1215. [Google Scholar] [CrossRef] [Green Version]
- Wu, B.; Zheng, G.; Chen, Y. An improved convolution neural network-based model for classifying foliage and woody components from terrestrial laser scanning data. Remote Sens. 2020, 12, 1010. [Google Scholar] [CrossRef] [Green Version]
- Wang, D.; Takoudjou, S.M.; Casella, E. LeWoS. A universal leaf-wood classification method to facilitate the 3D modelling of large tropical trees using terrestrial LiDAR. Methods Ecol. Evol. 2020, 11, 376–389. [Google Scholar] [CrossRef]
- Goodman, R.C.; Phillips, O.L.; Baker, T.R. The importance of crown dimensions to improve tropical tree biomass estimates. Ecol. Appl. 2014, 24, 680–698. [Google Scholar] [CrossRef] [Green Version]
- Budei, B.C.; St-Onge, B.; Hopkinson, C.; Audet, F.-A. Identifying the genus or species of individual trees using a three-wavelength airborne lidar system. Remote Sens. Environ. 2018, 204, 632–647. [Google Scholar] [CrossRef]
- Modzelewska, A.; Fassnacht, F.E.; Stereńczak, K. Tree species identification within an extensive forest area with diverse management regimes using airborne hyperspectral data. Int. J. Appl. Earth Obs. Geoinf. 2020, 84, 101960. [Google Scholar] [CrossRef]
- Harikumar, A.; Paris, C.; Bovolo, F.; Bruzzone, L. A crown quantization-based approach to tree-species classification using high-density airborne laser scanning data. IEEE Trans. Geosci. Remote Sens. 2021, 59, 4444–4453. [Google Scholar] [CrossRef]
- Reese, H.; Nyström, M.; Nordkvist, K.; Olsson, H. Combining airborne laser scanning data and optical satellite data for classification of alpine vegetation. Int. J. Appl. Earth Obs. Geoinf. 2014, 27, 81–90. [Google Scholar] [CrossRef]
- Prošek, J.; Šímová, P. UAV for mapping shrubland vegetation: Does fusion of spectral and vertical information derived from a single sensor increase the classification accuracy? Int. J. Appl. Earth Obs. Geoinf. 2019, 75, 151–162. [Google Scholar] [CrossRef]
- Bruggisser, M.; Hollaus, M.; Otepka, J.; Pfeifer, N. Influence of ULS acquisition characteristics on tree stem parameter estimation. ISPRS J. Photogramm. Remote Sens. 2020, 168, 28–40. [Google Scholar] [CrossRef]
- Vandendaele, B.; Fournier, R.A.; Vepakomma, U.; Pelletier, G.; Lejeune, P.; Martin-Ducup, O. Estimation of northern hardwood forest inventory attributes using UAV laser scanning (ULS): Transferability of laser scanning methods and comparison of automated approaches at the tree- and stand-level. Remote Sens. 2021, 13, 2796. [Google Scholar] [CrossRef]
- Politz, F.; Sester, M. Joint classification of ALS and DIM point clouds. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2019, XLII-2-W13, 1113–1120. [Google Scholar] [CrossRef] [Green Version]
- Taylor, J.R. An Introduction to Error Analysis: The Study of Uncertainties in Physical Measurements, 2nd ed.; University Science Books: Sausalito, CA, USA, 1997; ISBN 978-0-935702-42-2. [Google Scholar]

| Model Type | Equation |
|---|---|
| Quadratic | y = exp(αx2 + ωx + β) · ε |
| Power | y = β · xα · ε |
| Multiple Regression Power | y = β · x1α · x2ω · ε |
| Plot Name | # * of Black Spruce in Plot | Height for All Trees (m) | DBH for All Trees (cm) | TLS Measured Crown Area (m2) | Height for Sample Trees (m) | DBH for Sample Trees (cm) | Avg AGB for Sample Trees (kg) |
|---|---|---|---|---|---|---|---|
| V2B006 | 52 | 2.6 ± 1.0 (1.3; 5.7) | 2.9 ± 1.5 (0.5; 7.1) | 0.16 ± 0.11 (0.05; 0.43) | 2.6 ± 1.0 (1.6; 5.0) | 2.8 ± 1.3 (1.5; 6.0) | 1.55 ± 1.50 (0.41; 5.42) |
| V2B009 | 47 | 2.4 ± 1.0 (1.3; 5.4) | 2.4 ± 1.4 (0.3; 6.2) | 0.18 ± 0.09 (0.06; 0.35) | 2.7 ± 1.1 (1.4; 5.1) | 2.9 ± 1.5 (1.1; 6.2) | 1.93 ± 1.95 (0.37; 6.78) |
| V2B011 | 31 | 2.7 ± 1.3 (1.3; 6.2) | 2.9 ± 1.8 (0.3; 6.5) | 0.23 ± 0.10 (0.08; 0.41) | 2.7 ± 1.2 (1.3; 4.7) | 2.9 ± 1.6 (0.3; 5.1) | 1.85 ± 1.19 (0.46; 4.14) |
| V2B012 | 23 | 3.4 ± 1.7 (1.4; 7.7) | 3.7 ± 2.4 (0.6; 9.7) | 0.32 ± 0.21 (0.11; 0.66) | 3.4 ± 1.5 (1.5; 5.6) | 3.7 ± 2.1 (0.9; 6.7) | 3.80 ± 3.40 (0.60; 9.31) |
| V2B015 | 44 | 2.0 ± 0.7 (1.4; 4.6) | 2.0 ± 1.0 (0.3; 5.9) | 0.15 ± 0.10 (0.04; 0.35) | 2.2 ± 0.9 (1.6; 4.4) | 2.3 ± 1.2 (0.3; 4.7) | 1.02 ± 1.06 (0.11; 3.68) |
| V2B016 | 32 | 3.0 ± 1.2 (1.3; 5.8) | 3.1 ± 1.7 (0.4; 6.6) | 0.17 ± 0.05 (0.08; 0.23) | 2.9 ± 1.4 (1.3; 5.5) | 2.8 ± 1.6 (0.5; 5.4) | 1.72 ± 1.52 (0.28; 5.07) |
| V2B019 | 92 | 2.3 ± 0.7 (1.3; 5.0) | 1.9 ± 1.1 (0.3; 5.7) | 0.11 ± 0.05 (0.06; 0.22) | 2.4 ± 0.8 (1.4; 3.8) | 2.1 ± 1.0 (0.7; 4.1) | 0.93 ± 0.69 (0.24; 2.48) |
| V2B022 | 25 | 2.3 ± 0.7 (1.5; 4.7) | 2.3 ± 1.3 (0.6; 6.3) | 0.18 ± 0.11 (0.08; 0.49) | 2.4 ± 0.9 (1.5; 4.7) | 2.4 ± 1.5 (1.0; 6.3) | 1.50 ± 1.73 (0.51; 6.58) |
| V2B023 | 112 | 2.2 ± 0.8 (1.3; 7.1) | 2.1 ± 1.2 (0.3; 6.9) | 0.10 ± 0.07 (0.04; 0.27) | 2.5 ± 1.1 (1.5; 4.8) | 2.3 ± 1.4 (0.7; 4.8) | 1.10 ± 1.24 (0.15; 4.28) |
| V2B026 | 115 | 2.0 ± 0.6 (1.3; 4.6) | 1.8 ± 1.1 (0.3; 5.2) | 0.12 ± 0.05 (0.06; 0.20) | 2.2 ± 0.6 (1.6; 3.7) | 2.3 ± 1.2 (1.2; 5.2) | 0.95 ± 0.81 (0.34; 2.95) |
| Total | 573 | 2.3 ± 1.0 (1.3; 7.7) | 2.3 ± 1.4 (0.3; 9.7) | 0.17 ± 0.12 (0.04; 0.66) | 2.6 ± 1.1 (1.3; 5.6) | 2.6 ± 1.5 (0.3; 6.7) | 1.63 ± 1.83 (0.11; 9.31) |
| Model Type | Model Predictors * | Avg MAE | Avg RMSE (kg) | Avg Adj R2 | Final Ranking |
|---|---|---|---|---|---|
| Multi Pwr | CAxH and CDxH | 0.22 (0.21) | 0.34 (0.36) | 0.94 (0.94) | 1 |
| Pwr | V (Bounding Box) | 0.40 (0.39) | 0.59 (0.66) | 0.89 (0.89) | 2 |
| Pwr | H | 0.45 (0.41) | 0.63 (0.67) | 0.88 (0.88) | 3 |
| Multi Pwr | DBHxH | 0.46 (0.41) | 0.64 (0.67) | 0.88 (0.88) | 4 |
| Pwr | V (QSM) | 0.50 (0.46) | 0.70 (0.85) | 0.82 (0.82) | 5 |
| Pwr | CA and CD | 0.67 (0.66) | 0.95 (1.04) | 0.71 (0.71) | 6 |
| Quad | DBH | 0.83 (0.75) | 1.18 (1.30) | 0.66 (0.66) | 7 |
| Model Type | x1 | x2 | β | β std err | α | α std err | ω | ω std err |
|---|---|---|---|---|---|---|---|---|
| Multi Pwr | CA | H | 0.73 | 0.13 | 0.54 | 0.06 | 1.68 | 0.09 |
| Multi Pwr | CD | H | 0.64 | 0.10 | 1.07 | 0.11 | 1.68 | 0.09 |
| Multi Pwr | DBH (QSM) | H | 0.16 | 0.02 | 0.06 | 0.07 | 2.19 | 0.14 |
| Pwr | V (Bounding Box) | - | 1.35 | 0.05 | 0.97 | 0.04 | - | - |
| Pwr | H | - | 0.16 | 0.02 | 2.29 | 0.09 | - | - |
| Pwr | V (QSM) | - | 0.23 | 0.03 | 0.76 | 0.04 | - | - |
| Pwr | CA | - | 14.64 | 2.40 | 1.29 | 0.09 | - | - |
| Pwr | CD | - | 10.73 | 1.55 | 2.57 | 0.18 | - | - |
| Quad | DBH (QSM) | −0.97 | 0.13 | 0.40 | 0.08 | 0.25 | 0.15 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wagers, S.; Castilla, G.; Filiatrault, M.; Sanchez-Azofeifa, G.A. Using TLS-Measured Tree Attributes to Estimate Aboveground Biomass in Small Black Spruce Trees. Forests 2021, 12, 1521. https://doi.org/10.3390/f12111521
Wagers S, Castilla G, Filiatrault M, Sanchez-Azofeifa GA. Using TLS-Measured Tree Attributes to Estimate Aboveground Biomass in Small Black Spruce Trees. Forests. 2021; 12(11):1521. https://doi.org/10.3390/f12111521
Chicago/Turabian StyleWagers, Steven, Guillermo Castilla, Michelle Filiatrault, and G. Arturo Sanchez-Azofeifa. 2021. "Using TLS-Measured Tree Attributes to Estimate Aboveground Biomass in Small Black Spruce Trees" Forests 12, no. 11: 1521. https://doi.org/10.3390/f12111521
APA StyleWagers, S., Castilla, G., Filiatrault, M., & Sanchez-Azofeifa, G. A. (2021). Using TLS-Measured Tree Attributes to Estimate Aboveground Biomass in Small Black Spruce Trees. Forests, 12(11), 1521. https://doi.org/10.3390/f12111521








