Next Article in Journal
Investigation of Feller-Buncher Performance Using Weibull Distribution
Previous Article in Journal
Applying Machine Strength Grading System to Round Timber Used in Hydraulic Engineering Works
Previous Article in Special Issue
Assessment of Sentinel-2 Satellite Images and Random Forest Classifier for Rainforest Mapping in Gabon
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Forests
Volume 12
Issue 3
10.3390/f12030282
forests-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Accumulated Heating and Chilling Are Important Drivers of Forest Phenology and Productivity in the Algonquin-to-Adirondacks Conservation Corridor of Eastern North America

by
Michael A. Stefanuk
* and
Ryan K. Danby
School of Environmental Studies, Queen’s University, Kingston, ON K7L 3N6, Canada
*
Author to whom correspondence should be addressed.
Forests 2021, 12(3), 282; https://doi.org/10.3390/f12030282
Submission received: 5 February 2021 / Revised: 23 February 2021 / Accepted: 25 February 2021 / Published: 2 March 2021
(This article belongs to the Special Issue Random Forests for Forest Ecology)
Browse Figures
Review Reports Versions Notes

Abstract

:
Research Highlights: Forest phenology and productivity were responsive to seasonal heating and chilling accumulation, but responses differed across the temperature range. Background and Objectives: Temperate forests have responded to recent climate change worldwide, but the pattern and magnitude of response have varied, necessitating additional studies at higher spatial and temporal resolutions. We investigated climatic drivers of inter-annual variation in forest phenology and productivity across the Algonquin-to-Adirondacks (A2A) conservation corridor of eastern North America. Methods: We used remotely sensed indices from the AVHRR sensor series and a suite of gridded climate data from the Daymet database spanning from 1989–2014. We used random forest regression to characterize forest–climate relationships between forest growth indices and climatological variables. Results: A large portion of the annual variation in phenology and productivity was explained by climate (pR2 > 80%), with variation largely driven by accumulated heating and chilling degree days. Only very minor relationships with precipitation-related variables were evident. Conclusions: Our results indicate that anthropogenic climate change in the A2A has not yet reached the point of triggering widespread changes in forest phenology and productivity, but the sensitivity of forest growth to inter-annual variation in seasonal temperature accumulation suggests that more temperate forest area will be affected by climate change as warming continues.

1. Introduction

The phenology (i.e., timing of growth events, such as bud burst) and productivity (i.e., photosynthetic production over time) of temperate forests worldwide have responded to recent climate change [1,2]. Climate in eastern North America has generally become warmer and wetter over the past century [3,4,5]. Annual mean temperature has increased by approximately 1 °C since 1901, with most change occurring during winter [6]. The return rate of extreme temperature anomalies, especially unusually high winter temperatures, has increased in recent decades [7], corresponding to the overall increase in temperatures, which has largely been attributed to anthropogenic forcing [8]. Precipitation totals and intensity have also increased, especially in fall and spring, and models predict that this trend will continue [6,9]. A better understanding of the responses of forests to these recent changes, as well as the specific climatic variables which influence their growth, is necessary for an improved understanding of the impacts of continued climate change.
Temperate forest phenology is among the most sensitive indicators of environmental change, and is responsive to temperature cues [10]. In spring, phenological progression from bud burst to leaf development is cued by warm temperatures, accumulated over time [10]. In fall, progression from photosynthetically active foliage to leaf senescence and/or abscission are also largely cued by temperature but also precipitation and photoperiod, which serves as a limiting factor for the end-of-season date [11]. Together, the dates of the start and end of the growing season determine the overall length of the growing season, though studies of changes in fall phenology are not as common as studies of changes in spring phenology [10]. Changes in temperature, especially accumulated growing degree-days, have been implicated in advanced spring onset, delayed fall senescence, and overall lengthening of the growing season in temperate forests at global (ex., [1]), hemispheric and continental (ex., [12]), and local scales (ex., [13]).
Climate variables other than temperature and precipitation have also been shown to affect temperate forest phenology. Unusual ‘false spring’ events—when spring temperatures warm early and the insulating snow pack melts, followed by freezing temperatures—have been shown to cause physiological damage in opportunistic tree species, thus reducing annual production and vitality [14]. Droughts also affect phenology and productivity, as a drought can induce senescence and stop primary production [11]. However, phenology trends are not uniform in time or space. For example, spring advance had slowed since the year 2000 in the northern hemisphere [15]. Additionally, trends in the temperature sensitivity of fall phenology varied spatially within the United States [16].
Increases in forest productivity have also been associated with increased growing season length and increased air temperature [1,17,18]. Temperature is thought to drive increases in growing season length, which in turn creates a longer window in which trees can photosynthesize. Broadly, trends in forest greening (i.e., significant increases in productivity) and browning (i.e., significant decreases in productivity) have been spatially and temporally heterogeneous across different biomes of the northern hemisphere, which is thought to be caused by variation in the changes to growing-season length trends and the environmental characteristics of each biome [19]. The greatest productivity increase from climate warming has been in North America’s cooler ecoregions, but all ecoregions have had distinct responses [20]. In Canada and Alaska, 30% of forests were greening and 3% were browning from 1984–2012 [21], which is generally consistent with a dominant greening trend over browning across the northern hemisphere [19]. An increase in productivity in terms of carbon-uptake has been observed in temperate forest stands in Ontario [22] and New England [23], following productivity increases by opportunistic tree species that were able to take advantage of longer growing seasons.
There has been substantial research documenting temperate forest phenology and productivity at very broad [19,24] and very fine scales [25,26]. However, studies at intermediate regional scales have been less common. Some studies have been conducted at a regional scale, including an examination of productivity trends and their drivers in Yellowstone National Park [27], and one examining the drivers of the timing of the start and end of the growing season in Great Smoky Mountains National Park [28]. The regional scale of these studies allowed their authors to contextualize their results with the ecological, geographical, and climatic characteristics of their region, such as how Emmett et al. [27] were able to assess the influence of wildfire, insect, and human disturbance on forest productivity trends, or how Norman et al. [28] developed a greater understanding of forest phenology variation by filtering for landcover type, elevation, and disturbance. Regional studies can provide a bridge between highly specific small-scale studies (i.e., trees or stands) and highly general broad-scale studies (i.e., nations, continents, or hemispheres), across which small- and large-scale knowledge can be linked.
The majority of studies attempting to understand the drivers of forest growth trends do so using co-occurring trends in other environmental variables [29]. For example, Yuan et al. [30] examined global trends in climatic variables and in NDVI globally, and found that trends in atmospheric vapor pressure deficit switched from positive to negative around the year 2000, which coincided with a change in the direction of NDVI trends, implying that the change in vapor pressure deficit trends were driving the change in NDVI trends. However, this method becomes problematic in the current climatic era because of an increasing rate of anomalous weather events [7], which can reduce the effectiveness of trend detection methods [31]. Furthermore, this method is not particularly useful in areas where, or during periods when, trends are not detected (either increasing or decreasing). As an alternative, several recent studies have instead modeled inter-annual drivers of forest growth (ex., [29]). By modelling drivers of inter-annual variation, rather than drivers of trends, climatic anomalies can be treated as natural experiments and thus provide greater insight into the role of such extremes, to which forest phenology and productivity are likely to respond [32]. The challenge with this approach, however, is that it is computationally intense, and the potentially large number of interacting variables are not well suited to traditional linear modeling. Climatological variables are often highly inter-correlated, so it is difficult to identify and differentiate responses to specific aspects of climate. Machine learning approaches, such as random forest (RF), have become increasingly popular for modelling the influence of many interrelated independent variables. Rodriguez-Galiano et al. [29] modelled inter-annual variation in European forest phenology using RF regression, and they found that phenology-climate models had higher R2 (68%–90% vs. 39%–68%, respectively) and lower root mean squared error (0.92–0.43 vs. 1.04–1.40, respectively) than conventional linear models.
Our aim in this study was to examine the influence of climate on temperate forest growth at a regional scale in North America. We examined spring and fall phenology, growing season length, and foliar productivity, and compared these annual metrics to a suite of climatic variables hypothesized to influence them. We focused on the Algonquin-to-Adirondacks conservation corridor (A2A), which contains large diverse areas of temperate forest. Our research questions were: to what extent does climate influence the interannual variation in phenology and productivity of forests in the A2A region and what climate variables are the most important in driving variation? In order to address these questions, we required a method that would support analysis of a large number of inter-correlated climate variables, identify their relative importance, and characterize their individual influence on forest growth. As such, we applied RF regression modeling, which has been shown to be effective for this purpose [29].

2. Study Area

A2A is a continentally significant conservation corridor, which spans the Canada–United States border at the eastern extent of the Great Lakes in eastern North America (see Figure 1) [33]. It has become the focus of international conservation efforts because of its high concentration of large interconnected natural areas, many of which are protected forests. These forests are highly diverse, even in the context of the already high diversity of eastern North America.
The land area of A2A is >135,000 km2, of which 61% is forests (calculated using [34]). Most forests are deciduous (32% of total area), dominated by maples (Acer rubrum and Acer saccharum), red oak (Quercus rubra), and American Beech (Fagus grandifolia) [35,36]. Coniferous forests represent a smaller proportion (9% of total area), mainly in high elevation sites in Adirondacks and riparian areas, and are dominated by pines (Pinus strobus and Pinus banksiana), spruces (Picea rubens, Picea glauca, and Picea mariana), balsam fir (Aibes balsamea), eastern hemlock (Thuja canadensis), and white cedar (Thuja occidentalis). Communities containing a mixture of deciduous and coniferous species represent more area than coniferous communities alone (21% of the total area). Human settlement and agricultural lands are mainly in lowlands near the St Lawrence River.

3. Data

3.1. Forest Phenology and Productivity Indices

Forest growth data products based on remotely sensed photosynthetic activity were obtained from the United States Geological Survey (USGS) Earth Resources Observation and Science Center. These data were developed using the Advanced High Resolution Radiometer sensor series (AVHRR), which presented a relatively long temporal window for trend analysis (1989 to 2014) and had a spatial resolution (1 km2) relevant to analysis of forest landscapes. Indices were derived from annually compiled weekly composites of the normalized difference vegetation index, commonly referred to as NDVI [37].
Of the variables available from the USGS, we selected four ‘forest growth indices’, which were representative of the productivity and phenology of forests in A2A. We selected one productivity index: time integrated NDVI (TIN); and three phenology indices: length of growing season (LOS), start of growing season (SOS), and end of growing season (EOS). Details on each index are found in Table 1. Remotely sensed phenology indices at the spatial resolution of AVHRR do not capture distinct phenophases of individual plants represented within pixels, but rather a relative phenological change (ex., SOS may correspond to 25% leaf expansion on 50% of trees in a given pixel) of all vegetation within a given area (i.e., pixel) [38]. Likewise, TIN is a proxy metric of vegetation foliage productivity integrated across a given area (i.e., pixel) within a given annual growing season. In combination, these indices represent overall annual forest foliage production (which is represented over time as productivity, i.e., TIN), the portion of each year in which forests are growing (i.e., LOS), and the date of the start (i.e., SOS) and end (i.e., EOS) of the growing season, which both affect the LOS.
Only those pixels representing land dominated by forest were retained for analysis. Forested areas were identified by aggregating all forest classes in the 30 m resolution North American Landcover Classification [34] into a single ‘forest’ class. AVHRR pixels that were comprised of less than 50% forest were removed from further analysis.
Ji and Brown [39] found that the USGS AVHRR phenology data products are biased by the effects of satellite orbital drift, and they recommend removing data for 1992, 1993, 1994, 1999, and 2000. As such, orbital drift effects were removed by setting values in the affected layers as null, which reduced the number of available years from 26 to 21 but did not alter the timespan of the dataset.
We tested for trends in forest growth indices using least squares linear regression as part of exploratory data analysis. After accounting for temporal autocorrelation, we found no statistically significant (α = 0.05) trends in these forest growth indices over the study period (see Appendix A Table A2). Given the lack of forest growth trends we assumed that interannual variability in forest growth indices was not directional during the study period.
Z-scores were calculated for each forest growth index to represent inter-annual variability in forest growth (sensu [29]). The Z-score for a given year is calculated by scaling (subtracting the 1989–2014 mean, excluding the given year, from a given observation each year) and centering (dividing scaled values by the 1989–2014 standard deviation by pixel) the original observations. Z-scores representing little inter-annual variation (values within 1 standard deviation of the mean: −1 to 1) were removed because we were primarily interested in modelling drivers of variation in forest growth and Z-scores representing lesser variation were not as informative as those that we retained in that regard. Data manipulation was performed using the raster package [40] for R [41].

3.2. Climatological Variables

Climatological data were obtained from the Daymet database (available from daymet.ornl.gov, accessed on 4 July 2018), which offers gap-free, geospatially explicit, gridded climatological datasets covering North America [42]. Daymet datasets have a 1 km2 spatial resolution, a daily temporal resolution, and data beginning in 1980, with more recent years being added on an ongoing basis. These contiguous daily data were produced by interpolating daily observations from meteorological stations [43].
Minimum and maximum air temperature (hereafter ‘minimum temperature’ and ‘maximum temperature’, respectively), total precipitation (hereafter ‘precipitation’), snow-water equivalents (hereafter ‘snowpack’), day length, and net incident shortwave radiation (hereafter ‘solar radiation’) were obtained directly from Daymet. These data were used to calculate several secondary climatic variables. Mean monthly temperature (hereafter ‘mean temperature’) was derived by calculating the mean daily temperature (mean temperature = (maximum temperature + minimum temperature)/2) and averaging over the course of the month. Three thermal time indices were also calculated: accumulated heating degree days (floor of 4 °C) before the start of season (hereafter ‘spring heating’); accumulated heating degree days before the growing season maximum (hereafter ‘summer heating’); and accumulated chilling degree days (ceiling of 20 °C) between the growing season maximum and the end of the growing season (hereafter ‘fall chilling’) [13]. Windows for accumulated spring heating (1 January to 31 May), summer heating (1 January to 31 July), and fall chilling (1 August to 31 October) were defined to accumulate heating from the beginning of heat accumulation in winter until the end of spring, until approximately the typical date of maximum greenness during summer, and following the maximum until after typical EOS. The typical date of maximum greenness and EOS dates were defined by the observed median date within A2A (1989 to 2014, not including years affected by orbital drift). Spring heating and summer heating were derived separately so that temperature accumulation would not be represented beyond the time relevant to SOS (as summer heating would be). Accumulation periods were defined arbitrarily by calendar date to capture thermal time within consistent periods for intuitive inter-annual comparison. The standardized precipitation-evapotranspiration index (hereafter ‘SPEI’) was calculated to assess climatological drought [44]. SPEI is a useful drought index because it effectively models these conditions using only temperature and precipitation data as inputs, and has comparable results to more elaborate models, such as the Palmer Drought Severity Index [45]. Also calculated was root-freeze-risk, which represents the number of days each year where there is potential for frost damage to the roots of trees (for calculation methods, see Table 2). It has been shown that vegetation is sensitive to frost damage that would otherwise have been avoided by snow cover [10]. To the best of our knowledge, no index such as this has been incorporated into a study of forest growth at this scale. A description of all climatic variables used is provided in Table 2.
Independent temporally and spatially specific accuracy assessment can be performed on Daymet data using the station-level cross-validation dataset from the Oak Ridge National Laboratory [47]. We used these data to assess the accuracy of the minimum air temperature, maximum air temperature, and precipitation amounts within our study period and area of interest (see Appendix A Table A1). The R2 values of the linear models fit to data from stations within A2A were approximately 0.6 for precipitation and were > 0.9 for maximum air temperature and minimum air temperature. A lower R2 for precipitation was not unexpected given that Daymet is thought to underestimate total precipitation at higher elevations [48].

4. Methods

4.1. Modelling Schema

The relationship between climate and forest growth was modelled using RF regression [49]. RF is an ensemble machine learning method wherein the resulting model is the average of a large number of decision trees, which are constructed by recursive partitioning of bootstrap sub-samples of independent variables to describe the variance in the dependent variable [50]. RF maintains spatial and temporal independence through random sampling with replacement and ensures independence between independent variables by selecting the best variable to form the split at each node given a random subset of those independent variables. For a thorough description of RF, see [49,50].
A strength of RF is that the importance of given independent variables can be quantified by assessing changes in model accuracy when using different independent data to split training data within trees. Genuer et al. [51] proposed using RF’s built-in variable importance ranking mechanism to identify the most important independent variables within a preliminary RF model before fitting a final more robust RF model using only those important variables. They tested this method on a variety of regression and classification problems using highly dimensional datasets and found that RF variable selection is able to reliably identify the most important variables within a dataset, and that models that used only important variables had greater accuracy than models using all variables, thus making the models more parsimonious. We employed such a two-step RF modelling approach by constructing a preliminary and final model for each forest growth index. The preliminary model was used to efficiently identify climatological variables that were important drivers of inter-annual variation in forest growth, and the final model was to robustly model those forest–climate relationships. A graphical depiction of this method is illustrated in Figure 2. RF models were constructed using the randomForest package for R [52] using sequential processing [53,54].

4.2. Training and Validation Data

Gridded datasets were converted to tabular format for model training and validation. Data from pixels for which the Z-scores of a given forest growth index were <−1 or >1 were included in the data tables along with the corresponding climatological data. Climatological variables included with each forest growth index were determined a priori based on their hypothesized influence. Once compiled, these data were split randomly into training (75%) and validation (25%) subsets using the caret package for R [55]. Genuer et al. [56] used large simulated and real-world datasets to train RF models, and found that models trained on larger subsample proportions—even up to 100% of the data—had lesser prediction error but required substantially greater computational time. We chose a 75% training subsample size to balance the need for low predictive error and training time limitations, while still obtaining a substantial independent validation subsample.

4.3. Model Training

RF models are relatively insensitive to changes in model hyperparameters relative to other machine-learning methods but still require appropriate settings to optimize model accuracy and efficiency [50]. The number of trees (ntree), minimum node size (nodesize), and number of variables tested at each node (mtry) hyperparameters can be set for RF models. Hastie et al. [50] showed that modifying mtry affects both the correlation between predictions made by individual regression trees and the mean squared error of the resulting RF model, and emphasize that modifying the mtry value affects the relative benefit of averaging trees in a forest. mtry was tuned by performing a 5-fold cross-validation of model root-mean-squared error (RMSE), and selecting the setting with the lowest RMSE, which was done using the caret package for R [55]. RF models are less sensitive to ntree and nodesize settings, so given computational restrictions we did not train these statistically but instead experimented with various settings to identify a suitable balance of model efficiency and accuracy for preliminary and final models.
Preliminary models were trained with datasets including all climatological variables that we hypothesized to be important drivers of each forest growth index. The ntree was set to 150, nodesize was set to 0.001% of the number of observations, and mtry was trained a priori. Fifteen variables with the highest variable importance ranks were selected from the results of preliminary models for use in final models. We iteratively explored different numbers of variables and found that 15 provided an adequate balance between model error and interpretability.
Final models were trained with datasets including the 15 variables selected in preliminary models. The ntree was set to 1000, nodesize was set to 0.001% of the number of observations, and mtry was trained a priori. Final RF models were intended to be more robust than preliminary models, and to be representative of the relationship between climate and forest growth.
Variable importance was ranked using RF’s node purity metric (IncNodePurity), which is measured by taking the cumulative differences between the residual sum of squares before and after all splits using a given variable across all trees in a forest [49,52]. RF’s ‘out of the box’ variable importance metrics are vulnerable to bias from independent data characteristics, namely variable intercorrelation and inconsistent measurement scale (reviewed in [57]). Variable importance bias can persist in RF models regardless of the variable selection metric chosen because of the inherent use of the Gini node purity metric to select appropriate independent variables with which to split data at nodes within trees [58]. Knowing that some bias may be present in a variable importance metric, we interpreted the results in terms of relative ranking patterns over absolute values from variable importance metrics. The IncNodePurity, expressed as a percentage, of the 15 most important independent variables was used to assess the relative importance of variables for each forest growth index.
These forest–climate relationships form final RF models were visualized using variable importance and partial dependence plots. The marginal influence of each important independent variable was plotted using partial dependence plots [59,60]. Partial dependence plots show the amplitude and shape of the response of the dependent variable to a given independent variable with the effects of other independent variables averaged but not ignored [49].

4.4. Model Validation

The strength of the models was assessed using the root mean squared error (RMSE), and the coefficient of determination, reported as the percent of variance explained by a model (pR2) and representing the predictive accuracy of each model. These metrics were calculated for preliminary and final models using withheld 25% validation datasets with the caret package for R [55]. Genuer et al. [56] tested various applications of RF modelling on big data, and recommended validating RF prediction accuracy using an independent dataset that is smaller than the training dataset instead of using model out-of-bag error, which they found to be an unreliable indication of model error in big data applications.

5. Results

5.1. Model Characteristics

RF models, which used independent climatological data, explained a large proportion of the variation in forest growth indices of phenology and productivity in the A2A region (pR2 > 80%, see Table 3). RF models for each forest growth index were trained on different datasets, based on the forest pixels randomly included in the training set and the climatic variables that we hypothesized were important for each forest growth index (see Table 3). SOS was trained on the smallest temporal window (18 months) because months after the start of season were not relevant, while the LOS, EOS, and TIN models were trained on a larger window (23 months). SOS models had the fewest training observations (N = 393,369) following the removal of low-variance Z-scores, and the fewest independent variables (m = 151), whereas TIN had the most (N = 415,881, m = 197). TIN and LOS required less computational effort than SOS or EOS (mtry = 25 vs. 85 and 100, respectively). RMSE decreased and pR2 increased from the preliminary models to the final models for all four forest growth indices (see Table 3).

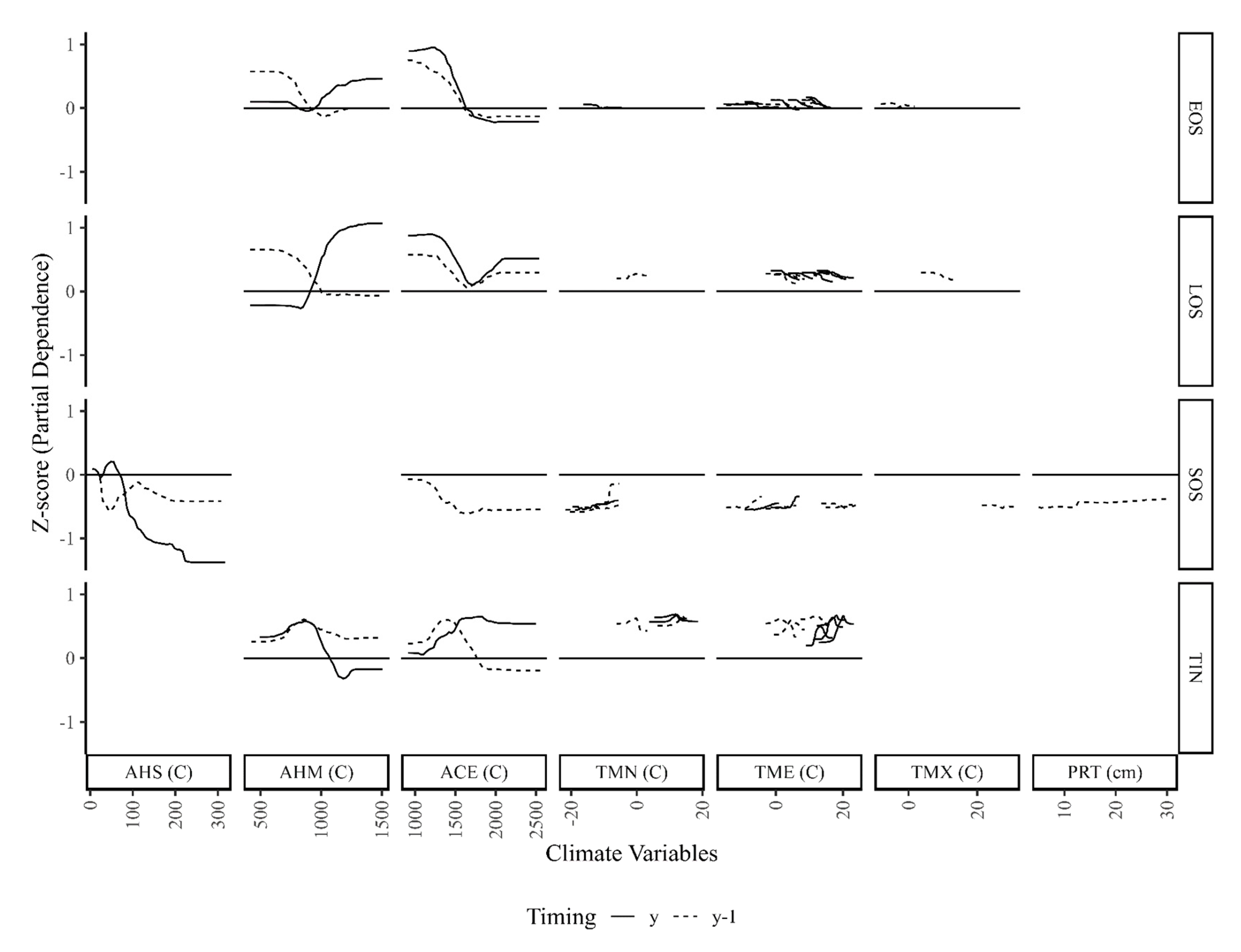
5.2. Forest-Climate Relationships

Spring and summer heating were the most important variables for SOS (spring), LOS, and TIN (summer) (see Table 4). Accumulated heating and chilling were ranked as being more important than monthly climate variables by a wide margin over other climatic variables considered here. Lagged effects of accumulated heating and chilling were generally ranked as being of lesser importance than current effects, except in the case of EOS, where lagged accumulated heating and chilling were ranked as more important than current accumulated heating. Greater accumulated heating resulted in earlier SOS and later EOS, though EOS was driven by greater current heating and lesser lagged heating (see Figure 3: AHS and AHM). LOS had a similar response to accumulated heating as EOS, with a larger response to greater current heat accumulation, which is consistent with the response of SOS. TIN responded negatively to heat accumulation below 1000 °C and responded positively above 1000 °C, with the largest responses in the mid-range of values, though TIN responded only positively to lagged heat accumulation. There was consistency in the inflection points of responses to accumulated heating, which appeared at approximately 900 and 1200 °C, and there was consistency in 0-crossovers at approximately 1000 °C.
Fall chilling accumulation was the most important variable for EOS, again by a wide margin over other climatic variables (see Table 4). Greater accumulated chilling resulted in earlier EOS, and lagged effects resulted in earlier SOS (see Figure 3: ACE). LOS responded positively to accumulated chilling, wherein lesser chilling resulted in longer LOS, and greater chilling also resulted in longer LOS to a lesser extent, but mid-range chilling had a neutral effect on LOS. LOS’ response to chilling appears to be a rough approximation of the most pronounced effects of chilling on SOS and EOS, wherein greater chilling resulted in a longer LOS at low, and to a lesser extent at high, levels of chilling accumulation. For EOS and LOS, the lagged effects of chilling were similar to current effects but with a lesser amplitude. TIN responded positively to accumulated chilling, with mid to high chilling accumulation resulting in higher TIN, though lagged chilling has a minimal effect at high chilling accumulation. TIN’s response to accumulated chilling mirrored the lagged response of SOS, which could indicate a relationship between these responses. Again, there was consistency in the inflection points of responses to accumulated chilling, which appeared at approximately 1200 and 1600 °C.
Monthly temperature variables, generally the mean, were ranked as being of some importance to forest phenology and productivity indices (see Table 4). The amplitude of their influence was less than that of accumulated heating and chilling (see Figure 3: TMN, TME, and TMX). SOS responded negatively to monthly temperature, whereas LOS and TIN responded positively, and EOS responses were relatively neutral. The relationships between monthly temperature and forest growth indices were generally similar in shape but were shifted along the x-axis depending on the range of temperatures in each month. Responses appeared in similar locations along the x-axis, indicating the range of monthly temperature means, minimums, and maximums that are most important for a given forest growth index.
Some climatic variables that we considered were not ranked among the 15 most important variables in preliminary RF models, and thus were not included in final RF models. Those variables were: drought, snowpack, root-freeze risk, solar radiation, and photoperiod. Precipitation was of some importance for SOS (rank 13/15, see Table 4).

6. Discussion

We assessed the inter-annual response of forest phenology and productivity indices to climatological variables in the forests of A2A from 1989–2014 with RF regression models, which allowed us to rank the importance of climatological variables for forest growth and characterize forest growth responses to climatological variables using partial dependence plots. We found that air temperature variables, in particular seasonal heating and chilling accumulation, explained much of the inter-annual variation in forest phenology and productivity in A2A. Forest growth responses to heating and chilling accumulation were non-linear, and variable across their range, and lagged responses differed from current responses.
A large proportion of inter-annual variation in phenology indices was explained by climatic variables. Accumulated heating and chilling were the most important variables in phenology models by a notable margin, especially for SOS and EOS. Generally, greater heat accumulation was associated with earlier SOS in spring and later EOS in fall, and greater chilling accumulation was associated with earlier SOS in the subsequent spring and earlier EOS in fall. This is broadly consistent with a large body of literature that has developed indicating that accumulated heating and chilling drives phenological development for temperate vegetation (reviewed in [10,61]). This is also consistent with local-scale field-based phenology observations, such as those by Richardson et al. [13], who found that logistic models based on accumulated warming degree-days (>4 °C) explained 90% of the variation in spring and fall phenophase progression timing in sugar maple, yellow birch, and American beech trees. Similarly, Yu et al. [62] trained species-level multiple linear regression predictive models of phenophase progression from field observations of deciduous trees, and found that models using accumulated growing degree days (>3 °C) were effective for simulating phenological progression in spring and fall. Our results demonstrate a similar relationship across A2A, which contains a diverse mixture of deciduous as well as coniferous trees. There has been some experimental work on differentiating species-specific sensitivity of different deciduous tree species’ phenology to climatic cues (ex. [26]), and we recommend future work on differentiating the responses of different forest communities at a regional scale, especially for largely coniferous communities. LOS response curves appeared to include the combined responses of SOS and EOS to temperature, which is logical because SOS and EOS dictate the endpoints of LOS. However, variation in LOS could be from either SOS or EOS so we considered them together here for context. Lower levels of accumulated heating were associated with later EOS and longer LOS in the following year, which could indicate a compensatory reaction to early fall senescence or short growing seasons assuming that conditions in the subsequent year are more favorable. EOS was later in years with lower chilling accumulation, indicating that forests responded opportunistically in warm years and continued their growth later into the fall. Interestingly, SOS was earlier in years when chilling was greater in the previous fall, suggesting that in years where EOS is early due to chilling, SOS may also be earlier.
Like phenology, we found that inter-annual variation in forest productivity was strongly linked to climate, and accumulated heating was the most important climatic variable for TIN. We observed productivity responses to be highest at moderate levels of heat accumulation, but that this response was negative at higher levels of heat accumulation. In contrast, productivity was higher with higher levels of chilling accumulation. Together, these could indicate that forest productivity is adapted to a mid-range heating and chilling envelope in this region, and that a potential future heating increase and chilling decrease could shift climatic conditions away from the fundamental niche of A2A’s current forest tree species. Wang et al. [63] also observed the responsiveness of forests in eastern North America to temperature. They tested for piecewise trends in NDVI productivity and spring temperature in North America and found that greening trends stalled around 2000 when spring temperature began to decline. However, studies at different scales have found that different factors drive forest productivity. At a very fine scale, studies using carbon flux as a proxy measure of productivity found that net ecosystem productivity is strongly correlated with photosynthetically active radiation in southern Ontario [22] and Massachusetts [23]. Zhu et al. [1] used trends in remotely sensed leaf area index, and found that atmospheric carbon fertilization explains much of the global greening that occurred from 1982–2009, and climate change explained only a small proportion of that greening. The contrast of our results with these finer- and coarser-scale studies suggests that there is inconsistency in the drivers of forest productivity when it is observed at different scales or using different methods. Myers-Smith et al. [64] explored a similar variation in productivity–climate relationships across the Arctic tundra biome when measured at different scales and our results point to the need for a parallel analysis for the temperate forest biome.
Many of the climatic variables that we included were not ranked as being important drivers of inter-annual variation in forest growth. Precipitation was of marginal importance for SOS, while drought, snowpack, root-freeze risk, solar radiation, and photoperiod were not ranked as being among the most important drivers of forest growth indices examined here. Photoperiod did not vary year-to-year, so it would not explain interannual variation. However, Yu et al. [62] found that photoperiod was an important variable in building reliable predictive models of the start and end of season dates, which indicates that the photoperiod can influence the date of a phenological shift but does not have a large influence on inter-annual variation in those dates. The limited importance of precipitation was surprising as precipitation is thought to provide necessary moisture for leaf development in spring and it has been shown to be important for phenological progression in spring and fall in other temperate regions [10,11]. Seyednasrollah et al. [24] examined environmental drivers of deciduous spring and fall phenology using PhenoCam data and a hierarchical multivariate joint model, and found that fall senescence advanced in parts of North America where mean annual precipitation was low, which indicates that forest sensitivity to precipitation depends on local climate. The limited importance of precipitation and drought in this case could indicate that the fall phenology of forests in A2A are insensitive to precipitation because of their climatic niche. Snow pack, or specifically the absence of snow pack, has been suggested as being a signal of the start of the growing season in high elevation or high-latitude environments [10], so it is logical that snowpack was not among the most important drivers of phenology in A2A, which is at low to middle elevations. However, snowpack serves to insulate roots from frost damage [65]. Major ‘false spring’ events, in which early snowmelt is followed by a cold snap, have resulted in notable root-freezing and damage in eastern North America in recent decades [14,66]. We designed the root-freeze risk index to quantify the potential for such damage and did not expect that it would be absent from the most important variables here because of known false spring events in A2A during the study period. However, these false springs were singular events, rather than continuous over time, so it is possible that they did not influence inter-annual variation over the entirety of the study period and thus were not ranked as being of high importance. It is possible that precipitation, photoperiod, and other variables have influenced forest phenology and productivity, but that these effects were ephemeral and were thus removed in the variable-selection stage following preliminary RF models. Other modelling approaches (ex. [24,62]) are more effective for identifying these subtleties for specific variables, and we recommend that future research examines the interrelated effects of episodic and continuous climatic variables on temperate forest growth.
Rodriguez-Galiano et al. [29] used RF regression to model climatic drivers of inter-annual variation in SOS and EOS across Europe, and following their success in its application recommended the use of RF to answer similar research questions elsewhere. We also found that RF was well suited to inter-annual forest-climate modelling. The ability to include large numbers of inter-correlated training variables—which climatic variables often are [38]—was especially useful as it allowed us to select the most important climatic variables from the many that could be influential. The ability to show non-linear relationships with partial dependence plots was also revealing because of the complexity of the forest–climate relationships that we found, which were not prototypical relationship forms (ex, linear, exponential). Our two-staged RF modelling approach made the modelled results more intuitive and parsimonious as less important climatic variables were not included in final results (sensu [51]). Recently, spatial cross-validation methods have been suggested to improve the predictive power of RF and other machine learning methods when using spatial data [67,68,69]. We did not apply spatial cross-validation in training, and our model validation metrics may be overly optimistic as a result. However predictive power and applicability outside of the area and time of interest were not as important as variable importance and partial dependence in answering our research questions, so those were the focus of this work. Studies in which greater predictive strength is required should consider applying such methods to avoid overfitting of spatially autocorrelated variables.

7. Conclusions

We used remotely sensed data and random forest regression to model forest–climate relationships for forest phenology and productivity indices in the Algonquin-to-Adirondack (A2A) conservation corridor from 1989–2014. In this analysis, we were able to compare forest phenology and productivity responses directly.
-
A large proportion of year-to-year variability in forest phenology and productivity was explained by climatic variables, particularly heating and chilling accumulation;
-
Accumulated heating was most important for SOS, EOS, and TIN, but accumulated chilling was most important for EOS;
-
Phenology was most responsive to temperature accumulation at low or high extremes, while productivity was most responsive to more moderate accumulations;
-
Lagged responses of EOS and LOS to accumulated heating, and of SOS to accumulated chilling had important distinctions from current responses;
-
Precipitation, photoperiod, and other climate variables were not ranked as being among the most important drivers of phenology or productivity.
The climate of eastern North America has warmed in the last century (+0.08 °C/decade), and more rapidly in recent decades (1970–2000: +0.25 °C/decade), though more of this warming has occurred in winter over summer [5,70]. These trends are projected to continue into future decades [3,4]. Given the relationships between forest growth and temperature that we observed, it seems likely that the growing season will be extended in A2A forests in coming years. These phenological changes have been anticipated using predictive models for forests in New England [71,72], lending support to this conclusion. However, our modeling indicates that warming could have a less predictable effect on total forest productivity in the future; moderate amounts of heating or chilling accumulation had a positive effect on TIN, but outside of that range, the effects of temperature accumulation were increasingly negative. This suggests that the warmer growing season temperatures expected in the future, which will likely include reduced chilling, could result in a decrease in forest productivity in some areas until forest composition changes to include higher proportions of tree species better suited to the future climate conditions.

Author Contributions

Conceptualization, M.A.S. and R.K.D.; methodology, M.A.S. and R.K.D.; software, M.A.S.; validation, M.A.S.; formal analysis, M.A.S.; investigation, M.A.S.; resources, R.K.D.; data curation, M.A.S.; writing—original draft preparation, M.A.S.; writing—review and editing, R.K.D. & M.A.S.; visualization, M.A.S.; supervision, R.K.D.; project administration, R.K.D.; funding acquisition, R.K.D. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the Canada Foundation for Innovation and Ontario Research Fund (LOF grant, file 22534), and by the School of Environmental Studies, Queen’s University.

Data Availability Statement

The data presented in this study are openly available in OSF at doi:10.17605/OSF.IO/ZWQ5A.

Acknowledgments

We would like to thank Paul Treitz, Brian Cumming and Anna Harrison for comments on an earlier draft, and editors and reviewers for their attention and suggestions which certainly improved this work.

Conflicts of Interest

The authors declare no conflict of interest.

Appendix A

Table
Table A1. Results of accuracy assessment of Daymet climatological data for A2A. Tests were performed using observed and predicted daily data for the beginning (1988) and end (2014) of the study period. The data used for validation are available for download [47]. Only the precipitation (prcp), minimum temperature (tmin), and maximum temperature (tmax) variables were available at the time that we performed this test. An ordinary-least squares linear model and a one-sided test of Pearson’s product moment correlation coefficient were used to assess the similarity between observed data from climatological stations and spatially corresponding predicted values from interpolated Daymet data.
Table A1. Results of accuracy assessment of Daymet climatological data for A2A. Tests were performed using observed and predicted daily data for the beginning (1988) and end (2014) of the study period. The data used for validation are available for download [47]. Only the precipitation (prcp), minimum temperature (tmin), and maximum temperature (tmax) variables were available at the time that we performed this test. An ordinary-least squares linear model and a one-sided test of Pearson’s product moment correlation coefficient were used to assess the similarity between observed data from climatological stations and spatially corresponding predicted values from interpolated Daymet data.
PrecipitationMinimum TemperatureMaximum Temperature
198820141988201419882014
Number of Stations1601401198411984
R-squared of linear model0.5810.6320.9770.9730.9690.965
Pearson’s correlation coefficient0.7620.7950.9880.9860.9840.982
p-value of Pearson’s correlation<0.0001<0.0001<0.0001<0.0001<0.0001<0.0001
Table
Table A2. Forest area with trends in growth, expressed as percent forest area within each ecoregion. Areas are presented as area of statistically significant trends (p ≤ 0.05) and statistically significant trends after correction for false-discovery rate (FDR). We used linear regression to identify annual trends in forest growth indices over the course of the 26-year study period. Time-ordered datasets for each forest pixel were first pre-whitened using the Yue-Pilon method [73]; wherein the series was transformed by subtracting the first autoregressive component from the series in order to remove temporal autocorrelation and avoid Type-1 error in trend testing [74]. Linear models were then fit using Sen’s slope [75], with the forest growth variable as the dependent variable and time (i.e., year) as the independent variable. The significance of models was assessed using p-values from a two-tailed Mann-Kendall significance test [76]. Testing many spatial pixels simultaneously presents a multiple-testing problem, wherein there was essentially a guarantee that false-positives would be identified without appropriate correction [77]. To address this, we adjusted p-values to account for the false-discovery rate using the Benjamini and Hochberg method [78]. Trend tests were performed using the zyp package for R [74].
Table A2. Forest area with trends in growth, expressed as percent forest area within each ecoregion. Areas are presented as area of statistically significant trends (p ≤ 0.05) and statistically significant trends after correction for false-discovery rate (FDR). We used linear regression to identify annual trends in forest growth indices over the course of the 26-year study period. Time-ordered datasets for each forest pixel were first pre-whitened using the Yue-Pilon method [73]; wherein the series was transformed by subtracting the first autoregressive component from the series in order to remove temporal autocorrelation and avoid Type-1 error in trend testing [74]. Linear models were then fit using Sen’s slope [75], with the forest growth variable as the dependent variable and time (i.e., year) as the independent variable. The significance of models was assessed using p-values from a two-tailed Mann-Kendall significance test [76]. Testing many spatial pixels simultaneously presents a multiple-testing problem, wherein there was essentially a guarantee that false-positives would be identified without appropriate correction [77]. To address this, we adjusted p-values to account for the false-discovery rate using the Benjamini and Hochberg method [78]. Trend tests were performed using the zyp package for R [74].
TINLOSSOSEOS
p ≤ 0.05FDRp ≤ 0.05FDRp ≤ 0.05FDRp ≤ 0.05FDR
+3.2%0.0%8.6%0.0%0.4%0.0%7.0%0.0%
00.0%0.0%0.0%0.0%0.0%0.0%0.0%0.0%
−1.1%0.0%0.0%0.0%0.7%0.0%0.1%0.0%

References

  1. Zhu, Z.; Piao, S.; Myneni, R.B.; Huang, M.; Zeng, Z.; Canadell, J.G.; Ciais, P.; Sitch, S.; Friedlingstein, P.; Arneth, A.; et al. Greening of the Earth and its drivers. Nat. Clim. Chang. 2016, 6, 791–795. [Google Scholar] [CrossRef]
  2. Garonna, I.; de Jong, R.; Schaepman, M.E. Variability and evolution of global land surface phenology over the past three decades (1982–2012). Glob. Chang. Biol. 2016, 22, 1456–1468. [Google Scholar] [CrossRef]
  3. Reidmiller, D.R.; Avery, C.W.; Easterling, D.R.; Kunkel, K.E.; Lewis, K.L.M.; Maycock, T.K.; Stewart, B.C. (Eds.) USGCRP, 2018: Impacts, Risks, and Adaptation in the United States, Fourth National Climate Assessment, Volume II; U.S. Global Change Research Program: Washington, DC, USA, 2018.
  4. Bush, E.; Lemmen, D.S. (Eds.) Canada’s Changing Climate Report; Government of Canada: Ottawa, ON, Canada, 2019.
  5. Huntington, T.G.; Richardson, A.D.; McGuire, K.J.; Hayhoe, K. Climate and hydrological changes in the northeastern United States: Recent trends and implications for forested and aquatic ecosystems. Can. J. For. Res. 2009, 39, 199–212. [Google Scholar] [CrossRef] [Green Version]
  6. Vincent, L.A.; Zhang, X.; Mekis, É.; Wan, H.; Bush, E.J. Changes in Canada’s Climate: Trends in Indices Based on Daily Temperature and Precipitation Data. Atmos. Ocean 2018, 56, 332–349. [Google Scholar] [CrossRef] [Green Version]
  7. Wang, X.L.; Feng, Y.; Vincent, L.A. Observed changes in one-in-20 year extremes of Canadian surface air temperatures. Atmos. Ocean 2014, 52, 222–231. [Google Scholar] [CrossRef]
  8. Wan, H.; Zhang, X.; Zwiers, F. Human influence on Canadian temperatures. Clim. Dyn. 2019, 52, 479–494. [Google Scholar] [CrossRef]
  9. Hoerling, M.; Eischeid, J.; Perlwitz, J.; Quan, X.W.; Wolter, K.; Cheng, L. Characterizing recent trends in U.S. heavy precipitation. J. Clim. 2016, 29, 2313–2332. [Google Scholar] [CrossRef]
  10. Richardson, A.D.; Keenan, T.F.; Migliavacca, M.; Ryu, Y.; Sonnentag, O.; Toomey, M. Climate change, phenology, and phenological control of vegetation feedbacks to the climate system. Agric. For. Meteorol. 2013, 169, 156–173. [Google Scholar] [CrossRef]
  11. Way, D.A.; Montgomery, R.A. Photoperiod constraints on tree phenology, performance and migration in a warming world. Plant Cell Environ. 2015, 38, 1725–1736. [Google Scholar] [CrossRef] [PubMed]
  12. Jeong, S.J.; Ho, C.H.; Gim, H.J.; Brown, M.E. Phenology shifts at start vs. end of growing season in temperate vegetation over the Northern Hemisphere for the period 1982-2008. Glob. Chang. Biol. 2011, 17, 2385–2399. [Google Scholar] [CrossRef]
  13. Richardson, A.D.; Bailey, A.S.; Denny, E.G.; Martin, C.W.; O’Keefe, J. Phenology of a northern hardwood forest canopy. Glob. Chang. Biol. 2006, 12, 1174–1188. [Google Scholar] [CrossRef] [Green Version]
  14. Hufkens, K.; Friedl, M.A.; Keenan, T.F.; Sonnentag, O.; Mailey, A.; O’Keefe, J.; Richardson, A.D. Ecological impacts of a widespread frost event following early spring leaf-out. Glob. Chang. Biol. 2012, 18, 2365–2377. [Google Scholar] [CrossRef]
  15. Wang, X.; Piao, S.; Xu, X.; Ciais, P.; Macbean, N.; Myneni, R.B.; Li, L. Has the advancing onset of spring vegetation green-up slowed down or changed abruptly over the last three decades? Glob. Ecol. Biogeogr. 2015, 24, 621–631. [Google Scholar] [CrossRef]
  16. Dragoni, D.; Rahman, A.F. Trends in fall phenology across the deciduous forests of the Eastern USA. Agric. For. Meteorol. 2012, 157, 96–105. [Google Scholar] [CrossRef]
  17. Myneni, R.B.; Keeling, C.D.; Tucker, C.J.; Asrar, G.; Nemani, R.R. Increased plant growth in the northern high latitudes from 1981 to 1991. Nature 1997, 386, 698–702. [Google Scholar] [CrossRef]
  18. Richardson, A.D.; Black, T.A.; Ciais, P.; Delbart, N.; Friedl, M.A.; Gobron, N.; Hollinger, D.Y.; Kutsch, W.L.; Longdoz, B.; Luyssaert, S.; et al. Influence of spring and autumn phenological transitions on forest ecosystem productivity. Philos. Trans. R. Soc. B Biol. Sci. 2010, 365, 3227–3246. [Google Scholar] [CrossRef] [Green Version]
  19. Wang, L.; Fensholt, R. Temporal changes in coupled vegetation phenology and productivity are biome-specific in the Northern Hemisphere. Remote Sens. 2017, 9, 1277. [Google Scholar] [CrossRef] [Green Version]
  20. Mekonnen, Z.A.; Grant, R.F.; Schwalm, C. Contrasting changes in gross primary productivity of different regions of North America as affected by warming in recent decades. Agric. For. Meteorol. 2016, 218–219, 50–64. [Google Scholar] [CrossRef] [Green Version]
  21. Ju, J.; Masek, J.G. The vegetation greenness trend in Canada and US Alaska from 1984-2012 Landsat data. Remote Sens. Environ. 2016, 176, 1–16. [Google Scholar] [CrossRef]
  22. Froelich, N.; Croft, H.; Chen, J.M.; Gonsamo, A.; Staebler, R.M. Trends of carbon fluxes and climate over a mixed temperate–boreal transition forest in southern Ontario, Canada. Agric. For. Meteorol. 2015, 211–212, 72–84. [Google Scholar] [CrossRef]
  23. Urbanski, S.; Barford, C.; Wofsy, S.; Kucharik, C.; Pyle, E.; Budney, J.; McKain, K.; Fitzjarrald, D.; Czikowsky, M.; Munger, J.W. Factors controlling CO2 exchange on timescales from hourly to decadal at Harvard Forest. J. Geophys. Res. Biogeosci. 2007, 112, 1–25. [Google Scholar] [CrossRef] [Green Version]
  24. Seyednasrollah, B.; Young, A.M.; Li, X.; Milliman, T.; Ault, T.; Frolking, S.; Friedl, M.; Richardson, A.D. Sensitivity of Deciduous Forest Phenology to Environmental Drivers: Implications for Climate Change Impacts Across North America. Geophys. Res. Lett. 2020, 47. [Google Scholar] [CrossRef]
  25. Richardson, A.D.; Hufkens, K.; Milliman, T.; Aubrecht, D.M.; Furze, M.E.; Nettles, R.; Heiderman, R.R.; Seyednasrollah, B.; Krassovski, M.B.; Latimer, J.M.; et al. Ecosystem warming extends vegetation activity but heightens vulnerability to cold temperatures. Nature 2018, 560, 368–371. [Google Scholar] [CrossRef]
  26. Flynn, D.F.B.; Wolkovich, E.M. Temperature and photoperiod drive spring phenology across all species in a temperate forest community. New Phytol. 2018, 219, 1353–1362. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  27. Emmett, K.D.; Renwick, K.M.; Poulter, B. Disentangling Climate and Disturbance Effects on Regional Vegetation Greening Trends. Ecosystems 2018, 22, 873–891. [Google Scholar] [CrossRef] [Green Version]
  28. Norman, S.P.; Hargrove, W.W.; Christie, W.M. Spring and Autumn Phenological Variability across Environmental Gradients of Great Smoky Mountains National Park, USA. Remote Sens. 2017, 9, 407. [Google Scholar] [CrossRef] [Green Version]
  29. Rodriguez-Galiano, V.F.; Sanchez-Castillo, M.; Dash, J.; Atkinson, P.M.; Ojeda-Zujar, J. Modelling interannual variation in the spring and autumn land surface phenology of the European forest. Biogeosciences 2016, 13, 3305–3317. [Google Scholar] [CrossRef] [Green Version]
  30. Yuan, W.; Zheng, Y.; Piao, S.; Ciais, P.; Lombardozzi, D. Increased atmospheric vapor pressure deficit reduces global vegetation growth. Sci. Adv. 2019, 6, 12. [Google Scholar] [CrossRef] [Green Version]
  31. Forkel, M.; Carvalhais, N.; Verbesselt, J.; Mahecha, M.D.; Neigh, C.S.R.; Reichstein, M. Trend Change detection in NDVI time series: Effects of inter-annual variability and methodology. Remote Sens. 2013, 5, 2113–2144. [Google Scholar] [CrossRef] [Green Version]
  32. Rafferty, N.E.; Caradonna, P.J.; Burkle, L.A.; Iler, A.M.; Bronstein, J.L. Phenological overlap of interacting species in a changing climate: An assessment of available approaches. Ecol. Evol. 2013, 3, 3183–3193. [Google Scholar] [CrossRef]
  33. Stephenson, B. The Algonquin to Adirondack Conservation Initiative: A key macro-landscape linkage in eastern North America. In Crossing Boundaries in Park Management; The George Wright Society: Hancock, MI, USA, 2001; pp. 303–310. [Google Scholar]
  34. CEC. Land Cover, 2010 (Landsat, 30 m). 2010. Available online: http://www.cec.org/north-american-environmental-atlas/land-cover-2010-landsat-30m/ (accessed on 6 July 2017).
  35. Crins, W.J. Ecozones, Ecoregions and Ecodistricts of Ontario; Inventory, Monitoring and Assessment; Ontario Ministry of Natural Resources: Peterborough, ON, Canada, 2002.
  36. Widmann, R.H.; Crawford, S.; Kurtz, C.M.; Nelson, M.D.; Miles, P.D.; Morin, R.S.; Riemann, R. New York Forests, 2012; U.S Department of Agriculture, Forest Service, Northern Research Station: Newtown Square, PA, USA, 2015.
  37. Eidenshink, J. A 16-year Time Series of 1 km AVHRR Satellite Data of the Conterminous United States and Alaska. Photogramm. Eng. Remote Sens. 2006, 72, 1027–1035. [Google Scholar] [CrossRef] [Green Version]
  38. de Beurs, K.M.; Henebry, G.M. Spatio-Temporal Statistical Methods for Modelling Land Surface Phenology. In Phenological Research: Methods for Environmental and Climate Change Analysis; Keatley, M.R., Hudson, I.L., Eds.; Springer Netherlands: Dordrecht, The Netherlands, 2010; pp. 147–158. ISBN 978-90-481-3334-5. [Google Scholar]
  39. Ji, L.; Brown, J.F. Effect of NOAA satellite orbital drift on AVHRR-derived phenological metrics. Int. J. Appl. Earth Obs. Geoinf. 2017, 62, 215–223. [Google Scholar] [CrossRef]
  40. Hijmans, R.J. Raster: Geographic Data Analysis and Modeling. 2017. Available online: cran.r-project.org/package=raster (accessed on 4 July 2018).
  41. R Core Team. R: A Language and Environment for Statistical Computing. 2017. Available online: r-project.org (accessed on 4 July 2018).
  42. Thornton, P.E.; Thornton, M.M.; Mayer, B.W.; Wei, Y.; Devarakonda, R.; Vose, R.S.; Cook, R.B. Daymet: Daily Surface Weather Data on a 1-km Grid for North America, 3rd ed.; 2017. Available online: daymet.ornl.gov (accessed on 4 July 2018).
  43. Menne, M.J.; Durre, I.; Vose, R.S.; Gleason, B.E.; Houston, T.G. An overview of the global historical climatology network-daily database. J. Atmos. Ocean. Technol. 2012, 29, 897–910. [Google Scholar] [CrossRef]
  44. Beguería, S.; Vicente-Serrano, S.M. Standardised Precipitation-Evapotranspiration Index. 2017. Available online: cran.r-project.org/package=SPEI (accessed on 4 July 2018).
  45. Beguería, S.; Vicente-Serrano, S.M.; Reig, F.; Latorre, B. Standardized precipitation evapotranspiration index (SPEI) revisited: Parameter fitting, evapotranspiration models, tools, datasets and drought monitoring. Int. J. Climatol. 2014, 34, 3001–3023. [Google Scholar] [CrossRef] [Green Version]
  46. Vicente-Serrano, S.M.; Beguería, S.; López-Moreno, J.I. A multiscalar drought index sensitive to global warming: The standardized precipitation evapotranspiration index. J. Clim. 2010, 23, 1696–1718. [Google Scholar] [CrossRef] [Green Version]
  47. Thornton, M.M.; Thornton, P.E.; Wei, Y.; Vose, R.S.; Boyer, A.G. Daymet: Station-Level Inputs and Model Predicted Values for North America, 3rd ed.; 2017. Available online: https://daac.ornl.gov/DAYMET/guides/Daymet_V3_Stn_Level_CrossVal.html (accessed on 2 May 2019).
  48. Henn, B.; Newman, A.J.; Livneh, B.; Daly, C.; Lundquist, J.D. An assessment of differences in gridded precipitation datasets in complex terrain. J. Hydrol. 2018, 556, 1205–1219. [Google Scholar] [CrossRef]
  49. Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
  50. Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
  51. Genuer, R.; Poggi, J.M.; Tuleau-Malot, C. Variable selection using random forests. Pattern Recognit. Lett. 2010, 31, 2225–2236. [Google Scholar] [CrossRef] [Green Version]
  52. Liaw, A.; Wiener, M. Classification and Regression by randomForest. R. News 2002, 2, 18–22. Available online: cran.r-project.org/package=randomForest (accessed on 2 May 2019).
  53. Microsoft; Weston, S. doSNOW: Foreach Parallel Adaptor for the “Snow” Package. 2017. Available online: cran.r-project.org/package=doSNOW (accessed on 2 May 2019).
  54. Microsoft; Weston, S. foreach: Provides Foreach Looping Construct for R. 2017. Available online: cran.r-project.org/package=foreach (accessed on 2 May 2019).
  55. Kuhn, M. caret: Classification and Regression Training. 2018. Available online: cran.r-project.org/package=caret (accessed on 2 May 2019).
  56. Genuer, R.; Poggi, J.M.; Tuleau-Malot, C.; Villa-Vialaneix, N. Random Forests for Big Data. Big Data Res. 2017, 9, 28–46. [Google Scholar] [CrossRef]
  57. Wei, P.; Lu, Z.; Song, J. Variable importance analysis: A comprehensive review. Reliab. Eng. Syst. Saf. 2015, 142, 399–432. [Google Scholar] [CrossRef]
  58. Strobl, C.; Boulesteix, A.L.; Zeileis, A.; Hothorn, T. Bias in random forest variable importance measures: Illustrations, sources and a solution. BMC Bioinf. 2007, 8. [Google Scholar] [CrossRef] [Green Version]
  59. Greenwell, B.M. pdp: An R Package for Constructing Partial Dependence Plots. R. J. 2017, 9, 421–436. Available online: cran.r-project.org/package=pdp (accessed on 2 May 2019). [CrossRef] [Green Version]
  60. Milborrow, S. Plotmo: Plot a Model’s Residuals, Response, and Partial Dependence Plots. 2018. Available online: cran.r-project.org/package=plotmo (accessed on 2 May 2019).
  61. Tang, J.; Körner, C.; Muraoka, H.; Piao, S.; Shen, M.; Thackeray, S.J.; Yang, X. Emerging opportunities and challenges in phenology: A review. Ecosphere 2016, 7, e01436. [Google Scholar] [CrossRef] [Green Version]
  62. Yu, R.; Schwartz, M.D.; Donnelly, A.; Liang, L. An observation-based progression modeling approach to spring and autumn deciduous tree phenology. Int. J. Biometeorol. 2016, 60, 335–349. [Google Scholar] [CrossRef] [PubMed]
  63. Wang, X.; Piao, S.; Ciais, P.; Li, J.; Friedlingstein, P.; Koven, C.; Chen, A. Spring temperature change and its implication in the change of vegetation growth in North America from 1982 to 2006. Proc. Natl. Acad. Sci. USA 2011, 108, 1240–1245. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  64. Myers-Smith, I.H.; Kerby, J.T.; Phoenix, G.K.; Bjerke, J.W.; Epstein, H.E.; Assmann, J.J.; John, C.; Andreu-Hayles, L.; Angers-Blondin, S.; Beck, P.S.A.; et al. Complexity revealed in the greening of the Arctic. Nat. Clim. Chang. 2020, 10, 106–117. [Google Scholar] [CrossRef] [Green Version]
  65. Körner, C.; Basler, D. Phenology Under Global Warming. Science 2010, 327, 1461–1462. [Google Scholar] [CrossRef] [PubMed]
  66. Gu, L.; Hanson, P.J.; Post, W.M.A.C.; Kaiser, D.P.; Yang, B.; Nemani, R.; Pallardy, S.G.; Meyers, T. The 2007 Eastern US Spring Freeze: Increased Cold Damage in a Warming World? Bioscience 2008, 58, 253–262. [Google Scholar] [CrossRef]
  67. Schratz, P.; Muenchow, J.; Iturritxa, E.; Richter, J.; Brenning, A. Hyperparameter tuning and performance assessment of statistical and machine-learning algorithms using spatial data. Ecol. Modell. 2019, 406, 109–120. [Google Scholar] [CrossRef] [Green Version]
  68. Meyer, H.; Reudenbach, C.; Hengl, T.; Katurji, M.; Nauss, T. Improving performance of spatio-temporal machine learning models using forward feature selection and target-oriented validation. Environ. Model. Softw. 2018, 101, 1–9. [Google Scholar] [CrossRef]
  69. Meyer, H.; Reudenbach, C.; Wöllauer, S.; Nauss, T. Importance of spatial predictor variable selection in machine learning applications—Moving from data reproduction to spatial prediction. Ecol. Modell. 2019, 411, 1–34. [Google Scholar] [CrossRef] [Green Version]
  70. Hayhoe, K.; Wake, C.P.; Huntington, T.G.; Luo, L.; Schwartz, M.D.; Sheffield, J.; Wood, E.; Anderson, B.; Bradbury, J.; DeGaetano, A.; et al. Past and future changes in climate and hydrological indicators in the US Northeast. Clim. Dyn. 2007, 28, 381–407. [Google Scholar] [CrossRef]
  71. Xie, Y.; Ahmed, K.F.; Allen, J.M.; Wilson, A.M.; Silander, J.A. Green-up of deciduous forest communities of northeastern North America in response to climate variation and climate change. Landsc. Ecol. 2015, 30, 109–123. [Google Scholar] [CrossRef]
  72. Xie, Y.; Wang, X.; Silander, J.A. Deciduous forest responses to temperature, precipitation, and drought imply complex climate change impacts. Proc. Natl. Acad. Sci. USA 2015, 112, 13585–13590. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  73. Yue, S.; Pilon, P.; Phinney, B.; Cavadias, G. The influence of autocorrelation on the ability to detect trend in hydrological series. Hydrol. Process. 2002, 16, 1807–1829. [Google Scholar] [CrossRef]
  74. Bronaugh, D.; Werner, A. Zyp: Zhang + Yue-Pilon Trends Package. 2013. Available online: cran.r-project.org/package=zyp (accessed on 2 May 2019).
  75. Sen, P.K. Estimates of the Regression Coefficient Based on Kendall’s Tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
  76. McLeod, A.I. Kendall: Kendall Rank Correlation and Mann-Kendall Trend Test. 2011. Available online: cran.r-project.org/package=Kendall (accessed on 2 May 2019).
  77. Cortés, J.; Mahecha, M.; Reichstein, M.; Brenning, A. Accounting for multiple testing in the analysis of spatio-temporal environmental data. Environ. Ecol. Stat. 2020, 27, 293–318. [Google Scholar] [CrossRef]
  78. Benjamini, Y.; Hochberg, Y. Controlling the False Discovery Rate: A Practical and Powerful Approach to Multiple Testing. J. R. Stat. Soc. Ser. B 1995, 57, 289–300. [Google Scholar] [CrossRef]
Forests 12 00282 g001 550
Figure 1. Map of the location and forest cover of A2A, with landcover classes from [34].
Figure 1. Map of the location and forest cover of A2A, with landcover classes from [34].
Forests 12 00282 g001
Forests 12 00282 g002 550
Figure 2. Flowchart of major steps in the forest-climate modelling workflow. This procedure was performed four times, once for each forest growth index. Inputs were AVHRR forest growth indices (the dependent variable) and pre-processed Daymet climatological data (the independent variables).
Figure 2. Flowchart of major steps in the forest-climate modelling workflow. This procedure was performed four times, once for each forest growth index. Inputs were AVHRR forest growth indices (the dependent variable) and pre-processed Daymet climatological data (the independent variables).
Forests 12 00282 g002
Forests 12 00282 g003 550
Figure 3. Partial dependence plots of important variables used in the final RF (Random Forest) models. Partial dependence (i.e., the marginal influence of a given variable with the effect of all other variables averaged out but not ignored) plots are grouped by variable class, and variables are divided by time (y = current, y − 1 = lagged). For plots with no lines, the corresponding variables were not ranked as important by preliminary RF models and were therefore not included in the final RF models. Forest growth indices: TIN = time-integrated NDVI; LOS = length of growing season; SOS = start of growing season; EOS = end of growing season. Climatic variables: AHS = accumulated heating (SOS); AHM = accumulated heating; ACE = accumulated chilling; TMX, TME, and TMN = maximum, mean and minimum temperature; PRT = precipitation.
Figure 3. Partial dependence plots of important variables used in the final RF (Random Forest) models. Partial dependence (i.e., the marginal influence of a given variable with the effect of all other variables averaged out but not ignored) plots are grouped by variable class, and variables are divided by time (y = current, y − 1 = lagged). For plots with no lines, the corresponding variables were not ranked as important by preliminary RF models and were therefore not included in the final RF models. Forest growth indices: TIN = time-integrated NDVI; LOS = length of growing season; SOS = start of growing season; EOS = end of growing season. Climatic variables: AHS = accumulated heating (SOS); AHM = accumulated heating; ACE = accumulated chilling; TMX, TME, and TMN = maximum, mean and minimum temperature; PRT = precipitation.
Forests 12 00282 g003
Table
Table 1. Forest growth indices selected from the USGS AVHRR phenology database. Data are accessible from https://www.usgs.gov/land-resources/eros/phenology, (accessed on 4 January 2018).
Table 1. Forest growth indices selected from the USGS AVHRR phenology database. Data are accessible from https://www.usgs.gov/land-resources/eros/phenology, (accessed on 4 January 2018).
NameAbbreviationCalculationDescription
Time-
integrated NDVI		TINTIN = accumulated daily NDVI between SOS and EOS above NDVI values at SOS and EOS (values between 0 and 100)Accumulated photosynthetic activity during the growing season, indicating foliage productivity
Length of growing
season		LOSLOS = EOS − SOSAmount of time between spring green-up and autumn senescence, or the amount of time in a year in which trees are photosynthetically productive
Start of
season date		SOSSOS = date that NDVI exceeds the backward-looking delayed-moving-average trend from the previous 18 observations, interpolated within 14-day compositesGreen-up of vegetation. This does not represent a distinct phenophase, but general ‘greening’ of vegetation that occurs in the spring
End of
season date		EOSEOS = date that NDVI becomes less than the forward-looking delayed-moving-average trend from the next 12 observations, interpolated within 14-day compositesBrown-down of vegetation. This does not represent a distinct phenophase, but a general ‘browning’ of vegetation that occurs in the fall
Table
Table 2. Climatic variables used as independent variables in forest-climate models, their definitions, and their temporal resolution following aggregation from a base daily resolution.
Table 2. Climatic variables used as independent variables in forest-climate models, their definitions, and their temporal resolution following aggregation from a base daily resolution.
NameDefinitionAggregate
Maximum temperatureMaximum air temperature at 2 mMonthly Mean
Minimum temperatureMinimum air temperature at 2 mMonthly Mean
Mean temperatureMean air temperature at 2 m
(mean of maximum and minimum air temperature)		Monthly Mean
PrecipitationDepth (mm) of precipitation in water equivalentMonthly Sum
SnowpackWeight (kg/m2) of on-ground snow, converted to water for measurement standardizationMonthly Sum
Spring heatingThe sum of daily temperatures above 4 °C for the winter and spring (1 January to 31 May)Annual Sum
Summer heatingThe sum of daily temperatures above 4 °C during the winter, spring and summer (1 January to 31 July)Annual Sum
Fall chillingThe sum of daily temperatures below 20 °C during the summer and fall (1 August to 31 October)Annual Sum
Root-freeze riskThe number of days with minimum air temperatures below 0 °C and snow-water equivalent depth of 0Monthly Sum
SPEI
(standardized precipitation—evapotranspiration index)		Index (mean = 0, SD = 1) of moisture stress, calculated using a 12-month rear-looking window [45,46]Monthly (within ‘SPEI’ R package)
Day lengthThe amount of time between dawn and disk (s)Monthly Mean
Solar radiationMean incident radiation flux density (W/m2)Monthly Mean
Table
Table 3. Inputs and outputs from preliminary and final RF (Random Forest) models. Model Inputs are the independent variables considered in each model and the time period considered (y−1 = lagged). N is the number of observations (pixels) used to train each model and was identical for the preliminary and final models. m is the number of independent variables used in each model. mtry is the number of randomly selected variables tested for best split at each node. RMSE is root-mean-squared error calculated using the validation dataset. pR2 (pseudo-R2) represents the percent of variance explained by the model. Forest growth indices: TIN = Time-integrated NDVI; LOS = length of growing season; SOS = start of season date; EOS = end of season date.
Table 3. Inputs and outputs from preliminary and final RF (Random Forest) models. Model Inputs are the independent variables considered in each model and the time period considered (y−1 = lagged). N is the number of observations (pixels) used to train each model and was identical for the preliminary and final models. m is the number of independent variables used in each model. mtry is the number of randomly selected variables tested for best split at each node. RMSE is root-mean-squared error calculated using the validation dataset. pR2 (pseudo-R2) represents the percent of variance explained by the model. Forest growth indices: TIN = Time-integrated NDVI; LOS = length of growing season; SOS = start of season date; EOS = end of season date.
Forest GrowthModel InputsPreliminary ModelFinal Model
MonthNmmtryRMSEpR2mmtryRMSEpR2
TINJany−1–Nov415,881197250.7669.171590.4486.69
LOSJany−1–Nov411,987197250.9064.7215100.5784.06
SOSJany−1–Jun393,3691511000.8663.3415130.6280.26
EOSJany−1–Nov401,890197850.8963.6015100.6480.34
Table
Table 4. Importance of climatic variables for modelling inter-annual variation in forest growth variables, ranked by scaled IncNodePurity. Variable importance (shown in the Imp. column for each final RF model) was scaled to a percentage (%) for comparison between final RF (Random Forest) models. Monthly climatic variables are labelled with the corresponding month, and lagged variables (i.e., from the previous year) are denoted with ‘y−1’. Forest growth indices: TIN = Time-integrated NDVI; LOS = length of growing season; SOS = start of season date; EOS = end of season date. Climatic variables: TMX, TME, TMN = maximum, mean and minimum temperature; precipitation = PRT.
Table 4. Importance of climatic variables for modelling inter-annual variation in forest growth variables, ranked by scaled IncNodePurity. Variable importance (shown in the Imp. column for each final RF model) was scaled to a percentage (%) for comparison between final RF (Random Forest) models. Monthly climatic variables are labelled with the corresponding month, and lagged variables (i.e., from the previous year) are denoted with ‘y−1’. Forest growth indices: TIN = Time-integrated NDVI; LOS = length of growing season; SOS = start of season date; EOS = end of season date. Climatic variables: TMX, TME, TMN = maximum, mean and minimum temperature; precipitation = PRT.
RankTINLOSSOSEOS
VariableImp.VariableImp.VariableImp.VariableImp.
1Acc. Heat.21.03Acc. Heat.29.49Acc. Heat.29.71Acc. Chill35.10
2Acc. Chill.20.19Acc. Chill24.36Acc. Heat.y−117.86Acc. Heat.y−113.27
3Acc. Chill.y−116.76Acc. Heat.y−112.55Acc. Chill.y−117.64Acc. Chill.y−113.11
4Acc. Heat.y−114.77Acc. Chill.y−18.22TME.APR4.08Acc. Heat.11.87
5TME.SEP6.23TME.SEP4.31TMN.DECy−13.53TMN.MAR3.67
6TME.OCTy−13.71TME.MAY3.48TME.FEBy−13.33TME.MAR3.20
7TME.NOVy−12.84TME.AUG3.45TMX.JULy−13.32TME.SEP3.02
8TME.JUL2.41TME.JUL2.90TME.MAR3.30TME.SEPy−12.83
9TMN.APRy−12.37TME.APR2.58TMN.JAN3.10TME.NOVy−12.65
10TME.JUN2.28TMX.OCTy−11.84TME.NOVy−13.06TMX.FEBy−12.61
11TME.SEPy−11.74TME.NOVy−11.73TME.AUGy−12.49TME.MAY2.37
12TMN.AUGy−11.73TME.OCT1.50TME.JULy−12.46TME.OCT1.88
13TME.AUG1.61TMN.APRy−11.42PRT.NOVy−12.35TME.FEBy−11.73
14TMN.AUG1.18TME.APRy−11.17TMN.MARy−12.24TME.APR1.53
15TMN.JUL1.15TME.OCTy−11.00TMN.FEBy−11.73TME.FEB1.17
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Stefanuk, M.A.; Danby, R.K. Accumulated Heating and Chilling Are Important Drivers of Forest Phenology and Productivity in the Algonquin-to-Adirondacks Conservation Corridor of Eastern North America. Forests 2021, 12, 282. https://doi.org/10.3390/f12030282

AMA Style

Stefanuk MA, Danby RK. Accumulated Heating and Chilling Are Important Drivers of Forest Phenology and Productivity in the Algonquin-to-Adirondacks Conservation Corridor of Eastern North America. Forests. 2021; 12(3):282. https://doi.org/10.3390/f12030282

Chicago/Turabian Style

Stefanuk, Michael A., and Ryan K. Danby. 2021. "Accumulated Heating and Chilling Are Important Drivers of Forest Phenology and Productivity in the Algonquin-to-Adirondacks Conservation Corridor of Eastern North America" Forests 12, no. 3: 282. https://doi.org/10.3390/f12030282

APA Style

Stefanuk, M. A., & Danby, R. K. (2021). Accumulated Heating and Chilling Are Important Drivers of Forest Phenology and Productivity in the Algonquin-to-Adirondacks Conservation Corridor of Eastern North America. Forests, 12(3), 282. https://doi.org/10.3390/f12030282

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop