Next Article in Journal
Editorial for Special Issue “Biodiversity and Management of Temperate Floodplain Forests”
Previous Article in Journal
Comparative Dynamics of Above-Ground Litter Production and Decomposition from Eucalyptus grandis Hill ex Maiden and Pinus taeda L., and Their Contribution to Soil Organic Carbon
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Forests
Volume 12
Issue 3
10.3390/f12030350
forests-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Stable Isotopes in Tree Rings of Pinus heldreichii Can Indicate Climate Variability over the Eastern Mediterranean Region

by
Ljubica Lukač
1,*,
Stjepan Mikac
1,
Otmar Urban
2,
Tomáš Kolář
2,3,
Michal Rybníček
2,3,
Alexander Ač
2,
Mirek Trnka
2,4 and
Michal V. Marek
2,5
1
Dendroecology Lab, Department of Forest Ecology and Silviculture, Faculty of Forestry, University of Zagreb, Svetošimunska Cesta 25, 10000 Zagreb, Croatia
2
Global Change Research Institute, Czech Academy of Sciences, Bělidla 986/4a, 603 00 Brno, Czech Republic
3
Department of Wood Science and Technology, Faculty of Forestry and Wood Technology, Mendel, University in Brno, Zemědělská 3, 613 00 Brno, Czech Republic
4
Faculty of AgriSciences, Institute of Agriculture Systems and Bioclimatology, Mendel University in Brno, Zemědělská 3, 613 00 Brno, Czech Republic
5
Institute of Management, Slovak Technical University Bratislava, Vazovova 5, 812 43 Bratislava, Slovakia
*
Author to whom correspondence should be addressed.
Forests 2021, 12(3), 350; https://doi.org/10.3390/f12030350
Submission received: 25 January 2021 / Revised: 8 March 2021 / Accepted: 12 March 2021 / Published: 16 March 2021
(This article belongs to the Section Forest Ecology and Management)
Browse Figures
Versions Notes

Abstract

:
A long-term context is important for understanding past climatic variability. Although tree-ring widths (TRWs) are widely used as a proxy for reconstructing past climate, the use of annually-resolved values of δ13C and δ18O tree-ring stable isotopes (TRSIs) is increasing and may provide further valuable information. Here, we present a 487-year-long TRW chronology and 240-year-long TRSI chronology for Bosnian pine (Pinus heldreichii H. Christ) and compare them to each other. We demonstrate that both δ13C and δ18O values are better proxies for temperature, precipitation, and drought than TRW. The correlations between these climate parameters and TRSIs are strongest for the combined summer (JJA) period. The results of temporal and spatial field correlation indicate that TRSI chronologies are stable, reliable proxies for JJA precipitation reconstruction over the whole Balkan Peninsula and surrounding eastern Mediterranean region. However, the stability of the temperature signal of the both δ13C and δ18O chronologies declines after the 1950s. Our work supports the emerging evidence that TRSI data track climate variability more accurately than a conventional TRW approach and can be subsequently used for the reconstruction of past climate.

1. Introduction

In addition to being geographically widespread, trees live for hundreds to thousands of years. Their longevity and sensitivity to their surrounding conditions makes trees valuable integrators of local environmental and climatic information [1,2,3]. These environmental changes are recorded on a yearly basis in tree rings. The growth and formation of individual tree rings reflect not only the internal physiology of wood formation, but also the influences of environmental conditions, particularly temperature and water availability. Tree rings therefore have enormous potential for the detection and reconstruction of past climatic conditions, including hydro-climatic extremes (e.g., [4]).
Besides conventional tree-ring width (TRW) analysis, tree-ring stable carbon (δ13C) and oxygen (δ18O) isotope ratios provide valuable climate-related information [5,6]. Changes in δ13C and δ18O values are closely connected to plant physiological processes, particularly to processes associated with photosynthetic CO2 uptake [7] and H2O transpiration [8]. These processes are strongly coupled to natural variations in factors determining day-to-day fluctuations in weather and changes in climatic conditions over longer time periods. In comparison to growth rate, tree-ring δ13C and δ18O values reflect particularly annual differences in temperature, precipitation, humidity, and light intensity [9,10].
Moreover, the δ13C and δ18O values reflect species-specific sensitivity to these environmental drivers, in addition to the overall habits of tree species, including the root system structure [11,12,13]. Previous studies have shown strong links between tree-ring stable isotopes (TRSIs) and many climatological phenomena including: drought/sunlight duration in the alpine region [14]; relative air humidity, cloud cover, and drought [15]; the Palmer drought severity index (PDSI; [16]); the standardized precipitation-evapotranspiration index (SPEI; [17]); and precipitation amounts [18]. However, the links between TRSIs and climate parameters are often stronger at wet sites than dry ones [19]. In dry environments, the δ13C value is predominantly influenced by fluctuations in vapor pressure deficit [20]. In wet environments where the diffusion of CO2 across the stomata is not limited, solar radiation and the photosynthetic properties of the Rubisco enzyme are key factors [21].
Dendrochronological research in the Dinarides, a mountain range in southern and southeastern Europe that separates the Balkan Peninsula from the Adriatic Sea, has been limited to date. There is therefore huge potential in this region for the development of long, climate-sensitive tree-ring chronologies suitable for the reconstruction of sunshine duration [22], summer temperature [23,24], and drought [25].
In this study, we analyzed and compared the climate signals of TRWs and TRSIs in primaeval forests of Bosnian pine (Pinus heldreichii H. Christ), known for their exceptional longevity (e.g., [26]). Existing studies of the climate sensitivity of Bosnian pine TRWs indicate that although this species offers great potential for creating long-term chronologies, the response of Bosnian pine to climate is generally limited [27,28,29].
The main aim of this research was therefore to determine whether alternative proxies such as isotope data offer stronger climate reconstruction potential in comparison to conventional TRW chronologies [22,24,30]. Our hypothesis is that isotope data (δ13C and δ18O values) are better proxies for high-resolution reconstructions of past hydroclimatic variability and can significantly improve the climate signal in Bosnian pine tree-ring data.

2. Materials and Methods

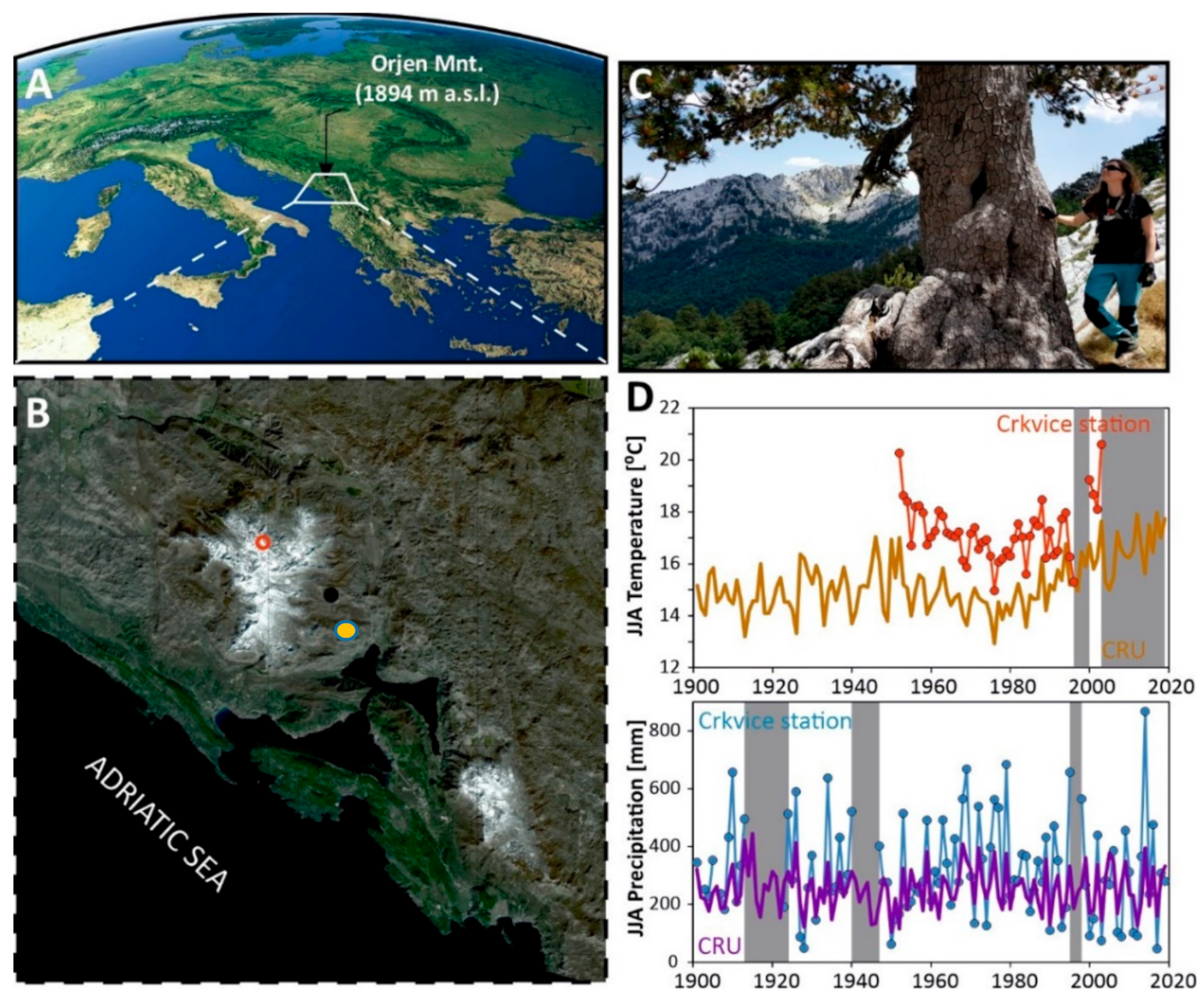
2.1. Research Area

The study area (42°34′ N, 18°32′ E, elevation 1894 m a.s.l.) is situated in the Orjen Mountains, a transboundary Dinaric Mediterranean limestone mountain range that stretches for about 25 km through Montenegro and Bosnia and Herzegovina. Orjen Peak is the highest peak in the sub-Adriatic Dinarides. The sub-Adriatic range contains evergreen deciduous forests and the vegetation transitions from temperate forests in its lower elevation belts to conifers and tundra in its northern and upper regions. The belt of primaeval Bosnian pine forest is located at the highest elevations above 1800 m a.s.l. The underlying forest soils are characterized by shallow layers of rendzina soil atop limestone and dolomite bedrock [31,32].
The Orjen Mountains are situated within the Mediterranean subtropical belt, at the intersection between Mediterranean and continental climates (Figure 1). At the study site, summers are hot and sunny with mean temperatures up to 19 °C in August, and autumn, winter, and spring constitute the rainy season and temperatures can drop to a minimum of −10 °C. Average annual precipitation (rain, snow) is about 5000 mm. Located as it is in the littoral Dinarides, the study area experiences strong precipitation contrasts throughout the year. November thunderstorms can deposit 2000 mm of rainwater over the course of just a few days, whereas August is frequently completely dry [33]. Forest fires are a frequent disturbance during the dry season [34].

2.2. Tree Core Sampling, Tree-Ring Width, and Stable Isotope Measurement

In total, 23 Bosnian pine trees were sampled in the primaeval forest. One core per tree was extracted at breast height (1.3 m) using a Pressler borer (Haglof Company Group, Sweden) with a 5-mm inner diameter. To avoid the compression of the wood, the cores were sampled in the direction parallel to the slope [35]. After careful surface preparation to maximize the visibility of the tree rings, all core samples were measured using a VIAS TimeTable measuring system (SCIEM, Vienna, Austria) with a measuring length of 78 cm and a resolution of 1/100 mm). The tree-ring width (TRW) was measured to an accuracy of 0.01 mm, and each series was cross-dated using PAST4 [36]. The series were statistically controlled using the COFECHA program version Cofecha (Laboratory of Tree-Ring Research, University of Arizona, Tucson, AZ, USA) [37].
Four core samples were selected for the isotopic analysis. Each of the precisely dated annual increments was separated with a scalpel under a stereomicroscope and packed into Teflon filter bags (F57; Ankom Technology, Macedon, NY, USA). The alpha-cellulose was then extracted via the modified Jayme–Wise isolation method [38]. Teflon filter bags were washed twice for two hours each using 5% NaOH solution at 60 °C, followed by washing with 7% NaClO2 solution (pH 4–5) for 30 hours at 60 °C. The samples were subsequently dried at 50 °C for 24 h, sealed in Eppendorf microtubes, and stored in the dark at room temperature (21 °C) before analysis. The samples of alpha-cellulose (0.2–1.0 mg) were weighed into tin boats and silver capsules (Elementar Analysensysteme, Langenselbold, Germany) for the determination of carbon and oxygen isotopes, respectively. For the δ13C measurements, the samples were combusted to CO2 at 960 °C; δ18O samples were pyrolyzed to CO at 1450 °C using a high-temperature combustion cell of an elemental analyzer (EA) varioPYRO cube (Elementar Analysensysteme, Germany). The stable isotopes in the CO2 and CO gases were then determined by a continuous flow isotope ratio mass spectrometer (irMS), ISOPRIME100 (Isoprime, Manchester, UK).
The system was calibrated using certified reference materials with known isotopic ratios from the International Atomic Energy Agency (IAEA, Vienna, Austria). The δ13C values were referenced to caffeine (IAEA-600) and graphite (USGS24). The δ18O values were referenced to benzoic acid (IAEA-601 and IAEA-602). The δ13C and δ18O values (‰) were given with respect to the deviation from the Vienna Pee Dee Belemnite (VPDB) and Vienna Standard Mean Ocean Water (VSMOW) standards, respectively. The long-term reproducibility of these standards, evaluated as standard deviation, was ≤0.05‰ (IAEA-600 and USGS24), ≤0.08‰ (IAEA-601), and ≤0.11‰ (IAEA-602). Standard deviations were ≤ 0.04‰ (δ13C) and ≤0.09‰ (δ18O) for five consecutive measurements of the homogenized alpha cellulose sample. For details see Urban et al. [39]. The δ13C time series were corrected for the δ13C decrease in the atmosphere [5]. The correction for atmospheric δ13C depletion was based on the compilation of ice core and direct measurements from Mauna Loa (https://www.esrl.noaa.gov/gmd/dv/data/). No additional physiological corrections of δ13C [18] were applied.
Because recent results show that stable isotopes manifest as a constant spread versus a level relationship over the lifespan of the tree [40], only the TRW datasets were standardized to suppress non-climatic factors. Negative exponential curves (NegExp), cubic smoothing splines (with a 50% frequency response cut-off at 150 years; spline150yr) and regional curve standardization (RCS) method were applied to remove age-related growth trends using the ARSTAN software version ARS41d_xp (Tree-Ring Laboratory, Lamont Doherty Earth Observatory of Columbia University, Palisades, NY, USA) [41]. TRW indices were calculated as residuals from estimated growth curves after applying an adaptive power transformation to the raw measurement series [42]. The final chronologies from each of the three detrending techniques were calculated using robust bi-weighted means. The expressed population signal (EPS; [43]) and inter-series correlation (Rbar) were calculated to assess the quality of each chronology. Because no significant differences were observed between the different chronology versions (Figure 2A), the residual chronology, after applying the 150-year smoothing spline, was selected to calculate the correlations with the monthly mean temperatures, precipitation sums, and Palmer drought severity index (PDSI; [44]). The correlations were calculated using the R package “treeclim” version 2.0.5.1 [45].
Temporal and spatial correlations between TRW and TRSI chronologies and seasonal climatic parameters were analyzed using monthly gridded data (0.5 × 0.5° grid) from the CRU TS3.24.01 database, available via the Royal Netherlands Meteorological Institute (KNMI) Climate Explorer platform (http://climexp.knmi.nl) [46]. Local climate observation data for the study area are very rare and time-limited, as is characteristic of the Dinaric region as a whole. For that reason, gridded CRU TS3.24.01 climatic data for the period of 1901−2018 were used. In our case, data from a nearby station (Crkvice) were compared with the CRU TS3.24.01 data to determine how well the downloaded data approximates local climate conditions (Figure 1D). Pearson’s correlation coefficients were calculated from April of the previous year to October of the current year for each climatic factor. The temporal stability of the climate signal was analyzed using moving window correlations with a 45-year interval plus 1 year. Analyses were performed with the most significant seasonal variables for the 1901–2018 period using CRU TS3.24.01 climate data.

3. Results

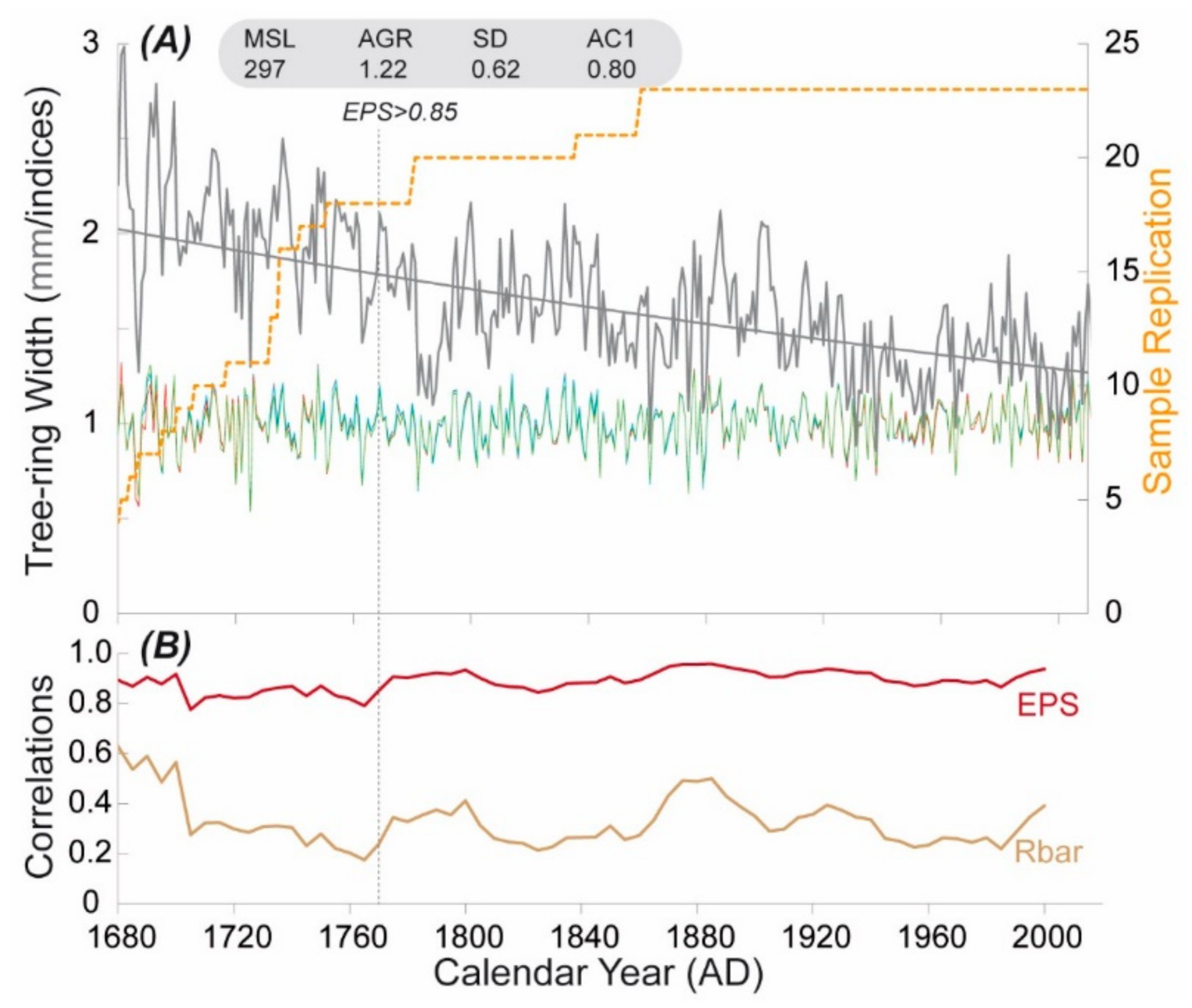
3.1. Tree-Ring Width Chronology

The 487-year TRW chronology covers the period of 1531–2018 (Figure 2). The minimum length of the TRW series (160 years) and the mean segment length (297 years) indicate that the chronology represents old trees. Although replication of the chronology decreases backwards in time, it does not drop below 23 TRW series during the studied period (1901–2018). The expressed population signal (EPS) fluctuates between 0.87 and 0.94. The high first-order autocorrelation (0.80) of the raw TRW chronology indicates large temporal memory.

3.2. Tree-Ring Stable Isotope Chronologies

Annually-resolved δ13C and δ18O chronologies obtained from four separate cores (Figure 3A) are highly synchronous over the 1780–2018 period as shown by EPS and Rbar (Figure 3B). Both the uncorrected δ13C time series and the time series corrected for the increase in CO2 concentration in the atmosphere are shown; hereafter, all presented δ13C time series are atmospheric-corrected data. The strength of the common signal over the whole period is confirmed by the consistently high mean Rbar (amounting to 0.51 and 0.55 for δ13C and δ18O, respectively) and EPS values (amounting to 0.80 and 0.83 for δ13C and δ18O, respectively).
The values of mean δ13C chronology range between −22.3‰ and −19.9‰ over the investigated period. The average δ13C value (±standard deviation) over the whole period is −21.0 ± 0.5‰; over the period 1901–2018, it is −21.2 ± 0.4‰. δ18O values show more variability, ranging between 24.8‰ and 30.2‰. Average values over the 1780–2018 and 1901–2018 periods are 27.7 ± 0.9‰ and 28.0 ± 0.9‰, respectively.

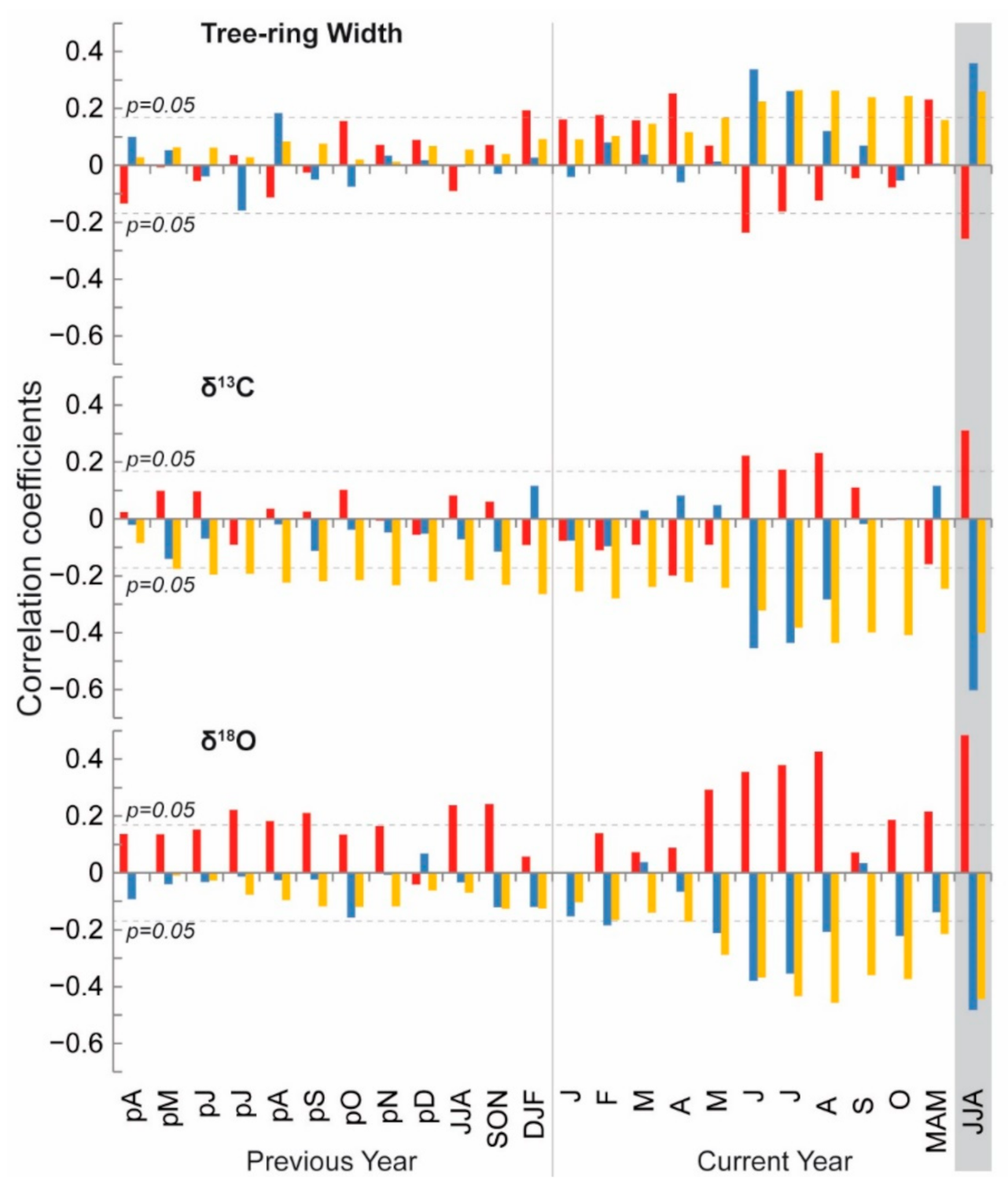
3.3. TRW and TRSI Responses to Climate

Correlations between TRW and TRSI chronologies and seasonal climatic parameters were obtained using the monthly gridded data (0.5 × 0.5° grid) from the CRU TS3.24.01 database. The sum of the current year summer precipitation is most strongly correlated with TRW (Figure 4). Summer (JJA) precipitation and PDSI are positively correlated with TRW, whereas monthly mean temperature over the same period is negatively correlated with TRW. Generally, correlations between radial growth and precipitation sum and PDSI of the previous growing season and the winter months are low and statistically non-significant. The correlation coefficients substantially increase during summer months of the current year. However, the mean monthly temperature of the previous growing season has no significant effect on TRW. The positive effect of winter temperatures on growth (up to April) gradually becomes negative in summer. This pattern suggests that the availability of water during the current summer is positively related to radial growth. Precipitation during the previous growing season is less important for pine growth.
The δ13C isotopic signal shows a significant positive correlation with temperature in June (r = 0.22) and August (r = 0.23) of the current year, and an even stronger negative correlation with precipitation during the summer months, particularly June (r = −0.45). For precipitation, the highest correlation is found when the whole summer period (JJA) is included (r = 0.60). Regarding the PDSI index, almost all months of both previous and current years are significantly negatively correlated with the δ13C record, with a maximum correlation in August of the current year (r = −0.44).
The δ18O isotope record is generally more strongly correlated with climate parameters than the δ13C record. Significant positive correlations with temperature are found in July, August, and September of the previous year and during the spring–summer period (May–August) of the current year. For individual months, the strongest correlation was found for August (r = 0.43); the correlation is even stronger for the combined JJA period (r = 0.48). Significant negative correlations with precipitation were found from May to August. As with temperature, the highest correlations between δ18O and precipitation and between δ18O and PDSI were observed for the JJA period (r of −0.48 and −0.43, respectively). Generally, the extension of JJA period and/or selection of other combined period does not improved the correlations of TRW and TRSI records with climate parameters (data not shown). Robust correlations between δ18O and PDSI index were also observed for separate months from May through October (Figure 4). Correlations of individual time series with climate parameters have shown similar results as the correlations of averaged δ13C and δ18O chronologies.

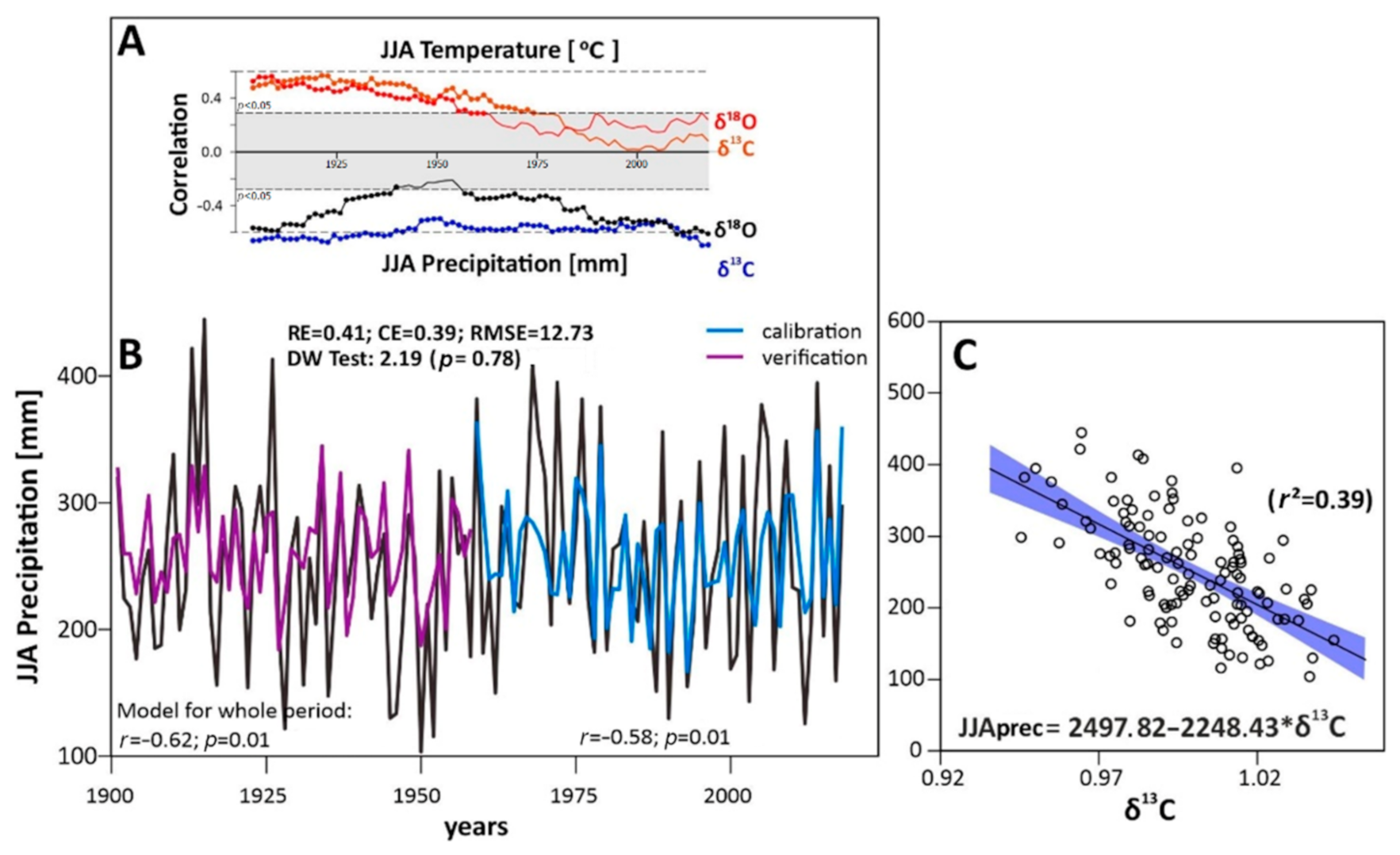
3.4. Temporal Stability of the Climate Signal

The temporal stability of the climate signal was analyzed using bootstrap correlations between the δ13C and δ18O chronologies and the most highly correlated climatic factors, which in our case are the JJA precipitation sum and the mean JJA temperature, respectively. The stability signal of JJA precipitation is prominent throughout the analyzed period (1901–2018; Figure 5A). In contrast to precipitation, the stability of the temperature signal of the both δ13C and δ18O chronologies declines slightly through the analyzed period, especially after 1950 (Figure 5A). In contrast to δ13C, the climate signal of the δ18O chronology is not stable over the analyzed period for either temperature or precipitation (Figure 5A). As with the δ13C temperature signal, the δ18O signal decreases over time, especially after the 1950s.
Our results confirm that the JJA precipitation sum is the most dominant and temporally stable climatic factor influencing the δ13C values in tree rings. We further tested the stability of the relationship between JJA precipitation and δ13C values using separate 60-year calibration and verification periods (Figure 5B). The calibration-verification model shows positive and significant (p ˂ 0.01) predictive capability, regardless of which period is used for the calibration (Figure 5B,C).

3.5. Spatial Field Correlations

The JJA precipitation sum and mean JJA temperatures downloaded from the CRU TS3.24.01 gridded dataset were further used to explore spatial field correlations. The strongest correlation between JJA precipitation sum and δ13C appears over the whole Balkan Peninsula (Figure 6). The δ13C and δ18O chronologies and mean JJA temperature only correlate strongly for the period 1901–1958, but diverge after the 1950s (Figure 6). The results of spatial field correlation indicate that the δ13C chronology is a stable, reliable proxy for JJA precipitation reconstruction over the eastern Mediterranean region.

4. Discussion

In the past decade, a number of studies have been published regarding the development of multi-century temperature- and precipitation-sensitive tree-ring chronologies from primaeval pine forests in the Balkans [28,47]. These studies show that the climate signal in the TRWs of pine species can be fairly weak [28,48], and more strongly dependent on local site conditions than on regional climate patterns [48]. However, the climatic signal in the width of late wood seems to be stronger (spring precipitation; [49]); maximum late wood density exhibits an even stronger climate signal (summer temperature; [28,47,49]).
In this study, we present a 487-year-long TRW chronology, thus extending the chronology for this region by 50 years [24,30]. Because the climate signal in TRW chronologies of P. heldreichii is relatively limited for robust climate reconstruction (also shown by [24]), we tested the hypothesis that TRSIs (δ13C and δ18O values) are better proxies for high-resolution reconstructions of hydroclimatic variability. Indeed, our results show higher correlations between TRSIs and climate parameters compared to TRW. The highest correlations were found when temperature, precipitation, and PDSI of the whole summer period (June–August; JJA) are included. These results are in general agreement with an earlier study by Hafner et al. [50] that confirm a robust positive relationship between δ13C and δ18O values and summer temperature, and a negative relationship with precipitation in the southeastern European Alps. Compared to the results of Levanič et al. [24], we observe a somewhat stronger relationship between δ13C and summer precipitation. They found correlations between δ13C and JJA temperature up to 0.6, although it was only −0.51 for JJA precipitation over the Balkan Peninsula. Even results from geographically distant locations of south-eastern China [16] confirmed that δ18O is a strong indicator of both precipitation and regional PDSI index reaching negative correlation coefficient below −0.6 for the June to October period of the current year. Similarly, we observe significant negative correlations between δ18O and the PDSI index and precipitation for the shorter JJA period. We observe a stronger relationship between PDSI and δ18O than between PDSI and δ13C, which is in accordance with the results of Esper et al. [19] and Rybníček et al. [51].
From an eco-physiological perspective, the tree-ring δ13C value is primarily modulated by the temperature-driven carboxylation rate and/or by the diffusive stomatal conductance of CO2 into the leaves. Particularly at humid sites, where stomatal conductance and intercellular CO2 concentration are not limiting factors of photosynthesis [52], higher temperatures result in higher δ13C values [53]. At dry sites, however, stomatal conductance may play a crucial role in 13C discrimination [54]. As shown by Farquhar et al. [55], low intercellular CO2 concentrations lead to reduced discrimination of 13C, thereby resulting in an increase in δ13C values. Such a mechanism is likely responsible for the higher δ13C values at low sum of JJA precipitation observed in our study.
The ratio of photosynthetic CO2 uptake to stomatal conductance, both of which are physiological processes contributing to carbon discrimination, is defined as plant water use efficiency (WUE). Accordingly, δ13C values of tree-ring cellulose are thought to provide particularly important insights into the tree’s WUE and other related physiological processes [7,56,57]. However, it is not possible to determine whether a change in WUE is caused by carboxylation, stomatal conductance, and/or a combination of the two.
Based on the theory, variability in δ18O values could potentially reflect changes in stomatal conductance due to a regulated rate of transpiration. It is assumed that δ18O values in plants are negatively correlated with stomatal conductance but independent of photosynthetic CO2 uptake [58]. Therefore, the combined analysis of δ13C and δ18O values represents a substantial improvement compared to previous work. It should be noted that both the isotopic signal of source water and post-photosynthetic and post-evaporative oxygen atom exchange processes could affect the final tree-ring δ18O signal [54]. Among other factors, vapor pressure deficit (VPD) is thought to influence the δ18O signal most substantially. When VPD increases (i.e., environmental conditions become drier), more evaporation occurs and the remaining water becomes enriched in 18O. This is because water molecules containing the lighter 16O isotope evaporate more readily than water molecules containing the heavier 18O isotope. VPD has been shown to be one of the most effective drivers of changes in stomatal aperture, leading to reductions in transpiration of H2O from leaves and the diffusion of CO2 into the leaves when VPD is high [52,59].
Indeed, several recent studies confirm that δ18O values can be a robust and reliable indicator of drought conditions and/or extreme hydroclimatic events [57,60,61]. We confirmed that δ18O values are tightly correlated with JJA precipitation sum over the substantial part of the Balkan Peninsula. The results of spatial field correlation, however, indicate that the δ13C chronology is an even stronger and more stable proxy for summer precipitation reconstruction. However, no spatio-temporal correlation between TRSIs and temperature during 1959–2018 was detected. This might be related to the widely documented phenomena known as “divergence”, where higher instrumental temperatures are not reflected in the TRWs proxies (e.g., [62]). We hypothesize that an increasing summer temperature over recent decades is no longer a limiting factor for growth of pines at high altitudes with very short vegetation periods. Moreover, lower amounts of summer precipitation, together with an increased evapotranspiration due to higher temperature, provide a stronger and stable precipitation signal over the past century. More research including an extended dataset and detailed analyses is necessary to explain the causality of the divergence phenomenon.
There are several hypotheses trying to explain this discrepancy, but probably combinations of different environmental and anthropogenic factors are involved (e.g., [63,64]). Stine and Huybers [63] showed that no divergence is observed in arctic ecosystems with sufficient (non-limiting) light availability (i.e., no volcanic/dimming/pollution effects); these authors recommend an isotopic signal analysis to account for the anomaly. Brownlee et al. [64] have shown that one of the suggested causes of divergence, drought, is not likely an explanatory factor in the Alaskan forests. A recent overview of divergence problem in the climate reconstruction is provided by Wilmking et al. [3], in which the need for correct statistical treatment of the data is strongly emphasized to avoid improper interpretation of the past climate changes and extremes. As many as two-thirds of published studies do not test for the stationarity of tree growth vs. climate reconstructions, whereas more than half of those which did found non-stationarity in the data. This suggests a dynamic nature of the tree–environment relationship; accordingly, all results should be interpreted with a caution, especially those not performing the stationarity test.

5. Conclusions

In this study, we present a 487-year-long TRW chronology, thus extending the chronology for this region by 50 years [24,30]. This is also the first study to use stable carbon and oxygen isotopes for climate reconstruction in this geographical region. By comparing TRW records with δ13C and δ18O records, we show that tree-ring stable isotopes from P. heldreichii growing at high elevations correlate strongly with factors reflecting the climate variability during the summer months (JJA). These correlations are stronger than those found for tree-ring widths. Values of δ18O and particularly δ13C are stable and reliable proxies of JJA precipitation and can be further used for paleoclimatic reconstructions of hydroclimatic conditions over the whole Balkan Peninsula and surrounding eastern Mediterranean region.

Author Contributions

Conceptualization, L.L., O.U., M.R., S.M., M.T. and M.V.M.; methodology, L.L., O.U., M.R., T.K. and S.M.; validation, M.V.M., S.M., O.U., A.A., T.K., M.R. and M.T.; formal analysis, A.A., T.K. and M.V.M.; investigation, L.L., M.R., T.K., O.U., and A.A.; resources, L.L.; data curation, L.L., O.U., A.A., M.R. and T.K.; writing—original draft preparation, L.L., O.U., M.V.M., T.K., M.R. and S.M.; writing—review and editing, M.V.M., M.R., S.M., A.A., T.K. and M.T.; visualization, T.K. and L.L., supervision, S.M. and M.V.M.; funding acquisition, M.V.M. and M.T. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by Ministry of Education, Youth and Sports of the Czech Republic (grant no. CZ.02.1.01/0.0/0.0/16_019/0000797), Czech Science Foundation (grant no. 18-17295S), European Regional Development Fund (grant no. KK.05.1.1.02), and by the Slovak Science Foundation VEGA (grant no. 2/0013/17).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The data presented in this study are available on request from the corresponding author.

Acknowledgments

This research was supported by the Ministry of Education, Youth and Sport under the project “SustES-Adaptation strategies for sustainable ecosystem services and food security under adverse environmental conditions” (project no. CZ.02.1.01/0.0/0.0/16_019/0000797) and by the Czech Science Foundation (18-17295S–Climate and air pollution effects on forest productivity). LL & SM were supported by the European Regional Development Fund under the project “Climate change adaptation measures for sustainable management of natural resources-MEMORIE, Scheme for strengthening applied research for climate change adaptation measures”, (ref. code: KK.05.1.1.02). MVM was supported by the Slovak Science Foundation VEGA (project no. 2/0013/17–The role of ecosystem services in support of landscape conservation under the global change”.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Briffa, K.R. Annual climate variability in the Holocene: Interpreting the message of ancient trees. Quat. Sci. Rev. 2000, 19, 87–105. [Google Scholar] [CrossRef]
  2. Burian, A.; Barbier de Reuille, P.; Kuhlemeier, C. Patterns of stem cell divisions contribute to plant longevity. Curr. Biol. 2016, 26, 1385–1394. [Google Scholar] [CrossRef] [Green Version]
  3. Wilmking, M.; van der Maaten-Theunissen, M.; van der Maaten, E.; Scharnweber, T.; Buras, A.; Biermann, C.; Gurskaya, M.; Hallinger, M.; Lange, J.; Shetti, R.; et al. Global assessment of relationships between climate and tree growth. Glob. Chang. Biol. 2020, 26, 3212–3220. [Google Scholar] [CrossRef] [Green Version]
  4. Morales, M.S.; Cook, E.R.; Barichivich, J.; Christie, D.A.; Villalba, R.; LeQuesne, C.; Srur, A.M.; Ferrero, M.E.; González-Reyes, Á.; Couvreux, F.; et al. Six hundred years of South American tree rings reveal an increase in severe hydroclimatic events since mid-20th century. Proc. Natl. Acad. Sci. USA 2020, 117, 16816–16823. [Google Scholar] [CrossRef] [PubMed]
  5. McCarroll, D.; Loader, N.J. Stable isotopes in tree rings. Quat. Sci. Rev. 2004, 23, 771–801. [Google Scholar] [CrossRef]
  6. De Boer, H.J.; Robertson, I.; Clisby, R.; Loader, N.J.; Gagen, M.; Young, G.H.F.; Wagner-Cremer, F.; Hipkin, C.R.; McCarroll, D.; Cernusak, L. Tree-ring isotopes suggest atmospheric drying limits temperature-growth responses of treeline bristlecone pine. Tree Physiol. 2019, 39, 983–999. [Google Scholar] [CrossRef]
  7. Farquhar, G.D.; Ehleringer, J.R.; Hubic, K.T. Carbon isotope discrimination and photosynthesis. Annu. Rev. Plant Physiol. Plant Mol. Biol. 1989, 40, 503–537. [Google Scholar] [CrossRef]
  8. Barbour, M.M.; Farquhar, G.D. Do pathways of water movement and leaf anatomical dimensions allow development of gradients in H218O between veins and the sites of evaporation within leaves? Plant Cell Environ. 2004, 27, 107–121. [Google Scholar] [CrossRef]
  9. Roden, J.S.; Lin, G.; Ehleringer, J.R. A mechanistic model for interpretation of hydrogen and oxygen isotope ratios in tree-ring cellulose-Evidence and implications for the use of isotopic signals transduced by plants. Geochim. Cosmochim. Acta 2000, 64, 21–35. [Google Scholar] [CrossRef]
  10. Leavitt, S.W. Tree-ring C–H–O isotope variability and sampling. Sci. Total Environ. 2010, 408, 5244–5253. [Google Scholar] [CrossRef]
  11. Ponton, S.; Dupouey, J.L.; Bréda, N.; Feuillat, F.; Bodénès, C.; Dreyer, E. Carbon isotope discrimination and wood anatomy variations in mixed stands of Quercus robur and Quercus petraea. Plant Cell Environ. 2001, 24, 861–868. [Google Scholar] [CrossRef] [Green Version]
  12. Song, X.; Farquhar, G.D.; Gessler, A.; Barbour, M.M. Turnover time of the non-structural carbohydrate pool influences δ18O of leaf cellulose. Plant Cell Environ. 2014, 37, 2500–2507. [Google Scholar] [CrossRef] [PubMed]
  13. Barbeta, A.; Peñuelas, J. Relative contribution of groundwater to plant transpiration estimated with stable isotopes. Sci. Rep. 2017, 7, 1–10. [Google Scholar] [CrossRef] [Green Version]
  14. Kress, A.; Saurer, M.; Siegwolf, R.T.W.; Frank, D.C.; Esper, J.; Bugmann, H. A 350-year drought reconstruction from Alpine tree ring stable isotopes. Global Biogeochem. Cycles 2010, 24, 1–16. [Google Scholar] [CrossRef] [Green Version]
  15. Nagavciuc, V.; Kern, Z.; Ionita, M.; Hartl, C.; Konter, O.; Esper, J.; Popa, I. Climate signals in carbon and oxygen isotope ratios of Pinus cembra tree-ring cellulose from the Călimani Mountains, Romania. Int. J. Climatol. 2020, 40, 2539–2556. [Google Scholar] [CrossRef]
  16. Liu, Y.; Fang, C.; Li, Q.; Song, H.; Ta, W.; Zhao, G.; Sun, C. Tree-ring δ18O based PDSI reconstruction in the Mt. Tianmu region since 1618 AD and its connection to the East Asian summer monsoon. Ecol. Indic. 2019, 104, 636–647. [Google Scholar] [CrossRef]
  17. Shestakova, T.A.; Voltas, J.; Saurer, M.; Siegwolf, R.T.W.; Kirdyanov, A.V. Warming effects on Pinus sylvestris in the cold-dry Siberian forest-steppe: Positive or negative balance of trade? Forests 2017, 8, 490. [Google Scholar] [CrossRef] [Green Version]
  18. Treydte, K.S.; Frank, D.C.; Saurer, M.; Helle, G.; Schleser, G.H.; Esper, J. Impact of climate and CO2 on a millennium-long tree-ring carbon isotope record. Geochim. Cosmochim. Acta 2009, 73, 4635–4647. [Google Scholar] [CrossRef]
  19. Esper, J.; Holzkämper, S.; Büntgen, U.; Schöne, B.; Keppler, F.; Hartl, C.; George, S.S.; Riechelmann, D.F.C.; Treydte, K. Site-specific climatic signals in stable isotope records from Swedish pine forests. Trees Struct. Funct. 2018, 32, 855–869. [Google Scholar] [CrossRef]
  20. Young, E.D.; Manning, C.E.; Schauble, E.A.; Shahar, A.; Macris, C.A.; Lazar, C.; Jordan, M. High-temperature equilibrium isotope fractionation of non-traditional stable isotopes: Experiments, theory, and applications. Chem. Geol. 2015, 395, 176–195. [Google Scholar] [CrossRef]
  21. Hafner, P.; McCarroll, D.; Robertson, I.; Loader, N.J.; Gagen, M.; Young, G.H.F.; Bale, R.J.; Sonninen, E.; Levanič, T. A 520-year record of summer sunshine for the eastern European Alps based on stable carbon isotopes in larch tree rings. Clim. Dyn. 2014, 43, 971–980. [Google Scholar] [CrossRef] [Green Version]
  22. Poljanšek, S.; Ceglar, A.; Levanič, T. Long-term summer sunshine/moisture stress reconstruction from tree-ring widths from Bosnia and Herzegovina. Clim. Past 2013, 9, 27–40. [Google Scholar] [CrossRef] [Green Version]
  23. Levanič, T.; Poljanšek, S.; Toromani, E. Early summer temperatures reconstructed from black pine (Pinus nigra Arnold) tree ring widths from Albania. Holocene 2014, 25, 469–481. [Google Scholar] [CrossRef]
  24. Levanič, T.; Jevšenak, J.; Hafner, P. Stable isotopes reveal climate signal hidden in tree rings of endemic Balkan pines. Atmosphere 2020, 11, 135. [Google Scholar] [CrossRef] [Green Version]
  25. Levanič, T.; Popa, I.; Poljanšek, S.; Nechita, C. A 323-year long reconstruction of drought for SW Romania based on black pine (Pinus nigra) tree ring widths. Int. J. Biometeorol. 2012, 57, 703–714. [Google Scholar] [CrossRef] [PubMed]
  26. Piovesan, G.; Biondi, F.; Baliva, M.; Dinella, A.; Di Fiore, L.; Marchiano, V.; Saba, E.P.; De Vivo, G.; Schettino, A.; Di Filippo, A. Tree growth patterns associated with extreme longevity: Implications for the ecology and conservation of primeval trees in Mediterranean mountains. Anthropocene 2019, 26, 100199. [Google Scholar] [CrossRef]
  27. Panayotov, M.; Bebi, P.; Trouet, V.; Yurukov, S. Climate signal in tree-ring chronologies of Pinus peuce and Pinus heldreichii from the Pirin Mountains in Bulgaria. Trees Struct. Funct. 2010, 24, 479–490. [Google Scholar] [CrossRef] [Green Version]
  28. Seim, A.; Büntgen, U.; Fonti, P.; Haska, H.; Herzig, F.; Tegel, W.; Trouet, W.; Treydte, K. Climate sensitivity of a millennium-long pine chronology from Albania. Clim. Res. 2012, 51, 217–228. [Google Scholar] [CrossRef]
  29. Bojaxhi, F.; Toromani, E. The growth of Bosnian pine (Pinus heldreichii Christ.) at tree line locations from Kosovo and its response to climate. Southeast Eur. For. 2016, 7, 109–118. [Google Scholar]
  30. Poljanšek, S.; Ballian, D.; Nagel, T.A.; Levanič, T. A 435-year-long European black pine (Pinus nigra) chronology for the central-western Balkan region. Tree Ring Res. 2012, 68, 31–44. [Google Scholar] [CrossRef]
  31. Stevanović, V.; Stevanović, B. Basic Climatic, Geological and Pedological Factors of Biodiversity of Terrestrial Ecosystems of Yugoslavia. In Biodiversity of Yugoslavia with List of Species of Special Importance; Radović, I., Angelus, J., Eds.; Ecolibri: Belgrade, Serbia, 1995; pp. 75–95. (In Serbian) [Google Scholar]
  32. Burić, D.; Ducić, V.; Mihajlović, J. The climate of Montenegro: Modificators and types-part two. Bull. Serb. Geogr. Soc. 2014, 94, 73–90. [Google Scholar]
  33. Walter, H.; Breckle, W.S. Ecological Systems of the Geobiosphere. 1. Ecological Principles in Global Perspectives; Springer: Berlin/Heidelberg, Germany, 1985; pp. 1–220. [Google Scholar]
  34. Nagel, T.A.; Firm, D.; Pisek, R.; Mihelič, T.; Hladnik, D.; de Groot, M.; Roženbergar, D. Evaluating the influence of integrative forest management on old-growth habitat structures in a temperate forest region. Biol. Conserv. 2017, 216, 101–107. [Google Scholar] [CrossRef]
  35. Gut, U.; Árvai, M.; Bijak, S.; Camarero, J.J.; Cedro, A.; Cruz-García, R.; Garamszegi, B.; Hacket-Pain, A.; Hevia, A.; Huang, W.; et al. No systematic effects of sampling direction on climate-growth relationships in a large-scale, multi-species tree-ring data set. Dendrochronologia 2019, 57, 125624. [Google Scholar] [CrossRef]
  36. Knibbe, B. PAST4—Personal Analysis System for Tree Ring Research Version4. Instruction Manual; SCIEM/Bernhard Knibbe: Vienna, Austria, 2004; pp. 1–140. [Google Scholar]
  37. Grissino-Mayer, H.D. Evaluating crossdating accuracy: A manual and tutorial for the computer program COFECHA. Tree Ring Res. 2001, 57, 205–221. [Google Scholar]
  38. Boettger, T.; Haupt, M.; Knöller, K.; Weise, S.M.; Waterhouse, J.S.; Rinne, K.T.; Loader, N.J.; Sonninen, E.; Jungner, H.; Masson-Delmotte, V.; et al. Wood cellulose preparation methods and mass spectrometric analyses of δ13C, δ18O, and nonexchangeable δ2H values in cellulose, sugar, and starch:  An interlaboratory comparison. Anal. Chem. 2007, 79, 4603–4612. [Google Scholar] [CrossRef]
  39. Urban, O.; Ač, A.; Kolář, T.; Rybníček, M.; Pernicová, N.; Koňasová, E.; Trnka, M.; Büntgen, U. The dendroclimatic value of oak stable isotopes. Dendrochronologia 2021, 65, 125804. [Google Scholar] [CrossRef]
  40. Büntgen, U.; Kolář, T.; Rybníček, M.; Koňasová, E.; Trnka, M.; Ač, A.; Krusic, P.J.; Esper, J.; Treydte, K.; Reinig, F.; et al. No age trends in oak stable isotopes. Paleoceanogr. Paleoclimatol. 2020, 34, 1–7. [Google Scholar] [CrossRef]
  41. Cook, E.R.; Krusic, P.J. Program ARSTAN: A Tree-Ring Standardization Program Based on Detrending and Autoregressive Time Series Modeling, with Interactive Graphics; Tree-Ring Laboratory, Lamont-Doherty Earth Observatory of Columbia University: Palisades, NY, USA, 2006. [Google Scholar]
  42. Cook, E.R.; Peters, K. Calculating unbiased tree-ring indices for the study of climatic and environmental change. Holocene 1997, 7, 361–370. [Google Scholar] [CrossRef]
  43. Wigley, T.M.L.; Briffa, K.R.; Jones, P.D. On the average value of correlated time series, with applications in dendroclimatology and hydrometeorology. J. Clim. Appl. Meteor. 1984, 23, 201–213. [Google Scholar] [CrossRef]
  44. Van der Schrier, G.; Briffa, K.R.; Jones, P.D.; Osborn, T.J. Summer moisture variability across Europe. J. Clim. 2006, 19, 2818–2834. [Google Scholar] [CrossRef]
  45. Zang, C.; Biondi, F. Treeclim: An R package for the numerical calibration of proxy-climate relationships. Ecography 2015, 38, 431–436. [Google Scholar] [CrossRef]
  46. Harris, I.; Jones, P.D.; Osborn, T.J.; Lister, D.H. Updated high-resolution grids of monthly climatic observations—The CRU TS3.10 Dataset. Int. J. Climatol. 2014, 34, 623–642. [Google Scholar] [CrossRef] [Green Version]
  47. Trouet, V. A tree-ring based late summer temperature reconstruction (AD 1675-1980) for the northeastern Mediterranean. Radiocarbon 2014, 56, 69–78. [Google Scholar] [CrossRef]
  48. Klippel, L.; Krusic, P.J.; Brandes, R.; Hartl-Meier, C.; Trouet, V.; Meko, M.; Esper, J. High-elevation inter-site differences in Mount Smolikas tree-ring width data. Dendrochronologia 2017, 44, 164–173. [Google Scholar] [CrossRef]
  49. Klesse, S.; Ziehmer, M.; Rousakis, G.; Trouet, V.; Frank, D. Synoptic drivers of 400 years of summer temperature and precipitation variability on Mt. Olympus, Greece. Clim. Dyn. 2014, 45, 807–824. [Google Scholar] [CrossRef]
  50. Hafner, P.; Robertson, I.; McCarroll, D.; Loader, N.J.; Gagen, M.; Bale, R.J.; Jungner, H.; Sonninen, E.; Hilasvuori, E.; Levanič, T. Climate signals in the ring widths and stable carbon, hydrogen and oxygen isotopic composition of Larix decidua growing at the forest limit in the southeastern European Alps. Trees Struct. Funct. 2011, 25, 1141–1154. [Google Scholar] [CrossRef]
  51. Rybníček, M.; Kolář, T.; Ač, A.; Balek, J.; Koňasová, E.; Trnka, M.; Urban, O.; Büntgen, U. Non-pooled oak (Quercus spp.) stable isotopes reveal enhanced climate sensitivity compared to ring widths. Clim. Res. 2021, 83, 27–41. [Google Scholar] [CrossRef]
  52. Lichtenthaler, H.K.; Ač, A.; Marek, M.V.; Kalina, J.; Urban, O. Differences in pigment composition, photosynthetic rates and chlorophyll fluorescence images of sun and shade leaves of four tree species. Plant Physiol. Biochem. 2007, 45, 577–588. [Google Scholar] [CrossRef]
  53. Lipp, J.; Trimborn, P.; Fritz, P.; Moser, H.; Becker, B.; Frenzel, B. Stable isotopes in tree ring cellulose and climatic change. Tellus 1991, 43, 322–330. [Google Scholar] [CrossRef] [Green Version]
  54. Gessler, A.; Ferrio, J.P.; Hommel, R.; Treydte, K.; Werner, R.A.; Monson, R.K. Stable isotopes in tree rings: Towards a mechanistic understanding of isotope fractionation and mixing processes from the leaves to the wood. Tree Physiol. 2014, 34, 796–818. [Google Scholar] [CrossRef] [Green Version]
  55. Farquhar, G.; O’Leary, M.H.; Berry, J. On the relationship between carbon isotope discrimination and the intercellular carbon dioxide concentration in leaves. Aust. J. Plant Physiol. 1982, 13, 281–292. [Google Scholar] [CrossRef]
  56. Seibt, U.; Rajabi, A.; Griffiths, H.; Berry, J. Carbon isotopes and water use efficiency: Sense and sensitivity. Oecologia 2008, 155, 441–454. [Google Scholar] [CrossRef] [PubMed]
  57. Pumijumnong, N.; Bräuning, A.; Sano, M.; Nakatsuka, T.; Muangsong, C.; Buajan, S. A 338-year tree-ring oxygen isotope record from Thai teak captures the variations in the Asian summer monsoon system. Sci. Rep. 2020, 10, 1–11. [Google Scholar] [CrossRef] [PubMed]
  58. Roden, J.; Siegwolf, R. Is the dual-isotope conceptual model fully operational? Tree Physiol. 2012, 32, 1179–1182. [Google Scholar] [CrossRef] [PubMed]
  59. Urban, O.; Klem, K.; Holišová, P.; Šigut, L.; Šprtová, M.; Teslová-Navrátilová, P.; Zitová, M.; Špunda, V.; Marek, M.V.; Grace, J. Impact of elevated CO2 concentration on dynamics of leaf photosynthesis in Fagus sylvatica is modulated by sky conditions. Environ. Pollut. 2014, 185, 271–280. [Google Scholar] [CrossRef] [Green Version]
  60. Ferrio, J.P.; Díez-Herrero, A.; Tarrés, D.; Ballesteros-Cánovas, J.A.; Aguilera, M.; Bodoque, J.M. Using stable isotopes of oxygen from tree-rings to study the origin of past flood events: First results from the Iberian peninsula. Quaternaire 2015, 26, 67–80. [Google Scholar] [CrossRef] [Green Version]
  61. Nagavciuc, V.; Ionita, M.; Perșoiu, A.; Popa, I.; Loader, N.J.; McCarroll, D. Stable oxygen isotopes in Romanian oak tree rings record summer droughts and associated large-scale circulation patterns over Europe. Clim. Dyn. 2019, 52, 6557–6568. [Google Scholar] [CrossRef] [Green Version]
  62. Frank, D.; Büntgen, U.; Böhm, R.; Maugeri, M.; Esper, J. Warmer early instrumental measurements versus colder reconstructed temperatures: Shooting at a moving target. Quat. Sci. Rev. 2007, 26, 3298–3310. [Google Scholar] [CrossRef]
  63. Stine, A.R.; Huybers, P. Arctic tree rings as recorders of variations in light availability. Nat. Commun. 2014, 5, 3836. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  64. Brownlee, A.H.; Sullivan, P.F.; Csank, A.Z.; Sveinbjörnsson, B.; Ellison, S.B.Z. Drought-induced stomatal closure probably cannot explain divergent white spruce growth in the Brooks Range, Alaska, USA. Ecology 2016, 97, 145–159. [Google Scholar] [CrossRef] [PubMed]
Forests 12 00350 g001 550
Figure 1. (A) Geographical position of the research area. (B) Satellite image of the Orjen Mountains. Red circle indicates the location of the Orjen Peak. Yellow point indicates the location of Crkvice meteorological station. (C) Example of an old pine tree on the sample plot. (D) Comparison of average summer (JJA) temperature and precipitation trends from the local meteorological station (Crkvice, 940 m a.s.l.) and gridded (0.5 × 0.5° grid) CRU TS3.24.01 data. Shaded areas indicate gaps in the climatological observations over the period of record.
Figure 1. (A) Geographical position of the research area. (B) Satellite image of the Orjen Mountains. Red circle indicates the location of the Orjen Peak. Yellow point indicates the location of Crkvice meteorological station. (C) Example of an old pine tree on the sample plot. (D) Comparison of average summer (JJA) temperature and precipitation trends from the local meteorological station (Crkvice, 940 m a.s.l.) and gridded (0.5 × 0.5° grid) CRU TS3.24.01 data. Shaded areas indicate gaps in the climatological observations over the period of record.
Forests 12 00350 g001
Forests 12 00350 g002 550
Figure 2. (A) Raw tree-ring width chronology with a trend approximated by an exponential function, sample replication, and three slightly different pine residual chronologies after applying three different standardization techniques: cubic smoothing splines with 50% frequency cut-off at 150 years, negative exponential functions, and regional curve standardization (RCS) method. The upper left inset provides insight into data characteristics. Basic statistical parameters (MSL—mean segment length; AGR–average growth rate; SD–standard deviation; AC1–first-order autocorrelation) are shown. (B) Expressed population signal (EPS) and inter-series correlation (Rbar) of the indexed TRW series. EPS and Rbar statistics were calculated over 30-year windows lagged by 25 years.
Figure 2. (A) Raw tree-ring width chronology with a trend approximated by an exponential function, sample replication, and three slightly different pine residual chronologies after applying three different standardization techniques: cubic smoothing splines with 50% frequency cut-off at 150 years, negative exponential functions, and regional curve standardization (RCS) method. The upper left inset provides insight into data characteristics. Basic statistical parameters (MSL—mean segment length; AGR–average growth rate; SD–standard deviation; AC1–first-order autocorrelation) are shown. (B) Expressed population signal (EPS) and inter-series correlation (Rbar) of the indexed TRW series. EPS and Rbar statistics were calculated over 30-year windows lagged by 25 years.
Forests 12 00350 g002
Forests 12 00350 g003 550
Figure 3. (A) Raw (grey lines) and averaged time series (1780–2018) of stable carbon (δ13C) and oxygen (δ18O) isotopic ratios in tree rings. Time series of δ13C data are presented as both uncorrected (black line) and corrected for an anthropogenic increase in CO2 concentration in the atmosphere (red line). (B) Expressed population signal (EPS; solid lines) and inter-series correlation (Rbar; dashed lines) of the raw δ13C and δ18O series are shown. EPS and Rbar statistics were calculated over 30-year windows lagged by 25 years. The average values of Rbar and EPS for both isotopes are >0.5 and >0.8, respectively.
Figure 3. (A) Raw (grey lines) and averaged time series (1780–2018) of stable carbon (δ13C) and oxygen (δ18O) isotopic ratios in tree rings. Time series of δ13C data are presented as both uncorrected (black line) and corrected for an anthropogenic increase in CO2 concentration in the atmosphere (red line). (B) Expressed population signal (EPS; solid lines) and inter-series correlation (Rbar; dashed lines) of the raw δ13C and δ18O series are shown. EPS and Rbar statistics were calculated over 30-year windows lagged by 25 years. The average values of Rbar and EPS for both isotopes are >0.5 and >0.8, respectively.
Forests 12 00350 g003
Forests 12 00350 g004 550
Figure 4. Pearson’s correlation coefficients between the TRW chronology and the two sets of isotope data with average temperature (red), Palmer drought severity index (PDSI) (yellow), and precipitation sums (blue) for the period of 1901–2018. The correlations are presented from April of the previous year (pA) to October of the current year (O); associated seasonal means are also shown. The grey vertical shadings indicate the summer (JJA) period of maximum response. Monthly gridded data (0.5 × 0.5° grid) from the CRU TS3.24.01 database were used to calculate the correlations.
Figure 4. Pearson’s correlation coefficients between the TRW chronology and the two sets of isotope data with average temperature (red), Palmer drought severity index (PDSI) (yellow), and precipitation sums (blue) for the period of 1901–2018. The correlations are presented from April of the previous year (pA) to October of the current year (O); associated seasonal means are also shown. The grey vertical shadings indicate the summer (JJA) period of maximum response. Monthly gridded data (0.5 × 0.5° grid) from the CRU TS3.24.01 database were used to calculate the correlations.
Forests 12 00350 g004
Forests 12 00350 g005 550
Figure 5. (A) Moving correlation analysis between tree-ring stable isotopes and JJA precipitation sum and mean JJA temperature. Correlation coefficients were calculated over 45-year periods and plotted on the central year. (B) Calibration-verification model for the JJA precipitation sum for the period 1901–2018. (C) Scatter plot of summer (JJA) precipitation sum (JJAprec; mm) and δ13C over the whole period 1901–2018. Abbreviations: RE (reduction error), CE (coefficient of efficiency), RSME (root mean square error), DW (Durbin-Watson statistics), r2 (squared Pearson’s correlation coefficient).
Figure 5. (A) Moving correlation analysis between tree-ring stable isotopes and JJA precipitation sum and mean JJA temperature. Correlation coefficients were calculated over 45-year periods and plotted on the central year. (B) Calibration-verification model for the JJA precipitation sum for the period 1901–2018. (C) Scatter plot of summer (JJA) precipitation sum (JJAprec; mm) and δ13C over the whole period 1901–2018. Abbreviations: RE (reduction error), CE (coefficient of efficiency), RSME (root mean square error), DW (Durbin-Watson statistics), r2 (squared Pearson’s correlation coefficient).
Forests 12 00350 g005
Forests 12 00350 g006 550
Figure 6. Spatial field correlations between δ13C and δ18O data and summer (JJA) precipitation sums and mean JJA temperatures for two subperiods. Subperiods are determined based on moving correlation analysis and split calibration-verification results. Spatial correlations between tree-ring stable isotope values and climatic variables were analyzed using monthly gridded data (0.5 × 0.5° grid) from the CRU TS3.24.01 database.
Figure 6. Spatial field correlations between δ13C and δ18O data and summer (JJA) precipitation sums and mean JJA temperatures for two subperiods. Subperiods are determined based on moving correlation analysis and split calibration-verification results. Spatial correlations between tree-ring stable isotope values and climatic variables were analyzed using monthly gridded data (0.5 × 0.5° grid) from the CRU TS3.24.01 database.
Forests 12 00350 g006
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Lukač, L.; Mikac, S.; Urban, O.; Kolář, T.; Rybníček, M.; Ač, A.; Trnka, M.; Marek, M.V. Stable Isotopes in Tree Rings of Pinus heldreichii Can Indicate Climate Variability over the Eastern Mediterranean Region. Forests 2021, 12, 350. https://doi.org/10.3390/f12030350

AMA Style

Lukač L, Mikac S, Urban O, Kolář T, Rybníček M, Ač A, Trnka M, Marek MV. Stable Isotopes in Tree Rings of Pinus heldreichii Can Indicate Climate Variability over the Eastern Mediterranean Region. Forests. 2021; 12(3):350. https://doi.org/10.3390/f12030350

Chicago/Turabian Style

Lukač, Ljubica, Stjepan Mikac, Otmar Urban, Tomáš Kolář, Michal Rybníček, Alexander Ač, Mirek Trnka, and Michal V. Marek. 2021. "Stable Isotopes in Tree Rings of Pinus heldreichii Can Indicate Climate Variability over the Eastern Mediterranean Region" Forests 12, no. 3: 350. https://doi.org/10.3390/f12030350

APA Style

Lukač, L., Mikac, S., Urban, O., Kolář, T., Rybníček, M., Ač, A., Trnka, M., & Marek, M. V. (2021). Stable Isotopes in Tree Rings of Pinus heldreichii Can Indicate Climate Variability over the Eastern Mediterranean Region. Forests, 12(3), 350. https://doi.org/10.3390/f12030350

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop