Optimization and Mechanical Properties of Fabricated 2D Wood Pyramid Lattice Sandwich Structure
Abstract
:1. Introduction
2. Materials and Methods
2.1. Unit Cell Design
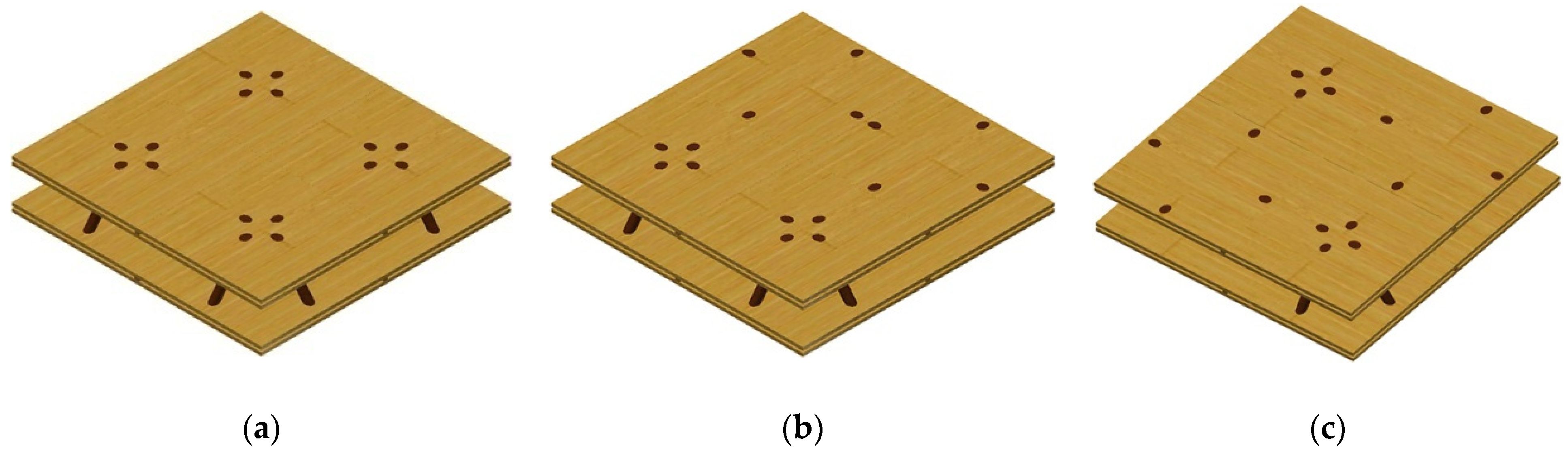
2.2. Specimen Structure
3. Experimental Programs
3.1. Mechanical Behaviors of Raw Materials
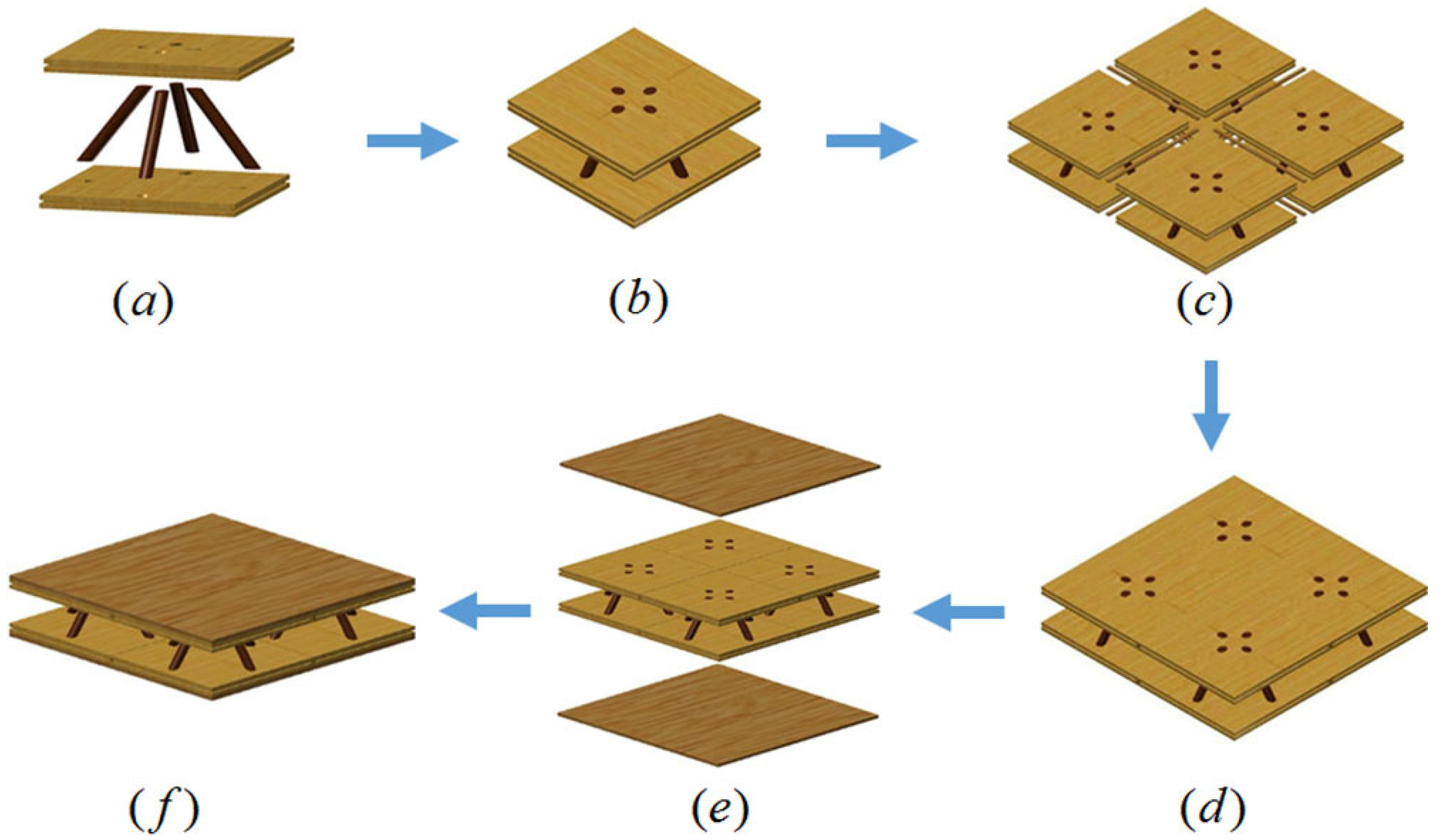
3.2. Fabrication
4. Results and Discussion
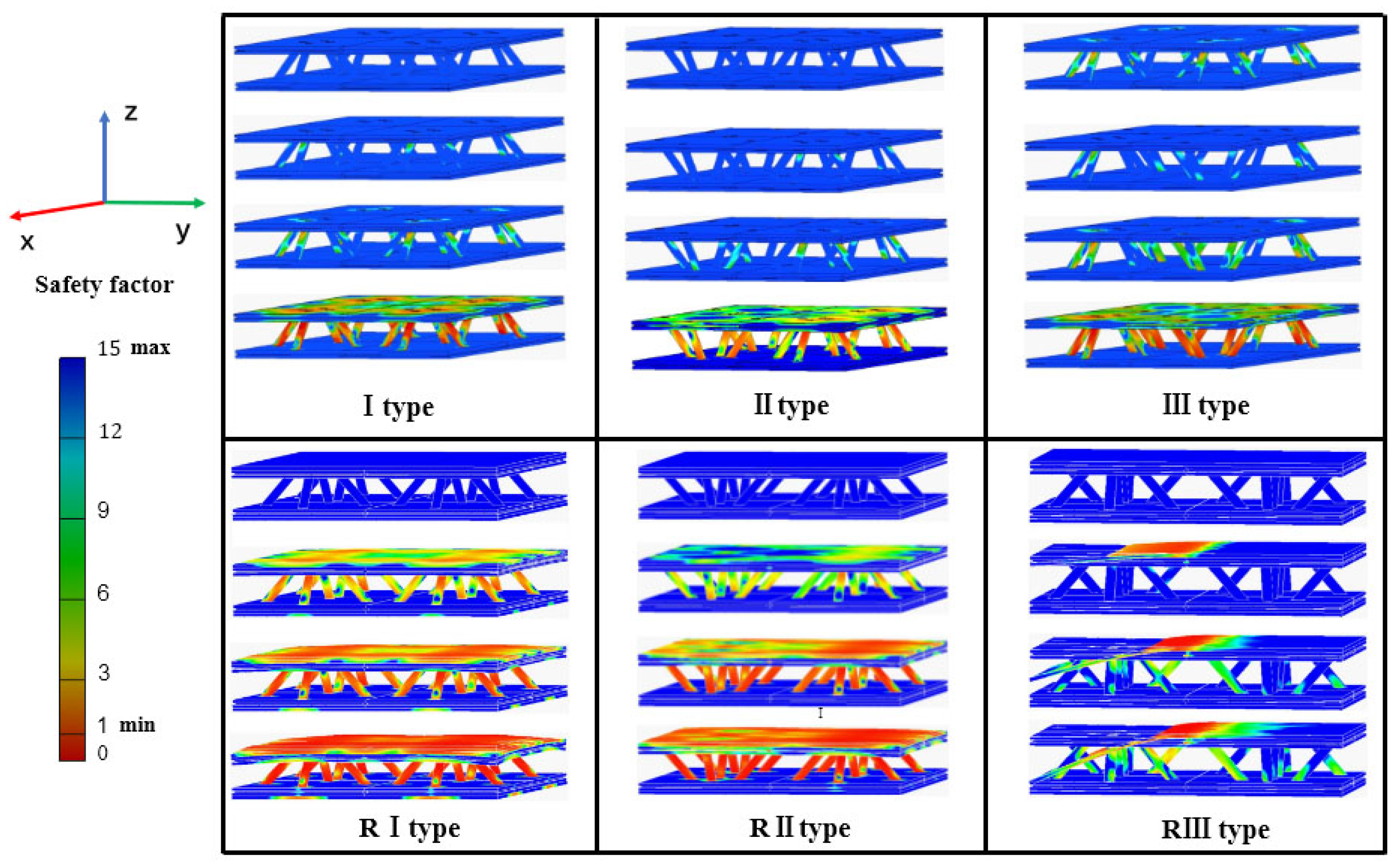
4.1. Compression Failure Mode of Specimens
4.2. Veneer Reinforcement
4.3. Theoretical Analysis
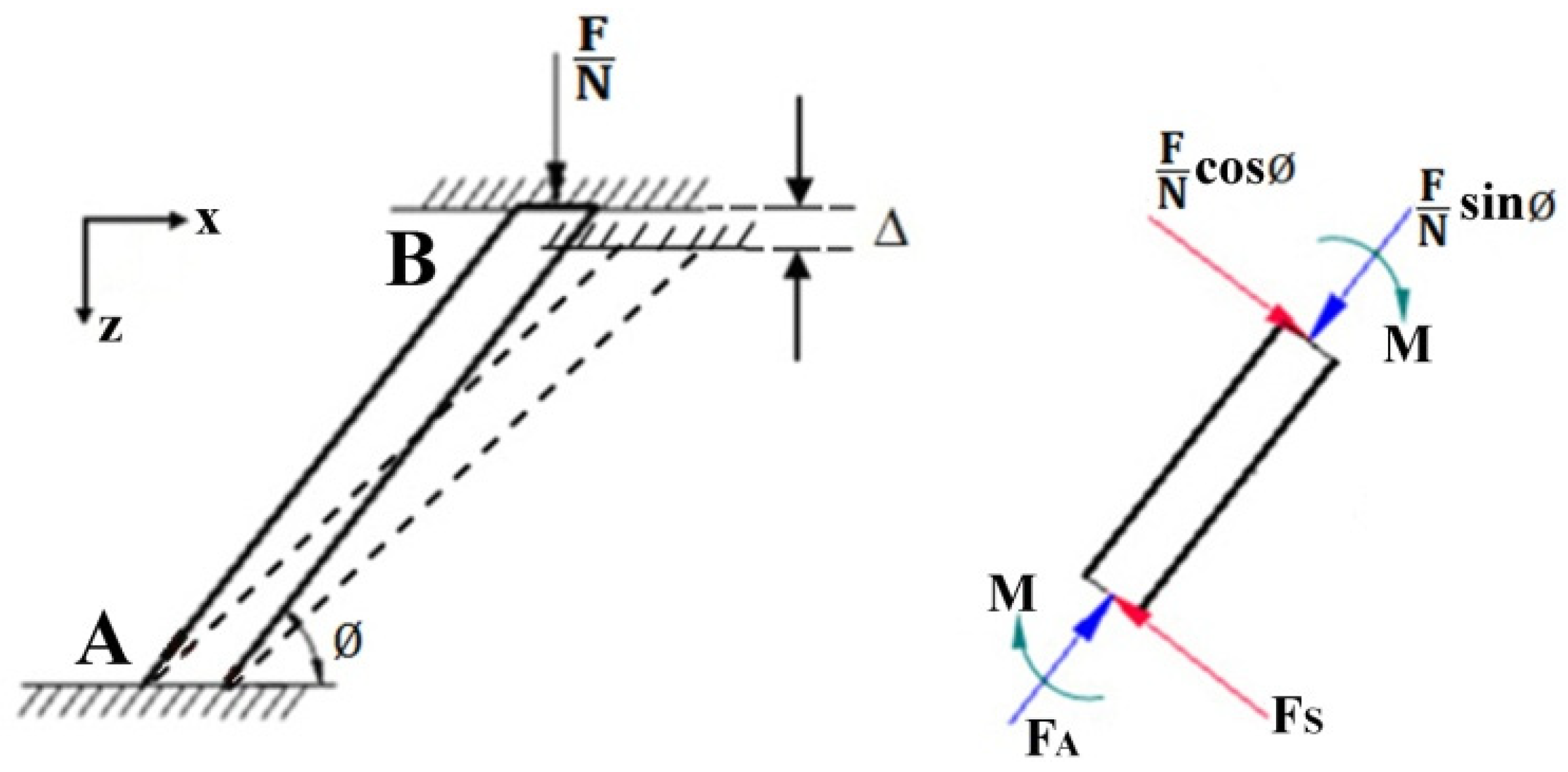
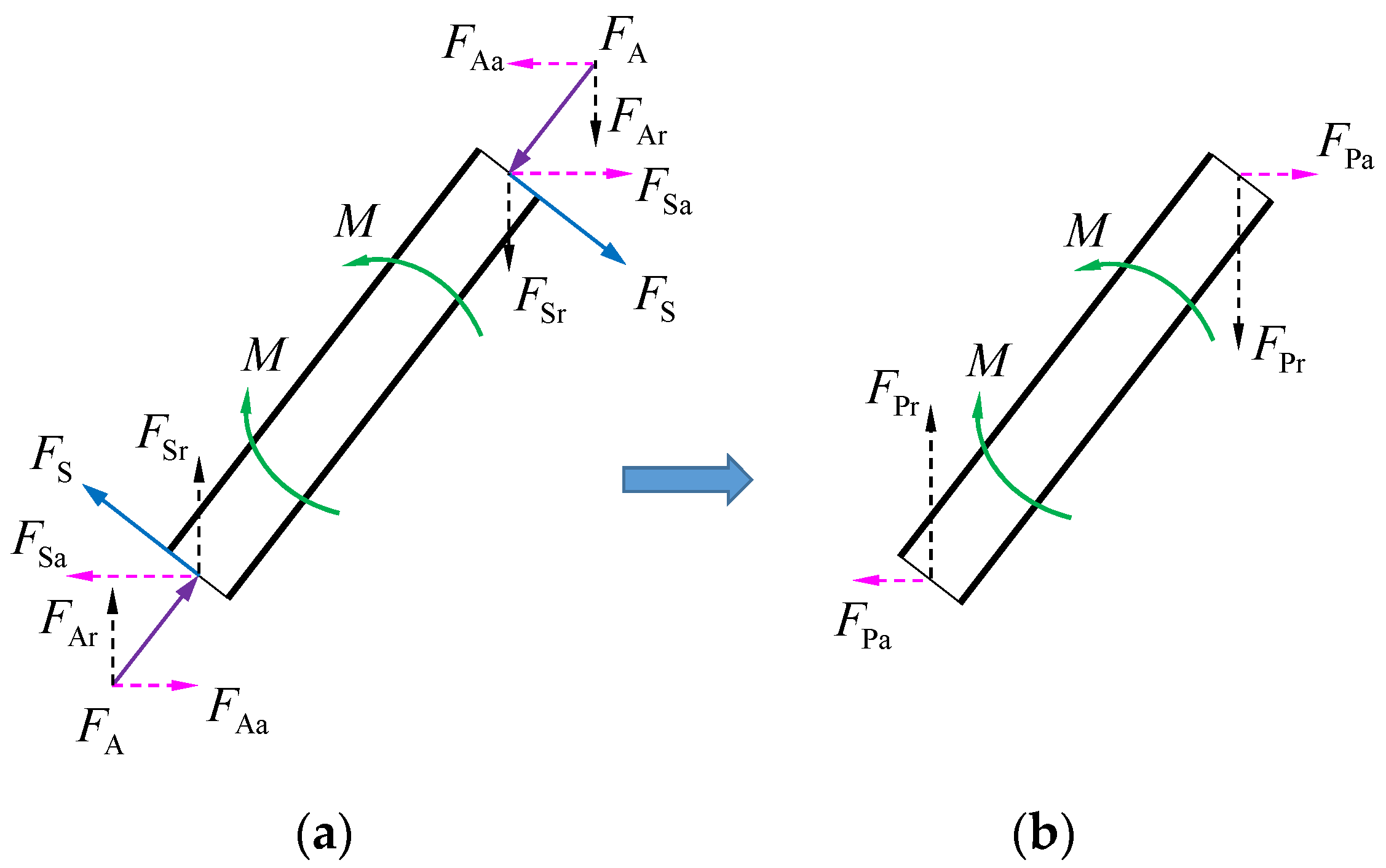
4.3.1. Stress Analysis of Core
4.3.2. Stress Analysis of Panel
4.4. Finite Element Analysis
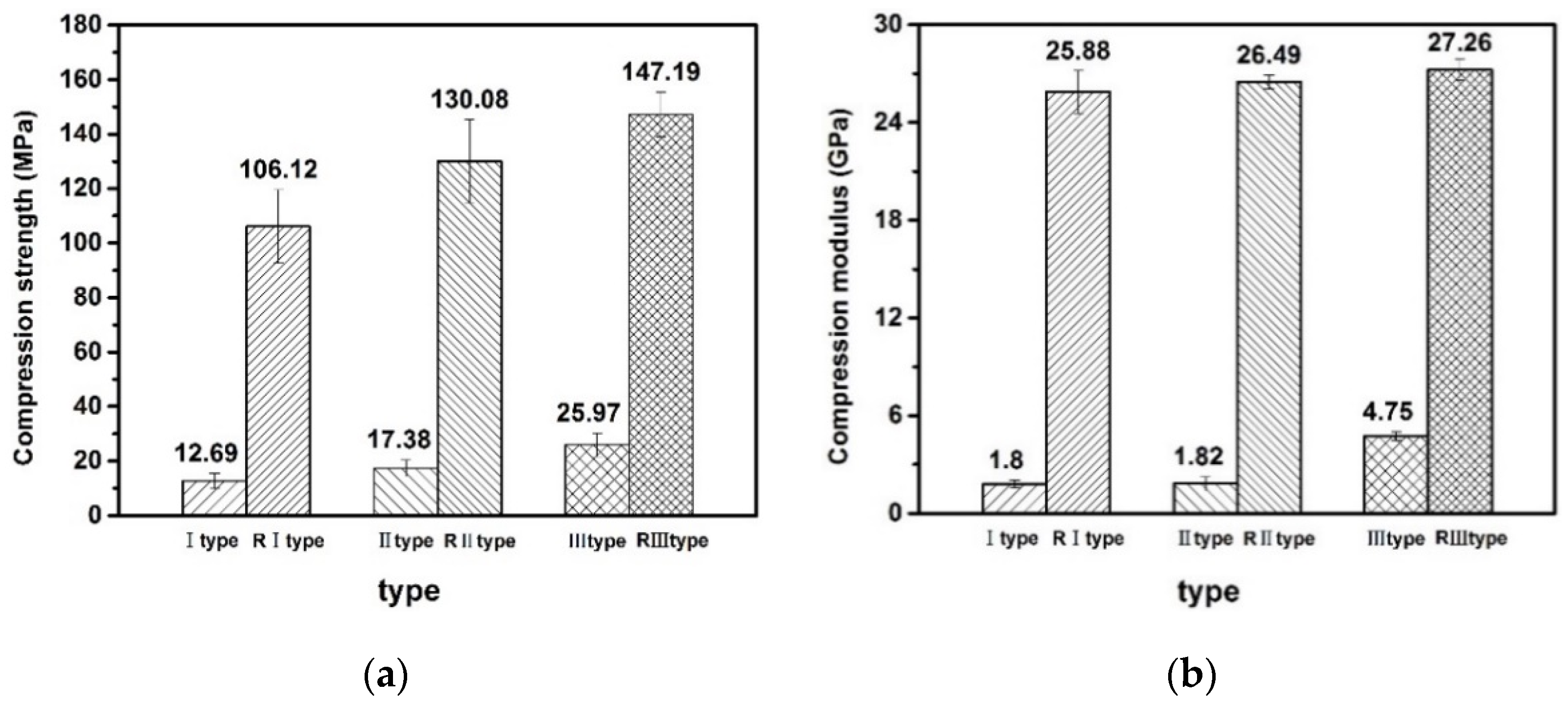
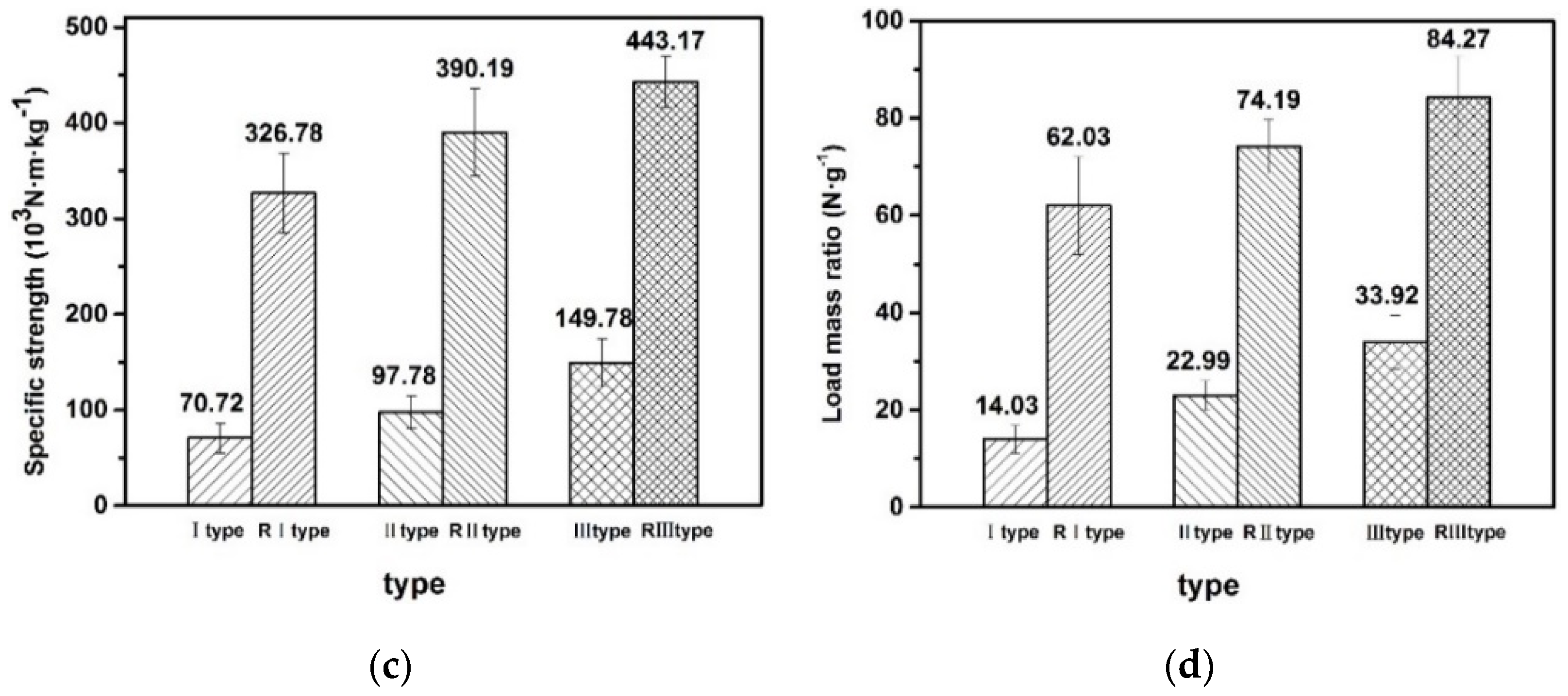
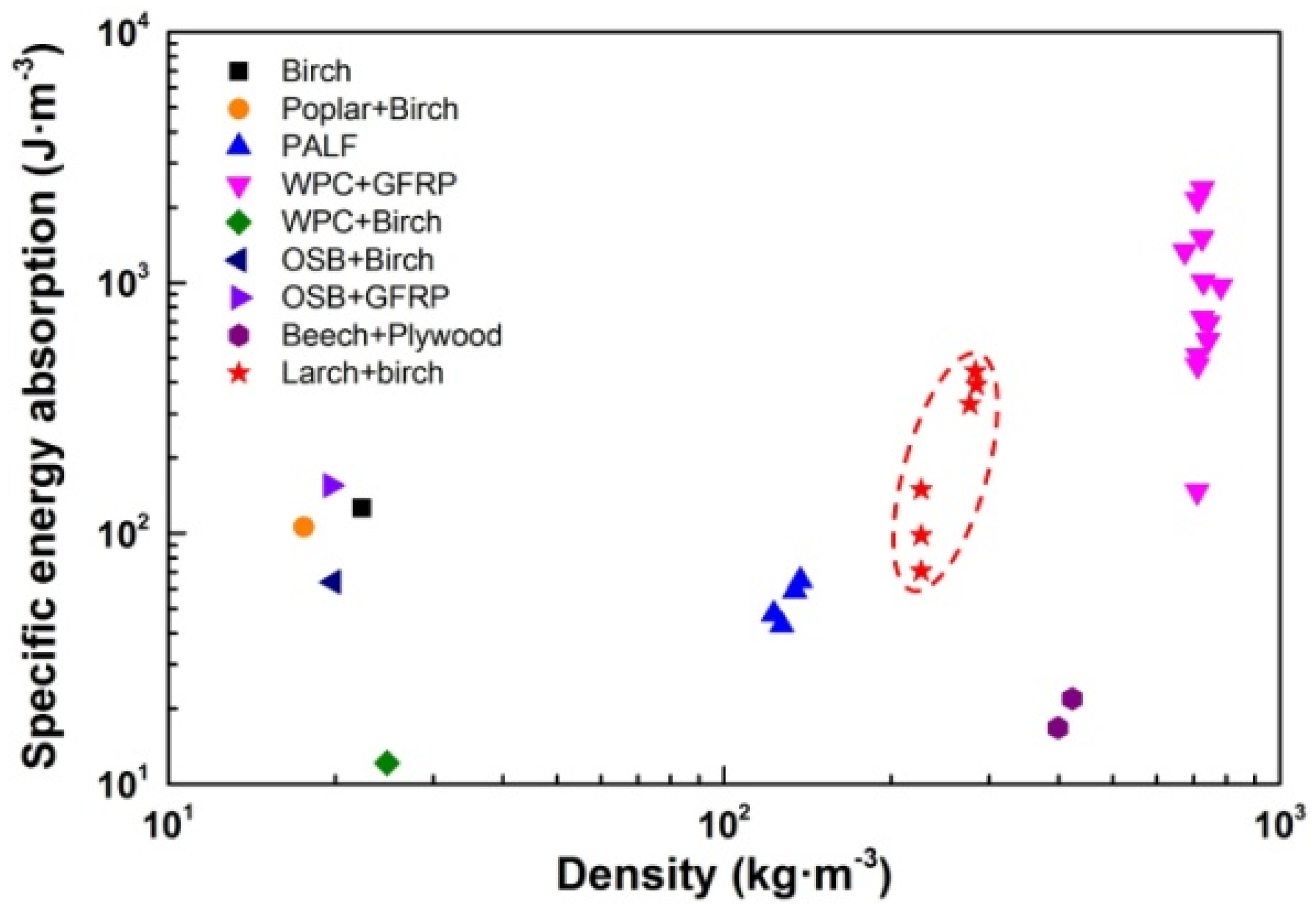
4.5. Performance Analysis
5. Conclusions
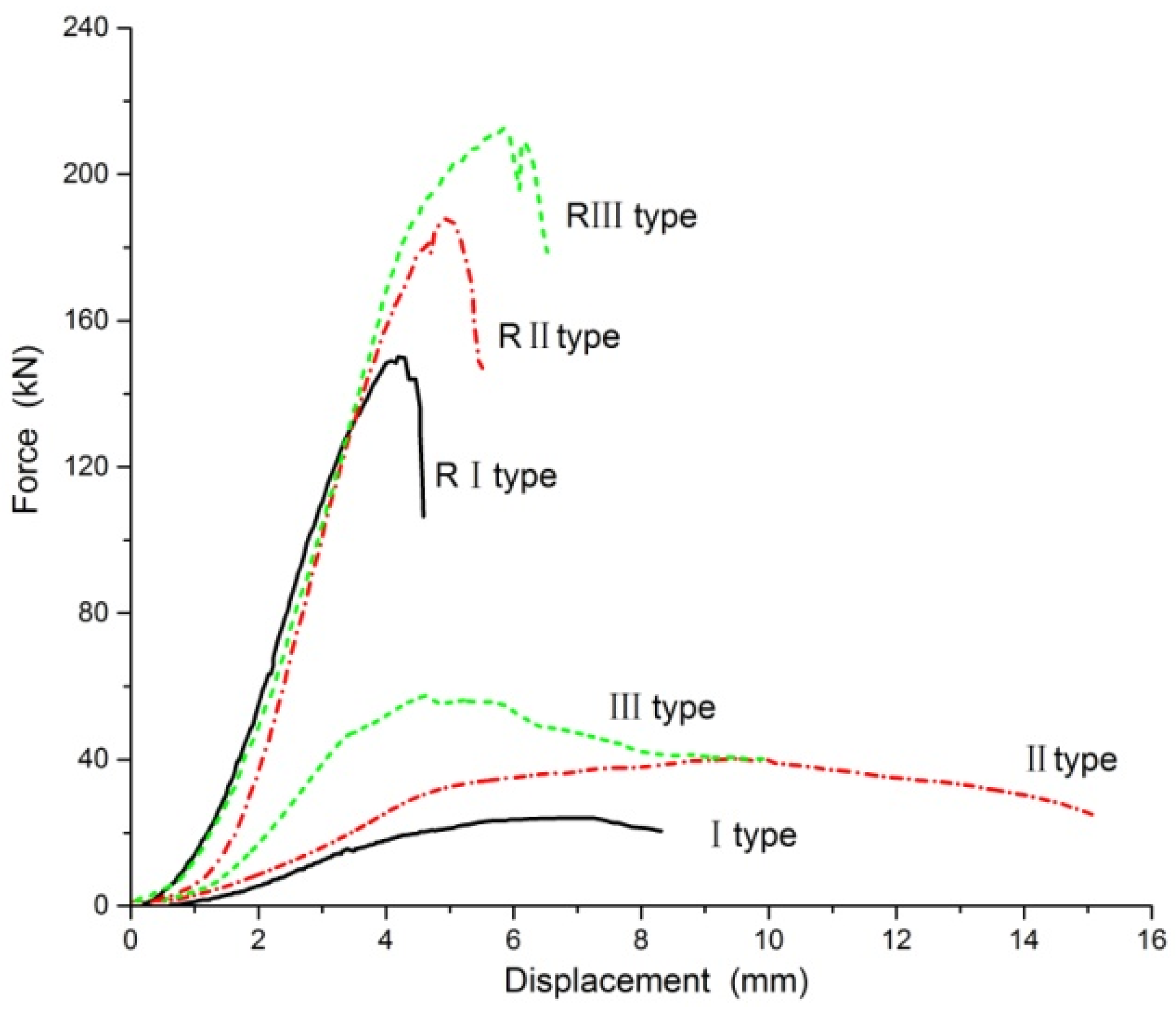
- The flat compression test shows that the arrangement of unit cells in the specimen affects the bearing capacity of the specimen. The load-carrying capacity of type III specimen is 2.4 times that of type I specimen. The load-carrying capacity of the specimens with veneer reinforcement is 6.35 times, 4.75 times, and 3.64 times higher than that of the specimens with unreinforced veneer. Compared with the unreinforced specimens, the specific strength and the load mass ratio are increased by 3–5 times and 2–5 times, respectively.
- The main failure modes of the specimens are core fracture and panel cracking. With the increase of the bearing capacity of the structure, the fracture mode of the core gradually moves upward from the root fracture and splitting of the core to the middle of the core, which is a shear fracture perpendicular to the axial direction. The results of compression performance, failure order and form obtained by finite element analysis are consistent with the experimental results. The failure of the specimen with unreinforced veneer starts from the root of the core, while the failure of specimen with reinforced veneer starts from the root of the core and the panel at the same time.
- The maximum load mass ratio of the structure with reinforced veneer is larger than that of the same type of wooden lattice sandwich structure, which proves that the structure with reinforced veneer is very significant to improve the flat compression performance of the structure.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yang, J.-S.; Ma, L.; Schmidt, R.; Qi, G.; Schröder, K.-U.; Xiong, J.; Wu, L.-Z. Hybrid lightweight composite pyramidal truss sandwich panels with high damping and stiffness efficiency. Compos. Struct. 2016, 148, 85–96. [Google Scholar] [CrossRef] [Green Version]
- Jiang, W.; Yang, B.; Guan, X.; Luo, Y. Bending and twisting springback prediction in the punching of the core for a lattice truss sandwich structure. Acta Metall. Sin. 2013, 26, 241–246. [Google Scholar] [CrossRef]
- Schaedler, T.A.; Chan, L.J.; Clough, E.C.; Stilke, M.A.; Hundley, J.M.; Masur, L.J. Nanocrystalline Aluminum Truss Cores for Lightweight Sandwich Structures. JOM 2017, 69, 2626–2634. [Google Scholar] [CrossRef] [Green Version]
- Zhang, G.; Wang, B.; Ma, L.; Xiong, J.; Yang, J.; Wu, L. The residual compressive strength of impact damaged sandwich structures with pyramidal truss cores. Compos. Struct. 2013, 105, 188–198. [Google Scholar] [CrossRef]
- Mohammadi, M.S.; Nairn, J.A. Crack propagation and fracture toughness of solid balsa used for cores of sandwich composites. J. Sandw. Struct. Mater. 2014, 16, 22–41. [Google Scholar] [CrossRef]
- Dimitrov, N.; Berggreen, C. Probabilistic fatigue life of balsa cored sandwich composites subjected to transverse shear. J. Sandw. Struct. Mater. 2015, 17, 562–577. [Google Scholar] [CrossRef]
- Brandner, R.; Dietsch, P.; Dröscher, J.; Schulte-Wrede, M.; Kreuzinger, H.; Sieder, M. Cross laminated timber (CLT) diaphragms under shear: Test configuration, properties and design. Constr. Build. Mater. 2017, 147, 312–327. [Google Scholar] [CrossRef]
- Dahy, H. Biocomposite materials based on annual natural fibres and biopolymers-Design, fabrication and customized applications in architecture. Constr. Build. Mater. 2017, 147, 212–220. [Google Scholar] [CrossRef]
- Qu, M.; Pelkonen, P.; Tahvanainen, L.; Arevalo, J.; Gritten, D. Experts’ assessment of the development of wood framed houses in China. J. Clean. Prod. 2012, 31, 100–105. [Google Scholar] [CrossRef]
- Rutkevičius, M.; Munusami, S.K.; Watson, Z.; Field, A.D.; Salt, M.; Stoyanov, S.D.; Petkovc, J.; Mehla, G.H.; Paunova, V.N. Fabrication of novel lightweight composites by a hydrogeltemplating technique. Mater. Res. Bull. 2012, 47, 980–986. [Google Scholar] [CrossRef]
- Qin, J.; Zheng, T.; Li, S.; Cheng, Y.; Xu, Q.; Ye, G.; Hu, Y. Core configuration and panel reinforcement affect compression properties of wood- based 2-D straight column lattice truss sandwich structure. Eur. J. Wood Wood Prod. 2019, 77, 539–546. [Google Scholar] [CrossRef]
- Zheng, T.; Yan, H.; Li, S.; Cheng, Y.; Zou, L.; Hu, Y. Compressive behavior and failure modes of the wood based double X type lattice sandwich structure. J. Build. 2020, 30, 1–10. [Google Scholar] [CrossRef]
- Yang, D.; Hu, Y.; Fan, C. Compression Behaviors of Wood Based Lattice Sandwich Structures. BioResources 2018, 13, 6577–6890. [Google Scholar]
- Li, S.; Hu, Y. Optimization of Connection Method of Wood based Lattice Sandwich Structure. J. Northwest For. Univ. 2019, 34, 225–230. [Google Scholar]
- Jin, M.; Hu, Y.; Wang, B. Compressive and bending behaviors of wood based two dimensional lattice truss core sandwich structures. Compos. Struct. 2015, 124, 337–344. [Google Scholar] [CrossRef]
- Wang, L.; Hu, Y.; Zhang, X.; Li, S.; Li, S.; Zhang, H. Design and compressive behavior of a wood based pyramidal lattice core sandwich structure. Eur. J. Wood Wood Prod. 2020, 78, 123–134. [Google Scholar] [CrossRef]
- Klímek, P.; Wimmer, R.; Brabec, M.; Sebera, V. Novel Sandwich Panel with Interlocking Plywood Kagome Lattice Core and Grooved Particleboard Facings. BioResources 2016, 11, 195–208. [Google Scholar] [CrossRef] [Green Version]
- Hao, M.; Hu, Y.; Wang, B.; Liu, S. Mechanical behavior of natural fiber-based isogrid lattice cylinder. Compos. Struct. 2017, 176, 117–123. [Google Scholar] [CrossRef]
- Li, S.; Qin, J.; Li, C.; Feng, Y.; Zhao, X.; Hu, Y. Optimization and compressive behavior of composite 2-D lattice structure. Mech. Adv. Mater. Struct. 2018, 27, 1213–1222. [Google Scholar] [CrossRef]
- Li, X. The Variant Design of Furniture Based Modules with 32mm System through Group Technology Optimization. Packag. Eng. 2015, 36, 55–59. [Google Scholar]
- Jaksch, S.; Franke, A.; Österreicher, D.; Treberspurg, M. A Systematic Approach to Sustainable Urban Densification using prefabricated timber based attic extension modules. Energy Procedia 2016, 96, 638–649. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Wang, Q.; LYU, S.; Frank, L.; Zhang, T. Relations Between Construction Process of Modern Timber Buildings and Prefabrication Design A Case Study of Canadian Construction Technology. Archit. J. 2018, 6, 106–111. [Google Scholar]
- ASTM C365-16. Standard Test Method for Flatwise Compressive Properties of Sandwich Cores; ASTM International: West Conshohocken, PA, USA, 2016. [Google Scholar]
- Lou, W.L.; Ren, H.Q.; Jiang, J.H.; Wang, Z.H.; Zhou, H.B.; Zhao, X.; Guo, W. Effects of Major Defects on Dimensional Larch Lumber Visual Grading. China Wood Ind. 2010, 2, 1–4. [Google Scholar]
- Jiang, J.H.; Lu, J.X.; Ren, H.Q. Study on Characteristic Values for Strength Properties of Chinese Larch Dimension Lumber. J. Build. Mater. 2012, 15, 361–365. [Google Scholar]
- Zhou, Z.; Bi, K.; Zhang, X. Effects of Cross Section Loading Mode and Finger Joint Type on the Bending Property of Larch Structural Finger Jointed Lumber in Large Dimension. Sci. Silvae Sinicae. 2016, 52, 82–89. [Google Scholar]
- Haiqing, R.; Wei, G.; Yafang, Y. Machine Grading of Lumber in North America. World For. Res. 2006, 19, 66–70. [Google Scholar]
- Wu, L.Z.; Xiong, J.; Ma, L.; Wang, B.; Zhang, G.; Yang, J. Processes in the study on novel composite sandwich panels with lattice truss cores. Adv. Mech. 2012, 42, 41–67. [Google Scholar]
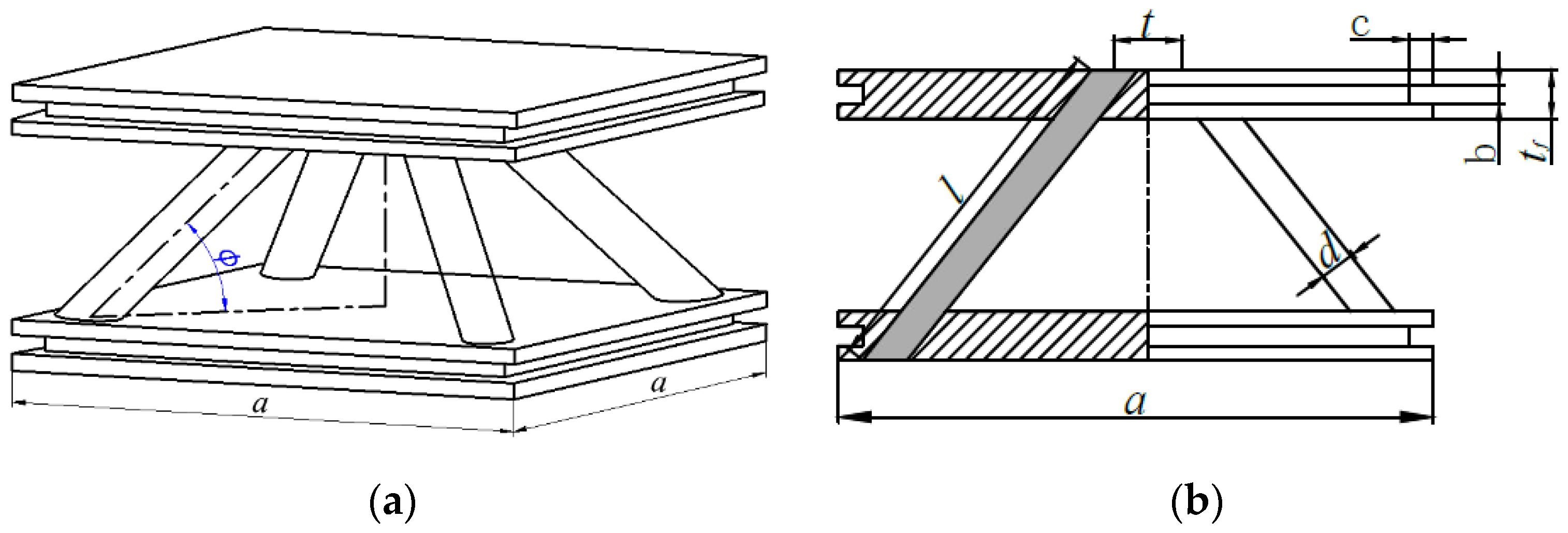



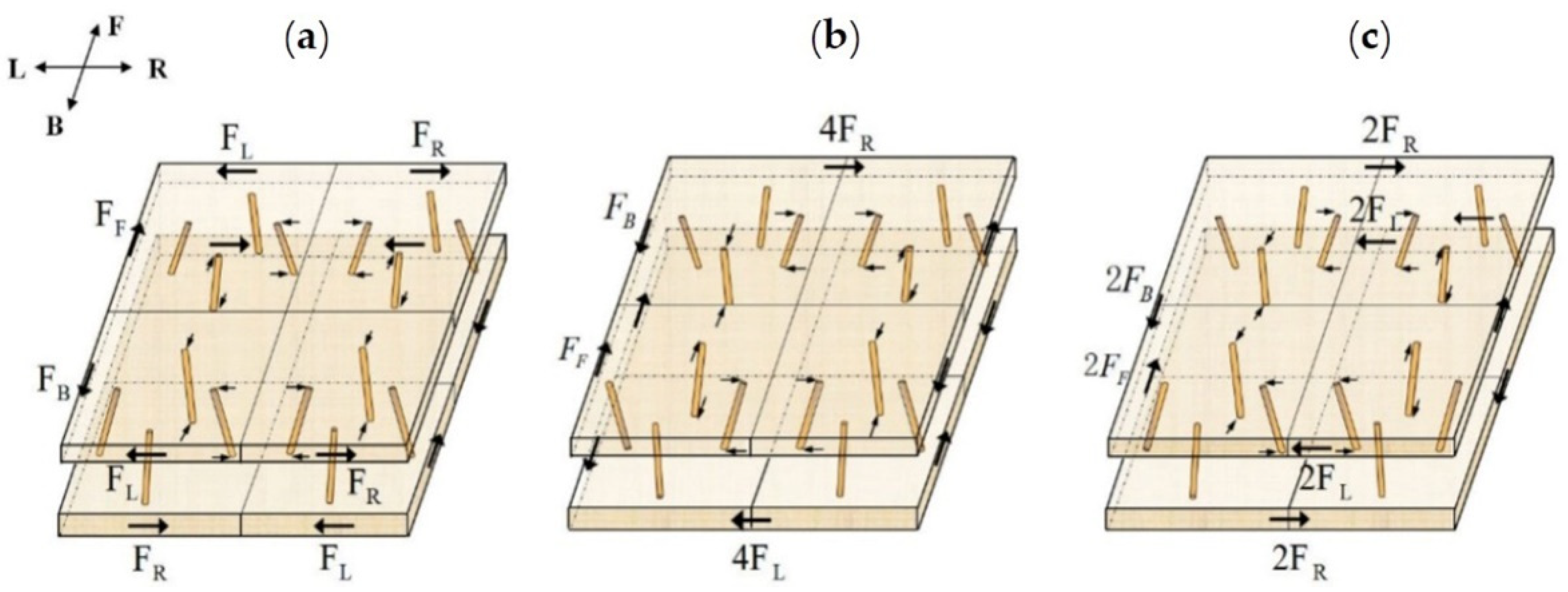

| Name | (mm) | (mm) | (mm) | (mm) | (mm) | (mm) | (°) |
|---|---|---|---|---|---|---|---|
| value | 180 | 3 | 12 | 12 | 3 | 46 | 52° |
| Material | Moisture Content | (kg/m3) | MOE (GPa) Compressive Flexural | MOR (MPa) Compressive Flexural | ||
|---|---|---|---|---|---|---|
| Larch finger-jointed lumber | 6.94% | 512.41 | 26.68 | 3.69 | 50.30 | 78.86 |
| Birch rod cores | 5.99% | 580.554 | 51.47 | 0.69 | 50.28 | 54.76 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, D.; Fan, C.; Hu, Y. Optimization and Mechanical Properties of Fabricated 2D Wood Pyramid Lattice Sandwich Structure. Forests 2021, 12, 607. https://doi.org/10.3390/f12050607
Yang D, Fan C, Hu Y. Optimization and Mechanical Properties of Fabricated 2D Wood Pyramid Lattice Sandwich Structure. Forests. 2021; 12(5):607. https://doi.org/10.3390/f12050607
Chicago/Turabian StyleYang, Dongxia, Changsheng Fan, and Yingcheng Hu. 2021. "Optimization and Mechanical Properties of Fabricated 2D Wood Pyramid Lattice Sandwich Structure" Forests 12, no. 5: 607. https://doi.org/10.3390/f12050607
APA StyleYang, D., Fan, C., & Hu, Y. (2021). Optimization and Mechanical Properties of Fabricated 2D Wood Pyramid Lattice Sandwich Structure. Forests, 12(5), 607. https://doi.org/10.3390/f12050607






