Effects of Grain Pattern on the Rolling Shear Properties of Wood in Cross-Laminated Timber

Abstract

Rolling shear modulus and strength are the key factors affecting the mechanical performance of some wood products such as cross-laminated timber (CLT). As reported, rolling shear property strongly depends on the sawing pattern such as the aspect ratio and grain direction (grain mode). However, the mechanism behind this phenomenon has not yet been clarified. In this work, the rolling shear modulus and strength of spruce-pine-fir (SPF) with different grain modes and aspect ratios were experimentally investigated. In addition, a theoretical investigation was carried out to reveal the mechanism behind this phenomenon. The results exhibited that the rolling shear moduli of 0° and 90° grain-mode wood were the same. This value can be called the pure rolling shear modulus. Rolling shear modulus of wood with angles other than 0° and 90° can be calculated from the pure rolling shear modulus and grain angle. Therefore, this modulus can be called the apparent rolling shear modulus. Thus, using 0° and 90° grain-mode specimens to determine the pure rolling shear modulus and strength of wood is recommended.

1. Introduction

Cross-laminated timber (CLT) is an innovative engineered wood product which consists of several layers of boards stacked crosswise and glued together [1]. CLT has gained its popularity in residential and nonresidential constructions in recent years due to its advantages of high material utilization rate, good dimensional stability, outstanding thermal insulation properties, and effective fire resistance [2].

The transverse laminations, which are oriented perpendicular to the major strength direction of CLT, work in rolling shear when subjected to the out-of-plane load. Considering that the rolling shear strength and modulus of wood are rather low, CLT members usually fracture due to cracks initiating from the transverse laminations [3]. Taking Norway spruce as an example, the rolling shear modulus is about 35 MPa, and the rolling shear strength is about 1.6 MPa [4]. Therefore, rolling shear modulus and strength are considered the key factors affecting the mechanical performance of CLT.

Several studies have been implemented in this domain. Zhou [5] found that the growth ring orientation has significant effects on the rolling shear modulus of wood. The study also found that the modulus of laminations with in-between grain was larger than that of the flat-sawn and quarter-sawn grain laminations. Ehrhart et al. [6] found that the sawing pattern influences the rolling shear modulus, and the lamination geometry influences the strength. Aicher et al. [7,8] found that the semi-quarter-sawn board has the largest rolling shear modulus in boards with different sawing patterns. Wang [9] tested the rolling shear property of poplar. The study exhibited that the shear modulus was the highest for semi-quarter-sawn boards. Cai [10] studied the effect of aspect ratio on the rolling shear property of fast-growing eucalyptus. The study exhibited that both rolling shear modulus and strength increase with the increase of aspect ratio. Ehrhart and Brandner [11] tested the rolling shear properties of six timber species with different board geometries and sawing patterns. They also investigated the system effects of multiple laminations.

As previously discussed, rolling shear modulus strongly depends on the sawing pattern, such as the aspect ratio, grain direction, and distance to pith. In addition, rolling shear strength depends on the tensile strength perpendicular to grain of wood. However, the mechanism behind this phenomenon has not yet been clarified. In this work, the rolling shear modulus and strength of SPF with different grain modes and aspect ratios were experimentally investigated. Afterward, a theoretical investigation was carried out to reveal the mechanism behind this phenomenon.

2. Materials and Methods

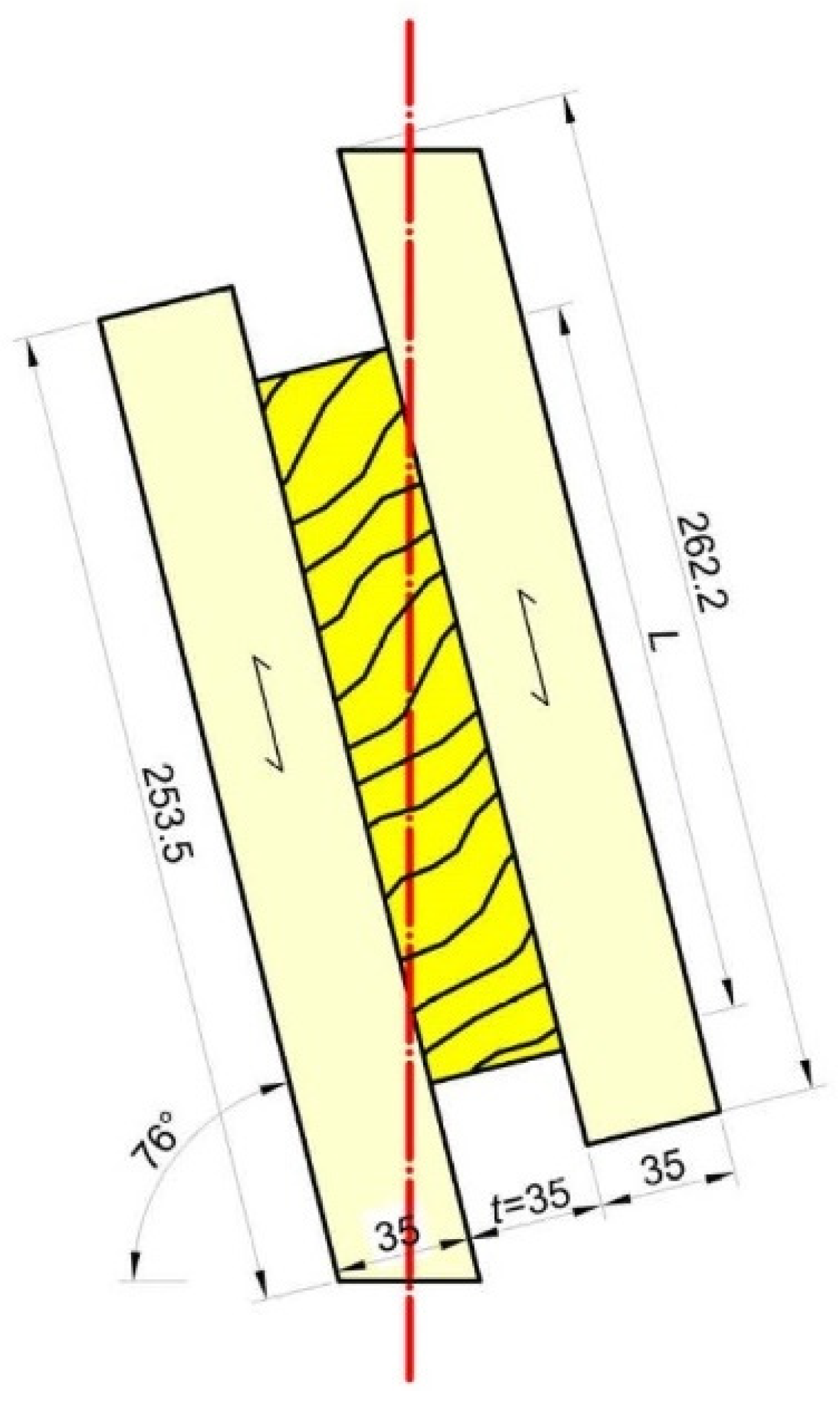
2.1. Materials

The specimens were manufactured from 50 mm × 100 mm, 50 mm × 150 mm, and 50 mm × 200 mm visually graded No. 2 SPF dimension lumbers imported from Canada. The lumbers were randomly picked from the wood stock of a domestic wood product supplier (Crown homes Ltd., Suzhou, China).

A sandwich-structured specimen was designed. The inner lamination was the test block, whereas the outer laminations were used to apply the force. To manufacture the designed specimen, the dimension lumbers were first double-surface planned into the thinness of 35 mm. Afterward, they were cut into 140 mm-long test blocks and certain-length outer laminations. The laminations were glued together using 1-component polyurethane adhesive (Purbond HB S309) and pressed with a pressure of about 1.0 MPa. After curing, the outer layers were cut into the designed shape as shown in Figure 1. The length and the shape of the outer laminations were designed to ensure that the applied load passed through the center of the test block. The inclination angle of the specimen was 17°.

The wood of the specimens had an average density of 459 kg/m³ and an average moisture content of 11.4%. The test blocks made from dimension lumber with dimensions of 50 mm × 100 mm, 50 mm × 150 mm, and 50 mm × 200 mm were labeled as I, II, and III, respectively. These test blocks (I, II, and III) had aspect ratios of 89:35 (2.54:1), 140:35 (4:1), and 184:35 (25.26:1), respectively. The grain modes, represented by the angle β between the tangential and the loading directions, were labeled as 0°, 45°, 90°, respectively, as shown in Figure 2. Therefore, the specimens were denoted with the aspect ratio and grain pattern. For example, I-45 indicates that the aspect ratio of the test block is 89:35 and the angle β is 45°.

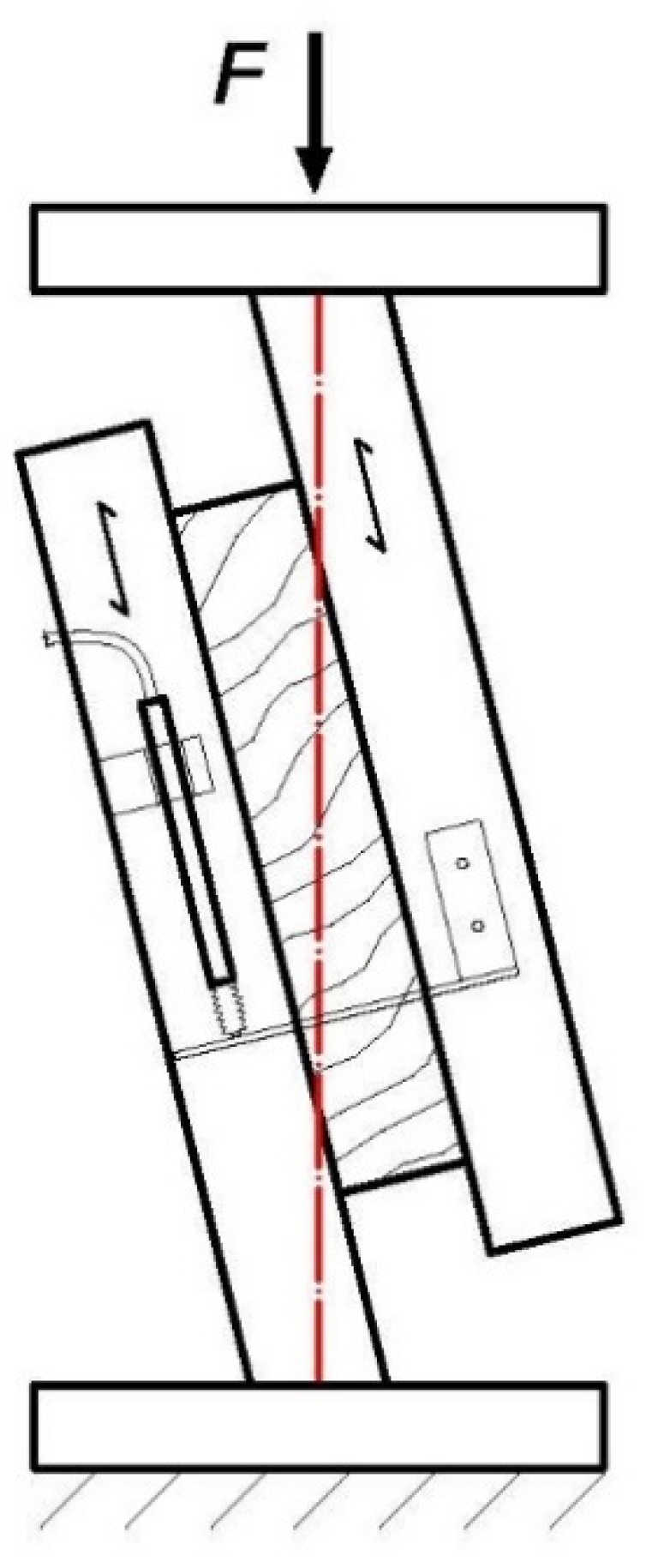
2.2. Methods

There is a variety of testing methods available to determine the rolling shear modulus and strength. However, there are still no widely accepted standardized test configurations and methods. In this study, the test configuration given in the Chinese standard “Cross Laminated Timber (LY/T 3039-2018)” [12] was adopted. It is equivalent to the test configuration given in EN 408 [13] and considers the modifications suggested by Mestek [14].

As shown in Figure 3, the compressive load was applied to the outer lamination of the specimen to provide uniform shear stress in the test block. The specimen was designed and placed in a way to ensure the passage of the load path through the geometric center of the test block. The tests were performed by a universal test machine (Instron 5512, Beijing, China) with a loading rate of 0.5 mm/min. LVDTs were attached to the outer laminations using specially designed clips to measure the relative displacement between the 2 outer laminations. To protect the LVDT, it was removed at about 50% of the estimated ultimate load of the specimen. The load and displacement were recorded by the test machine at a frequency of 5 Hz. The attained data were used to determine the apparent rolling shear modulus (${\check{G}}_{rt}$) and the rolling shear strength (${\tau }_{rt}$). ${\check{G}}_{rt}$ and ${\tau }_{rt}$ can be calculated by Equations (1) and (2), respectively.

$${\check{G}}_{rt}=\frac{t\cos 17°}{Lw}\times k$$

(1)

$${\tau }_{rt}=P_{\max }\times \cos 17°/\left(Lw\right)$$

(2)

where t, L, and w are the thickness, length, and width of the test block or the cross lamination, respectively; k is the slope of the load-deformation curve in the linear range; and $P_{\max }$ is the ultimate load.

3. Results and Discussion

3.1. Failure Modes

For 89 mm × 35 mm specimens (Groups I-0, I-45 and I-90), the failure modes of the specimens with 0° and 90° grain angles were similar. Cracks initiated and propagated parallel to the load path and near the glue line (Figure 4a,b). Furthermore, the crack of the specimens of Group I-0 seemed smoother than that of the specimens of Group I-90. The crack in the case of Group I-90 deviated from the initial path and extended along the growth ring (Figure 4c). For the specimens of Group I-45, the crack propagated about 45° to the load path (parallel or perpendicular to the wood grain) (Figure 4d).

The failure of the specimens with larger aspect ratios (Groups II and III) was similar to that of Group I. However, some differences were found due to the deviation of the grain angles of the test blocks from the designed angle considering that the test blocks were full-sized specimens cut from dimension lumbers. As an example, photos of the specimen of Group II-45 (Figure 5a) and Group III-0 (Figure 5b) are presented. As can be seen in Figure 5a, the directions of cracks varied with the grain angles. However, all the cracks were about 45° to the load path. For the specimen of Group III-0, the crack first propagated parallel to the glue line. Afterward, it propagated along the growth ring because the grain was not perfectly parallel to the loading direction.

3.2. Rolling Shear Modulus and Strength

A summary of the rolling shear strength and rolling shear modulus of all the test groups is listed in

Table 1. The apparent rolling shear modulus and rolling shear strength of different configurations.

Group	Apparent Rolling Shear Modulus ${\check{\mathit{G}}}_{\mathit{r}\mathit{t}}$			Rolling Shear Strength ${\mathit{\tau }}_{\mathit{r}\mathit{t}}$
	Average (MPa)	COV	Sig 1	Average (MPa)	COV	Sig
I-0	64.9	0.40	ab	1.26	0.38	ab
I-45	94.9	0.24	a	1.00	0.18	a
I-90	52.2	0.48	b	1.68	0.13	b
II-0	66.5	0.25	ab	1.74	0.12	a
II-45	154.5	0.57	c	1.38	0.39	a
II-90	79.5	0.19	a	1.67	0.17	a
III-0	51.6	0.43	a	1.44	0.11	a
III-45	184.1	0.29	b	1.73	0.16	a
III-90	96.5	0.16	ac	1.82	0.22	a
Average	93.9	0.33	-	1.52	0.21	-

¹ Different letters indicate that the difference of the means is significant at the 0.05 level.

. The mean apparent rolling shear modulus of all the specimens was 93.9 MPa with a coefficient of variation (COV) of 0.33. The mean rolling shear strength was 1.52 MPa with a COV of 0.21. One-way ANOVA at a level of 0.05 was used to compare the statistical differences between the tested values within Groups I, II, and III. The results are listed in Table 1.

Table 1 shows that the apparent rolling shear modulus of the specimen with 45° grain mode was larger than those of 0° and 90° specimens. This finding is in line with other researchers’ results [5,7,8]. In addition, there was an increasing trend with the increase of the aspect ratio. The rolling shear strength increased slightly with the increase of the aspect ratio, as the longer the test block, the less significant the stress concentration [11].

4. Theoretical Work

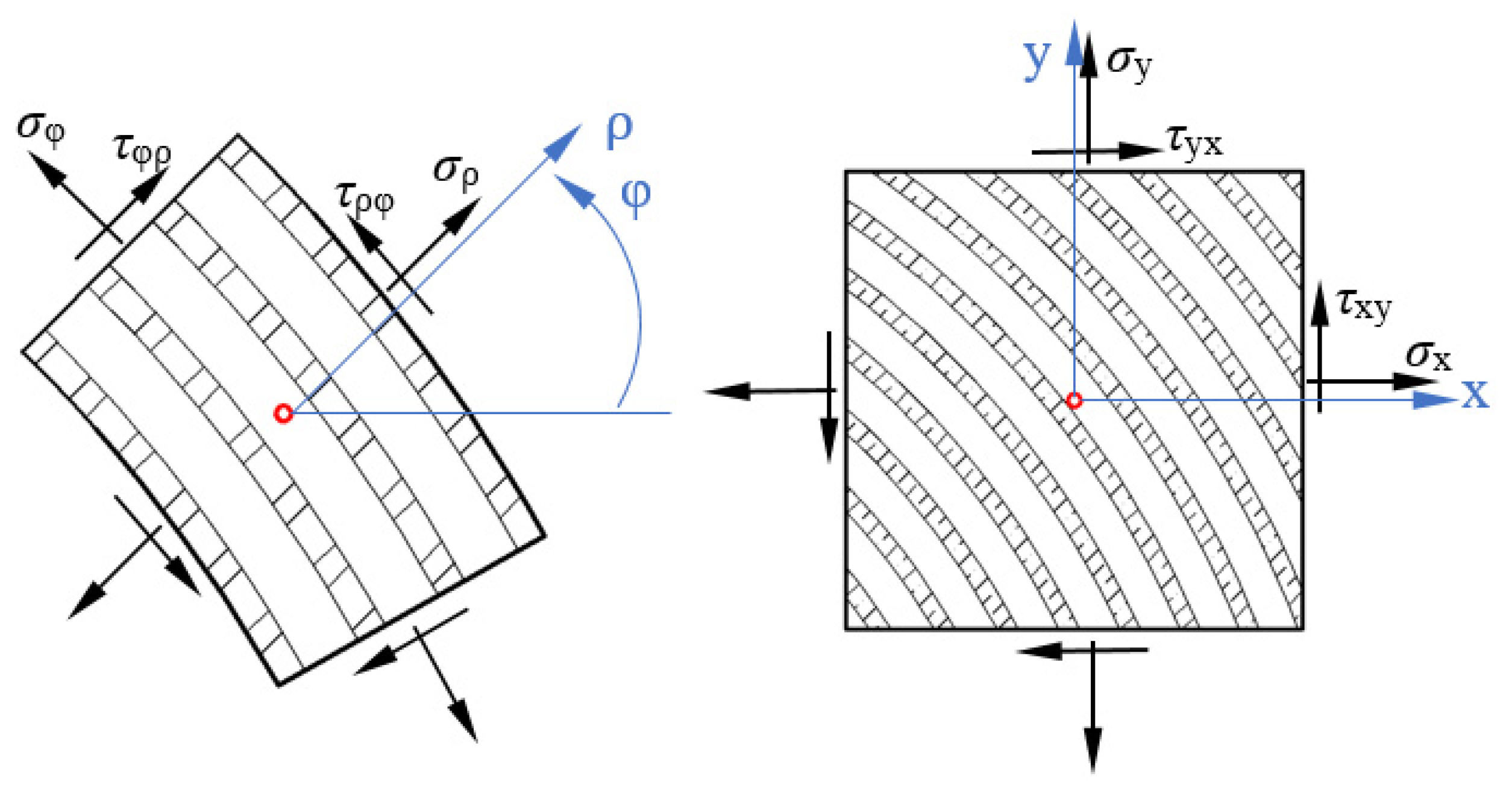
4.1. Mechanism of the Rolling Shear

As a kind of anisotropic biomass material, wood, with its natural growth ring, can be treated as cylindrical anisotropy material [15]. However, due to similarity of the properties in the tangential and radial directions, the grain patterns are usually not traced in swan lumber and lamination-based engineered wood products. Therefore, the wood is often treated as transversely isotropic material [16]. In such a model, tangential and radial directions are both viewed as transverse directions. Eventually, the wood properties are defined and determined in a Cartesian coordinate system. Under currently available standards, there are no requirements on the grain mode of specimen to determine the rolling shear property. In addition, these standards consider the cross section of the test block rectangular. Following the current standards, the rolling shear modulus depends on the grain angle and aspect ratio of the test block. The properties of the rolling shear are closer to the system properties than the material properties of the wood in the Cartesian coordinate system due to the cylindrical distributed growth ring. The properties of rolling shear should be evaluated in the polar coordinate system. The properties of rolling shear in the Cartesian coordinate system can be represented by the properties in the polar coordinate system based on mechanic theory.

For wood, at the same material point, the relationship between stress and strain can be expressed either in the polar coordinate or the Cartesian coordinate system as shown in Figure 6.

The stress–strain relationship for wood in the polar coordinate system is given by Equation (3) [17].

$${\sigma }_{ij}=D_{ijkl}{\epsilon }_{kl}$$

(3)

where ${\sigma }_{ij}$ and ${\epsilon }_{ij}$ are the stress and strain tensors, respectively, whereas $D_{ijkl}$ is the elasticity tensor.

For radial-tangential 2D problem, Equation (3) can be rewritten with the stress and strain components in Voigt notation as shown in Equation (4) [18].

$$\left\{\begin{array}{c}{\sigma }_{\rho }\\ {\sigma }_{\phi }\\ {\tau }_{\rho \phi }\end{array}\right\}=\left[\begin{array}{ccc}\frac{-E_{\rho }}{{\nu }_{\rho \phi }{\nu }_{\phi \rho }-1}& \frac{-E_{\rho }{\nu }_{\phi \rho }}{{\nu }_{\rho \phi }{\nu }_{\phi \rho }-1}& 0\\ \frac{-E_{\phi }{\nu }_{\rho \phi }}{{\nu }_{\rho \phi }{\nu }_{\phi \rho }-1}& \frac{-E_{\phi }}{{\nu }_{\rho \phi }{\nu }_{\phi \rho }-1}& 0\\ 0& 0& 2G_{rt}\end{array}\right]\left\{\begin{array}{c}{\epsilon }_{\rho }\\ {\epsilon }_{\phi }\\ {\epsilon }_{\rho \phi }\end{array}\right\}$$

(4)

Or simply written as shown in Equation (5).

$$\sigma =\mathit{D} \epsilon$$

(5)

where σ and ε are the stress and strain vectors, respectively, whereas D is the elasticity matrix.

The strain stress relationship for wood in the Cartesian coordinate system can be written as shown in Equation (6).

$$\check{\sigma }=\check{\mathit{D}} \check{\epsilon }$$

(6)

where $\check{\sigma }$ and $\check{\epsilon }$ are the stress and strain vectors, and $\check{\mathit{D}}$ is the elasticity matrix in the Cartesian coordinate system.

Without loss of generality, the angle between the x-axis and the ρ-axis is taken as β. The stress–strain relationship for wood in the Cartesian coordinate system and the polar coordinate system can be established by the rotation matrix T, which depends on β. To define the rotation matrix, m and n are defined as the cosine and sine of β.

$$m=\cos \beta$$

(7)

$$n=\sin \beta$$

(8)

Afterward, the stress and strain in the Cartesian coordinate system can be represented by the corresponding components by Equations (9) and (10).

$$\sigma =\mathit{T}\check{\sigma }$$

(9)

$$\epsilon =\mathit{T}\check{\epsilon }$$

(10)

where T is a rotation matrix defined by Equation (11).

$$\mathit{T}=\left[\begin{array}{ccc}{m}^2& n^2& -2mn\\ n^2& m^2& 2mn\\ mn& -mn& m^2-n^2\end{array}\right]$$

(11)

Therefore, the stress–strain relationship in the Cartesian coordinate system can be expressed by the elasticity constants given in Equation (4), as shown in Equation (12).

$$\sigma =\mathit{T}\check{\mathit{D}}{\mathit{T}}^{-1}\epsilon$$

(12)

where D is given by Equation (13).

$$\mathit{D}=\mathit{T}\check{\mathit{D}}{\mathit{T}}^{-1}$$

(13)

and D can be written as shown in Equation (14).

$$\mathit{D}=\left[\begin{array}{ccc}{d}_{11}& d_{12}& d_{13}\\ d_{21}& d_{22}& d_{23}\\ d_{31}& d_{32}& 2d_{33}\end{array}\right]$$

(14)

where every element can be determined, in which

$$d_{33}={\check{G}}_{rt}=G_{rt}\cos 2\beta -\frac{{\sin }^2\beta {\cos }^2\beta }{\frac{E_t}{E_r}{\nu }_{rt}^2-1}\left(E_r+E_t-2E_t{\nu }_{rt}\right)$$

(15)

Thus, d₃₃ can be considered as the apparent or equivalent rolling shear modulus (${\check{G}}_{rt}$). From Equation (15), ${\check{G}}_{rt}$ is a function of the pure shear modulus ($G_{rt}$), modulus of elasticity ($E_t), (E_r)$, Poisson’s ratio, (${\nu }_{rt}$), and the angle β. ${\check{G}}_{rt}$ is the same as $G_{rt}$ when β is equal to 0° or 90°. Thus, the rolling shear moduli determined from 0° and 90° specimens are the pure rolling shear moduli.

4.2. Relationship of Grain and Rolling Shear Modulus

Based on Equation (15), the apparent rolling shear modulus is a function of the grain angle. Therefore, the apparent rolling shear moduli of groups I, II, and III were predicted based on the pure rolling shear modulus, which is the average rolling shear moduli of grain mode 0° and 90°. As shown in Figure 7, the apparent rolling shear modulus increased with the increase of the grain angle. It reached the maximum at an angle of 45°. Afterward, it decreased with the increase of the grain angle. However, at the angle of 90°, it was equal to the pure rolling shear modulus.

The rolling shear moduli of different groups from the test are also marked in Figure 7. The test results basically follow the predicted trend. However, the values are not the same as the predicted ones. Two probable reasons are behind this phenomenon. First, the test block is a full-sized specimen, not clear wood. As wood is a kind of biomaterial, there were potential defects distributed in the test block. The coefficient of variance (COV) of the mechanical properties of timber is large. For No. 2 visually graded dimension lumber, the COVs of bending and compression strength are more than 0.41 [19]. For rolling shear modulus, the COV is even lager, as reported by Flaig [20], and can reach as high as 0.74. Considering the limited replicates and large COV, the test results may deviate from the prediction. Second, the shear stress was not uniformly distributed in the test block. Instead, there were concentrations of stresses in the test block. Therefore, the test block was not in pure shearing deformation, and there are other deformations, such as bending. For the specimens with a smaller aspect ratio, the stress concentration and non-shear deformation were severer. Therefore, the measured shear modulus was more like to deviate from the predicted value.

5. Conclusions

The rolling shear properties of the wood were experimentally and theoretically investigated. Based on the experimental investigation, it was found that:

(1)

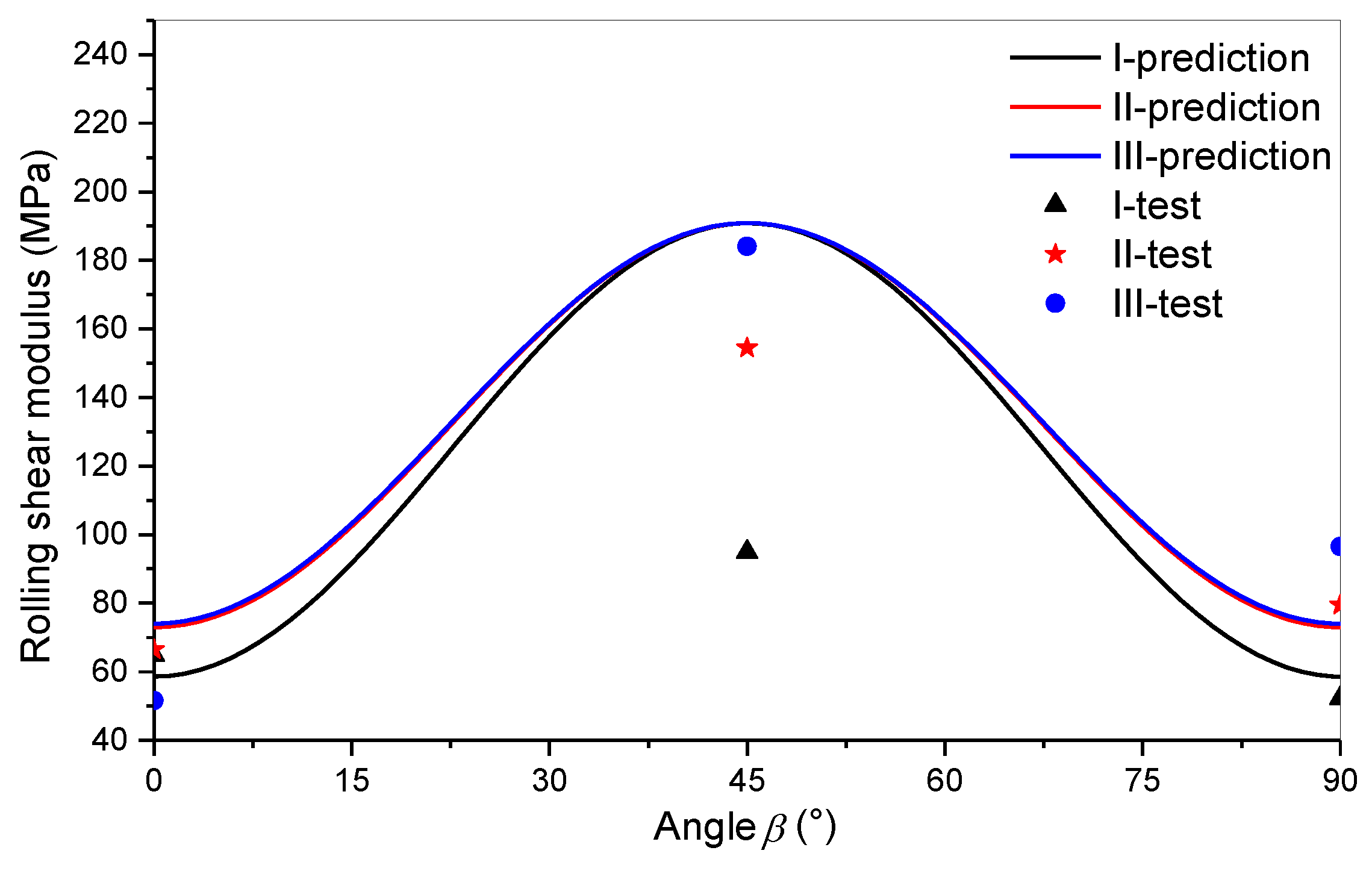
The apparent rolling shear modulus was the largest for the in-between grain-mode specimens (at a grain angle of 45°). However, it had the lowest values for parallel (0°) and right angle (90°) grain-mode specimens.

(2)

The rolling shear strength of the wood increased slightly with the aspect ratio because the stress concentration is very severe in small aspect ratio specimens.

Based on the theoretical investigation, it was found that:

(1)

The rolling shear moduli of 0° and 90° grain-mode of the wood were the same. This value can be called the pure rolling shear modulus.

(2)

The rolling shear moduli of the wood with angles other than 0° and 90° can be calculated from the pure rolling shear modulus and grain angle. Therefore, these moduli can be called the apparent rolling shear moduli.

(3)

Using 0° and 90° grain-mode specimens to determine the pure rolling shear modulus and strength of the wood is recommended.