Analytical Model for the Load-Bearing Capacity Analysis of Winter Forest Roads: Experiment and Estimation
Abstract
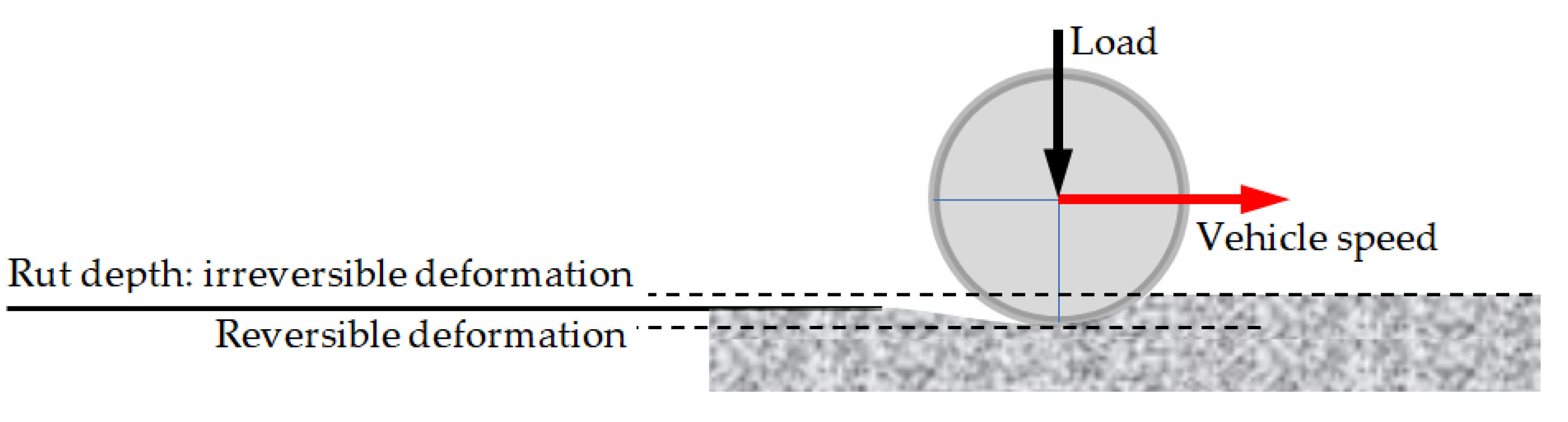
:1. Introduction
2. Methodology
2.1. Degrading Material as a Macro-Object Consisting of Mesoscale Elements
2.2. Hypothesis about the Law of Stiffness Degradation
2.3. Substantiation of the Analytical Relationship between Load and Displacement
3. Results and Comments
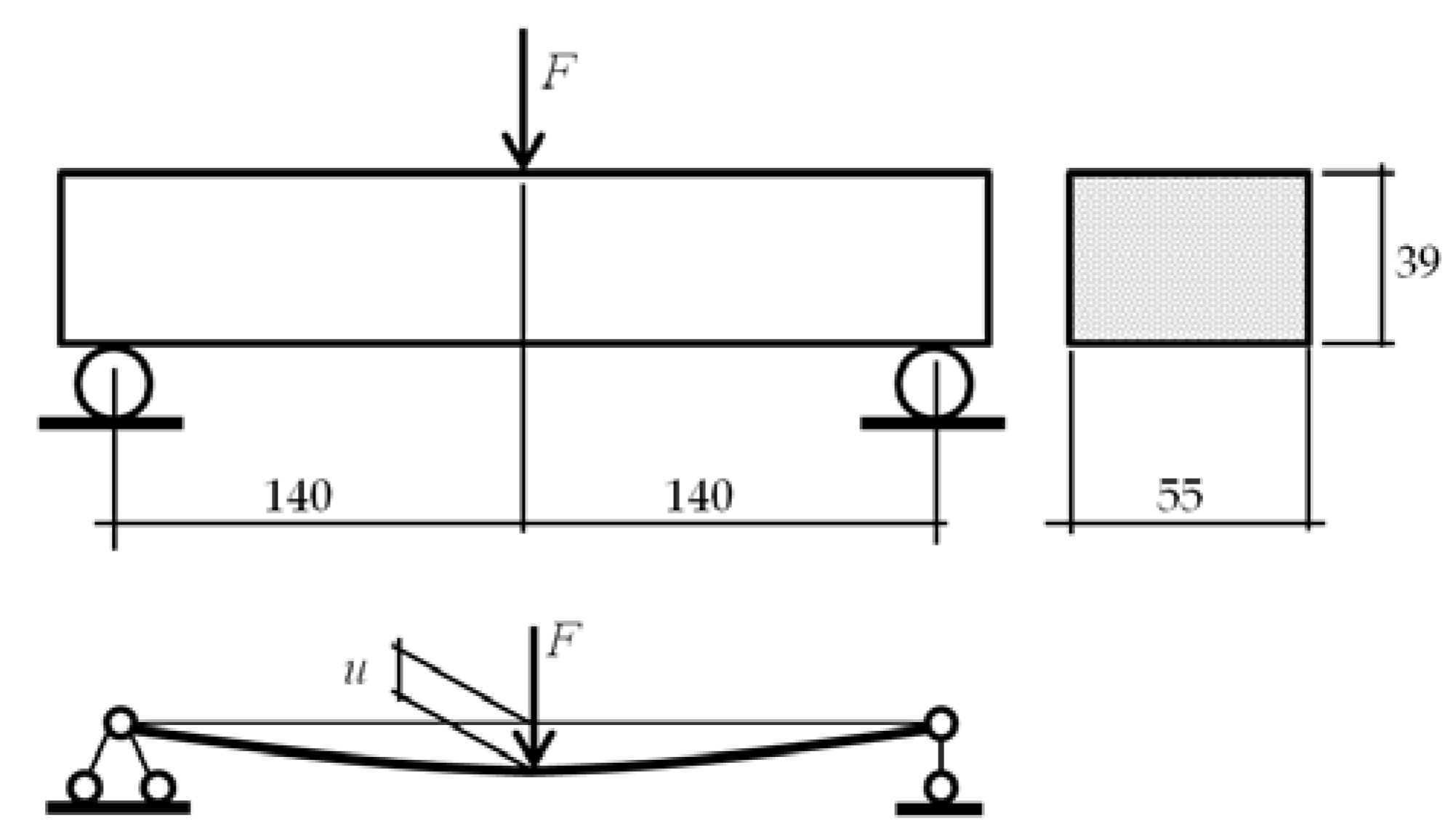
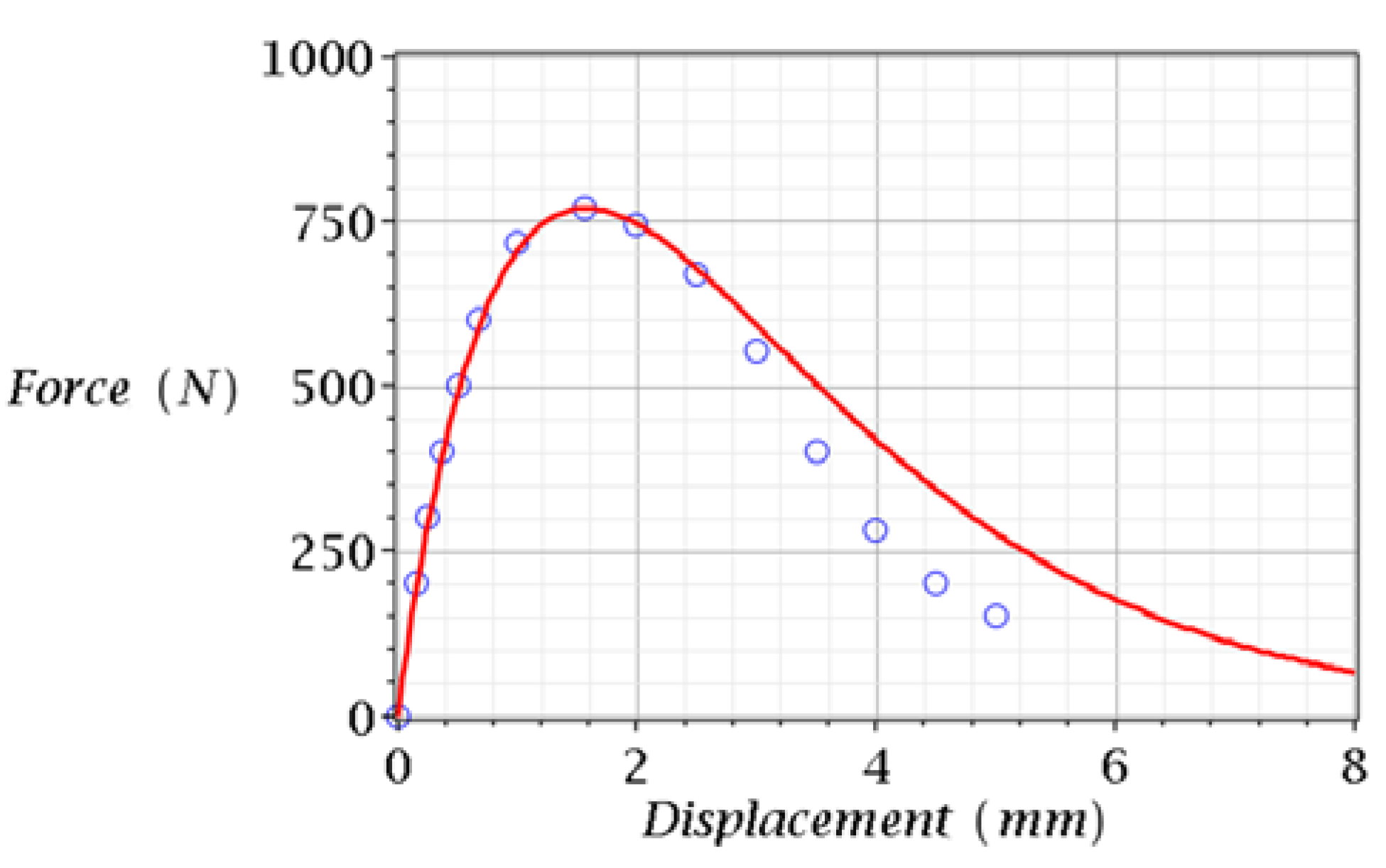
3.1. Comparison of Model and Experimental Data: Bending of a Beam from Frozen Sandy Loam
3.2. Prediction of and Values in Case of Bending
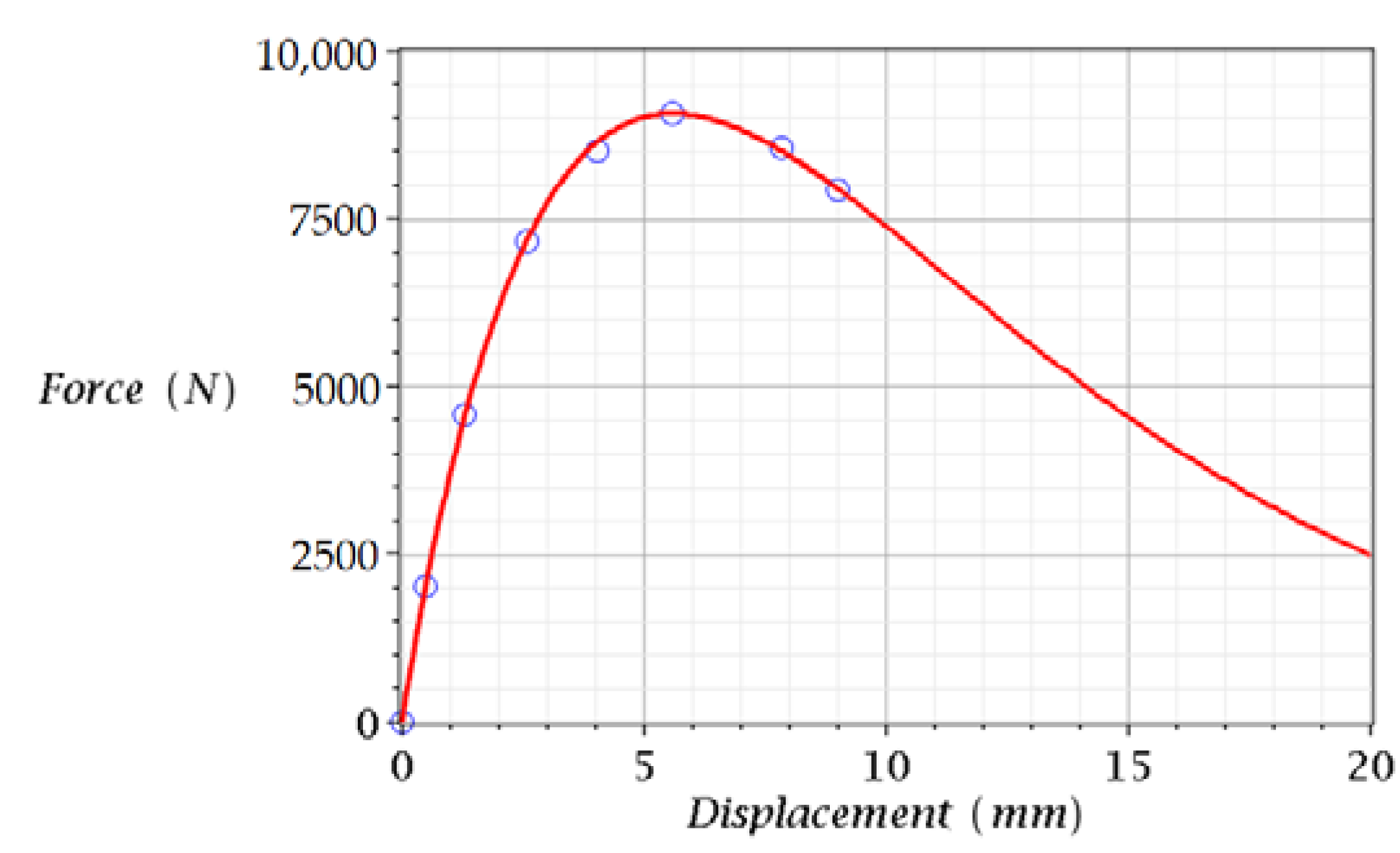
3.3. Comparison of Model and Experimental Data: Uniaxial Compression of Frozen Sandy Soil
3.4. Prediction of and Values under Uniaxial Compression of Frozen Sandy Soil
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kuloglu, T.Z.; Anderson, A.E.; Lieffers, V.J. Cost comparison of non-frozen and frozen forest road construction in changing climates. Int. J. For. Eng. 2021, 32, 103–111. [Google Scholar] [CrossRef]
- Evirgen, B.; Tuncan, M. A physical soil freezing model for laboratory applications. Cold Reg. Sci. Technol. 2019, 159, 29–39. [Google Scholar] [CrossRef]
- Petrovic, J.J. Mechanical properties of ice and snow. J. Mater. Sci. 2003, 38, 1–6. Available online: https://www.researchgate.net/publication/227158247_Review_Mechanical_properties_of_ice_and_snow (accessed on 20 September 2021). [CrossRef]
- Antonson, H.; Buckland, P.; Blomqvist, G. Road Salt Damage to Historical Milestones Indicates Adaptation of Winter Roads to Future Climate Change May Damage Arctic Cultural Heritage. Climate 2021, 9, 149. [Google Scholar] [CrossRef]
- Madsen, S.S.; Pedersen, N.L. Comparison of RAPTOR measurements with falling weight deflectometer deflections using backcalculation. In Eleventh International Conference on the Bearing Capacity of Roads, Railways and Airfields, 1st ed.; Hoff, I., Mork, H., Saba, R., Eds.; CRC Press: London, UK, 2022; Volume 3, pp. 33–44. [Google Scholar] [CrossRef]
- Martin, A.M.; Owende, P.M.O.; O’Mahony, M.J.; Ward, S.M. Estimation of the serviceability of forest access roads. J. For. Eng. 1999, 10, 55–61. [Google Scholar] [CrossRef]
- Uglova, E.V.; Tiraturyan, A.N.; Liapin, A.A. Integrated approach to studying characteristics of dynamic deformation on flexible pavement surface using nondestructive testing. PNRPU Mech. Bull. 2016, 2, 111–130. [Google Scholar] [CrossRef]
- Kaakkurivaara, T.; Vuorimies, N.; Kolisoja, P.; Uusitalo, J. Applicability of portable tools in assessing the bearing capacity of forest roads. Silva Fenn. 2015, 49, 1239. [Google Scholar] [CrossRef]
- Gavrilov, T.A.; Kolesnikov, G.N. Evolving crack influence on the strength of frozen sand soils. Mag. Civ. Eng. 2020, 2, 54–64. [Google Scholar] [CrossRef]
- Hwang, B.; Cho, W. The Effect of Fines and Temperature on the Mode I Fracture Characteristics of the Frozen Sand. Adv. Civ. Eng. 2022, 2022, 9917378. [Google Scholar] [CrossRef]
- Chen, J.; Wang, L.; Yao, Z. Physical and mechanical performance of frozen rocks and soil in different regions. Adv. Civ. Eng. 2020, 2020, 8867414. [Google Scholar] [CrossRef]
- Cornetti, P.; Pugno, N.; Carpinteri, A.; Taylor, D. Finite fracture mechanics: A coupled stress and energy failure criterion. Eng. Fract. Mech. 2006, 73, 2021–2033. [Google Scholar] [CrossRef]
- Wei, S.; Tao, Y.; Ying, G.; Zhichao, X.; Chengcheng, Z. Establishment and Experimental Verification of Stress-Temperature Coupled Damage Model of Warm Frozen Soil. Geofluids 2022, 2022, 5101425. [Google Scholar] [CrossRef]
- Liu, D.; He, M.; Cai, M. A damage model for modeling the complete stress–strain relations of brittle rocks under uniaxial compression. Int. J. Damage Mech. 2018, 27, 1000–1019. [Google Scholar] [CrossRef]
- Zhang, F.; Zhu, Z.; Fu, T.; Jia, J. Damage mechanism and dynamic constitutive model of frozen soil under uniaxial impact loading. Mech. Mater. 2020, 140, 103217. [Google Scholar] [CrossRef]
- Xu, J.J.; Tang, C.S.; Cheng, Q.; Xu, Q.L.; Inyang, H.I.; Lin, Z.Y.; Shi, B. Investigation on desiccation cracking behavior of clayey soils with a perspective of fracture mechanics: A review. J. Soils Sediments 2021, 22, 859–888. [Google Scholar] [CrossRef]
- Mohammadnejad, M.; Liu, H.; Chan, A.; Dehkhoda, S.; Fukuda, D. An overview on advances in computational fracture mechanics of rock. Geosystem Eng. 2021, 24, 206–229. [Google Scholar] [CrossRef]
- Makarov, P.V. Evolutionary nature of structure formation in lithospheric material: Universal principle for fractality of solids. Russ. Geol. Geophys. 2007, 48, 558–574. [Google Scholar] [CrossRef]
- Smolin, I.Y.; Eremin, M.O.; Makarov, P.V.; Buyakova, S.P.; Kul’kov, S.N.; Evtushenko, E.P. Numerical modelling of mechanical behaviour of model brittle porous materials at the mesoscale. Tomsk. State Univ. J. Math. Mech. 2013, 5, 78–90. Available online: http://mi.mathnet.ru/eng/vtgu/y2013/i5/p78 (accessed on 20 August 2021).
- Kolesnikov, G. Analysis of Concrete Failure on the Descending Branch of the Load-Displacement Curve. Crystals 2020, 10, 921. [Google Scholar] [CrossRef]
- Kolesnikov, G.; Gavrilov, T. Sandstone Modeling under Axial Compression and Axisymmetric Lateral Pressure. Symmetry 2022, 14, 796. [Google Scholar] [CrossRef]
- Baldwin, R.; North, M.A. Stress-strain curves of concrete at high temperature—A review. Fire Saf. Sci. 1969, 785, 1. Available online: http://www.iafss.org/publications/frn/785/-1/view/frn_785.pdf (accessed on 31 March 2022).
- Stojković, N.; Perić, D.; Stojić, D.; Marković, N. New stress-strain model for concrete at high temperatures. Teh. Vjesn. 2017, 24, 863–868. [Google Scholar] [CrossRef]
- Aksenov, V.I.; Gevorkyan, S.G.; Doroshin, V.V. Dependence of Strength and Physical Properties of Frozen Sands on Moisture Content. Soil Mech. Found. Eng. 2018, 54, 420–424. [Google Scholar] [CrossRef]
- Li, K.; Li, Q.; Liu, C. Impacts of Water Content and Temperature on the Unconfined Compressive Strength and Pore Characteristics of Frozen Saline Soils. KSCE J. Civ. Eng. 2022, 26, 1652–1661. [Google Scholar] [CrossRef]
- Zhao, Y.; Han, Y.; Chen, C.; Seo, H. Crack Detection in Frozen Soils Using Infrared Thermographic Camera. Sensors 2022, 22, 885. [Google Scholar] [CrossRef] [PubMed]
- Zuan, P.; Yang, L.; Fei, L. Particle breakage behavior in frozen sands during triaxial shear tests based on the energy principle. Cold Reg. Sci. Technol. 2022, 199, 103571. [Google Scholar] [CrossRef]
- Hu, F.; Li, Z.; Tian, Y.; Hu, R. Failure Patterns and Morphological Soil–Rock Interface Characteristics of Frozen Soil–Rock Mixtures under Compression and Tension. Appl. Sci. 2021, 11, 461. [Google Scholar] [CrossRef]
- Gaspar, G.; Dudak, J.; Behulova, M.; Stremy, M.; Budjac, R.; Sedivy, S.; Tomas, B. IoT-Ready Temperature Probe for Smart Monitoring of Forest Roads. Appl. Sci. 2022, 12, 743. [Google Scholar] [CrossRef]
- Blagojević, M.; Pešić, D.; Mijalković, M.; Glišović, S. Unique function for describing stress and strain behaviour of fire-affected concrete [Jedinstvena funkcija za opisivanje naprezanja i deformacije betona u požaru]. Gradjevinar 2011, 63, 19–24. Available online: https://hrcak.srce.hr/64221 (accessed on 20 August 2021).
- He, S.-H.; Zhang, Q.-F.; Ding, Z.; Xia, T.-D.; Gan, X.-L. Experimental and Estimation Studies of Resilient Modulus of Marine Coral Sand under Cyclic Loading. J. Mar. Sci. Eng. 2020, 8, 287. [Google Scholar] [CrossRef]
- Xia, P.; Shao, L.; Deng, W.; Zeng, C. Evolution Prediction of Hysteresis Behavior of Sand under Cyclic Loading. Processes 2022, 10, 879. [Google Scholar] [CrossRef]
- Tsuha, C.D.H.C.; Foray, P.Y.; Jardine, R.J.; Yang, Z.X.; Silva, M.; Rimoy, S. Behaviour of displacement piles in sand under cyclic axial loading. Soils Found. 2012, 52, 393–410. [Google Scholar] [CrossRef]
- Liu, Y.; Dai, F. A review of experimental and theoretical research on the deformation and failure behavior of rocks subjected to cyclic loading. J. Rock Mech. Geotech. Eng. 2021, 13, 1203–1230. [Google Scholar] [CrossRef]
- Bergman, R.; Sahoo, K.; Englund, K.; Mousavi-Avval, S.H. Lifecycle Assessment and Techno-Economic Analysis of Biochar Pellet Production from Forest Residues and Field Application. Energies 2022, 15, 1559. [Google Scholar] [CrossRef]
- O’Mahony, M.J.; Ueberschaer, A.; Owende, P.M.O.; Ward, S.M. Bearing capacity of forest access roads built on peat soils. J. Terramechanics 2000, 37, 127–138. [Google Scholar] [CrossRef]
- Ovaskainen, H.; Riekki, K. Computation of Strip Road Networks Based on Harvester Location Data. Forests 2022, 13, 782. [Google Scholar] [CrossRef]




| Point Selection Options 1 and 2 | (mm) | (mm) | (N) | (N) | (mm) | (N) |
|---|---|---|---|---|---|---|
| Indirect measurements: | ||||||
| 1 | 0.163 | 0.259 | 200 | 300 | 1.667 (105%) | 829 (108%) |
| 2 | 0.163 | 0.375 | 200 | 400 | 1.514 (96%) | 761 (99%) |
| 3 | 0.259 | 0.375 | 300 | 400 | 1.407 (89%) | 721 (94%) |
| Average values: | 1.529 (97%) | 770 (100%) | ||||
| Direct measurements 1: | 1.574 (100%) | 769 (100%) | ||||
| Point Selection Options 1 and 2 | (mm) | (mm) | (N) | (N) | (mm) | (N) |
|---|---|---|---|---|---|---|
| Indirect measurements: | ||||||
| 1 | 0.486 | 1.292 | 2018 | 4560 | 4.926 (114%) | 8313 (109%) |
| 2 | 0.486 | 2.609 | 2018 | 7140 | 5.082 (110%) | 8549 (106%) |
| 3 | 1.292 | 2.609 | 4560 | 7140 | 5.182 (108%) | 8631 (105%) |
| Average values: | 5.063 (111%) | 8498 (107%) | ||||
| Direct measurements 1: | 5.604 (100%) | 9061 (100%) | ||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Katarov, V.; Syunev, V.; Kolesnikov, G. Analytical Model for the Load-Bearing Capacity Analysis of Winter Forest Roads: Experiment and Estimation. Forests 2022, 13, 1538. https://doi.org/10.3390/f13101538
Katarov V, Syunev V, Kolesnikov G. Analytical Model for the Load-Bearing Capacity Analysis of Winter Forest Roads: Experiment and Estimation. Forests. 2022; 13(10):1538. https://doi.org/10.3390/f13101538
Chicago/Turabian StyleKatarov, Vasily, Vladimir Syunev, and Gennady Kolesnikov. 2022. "Analytical Model for the Load-Bearing Capacity Analysis of Winter Forest Roads: Experiment and Estimation" Forests 13, no. 10: 1538. https://doi.org/10.3390/f13101538
APA StyleKatarov, V., Syunev, V., & Kolesnikov, G. (2022). Analytical Model for the Load-Bearing Capacity Analysis of Winter Forest Roads: Experiment and Estimation. Forests, 13(10), 1538. https://doi.org/10.3390/f13101538






