G×E Analysis of Early Growth Traits of Populus deltoides in East China by Using BLUP-GGE
Abstract
1. Introduction
2. Materials and Methods
2.1. Test Sites and Conditions
2.2. Test Design
2.3. Statistical Analysis
3. Results
3.1. Genetic Variation Analysis of Tree Height and DBH
3.2. Mixed Linear Model Test for Tree Height and DBH
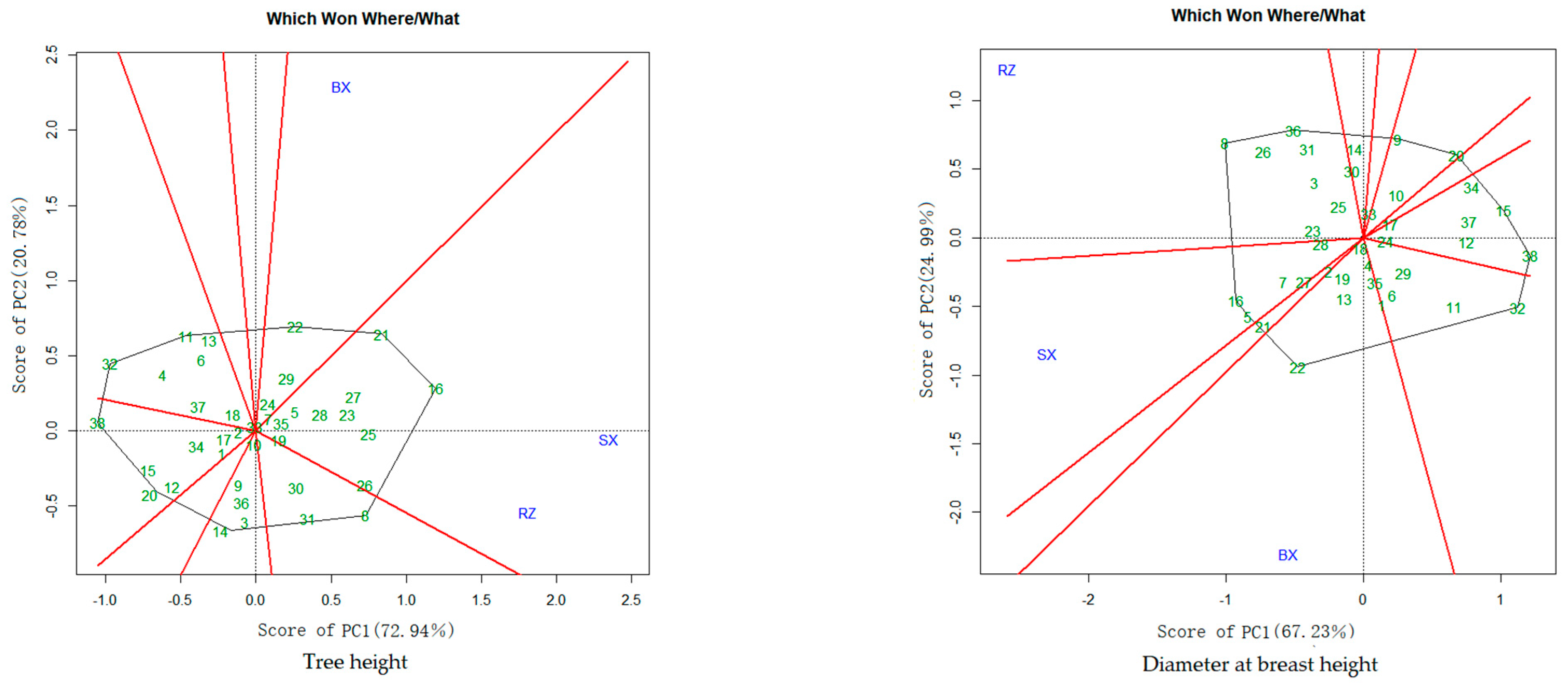
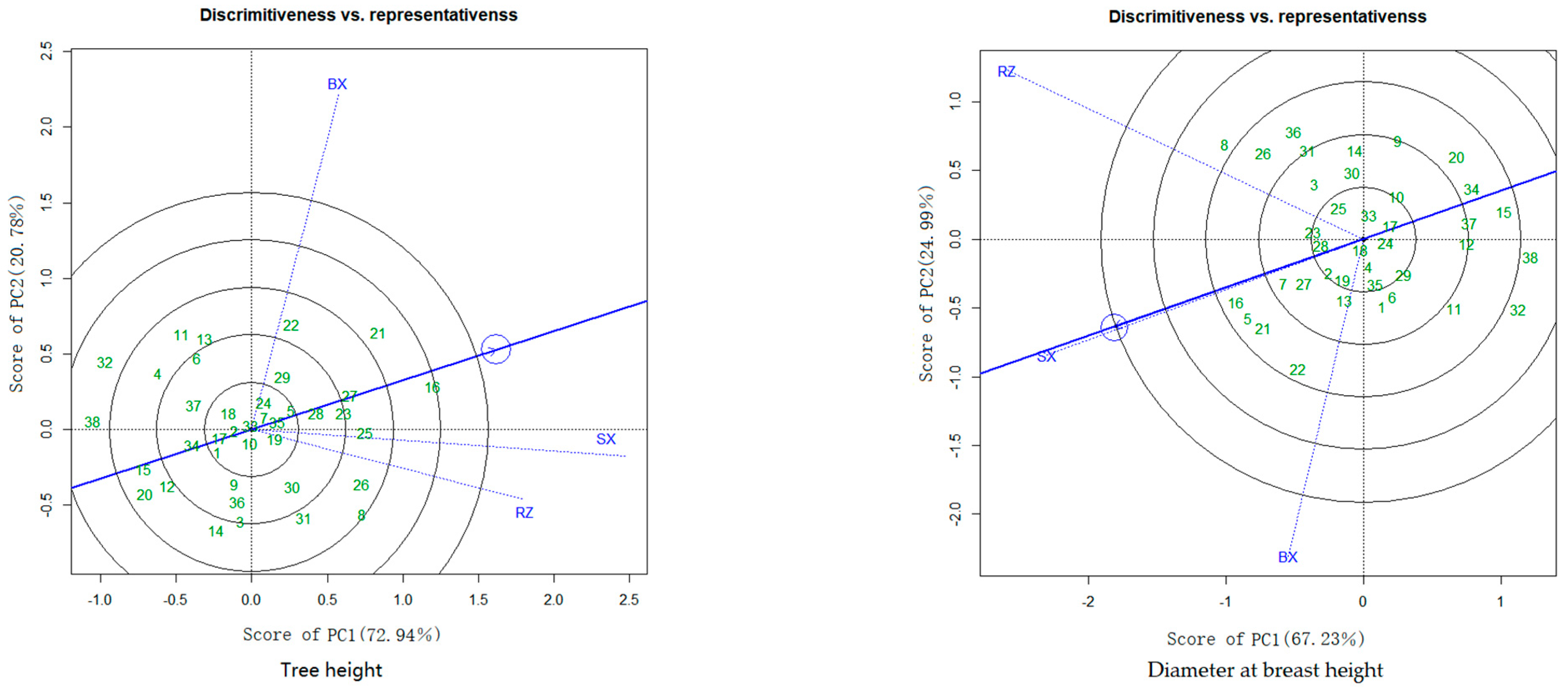
3.3. BLUP-GGE Analysis for Tree Height and DBH
3.3.1. Group of the Locations and Optimal Genotypes for Each Location
3.3.2. Discrimination and Representativeness of the Trial Sites
3.3.3. High Yield and Stability
3.4. High DBH Yield of Genotypes
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Stobrawa, K. Poplars (Populus spp.): Ecological role, applications and scientific perspectives in the 21st century. Balt. For. 2014, 20, 204–213. [Google Scholar]
- Richardson, J.; Isebrands, J.G. Multiple social and environmental benefits of poplars and willows-Mini Review. CABI Rev. 2014, 2013, 1–3. [Google Scholar] [CrossRef]
- Kumar, D.; Singh, N.B. Age-age correlation for early selection of clones of Populus in India. Silvae Genet. 2001, 50, 103–107. [Google Scholar]
- Kaczmarek, D.J.; Coyle, D.R.; Coleman, M.D. Survival and growth of a range of Populus clones in central South Carolina USA through age ten: Do early assessments reflect longer-term survival and growth trends? Biomass Bioenerg. 2013, 49, 260–272. [Google Scholar] [CrossRef]
- Li, Y.; Suontama, M.; Burdon, R.D.; Dungey, H.S. Genotype by environment interactions in forest tree breeding: Review of methodology and perspectives on research and application. Tree Genet. Genomes 2017, 13, 60. [Google Scholar] [CrossRef]
- Romagosa, I.; Fox, R.N. Genotype × environment interaction and adaptation; Principles and prospects. In Plant Breeding; Springer: Berlin, Germany, 1993; pp. 373–390. [Google Scholar]
- Yan, W. GGEbiplot—A Windows application for graphical analysis of multienvironment trial data and other types of two-way data. Agron. J. 2001, 93, 1111–1118. [Google Scholar] [CrossRef]
- Yan, W.K. Optimal use of biplots in analysis of multi-location variety test data. Acta Agron. Sin. 2010, 36, 1805–1819. [Google Scholar]
- Liu, N.; Ding, C.; Li, B.; Ding, M.; Su, X.; Huang, Q. Analysis of the Genotype Interaction of Four-Year-Old Populus euramericana Using the BLUP-GGE Technique. Forests 2021, 12, 1759. [Google Scholar] [CrossRef]
- Yan, W.; Rajcan, I. Biplot analysis of test sites and trait relations of soybean in Ontario. Crop Sci. 2002, 42, 11–20. [Google Scholar] [CrossRef]
- Sun, J.; Jiao, W.; Wang, Q.; Wang, T.; Yang, H.; Jin, J.; Feng, H.; Guo, J.; Feng, L.; Xu, X.; et al. Potential habitat and productivity loss of Populus deltoides industrial forest plantations due to global warming. For. Ecol. Manag. 2021, 496, 119474. [Google Scholar] [CrossRef]
- Butler, D.G.; Cullis, B.R.; Gilmour, A.R.; Gogel, B.J.; Thompson, R. ASReml-R Reference Manual Version 4; VSN International Ltd.: Hemel Hempstead, UK, 2017; pp. 8–81. [Google Scholar]
- Avola, G.; Riggi, E.; Gresta, F.; Sortino, O.; Onofri, A. Random effects models, BLUPs and redundancy analyses for grain legume crops in semi-arid environments. Eur. J. Agron. 2018, 93, 18–26. [Google Scholar] [CrossRef]
- Isik, F.; Holland, J.; Maltecca, C. Genetic Data Analysis for Plant and Animal Breeding; Springer International Publishing: Cham, Switzerland, 2017. [Google Scholar]
- Silva, G.A.P.; Gezan, S.A.; de Carvalho, M.P.; Gouvêa, L.R.L.; Verardi, C.K.; de Oliveira, A.L.; Gonçalves, P.S. Genetic parameters in a rubber tree population: Heritabilities, genotype-by-environment interactions and multi-trait correlations. Tree Genet. Genomes 2014, 10, 1511–1518. [Google Scholar] [CrossRef]
- Yan, W.; Kang, M.S. Gge Biplot Analysis: A Graphical Tool for Breeders, Geneticists, and Agronomists; CRC Press: Boca Raton, FL, USA, 2002. [Google Scholar]
- Kätzel, R. Conservation of forest genetic resources: The basis for adaptability in managed forests. In Sustainable Forest Management in a Changing World; Springer: Berlin, Germany, 1993; pp. 93–114. [Google Scholar]
- Burdon, R.D. Genetic diversity and disease resistance: Some considerations for research, breeding, and deployment. Can. J. Forest Res. 2001, 31, 596–606. [Google Scholar] [CrossRef]
- Yanchuk, A.D.; Jaquish, B. Forest genetic resource management: Is there a fit among conservation, breeding and biotechnology? Forest 2003, 780, B4. [Google Scholar]
- Zhao, X.; Hou, W.; Zheng, H.; Zheng, Z. Analyses of genotypic variation in white poplar clones at four sites in China. Silvae Gene 2013, 62, 187–195. [Google Scholar] [CrossRef]
- Zhang, P.; Wu, F.; Kang, X. Genotypic variation in wood properties and growth traits of triploid hybrid clones of Populus tomentosa at three clonal trials. Tree Genet. Genomes 2012, 8, 1041–1050. [Google Scholar] [CrossRef]
- Pliura, A.; Zhang, S.Y.; MacKay, J.; Bousquet, J. Genotypic variation in wood density and growth traits of poplar hybrids at four clonal trials. For. Ecol. Manag. 2007, 238, 92–106. [Google Scholar] [CrossRef]
- Ekomono, C.G.M.; Rambolarimanana, T.; Bouvet, J.M. Preponderance of additive and non-additive variances for growth, ecophysiological and wood traits in Eucalyptus hybrid genotype-by-spacing interaction. Tree Genet. Genomes 2022, 18, 32. [Google Scholar] [CrossRef]
- Ling, J.; Xiao, Y.; Hu, J.; Wang, F.; Ouyang, F.; Wang, J.; Zhang, H. Genotype by environment interaction analysis of growth of Picea koraiensis families at different sites using BLUP-GGE. New For. 2021, 52, 113–127. [Google Scholar] [CrossRef]
- Pliura, A.; Suchockas, V.; Sarsekova, D.; Gudynaitė, V. Genotypic variation and heritability of growth and adaptive traits, and adaptation of young poplar hybrids at northern margins of natural distribution of Populus nigra in Europe. Biomass Bioenerg. 2014, 70, 513–529. [Google Scholar] [CrossRef]
- Lai, M.; Dong, L.; Yi, M.; Sun, S.; Zhang, Y.; Fu, L.; Xu, Z.; Lei, L.; Leng, C.; Zhang, L. Genetic variation, heritability and genotype × environment interactions of resin yield, growth traits and morphologic traits for Pinus elliottii at three progeny trials. Forests 2017, 8, 409. [Google Scholar] [CrossRef]
- Xiao, Y.; Ma, W.; Lu, N.; Wang, Z.; Wang, N.; Zhai, W.; Zhai, W.; Kong, L.; Qu, G.; Wang, Q.; et al. Genetic Variation of Growth Traits and Genotype-by-Environment Interactions in Clones of Catalpa bungei and Catalpa fargesii f. duclouxii. Forests 2019, 10, 57. [Google Scholar] [CrossRef]
- Yuan, C.; Zhang, Z.; Jin, G.; Zheng, Y.; Zhou, Z.; Sun, L.; Tong, H. Genetic parameters and genotype by environment interactions influencing growth and productivity in Masson pine in east and central China. For. Eco. Mana. 2021, 487, 118991. [Google Scholar] [CrossRef]
- Wang, R.; Hu, D.; Zheng, H.; Yan, S.; Wei, R. Genotype × nvironmental interaction by AMMI and GGE biplot analysis for the provenances of Michelia chapensis in South China. J. For. Res. 2016, 27, 659–664. [Google Scholar] [CrossRef]
- Namkoong, G.; Kang, H.C.; Brouard, J.S. Tree Breeding: Principles and Strategies: Principles and Strategies; Springer Science & Business Media: Berlin, Germany, 2012; Volume 11. [Google Scholar]
- Isebrands, J.G.; Richardson, J. Poplars and willows: Trees for Society and the Environment; CABI: Wallingford, UK, 2014; pp. 527–561. [Google Scholar]
- Zhang, S.; Yu, Q.; Chauret, G.; Koubaa, A. Selection for both growth and wood properties in hybrid poplar clones. For. Sci. 2003, 6, 901–908. [Google Scholar]
- Keča, L.; Keča, N. Market potential dynamics for plantation-grown poplar forest products in Serbia. In Proceedings of the International Conference: Reforestation Challenges, Belgrade, Serbia, 3–6 June 2015. [Google Scholar]


| Number | Parents | Number | Parents |
|---|---|---|---|
| 1 | P. deltoides ‘1’ × P. deltoides | 20 | P. deltoides ‘1’ × P. deltoides |
| 2 | P. deltoides ‘1’ × P. deltoides | 21 | P. deltoides ‘1’ × P. deltoides |
| 3 | P. deltoides ‘1’ × P. deltoides | 22 | P. deltoides ‘1’ × P. deltoides |
| 4 | P. deltoides ‘1’ × P. deltoides | 23 | P. deltoides ‘1’ × P. deltoides |
| 5 | P. deltoides ‘1’ × P. deltoides | 24 | P. deltoides ‘3’ × P. deltoides |
| 6 | P. deltoides ‘3’ × P. deltoides | 25 | P. deltoides ‘3’ × P. deltoides |
| 7 | P. deltoides ‘3’ × P. deltoides | 26 | P. deltoides ‘3’ × P. deltoides |
| 8 | P. deltoides ‘4’ × P. deltoides | 27 | P. deltoides ‘2’ × P. deltoides |
| 9 | P. deltoides ‘4’ × P. deltoides | 28 | P. deltoides ‘2’ × P. deltoides |
| 10 | P. deltoides ‘4’ × P. deltoides | 29 | P. deltoides ‘2’ × P. deltoides |
| 11 | P. deltoides ‘0’ × P. deltoides | 30 | P. deltoides ‘8’ × P. deltoides |
| 12 | P. deltoides ‘0’ × P. deltoides | 31 | P. deltoides ‘8’ × P. deltoides |
| 13 | P. deltoides ‘0’ × P. deltoides | 32 | P. deltoides ‘0’ × P. deltoides |
| 14 | P. deltoides ‘6’ × P. deltoides | 33 | P. deltoides ‘0’ × P. deltoides |
| 15 (Zhonghe 1) | P. deltoides cv. ‘Zhonghe 1’ | 34 | P. deltoides ‘0’ × P. deltoides |
| 16 | P. deltoides ‘1’ × P. deltoides | 35 | P. deltoides ‘6’ × P. deltoides |
| 17 | P. deltoides ‘1’ × P. deltoides | 36 | P. deltoides ‘6’ × P. deltoides |
| 18 | P. deltoides ‘1’ × P. deltoides | 37 (I-69) | P. deltoides cv. ‘Lux I-69’ |
| 19 | P. deltoides ‘1’ × P. deltoides | 38 (T-66) | P. deltoides cv. ‘PE-19-66’ |
| Environment Factor | Rizhao (RZ) | Shanxian (SX) | Boxing (BX) |
|---|---|---|---|
| Longitude/E | 119°31′ | 115°91′ | 118°29′ |
| Latitude/N | 35°46′ | 34°66′ | 37°19′ |
| Average annual temperature/°C | 11.6 | 13.9 | 12.5 |
| Maximum monthly average temperature/°C | 23.9 | 27.8 | 26.5 |
| Minimum monthly average temperature/°C | −0.3 | −0.9 | −3.0 |
| Average annual rainfall/mm | 813.0 | 737.1 | 627.3 |
| Average annual sunshine duration/h | 2432.8 | 2388.1 | 2632.5 |
| Agrotype | loam | sandy loam | saline-alkali soil |
| Trait | Site | Mean (±S.E.) | Coefficient of Variation (%) | Repeatability | Heritability | Phenotypic Coefficient of Variation (%) | Coefficient of Genetic Variation (%) |
|---|---|---|---|---|---|---|---|
| H/m | RZ | 11.9 ± 0.08 | 15.4 | 0.95 | 0.56 | 11.2 | 8.4 |
| SX | 19.8 ± 0.12 | 11.8 | 0.96 | 0.66 | 8.8 | 7.1 | |
| BX | 9.0 ± 0.10 | 17.2 | 0.87 | 0.47 | 15.0 | 10.3 | |
| DBH/cm | RZ | 13.4 ± 0.14 | 22.3 | 0.93 | 0.47 | 18.5 | 12.7 |
| SX | 20.1 ± 0.16 | 15.0 | 0.86 | 0.34 | 13.3 | 7.6 | |
| BX | 11.1 ± 0.15 | 21.3 | 0.79 | 0.33 | 19.0 | 10.9 |
| Effect Variable | DBH | Height | ||||||
|---|---|---|---|---|---|---|---|---|
| Df | SSD | Wald | Df | SSD | Wald | |||
| Site | 2 | 583.77 | 583.77 | <2.2 × 10−16 ** | 2 | 1715.7 | 2341.7 | <2.22 × 10−16 ** |
| Residual (MS) | - | 1.0 | - | - | - | 1.0 | - | - |
| Effect Variable | DBH | Height | ||||
|---|---|---|---|---|---|---|
| Variance Component | Standard Error | z Ratio | Variance Component | Standard Error | z Ratio | |
| Block | 0.1083 | 0.1055 | 1.03 | 0.2036 | 0.1703 | 1.20 |
| Genotype | 0.8261 | 0.4411 | 1.87 * | 0.5462 | 0.2417 | 2.26 * |
| G×E | 1.9202 | 0.4527 | 4.24 ** | 0.9467 | 0.2142 | 4.19 ** |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, Z.; Dong, Y.; Liu, N.; Li, S.; Zhang, W.; Wang, Y.; Han, Y.; Zhuang, R.; Zhang, X.; Su, X.; et al. G×E Analysis of Early Growth Traits of Populus deltoides in East China by Using BLUP-GGE. Forests 2022, 13, 1808. https://doi.org/10.3390/f13111808
Yuan Z, Dong Y, Liu N, Li S, Zhang W, Wang Y, Han Y, Zhuang R, Zhang X, Su X, et al. G×E Analysis of Early Growth Traits of Populus deltoides in East China by Using BLUP-GGE. Forests. 2022; 13(11):1808. https://doi.org/10.3390/f13111808
Chicago/Turabian StyleYuan, Zhengsai, Yufeng Dong, Ning Liu, Shanwen Li, Weixi Zhang, Yanping Wang, Youji Han, Ruonan Zhuang, Xiaoyan Zhang, Xiaohua Su, and et al. 2022. "G×E Analysis of Early Growth Traits of Populus deltoides in East China by Using BLUP-GGE" Forests 13, no. 11: 1808. https://doi.org/10.3390/f13111808
APA StyleYuan, Z., Dong, Y., Liu, N., Li, S., Zhang, W., Wang, Y., Han, Y., Zhuang, R., Zhang, X., Su, X., Ding, C., & Liu, G. (2022). G×E Analysis of Early Growth Traits of Populus deltoides in East China by Using BLUP-GGE. Forests, 13(11), 1808. https://doi.org/10.3390/f13111808







