Modeling Tree Growth Responses to Climate Change: A Case Study in Natural Deciduous Mountain Forests
Abstract
1. Introduction
2. Materials and Methods
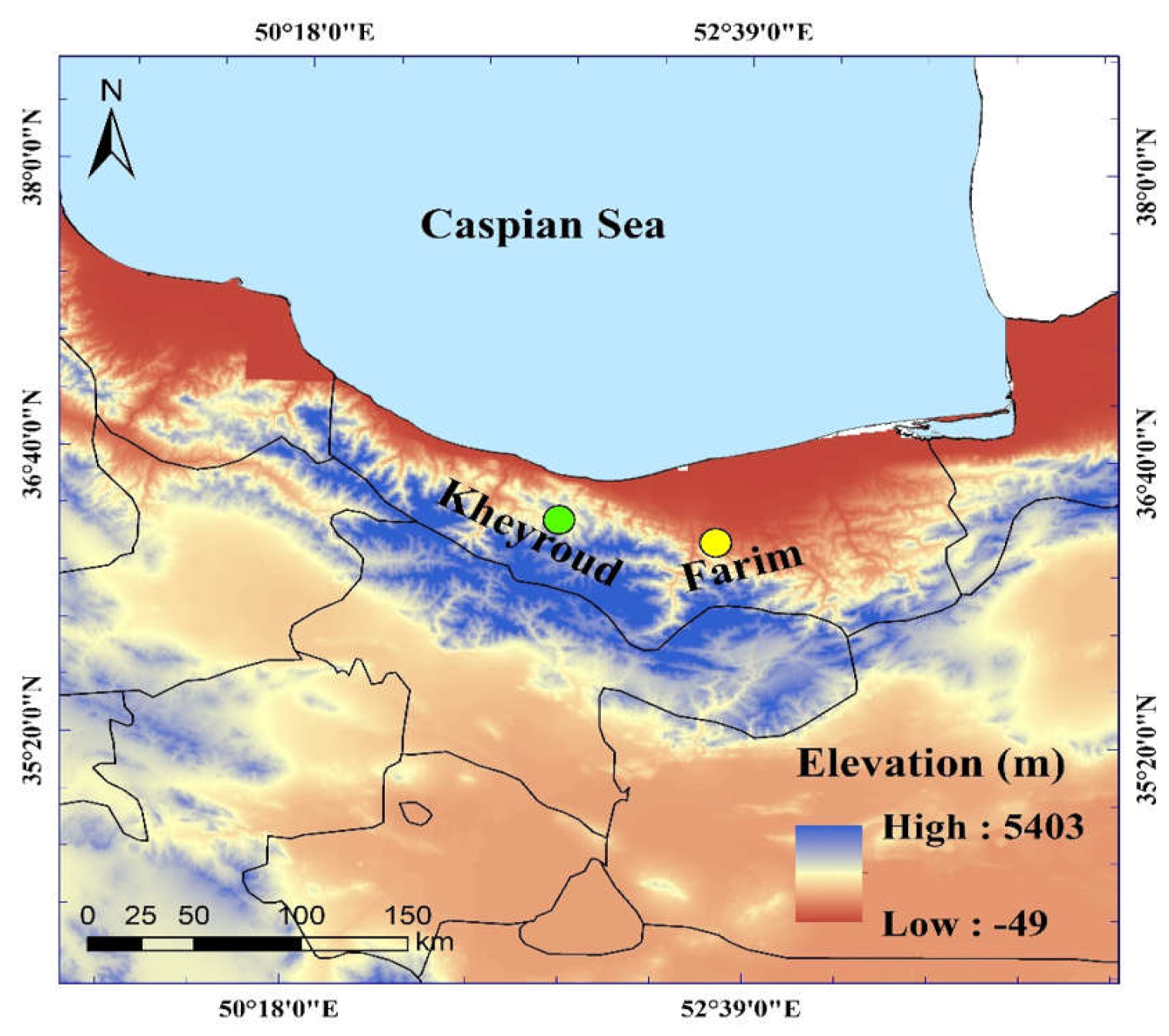
2.1. Study Area
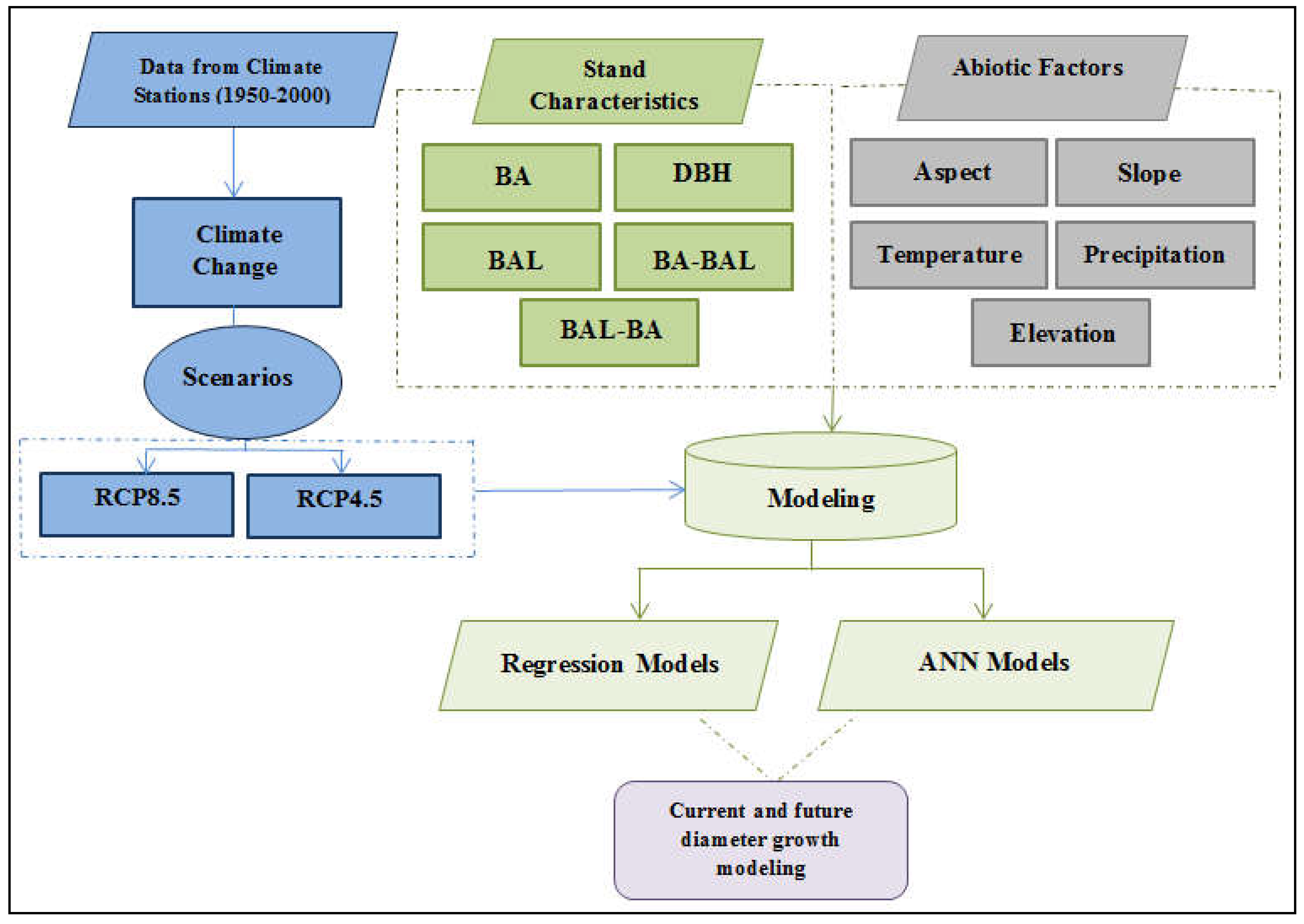
2.2. Methodology
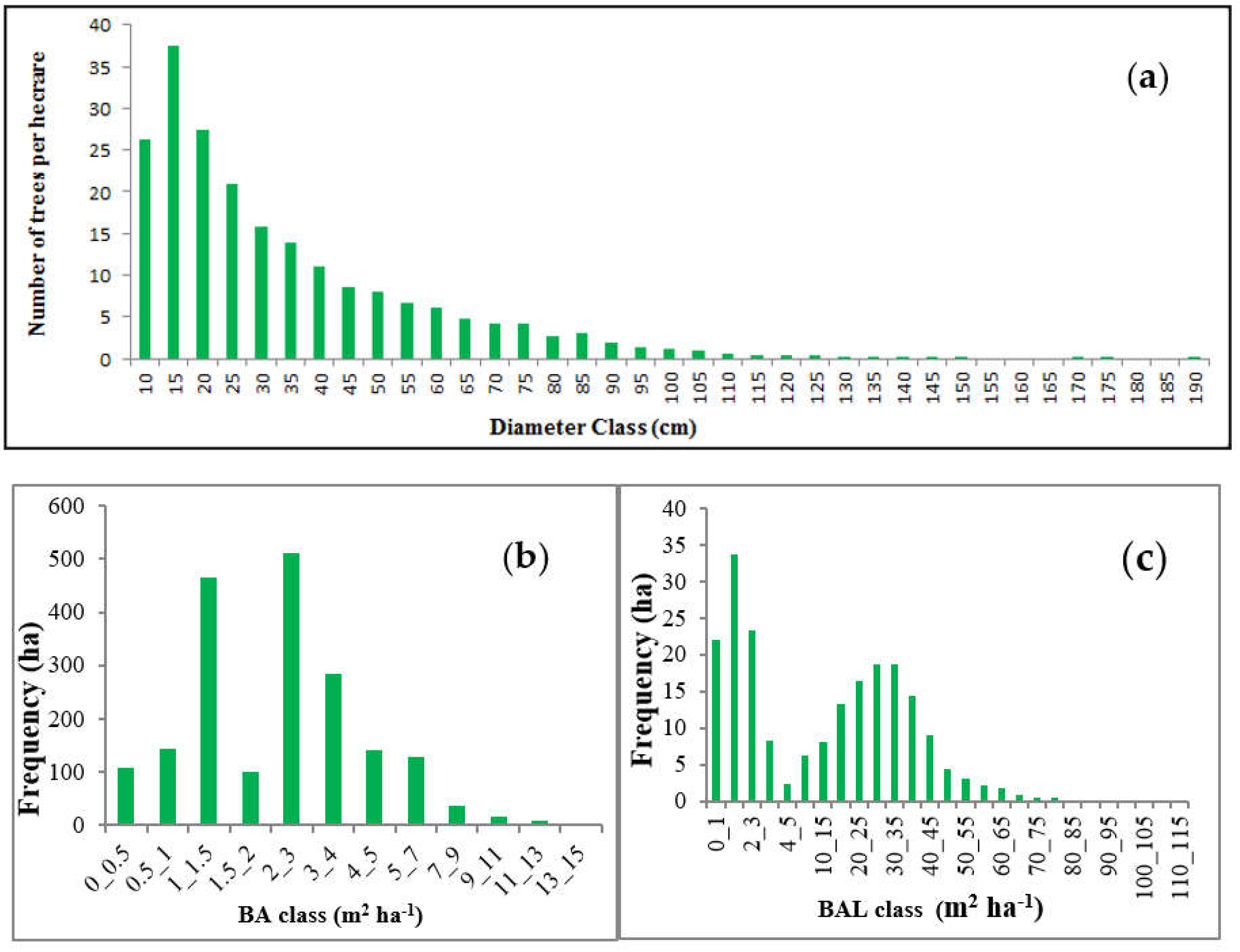
2.3. Data Used
2.3.1. Dependent Variable: Increment Data
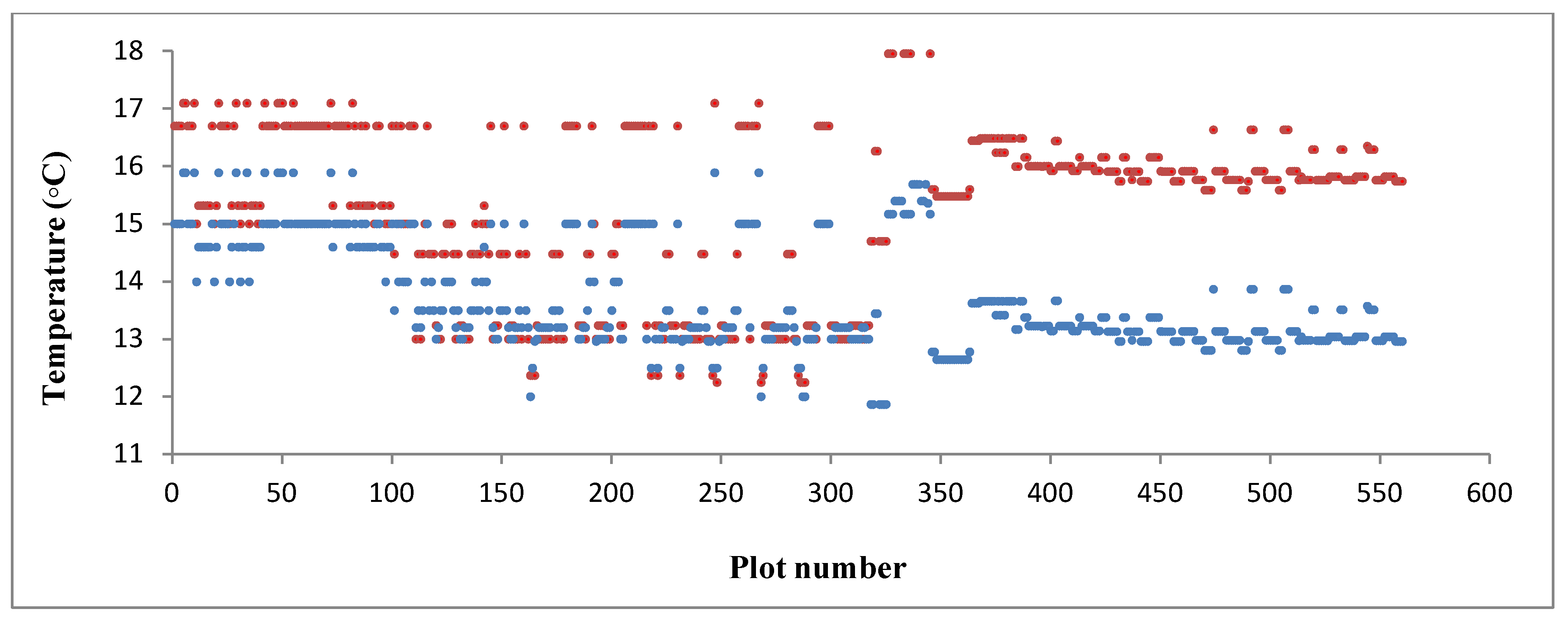
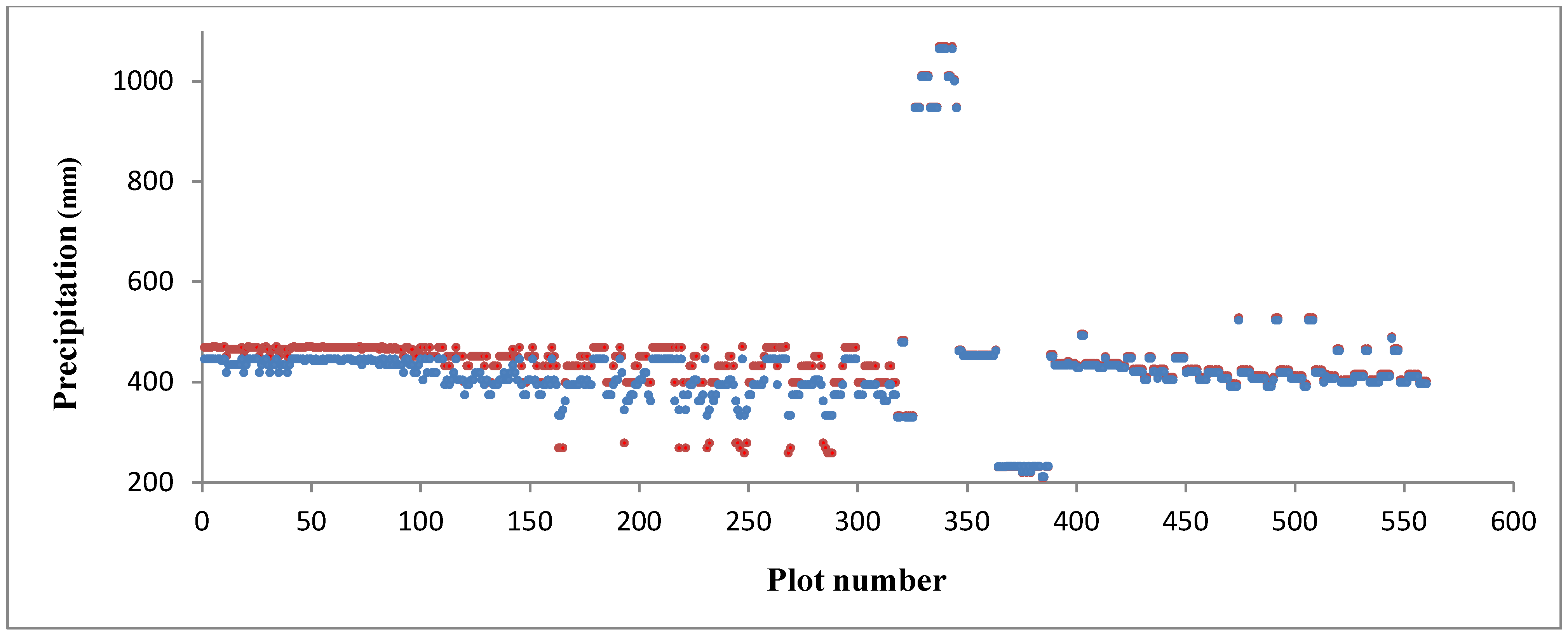
2.3.2. Independent Variables: Climate Data
2.3.3. Other Independent Variables
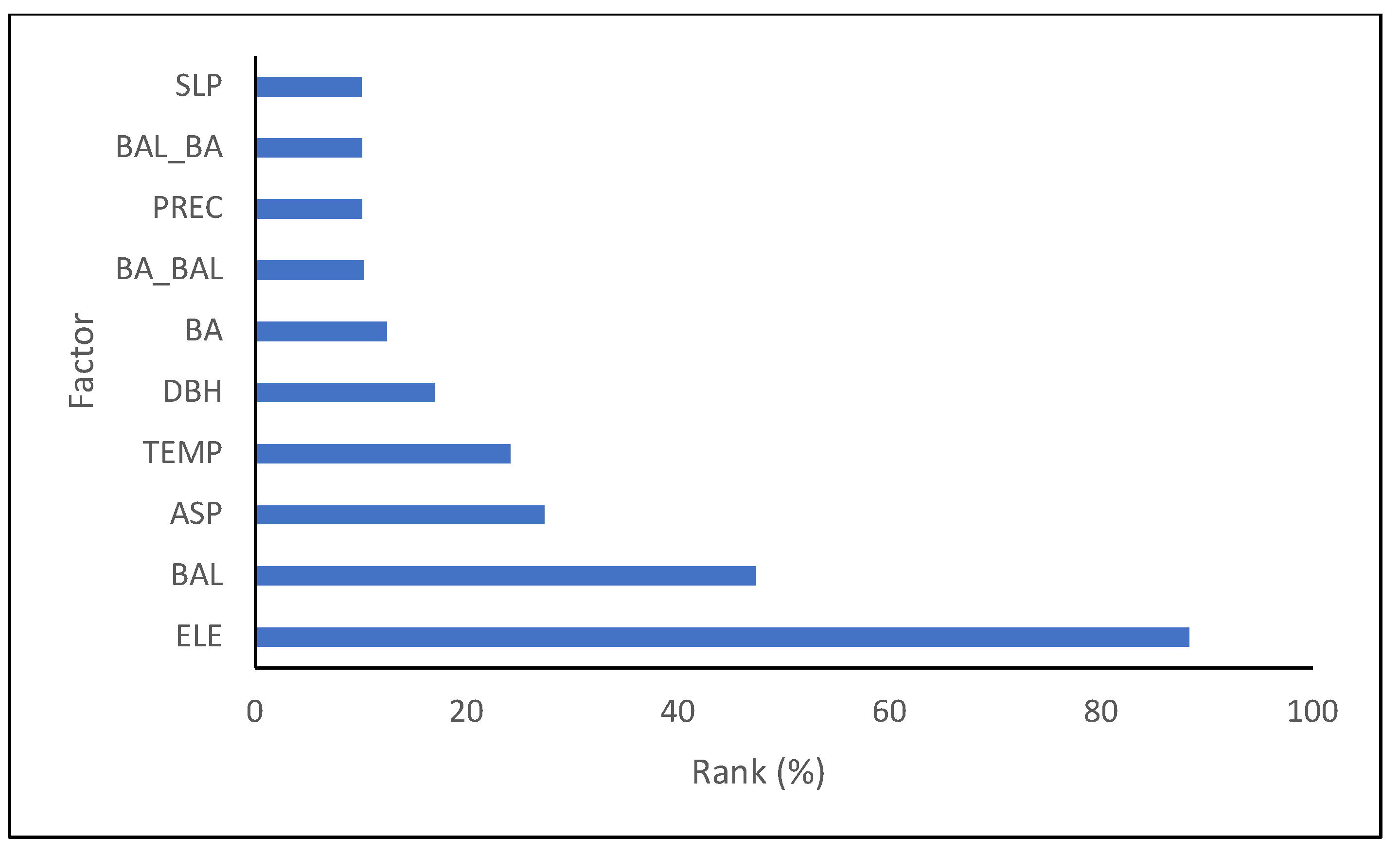
2.4. Models Used
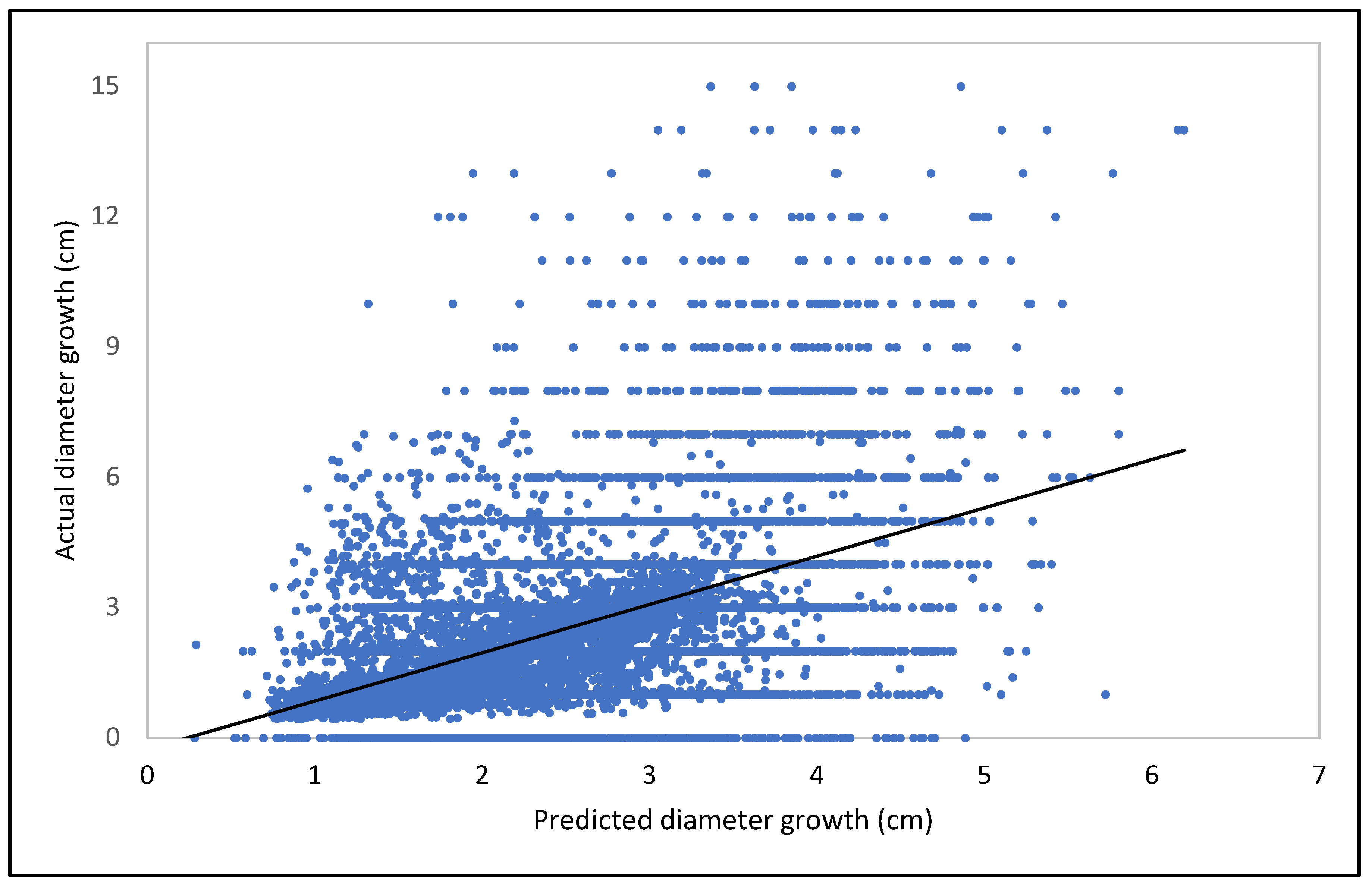
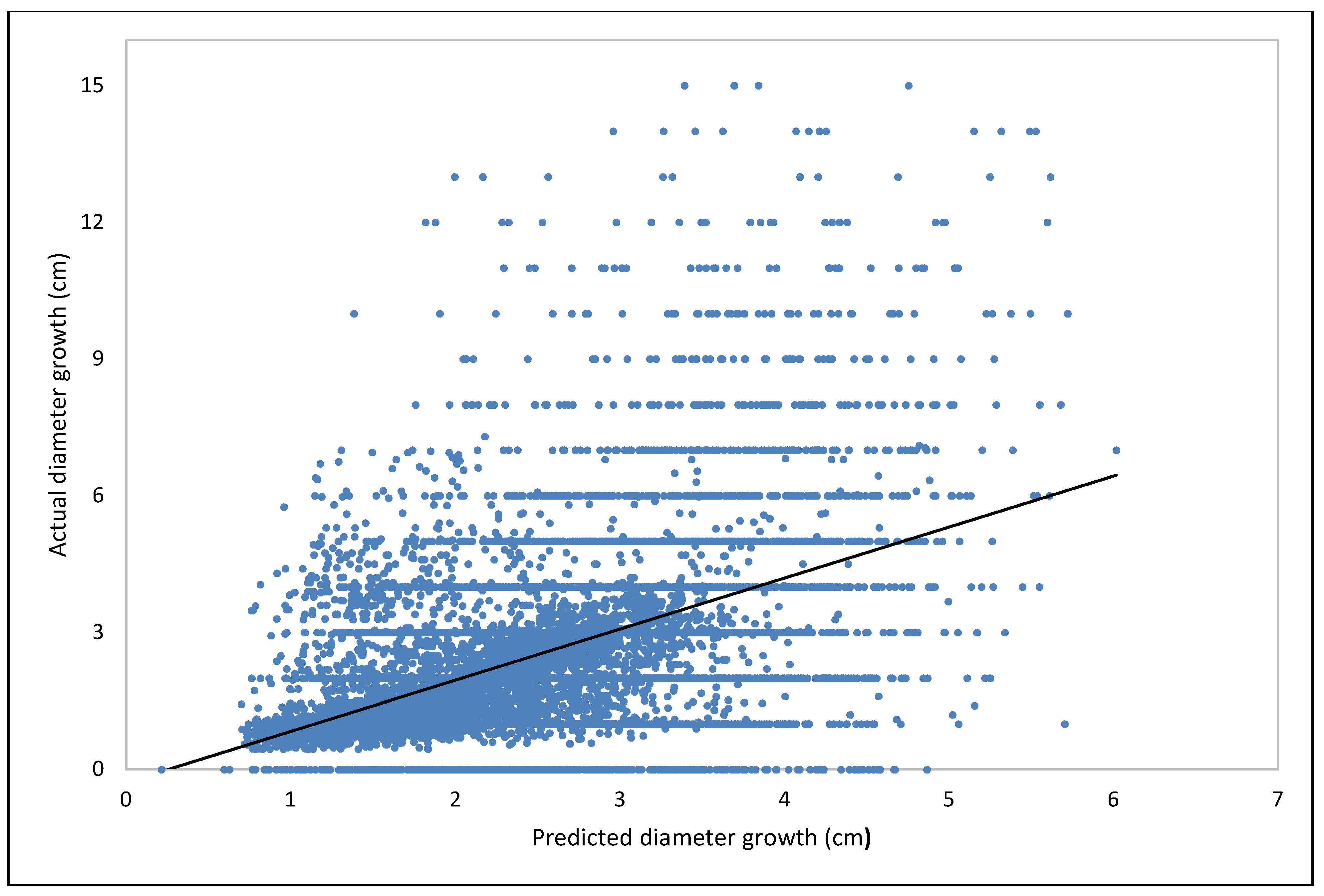
Model Training and Validation
3. Results
3.1. Modeling Results for Each Species
3.1.1. Fagus
0.0016 (ASP) − 0.0027 (ELE) − 0.77 (TEMP) + 0.0022 (PRPE) + eij
3.1.2. Carpinus
1.04 (BA-BAL) + 1.04 (BAL-BA) + 0.0011(ASP) −
0.0013 (ELE) − 0.30 (TEMP) + 0.00052 (PRPE) + eij
3.1.3. Quercus
5.49 (BA) + 0.02 (BAL) –
0.0014 (ELE) − 0.65 (TEMP) + eij
3.1.4. Others Species
0.0003 (BAL-BA) − 0.0014 (ELE) –
0.63 (TEMP) + eij
3.2. Modeling Results for the Current Conditions
0.032 (BA/BAL) − 0.00029 (BAL/BA) –
0.0022 (elevation) + 0.0021 (aspect) –
0.62 (temperature) + 0.0014 (precipitation) + eij
3.3. Modeling Results for the Next 50 Years
0.031 (BA/BAL) + 0.00306 (BAL/BA) +
0.0101 (elevation) + 0.0028 (aspect) +
0.234 (precipitation) − 0.0123 (PREC) + eij
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yue, Z.; Zhou, W.; Li, T. Impact of the Indian Ocean dipole on evolution of the subsequent ENSO: Relative roles of dynamic and thermodynamic processes. J. Clim. 2021, 34, 3591–3607. [Google Scholar] [CrossRef]
- Longo, M.; Knox, R.G.; Levine, N.M.; Alves, L.F.; Bonal, D.; Camargo, P.B.; Fitzjarrald, D.R.; Hayek, M.N.; Restrepo-Coupe, N.; Saleska, S.R. Ecosystem heterogeneity and diversity mitigate Amazon forest resilience to frequent extreme droughts. New Phytol. 2018, 219, 914–931. [Google Scholar] [CrossRef] [PubMed]
- Hamidi, S.K.; de Luis, M.; Bourque, C.P.-A.; Bayat, M.; Serrano-Notivoli, R. Projected biodiversity in the Hyrcanian Mountain Forest of Iran: An investigation based on two climate scenarios. Biodivers. Conserv. 2022, 1–18. [Google Scholar] [CrossRef]
- Quan, Q.; Liang, W.; Yan, D.; Lei, J. Influences of joint action of natural and social factors on atmospheric process of hydrological cycle in Inner Mongolia, China. Urban Clim. 2022, 41, 101043. [Google Scholar] [CrossRef]
- Tollefson, J. IPCC climate report: Earth is warmer than it’s been in 125,000 years. Nature 2021, 596, 171–172. [Google Scholar] [CrossRef]
- Lo Piccolo, E.; Landi, M. Red-leafed species for urban “greening” in the age of global climate change. J. For. Res. 2021, 32, 151–159. [Google Scholar] [CrossRef]
- Crookston, N.L.; Rehfeldt, G.E.; Dixon, G.E.; Weiskittel, A.R. Addressing climate change in the forest vegetation simulator to assess impacts on landscape forest dynamics. For. Ecol. Manag. 2010, 260, 1198–1211. [Google Scholar] [CrossRef]
- Littell, J.S.; McKenzie, D.; Kerns, B.K.; Cushman, S.; Shaw, C.G. Managing uncertainty in climate-driven ecological models to inform adaptation to climate change. Ecosphere 2011, 2, 1–19. [Google Scholar] [CrossRef]
- Escoriza, D.; Hernandez, A. Buffered microclimate determines the presence of Salamandra corsica. J. For. Res. 2021, 32, 1089–1093. [Google Scholar] [CrossRef]
- Kirschbaum, M.U. Forest growth and species distribution in a changing climate. Tree Physiol. 2000, 20, 309–322. [Google Scholar] [CrossRef]
- Yang, Y.; Li, T.; Wang, Y.; Cheng, H.; Chang, S.X.; Liang, C.; An, S. Negative effects of multiple global change factors on soil microbial diversity. Soil Biol. Biochem. 2021, 156, 108229. [Google Scholar] [CrossRef]
- Limaki, M.K.; Nimvari, M.E.-h.; Alavi, S.J.; Mataji, A.; Kazemnezhad, F. Potential elevation shift of oriental beech (Fagus orientalis L.) in Hyrcanian mixed forest ecoregion under future global warming. Ecol. Model. 2021, 455, 109637. [Google Scholar] [CrossRef]
- Yang, Y.; Li, T.; Pokharel, P.; Liu, L.; Qiao, J.; Wang, Y.; An, S.; Chang, S.X. Global effects on soil respiration and its temperature sensitivity depend on nitrogen addition rate. Soil Biol. Biochem. 2022, 174, 108814. [Google Scholar] [CrossRef]
- Strömgren, M.; Linder, S. Effects of nutrition and soil warming on stemwood production in a boreal Norway spruce stand. Glob. Change Biol. 2002, 8, 1194–1204. [Google Scholar] [CrossRef]
- Yang, Y.; Watanabe, M.; Li, F.; Zhang, J.; Zhang, W.; Zhai, J. Factors affecting forest growth and possible effects of climate change in the Taihang Mountains, northern China. For. Int. J. For. Res. 2006, 79, 135–147. [Google Scholar] [CrossRef]
- Dunn, R.J.; Hurst, D.F.; Gobron, N.; Willett, K.M. Global climate [in “state of the climate in 2016”]. Bull. Amer. Meteor. Soc 2017, 98, 5–62. [Google Scholar]
- Jactel, H.; Koricheva, J.; Castagneyrol, B. Responses of forest insect pests to climate change: Not so simple. Curr. Opin. Insect Sci. 2019, 35, 103–108. [Google Scholar] [CrossRef]
- Coelho, L.; Nascimento, A.R.T.; Santos, J.C.; Silva, V.F. Unveiling an important interaction in forestry: Ectomyelois muriscis and Khaya grandifoliola cankers and tree growth. J. For. Res. 2021, 32, 1287–1293. [Google Scholar] [CrossRef]
- Li, W.; Shi, Y.; Zhu, D.; Wang, W.; Liu, H.; Li, J.; Shi, N.; Ma, L.; Fu, S. Fine root biomass and morphology in a temperate forest are influenced more by the nitrogen treatment approach than the rate. Ecol. Indic. 2021, 130, 108031. [Google Scholar] [CrossRef]
- Ashraf, M.I.; Meng, F.-R.; Bourque, C.P.-A.; MacLean, D.A. A novel modelling approach for predicting forest growth and yield under climate change. PLoS ONE 2015, 10, e0132066. [Google Scholar] [CrossRef]
- Hamidi, S.K.; Weiskittel, A.; Bayat, M.; Fallah, A. Development of individual tree growth and yield model across multiple contrasting species using nonparametric and parametric methods in the Hyrcanian forests of northern Iran. Eur. J. For. Res. 2021, 140, 421–434. [Google Scholar] [CrossRef]
- Pretzsch, H.; Bielak, K.; Block, J.; Bruchwald, A.; Dieler, J.; Ehrhart, H.-P.; Kohnle, U.; Nagel, J.; Spellmann, H.; Zasada, M. Productivity of mixed versus pure stands of oak (Quercus petraea (Matt.) Liebl. and Quercus robur L.) and European beech (Fagus sylvatica L.) along an ecological gradient. Eur. J. For. Res. 2013, 132, 263–280. [Google Scholar] [CrossRef]
- Adeniyi, M.O. The consequences of the IPCC AR5 RCPs 4.5 and 8.5 climate change scenarios on precipitation in West Africa. Clim. Change 2016, 139, 245–263. [Google Scholar] [CrossRef]
- Yang, Y.; Chen, X.; Liu, L.; Li, T.; Dou, Y.; Qiao, J.; Wang, Y.; An, S.; Chang, S.X. Nitrogen fertilization weakens the linkage between soil carbon and microbial diversity: A global meta-analysis. Glob. Change Biol. 2022, 28, 6446–6461. [Google Scholar] [CrossRef] [PubMed]
- Bayat, M.; Pukkala, T.; Namiranian, M.; Zobeiri, M. Productivity and optimal management of the uneven-aged hardwood forests of Hyrcania. Eur. J. For. Res. 2013, 132, 851–864. [Google Scholar] [CrossRef]
- Hamidi, S.K.; Zenner, E.K.; Bayat, M.; Fallah, A. Analysis of plot-level volume increment models developed from machine learning methods applied to an uneven-aged mixed forest. Ann. For. Sci. 2021, 78, 4. [Google Scholar] [CrossRef]
- Bayat, M.; Burkhart, H.; Namiranian, M.; Hamidi, S.K.; Heidari, S.; Hassani, M. Assessing biotic and abiotic effects on biodiversity index using machine learning. Forests 2021, 12, 461. [Google Scholar] [CrossRef]
- Bourque, C.P.-A.; Bayat, M. Landscape variation in tree species richness in northern Iran forests. PLoS ONE 2015, 10, e0121172. [Google Scholar] [CrossRef]
- Munyasya, A.N.; Koskei, K.; Zhou, R.; Liu, S.-T.; Indoshi, S.N.; Wang, W.; Zhang, X.-C.; Cheruiyot, W.K.; Mburu, D.M.; Nyende, A.B. Integrated on-site & off-site rainwater-harvesting system boosts rainfed maize production for better adaptation to climate change. Agric. Water Manag. 2022, 269, 107672. [Google Scholar]
- Tian, H.; Qin, Y.; Niu, Z.; Wang, L.; Ge, S. Summer Maize Mapping by Compositing Time Series Sentinel-1A Imagery Based on Crop Growth Cycles. J. Indian Soc. Remote Sens. 2021, 49, 2863–2874. [Google Scholar] [CrossRef]
- Bayat, M.; Bettinger, P.; Hassani, M.; Heidari, S. Ten-year estimation of Oriental beech (Fagus orientalis Lipsky) volume increment in natural forests: A comparison of an artificial neural networks model, multiple linear regression and actual increment. For. Int. J. For. Res. 2021, 94, 598–609. [Google Scholar] [CrossRef]
- Burkhart, H.E.; Tomé, M. Modeling Forest Trees and Stands; Springer Science & Business Media: Cham, Switzerland, 2012. [Google Scholar]
- Chen, J.; Du, L.; Guo, Y. Label constrained convolutional factor analysis for classification with limited training samples. Inf. Sci. 2021, 544, 372–394. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, K.; Li, Z.; Liu, Z.; Wang, J.; Huang, P. A hybrid runoff generation modelling framework based on spatial combination of three runoff generation schemes for semi-humid and semi-arid watersheds. J. Hydrol. 2020, 590, 125440. [Google Scholar] [CrossRef]
- Zhou, R.; Wu, D.; Zhou, R.; Fang, L.; Zheng, X.; Lou, X. Estimation of DBH at forest stand level based on multi-parameters and generalized regression neural network. Forests 2019, 10, 778. [Google Scholar] [CrossRef]
- García-Gutiérrez, J.; Martínez-Álvarez, F.; Troncoso, A.; Riquelme, J.C. A comparison of machine learning regression techniques for LiDAR-derived estimation of forest variables. Neurocomputing 2015, 167, 24–31. [Google Scholar] [CrossRef]
- Kuehne, C.; Russell, M.; Weiskittel, A.; Kershaw, J., Jr. Comparing strategies for representing individual-tree secondary growth in mixed-species stands in the Acadian Forest region. For. Ecol. Manag. 2020, 459, 117823. [Google Scholar] [CrossRef]
- Kweon, D.; Comeau, P.G. Relationships between tree survival, stand structure and age in trembling aspen dominated stands. For. Ecol. Manag. 2019, 438, 114–122. [Google Scholar] [CrossRef]
- Primicia, I.; Camarero, J.J.; Janda, P.; Čada, V.; Morrissey, R.C.; Trotsiuk, V.; Bače, R.; Teodosiu, M.; Svoboda, M. Age, competition, disturbance and elevation effects on tree and stand growth response of primary Picea abies forest to climate. For. Ecol. Manag. 2015, 354, 77–86. [Google Scholar] [CrossRef]
- Askarizadeh, D.; Arzani, H.; Jafary, M.; Bazrafshan, J.; Prentice, I.C. Surveying of the past, present, and future of vegetation changes in the central Alborz ranges in relation to climate change. J. RS GIS Nat. Resour. 2018, 9, 1–18. [Google Scholar]
- Burkhart, H.E.; Brooks, E.B.; Dinon-Aldridge, H.; Sabatia, C.O.; Gyawali, N.; Wynne, R.H.; Thomas, V.A. Regional simulations of loblolly pine productivity with CO2 enrichment and changing climate scenarios. For. Sci. 2018, 64, 349–357. [Google Scholar] [CrossRef]
- Subedi, N.; Sharma, M. Climate-diameter growth relationships of black spruce and jack pine trees in boreal Ontario, Canada. Glob. Change Biol. 2013, 19, 505–516. [Google Scholar] [CrossRef] [PubMed]
- Sharma, M. Modelling climate effects on diameter growth of red pine trees in boreal Ontario, Canada. Trees For. People 2021, 4, 100064. [Google Scholar] [CrossRef]
- Wilmking, M.; Juday, G.P. Longitudinal variation of radial growth at Alaska’s northern treeline—Recent changes and possible scenarios for the 21st century. Glob. Planet. Change 2005, 47, 282–300. [Google Scholar] [CrossRef]
- Goldblum, D.; Rigg, L. Tree growth response to climate change at the deciduous boreal forest ecotone, Ontario, Canada. Can. J. For. Res. 2005, 35, 2709–2718. [Google Scholar] [CrossRef]
- Oboite, F.O.; Comeau, P.G. Climate sensitive growth models for predicting diameter growth of western Canadian boreal tree species. For. Int. J. For. Res. 2021, 94, 363–373. [Google Scholar] [CrossRef]
- Laubhann, D.; Sterba, H.; Reinds, G.J.; De Vries, W. The impact of atmospheric deposition and climate on forest growth in European monitoring plots: An individual tree growth model. For. Ecol. Manag. 2009, 258, 1751–1761. [Google Scholar] [CrossRef]


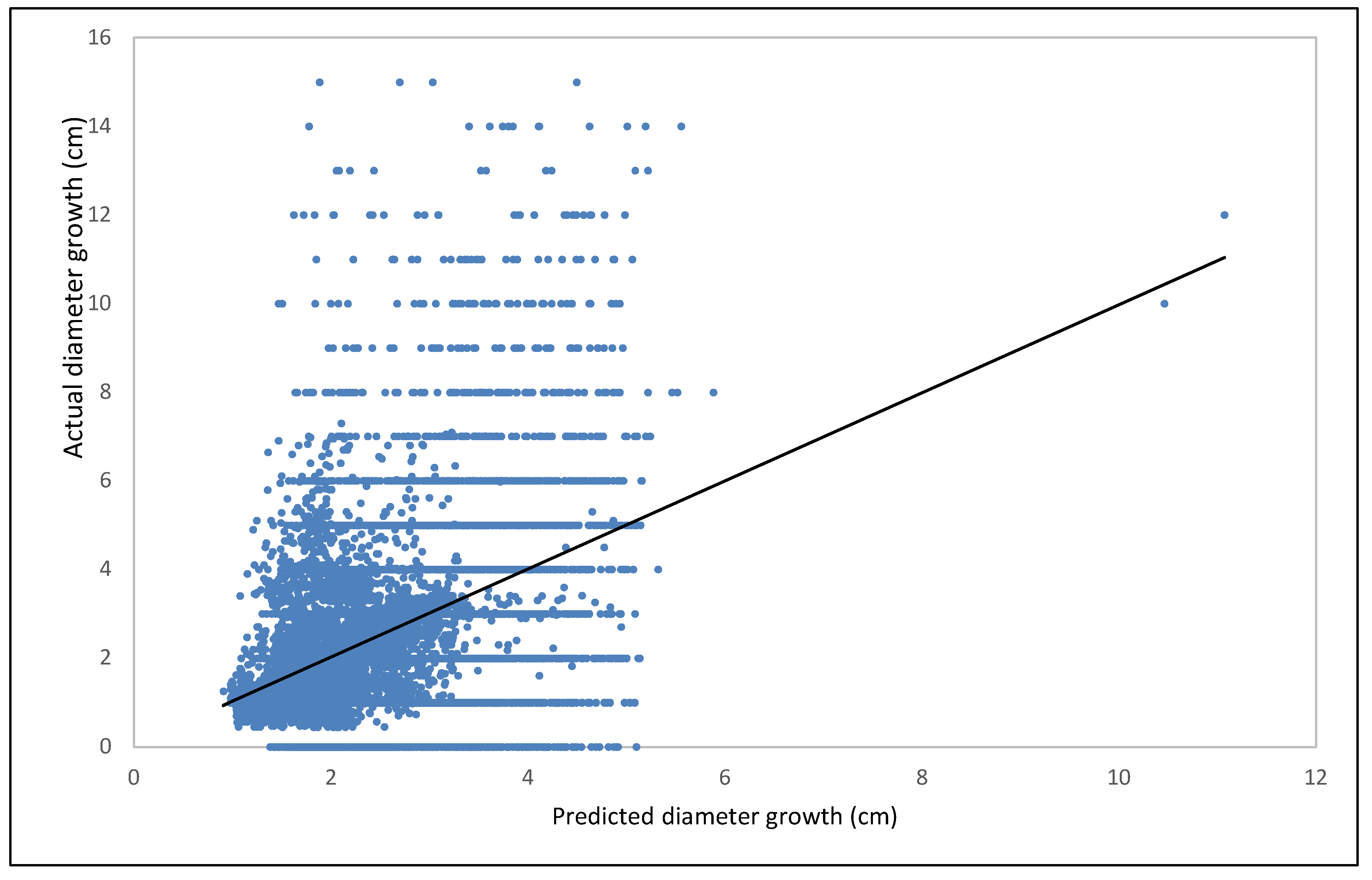
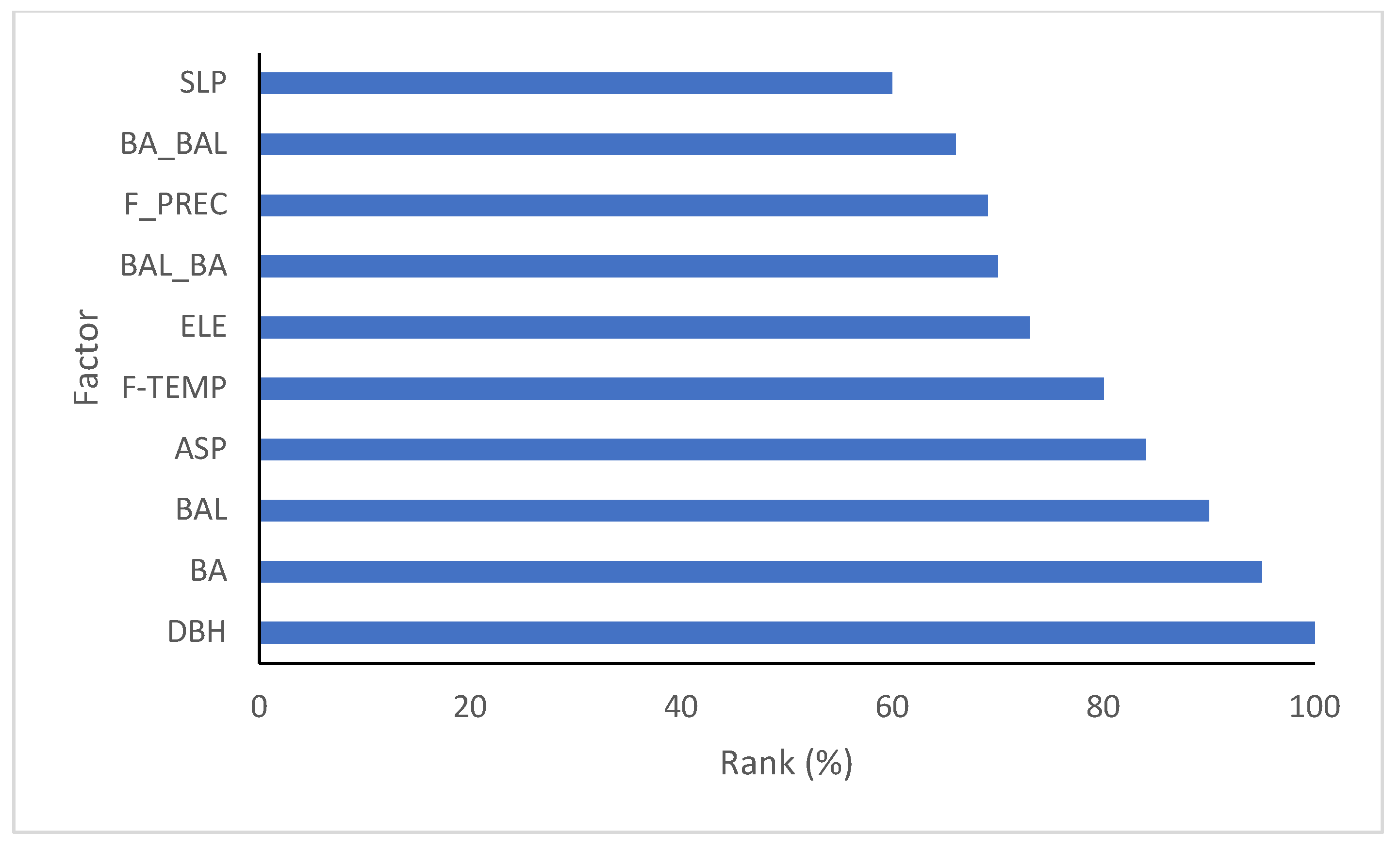
| Fagus | Estimate | Std. Error | t Value | Pr (>|t|) |
|---|---|---|---|---|
| Intercept | 13.86678 | 1.202374 | 11.5328 | 0.000000 |
| DBH | 0.03621 | 0.003532 | 10.2515 | 0.000000 |
| BA | −1.24626 | 0.372723 | −3.3437 | 0.000833 |
| BAL | 0.00724 | 0.001901 | 3.8095 | 0.000141 |
| BA_BAL | −0.11809 | 0.124150 | −0.9512 | 0.341546 |
| BAL_BA | −0.00004 | 0.000022 | −1.7320 | 0.083342 |
| ASP | 0.00169 | 0.000306 | 5.5352 | 0.000000 |
| SLP | 0.00031 | 0.001607 | 0.1940 | 0.846222 |
| ELE | −0.00272 | 0.000265 | −10.2758 | 0.000000 |
| TEMP | −0.77897 | 0.072303 | −10.7738 | 0.000000 |
| PREC | 0.00226 | 0.000321 | 7.0347 | 0.000000 |
| Carpinus | Estimate | Std. Error | t Value | Pr (>|t|) |
|---|---|---|---|---|
| Intercept | 6.51818 | 0.801555 | 8.13192 | 0.000000 |
| DBH | 0.04583 | 0.004726 | 9.69805 | 0.000000 |
| BA | −2.23963 | 0.604983 | −3.70198 | 0.000217 |
| BAL | 0.00041 | 0.001998 | 0.20604 | 0.836767 |
| BA_BAL | −1.04600 | 0.287918 | −3.63298 | 0.000284 |
| BAL_BA | 0.00008 | 0.000011 | 7.16247 | 0.000000 |
| ASP | 0.00110 | 0.000298 | 3.68348 | 0.000233 |
| SLP | −0.00243 | 0.002056 | −1.18355 | 0.236659 |
| ELE | −0.00137 | 0.000218 | −6.26503 | 0.000000 |
| TEMP | −0.30486 | 0.048397 | −6.29913 | 0.000000 |
| PREC | 0.00052 | 0.000221 | 2.35220 | 0.018710 |
| Quercus | Estimate | Std. Error | t Value | Pr (>|t|) |
|---|---|---|---|---|
| Intercept | 11.23192 | 2.848557 | 3.94302 | 0.000091 |
| DBH | 0.08955 | 0.018065 | 4.95705 | 0.000001 |
| BA | −5.49099 | 2.172556 | −2.52743 | 0.011780 |
| BAL | 0.02703 | 0.009387 | 2.87913 | 0.004149 |
| BA_BAL | −0.47566 | 0.648376 | −0.73362 | 0.463506 |
| BAL_BA | −0.00011 | 0.000085 | −1.28709 | 0.198626 |
| ASP | −0.00009 | 0.000994 | −0.09118 | 0.927383 |
| SLP | −0.00168 | 0.005095 | −0.32890 | 0.742362 |
| ELE | −0.00140 | 0.000695 | −2.00836 | 0.045113 |
| TEMP | −0.65842 | 0.158488 | −4.15439 | 0.000038 |
| PREC | 0.00025 | 0.000856 | 0.28801 | 0.773449 |
| Others Species | Estimate | Std. Error | t Value | Pr (>|t|) |
|---|---|---|---|---|
| Intercept | 12.37578 | 1.823423 | 6.78711 | 0.000000 |
| DBH | 0.00689 | 0.006085 | 1.13154 | 0.257977 |
| BA | 0.96779 | 0.602838 | 1.60539 | 0.108578 |
| BAL | 0.02499 | 0.004180 | 5.97897 | 0.000000 |
| BA_BAL | −0.44267 | 0.386819 | −1.14440 | 0.252608 |
| BAL_BA | −0.00033 | 0.000055 | −5.99956 | 0.000000 |
| ASP | −0.00010 | 0.000581 | −0.16392 | 0.869808 |
| SLP | 0.00043 | 0.002916 | 0.14735 | 0.882876 |
| ELE | −0.00142 | 0.000462 | −3.06661 | 0.002196 |
| TEMP | −0.63779 | 0.102897 | −6.19840 | 0.000000 |
| PREC | 0.00087 | 0.000479 | 1.82720 | 0.067831 |
| Species | Network Name | Algorithm | Error Function | Hidden Activation | R2 | RMSE | % RMSE | BIAS | % BIAS |
|---|---|---|---|---|---|---|---|---|---|
| Fagus | MLP 10-6-1 | BFGS 46 | SOS | Logistic | 0.50 | 0.43 | 18.69 | 0.0005 | 0.029 |
| Carpinus | MLP 10-4-1 | BFGS 53 | SOS | Tanh | 0.37 | 0.69 | 31.08 | 0.0025 | 0.079 |
| Quercus | MLP 10-12-1 | BFGS 26 | SOS | Logistic | 0.57 | 0.40 | 17.77 | 0.0004 | 0.026 |
| Others | MLP 10-11-1 | BFGS 33 | SOS | Exponential | 0.42 | 0.58 | 26.24 s | 0.0017 | 0.030 |
| Species | Network Name | Algorithm | Error Function | Hidden Activation | R2 | RMSE | % RMSE | BIAS | % BIAS |
|---|---|---|---|---|---|---|---|---|---|
| Fagus | MLP 10-6-1 | BFGS 46 | SOS | Logistic | 0.47 | 0.50 | 22.52 | 0.0009 | 0.006 |
| Carpinus | MLP 10-4-1 | BFGS 53 | SOS | Tanh | 0.41 | 0.61 | 27.47 | 0.0028 | 0.017 |
| Quercus | MLP 10-12-1 | BFGS 26 | SOS | Logistic | 0.58 | 0.41 | 18.56 | 0.0006 | 0.004 |
| Others | MLP 10-11-1 | BFGS 33 | SOS | Exponential | 0.42 | 0.63 | 28.12 | 0.0023 | 0.011 |
| Estimate | Std. Error | t Value | Pr (>|t|) | |
|---|---|---|---|---|
| Intercept | 1.176 × 101 | 1.134e × 10 | 10.367 | <2 × 10−16 *** |
| DBH | 4.393 × 10−2 | 2.440 × 10−3 | 18.001 | <2 × 10−16 *** |
| BA | −2.201 × 10 | 2.645 × 10−1 | −8.323 | <2 × 10−16 *** |
| BAL | −1.846 × 10−3 | 1.901 × 10−3 | −0.971 | 0.33195 |
| BA_BAL | −3.250 × 10−1 | 1.071 × 10−1 | −3.035 | 0.00241 ** |
| BAL_BA | 2.958 × 10−5 | 9.427 × 10−6 | 3.138 | 0.00171 ** |
| ASP | 2.157 × 10−3 | 3.677 × 10−4 | 5.865 | 8.88 × 10−9 *** |
| ELE | −2.219 × 10−3 | 2.698 × 10−4 | −8.223 | 2.22 × 10−15 *** |
| SLP | −3.050 × 10−3 | 2.003 × 10−3 | −1.523 | 0.12846 |
| TEMP | −6.222 × 10−1 | 6.650 × 10−2 | −9.356 | <2 × 10−16 *** |
| PREC | 1.488 × 10−3 | 3.137 × 10−4 | 4.744 | 2.83 × 10−6 *** |
| Sample | Network | Algorithm | Error Function | Hidden Activation | R2 | RMSE | % RMSE | BIAS | % BIAS |
|---|---|---|---|---|---|---|---|---|---|
| Train | MLP 10-9-1 | BFGS 106 | SOS | Tanh | 0.48 | 0.52 | 21.84 | 0.0008 | 0.0336 |
| Validation | MLP 10-9-1 | BFGS 106 | SOS | Tanh | 0.44 | 0.63 | 26.47 | 0.0010 | 0.04201 |
| Variable | Estimate | Std. Error | t Value | Pr (>|t|) |
|---|---|---|---|---|
| Intercept | −3.128 ×10 | 9.376 ×10−1 | −3.337 | 0.000911 *** |
| DBH | 4.453 ×10−2 | 2.451 ×10−3 | 18.169 | <2 ×10−16 *** |
| BA | −2.282 ×10 | 2.657 ×10−1 | −8.589 | <2 ×10−16 *** |
| BAL | −1.825 ×10−3 | 2.057 ×10−3 | −0.887 | 0.375212 |
| BA_BAL | −3.312 ×10−1 | 1.075 ×10−1 | −3.081 | 0.002065 ** |
| BAL_BA | 3.066 ×10−5 | 9.440 ×10−6 | 3.248 | 0.001166 ** |
| ASP | 2.877 ×10−3 | 3.820 ×10−4 | 7.531 | 2.90 ×10−13 *** |
| ELE | 1.011 ×10−3 | 2.944 ×10−4 | 3.435 | 0.000644 *** |
| SLP | −1.393 ×10−3 | 2.146 ×10−3 | −0.649 | 0.516438 |
| TEMP | 2.346 ×10−1 | 4.451 ×10−2 | 5.272 | 2.00 ×10−7 *** |
| PREC | −1.232 ×10−3 | 2.880 ×10−4 | −4.277 | 2.33 ×10−5 *** |
| Sample | Network Name | Algorithm | Error Function | Hidden Activation | R2 | RMSE | %RMSE | BIAS | %BIAS |
|---|---|---|---|---|---|---|---|---|---|
| Train | MLP 10-11-1 | BFGS 196 | SOS | Exponential | 0.49 | 0.50 | 20.92 | 0.0005 | 0.020 |
| Validation | MLP 10-11-1 | BFGS 196 | SOS | Exponential | 0.44 | 0.76 | 31.79 | 0.0019 | 0.079 |
| Climate Condition | Species | Linear Mixed-Effect Model | MLP |
|---|---|---|---|
| Current | Fagus | 2.30 | 2.31 |
| Carpinus | 2.22 | 2.24 | |
| Quercus | 2.96 | 2.98 | |
| Other | 2.85 | 2.86 | |
| All | 2.39 (cm) | 2.40 (cm) | |
| Future time | Fagus | 2.30 | 2.31 |
| Carpinus | 2.22 | 2.25 | |
| Quercus | 2.94 | 2.98 | |
| Other | 2.85 | 2.86 | |
| All | 2.38 (cm) | 2.39 (cm) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bayat, M.; Knoke, T.; Heidari, S.; Hamidi, S.K.; Burkhart, H.; Jaafari, A. Modeling Tree Growth Responses to Climate Change: A Case Study in Natural Deciduous Mountain Forests. Forests 2022, 13, 1816. https://doi.org/10.3390/f13111816
Bayat M, Knoke T, Heidari S, Hamidi SK, Burkhart H, Jaafari A. Modeling Tree Growth Responses to Climate Change: A Case Study in Natural Deciduous Mountain Forests. Forests. 2022; 13(11):1816. https://doi.org/10.3390/f13111816
Chicago/Turabian StyleBayat, Mahmoud, Thomas Knoke, Sahar Heidari, Seyedeh Kosar Hamidi, Harold Burkhart, and Abolfazl Jaafari. 2022. "Modeling Tree Growth Responses to Climate Change: A Case Study in Natural Deciduous Mountain Forests" Forests 13, no. 11: 1816. https://doi.org/10.3390/f13111816
APA StyleBayat, M., Knoke, T., Heidari, S., Hamidi, S. K., Burkhart, H., & Jaafari, A. (2022). Modeling Tree Growth Responses to Climate Change: A Case Study in Natural Deciduous Mountain Forests. Forests, 13(11), 1816. https://doi.org/10.3390/f13111816







