Study on Biomass Models of Artificial Young Forest in the Northwestern Alpine Region of China
Abstract
:1. Introduction
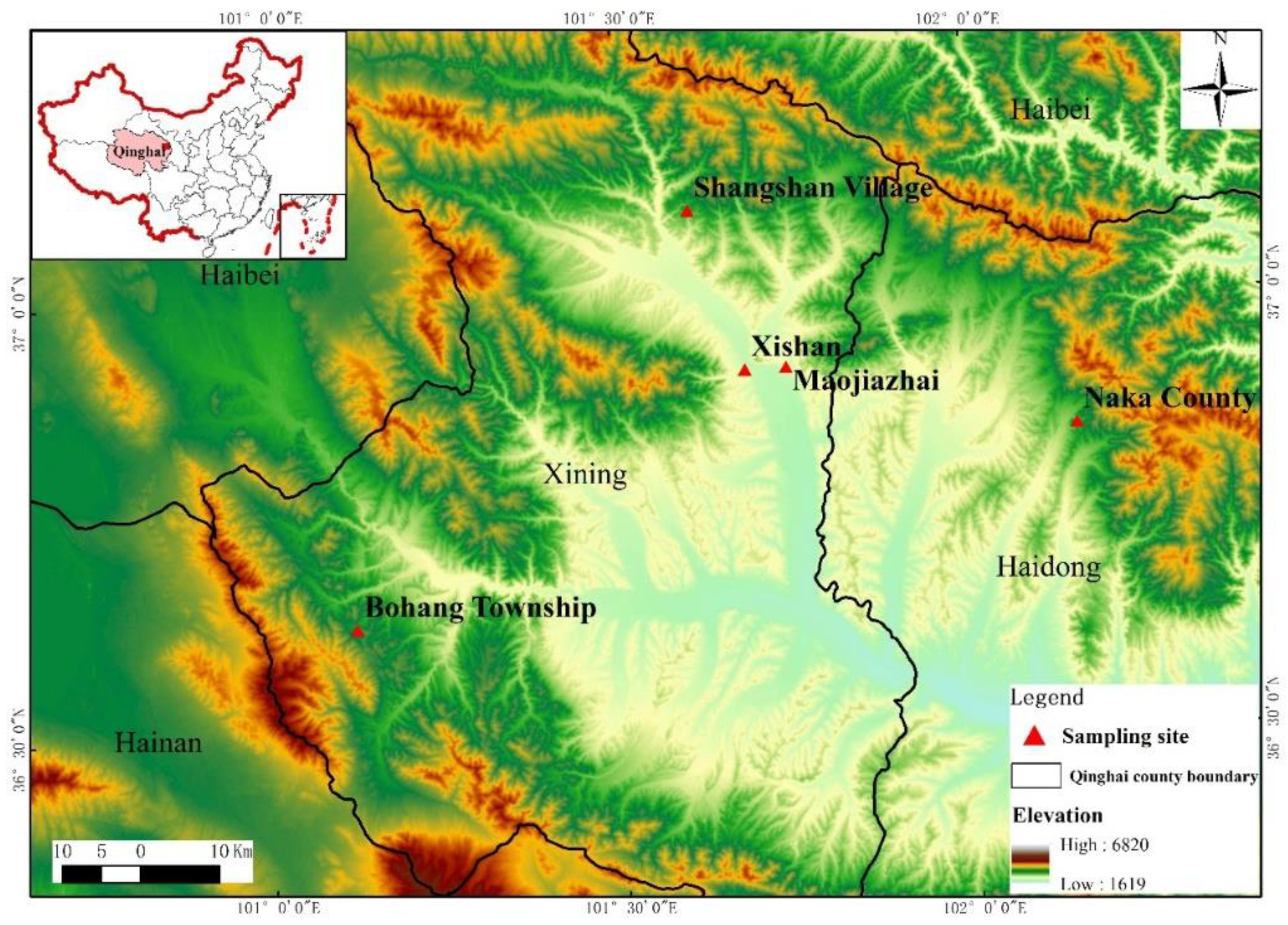
2. Study Area
3. Methods
3.1. Data Collection
3.2. Biomass Model Establishment
3.2.1. Independent Models
3.2.2. Compatible Models
Component-Additive Method
Total-Control Method
3.3. Model Evaluation and Accuracy Tests
4. Results
4.1. Correlation Analysis between Modeling Variables and The Biomass of Each Component
4.2. Establishment of an Independent Biomass Model for Young Trees
4.3. Establishment of Compatible Biomass Models for Young Trees
4.4. Biomass Distribution Characteristics of Each Component of Young Trees
5. Discussion
6. Conclusions
- (1)
- Multiple regression with two independent variables was superior to univariate models for all three tree species. For Pinus tabulaeformis and Picea crassifolia, base diameter was the best-fitting variable of the univariate model, and when the base diameter and crown diameter were used as multivariate model variables, model accuracy was significantly improved. For Sabina przewalskii, tree height was the best-fitting variable of the univariate model; when tree height and crown diameter were used as multivariate model variables, model accuracy was significantly improved, which might be related to the biological characteristics of Sabina przewalskii (namely, their tendency to have multiple trunks).
- (2)
- The optimal biomass models were those in which the multivariate components were added to the compatibility models. When calculating the amount of single wood biomass, the independent biomass model has high accuracy; when calculating the biomass of the sample wood area (whole plant and each component), the nonlinear joint estimation of the compatibility model is more compatible with the independent model error. Although error is slightly large, the model maintains good compatibility between each component, and it can effectively predict the biomass of the area. Although there were no significant differences in the fitting accuracy of compatibility models constructed using the component-additive and total-control methods, the component-additive models were slightly superior in general, especially the multiple regression with two independent variables, which had the best fitting effect, and leaf and root biomass, which had poor fitting accuracy.
- (3)
- The largest biomass component of the three tree species was the leaves (26%–68%), followed by the branches (10%–46%) and trunks (11%–55%). As the base diameter increased, the proportion of leaf biomass decreased significantly, and the proportion of branch and trunk biomass increased significantly, especially for the proportion of Pinus tabulaeformis trunk, which was as high as 55%. Aboveground biomass was higher than root (belowground) biomass. As the base diameter increased from 0 to 11 cm, the proportion of aboveground biomass of Picea crassifolia increased, and the proportion of aboveground biomass of Pinus tabulaeformis and Sabina przewalskii decreased slightly.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Yang, Y.H.; Shi, Y.; Sun, W.J. Terrestrial carbon sinks in China and around the world and their contribution to carbon neutrality. Sci. China Ser. D 2022, 52, 534–574. [Google Scholar]
- Li, M.Y. Carbon Storages and Carbon Sequestration Potentials of the Terrestrial Ecosystems on the Loess Plateau. Master’s Thesis, University of Chinese Academy of Sciences, Beijing, China, 2021. [Google Scholar]
- Wang, Y.Y. Coupling Associations between Plant Species Composition Traits and Biomass Carbon Sink Function and Mechanism of Forests in the Greater and Lesser Khingan Mountains. Ph.D. Thesis, University of Chinese Academy of Sciences, Beijing, China, 2021. [Google Scholar]
- Guo, Z.X.; Cao, C.; Liu, P. Construction of biomass model of Chinese fir plantation in Guangdong based on Lianqing data. J. Cent. South Univ. For. Technol. 2022, 42, 78–89. [Google Scholar] [CrossRef]
- Sun, W.T.; Zhou, J.; Li, L.H. Biomass and carbon density distribution characteristics of Pinus taiwanensis at different forest ages. J. Shandong Agric. Univ. (Nat. Sci. Ed.) 2022, 53, 469–474. [Google Scholar]
- Fan, B.M.; Li, X.H.; Du, J. Review and Prospect of Forestry Policies of the CPC in the Past Century. For. Econ. 2021, 43, 5–23. [Google Scholar]
- Zhang, L. Analysis of Carbon Storage and Carbon Density in Arbor Forest of Genhe Forestry Bureau. Master’s Thesis, Inner Mongolia Agricultural University, Hohhot, China, 2021. [Google Scholar]
- Liang, R.T.; Wang, Y.F.; Qiu, S.Y. Comparison of artificial neural network with compatible biomass model for predicting aboveground biomass of individual tree. Chin. J. Appl. Ecol. 2022, 33, 9–16. [Google Scholar]
- Huang, X.N. The Response and Simulation of the Biomass of Larix Principis-Rupprechtii Plantation in Liupan Mountains to Site Condition and Stand Structure. Master’s Thesis, Beijing Forestry University, Beijing, China, 2020. [Google Scholar]
- Vuorinne, I.; Heiskanen, J.; Maghenda, M.; Mwangala, L.; Muukkonen, P.; Pellikka, P.K. Allometric models for estimating leaf biomass of sisal in a semi-arid environment in Kenya. Biomass Bioenergy 2021, 155, 106294. [Google Scholar] [CrossRef]
- Das, M.; Nath, P.C.; Sileshi, G.W.; Pandey, R.; Nath, A.J.; Das, A.K. Biomass models for estimating carbon storage in Areca palm plantations. Environ. Sustain. Indic. 2021, 10, 100115. [Google Scholar] [CrossRef]
- Siddique, M.R.H.; Mahmood, H.; Siddiqui, M.B.N.; Abdullah, S.R.; Akhter, M.; Sola, G.; Iqbal, M.Z.; Henry, M. Conventional and additive models for estimating the biomass, carbon and nutrient stock in individual Shorea robusta Gaertn. f. tree of the Sal forests of Bangladesh. Environ. Chall. 2021, 4, 100178. [Google Scholar] [CrossRef]
- Gao, Y. Carbon Density and Storage of Forest and Grassl and Ecosystems in the Loess Plateau Region. Ph.D. Thesis, Northwest A & F University, Xianyang, China, 2014. [Google Scholar]
- Ter-Mikaelian, M.T.; Korzukhin, M.D. Biomass equations for sixty-five North American tree species. For. Ecol. Manag. 1997, 97, 1–24. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.F. Modeling Study of Generic Allometyic Biomass Equations for Common Tree Species in China. Master’s Thesis, Zhejiang Normal University, Jinhua, China, 2021. [Google Scholar]
- Zhang, J.; Fiddler, G.O.; Young, D.H.; Shestak, C.; Carlson, R. Allometry of tree biomass and carbon partitioning in ponderosa pine plantations grown under diverse conditions. For. Ecol. Manag. 2021, 497, 119526. [Google Scholar] [CrossRef]
- Luo, X.B.; Zeng, W.S.; He, D.B. Study on the establishment and application of aboveground biomass model of standing trees. J. Nat. Resour. 1999, 14, 271–277. [Google Scholar]
- Cao, L.; Li, H.K. Establishment and analysis of compatible biomass model for Cinnamomum camphora in Guangdong Province. J. For. Environ. 2018, 38, 458–465. [Google Scholar]
- Cao, L.; Li, H.K. Comparison of two compatible biomass models: A case study from three broadleaved tree species in Guangdong. Chin. J. Ecol. 2019, 38, 1916–1925. [Google Scholar]
- Liu, J.F.; Ni, J. Comparison of general allometric equations of biomass estimation for major tree species types in China. Quat. Sci. 2021, 41, 1169–1180. [Google Scholar]
- Dutcă, I.; Mather, R.; Blujdea, V.N.B.; Ioraș, F.; Olari, M.; Abrudan, I.V. Site-Effects on Biomass Allometric Models for Early Growth Plantations of Norway Spruce (Picea abies (L.) Karst.). Biomass Bioenergy 2018, 116, 8–17. [Google Scholar] [CrossRef]
- Ouédraogo, K.; Dimobe, K.; Thiombiano, A. Allometric models for estimating aboveground biomass and carbon stock for Diospyros mespiliformis in West Africa. Silva Fenn. 2020, 54, 10215. [Google Scholar] [CrossRef] [Green Version]
- He, X.; Lei, X.D.; Dong, L.H. How large is the difference in large-scale forest biomass estimations based on new climate-modified stand biomass models? Ecol. Indic. 2021, 126, 107569. [Google Scholar] [CrossRef]
- Liu, R.S.; Wang, D.M.; Li, P. Plant diversity, ground biomass characteristics and their relationships of typical plantations in the alpine region of Qinghai. Acta Ecol. Sin. 2020, 40, 692–700. [Google Scholar]
- Cao, H. The Hydrological Function of the Soil and Litter for Different Artificial Forest in Alpine Region of Qinghai. Master’s Thesis, Beijing Frestry University, Beijing, China, 2014. [Google Scholar]
- Zeng, W.S.; Xiao, Q.H. Study on Explainable Ability of Various Diameters of Saplings to Individual Volume and Biomass. Cent. South For. Inventory Plan. 2011, 30, 1–4. [Google Scholar]
- Zhang, R.S.; Wang, Q.; Liu, Y.P. Research on Diameter and DBH of Pinusdensiflora on Sand Landof Northwestern Liaoning Province Based on the Regression Analysis. J. Jilin For. Sci. Technol. 2018, 47, 17–19. [Google Scholar]
- LY/T 2259-2014; Technical Regulation on Sample Collections for Tree Biomass Modeling. State Forestry Administration: Beijing, China, 2014.
- LY/T 2258-2014; Technical Regulation on Methodology for Tree Biomass Modeling. State Forestry Administration: Beijing, China, 2014.
- Dong, L.; Zhang, L.; Li, F. Additive biomass equations based on different dendrometric variables for two dominant species (Larix gmelini Rupr. and Betula platyphylla Suk.) in natural forests in the Eastern Daxing’an Mountains, Northeast China. Forests 2018, 9, 261. [Google Scholar] [CrossRef]
- Zeng, W.S. Comparison of Different Weight Functions in Weighted Regression. For. Resour. Manag. 2013, 5, 55–61. [Google Scholar]
- Dutcă, I.; McRoberts, R.E.; Næsset, E.; Blujdea, V.N. Accommodating heteroscedasticity in allometric biomass models. For. Ecol. Manag. 2022, 505, 119865. [Google Scholar] [CrossRef]
- Zeng, W.S.; Tang, S.Z. Goodness Evaluation and Precision Analysis of Tree Biomass Equations. Sci. Silvae Sin. 2011, 47, 106–113. [Google Scholar]
- Cai, H.D.; Nong, S.Q.; Zhang, W. The research and construction of the main tree biomass model in Guangxi. For. Resour. Manag. 2014, 66, 58–61. [Google Scholar]
- Li, Y.F.; Qin, J.S.; Ma, J.M.; Yang, Z.Q.; Li, M.J.; Lu, S.H.; Song, Z.R. Establishment of above-ground biomass model and distribution characteristics of Pinus massoniana plantations in southern subtropical. J. Guangxi Norm. Univ. (Nat. Sci. Ed.) 2021, 39, 170–180. [Google Scholar]
- Alvarez, E.; Duque, A.; Saldarriaga, J.; Cabrera, K.; de Las Salas, G.; del Valle, I.; Lema, A.; Moreno, F.; Orrego, S.; Rodríguez, L. Tree above-ground biomass allometries for carbon stocks estimation in the natural forests of Colombia. For. Ecol. Manag. 2012, 267, 297–308. [Google Scholar] [CrossRef]
- LY/T 2655-2016; Tree Biomass Models and Related Parameters to Carbon Accounting for Picea. State Forestry Administration: Beijing, China, 2016.
- LY/T 2660-2014; Tree Biomass Models and Related Parameters to Carbon Accounting for Pinus Tabulaeformis. State Forestry Administration: Beijing, China, 2014.
- Wang, F.; Guo, Y.D.; Zhang, Q.L. Construction of Xing’an Following Leaves Pine Forest Biomass Model. J. Inn. Mong. Agric. Univ. (Nat. Sci. Ed.) 2015, 36, 44–47. [Google Scholar]
- Bond, L.B.; Wang, C.; Gower, S.T. Aboveground and belowground biomass and sapwood area allometric equations for sixboreal tree species of northern Manitoba. Can. J. For. Res. 2002, 32, 1441–1450. [Google Scholar] [CrossRef]


| Variable Name | Picea crassifolia | Pinus tabuliformis | Sabina przewalskii | ||||||
|---|---|---|---|---|---|---|---|---|---|
| AVG | Range | SD | AVG | Range | SD | AVG | Range | SD | |
| Base Diameter (D)/cm | 4.71 | 0.82–10.5 | 2.66 | 4.33 | 0.87–9.0 | 2.26 | 4.62 | 0.62–10.9 | 3.09 |
| Crown Diameter (C)/m | 1.07 | 0.16–2.67 | 0.66 | 0.95 | 0.29–2.88 | 0.66 | 3.90 | 1.55–7.75 | 1.66 |
| Tree Height (H)/m | 1.70 | 0.30–4.45 | 1.04 | 1.62 | 0.46–3.48 | 0.81 | 1.38 | 0.39–3.47 | 0.81 |
| Leaf Biomass/kg | 1.57 | 0.008–6.0 | 1.76 | 0.62 | 0.026–3.2 | 0.83 | 0.60 | 0.005–2.3 | 0.67 |
| Branch Biomass/kg | 1.20 | 0.004–6.4 | 1.46 | 0.47 | 0.01–2.8 | 0.69 | 0.37 | 0.002–2.2 | 0.51 |
| Trunk Biomass/kg | 0.85 | 0.005–4.2 | 1.08 | 0.68 | 0.013–3.6 | 1.02 | 0.36 | 0.003–2.4 | 0.51 |
| Root Biomass/kg | 0.88 | 0.006–3.9 | 0.98 | 0.59 | 0.02–3.04 | 0.86 | 0.57 | 0.004–2.8 | 0.71 |
| Relevance | D | C | H | CH | DH | D2H | C2H | D2C | |
|---|---|---|---|---|---|---|---|---|---|
| Picea crassifolia | Leaves | 0.893 ** | 0.887 ** | 0.913 ** | 0.910 ** | 0.944 ** | 0.928 ** | 0.842 ** | 0.888 ** |
| Branches | 0.888 ** | 0.903 ** | 0.828 ** | 0.885 ** | 0.904 ** | 0.931 ** | 0.856 ** | 0.968 ** | |
| Trunk | 0.891 ** | 0.904 ** | 0.900 ** | 0.945 ** | 0.965 ** | 0.984 ** | 0.911 ** | 0.972 ** | |
| Root | 0.877 ** | 0.860 ** | 0.825 ** | 0.829 ** | 0.877 ** | 0.884 ** | 0.762 ** | 0.889 ** | |
| Sum | 0.934 ** | 0.935 ** | 0.915 ** | 0.941 ** | 0.972 ** | 0.980 ** | 0.888 ** | 0.975 ** | |
| Pinus tabuliformis | Leaves | 0.866 ** | 0.918 ** | 0.813 ** | 0.929 ** | 0.902 ** | 0.925 ** | 0.907 ** | 0.960 ** |
| Branches | 0.847 ** | 0.936 ** | 0.808 ** | 0.953 ** | 0.895 ** | 0.919 ** | 0.950 ** | 0.966 ** | |
| Trunk | 0.888 ** | 0.904 ** | 0.850 ** | 0.943 ** | 0.952 ** | 0.988 ** | 0.908 ** | 0.980 ** | |
| Root | 0.806 ** | 0.905 ** | 0.770 ** | 0.890 ** | 0.838 ** | 0.853 ** | 0.866 ** | 0.896 ** | |
| Sum | 0.883 ** | 0.946 ** | 0.840 ** | 0.960 ** | 0.930 ** | 0.956 ** | 0.937 ** | 0.984 ** | |
| Sabina przewalskii | Leaves | 0.859 ** | 0.908 ** | 0.938 ** | 0.950 ** | 0.924 ** | 0.865 ** | 0.916 ** | 0.874 ** |
| Branches | 0.789 ** | 0.860 ** | 0.917 ** | 0.963 ** | 0.922 ** | 0.876 ** | 0.965 ** | 0.903 ** | |
| Trunk | 0.737 ** | 0.840 ** | 0.884 ** | 0.949 ** | 0.888 ** | 0.845 ** | 0.970 ** | 0.877 ** | |
| Root | 0.803 ** | 0.825 ** | 0.896 ** | 0.916 ** | 0.904 ** | 0.845 ** | 0.904 ** | 0.886 ** | |
| Sum | 0.837 ** | 0.896 ** | 0.949 ** | 0.984 ** | 0.950 ** | 0.923 ** | 0.975 ** | 0.895 ** | |
| Tree Species | Component | Models | Evaluation Indicators | |||||
|---|---|---|---|---|---|---|---|---|
| R2 | SEE (kg) | MPE (%) | TRE (%) | ASE (%) | MPSE (%) | |||
| Picea crassifolia n = 41 | Leaves | M = 0.0292D2.3167 | 0.832 | 0.73 | 14.7 | −0.03 | −7.8 | 27.8 |
| M = 0.0736D1.4174 × H0.8874 | 0.888 | 0.6 | 12.18 | −0.02 | −5.97 | 26.68 | ||
| M = 0.0566D1.8808 × C0.400 | 0.838 | 0.73 | 14.66 | −0.04 | −8.25 | 27.66 | ||
| Branches | M = 0.0133D2.5840 | 0.911 | 0.44 | 11.55 | 0.00 | −3.41 | 27.39 | |
| M = 0.0105D2.8034 × H−0.2157 | 0.913 | 0.44 | 11.55 | 0.00 | −3.39 | 27.58 | ||
| M = 0.0488D1.7228 × C0.7957 | 0.936 | 0.38 | 9.9 | 0.00 | −3.16 | 27.44 | ||
| Trunk | M = 0.0056D2.8441 | 0.929 | 0.29 | 10.79 | 0.00 | 10.29 | 23.51 | |
| M = 0.0101D2.0347 × H1.0277 | 0.969 | 0.2 | 7.23 | 2.16 | 17.19 | 25.93 | ||
| M = 0.0172D2.1072 × C0.6717 | 0.948 | 0.25 | 9.36 | 0.00 | 0.68 | 20.43 | ||
| Root | M = 0.021D2.198 | 0.827 | 0.41 | 14.78 | 0.00 | −6.7 | 38.92 | |
| M = 0.021D2.18 × H0.018 | 0.827 | 0.42 | 14.98 | 0.00 | −6.70 | 38.93 | ||
| M = 0.035D1.8491 × C0.322 | 0.828 | 0.42 | 14.95 | 0.00 | −6.60 | 38.80 | ||
| Sum | M = 0.064D2.458 | 0.960 | 1.02 | 7.14 | 0.00 | −3.95 | 18.42 | |
| M = 0.098D2.048 × H0.403 | 0.972 | 0.86 | 6.02 | 0.00 | −3.63 | 17.89 | ||
| M = 0.159D1.853 × C0.557 | 0.972 | 0.86 | 6.06 | 0.00 | −4.12 | 18.07 | ||
| Pinus tabuliformis n = 27 | Leaves | M = 0.0106D2.5002 | 0.867 | 0.31 | 19.64 | 0.03 | 8.52 | 32.13 |
| M = 0.0131D2.2799 × H0.2271 | 0.868 | 0.32 | 20.3 | 0.07 | 6.47 | 29.11 | ||
| M = 0.0572D1.4129 × C0.8408 | 0.925 | 0.24 | 15.08 | 0.01 | 1.13 | 23.47 | ||
| Branches | M = 0.0045D2.8083 | 0.835 | 0.29 | 23.88 | 0.00 | 7.52 | 41.17 | |
| M = 0.0068D2.3661 × H0.4915 | 0.842 | 0.29 | 23.93 | 0.00 | 5.19 | 36.55 | ||
| M = 0.0668D1.0731 × C1.3120 | 0.954 | 0.15 | 12.85 | −0.01 | −3.92 | 27.14 | ||
| Trunk | M = 0.0038D3.0850 | 0.974 | 0.17 | 9.79 | 0.04 | −9.83 | 33.66 | |
| M = 0.0072D2.3241 × H0.9052 | 0.982 | 0.14 | 8.36 | 0.01 | −0.21 | 28.35 | ||
| M = 0.0112D2.3979 × C0.5109 | 0.977 | 0.16 | 9.36 | 0.05 | 14.78 | 35.53 | ||
| Root | M = 0.007D2.663 | 0.733 | 0.45 | 30.63 | 0.00 | 7.9 | 66.38 | |
| M = 0.015D1.896 × H0.814 | 0.729 | 0.47 | 31.56 | 0.03 | −0.69 | 52.53 | ||
| M = 0.239D0.405 × C0.1.72 | 0.83 | 0.37 | 24.74 | −0.07 | −10.90 | 39.30 | ||
| Sum | M = 0.024D2.766 | 0.92 | 0.97 | 16.36 | 0.01 | 13.35 | 39.88 | |
| M = 0.043D2.161 × H0.653 | 0.92 | 0.99 | 16.72 | 0.04 | 7.62 | 31.23 | ||
| M = 0.213D1.369 × C1.067 | 0.97 | 0.54 | 9.15 | 0.00 | −0.35 | 24.13 | ||
| Sabina przewalskii n = 28 | Leaves | M = 0.2467H1.9446 | 0.866 | 0.25 | 16.1 | −0.13 | −15.36 | 39.1 |
| M = 0.1432D0.4502 × H1.5075 | 0.878 | 0.24 | 15.74 | −0.14 | −15.97 | 36.92 | ||
| M = 0.0635C1.1437 × H1.1830 | 0.881 | 0.24 | 15.51 | −0.16 | −14.83 | 37.7 | ||
| Branches | M = 0.1040H2.4482 | 0.918 | 0.15 | 15.52 | −0.03 | −15.14 | 39.93 | |
| M = 0.0867D0.1533 × H2.2986 | 0.919 | 0.15 | 15.81 | −0.04 | −15.62 | 39.4 | ||
| M = 0.0348C0.9302 × H1.8203 | 0.932 | 0.14 | 14.46 | −0.05 | −14.78 | 38.82 | ||
| Trunk | M = 0.1081H2.3846 | 0.909 | 0.16 | 16.8 | −0.01 | −7.78 | −38.42 | |
| M = 0.1030D0.0495 × H2.3212 | 0.907 | 0.16 | 17.32 | 0.06 | −8.55 | 39.08 | ||
| M = 0.0225C1.3266 × H1.4931 | 0.94 | 0.13 | 13.95 | 0.03 | −6.34 | 37.66 | ||
| Root | M = 0.036H1.666 | 0.682 | 0.41 | 27.85 | −0.02 | −8.33 | 64.59 | |
| M = 0.148D0.274 × H1.856 | 0.846 | 0.29 | 19.81 | −0.02 | −15.51 | 46.46 | ||
| M = 0.195C0.059 × H2.067 | 0.84 | 0.29 | 20.18 | −0.05 | −15.88 | 47.57 | ||
| Sum | M = 0.113H1.698 | 0.73 | 1.21 | 24.71 | 0.00 | −8.96 | 56.44 | |
| M = 0.030D0.548 × H2.157 | 0.90 | 0.75 | 15.33 | 0.07 | −13.59 | 40.48 | ||
| M = 0.484C0.261 × H1.923 | 0.95 | 0.52 | 10.63 | −0.03 | −14.32 | 32.94 | ||
| Tree Species | Models | Variables | Evaluation Indicators | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| a1 | b1 | m1 | a2 | b2 | m3 | a3 | b3 | m3 | a4 | b4 | m4 | |||
| Picea crassifolia | (4) | D | 0.042 | 2.139 | 0.009 | 2.749 | 0.005 | 2.935 | 0.021 | 2.187 | ||||
| D,H | 0.092 | 1.244 | 1.005 | 0.008 | 2.918 | −0.20 | 0.009 | 2.123 | 0.969 | 0.023 | 2.136 | 0.014 | ||
| D,C | 0.102 | 1.548 | 0.540 | 0.044 | 1.759 | 0.858 | 0.021 | 1.945 | 0.881 | 0.029 | 1.990 | 0.160 | ||
| (5) | D | 0.068 | 2.425 | 1.466 | −0.03 | 8.089 | −0.75 | 3.265 | −0.59 | |||||
| D,H | 0.093 | 2.023 | 0.490 | 0.943 | 0.747 | −1.10 | 10.25 | −0.86 | 0.007 | 2.673 | −0.04 | −0.89 | ||
| D,C | 0.183 | 1.764 | 0.625 | 2.197 | −0.21 | −0.03 | 4.853 | −0.40 | −0.34 | 1.479 | 0.010 | −0.72 | ||
| Pinus tabuliformis | (4) | D | 0.007 | 2.693 | 0.004 | 2.847 | 0.002 | 3.359 | 0.007 | 2.665 | ||||
| D,H | 0.005 | 2.744 | 0.228 | 0.004 | 2.269 | 1.139 | 0.003 | 2.782 | 0.762 | 0.006 | 2.474 | 0.589 | ||
| H,C | 1.151 | −1.70 | 2.996 | 0.848 | −1.84 | 3.328 | 0.300 | 0.933 | 1.331 | 1.760 | −2.51 | 3.545 | ||
| (5) | D | 0.017 | 2.932 | 1.764 | −0.47 | 3.097 | −0.63 | 3.019 | −0.65 | |||||
| D,H | 0.015 | 2.655 | 0.715 | 0.948 | −0.42 | 0.472 | 1.247 | 0.039 | −0.48 | 1.352 | −0.21 | −0.10 | ||
| H,C | 2.123 | −0.27 | 2.099 | 2.788 | −2.37 | 1.485 | 3.464 | −2.10 | 1.103 | 10.48 | −4.30 | 2.605 | ||
| Sabina przewalskii | (4) | H | 0.299 | 1.710 | 0.118 | 2.308 | 0.085 | 2.624 | 0.232 | 1.977 | ||||
| D,H | 0.206 | 0.306 | 1.420 | 0.107 | 0.080 | 2.232 | 0.100 | −0.13 | 2.736 | 0.162 | 0.287 | 1.718 | ||
| H,C | 0.094 | 0.993 | 1.012 | 0.029 | 1.438 | 1.220 | 0.010 | 1.251 | 1.886 | 0.129 | 1.616 | 0.513 | ||
| (5) | H | 0.713 | 2.080 | 1.409 | −0.33 | 3.651 | −0.95 | 2.805 | −0.67 | |||||
| D,H | 0.575 | 0.172 | 1.924 | 1.104 | 0.199 | −0.52 | 2.208 | 0.409 | −1.33 | 1.727 | 0.387 | −1.02 | ||
| H,C | 0.209 | 1.309 | 1.078 | 2.952 | 0.177 | −0.67 | 9.498 | −0.31 | −0.86 | 13.02 | 0.353 | −1.38 | ||
| Tree Species | Models | Variables | R2 | SEE | MPE | TRE | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Leaves | Branches | Trunk | Root | Sum | Leaves | Branches | Trunk | Root | Sum | Leaves | Branches | Trunk | Root | Sum | Leaves | Branches | Trunk | Root | Sum | |||
| Picea crassifolia | (4) | D | 0.838 | 0.913 | 0.928 | 0.827 | 0.960 | 0.72 | 0.45 | 0.31 | 0.45 | 1.14 | 14.46 | 11.75 | 11.49 | 16.16 | 8.10 | −1.34 | 1.55 | 1.05 | 0.11 | 0.16 |
| D,H | 0.891 | 0.915 | 0.969 | 0.827 | 0.974 | 0.59 | 0.44 | 0.20 | 0.45 | 0.93 | 11.88 | 11.64 | 7.58 | 16.17 | 6.56 | 0.24 | 1.30 | 2.24 | −0.5 | 0.75 | ||
| D,C | 0.844 | 0.938 | 0.948 | 0.829 | 0.972 | 0.70 | 0.38 | 0.26 | 0.45 | 0.95 | 14.19 | 9.94 | 9.73 | 16.10 | 6.75 | −1.17 | 0.93 | 0.98 | −0.3 | 0.0 | ||
| (5) | D | 0.840 | 0.912 | 0.929 | 0.827 | 0.960 | 0.71 | 0.45 | 0.31 | 0.45 | 1.14 | 14.37 | 11.79 | 11.39 | 16.19 | 8.05 | −2.31 | 2.11 | −0.42 | 0.99 | −0.1 | |
| D,H | 0.891 | 0.912 | 0.968 | 0.828 | 0.973 | 0.59 | 0.45 | 0.21 | 0.45 | 0.94 | 11.85 | 11.82 | 7.69 | 16.14 | 6.67 | 0.16 | 1.72 | 2.25 | 0.09 | 0.97 | ||
| D,C | 0.844 | 0.937 | 0.948 | 0.829 | 0.972 | 0.70 | 0.38 | 0.26 | 0.45 | 0.95 | 14.17 | 9.97 | 9.75 | 16.10 | 6.73 | −0.43 | 1.01 | 1.42 | −0.2 | 0.35 | ||
| Pinus tabuliformis | (4) | D | 0.870 | 0.836 | 0.977 | 0.733 | 0.917 | 0.30 | 0.30 | 0.17 | 0.52 | 1.17 | 19.38 | 24.99 | 10.10 | 35.71 | 20.14 | 1.66 | 0.31 | 2.38 | 0.55 | 1.32 |
| D,H | 0.867 | 0.842 | 0.987 | 0.729 | 0.918 | 0.31 | 0.29 | 0.13 | 0.52 | 1.16 | 19.64 | 24.50 | 7.73 | 35.96 | 20.01 | 6.51 | 7.10 | 3.26 | 6.66 | 5.73 | ||
| H,C | 0.860 | 0.932 | 0.877 | 0.864 | 0.961 | 0.32 | 0.19 | 0.40 | 0.37 | 0.80 | 20.09 | 16.12 | 23.42 | 25.47 | 13.73 | 9.41 | 8.58 | 3.78 | 1.99 | 0.83 | ||
| (5) | D | 0.870 | 0.836 | 0.977 | 0.732 | 0.916 | 0.30 | 0.30 | 0.17 | 0.52 | 1.17 | 19.39 | 24.99 | 10.13 | 35.73 | 20.17 | 2.38 | 1.08 | 2.40 | 1.54 | 1.92 | |
| D,H | 0.863 | 0.838 | 0.987 | 0.724 | 0.915 | 0.31 | 0.30 | 0.13 | 0.53 | 1.18 | 19.94 | 24.83 | 7.74 | 36.28 | 20.32 | 8.95 | 9.86 | 3.40 | 9.50 | 7.67 | ||
| H,C | 0.883 | 0.947 | 0.888 | 0.864 | 0.932 | 0.29 | 0.17 | 0.38 | 0.37 | 1.06 | 18.40 | 14.16 | 22.30 | 25.44 | 18.19 | 2.49 | 1.78 | 1.73 | 0.42 | 1.61 | ||
| Sabina przewalskii | (4) | H | 0.880 | 0.922 | 0.911 | 0.842 | 0.953 | 0.23 | 0.15 | 0.17 | 0.33 | 0.61 | 15.22 | 15.86 | 18.18 | 22.69 | 12.72 | −3.30 | −1.43 | 4.72 | −1.5 | −0.9 |
| D,H | 0.891 | 0.922 | 0.913 | 0.848 | 0.956 | 0.22 | 0.15 | 0.17 | 0.32 | 0.59 | 14.54 | 15.83 | 18.05 | 22.24 | 12.33 | −3.26 | −1.43 | 4.56 | −1.2 | −0.8 | ||
| H,C | 0.899 | 0.938 | 0.944 | 0.846 | 0.968 | 0.22 | 0.13 | 0.13 | 0.32 | 0.50 | 13.99 | 14.13 | 14.49 | 22.44 | 10.43 | −4.47 | −2.50 | 2.62 | −1.9 | −2.0 | ||
| (5) | H | 0.883 | 0.922 | 0.910 | 0.842 | 0.953 | 0.23 | 0.15 | 0.17 | 0.33 | 0.61 | 15.04 | 15.83 | 18.34 | 22.70 | 12.67 | −3.05 | −0.97 | 5.39 | −1.1 | −0.5 | |
| D,H | 0.893 | 0.922 | 0.911 | 0.848 | 0.956 | 0.22 | 0.15 | 0.17 | 0.32 | 0.59 | 14.42 | 15.82 | 18.23 | 22.27 | 12.36 | −2.87 | −0.90 | 5.40 | −0.7 | −0.3 | ||
| H,C | 0.903 | 0.938 | 0.943 | 0.845 | 0.969 | 0.21 | 0.13 | 0.14 | 0.32 | 0.49 | 13.73 | 14.09 | 14.61 | 22.45 | 10.32 | −4.54 | −2.06 | 3.31 | −1.2 | −1.6 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mao, C.; Yi, L.; Xu, W.; Dai, L.; Bao, A.; Wang, Z.; Zheng, X. Study on Biomass Models of Artificial Young Forest in the Northwestern Alpine Region of China. Forests 2022, 13, 1828. https://doi.org/10.3390/f13111828
Mao C, Yi L, Xu W, Dai L, Bao A, Wang Z, Zheng X. Study on Biomass Models of Artificial Young Forest in the Northwestern Alpine Region of China. Forests. 2022; 13(11):1828. https://doi.org/10.3390/f13111828
Chicago/Turabian StyleMao, Chunyan, Lubei Yi, Wenqiang Xu, Li Dai, Anming Bao, Zhengyu Wang, and Xueting Zheng. 2022. "Study on Biomass Models of Artificial Young Forest in the Northwestern Alpine Region of China" Forests 13, no. 11: 1828. https://doi.org/10.3390/f13111828
APA StyleMao, C., Yi, L., Xu, W., Dai, L., Bao, A., Wang, Z., & Zheng, X. (2022). Study on Biomass Models of Artificial Young Forest in the Northwestern Alpine Region of China. Forests, 13(11), 1828. https://doi.org/10.3390/f13111828






