Evaluation of Softwood Timber Quality—A Case Study on Two Silvicultural Systems in Central Germany
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Sites and Study Objects
2.1.1. Annual Ring Analysis
2.1.2. Wood Density
2.1.3. Visual Timber Grading and Four-Point Bending Strength
2.1.4. Point Cloud Processing
2.2. Statistical Analysis
3. Results
3.1. Mean Ring Width and Mean Density
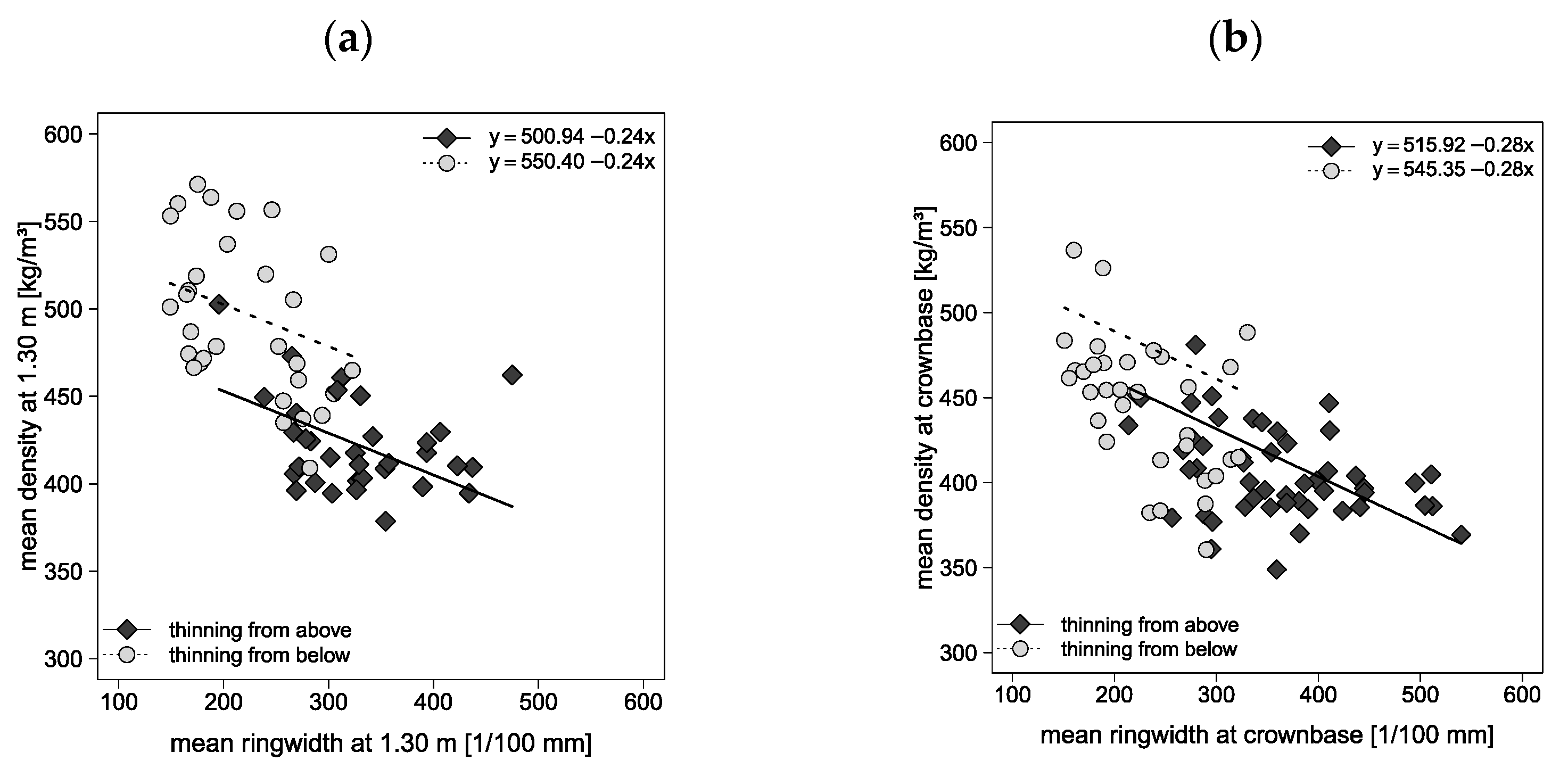
3.2. Relation between Mean Ring Width and Mean Density
3.3. Visual Timber Grading and Bending Strength
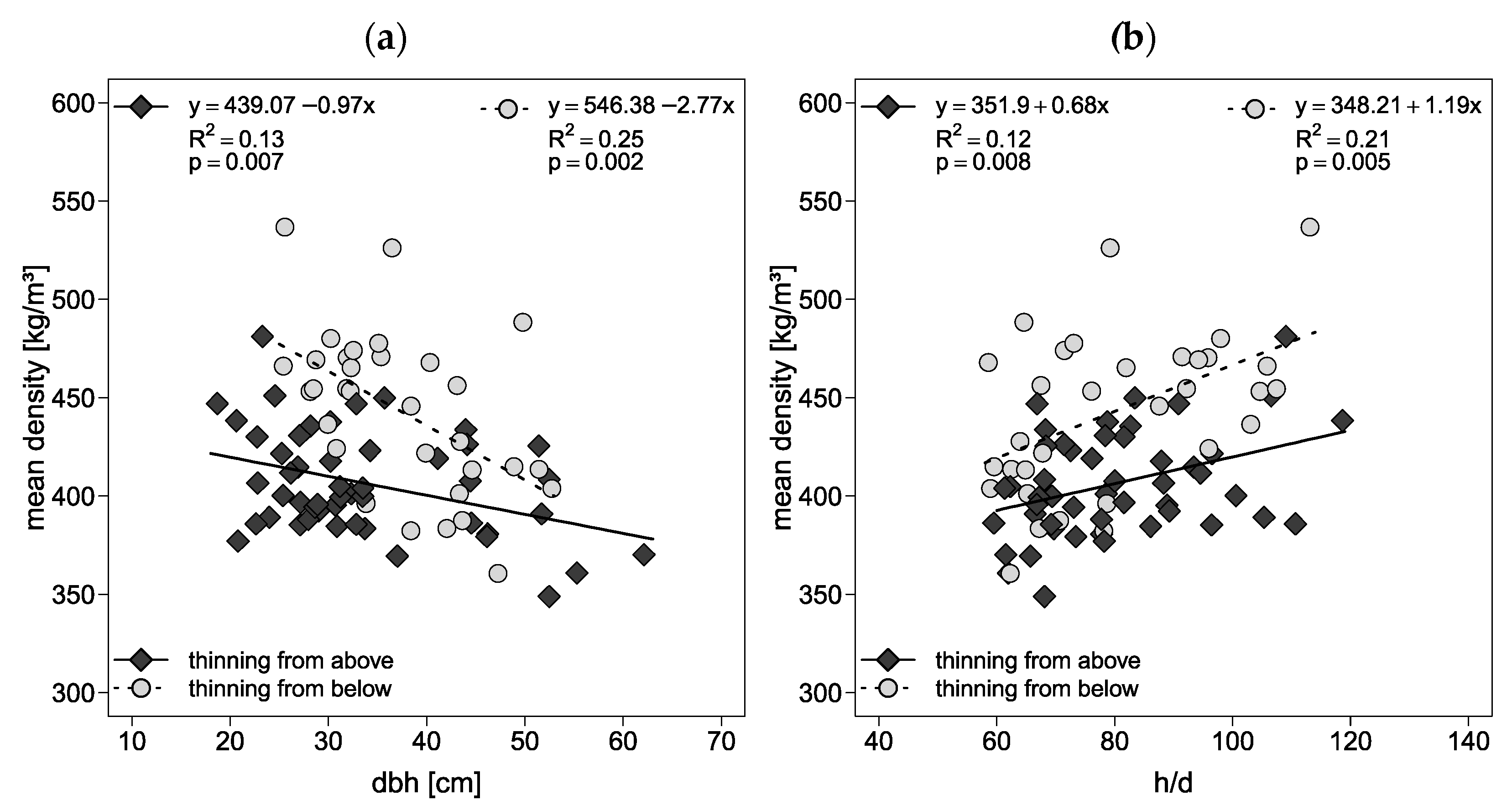
3.4. Relationship between Tree Morphology and Mean Density
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- IPCC. Summary for Policymakers. In Climate Change and Land: An IPCC Special Report on Climate Change, Desertification, Land Degradation, Sustainable Land Management, Food Security, and Greenhouse Gas Fluxes in Terrestrial Ecosystems; Shukla, P.R., Skea, J., Buendia, E.C., Masson-Delmotte, V., Pörtner, H.-O., Roberts, D.C., Zhai, P., Slade, R., Connors, S., van Diemen, R., et al., Eds.; IPCC: Geneva, Switzerland, 2019; Available online: https://www.ipcc.ch/srccl/ (accessed on 26 September 2022).
- BMEL. Deutschlands Wald im Klimawandel-Eckpunkte und Maßnahmen: Diskussionspapier zum Nationalen Waldgipfel. 25 September 2019. Available online: https://www.bmel.de/SharedDocs/Downloads/DE/Broschueren/waldgipfel-2019-diskussionspapier.html (accessed on 28 January 2021).
- Schuldt, B.; Buras, A.; Arend, M.; Vitasse, Y.; Beierkuhnlein, C.; Damm, A.; Gharun, M.; Grams, T.E.; Hauck, M.; Hajek, P.; et al. A first assessment of the impact of the extreme 2018 summer drought on Central European forests. Basic Appl. Ecol. 2020, 45, 86–103. [Google Scholar] [CrossRef]
- Spiecker, H. (Ed.) Growth of Norway Spruce (Picea abies [L.] Karst.) under Changing Environmental Conditions in Europe. In Spruce Monocultures in Central Europe. Problems and Prospects; European Forest Institute: Joensuu, Finland, 2000. [Google Scholar]
- Spiecker, H. Silvicultural management in maintaining biodiversity and resistance of forests in Europe—Temperate zone. J. Environ. Manag. 2003, 67, 55–65. [Google Scholar] [CrossRef]
- von Lüpke, B.; Ammer, C.; Braciamacchie, M.; Brunner, A.; Ceitel, J.; Collet, C.; Deu-leuze, C.; Di Placido, J.; Huss, J.; Jankovic, J.; et al. Silvicultural strategies for conversion. In Norway Spruce Conversion—Options and Consequences; Spiecker, H., Hansen, J., Klimo, E., Skovsgaard, J., Sterba, H., von Teuffel, K., Eds.; Brill: Leiden, The Netherlands; Boston, MA, USA, 2004; pp. 121–164. [Google Scholar]
- Ammer, C.; Bickel, E.; Kölling, C. Converting Norway spruce stands with beech–a review of arguments and techniques. Austrian J. For. Sci. 2008, 125, 3–26. [Google Scholar]
- Röhrig, E.; Bartsch, N.; Lüpke, B.V. Waldbau auf Ökologischer Grundlage, 7; Vollständig Aktualisierte, Auflage; Ulmer: Stuttgart, Germany, 2006; ISBN 3800145952. [Google Scholar]
- Seifert, T.; Breibeck, J.; Nickel, M.; Klemmt, H.J.; Pretzsch, H. Holzeigenschaften der Fichte bei unterschiedlicher Bestandesdichte. AFZ-Der. Wald. 2009, 2, 89–91. [Google Scholar]
- Bartsch, N.; von Lüpke, B.; Röhrig, E. Waldbau auf ökologischer Grundlage, 8; Vollständig Überarbeitete und Erweiterte Auflage; Eugen Ulmer KG: Stuttgart, Germany, 2020; ISBN 978-3-8385-8754-7. [Google Scholar]
- Beinhofer, B. Weitständig erzogene Nadelholzbestände–eine lukrative Alternative? Allg. Forst-Und Jagdzeitung. 2009, 180, 65–75. [Google Scholar]
- Kollmann, F.F.P.; Côté, W.A. Solid wood. In Principles of Wood Science and Technology; Springer: Tokyo, Japan, 1984; Volume 1, p. 180. [Google Scholar]
- Mäkinen, H.; Saranpää, P.; Linder, S. Wood-density variation of Norway spruce in relation to nutrient optimization and fibre dimensions. Can. J. For. Res. 2002, 32, 185–194. [Google Scholar] [CrossRef]
- Niemz, P.; Sonderegger, W. Holzphysik: Physik des Holzes und der Holzwerkstoffe; Carl Hanser Verlag GmbH Co KG: München, Germany, 2017; ISBN 3446445463. [Google Scholar]
- 4074-1:2012-06; Sortierung von Holz nach der Tragfähigkeit-Teil 1: Nadelschnittholz. Beuth Verlag GmbH: Berlin, Germany, 2012.
- 338:2016-07; Bauholz für tragende Zwecke-Festigkeitsklassen: Deutsche Fassung EN 338:2016. Beuth Verlag GmbH: Berlin, Germany, 2016.
- Ammer, C. Diversity and forest productivity in a changing climate. New Phytol. 2019, 221, 50–66. [Google Scholar] [CrossRef] [Green Version]
- Metz, J.; Seidel, D.; Schall, P.; Scheffer, D.; Schulze, E.-D.; Ammer, C. Crown modeling by terrestrial laser scanning as an approach to assess the effect of aboveground intra- and interspecific competition on tree growth. For. Ecol. Manag. 2013, 310, 275–288. [Google Scholar] [CrossRef]
- Liang, X.; Kankare, V.; Hyyppä, J.; Wang, Y.; Kukko, A.; Haggrén, H.; Yu, X.; Kaartinen, H.; Jaakkola, A.; Guan, F.; et al. Terrestrial laser scanning in forest inventories. ISPRS J. Photogramm. Remote Sens. 2016, 115, 63–77. [Google Scholar] [CrossRef]
- Höwler, K.; Annighöfer, P.; Ammer, C.; Seidel, D. Competition improves quality-related external stem characteristics of Fagus sylvatica. Can. J. For. Res. 2017, 47, 1603–1613. [Google Scholar] [CrossRef]
- Stal, C.; Verbeurgt, J.; de Sloover, L.; de Wulf, A. Assessment of handheld mobile terrestrial laser scanning for estimating tree parameters. J. For. Res. 2021, 32, 1503–1513. [Google Scholar] [CrossRef]
- Heidenreich, M.G.; Seidel, D. Assessing Forest Vitality and Forest Structure Using 3D Data: A Case Study From the Hainich National Park, Germany. Front. For. Glob. Chang. 2022, 5, 929106. [Google Scholar] [CrossRef]
- Neudam, L.; Annighöfer, P.; Seidel, D. Exploring the Potential of Mobile Laser Scanning to Quantify Forest Structural Complexity. Front. Remote Sens. 2022, 3. [Google Scholar] [CrossRef]
- Grammel, R. Zusammenhänge zwischen Wachstumsbedingungen und holztechnologischen Eigenschaften der Fichte. Eur. J. For. Res. 1990, 109, 119–129. [Google Scholar] [CrossRef]
- Dutilleul, P.; Herman, M.; Avella-Shaw, T. Growth rate effects on correlations among ring width, wood density, and mean tracheid length in Norway spruce (Picea abies). Can. J. For. Res. 1998, 28, 56–68. [Google Scholar] [CrossRef]
- Kraft, G. Beiträge zur Lehre von den Durchforstungen, Schlagstellungen und Lichtungshieben; Verlag Klindworth: Hannover, Germany, 1884. [Google Scholar]
- DWD. Climate Data Center. Available online: https://cdc.dwd.de/portal/ (accessed on 26 September 2022).
- DWD. Nutzung klimatologischer Referenzperioden ab 2021. Available online: https://www.dwd.de/DE/leistungen/besondereereignisse/verschiedenes/20210119_neue_referenzperiode.html (accessed on 27 October 2022).
- Williamson, G.B.; Wiemann, M.C. Measuring wood specific gravity…Correctly. Am. J. Bot. 2010, 97, 519–524. [Google Scholar] [CrossRef] [Green Version]
- 408:2022-10; Holzbauwerke-Bauholz für Tragende Zwecke und Brettschichtholz-Bestimmung Einiger Physikalischer Und Mechanischer Eigenschaften: Deutsche Fassung EN 408:2010 +A1:2012. Beuth Verlag GmbH: Berlin, Germany, 2012.
- Piboule, A.; Krebs, M.; Esclatine, L.; Hervé, J.C. (Eds.) Computree: A collaborative platform for use of terrestrial lidar in dendrometry. In Proceedings of the International IUFRO Conference MeMoWood, Nancy, France, 1–4 October 2013. [Google Scholar]
- Burkardt, K.; Annighöfer, P.; Seidel, D.; Ammer, C.; Vor, T. Intraspecific Competition Affects Crown and Stem Characteristics of Non-Native Quercus rubra L. Stands in Germany. Forests 2019, 10, 846. [Google Scholar] [CrossRef] [Green Version]
- Seidel, D.; Leuschner, C.; Müller, A.; Krause, B. Crown plasticity in mixed forests—Quantifying asymmetry as a measure of competition using terrestrial laser scanning. For. Ecol. Manag. 2011, 261, 2123–2132. [Google Scholar] [CrossRef]
- Seidel, D.; Schall, P.; Gille, M.; Ammer, C. Relationship between tree growth and physical dimensions of Fagus sylvatica crowns assessed from terrestrial laser scanning. Iforest-Biogeosci. For. 2015, 8, 735–742. [Google Scholar] [CrossRef]
- Juchheim, J.; Annighöfer, P.; Ammer, C.; Calders, K.; Raumonen, P.; Seidel, D. How management intensity and neighborhood composition affect the structure of beech (Fagus sylvatica L.) trees. Trees 2017, 31, 1723–1735. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; The R Foundation: Vienna, Austria, 2021; Available online: https://www.R-project.org/ (accessed on 26 September 2022).
- OriginLab Corporation. OriginPro, Distributor for Germany, Switzerland, Austria and Liechtenstein: Northampton, MA, USA; Additive GmbH: Friedrichsdorf, Germany, 2021.
- Bates, D.; Mächler, M.; Bolker, B.; Walker, S. Fitting Linear Mixed-Effects Models Using lme4. arXiv 2014, arXiv:1406.5823. [Google Scholar] [CrossRef]
- Lindström, H. Basic density in Norway spruce. Part, I. A literature review. Wood Fiber Sci. 1996, 28, 15–27. [Google Scholar]
- Jaakkola, T.; Mäkinen, H.; Saranpää, P. Wood density of Norway spruce: Responses to timing and intensity of first commercial thinning and fertilisation. For. Ecol. Manag. 2006, 237, 513–521. [Google Scholar] [CrossRef]
- Pretzsch, H.; Rais, A. Wood quality in complex forests versus even-aged monocultures: Review and perspectives. Wood Sci. Technol. 2016, 50, 845–880. [Google Scholar] [CrossRef]
- Krajnc, L.; Farrelly, N.; Harte, A.M. The effect of thinning on mechanical properties of Douglas fir, Norway spruce, and Sitka spruce. Ann. For. Sci. 2019, 76, 3. [Google Scholar] [CrossRef] [Green Version]
- Brüchert, F.; Becker, G.; Speck, T. The mechanics of Norway spruce [Picea abies (L.) Karst]: Mechanical properties of standing trees from different thinning regimes. For. Ecol. Manag. 2000, 135, 45–62. [Google Scholar] [CrossRef]
- Pape, R. Effects of Thinning Regime on the Wood Properties and Stem Quality of Picea abies. Scand. J. For. Res. 1999, 14, 38–50. [Google Scholar] [CrossRef]
- Pape, R. Influence of Thinning and Tree Diameter Class on the Development of Basic Density and Annual Ring Width in Picea abies. Scand. J. For. Res. 1999, 14, 27–37. [Google Scholar] [CrossRef]
- Lindström, H. Basic density in Norway spruce, Part III. Development from pith outwards. Wood Fiber Sci. 1996, 28, 391–405. [Google Scholar]
- Mäkinen, H.; Isomäki, A. Thinning intensity and growth of Norway spruce stands in Finland. Forestry 2004, 77, 349–364. [Google Scholar] [CrossRef] [Green Version]
- Jaakkola, T.; Mäkinen, H.; Saranpää, P. Wood density in Norway spruce: Changes with thinning intensity and tree age. Can. J. For. Res. 2005, 35, 1767–1778. [Google Scholar] [CrossRef]
- Pretzsch, H. (Ed.) Forest Dynamics, Growth and Yield; Springer: Berlin/Heidelberg, Germany, 2009; ISBN 978-3-540-88306-7. [Google Scholar]
- Hein, S. Knot attributes and occlusion of naturally pruned branches of Fagus sylvatica. For. Ecol. Manag. 2008, 256, 2046–2057. [Google Scholar] [CrossRef]
- Jyske, T.; Mäkinen, H.; Saranpää, P. Wood density within Norway spruce stems. Silva Fenn. 2008, 42, 439–455. [Google Scholar] [CrossRef] [Green Version]
- Knigge, W. Untersuchungen ueber die Beziehungen zwischen Holzeigenschaften und Wuchs der Gastbaumart Douglasie (Pseudotsuga taxifolia Britt.). In Schriftenreihe der Forstlichen Fakultaet der Universitaet Goettingen und Mitteilungen der Niedersaechsischen Forstlichen Versuchsanstalt (Bd. 20); J. D. Sauerländer’s Verlag, Frankfurt am Main: Bad Orb, Germany, 1958. [Google Scholar]
- Sauter, U. Technologische Holzeigenschaften der Douglasie (Pseudotsuga Menziesii (Mirb.) Franco) Als Ausprägung Unterschiedlicher Wachstumsbedingungen. Ph.D. Thesis. 1992. Available online: https://hal.archives-ouvertes.fr/hal-00981419 (accessed on 26 September 2022).
- Bachmann, P. Wirtschaftliche Überlegungen zur Waldpflege. Hespa Mitt. 1970, 20, 1–24. [Google Scholar]
- Kint, V.; Hein, S.; Campioli, M.; Muys, B. Modelling self-pruning and branch attributes for young Quercus robur L. and Fagus sylvatica L. trees. For. Ecol. Manag. 2010, 260, 2023–2034. [Google Scholar]
- Richter, C. Holzmerkmale der Bäume: Beschreibung der Merkmale, Ursachen, Vermeidung, Auswirkungen auf die Verwendung des Holzes, Technologische Anpassung, 1; Auflage; DRW-Verlag: Leinfelden-Echterdingen, Germany, 2019; ISBN 3871819352. [Google Scholar]
- Osborne, N.L.; Maguire, D.A. Modeling knot geometry from branch angles in Douglas-fir (Pseudotsuga menziesii). Can. J. For. Res. 2016, 46, 215–224. [Google Scholar] [CrossRef] [Green Version]
- 1927-1:2008-06; Qualitäts-Sortierung von Nadel-Rundholz-Teil 1: Fichten und Tannen: Deutsche Fassung EN 1927-1:2008. Beuth Verlag GmbH: Berlin, Germany, 2008.
- Burawska-Kupniewska, I.; Krzosek, S.; Mańkowski, P. Efficiency of Visual and Machine Strength Grading of Sawn Timber with Respect to Log Type. Forests 2021, 12, 1467. [Google Scholar] [CrossRef]
- 14081-1:2016+A1:2019; Holzbauwerke-Nach Festigkeit sortiertes Bauholz für tragende Zwecke mit rechteckigem Querschnitt: Teil 1: Allgemeine Anforderungen; Deutsche Fassung EN. Beuth Verlag GmbH: Berlin, Germany, 2019.
- Kessel, M.H.; Sandoz, J.L. Zur Effizienz der Festigkeitssortierung von Fichtenkantholz. Eur. J. Wood Prod. 1989, 47, 323–327. [Google Scholar] [CrossRef]
- Hecker, M.; Ressmann, J.; Becker, G.; Merforth, C. Prognose der Schnittholz-Qualität auf der Grundlage der Rundholz-Sortierung. Eur. J. Wood Prod. 2000, 58, 168–176. [Google Scholar] [CrossRef]
- Llana, D.F.; Short, I.; Harte, A.M. Use of non-destructive test methods on Irish hardwood standing trees and small-diameter round timber for prediction of mechanical properties. Ann. For. Sci. 2020, 77, 62. [Google Scholar] [CrossRef]
- Russo, D.; Marziliano, P.A.; Macri, G.; Proto, A.R.; Zimbalatti, G.; Lombardi, F. Does Thinning Intensity Affect Wood Quality? An Analysis of Calabrian Pine in Southern Italy Using a Non-Destructive Acoustic Method. Forests 2019, 10, 303. [Google Scholar] [CrossRef] [Green Version]
- Pretzsch, H. Density and growth of forest stands revisited. Effect of the temporal scale of observation, site quality, and thinning. For. Ecol. Manag. 2020, 460, 117879. [Google Scholar] [CrossRef]
- Kankare, V.; Joensuu, M.; Vauhkonen, J.; Holopainen, M.; Tanhuanpää, T.; Vastaranta, M.; Hyyppä, J.; Hyyppä, H.; Alho, P.; Rikala, J.; et al. Estimation of the Timber Quality of Scots Pine with Terrestrial Laser Scanning. Forests 2014, 5, 1879–1895. [Google Scholar] [CrossRef] [Green Version]
- Höwler, K.; Vor, T.; Seidel, D.; Annighöfer, P.; Ammer, C. Analyzing effects of intra-and interspecific competition on timber quality attributes of Fagus sylvatica L.—From quality assessments on standing trees to sawn boards. Eur. J. For. Res. 2019, 138, 327–343. [Google Scholar] [CrossRef]








| P2 | P3 | P4 | P5 | P6 | ||
|---|---|---|---|---|---|---|
| 226-2 | 227 A1 | 1528a | 2226c | 1517b2 | ||
| GPS-Coordinates (Degrees, Minutes, Seconds) | 50°52′31.39″ N 8°23′1.33″ E | 50°52′39.69″ N 8°23′25.71″ E | 51°43′01.0″ N 10°25′00.3″ E | 51°43′03.7″ N 10°25′16.9″ E | 51°42′13.9″ N 10°25′18.4″ E | |
| Site condition | Altitude above sea level | 450–490 m | 430–520 m | 551–600 m | 501–550 m | 551–600 m |
| Slope exposure | N (≤36%) | NW–W (≤36%) | N | S | S | |
| Soil condition | Mesotrophic | Mesotrophic | Mesotrophic | Mesptrophic | Mesotrophic | |
| Moisture condition | Moderately fresh | Moderately fresh | Fresh | Fresh | Fresh | |
| Annual average temp. 1 | 1961–1990 (7.7 °C); 1991–2020 (9.7 °C) 1961–1990 (902 mm); 1991–2020 (822 mm) | 1961–1990 (5.9 °C); 1991–2020 (6.9 °C) | ||||
| Annual total precipitation | 1961–1990 (1263 mm); 1991–2020 (1303 mm) | |||||
| Stand description | Share [%] | 100 | 100 | 95 | 90 | 100 |
| Area [ha] | 1.7 | 2.3 | 16.4 | 5.9 | 6.3 | |
| Tree species | PCAB 4 | PCAB | PCAB | PCAB | PCAB | |
| Age 2 | 41 | 83 | 80 | 80 | 39 | |
| Dominant height [m] | 30.8 | 29.3 | 18 | |||
| Basal area [m²∙ha−1] | 34.1 | 37.2 | 37.1 | 28.3 | 35 | |
| MAImax 3 | 17.8 | 11.4 | 12 | 11 | 12 | |
| Sample tree information | Mean height [m] | 25.3 | 29.8 | 33.8 | 28.2 | 20.5 |
| Mean DBH [cm] | 28.5 | 32.3 | 46.3 | 42.4 | 28.6 | |
| Visually graded boards | 132 | 97 | 231 | 177 | 59 | |
| Mechanically tested boards | 15 | 14 | 44 | 23 | 14 | |
| Thinning category | TFA 5 | TFB 6 | TFA | TFB | TFA | |
| Thinning interventions [m3∙ha−1] | 2012 (67) | 2012 (71) | 2014 (2.9); 2018 (12.7) | 2014 (25.9) | 2014 (41.3) | |
| Spearman’s Rank Correlation | Mean Ring Width | Mean Density | ||||
|---|---|---|---|---|---|---|
| DBH | CBH | DBH | CBH | |||
| mean ring width | DBH | ρ | 0.937 | −0.754 | −0.634 | |
| p value | <0.001 | <0.001 | <0.001 | |||
| CBH | ρ | −0.763 | −0.612 | |||
| p value | <0.001 | <0.001 | ||||
| mean density | DBH | ρ | 0.754 | |||
| p value | <0.001 | |||||
| Fixed Effects | Estimates | SE | df | t-Value | p-Value | R²m | R²c | Random Effect | Variance | SD | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| DBH | Intercept | 500.94 | 25.36 | 64 | 19.75 | <0.001 | 0.59 | 0.59 | SC 3 | 0.00 | 0.00 |
| MRW 1 | −0.24 | 0.07 | −3.28 | 0.002 | Residual | 1081 | 32.87 | ||||
| TFB 2 | 49.47 | 16.48 | 3.00 | 0.004 | |||||||
| Age 80 | −2.99 | 16.43 | −0.18 | 0.86 | |||||||
| CBH | Intercept | 515.92 | 19.70 | 83 | 26.20 | <0.001 | 0.47 | 0.47 | SC | 0.00 | 0.00 |
| MRW | −0.28 | 0.05 | −5.63 | <0.001 | Residual | 759.4 | 27.56 | ||||
| TFB | 29.43 | 9.40 | 3.13 | 0.002 | |||||||
| Age 80 | −34.30 | 10.21 | −3.36 | 0.001 | |||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Höwler, K.; Seidel, D.; Krenn, T.; Berthold, D.; Ehbrecht, M.; Müller, J.; Kietz, B. Evaluation of Softwood Timber Quality—A Case Study on Two Silvicultural Systems in Central Germany. Forests 2022, 13, 1910. https://doi.org/10.3390/f13111910
Höwler K, Seidel D, Krenn T, Berthold D, Ehbrecht M, Müller J, Kietz B. Evaluation of Softwood Timber Quality—A Case Study on Two Silvicultural Systems in Central Germany. Forests. 2022; 13(11):1910. https://doi.org/10.3390/f13111910
Chicago/Turabian StyleHöwler, Kirsten, Dominik Seidel, Tobias Krenn, Dirk Berthold, Martin Ehbrecht, Jan Müller, and Bettina Kietz. 2022. "Evaluation of Softwood Timber Quality—A Case Study on Two Silvicultural Systems in Central Germany" Forests 13, no. 11: 1910. https://doi.org/10.3390/f13111910
APA StyleHöwler, K., Seidel, D., Krenn, T., Berthold, D., Ehbrecht, M., Müller, J., & Kietz, B. (2022). Evaluation of Softwood Timber Quality—A Case Study on Two Silvicultural Systems in Central Germany. Forests, 13(11), 1910. https://doi.org/10.3390/f13111910






