Verifying the Lifting and Slewing Dynamics of a Harvester Crane with Possible Levelling When Operating on Sloping Grounds
Abstract
:1. Introduction
2. Materials and Methods
2.1. The Machine
2.2. 3D Model
2.2.1. The Components Provided
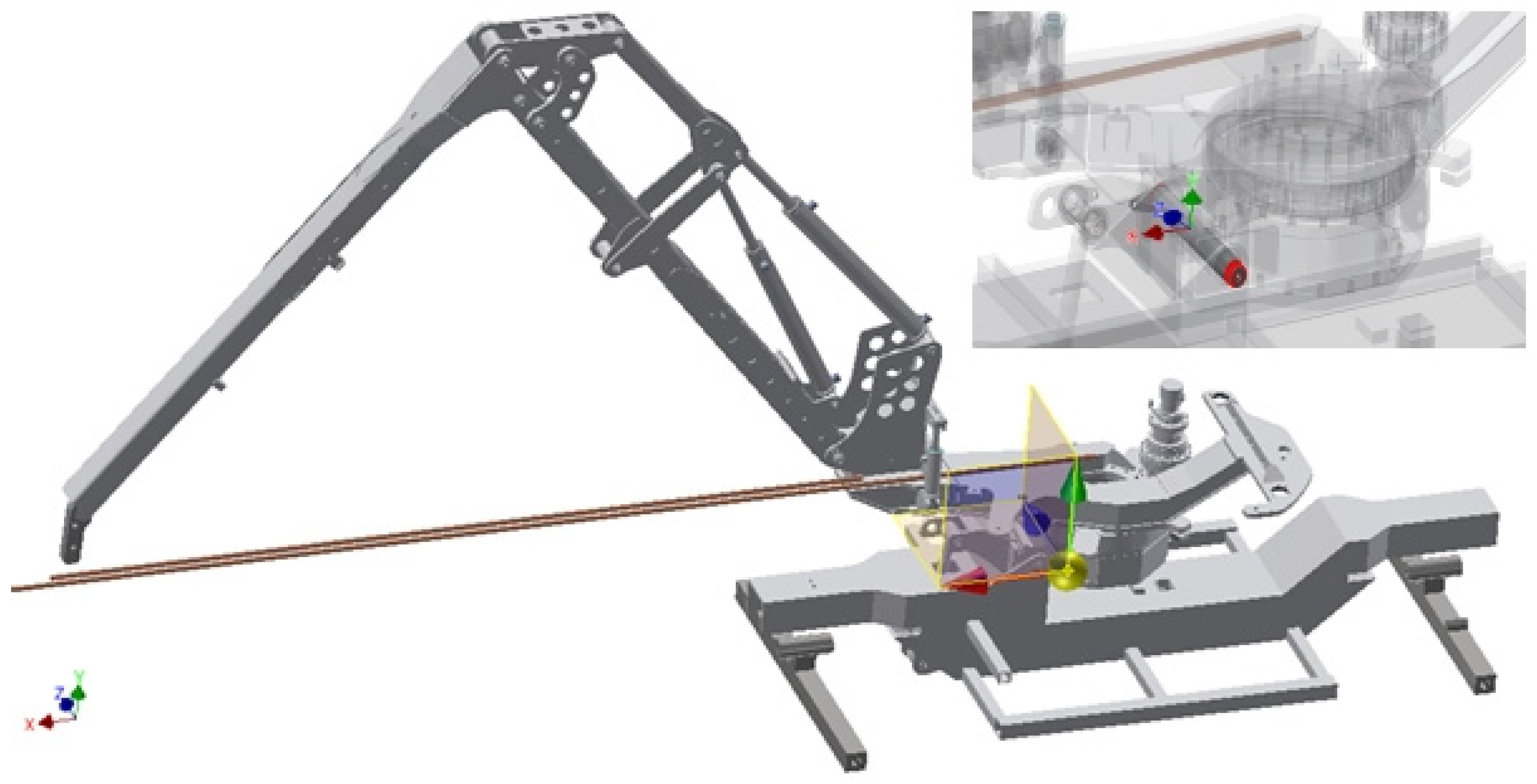
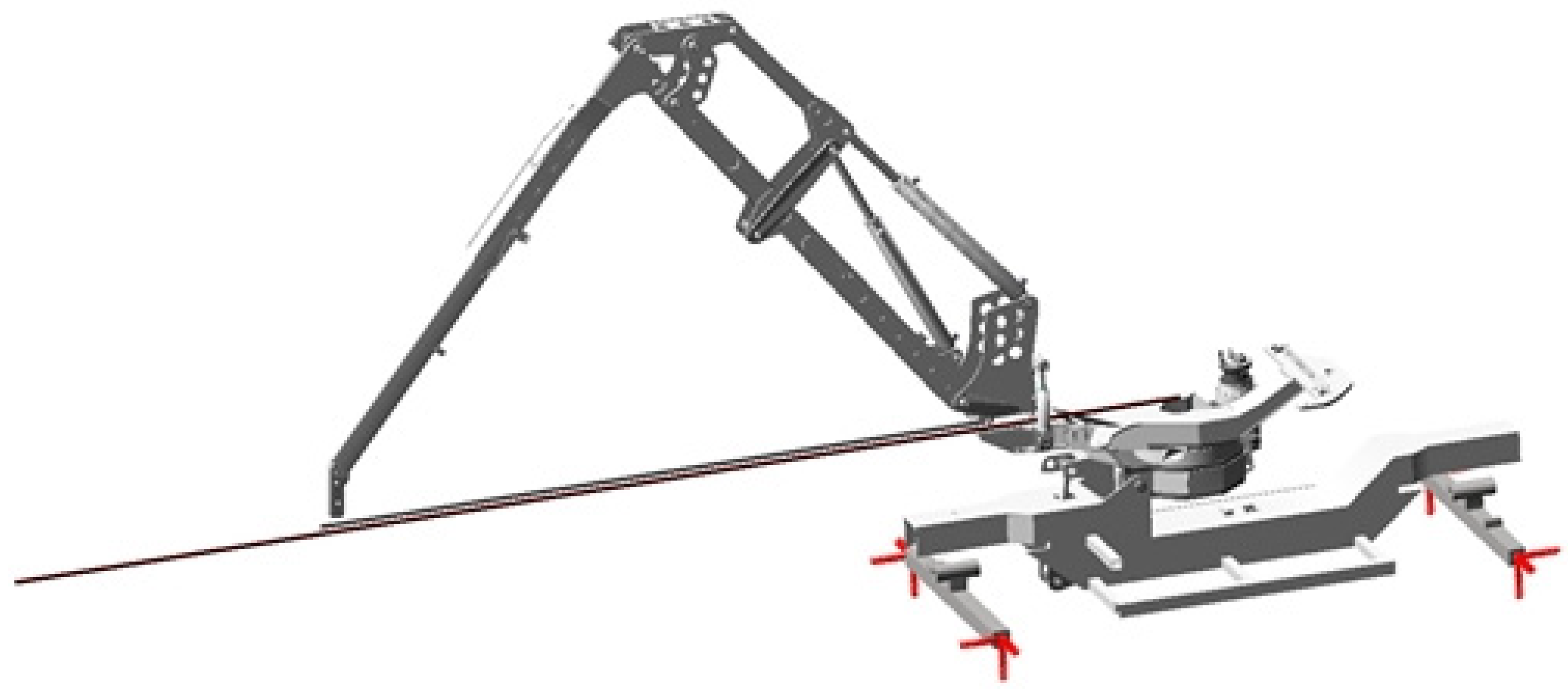
2.2.2. Coordinate System
2.3. Adams—The Numerical Simulation Model
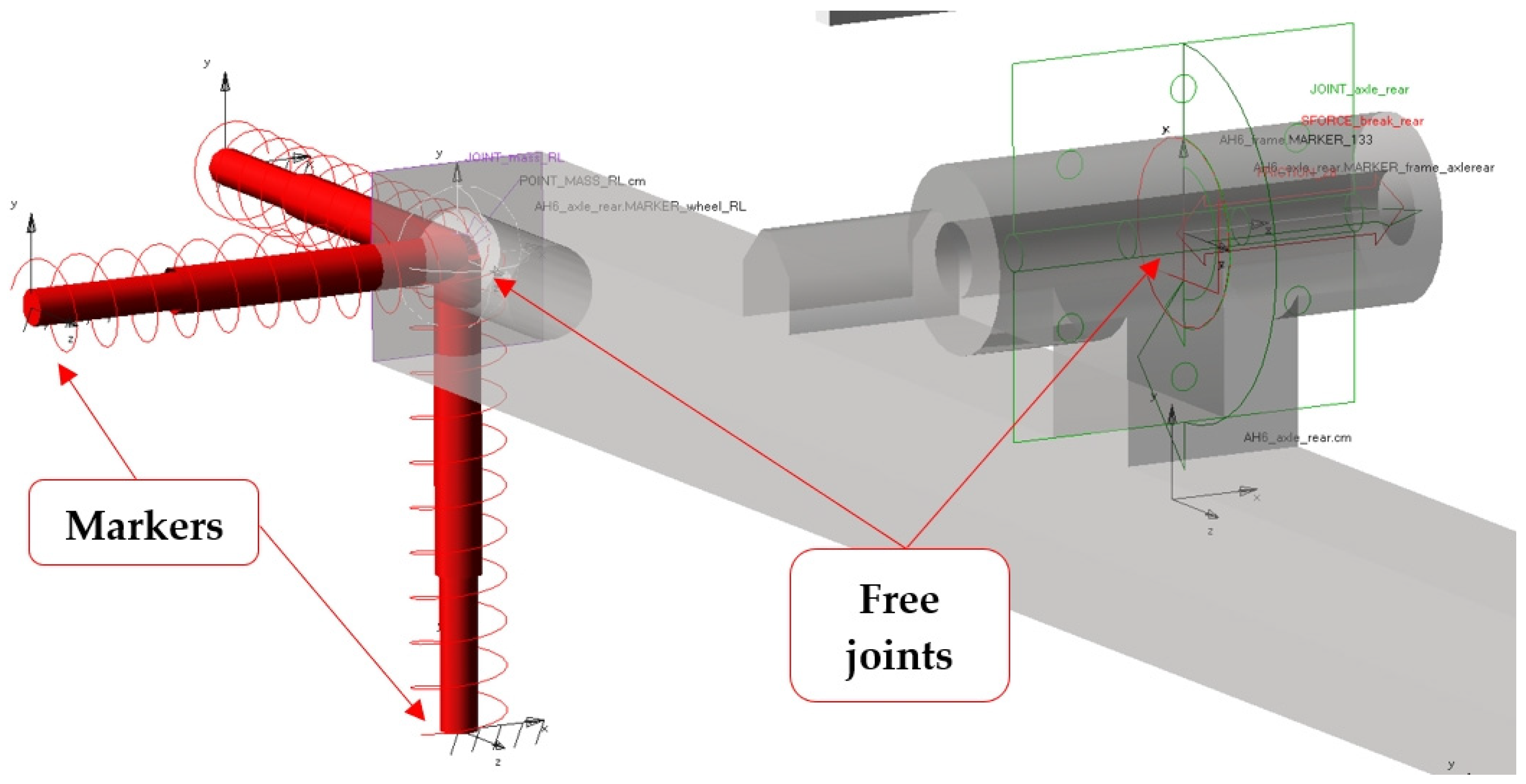
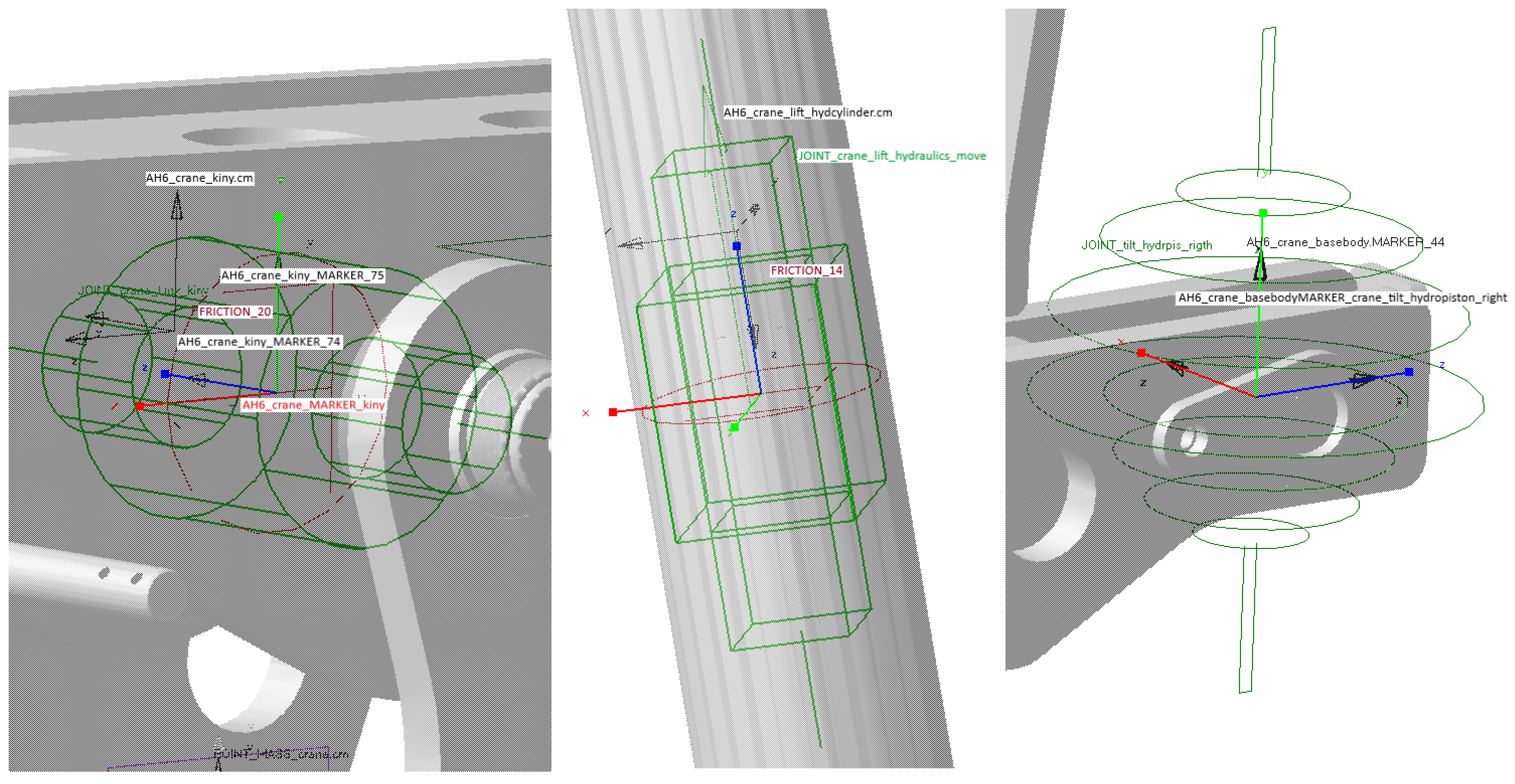
2.3.1. Joints between the Components
2.3.2. Types of Attachment of the Dynamic System
2.4. Validation of the Experiment
2.4.1. Determining the Lifting Torque
2.4.2. Determining the Slewing Torque
2.5. Statistical Analyses
3. Results
3.1. Lifting Torque of the Crane
3.2. Slewing Torque
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Visser, R.; Stampfer, K. Expanding Ground-based Harvesting onto Steep Terrain: A Review. Croat. J. For. Eng. 2015, 36, 321–331. [Google Scholar]
- Visser, R.; Berkett, H. Effect of terrain steepness on machine slope when harvesting. Int. J. For. Eng. 2015, 26, 1–9. [Google Scholar] [CrossRef]
- Enache, A.; Kühmaier, M.; Visser, R.; Stampfer, K. Forestry operations in the European mountains: A study of current practices and efficiency gaps. Scand. J. For. Res. 2016, 31, 412–427. [Google Scholar] [CrossRef]
- Cavalli, R.; Amishev, D. Steep terrain forest operations—challenges, technology development, current implementation, and future opportunities. Int. J. For. Eng. 2019, 30, 175–181. [Google Scholar] [CrossRef]
- Axelsson, S.Å. The mechanization of logging operations in Sweden and its effect on occupational safety and health. Int. J. For. Eng. 1998, 9, 25–31. [Google Scholar] [CrossRef]
- Bell, R.K. Changes in logging injury rates associated with use of feller-bunchers in West Virginia. J. Saf. Res. 2002, 33, 463–471. [Google Scholar] [CrossRef]
- Raymond, K. Innovative Harvesting Solutions: A Step Change Harvesting Research Programme. N. Z. J. For. 2010, 55, 4–9. [Google Scholar]
- Ghaffariyan, M.R.; Acuna, M.; Ackerman, P. Review of new ground-based logging technologies for steep terrain. CRC For. Bull. Hobart Tasman. Aust. 2012, 21, 1–5. [Google Scholar]
- Jodłowski, K.; Kalinowski, M. Current possibilities of mechanized logging in mountain areas. For. Res. Pap. 2018, 79, 365–375. [Google Scholar] [CrossRef] [Green Version]
- Neruda, J. Harvestorové Technologie Lesní Těžby, 1st ed.; Mendel University in Brno: Brno, Czech Republic, 2013; pp. 1–165. [Google Scholar]
- Schiess, P.; Schuh, D.; Miyata, E.S.; Mann, C.N. Concept Evaluation of a Walking Feller-Buncher—The Kaiser X5M Spider Concept Evaluation of a Walking Feller-Buncher—The Kaiser X5M Spider. In Proceedings of the 1st Technical Conference on Timber Harvesting in the Central Rockies, Ft. Collins, CO, USA, 4–6 January 1983; pp. 40–52. [Google Scholar]
- Amishev, D.; Evanson, T. Innovative methods for steep terrain harvesting. In Proceedings of the FORMEC 2010 Forest Engineering: Meeting the Needs of the Society and the Environment, Padova, Italy, 11–14 July 2010; pp. 1–9. [Google Scholar]
- Omar, M.A. Modeling and simulation of structural components in recursive closed-loop multibody systems. Multibody Syst. Dyn. 2017, 41, 47–74. [Google Scholar] [CrossRef]
- Rill, G. A modified implicit Euler algorithm for solving vehicle dynamic equations. Multibody Syst. Dyn. 2006, 15, 1–24. [Google Scholar] [CrossRef]
- Rahikainen, J.; Gonzalez, F.; Naya, M.A.; Sopanen, J.; Mikkola, A. On the cosimulation of multibody systems and hydraulic dynamics. Multibody Syst. Dyn. 2020, 50, 143–167. [Google Scholar] [CrossRef] [Green Version]
- Drapal, L.; Novotny, P. Torsional vibration analysis of crank train with low friction losses. J. Vibroeng. 2017, 19, 5691–5701. [Google Scholar] [CrossRef]
- González, M.; Dopico, D.; Lugrís, U.; Cuadrado, J. A benchmarking system for MBS simulation software: Problem standardization and performance measurement. Multibody Syst. Dyn. 2006, 16, 179–190. [Google Scholar] [CrossRef]
- Arnold, M.; Burgermeister, B.; Führer, C.; Hippmann, G.; Rill, G. Numerical methods in vehicle system dynamics: State of the art and current developments. Veh. Syst. Dyn. 2011, 49, 1159–1207. [Google Scholar] [CrossRef]
- Fehr, J.; Eberhard, P. Error-controlled model reduction in flexible multibody dynamics. J. Comput. Nonlinear Dyn. 2010, 5, 031005. [Google Scholar] [CrossRef]
- Larsson, J.; Krus, P.; Palmberg, J. Modelling, simulation and validation of complex fluid and mechanical systems. In Proceedings of the 5th International Conference on Fluid Power Transmission and Control (ICFP 2001), Hangzhou, China, 3–5 April 2001; pp. 338–343. [Google Scholar]
- MSC Software Reference Manual of ADAMS Help Documentation. Available online: https://help.mscsoftware.com/bundle/adams_2021.2/page/adams_main.htm (accessed on 27 January 2022).
- Schaub, M.; Simeon, B. Automatic H-scaling for the efficient time integration of stiff mechanical systems. Multibody Syst. Dyn. 2002, 8, 329–345. [Google Scholar] [CrossRef]
- Fojtášek, J. Heavy Commercial Vehicle Yaw Control Simulation. Vibroeng. Procedia 2018, 18, 138–143. [Google Scholar] [CrossRef]
- ISO 6814:2015; Machinery for Forestry—Mobile and Self-Propelled Machinery—Terms, Definitions and Classification. ISO: Geneva, Switzerland, 2015.
- EN 12999:2011; Cranes—Loader Cranes. ISO: Geneva, Switzerland, 2021.
- Yuming, Y.; Subhash, R.; Boileau, P.E. Multi-performance analyses and design optimisation of hydro-pneumatic suspension system for an articulated frame-steered vehicle. Veh. Syst. Dyn. 2019, 57, 108–133. [Google Scholar] [CrossRef]
- Drapal, L.; Voparil, J. Design Concept of a Crankshaft for Reduction of Main Bearings Power Losses and a Deep Skirt Engine Block Load. In Proceedings of the 18th International Conference on Mechatronics—Mechatronika, Brno, Czech Republic, 5–7 December 2018; pp. 533–536. [Google Scholar]
- Akhadkar, N.; Acary, V.; Brogliato, B. Multibody systems with 3D revolute joints with clearances: An industrial case study with an experimental validation. Multibody Syst. Dyn. 2018, 42, 249–282. [Google Scholar] [CrossRef] [Green Version]
- Heirman, G.H.K.; Desmet, W. Interface reduction of flexible bodies for efficient modeling of body flexibility in multibody dynamics. Multibody Syst. Dyn. 2010, 24, 219–234. [Google Scholar] [CrossRef]
- Wong, J.Y. Theory of Ground Vehicles, 4th ed.; Wiley: Hoboken, NJ, USA, 2008; pp. 1–90. [Google Scholar]



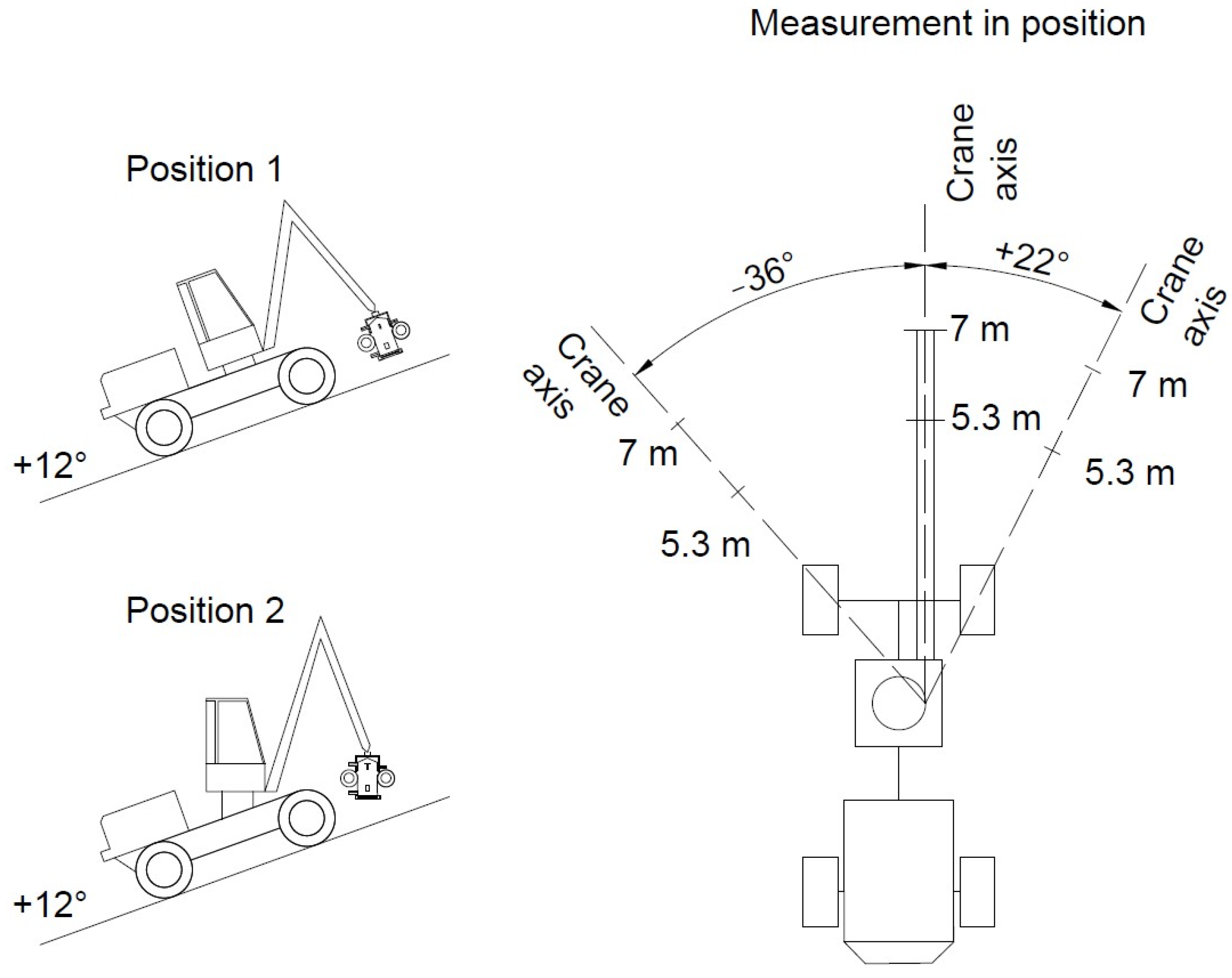
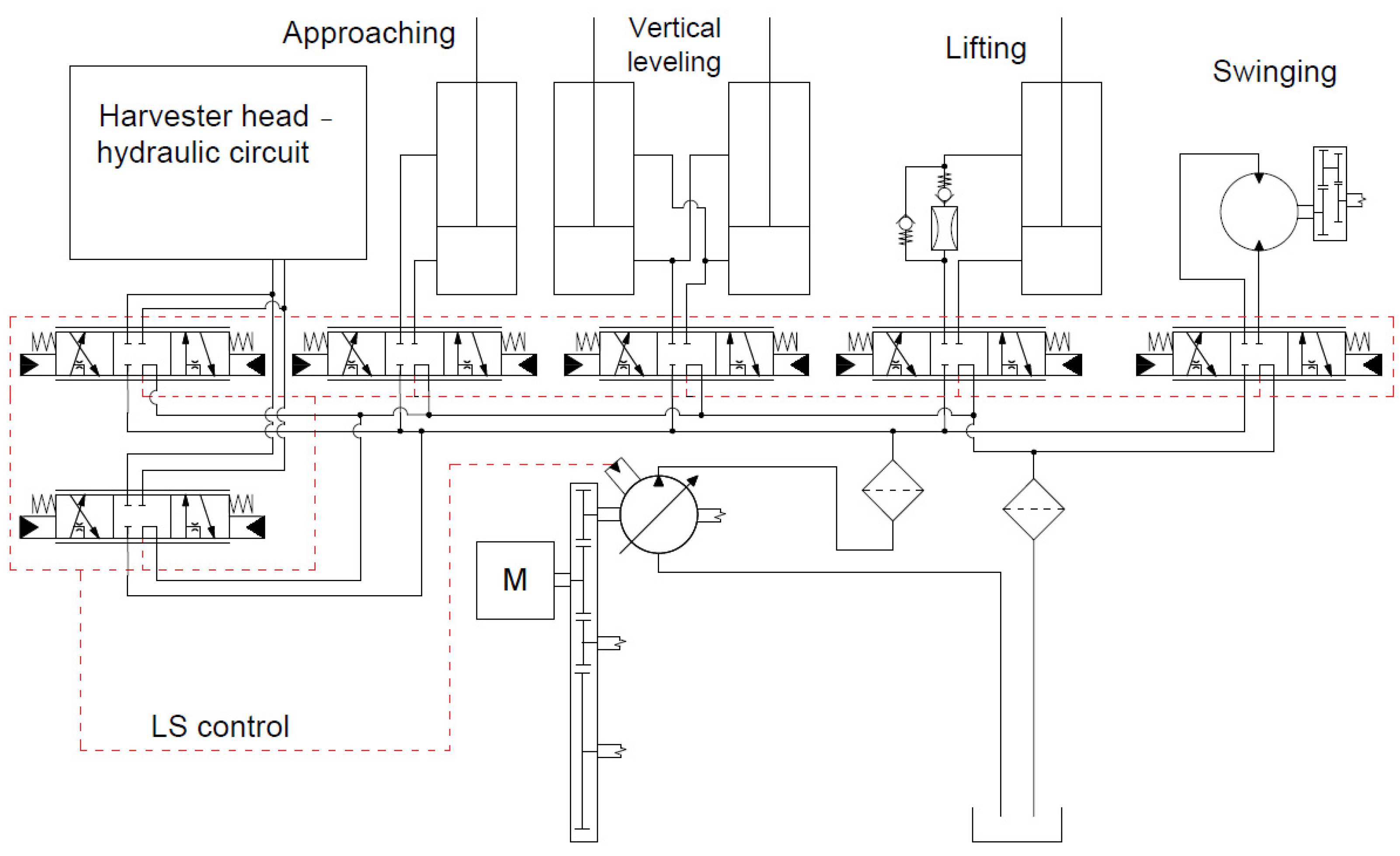




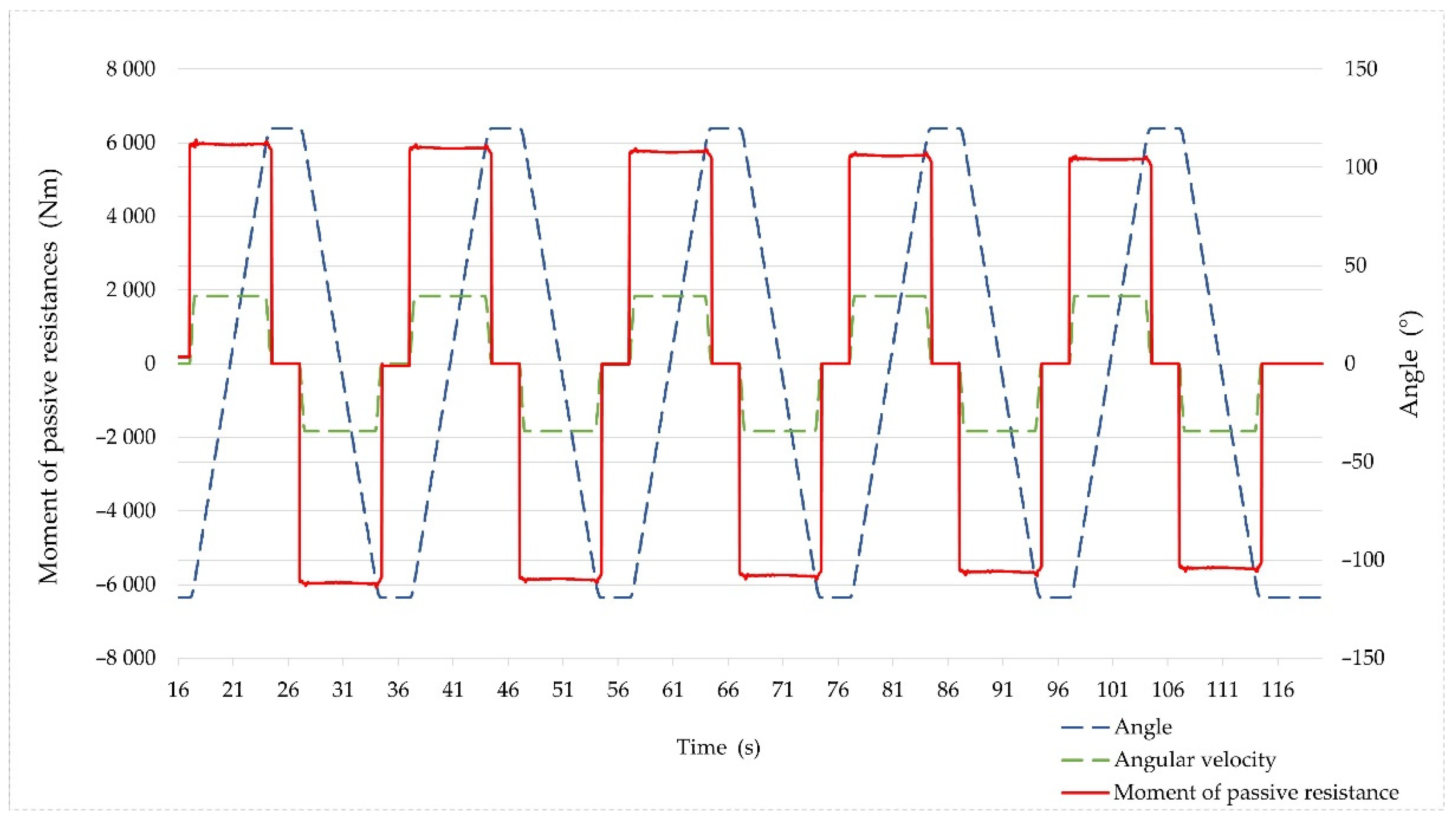
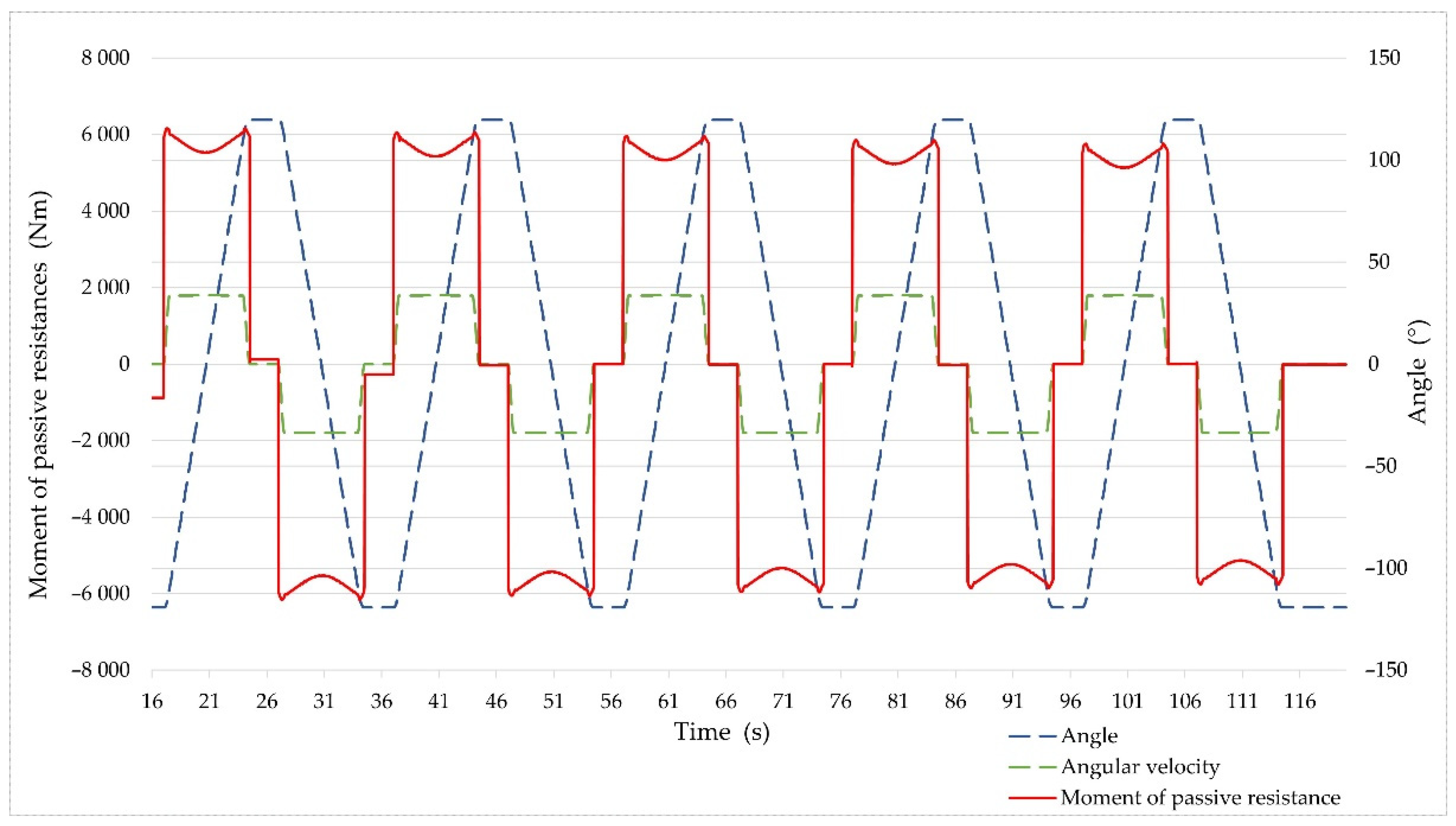
| Reach (m) | Axis (°) | Slope of the Slewing Bearing (°) | Maximum Lifting Force (N) | ||||
|---|---|---|---|---|---|---|---|
| Measurement 1 | Measurement 2 | Measurement 3 | Measurement 4 | Measurement 5 | |||
| 5.3 | −36 | −12 | 5246.56 | 5315.20 | 5285.78 | 5285.78 | 5236.75 |
| 0 | 7423.63 | 7413.83 | 7492.28 | 7570.73 | 7531.51 | ||
| 0 | −12 | 8345.46 | 8561.21 | 8335.65 | 8286.62 | 8208.17 | |
| 0 | 5452.50 | 5893.80 | 5521.14 | 5629.02 | 5678.05 | ||
| +22 | −12 | 7374.60 | 7433.44 | 7423.63 | 7413.83 | 7404.02 | |
| 0 | 5099.46 | 5021.00 | 5099.46 | 5109.26 | 5109.26 | ||
| 7 | −36 | −12 | 2843.93 | 2745.86 | 2971.41 | 3020.45 | 2971.41 |
| 0 | 3255.81 | 3324.45 | 3314.65 | 3285.23 | 3324.45 | ||
| 0 | −12 | 3589.23 | 3648.07 | 3559.81 | 3746.14 | 3726.53 | |
| 0 | 3373.49 | 3246.00 | 3334.26 | 3255.81 | 3314.65 | ||
| +22 | −12 | 2794.90 | 2853.74 | 2892.96 | 2873.35 | 2902.77 | |
| 0 | 3177.35 | 3246.00 | 3206.77 | 3196.97 | 3285.23 | ||
| Reach (m) | Axis (°) | Slope of the Slewing Bearing (°) | Result of Statistical Analyses |
|---|---|---|---|
| 5.3 | −36 | −12 | ˂0.001 |
| 0 | |||
| 0 | −12 | ˂0.001 | |
| 0 | |||
| +22 | −12 | 0.012186 | |
| 0 | |||
| 7 | −36 | −12 | 0.000071 |
| 0 | |||
| 0 | −12 | 0.000045 | |
| 0 | |||
| +22 | −12 | ˂0.001 | |
| 0 |
| Reach (m) | Axis (°) | Slope of the Slewing Bearing (°) | Result of Statistical Analyses |
|---|---|---|---|
| 5.3 | −36 | −12 | <0.001 |
| 0 | <0.001 | ||
| 0 | −12 | <0.001 | |
| 0 | <0.001 | ||
| +22 | −12 | <0.001 | |
| 0 | <0.001 | ||
| 7 | −36 | −12 | <0.001 |
| 0 | <0.001 | ||
| 0 | −12 | <0.001 | |
| 0 | <0.001 | ||
| +22 | −12 | <0.001 | |
| 0 | <0.001 |
| Reach (m) | Axis (°) | Slope of the Slewing Bearing (°) | Mean Pressure (Bar) | Deviation (%) | |
|---|---|---|---|---|---|
| Reality | Model | ||||
| 5.3 | −36 | −12 | 193.25 | 174.35 | 9.78 |
| 0 | 190.84 | 149.43 | 21.70 | ||
| 0 | −12 | 190.71 | 183.73 | 3.66 | |
| 0 | 190.05 | 154.54 | 18.68 | ||
| +22 | −12 | 192.04 | 171.87 | 10.51 | |
| 0 | 191.68 | 146.64 | 23.50 | ||
| 7 | −36 | −12 | 192.54 | 195.72 | 1.65 |
| 0 | 192.14 | 204.70 | 6.54 | ||
| 0 | −12 | 189.48 | 204.40 | 7.88 | |
| 0 | 189.52 | 204.41 | 7.86 | ||
| +22 | −12 | 191.41 | 190.96 | 0.23 | |
| 0 | 191.32 | 202.62 | 5.90 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mergl, V.; Kašpárek, J. Verifying the Lifting and Slewing Dynamics of a Harvester Crane with Possible Levelling When Operating on Sloping Grounds. Forests 2022, 13, 357. https://doi.org/10.3390/f13020357
Mergl V, Kašpárek J. Verifying the Lifting and Slewing Dynamics of a Harvester Crane with Possible Levelling When Operating on Sloping Grounds. Forests. 2022; 13(2):357. https://doi.org/10.3390/f13020357
Chicago/Turabian StyleMergl, Václav, and Jaroslav Kašpárek. 2022. "Verifying the Lifting and Slewing Dynamics of a Harvester Crane with Possible Levelling When Operating on Sloping Grounds" Forests 13, no. 2: 357. https://doi.org/10.3390/f13020357
APA StyleMergl, V., & Kašpárek, J. (2022). Verifying the Lifting and Slewing Dynamics of a Harvester Crane with Possible Levelling When Operating on Sloping Grounds. Forests, 13(2), 357. https://doi.org/10.3390/f13020357






