Bulk Density of Shrub Types and Tree Crowns to Use with Forest Inventories in the Iberian Peninsula
Abstract
:1. Introduction
2. Materials and Methods
2.1. Establishing Common Groups of Trees and Shrub Species for the Iberian Peninsula
2.2. Methods for Estimating Bulk Densities from Individual Shrubs and Trees to Shrubs Formations and Forest Canopies
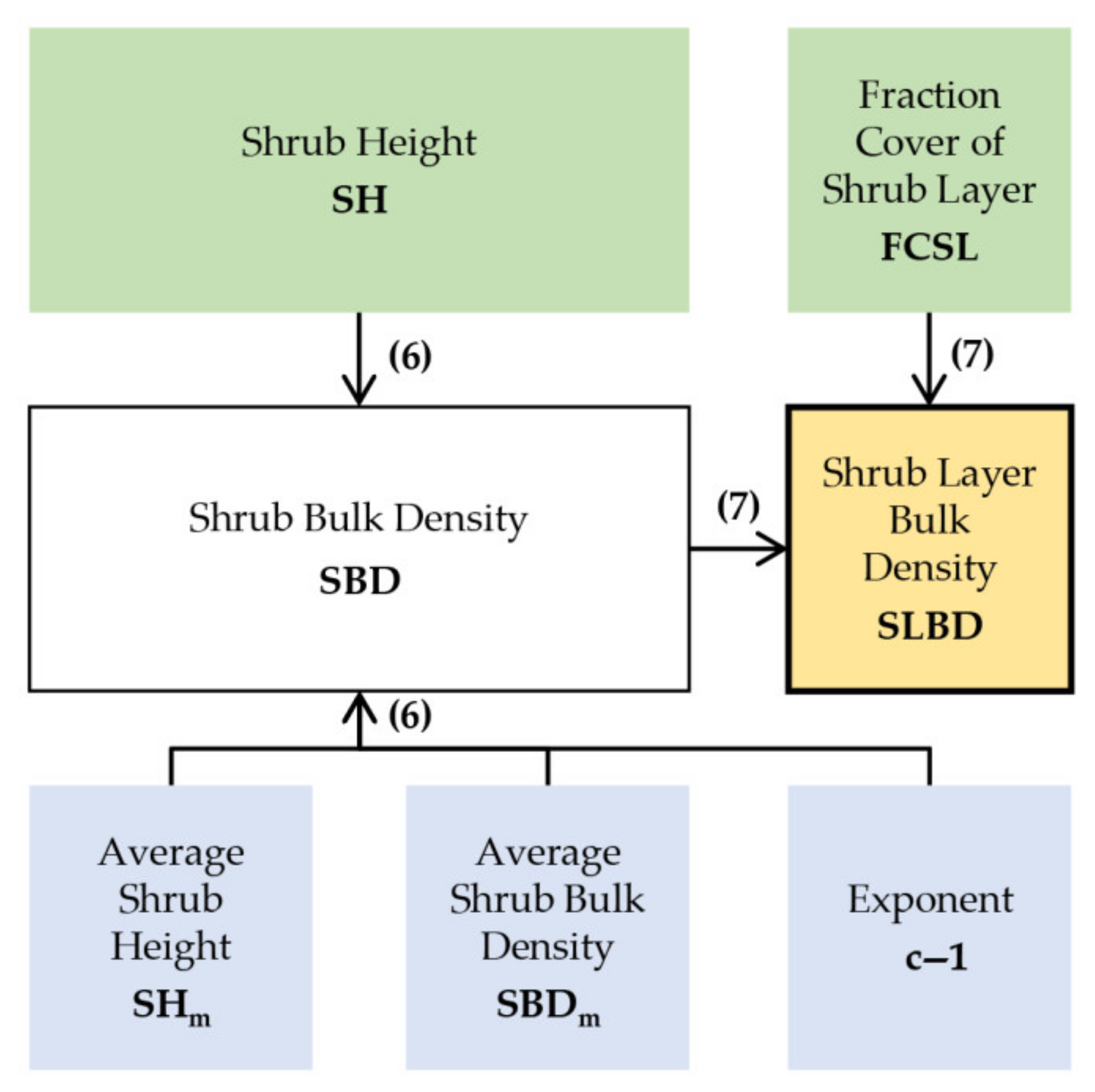
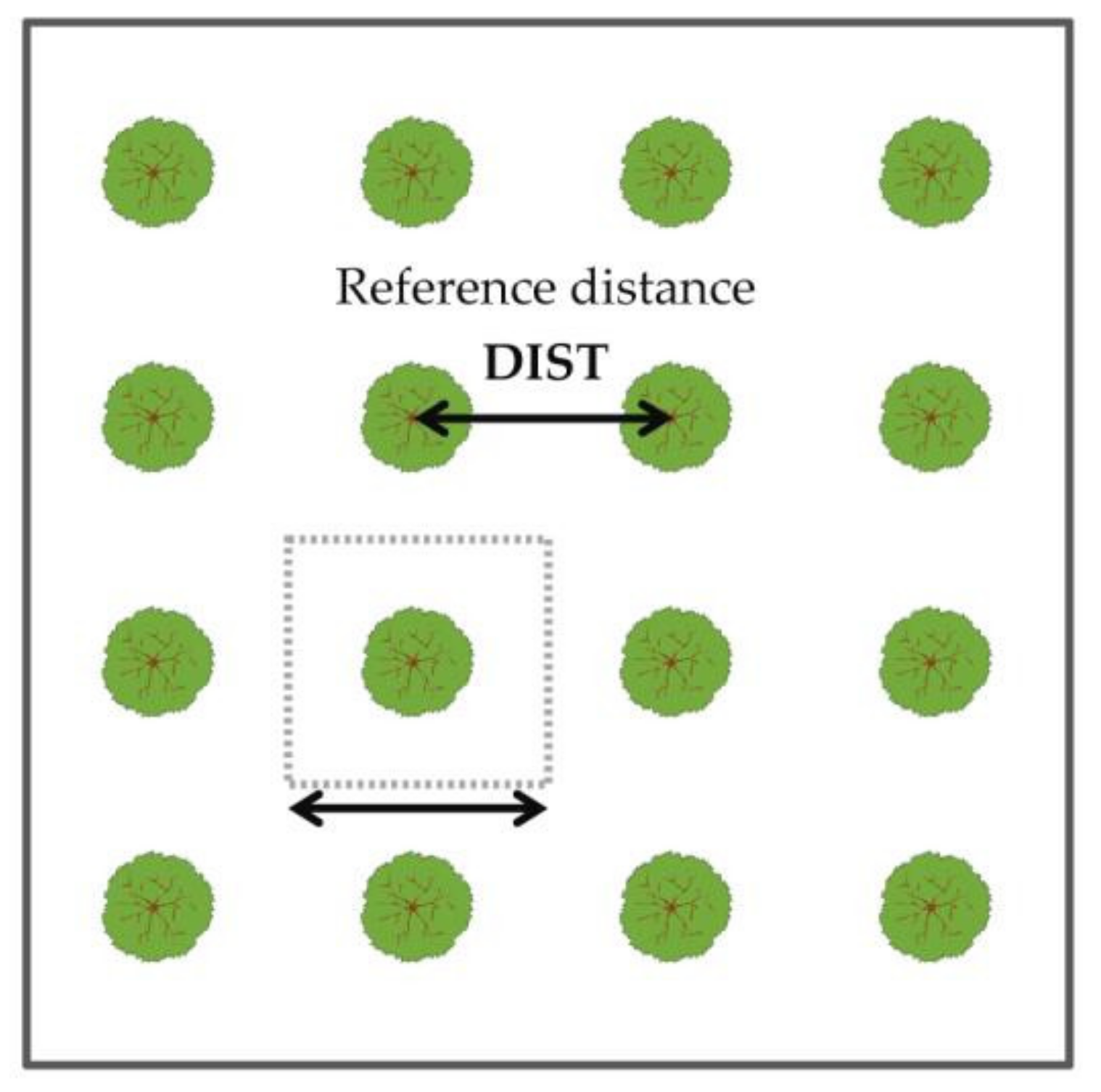
2.3. Estimating Bulk Densities for Shrubs and Shrub Layers
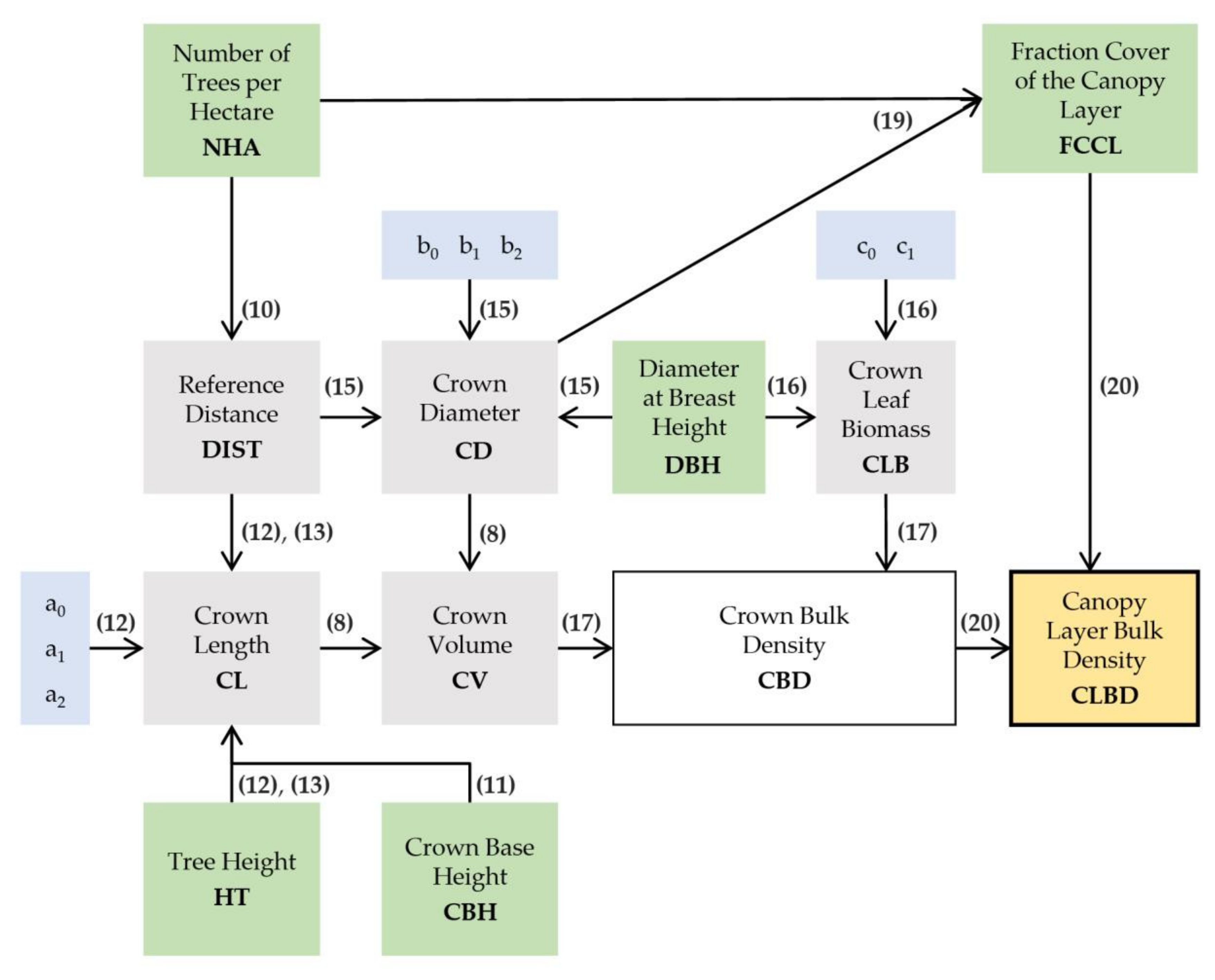
2.4. Estimating Bulk Densities for Tree Crowns and Canopies
3. Results
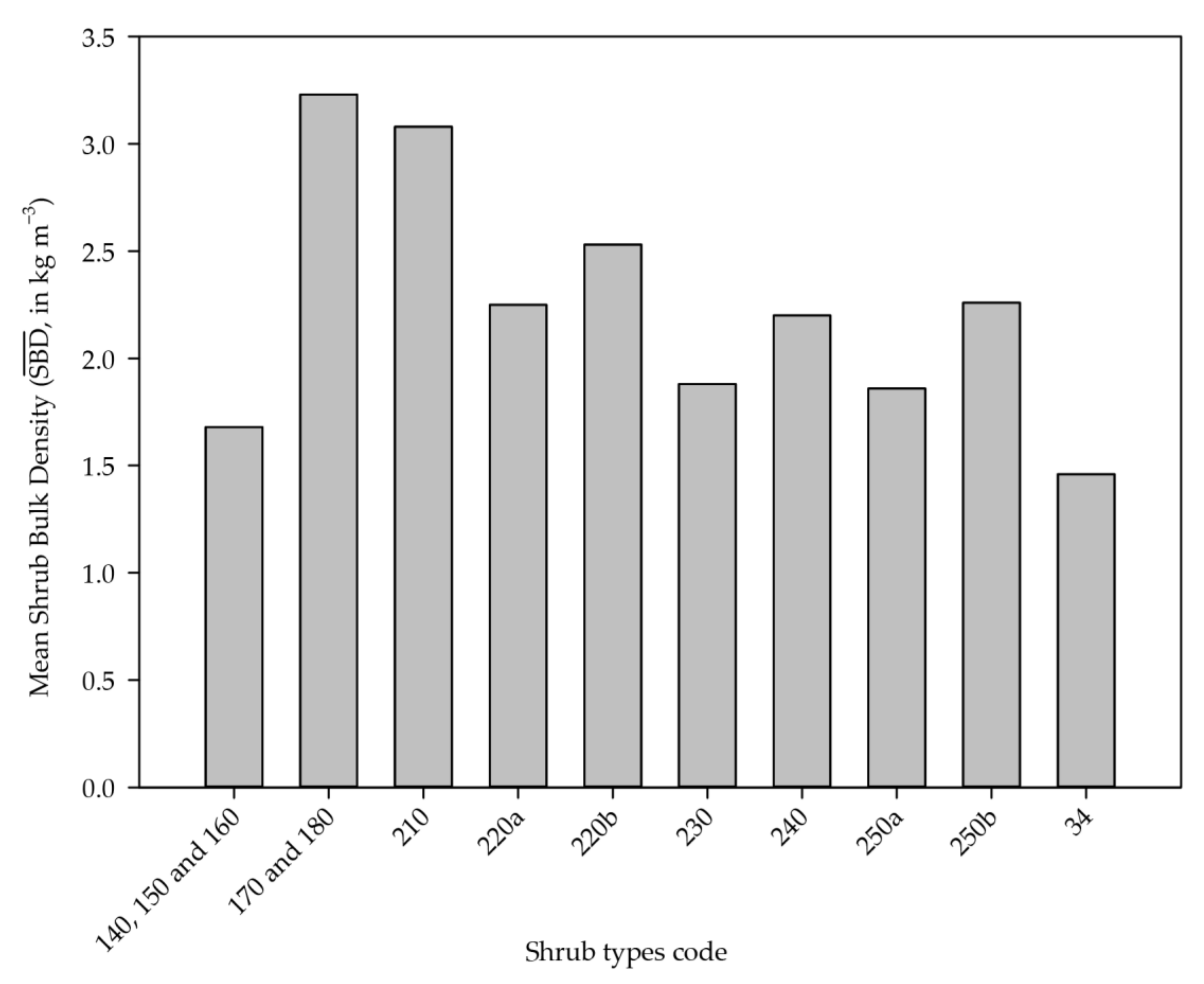
3.1. Shrub Bulk Densities
3.2. Bulk Density for Tree Crowns and Canopies
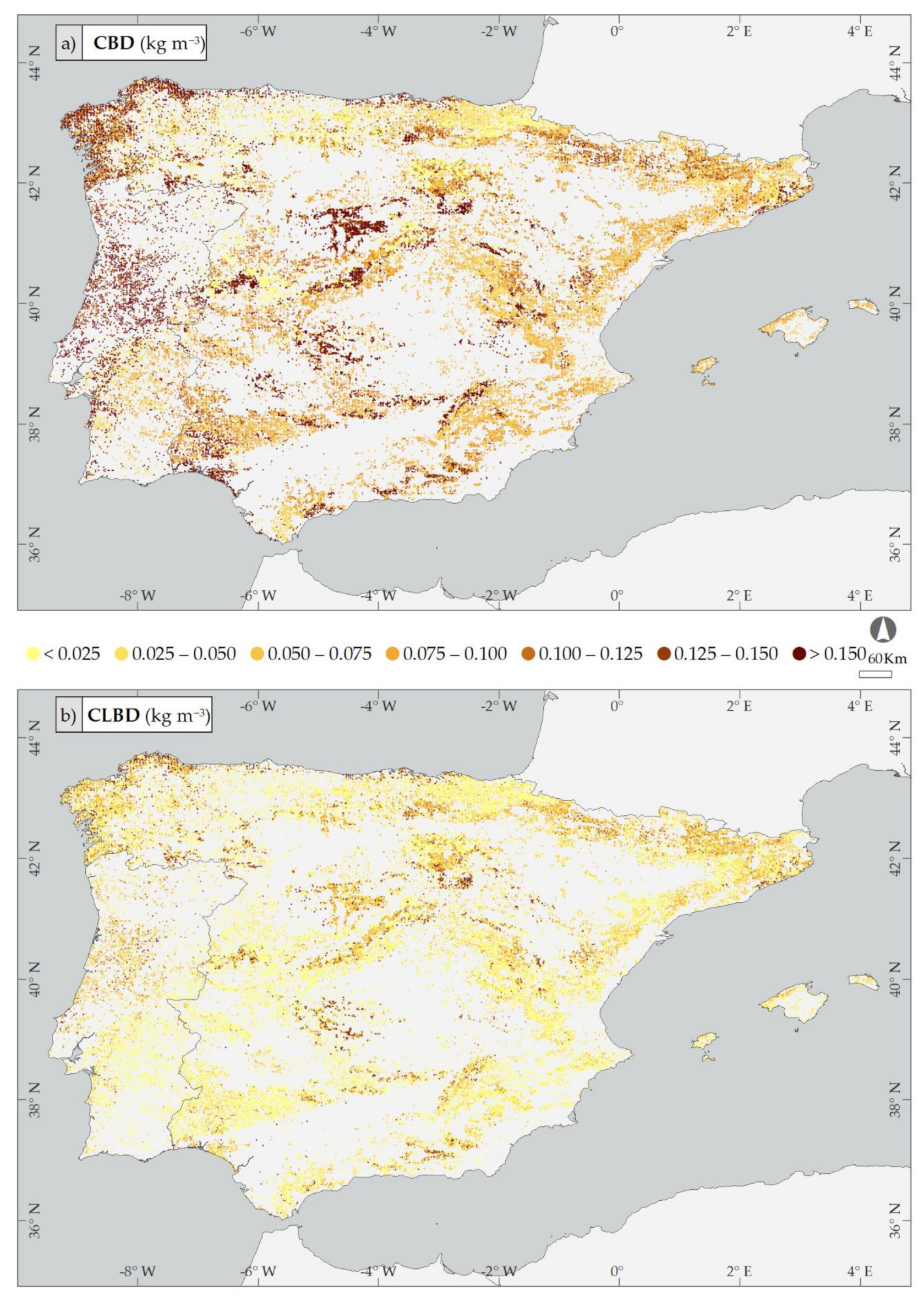
3.3. Application of Bulk Density Results to the National Forest Inventories of the Iberian Peninsula
4. Discussion
5. Summary
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Alberdi, I.; Condés, S.; McRoberts, R.E.; Winter, S. Mean species cover: A harmonized indicator of shrub cover for forest inventories. Eur. J. For. Res. 2018, 137, 265–278. [Google Scholar] [CrossRef] [Green Version]
- Nunes, L.; Moreno, M.; Alberdi, I.; Álvarez-González, J.G.; Godinho-Ferreira, P.; Mazzoleni, S.; Castro Rego, F. Harmonized Classification of Forest Types in the Iberian Peninsula Based on National Forest Inventories. Forests 2020, 11, 1170. [Google Scholar] [CrossRef]
- ICNF. 10o Relatório Provisório de Incêndios Florestais—2017: 01 de Janeiro a 31 de Outubro; Departamento de Gestão de Áreas Públicas e de Proteção, Instituto da Conservação da Natureza e das Florestas: Lisbon, Portugal, 2017. [Google Scholar]
- MAPAMA. Estadística General de Incendios Forestales; Ministerio de Agricultura y Pesca, Alimentación y Medio Ambiente: Madrid, Spain, 2017. Available online: https://www.miteco.gob.es/es/biodiversidad/temas/inventarios-nacionales/inventario-espanol-patrimonio-natural-biodiv/sistema-indicadores/06c-estadistica-incendios-forestales.aspx (accessed on 30 June 2020).
- González, J.R.; Palahí, M.; Trasobares, A.; Pukkala, T. A fire probability model for forest stands in Catalonia (north-east Spain). Ann. For. Sci. 2006, 63, 169–176. [Google Scholar] [CrossRef]
- ICNF. Incêndios Rurais. Informação Sobre Áreas Ardidas e Ocorrências de 2001 a 2021. Available online: http://www2.icnf.pt/portal/florestas/dfci/relat/rel-if (accessed on 30 October 2021).
- San-Miguel-Ayanz, J.; Moreno, J.M.; Camia, A. Analysis of large fires in European Mediterranean landscapes: Lessons learned and perspectives. For. Ecol. Manag. 2013, 294, 11–22. [Google Scholar] [CrossRef]
- Rego, F.; Catry, F.X.; Montiel, C.; Karlsson, O. Influence of territorial variables on the performance of wildfire detection systems in the Iberian Peninsula. For. Policy Econ. 2013, 29, 26–35. [Google Scholar] [CrossRef]
- Nunes, L.; Álvarez-González, J.G.; Alberdi, I.; Silva, V.; Rocha, M.; Rego, F.C. Analysis of the occurrence of wildfires in the Iberian Peninsula based on harmonised data from national forest inventories. Ann. For. Sci. 2019, 76, 27. [Google Scholar] [CrossRef] [Green Version]
- Nunes, M.C.S.; Vasconcelos, M.J.; Pereira, J.M.C.; Dasgupta, N.; Alldredge, R.J.; Rego, F.C. Land Cover Type and Fire in Portugal: Do Fires Burn Land Cover Selectively? Landsc. Ecol. 2005, 20, 661–673. [Google Scholar] [CrossRef]
- Papió, C.; Trabaud, L. Comparative study of the aerial structure of five shrubs of mediterranean shrublands. For. Sci. 1991, 37, 146–159. [Google Scholar] [CrossRef]
- Cruz, M.G.; Alexander, M.E.; Wakimoto, R.H. Assessing canopy fuel stratum characteristics in crown fire prone fuel types of western North America. Int. J. Wildl. Fire 2003, 12, 39–50. [Google Scholar] [CrossRef] [Green Version]
- Botequim, B.; Zubizarreta-Gerendiain, A.; Garcia-Gonzalo, J.; Silva, A.; Marques, S.; Fernandes, P.M.; Pereira, J.M.C.; Tomé, M. A model of shrub biomass accumulation as a tool to support management of portuguese forests. IForest 2014, 8, 114–125. [Google Scholar] [CrossRef] [Green Version]
- Hevia, A.; Álvarez-González, J.G.; Ruiz-Fernández, E.; Prendes, C.; Ruiz-González, A.D.; Majada, J.; González-Ferreiro, E. Modelling canopy fuel and forest stand variables and characterizing the influence of thinning in the stand structure using airborne LiDAR. Rev. Teledetec. 2016, 2016, 3979. [Google Scholar] [CrossRef] [Green Version]
- ICNF. 6.o Inventário Florestal Nacional IFN6. Relatório Final; Instituto da Conservação da Natureza e das Florestas: Lisbon, Portugal, 2019; Available online: http://www2.icnf.pt/portal/florestas/ifn/resource/doc/ifn/ifn6/IFN6_Relatorio_completo-2019-11-28.pdf (accessed on 18 January 2022).
- MITECO. Anuario de Estadística Forestal. 2018. Available online: https://www.miteco.gob.es/es/biodiversidad/estadisticas/forestal_anuario_2018.aspx (accessed on 15 September 2021).
- Van Wagner, C.E. Conditions for the start and spread of crown fire. Can. J. For. Res. 1977, 7, 23–34. [Google Scholar] [CrossRef]
- Cruz, M.G.; Alexander, M.E.; Wakimoto, R.H. Development and testing of models for predicting crown fire rate of spread in conifer forest stands. Can. J. For. Res. 2005, 35, 1626–1639. [Google Scholar] [CrossRef]
- Scott, J.H.; Reinhardt, E.D. Assessing Crown Fire Potential by Linking Models of Surface and Crown Fire Behavior; Rocky Mountain Research Station. Research Paper RMRS-RP-29; USDA Forest Service: Ogden, UT, USA, 2001.
- Thomas, P.H. Some Aspects of the Growth and Spread of Fire in the Open. For. Int. J. For. Res. 1967, 40, 139–164. [Google Scholar] [CrossRef] [Green Version]
- Alexander, M.E.; Cruz, M.G.; Vaillant, N.M.; Peterson, D.L. Crown Fire Behavior Characteristics and Prediction in Conifer Forests: A State-of-Knowledge Synthesis; Final Report to the Joint Fire Science Program; Joint Fire Science Program: Boise, ID, USA, 2013.
- Scott, J.H.; Reinhardt, E.D. Stereo Photo Guide for Estimating Canopy Fuel Characteristics in Conifer Stands; Gen. Tech. Rep. RMRS-GTR-145; Department of Agriculture, Forest Service, Rocky Mountain Research Station: Fort Collins, CO, USA; Boise, ID, USA, 2005. [CrossRef] [Green Version]
- Rego, F.C.; Morgan, P.; Fernandes, P.; Hoffman, C. Fire Science: From Chemistry to Landscape Management; Textbooks in Earth Sciences, Geography and Environment; Springer: New York, NY, USA, 2021; ISBN 9783030698157. [Google Scholar]
- Anderson, W.R.; Cruz, M.G.; Fernandes, P.M.; McCaw, L.; Vega, J.A.; Bradstock, R.A.; Fogarty, L.; Gould, J.; McCarthy, G.; Marsden-Smedley, J.B.; et al. A generic, empirical-based model for predicting rate of fire spread in shrublands. Int. J. Wildl. Fire 2015, 24, 443–460. [Google Scholar] [CrossRef] [Green Version]
- Fernandes, P.M.; Catchpole, W.R.; Rego, F.C. Shrubland fire behaviour modelling with microplot data. Can. J. For. Res. 2000, 30, 889–899. [Google Scholar] [CrossRef]
- Fernandes, P.A.; Pereira, J.P. Caracterização de combustíveis na Serra da Arrábida. Silva Lusit. 1993, 1, 237–260. [Google Scholar]
- Pasalodos-Tato, M.; Ruiz-Peinado, R.; del Río, M.; Montero, G. Shrub biomass accumulation and growth rate models to quantify carbon stocks and fluxes for the Mediterranean region. Eur. J. For. Res. 2015, 134, 537–553. [Google Scholar] [CrossRef]
- Mitsopoulos, I.; Mallinis, G.; Arianoutsou, M. Wildfire Risk Assessment in a Typical Mediterranean Wildland–Urban Interface of Greece. Environ. Manag. 2014, 55, 900–915. [Google Scholar] [CrossRef]
- Keane, R.E.; Reinhardt, E.D.; Scott, J.; Gray, K.; Reardon, J. Estimating forest canopy bulk density using six indirect methods. Can. J. For. Res. 2005, 35, 724–739. [Google Scholar] [CrossRef]
- Skowronski, N.S.; Clark, K.L.; Duveneck, M.; Hom, J. Three-dimensional canopy fuel loading predicted using upward and downward sensing LiDAR systems. Remote Sens. Environ. 2011, 115, 703–714. [Google Scholar] [CrossRef]
- Riaño, D.; Chuvieco, E.; Condés, S.; González-Matesanz, J.; Ustin, S.L. Generation of crown bulk density for Pinus sylvestris L. from lidar. Remote Sens. Environ. 2004, 92, 345–352. [Google Scholar] [CrossRef]
- Andersen, H.E.; McGaughey, R.J.; Reutebuch, S.E. Estimating forest canopy fuel parameters using LIDAR data. Remote Sens. Environ. 2005, 94, 441–449. [Google Scholar] [CrossRef]
- Hermosilla, T.; Ruiz, L.A.; Kazakova, A.N.; Coops, N.C.; Moskal, L.M. Estimation of forest structure and canopy fuel parameters from small-footprint full-waveform LiDAR data. Int. J. Wildl. Fire 2014, 23, 224–233. [Google Scholar] [CrossRef] [Green Version]
- González-Ferreiro, E.; Diéguez-Aranda, U.; Crecente-Campo, F.; Barreiro-Fernández, L.; Miranda, D.; Castedo-Dorado, F. Modelling canopy fuel variables for Pinus radiata D. Don in NW Spain with low-density LiDAR data. Int. J. Wildl. Fire 2014, 23, 350–362. [Google Scholar] [CrossRef]
- Marino, E.; Tomé, J.L.; Madrigal, J.; Hernando, C. Effect of airborne LiDAR pulse density on crown fuel modelling. In Proceedings of the 6th International Fire Behavior and Fuels Conference, Marseille, France, 29 April–3 May 2019; pp. 1–6. [Google Scholar]
- Saatchi, S.; Halligan, K.; Despain, D.G.; Crabtree, R.L. Estimation of forest fuel load from radar remote sensing. IEEE Trans. Geosci. Remote Sens. 2007, 45, 1726–1740. [Google Scholar] [CrossRef]
- Arellano-Pérez, S.; Castedo-Dorado, F.; López-Sánchez, C.A.; González-Ferreiro, E.; Yang, Z.; Díaz-Varela, R.A.; Álvarez-González, J.G.; Vega, J.A.; Ruiz-González, A.D. Potential of Sentinel-2A data to model surface and canopy fuel characteristics in relation to crown fire hazard. Remote Sens. 2018, 10, 1645. [Google Scholar] [CrossRef] [Green Version]
- Cruz, M.G.; Alexander, M.E. Evaluating regression model estimates of canopy fuel stratum characteristics in four crown fire-prone fuel types in western North America. Int. J. Wildl. Fire 2012, 21, 168–179. [Google Scholar] [CrossRef]
- Alberdi, I.; Condés, S.; Millán, J.; Saura, S.; Sánchez, G.; Pérez, F.; Villanueva, J.; Vallejo, R. National Forest Inventories Report, Spain. In National Forest Inventories. Pathways for Common Reporting; Tomppo, E., Gschwantner, T., Lawrence, M., McRoberts, R., Eds.; Springer: New York, NY, USA, 2010; pp. 529–540. [Google Scholar]
- AFN. Inventário Florestal Nacional. In Portugal Continental—IFN5 2005-2006; Relatório Final; Autoridade Florestal Nacional: Lisbon, Portugal, 2010. [Google Scholar]
- Castroviejo, S. Coord. gen. (1986–2019). In Flora iberica 1–8, 10–15, 17–18, 20–21; Real Jardín Botánico CSIC: Madrid, Spain, 2019. [Google Scholar]
- MAPAMA. 2007 Mapa Forestal de España. Escala 1:25.000 (MFE25); Ministerio de Agricultura y Pesca, Alimentación y Medio Ambiente. Dirección General de Desarrollo Rural y Política Forestal: Madrid, Spain, 2017.
- AFN. Instruções Para o Trabalho de Campo do Inventário Florestal Nacional—IFN 2005/2006; Autoridade Florestal Nacional, Direcção Nacional de Gestão Florestal: Lisbon, Portugal, 2009. [Google Scholar]
- Costa, J.C.; Aguiar, C.; Capelo, J.H.; Lousã, M.; Neto, C. Biogeografia de Portugal Continental. Quercetea 1998, 1, 5–56. [Google Scholar]
- Rivas-Martínez, S.; Penas, A.; Díaz González, T.E.; Cantó, P.; del Río, S.; Costa, J.C.; Herrero, L.; Molero, J. Biogeographic Units of the Iberian Peninsula and Baelaric Islands to District Level. A Concise Synopsis. In The Vegetation of the Iberian Peninsula. Plant and vegetation; Loidi, J., Ed.; Springer: Berlin/Heidelberg, Germany, 2017; pp. 131–188. [Google Scholar]
- Vega, J.A.; Fernandes, P.; Cuiñas, P.; Fontúrbel, M.T.; Pérez, J.R.; Loureiro, C. Fire spread analysis of early summer field experiments in shrubland fuel types of northwestern Iberia. For. Ecol. Manag. 2006, 234, S102. [Google Scholar] [CrossRef]
- West, G.B.; Brown, J.H.; Enquist, B.J. A general model for the origin of allometric scaling laws in biology. Science 1997, 276, 122–126. [Google Scholar] [CrossRef] [PubMed]
- Instituto Nacional para la Conservación de la Naturaleza (España). Segundo Inventario Forestal Nacional, 1986–1995. Explicaciones y Métodos; ICONA: Madrid, Spain, 1990. [Google Scholar]
- Cruz, M.G.; Alexander, M.E.; Wakimoto, R.H. Modeling the likelihood of crown fire occurrence in conifer forest stands. For. Sci. 2004, 50, 640–658. [Google Scholar]
- Tomppo, E.; Gschwantner, T.; Lawrence, M.; McRoberts, R.E. National Forest Inventories: Pathways for Common Reporting; Springer: Berlin, Germany, 2010; ISBN 978-90-481-3232-4. [Google Scholar]
- Montero, G.; Ruiz-peinado, R.; Muñoz, M. Producción de Biomassa y Fijación de CO2 por los Bosques Españoles; Florestal, M.I.S., Ed.; INIA: Madrid, Spain, 2005; ISBN 2014000050000. [Google Scholar]
- Lopes, D. Estimating Net Primary Production in Eucalyptus Globulus and Pinus Pinaster Ecossytems in Portugal. Ph.D. Thesis, Kingston University, Surrey, UK, 2005. [Google Scholar]
- Mendes, A.; Nunes, L.; Lopes, D.; Soares, P. Ajuste de equações de biomassa total e por componentes para carvalho-negral e pinheiro-bravo no distrito de Vila Real. In 7o Congresso Florestal Nacional. Conhecimento e Inovação, 05-08 Junho; SPCF: Vila Real e Bragança, Portugal, 2013; Available online: http://hdl.handle.net/10400.5/21578 (accessed on 18 January 2022).
- Mitsopoulos, I.D.; Dimitrakopoulos, A.P. Estimation of canopy fuel characteristics of Aleppo pine (Pinus halepensis Mill.) forests in Greece based on common stand parameters. Eur. J. For. Res. 2014, 133, 73–79. [Google Scholar] [CrossRef]
- Leonardi, S.; Santa Regina, I.; Rapp, M.; Gallego, H.A.; Rico, M. Biomass, litterfall and nutrient content in Castanea sativa coppice stands of southern Europe. Ann. For. Sci. 1996, 53, 1071–1081. [Google Scholar] [CrossRef]
- Jiménez, E.; Vega, J.A.; Ruiz-González, A.D.; Guijarro, M.; Alvarez-González, J.G.; Madrigal, J.; Cuiñas, P.; Hernando, C.; Fernández-Alonso, J.M. Carbon emissions and vertical pattern of canopy fuel consumption in three Pinus pinaster Ait. active crown fires in Galicia (NW Spain). Ecol. Eng. 2013, 54, 202–209. [Google Scholar] [CrossRef]
- Tachajapong, W.; Lozano, J.; Mahalingam, S.; Xiangyang, Z.; Weise, D.R. An investigation of crown fuel bulk density effects on the dynamics of crown fire initiation in Shrublands. Combust. Sci. Technol. 2008, 180, 593–615. [Google Scholar] [CrossRef] [Green Version]
- Byram, G.M. Combustian of Forest Fuels. In Forest Fire Control and Use; Davis, K.P., Ed.; McGraw-Hill Book Company: New York, NY, USA, 1959; pp. 61–89. [Google Scholar]
- Pimont, F.; Dupuy, J.L.; Rigolot, E. A simple model for shrub-strata-fuel dynamics in Quercus coccifera L. communities. Ann. For. Sci. 2018, 75, 44. [Google Scholar] [CrossRef] [Green Version]
- Scott, J.H.; Burgan, R.E. Standard Fire Behavior Fuel Models: A Comprehensive Set for Use with Rothermel’s Surface Fire Spread Model. Gen. Tech. Rep. RMRS-GTR-153; Department of Agriculture, Forest Service, Rocky Mountain Research Station: Fort Collins, CO, USA; Boise, ID, USA, 2005. [Google Scholar]
- Countryman, C.M.; Philpot, C.W. Physical Characteristics of Chamise as a Wildland Fuel; Research Paper PSW-66; USDA Forest Service, Pacific Southwest, Forest and Range Experimental Station: Berkeley, CA, USA, 1970.
- Silva, T.P.; Pereira, J.M.C.; Paúl, J.C.P.; Santos, M.T.N.; Vasconcelos, M.J.P. Estimativa de Emissões Atmosféricas Originadas por Fogos Rurais em Portugal. Silva Lusit. 2006, 14, 239–263. [Google Scholar]
- Paúl, J.C. Caracterização Biofisica e Georreferenciação de Parcelas de Inventário de Vegetação o Parque Natural das Serras de Airee Candeeiros; ISA: Lisbon, Portugal, 1993. [Google Scholar]
- Armand, D.; Etienne, M.; Legrand, C.; Marechal, J.; Valette, J.C. Phytovolume, phytomasse et relations structurales chez quelques arbustes méditerranéens. Ann. Sci. For. 1993, 50, 79–89. [Google Scholar] [CrossRef] [Green Version]
- Pereira, J.M.C.; Sequeira, N.M.S.; Carreiras, J.M.B. Structural properties and dimensional relations of some mediterranean shrub fuels. Int. J. Wildl. Fire 1995, 5, 35–42. [Google Scholar] [CrossRef]
- Pausas, J.G.; Alessio, G.A.; Moreira, B.; Corcobado, G. Fires enhance flammability in Ulex parviflorus. New Phytol. 2012, 193, 18–23. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Arellano, S.; Vega, J.A.; Ruiz, A.D.; Arellano, A.; Álvarez, J.G.; Vega, D.J.; Pérez, P. Foto-Guía de Combustibles Forestales de Galicia y Comportamiento del Fuego Asociado; Andavira Editora: Santiago de Compostela, Spain, 2017; ISBN 9788484089865. [Google Scholar]
- Jaime, M.; Berná, B. Aspectos Ecológicos y Técnicas de Control del Combustiblecombustible (Roza y Quema Controlada) en Matorrales con alto Riesgo de Incendio, Dominados por Ulex Parviflorus (Pourr.); Universidad de Alicante: Alicante, Spain, 2001. [Google Scholar]
- Marino, E.; Hernando, C.; Madrigal, J.; Guijarro, M. Short-term effect of fuel treatments on fire behaviour in a mixed heathland: A comparative assessment in an outdoor wind tunnel. Int. J. Wildl. Fire 2014, 23, 1097–1107. [Google Scholar] [CrossRef]
- Vega, J.A.; Cuiñas, P.; Fonturbel, T.; Pérez-Gorostiaga, P.; Fernández, C. Predicting fire behaviour in Galician (NW Spain) shrubland fuel complexes. In Proceedings of the 3rd International Conference on Forest Fire Research and 14th Fire and Forest Meteorology, Luso, Portugal, 16–20 November; Viegas, D., Ed.; Universidade de Coimbra: Coimbra, Portugal, 1998; pp. 713–728. [Google Scholar]
- Fernandes, P. Fire spread prediction in shrub fuels in Portugal. For. Ecol. Manag. 2001, 144, 67–74. [Google Scholar] [CrossRef]
- Marino, E.; Hernando, C.; Madrigal, J.; Dez, C.; Guijarro, M. Fuel management effectiveness in a mixed heathland: A comparison of the effect of different treatment types on fire initiation risk. Int. J. Wildl. Fire 2012, 21, 969–979. [Google Scholar] [CrossRef]
- Vega, J.A.; Jiḿnez, E.; Dupuy, J.L.; Linn, R.R. Effects of flame interaction on the rate of spread of heading and suppression fires in shrubland experimental fires. Int. J. Wildl. Fire 2012, 21, 950–960. [Google Scholar] [CrossRef]
- Fernandes, P.; Rego, F.C. Changes in fuel structure and fire behavior with heathland aging in northern Portugal. In Proceedings of the 13th Fire Forest Meteorology Conference, Lorne, Australia, 27–31 October 1996; 1998; pp. 433–436. [Google Scholar]
- Baeza, M.J.; Raventós, J.; Escarré, A. Structural changes in relation to age in prone Mediterranean shrublands. In Proceedings of the 3rd International Conference of Forest Fire Research, Luso, Portugal, 16–20 November 1998; Viegas, D.X., Ed.; Associação para o Desenvolvimento da Aerodinamica Industrial: Coimbra, Portugal, 1998; Volume II, pp. 2567–2578. [Google Scholar]
- Conroy, B. Fuel data for fire management. In Bushfire Management in Natural Areas; Conroy, B., Ed.; National Parks and Wildlife Service: Sydney, NSW, Australia, 1987; pp. 43–59. [Google Scholar]
- McFarland, D.C. Fire and the vegetation composition and structure of subtropical heathlands in southeastern Queensland. Aust. J. Bot. 1988, 36, 533–546. [Google Scholar] [CrossRef]
- Davies, G.M.; Legg, C.J.; Smith, A.A.; MacDonald, A.J. Rate of spread of fires in Calluna vulgaris-dominated moorlands. J. Appl. Ecol. 2009, 46, 1054–1063. [Google Scholar] [CrossRef]
- Fernandes, P. Fuel dynamics in Northern Portugal low shrubland. In Proceedings of the Workshop on Fire Ecology and the European Biota; European Commission: Brussels, Belgium, 1996. [Google Scholar]
- Marino, E.; Guijarro, M.; Hernando, C.; Madrigal, J.; Diez, C. Fire hazard after prescribed burning in a gorse shrubland: Implications for fuel management. J. Environ. Manag. 2011, 92, 1003–1011. [Google Scholar] [CrossRef]
- Marino, E.; Dupuy, J.L.; Pimont, F.; Guijarro, M.; Hernando, C.; Linn, R. Fuel bulk density and fuel moisture content effects on fire rate of spread: A comparison between FIRETEC model predictions and experimental results in shrub fuels. J. Fire Sci. 2012, 30, 277–299. [Google Scholar] [CrossRef]
- CEABN. Fireland. In Efeitos do Fogo sobre a Dinâmica da Vegetação à Escala da Paisagem em Portugal; FCT Project PTDC/AGR-CFL/104651/2008; CEABN-ISA: Lisbon, Portugal, 2013. [Google Scholar]
- MAPAMA. Los Incendios Forestales en España. Decenio 2001–2010. Available online: http://www.mapama.gob.es/es/desarrollo-rural/estadisticas/incendiosforestales2001-2010finalmod1_tcm7-349255.pdf (accessed on 16 November 2020).
- Marino, E.; Guijarro, M.; Madrigal, J.; Hernando, C.; Diez, C. Assessing fire propagation empirical models in shrub fuel complexes using wind tunnel data. WIT Trans. Ecol. Environ. 2008, 119, 121–130. [Google Scholar] [CrossRef] [Green Version]
- Fernandes, P.; Loureiro, C.; Botelho, H.; Ferreira, A.; Fernandes, M. Avaliação Indirecta da Carga de Combustível em Pinhal Bravo. Silva Lusit. 2002, 1, 73–90. [Google Scholar]
- Fernandes, P.; Loureiro, C.; Botelho, H. Fire behaviour and severity in a maritime pine stand under differing fuel conditions. Ann. For. Sci. 2004, 61, 537–544. [Google Scholar] [CrossRef] [Green Version]
- Gómez-Vázquez, I.; Crecente-Campo, F.; Diéguez-Aranda, U.; Castedo-Dorado, F. Modelling canopy fuel variables in Pinus pinaster Ait. and Pinus radiata D. Don stands in northwestern Spain. Ann. For. Sci. 2013, 70, 161–172. [Google Scholar] [CrossRef] [Green Version]
- Dieguez-Aranda, U.; Vargas, M.; Castedo, D.; Cano, J.; Barrio, A.; Abarzua, F.; González, M.; Juárez, C.; Rodriguez, R.; Lopez, F.; et al. Herramientas Selvícolas para la Gestión Forestal Sostenible en Galicia; Xunta de Galicia: Santiago de Compostela, Spain, 2009; Volume 82, ISBN 9788469273951. [Google Scholar]
- Ruiz-González, A.D.; Castedo-Dorado, F.; Vega, J.A.; Jiménez, E.; Fernández-Alonso, J.M.; Álvarez-González, J.G. Modelling canopy fuel dynamics of maritime pine stands in north-west Spain. Int. J. Wildl. Fire 2015, 24, 92–102. [Google Scholar] [CrossRef]
- Faias, S. Analysis of Biomass Expansion Factors for the Most Important Tree Species in Portugal. Master’s Thesis, Instituto Superior de Agronomia, Lisbon, Portugal, 2009. [Google Scholar] [CrossRef]
- Botequim, B.; Fernandes, P.M.; Garcia-Gonzalo, J.; Silva, A.; Borges, J.G. Coupling fire behaviour modelling and stand characteristics to assess and mitigate fire hazard in a maritime pine landscape in Portugal. Eur. J. For. Res. 2017, 136, 527–542. [Google Scholar] [CrossRef]
- Botequim, B.; Fernandes, P.M.; Borges, J.G.; González-Ferreiro, E.; Guerra-Hernández, J. Improving silvicultural practices for Mediterranean forests through fire behaviour modelling using LiDAR-derived canopy fuel characteristics. Int. J. Wildl. Fire 2019, 28, 823–839. [Google Scholar] [CrossRef]
- Molina, J.R.; Rodriguez y Silva, F.; Herrera, M.A. Comportamiento potencial del fuego de copas en masas de pinus pinea bajo diferentes tratamientos selvícolas. For. Syst. 2011, 20, 266–277. [Google Scholar] [CrossRef] [Green Version]
- Balboa-Murias, M.A.; Rodríguez-Soalleiro, R.; Merino, A.; Álvarez-González, J.G. Temporal variations and distribution of carbon stocks in aboveground biomass of radiata pine and maritime pine pure stands under different silvicultural alternatives. For. Ecol. Manag. 2006, 237, 29–38. [Google Scholar] [CrossRef]
- Ruiz-González, A.D.; Álvarez-González, J.G. Canopy bulk density and canopy base height equations for assessing crown fire hazard in Pinus radiata plantations. Can. J. For. Res. 2011, 41, 839–850. [Google Scholar] [CrossRef]
- Fernández-Alonso, J.M.; Alberdi, I.; Álvarez-González, J.G.; Vega, J.A.; Cañellas, I.; Ruiz-González, A.D. Canopy fuel characteristics in relation to crown fire potential in pine stands: Analysis, modelling and classification. Eur. J. For. Res. 2013, 132, 363–377. [Google Scholar] [CrossRef]
- Reinhardt, E.; Scott, J.; Gray, K.; Keane, R. Estimating canopy fuel characteristics in five conifer stands in the western United States using tree and stand measurements. Can. J. For. Res. 2006, 36, 2803–2814. [Google Scholar] [CrossRef]
- Plucinski, M.P. The Investigation of Factors Governing Ignition and Development of Fires in Heathland Vegetation. Ph.D. Thesis, University of New South Wales, Canberra, Australia, 2003. [Google Scholar]
- Catchpole, W.R. Heathland Fuel and Fire Modelling. Ph.D. Thesis, University of New South Wales, Canberra, Australia, 1987. [Google Scholar]


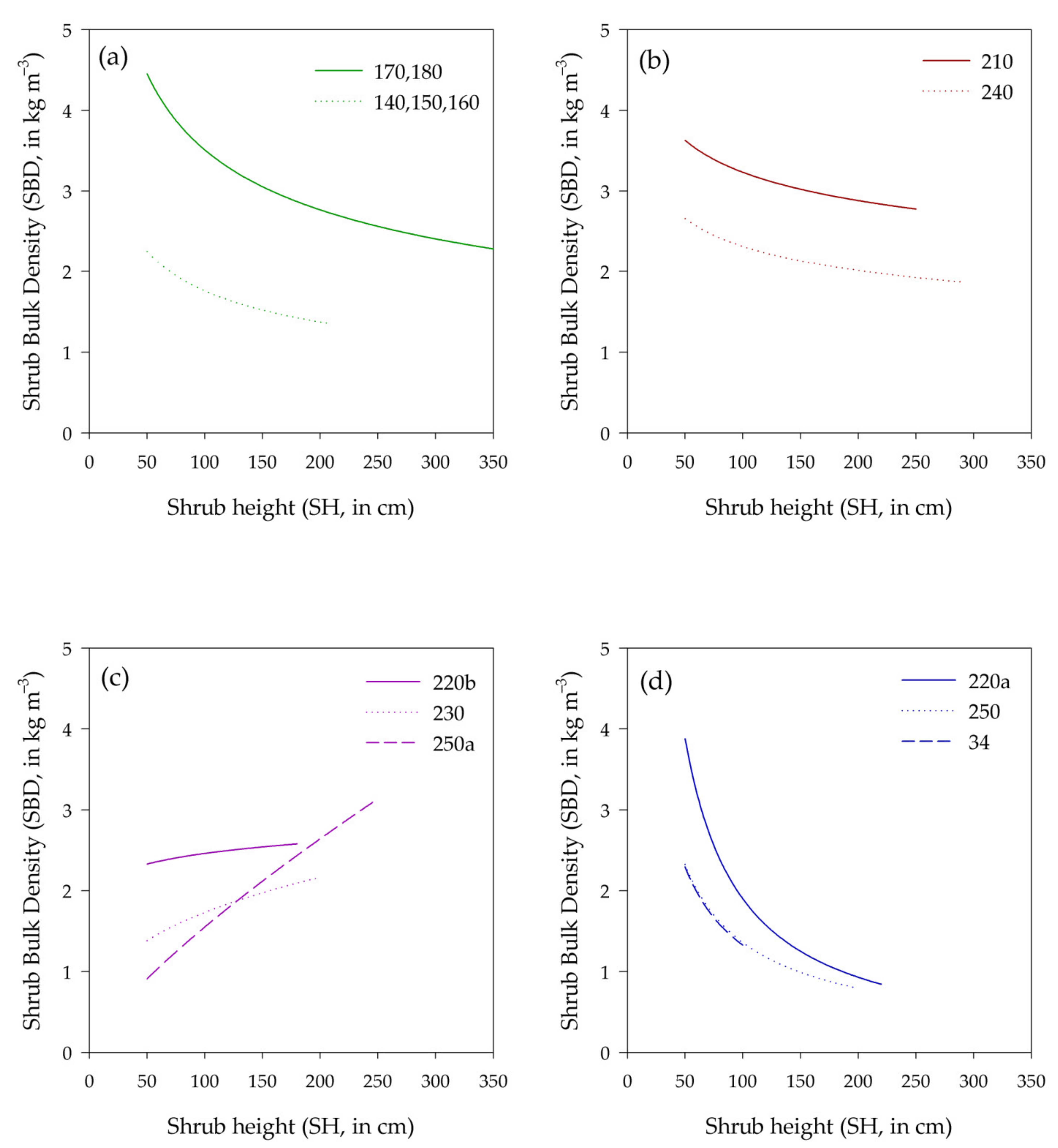
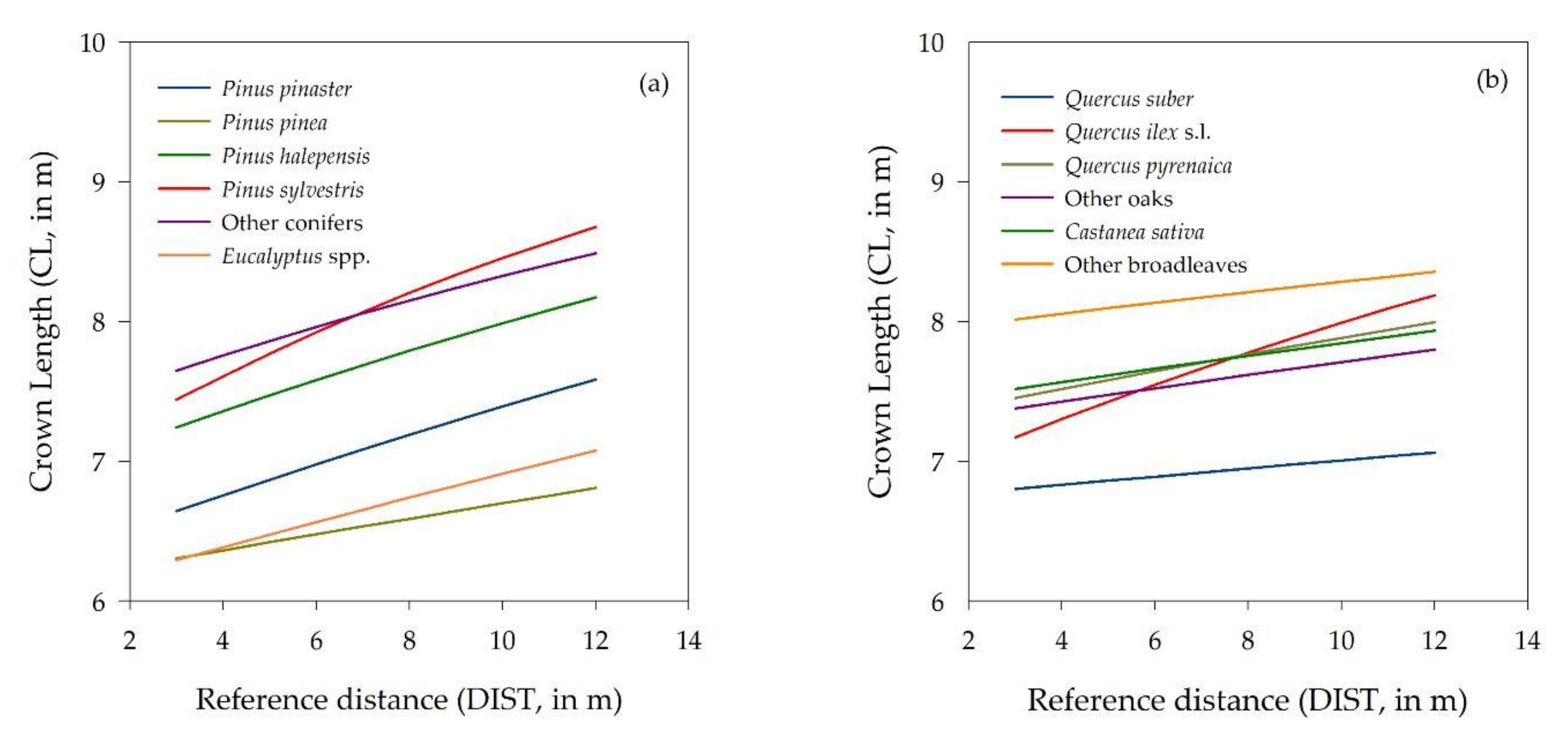
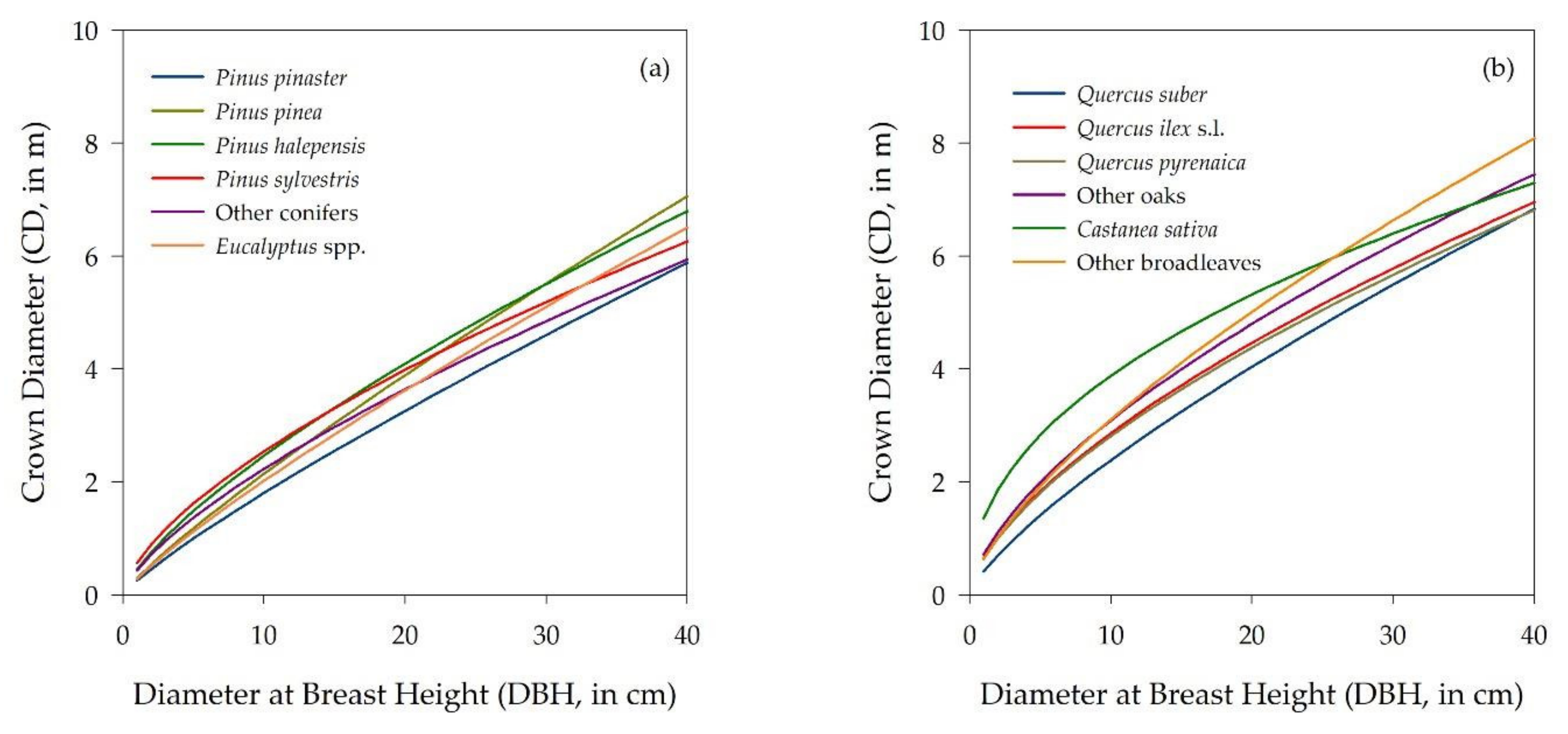

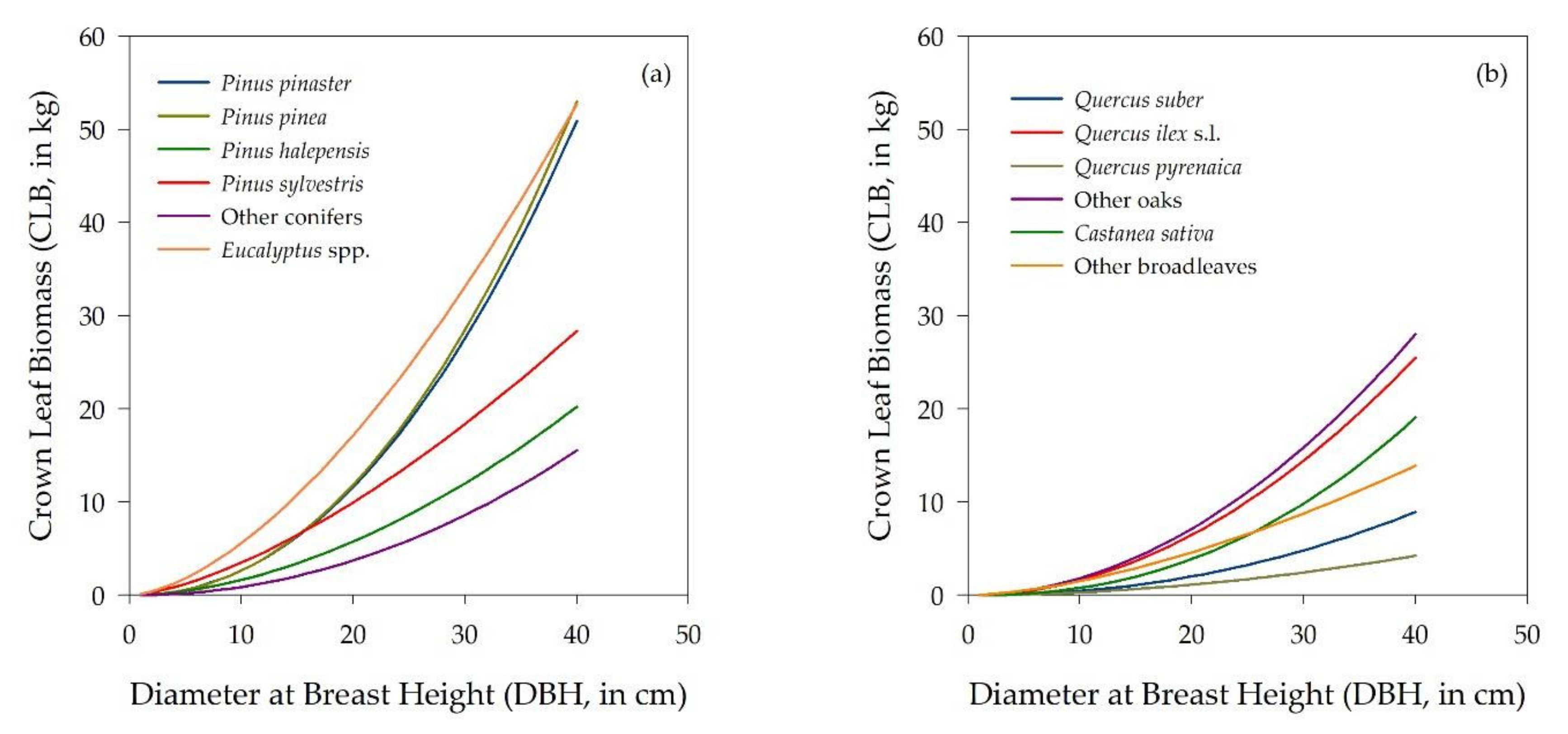
| Shrub Types | Codes [27] | Number of Plots | (cm) | (kg m−3) | Coefficient for the Dependency on Height (c −1 ) | R2 |
|---|---|---|---|---|---|---|
| Machias, terebinthus, garrigues | 140, 150 and 160 | 52 | 114 | 1.68 | −0.358 | 0.61 |
| Quercus coccifera and Pistacia lentiscus | 170 and 180 | 92 | 128 | 3.23 | −0.343 | 0.51 |
| Heathers, Ericaceae shrubs and related groups | 210 | 71 | 134 | 3.08 | −0.166 | 0.74 |
| Small size Cistaceae shrubs | 220a | 27 | 85 | 2.25 | −1.030 | 0.52 |
| Big size Cistaceae shrubs | 220b | 144 | 141 | 2.53 | 0.079 | 0.62 |
| Mixture of broom leguminous shrubs | 230 | 48 | 128 | 1.88 | 0.324 | 0.58 |
| Ulex spp. shrubs and related groups | 240 | 69 | 129 | 2.20 | −0.201 | 0.48 |
| Rosmarinus officinalis | 250a | 75 | 127 | 1.86 | 0.769 | 0.66 |
| Lavandula spp., Rosmarinus officinalis, Thymus spp. shrubland and Phlomis purpurea | 250b | 105 | 52 | 2.26 | −0.777 | 0.36 |
| Ampelodesmos spp. and other grasses | 34 | 25 | 89 | 1.46 | −0.791 | 0.45 |
| Species/Group | Sample Size | a0 | a1 | R2 |
|---|---|---|---|---|
| Pinus pinaster | 4382 | 0.589 | 0.051 | 0.377 |
| Pinus pinea | 1273 | 0.626 | 0.024 | 0.416 |
| Pinus halepensis | 5662 | 0.455 | 0.059 | 0.588 |
| Pinus sylvestris | 4657 | 0.451 | 0.090 | 0.489 |
| Other conifers | 4956 | 0.369 | 0.061 | 0.556 |
| Eucalypts | 1263 | 0.662 | 0.039 | 0.258 |
| Quercus suber | 46 | 0.490 | 0.014 | 0.874 |
| Quercus ilex s.l. | 621 | 0.478 | 0.064 | 0.724 |
| Quercus pyrenaica | 1204 | 0.379 | 0.034 | 0.691 |
| Other oaks | 1431 | 0.384 | 0.026 | 0.724 |
| Castanea sativa | 122 | 0.357 | 0.027 | 0.798 |
| Other broadleaves | 302 | 0.267 | 0.026 | 0.742 |
| Species/Group | Sample Size | b0 | b1 | b2 | R2 |
|---|---|---|---|---|---|
| Pinus pinaster | 38,311 | 0.225 | 0.851 | 0.078 | 0.725 |
| Pinus pinea | 9147 | 0.277 | 0.859 | 0.043 | 0.808 |
| Pinus halepensis | 35,194 | 0.421 | 0.731 | 0.052 | 0.675 |
| Pinus sylvestris | 27,961 | 0.527 | 0.650 | 0.047 | 0.627 |
| Other conifers | 35,542 | 0.416 | 0.705 | 0.035 | 0.649 |
| Eucalypts | 9359 | 0.256 | 0.843 | 0.078 | 0.719 |
| Quercus suber | 8715 | 0.362 | 0.758 | 0.088 | 0.700 |
| Quercus ilex s.l. | 38,424 | 0.579 | 0.640 | 0.078 | 0.742 |
| Quercus pyrenaica | 11,660 | 0.608 | 0.638 | 0.039 | 0.629 |
| Other oaks | 19,904 | 0.679 | 0.634 | 0.036 | 0.651 |
| Castanea sativa | 4563 | 1.236 | 0.455 | 0.060 | 0.592 |
| Other broadleaves | 12,336 | 0.585 | 0.690 | 0.051 | 0.644 |
| Species/Group | c0 | c1 | R2 | Source of Data |
|---|---|---|---|---|
| Pinus pinaster | 0.0197 | 2.130 | 0.760 | Lopes [52] |
| Pinus pinea | 0.0184 | 2.159 | 0.937 | Montero et al. [51] |
| Pinus halepensis | 0.0254 | 1.811 | 0.843 | Mitsopoulos and Dimitrakopoulos [54] |
| Pinus sylvestris | 0.1081 | 1.510 | 0.625 | Montero et al. [51] |
| Other conifers | 0.0078 | 2.058 | 0.739 | Pinus radiata in Montero et al. [51] |
| Eucalypts | 0.1349 | 1.618 | 0.859 | Montero et al. [51] |
| Quercus suber | 0.0033 | 2.145 | 0.648 | Montero et al. [51] |
| Quercus ilex s.l. | 0.0176 | 1.973 | 0.850 | Montero et al. [51] |
| Quercus pyrenaica | 0.0040 | 1.888 | 0.830 | Mendes et al. [53] |
| Other oaks | 0.0197 | 1.968 | 0.884 | Quercus faginea in Montero et al. [51] |
| Castanea sativa | 0.0040 | 2.296 | 0.856 | Leonardi et al. [55] |
| Other broadleaves | 0.0386 | 1.596 | 0.727 | Populus euroamericana in Montero et al. [51] |
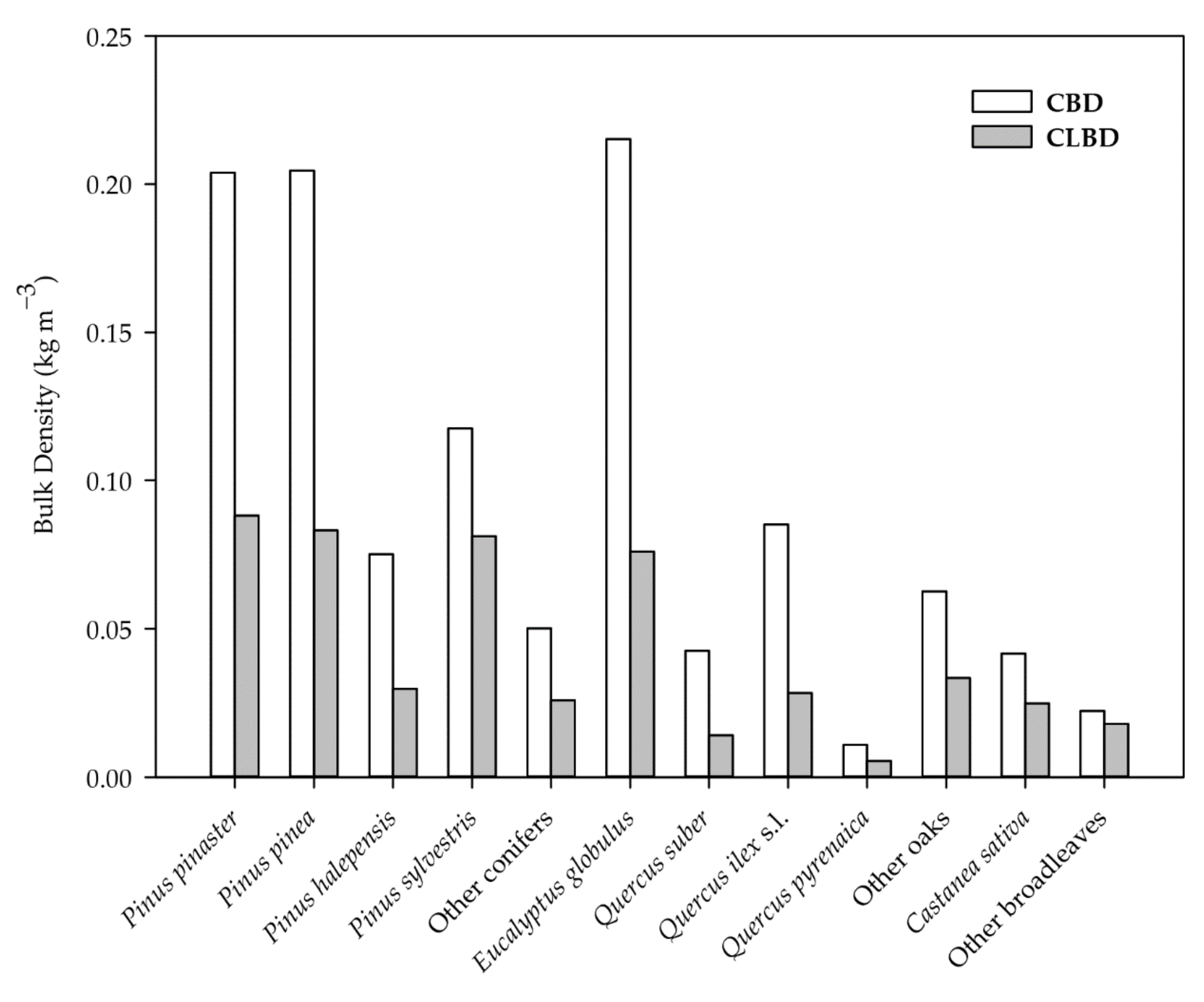
| Species/Group | Sample Size | DBH (cm) | HT (m) | NHA (Trees ha−1) | G (m2 ha−1) | CBD (kg m−3) | CLBD (kg m−3) | |
|---|---|---|---|---|---|---|---|---|
| Portugal | Spain | |||||||
| Pinus pinaster | 1423 | 7369 | 19.2 (10.1) | 11.1 (4.2) | 739 (806) | 18.2 (13.3) | 0.191 (0.072) | 0.073 (0.060) |
| Pinus pinea | 165 | 2152 | 22.2 (11.8) | 8.3 (2.9) | 406 (460) | 11.9 (8.7) | 0.195 (0.065) | 0.070 (0.050) |
| Pinus halepensis | 8 | 9264 | 18.5 (7.3) | 7.8 (2.5) | 422 (420) | 9.5 (7.6) | 0.073 (0.019) | 0.026 (0.019) |
| Pinus sylvestris | 14 | 6053 | 18.5 (7.7) | 10.2 (3.6) | 909 (796) | 22.5 (14.2) | 0.115 (0.038) | 0.075 (0.039) |
| Other conifers | 22 | 6312 | 19.4 (9.7) | 10.2 (5.1) | 744 (686) | 18.6 (13.8) | 0.048 (0.016) | 0.023 (0.014) |
| Eucalyptus globulus | 1059 | 2816 | 13.3 (6.8) | 14.3 (4.9) | 881 (964) | 12.9 (11.3) | 0.217 (0.101) | 0.073 (0.080) |
| Quercus suber | 1051 | 2927 | 24.6 (16.2) | 6.5 (2.7) | 244 (461) | 7.1 (7.2) | 0.039 (0.086) | 0.011 (0.063) |
| Quercus ilex s.l. | 828 | 10,768 | 25.9 (17.2) | 6.3 (1.7) | 356 (555) | 6.7 (6.0) | 0.082 (0.018) | 0.027 (0.023) |
| Quercus pyrenaica | 144 | 3201 | 17.6 (12.5) | 8.7 (2.9) | 686 (720) | 11.3 (9.9) | 0.010 (0.003) | 0.005 (0.004) |
| Other oaks | 58 | 3431 | 20.4 (15.9) | 8.9 (4.1) | 584 (669) | 11.8 (10.5) | 0.059 (0.021) | 0.029 (0.021) |
| Castanea sativa | 36 | 758 | 28.4 (25.9) | 11.0 (3.4) | 689 (923) | 20.7 (17.4) | 0.035 (0.039) | 0.019 (0.020) |
| Other broadleaves | 67 | 2499 | 27.2 (15.9) | 15.1 (5.4) | 584 (606) | 23.1 (13.0) | 0.022 (0.008) | 0.017 (0.008) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nunes, L.; Pasalodos-Tato, M.; Alberdi, I.; Sequeira, A.C.; Vega, J.A.; Silva, V.; Vieira, P.; Rego, F.C. Bulk Density of Shrub Types and Tree Crowns to Use with Forest Inventories in the Iberian Peninsula. Forests 2022, 13, 555. https://doi.org/10.3390/f13040555
Nunes L, Pasalodos-Tato M, Alberdi I, Sequeira AC, Vega JA, Silva V, Vieira P, Rego FC. Bulk Density of Shrub Types and Tree Crowns to Use with Forest Inventories in the Iberian Peninsula. Forests. 2022; 13(4):555. https://doi.org/10.3390/f13040555
Chicago/Turabian StyleNunes, Leónia, María Pasalodos-Tato, Iciar Alberdi, Ana Catarina Sequeira, José Antonio Vega, Vasco Silva, Pedro Vieira, and Francisco Castro Rego. 2022. "Bulk Density of Shrub Types and Tree Crowns to Use with Forest Inventories in the Iberian Peninsula" Forests 13, no. 4: 555. https://doi.org/10.3390/f13040555
APA StyleNunes, L., Pasalodos-Tato, M., Alberdi, I., Sequeira, A. C., Vega, J. A., Silva, V., Vieira, P., & Rego, F. C. (2022). Bulk Density of Shrub Types and Tree Crowns to Use with Forest Inventories in the Iberian Peninsula. Forests, 13(4), 555. https://doi.org/10.3390/f13040555








