Understanding Effects of Competition and Shade Tolerance on Carbon Allocation with a Carbon Balance Model
Abstract
:1. Introduction
2. Data Acquisition
3. Model Description and Parameterization
3.1. Biomass of Compartments
3.2. Carbon Balance and Allocation
3.2.1. Photosynthesis and Respiration
3.2.2. Compartment Senescence and Stem Mortality
3.3. Stem Volume, Diameter, Basal Area, and Growth Estimate
4. Model Validation and Tuning
5. Simulation Experiments
6. Results
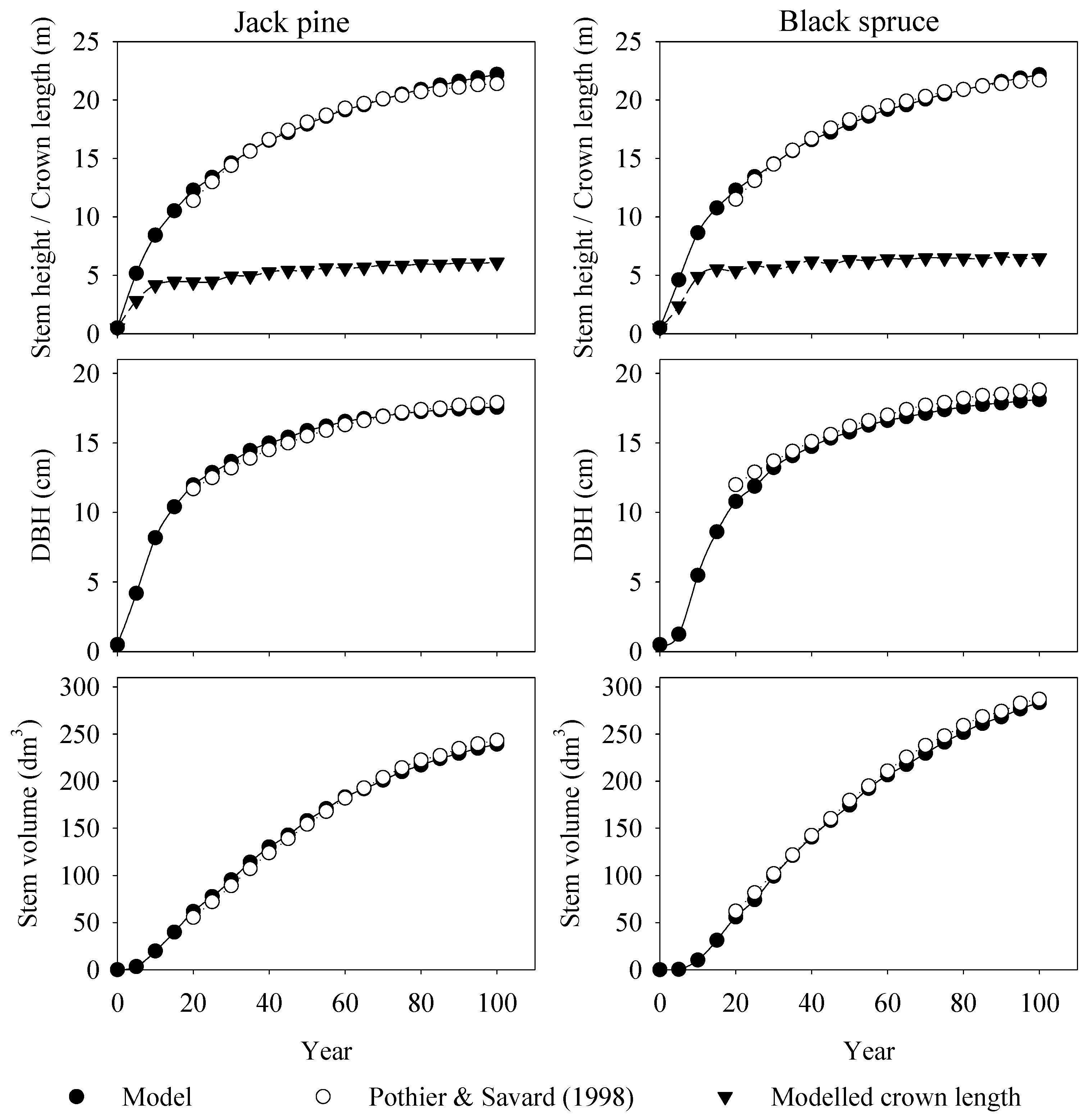
6.1. Model Validation and Assessment
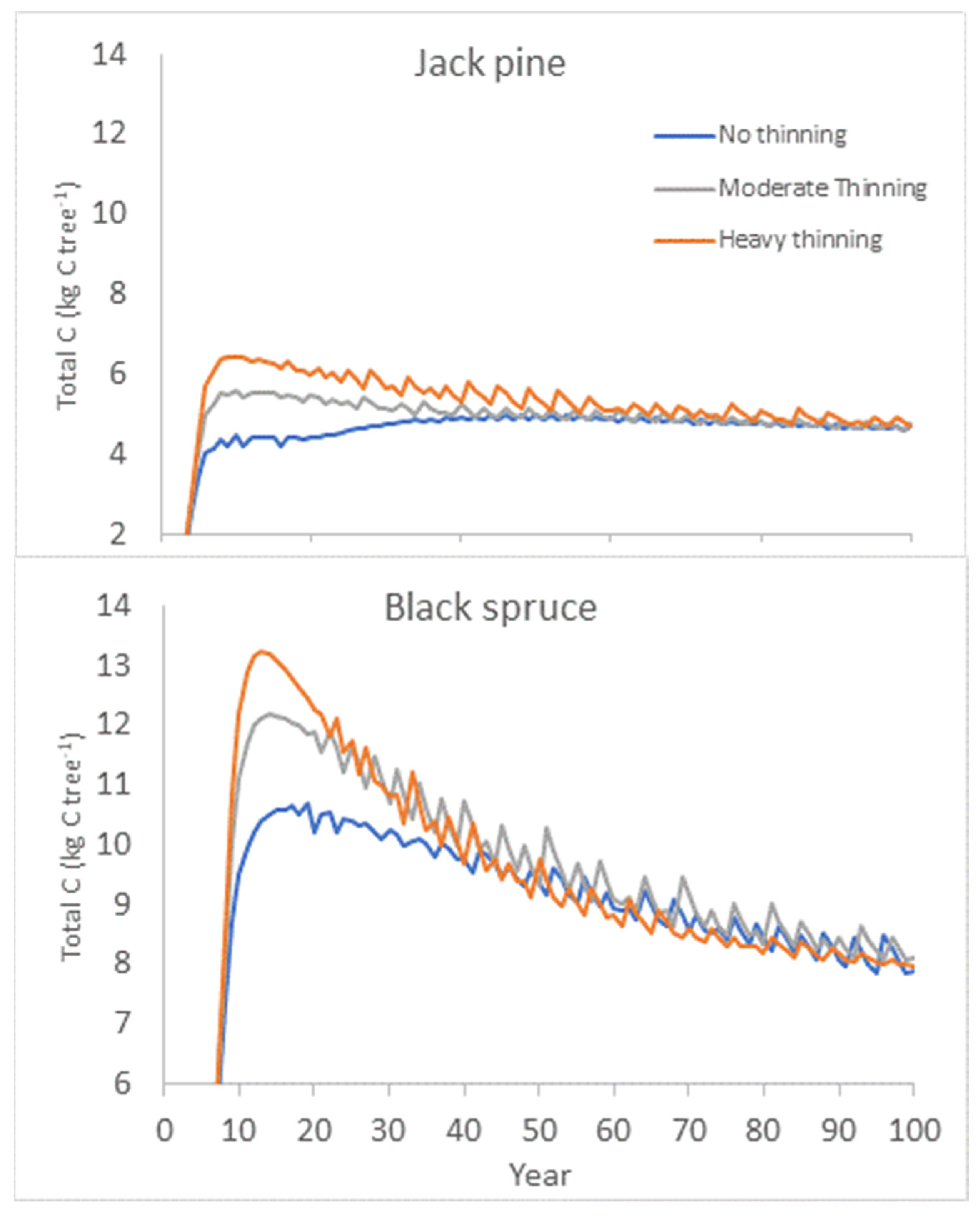
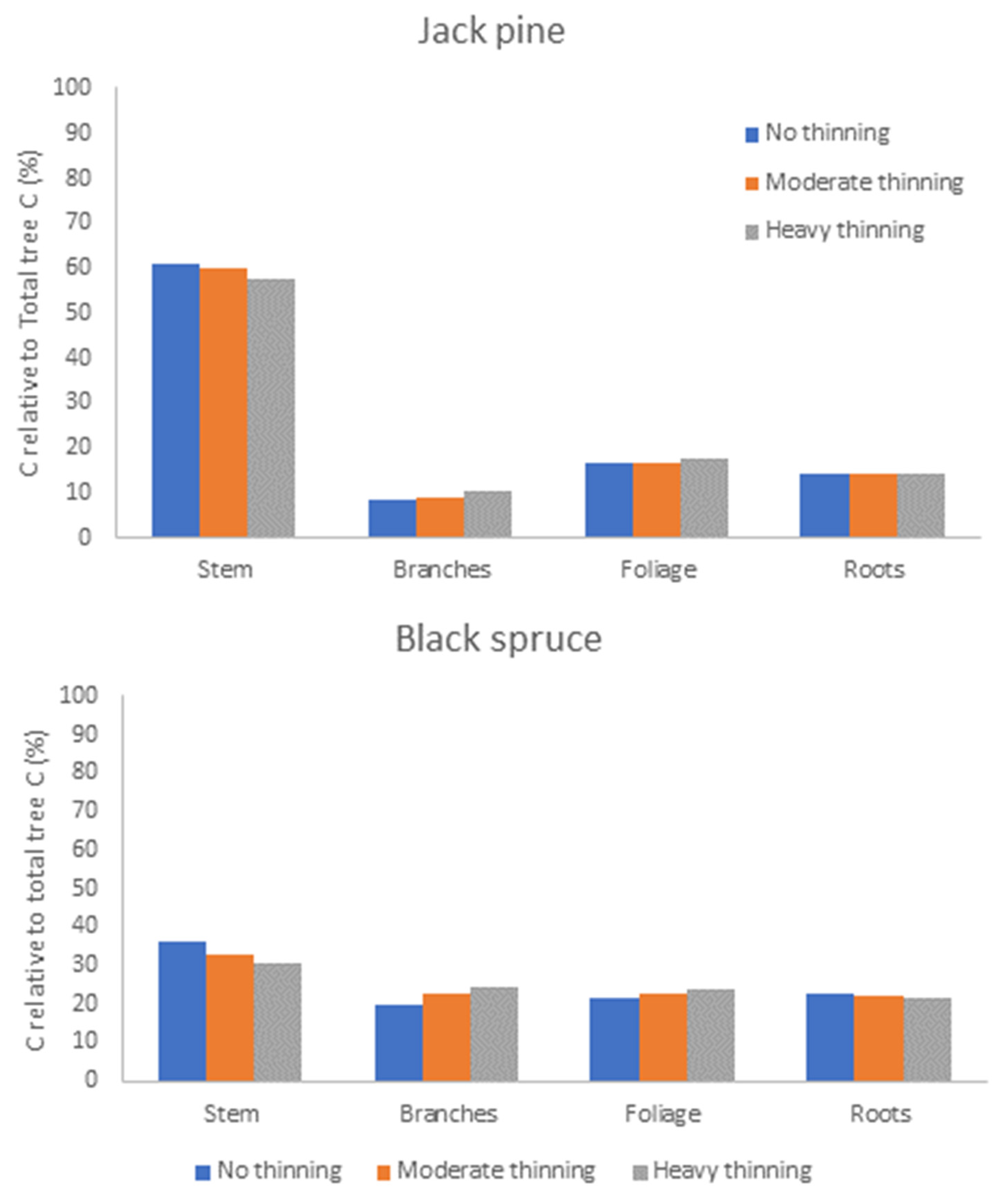
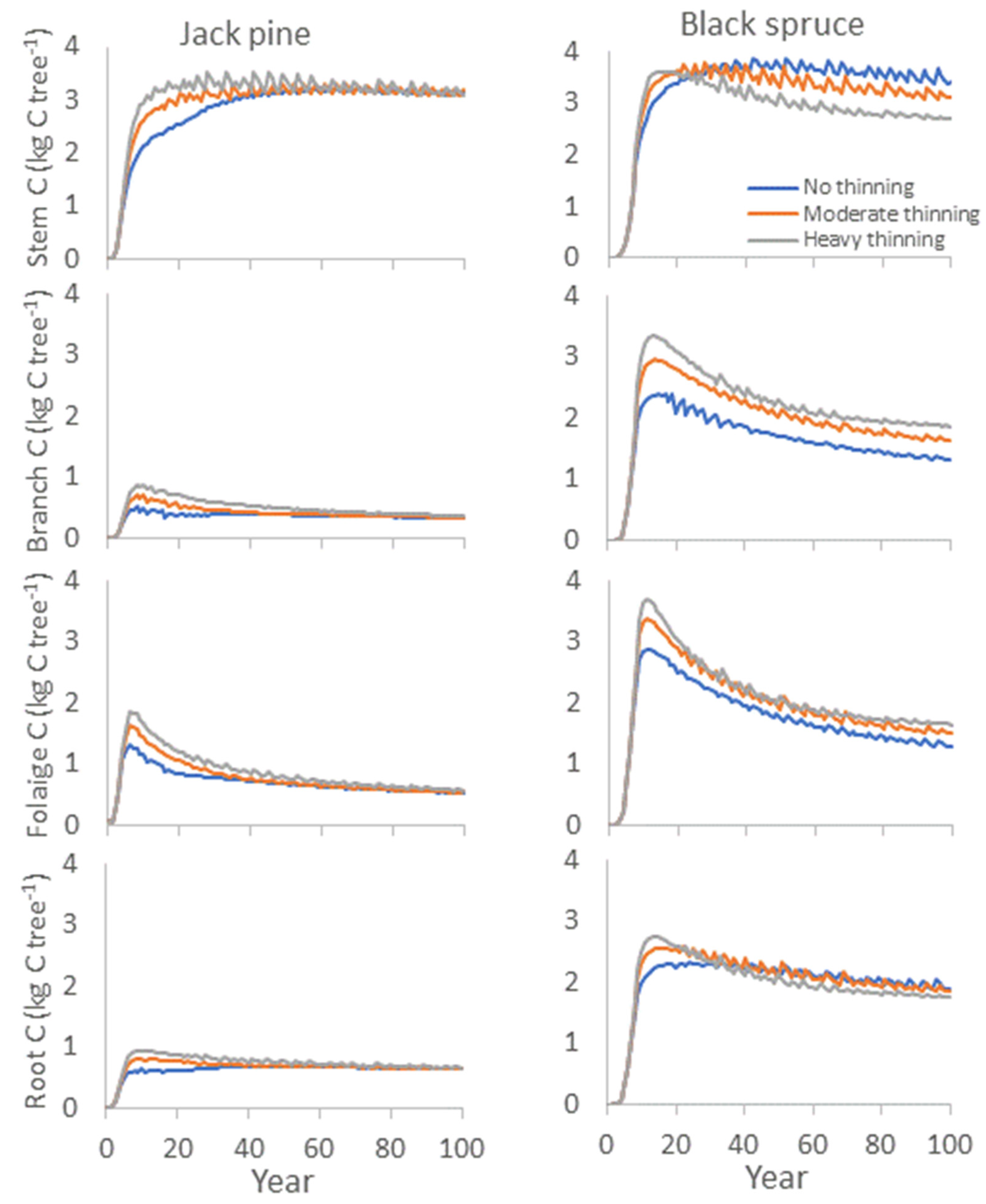
6.2. Model Competition Simulations and Effects on Carbon Allocation
7. Discussion
8. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pearsall, W. Growth studies: VI. On the relative sizes of growing plant organs. Ann. Bot. 1927, 41, 549–556. [Google Scholar] [CrossRef]
- Loach, K. Shade Tolerance in Tree Seedlings. I. Leaf Photosynthesis and Respiration in Plants Raised Under Artificial Shade. New Phytol. 1967, 66, 607–621. [Google Scholar] [CrossRef]
- Lacointe, A. Carbon allocation among tree organs: A review of basic processes and representation in functional-structural tree models. Ann. For. Sci. 2000, 57, 521–533. [Google Scholar] [CrossRef] [Green Version]
- Schall, P.; Lödige, C.; Beck, M.; Ammer, C. Biomass allocation to roots and shoots is more sensitive to shade and drought in European beech than in Norway spruce seedlings. For. Ecol. Manag. 2012, 266, 246–253. [Google Scholar] [CrossRef]
- Franceschini, T.; Schneider, R. Influence of shade tolerance and development stage on the allometry of ten temperate tree species. Oecologia 2014, 176, 739–749. [Google Scholar] [CrossRef]
- Gower, S.; Vogel, J.; Norman, J.; Kucharik, C.; Steele, S.; Stow, T. Carbon distribution and aboveground net primary production in aspen, jack pine, and black spruce stands in Saskatchewan and Manitoba, Canada. J. Geophys. Res. Atmos. 1997, 102, 29029–29041. [Google Scholar] [CrossRef]
- Dickson, R.E. Carbon and nitrogen allocation in trees. Ann. Des Sci. For. 1989, 46, 631s–647s. [Google Scholar] [CrossRef] [Green Version]
- Franklin, O.; Johansson, J.; Dewar, R.C.; Dieckmann, U.; McMurtrie, R.E.; Brännström, Å.; Dybzinski, R. Modeling carbon allocation in trees: A search for principles. Tree Physiol. 2012, 32, 648–666. [Google Scholar] [CrossRef] [Green Version]
- Schneider, R.; Berninger, F.; Ung, C.H.; Mäkelä, A.; Swift, D.E.; Zhang, S.Y. Within crown variation in the relationship between foliage biomass and sapwood area in jack pine. Tree Physiol. 2011, 31, 22–29. [Google Scholar] [CrossRef] [Green Version]
- Goudiaby, V.; Brais, S.; Berninger, F.; Schneider, R. Vertical patterns in specific volume increment along stems of dominant jack pine (Pinus banksiana) and black spruce (Picea mariana) after thinning. Can. J. For. Res. 2012, 42, 733–748. [Google Scholar] [CrossRef]
- Kantola, A.; Mäkinen, H.; Mäkelä, A. Stem form and branchiness of Norway spruce as a sawn timber—Predicted by a process based model. For. Ecol. Manag. 2007, 241, 209–222. [Google Scholar] [CrossRef]
- Rastetter, E.B.; Aber, J.D.; Peters, D.P.C.; Ojima, D.S.; Burke, I.C. Using Mechanistic Models to Scale Ecological Processes across Space and Time. BioScience 2003, 53, 68–76. [Google Scholar] [CrossRef] [Green Version]
- Mäkelä, A. A carbon balance model of growth and self-pruning in trees based on structural relationships. For. Sci. 1997, 43, 7–24. [Google Scholar]
- Johnstone, J.; Chapin, F.S., III. Effects of Soil Burn Severity on Post-Fire Tree Recruitment in Boreal Forest. Ecosystems 2006, 9, 14–31. [Google Scholar] [CrossRef]
- Naydenov, K.; Tremblay, F.; Bergeron, Y.; Goudiaby, V. Effect of active charcoal on the primary growth of jack pine seedlings, Influence du charbon actif sur la croissance primaire des plantules de pin gris. Can. J. For. Res. 2006, 36, 761–767. [Google Scholar] [CrossRef]
- Portsmuth, A.; Niinemets, Ü. Structural and physiological plasticity in response to light and nutrients in five temperate deciduous woody species of contrasting shade tolerance. Funct. Ecol. 2007, 21, 61–77. [Google Scholar] [CrossRef]
- Gendreau-Berthiaume, B.; Kneeshaw, D.D.; Harvey, B.D. Effects of partial cutting and partial disturbance by wind and insects on stand composition, structure and growth in boreal mixedwoods. For. Int. J. For. Res. 2012, 85, 551–565. [Google Scholar] [CrossRef]
- Goudiaby, V.; Brais, S.; Berninger, F.; Schneider, R.; Grenier, Y. Thinning Effects on Jack Pine and Black Spruce Photosynthesis in Eastern Boreal Forests of Canada. Silva Fenn. 2011, 45, 595–609. [Google Scholar] [CrossRef] [Green Version]
- Moulinier, J.; Brais, S.; Harvey, B.D.; Koubaa, A. Response of boreal jack pine (Pinus banksiana Lamb.) stands to a gradient of commercial thinning intensities, with and without N fertilization. Forests 2015, 6, 2678–2702. [Google Scholar] [CrossRef] [Green Version]
- Environment Canada. National Climate Data and Information Archive. Available online: http://www.climate.weatheroffice.ec.gc.ca/Welcome_e.html?&& (accessed on 10 October 2021).
- Shinozaki, K.; Yoda, K.; Hozumi, K.; Kira, T. A quantitative analysis of plant form-the pipe model theory: II. Further evidence of the theory and its application in forest ecology. Jpn. J. Ecol. 1964, 14, 133–139. [Google Scholar]
- Brouwer, R. Distribution of dry matter in the plant. Neth. J. Agric. Sci. 1962, 10, 361–376. [Google Scholar] [CrossRef]
- Zeide, B.; Gresham, C.A. Fractal dimensions of tree crowns in three loblolly pine plantations of coastal South Carolina. Can. J. For. Res. 1991, 21, 1208–1212. [Google Scholar] [CrossRef]
- Waring, R.H.; Schroeder, P.E.; Oren, R. Application of the pipe model theory to predict canopy leaf area. Can. J. For. Res. 1982, 12, 556–560. [Google Scholar] [CrossRef]
- Landsberg, J.J.; Waring, R.H. A generalised model of forest productivity using simplified concepts of radiation-use efficiency, carbon balance and partitioning. For. Ecol. Manag. 1997, 95, 209–228. [Google Scholar] [CrossRef]
- Yin, X. Reconstructing monthly global solar radiation from air temperature and precipitation records: A general algorithm for Canada. Ecol. Model. 1996, 88, 39–44. [Google Scholar] [CrossRef]
- Jacovides, C.P.; Tymvios, F.S.; Asimakopoulos, D.N.; Theofilou, K.M.; Pashiardes, S. Global photosynthetically active radiation and its relationship with global solar radiation in the Eastern Mediterranean basin. Theor. Appl. Climatol. 2003, 74, 227–233. [Google Scholar] [CrossRef]
- Ryan, M.G.; Lavigne, M.B.; Gower, S.T. Annual carbon cost of autotrophic respiration in boreal forest ecosystems in relation to species and climate. J. Geophys. Res. Atmos. 1997, 102, 28871–28883. [Google Scholar] [CrossRef] [Green Version]
- Steele, S.J.; Gower, S.T.; Vogel, J.G.; Norman, J.M. Root mass, net primary production and turnover in aspen, jack pine and black spruce forests in Saskatchewan and Manitoba, Canada. Tree Physiol. 1997, 17, 577–587. [Google Scholar] [CrossRef] [Green Version]
- Pothier, D.; Savard, F. Actualisation des Tables de Production Pour les Principales ESPèces du QUébec; Gouvernement du Québec, Ministère des Ressources Naturelles, Bibliothèque Nationale du Québec, RN98 3054: Québec, QC, Canada, 1998. [Google Scholar]
- Nikolova, P.; Blaschke, H.; Matyssek, R.; Pretzsch, H.; Seifert, T. Combined application of computer tomography and light microscopy for analysis of conductive xylem area in coarse roots of European beech and Norway spruce. Eur. J. For. Res. 2009, 128, 145–153. [Google Scholar] [CrossRef]
- Singh, T. Wood density variation of six major tree species of the Northwest Territories. Can. J. For. Res. 1986, 16, 127–129. [Google Scholar] [CrossRef]
- Bond-Lamberty, B.; Wang, C.; Gower, S. Aboveground and belowground biomass and sapwood area allometric equations for six boreal tree species of northern Manitoba. Can. J. For. Res. 2002, 32, 1441–1450. [Google Scholar] [CrossRef]
- Kyker-Snowman, T.D.; Wilson, B.F. Total wood, sapwood, and heartwood in branch bases of three conifers. Can. J. For. Res. 1988, 18, 1332–1336. [Google Scholar] [CrossRef]
- Lavigne, M.; Ryan, M. Growth and maintenance respiration rates of aspen, black spruce and jack pine stems at northern and southern BOREAS sites. Tree Physiol. 1997, 17, 543–551. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Armentano, T.V.; Menges, E.S. Air-pollution-induced foliar injury to natural populations of jack and white pine in a chronically polluted environment. Water Air Soil Pollut. 1987, 33, 395–409. [Google Scholar] [CrossRef]
- Hom, J.L.; Oechel, W.C. The photosynthetic capacity, nutrient content, and nutrient use efficiency of different needle age-classes of black spruce (Picea mariana) found in interior Alaska. Can. J. For. Res. 1983, 13, 834–839. [Google Scholar] [CrossRef]
- Brooks, J.R.; Flanagan, L.B.; Varney, G.T.; Ehleringer, J.R. Vertical gradients in photosynthetic gas exchange characteristics and refixation of respired CO2 within boreal forest canopies. Tree Physiol. 1997, 17, 1–12. [Google Scholar] [CrossRef]
- Aubin, I.; Beaudet, M.; Messier, C. Light extinction coefficients specific to the understory vegetation of the southern boreal forest, Quebec. Can. J. For. Res. 2000, 30, 168–177. [Google Scholar] [CrossRef]
- Pinjuv, G.; Mason, E.G.; Watt, M. Quantitative validation and comparison of a range of forest growth model types. For. Ecol. Manag. 2006, 236, 37–46. [Google Scholar] [CrossRef]
- Valentine, H.T.; Mäkelä, A. Bridging process-based and empirical approaches to modeling tree growth. Tree Physiol. 2005, 25, 769–779. [Google Scholar] [CrossRef]
- Wright, S.D.; McConnaughay, K.D.M. Interpreting phenotypic plasticity: The importance of ontogeny. Plant Species Biol. 2002, 17, 119–131. [Google Scholar] [CrossRef]
- McConnaughay, K.D.M.; Coleman, J.S. Biomass allocation in plants: Ontogeny or optimality? A test along three resource gradients. Ecology 1999, 80, 2581–2593. [Google Scholar] [CrossRef]
- Evans, G.C. The Quantitative Analysis of Plant Growth; University of California Press: Berkeley, CA, USA, 1972; Volume 1. [Google Scholar]
- Claveau, Y.; Messier, C.; Comeau, P.G.; Coates, K.D. Growth and crown morphological responses of boreal conifer seedlings and saplings with contrasting shade tolerance to a gradient of light and height. Can. J. For. Res. 2002, 32, 458–468. [Google Scholar] [CrossRef] [Green Version]
- McCarthy, M.C.; Enquist, B.J. Consistency between an allometric approach and optimal partitioning theory in global patterns of plant biomass allocation. Funct. Ecol. 2007, 21, 713–720. [Google Scholar] [CrossRef]
- Sims, R.A.; Kersaw, H.M.; Wickware, G.M. The Autecology of Major Tree Species in the North Central Region of Ontario; Forestry Canada, Ontario Region: Sault Ste. Marie, ON, Canada, 1990; 126p. [Google Scholar]
- Humbert, L.; Gagnon, D.; Kneeshaw, D.; Messier, C. A shade tolerance index for common understory species of northeastern North America. Ecol. Indic. 2007, 7, 195–207. [Google Scholar] [CrossRef] [Green Version]
- Newton, P.F.; Jolliffe, P.A. Aboveground dry matter partitioning responses of black spruce to directional-specific indices of local competition. Can. J. For. Res. 2003, 33, 1832–1845. [Google Scholar] [CrossRef]
- Walters, M.B.; Reich, P.B. Research Review: Low-Light Carbon Balance and Shade Tolerance in the Seedlings of Woody Plants: Do Winter Deciduous and Broad-Leaved Evergreen Species Differ? New Phytol. 1999, 143, 143–154. [Google Scholar] [CrossRef]
- Albrektson, A. Sapwood basal area and needle mass of Scots pine (Pinus sylvestris L.) trees in central Sweden. For. Int. J. For. Res. 1984, 57, 35–43. [Google Scholar] [CrossRef]
- Shelburne, V.; Hedden, R.; Allen, R. The effect of site, stand density, and sapwood permeability on the relationship between leaf area and sapwood area in loblolly pine (Pinus taeda L.). For. Ecol. Manag. 1993, 58, 193–209. [Google Scholar] [CrossRef]
- O’Hara, K.L. The historical development of uneven-aged silviculture in North America. Forestry 2002, 75, 339–346. [Google Scholar] [CrossRef]

| Jack Pine | Black Spruce | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Mean (SD) | Mean (SD) | |||||||||
| Gr | 0% | 1–31% | 32–40% | 41–66% | 0% | 1–31% | 32–40% | 41–66% | ||
| Nb | 2625 | 2321 | 2838 | 2790 | 2000 (891) | 2375 | 2283 | 2090 | 2364 | 2257 (521) |
| Na | 2625 | 1250 | 1188 | 1050 | 1505 (800) | 2375 | 1475 | 1260 | 1171 | 1435 (641) |
| Gb | 27.5 | 23.2 | 20.2 | 18.5 | 21.6 (5.66) | 38.85 | 33.43 | 34.24 | 29.29 | 32.6 (5.5) |
| Ga | 27.5 | 16.9 | 13.1 | 11.7 | 19.0 (6.55) | 38.85 | 27.9 | 28.01 | 21.59 | 26.7 (8.6) |
| Vb | 121.4 | 112 | 101.4 | 101.1 | 101.3 (25.97) | 187.1 | 164.1 | 174.4 | 140.1 | 159.5 (29) |
| Va | 96.9 | 58.6 | 36.4 | 34.3 | 62.6 (27.46) | 187.1 | 138.2 | 146.7 | 104.9 | 132.8 (43.6) |
| DBHb | 11.3 | 10.5 | 9 | 8.7 | 11.6 (2.15) | 14.4 | 13.4 | 13.7 | 11.9 | 13.1 (1.75) |
| DBHa | 11.3 | 12.5 | 11.3 | 12 | 12.5 (1.75) | 14.4 | 15.3 | 16.4 | 14.9 | 15.3 (1.72) |
| Htotb | 13.7 | 17.3 | 20.5 | 23.6 | 16.2 (4.60) | 15.3 | 15.9 | 15.9 | 15.3 | 15.6 (0.93) |
| Htota | 11.5 | 11.3 | 9.6 | 9.8 | 10.7 (1.28) | 15.3 | 15.9 | 16.6 | 15.2 | 15.7 (1.14) |
| Hcb | 5.2 | 6.4 | 7.5 | 8.6 | 5.9 (1.82) | 5.6 | 5.8 | 5.9 | 5.6 | 5.7 (0.34) |
| Hca | 4.4 | 4.3 | 3.7 | 3.7 | 4.1 (0.47) | 5.6 | 5.8 | 6.1 | 5.6 | 5.8 (0.41) |
| Vtotb | 52.6 | 48.6 | 35.6 | 37.7 | 56.8 (24.24) | 86 | 78.5 | 86.3 | 61.4 | 74.7 (23.65) |
| Vtota | 40.7 | 48.5 | 30.2 | 35.3 | 44.3 (14.10) | 86 | 97.7 | 117.7 | 90.9 | 98.0 (26.88) |
| Fma | 4.76 | 5.62 | 5.50 | 6.50 | 5.54 (1.77) | 4.94 | 3.63 | 5.14 | 5.89 | 5.32 (1.88) |
| Fmb | — | — | — | — | — | — | — | — | — | — |
| Symbol * | Meaning | Jack Pine | Black Spruce | Unit | References |
|---|---|---|---|---|---|
| φs | Form factor of stemwood in stem below crown | 1.629 | 1.0 | - | Based on pipe model assumption |
| φc | Form factor of stemwood in stem within crown | 0.563 | 0.563 | - | Based on conical form assumption |
| φ’b | Form factor of stemwood in branches | 1.071 | 1.071 | - | Estimated |
| φ’t | Form factor of stemwood in transport root | 1 | 1 | - | [24] |
| cb | Ratio of crown radius to crown length | 0.20 | 0.15 | - | [13,18] |
| ct | Ratio of transport root length to stem length | 1 | 1 | - | [13] |
| ρs, ρb, ρt | Density of wood | 421 | 454 | kg·m−3 | [25] |
| αs | Sapwood area: foliage biomass ratio in stem | 4.2 × 10−4 | 3.0 × 10−4 | m2·kg−1 | [18], stem sapwood area from Reference [26] |
| αb | Sapwood area: foliage biomass ratio in branches | 1.03 × 10−3 | 2.13 × 10−3 | m2·kg−1 | [10]; branch sapwood area estimated from Reference [27] |
| αt | Sapwood area: foliage biomass ratio in transport roots | 1.02 × 10−4 | 1.26 × 10−4 | m2·kg−1 | This paper; root sapwood area from Reference [26] |
| αr | Fine root: foliage biomass ratio | 0.15 | 0.2 | - | This paper; fine-root biomass [28] |
| β1 | Parameter 1 for crown height estimation | 0.5377 | 0.5948 | - | Trial and error |
| β2 | Parameter 2 for crown height estimation | −0.0659 | −0.0248 | - | Trial and error |
| β3 | Parameter 3 for crown height estimation | 0.5543 | 0.4252 | - | Trial and error |
| 2z | “Fractal dimension” of foliage in crown | 1.121 | 1.7926 | - | [18] |
| ξ | “Surface area density” of foliage | 0.5139 | 0.2231 | kg·m−2.7 (jack pine) kg·m−2.4 (black spruce) | [10], using Equation (5c) from Reference [13] |
| Carbon use efficiency | 0.587 | 0.37 | kg·C·kg−1 DW | [29] | |
| r1 | Specific maintenance respiration rate of foliage + fine roots | 0.31 | 0.09 | kg·C·kg−1 DW·year−1 | [30] |
| r2 | Specific maintenance respiration rate of wood | 0.02 | 0.07 | kg·C·kg−1 DW·year−1 | [29] |
| sf | Specific senescence rate of foliage | 0.33 | 0.08 | year−1 | Based on needle lifetime of 13 years for black spruce [30] and 3 years for jack pine [31] |
| sr | Specific senescence rate of fine roots | 3.3 | 3.3 | year−1 | [28] |
| ds0, db0, dt0 | Specific sapwood area turnover rate per unit relative pruning | 1 | 1 | - | [13] |
| ds1 | Specific stem sapwood area turnover rate in case of pruning | 0.02 | 0.05 | year−1 | Estimated based on Reference [13] |
| db1 | Specific branch sapwood area turnover rate in case of pruning | 0.05 | 0.05 | [13] | |
| dt1 | Specific transport root sapwood area turnover rate in case of pruning | 0.05 | 0.05 | [13] | |
| ψs | Form factor of senescent sapwood in stem below crown | 1.629 | 1.0 | - | Implied by pipe model |
| ψc | Form factor of senescent sapwood in stem inside crown | 0.5 | 0.5627 | - | Trial and error |
| ψ’b | Form factor of senescent sapwood in branches | 0.9 | 0.9 | - | [13] |
| ψ’t | Form factor of senescent sapwood in transport roots | 0.46 | 0.46 | - | [13,24] |
| an | Specific leaf area | 3.5 | 4.4 | m3·kg−1 | [18] |
| P0 | Maximum rate of canopy photosynthesis per unit area | 2.20 | 1.46 | kg·C·m−2 year−1 | Computed from Reference [10] |
| aσ | Decrease of photosynthesis per unit crown length | 0.094 | 0.11 | m−1 | [32] |
| K | Extinction coefficient | 0.53 | 0.52 | - | [33] |
| Cmax | Crown coverage | 1.52 | 1.91 | - | Computed from Reference [10] |
| fe | Bark factor | 0.225 | 0.737 | - | This paper |
| φs.tot | Parameter for stem volume and basal area stem height | 0.0578 | 0.3145 | - | This paper |
| δ | Parameter for quadratic and arithmetic stem diameter at 1.30 m relationship | 0.989 | 0.985 | - | This paper |
| ε1 | Parameter 1 related to quantum efficiency | 0.0432 | 0.5948 | - | Trial and error |
| ε2 | Parameter 2 related to quantum efficiency | 0.0012 | 0.0247 | - | Trial and error |
| ε3 | Parameter 3 related to quantum efficiency | 0.0003 | 0.4252 | - | Trial and error |
| Variables | MB (%) | EF (%) |
|---|---|---|
| Jack Pine | ||
| iDBH | 11 | 53 |
| iHtot | 6 | 55 |
| ivtot | 6 | 99 |
| Fm | 1 | 36 |
| Black Spruce | ||
| iDBH | 14 | 84 |
| iHtot | 10 | 69 |
| ivtot | 18 | 55 |
| Fm | 9 | 91 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Goudiaby, V.; Schneider, R.; Brais, S.; Raulier, F.; Berninger, F. Understanding Effects of Competition and Shade Tolerance on Carbon Allocation with a Carbon Balance Model. Forests 2022, 13, 572. https://doi.org/10.3390/f13040572
Goudiaby V, Schneider R, Brais S, Raulier F, Berninger F. Understanding Effects of Competition and Shade Tolerance on Carbon Allocation with a Carbon Balance Model. Forests. 2022; 13(4):572. https://doi.org/10.3390/f13040572
Chicago/Turabian StyleGoudiaby, Venceslas, Robert Schneider, Suzanne Brais, Frédéric Raulier, and Frank Berninger. 2022. "Understanding Effects of Competition and Shade Tolerance on Carbon Allocation with a Carbon Balance Model" Forests 13, no. 4: 572. https://doi.org/10.3390/f13040572
APA StyleGoudiaby, V., Schneider, R., Brais, S., Raulier, F., & Berninger, F. (2022). Understanding Effects of Competition and Shade Tolerance on Carbon Allocation with a Carbon Balance Model. Forests, 13(4), 572. https://doi.org/10.3390/f13040572







