Predicting the Average Compression Strength of CLT by Using the Average Density or Compressive Strength of Lamina

Abstract

The compressive strength in the major direction of cross-laminated timber CLT is the key to supporting the building load when CLT is used as load-bearing walls in high-rise wood structures. This study mainly aims to present a model for predicting the average compressive strength of CLT and promoting the utilization of CLT made out of planted larch. The densities and compressive strengths of lamina specimens and CLT samples with widths of 89 and 178 mm were evaluated, and their relationship was analyzed to build a prediction model by using Monte Carlo simulation. The results reveal that the average density of the lamina and CLT were about equal, whereas the average compressive strength of the CLT was just about 72% of that of the lamina. Width exerted no significant effect on the average compressive strength of the CLT, but homogenization caused the wider CLT to have a smaller variation than that of the lamina. The average compressive strength of the lamina could be calculated by using the average density of lamina multiply by 103.10, and the average compressive strength of the CLT could be calculated according to the compression strength of lamina in major and minor direction, therefore, a new prediction model is determined to predict the average compression strength of CLT by using the average density of lamina or CLT, the average compression strength of CLT made in this study is about 74.23 times of the average density of the lamina. The results presented in this study can be used to predict the average compressive strength of CLT by using the average density of lamina and provide a fundamental basis for supporting the utilization of CLT as load-bearing walls.

1. Introduction

Cross-laminated timber (CLT) is an ideal material for multistory constructions and high-rise buildings. As a prefabricated massive engineering wood product, CLT is a new solid-engineered wood product fabricated by gluing more than three layers of sawn lumber or wood composite panels, stacked crosswise to form a large-scale panel [1]. CLT exhibits mechanical and physical properties superior to those of other engineering wood products (such as glued laminated timber, oriented strand board, and laminated veneer lumber), as its adjacent wood layers is assembled orthogonally. Owing to its good in-plane and out-of-plane compressive strength, excellent dimensional stability, and a high level of prefabrication, CLT panels are widely used as prefabricated structural components, such as wall panels, floors, and roofs in residential and high-rise wood buildings [2].

In Europe and North America where it has drawn considerable attention, CLT is widely applied in high-rise buildings because it is environment-friendly and energy-efficient and shows superior physical and mechanical properties to those of steel and concrete, such as the CLT has the greater strength to weight ratio and better insulation performance. CLT has been used as prefabricated floor and exterior wall in an 18-floor student apartment at the University of British Columbia in Canada [3]. Prefabricated CLT components produced using local wood from Norway have been used to build the Tower of Lake Mjøsa with a height of 85.4 m, thus far the tallest wood apartment globally.

Numerous studies have been conducted on manufacturing and building technologies for CLT to promote and expand the application of CLT [4] by studying the compressive performance [5], bending properties [6], rolling shear performance [7], fire resistance [8], and thermal and insulation performance [9] of CLT. Safety under the force of wood building mainly depends on the safety and load resistance capacity of load-bearing components. Specifically, the resistance capacity of the load-bearing wall is mostly determined by the in-plane compressive strength of the CLT used in high-rise buildings.

The resistance capacity of CLT under compressive load is usually investigated by statistical analysis of the load-bearing capacity of full-size CLT components. Nonetheless, large-scale testing has several disadvantages, such as time costs, significant material preparation requirements, and high costs because variations in manufacturing parameters influence the mechanical properties of CLT [10,11,12]. Such disadvantages may be overcome by developing theories and models for the prediction and calculation of the compressive strength of CLT. Once verified using experimental data, the proposed prediction model may be used to guide the production process of CLT [10,13]. In one study, the compressive strength was calculated and predicted using the formula $F_{CLT}{A}_{CLT}={{\displaystyle \sum }}^{}{F}_i{A}_i$ ($F_{CLT}$ is the compressive strength of CLT; $A_{CLT}$ is the cross-sectional area of CLT; $F_i$ is the compressive strength of the ith lamina; and $A_i$ is the cross-sectional area of the ith lamina) derived from the mechanical theory of composites and calculated the compressive resistance capacity of the lamina in each layer [14]. Another study reported that the resistance capacity of layers stacked crosswise should be ignored and considered to be zero in calculating the compressive strength of CLT because the compressive strength ratio was found to be around 10% between the timber perpendicular and parallel to the wood grain [15,16]. However, the horizontal compressive strength of CLT was reported to be 30%—that is, greater than the glulam—given the effects of restraint and reinforcement between adjacent layers perpendicular to each other [5].

The compressive strength of larch lamina can be used to predict the compressive strength of CLT. Moreover, the mechanical properties of wood are typically related to its density [17]. Compressive strength parallel to the grain exhibits a good linear correlation (R² = 0.5195) with density in small clear wood samples [18]. The linear correlation between the strength and density of dimensional lumber was not sufficient because of wood variability [19]. To reduce the effect of wood variation, a good linear correlation was established by grouping the lumber first according to the density of lumber, and then study the relationship between the mean strength and elastic modulus of dimensional lumber [20]. This method can reduce the effect of wood variation and improve the accuracy of the strength prediction model. Therefore, a prediction model to calculate the average compressive strength of CLT combining the following two models can be presented: a mechanical model to calculate the average of CLT by using the average compressive strength of lamina and a prediction model to determine the average compressive strength of lamina by using the average density.

As the mean value of compressive strength is necessary to calculate the characteristic value of CLT and will be very helpful to determine the design value for the CLT using as wall planes. This study aims to complete and verify predictive modeling to determine the average compressive strength by using the average compressive strength or density of lamina. Lamina samples with a cross-section of 21 mm × 89 mm and CLT samples with cross-sections of 63 mm × 89 mm and 63 mm × 178 mm were fabricated. The density and compressive strength of the lamina and CLT samples parallel to the grain were analyzed. A prediction model for the average compressive strength and average density of the lamina was established by Monte Carlo simulation (MCS) [21,22]. The simplified formula for determining the average compressive strength of CLT was obtained using the average compressive strength of the CLT lamina.

A prediction model was then established to calculate and predict the average compressive strength of CLT, based on the combination of the prediction model and simplified calculation formula. The prediction model proposed in this study could complement the theoretical formula for the compressive strength of CLT and efficiently determine the average compressive strength of CLT for wood building design.

2. Materials and Methods

2.1. Properties of the Lamina

Larch logs (Larix kaempferi) from a plantation in Liaoning, China were used to prepare lamina and CLT specimens. Logs with a diameter of 18–30 cm and about 15–20 growth rings were processed by sawing, kiln drying, rough planning, and fine planning to produce lumber with a cross-section of 21 mm × 89 mm. To reduce the defects, visual grading of the lumber was performed in accordance with Chinese Standard GB 5005-2017 [23]. Only the lumber could meet the requirement for the visual Ⅱ_c grade, similar to the visual SS grade in North America, and was selected to produce the lamina and CLT samples. Lamina specimens measuring 21 mm × 89 mm × 150 mm with a number of 102 and with a slenderness ratio lower than 17 and were cut from the selected lumber with a moisture content of 12 ± 2%. To maintain the representative of the wood sample and reduce the effect of the maximum defect of each lumber on the test results, the lamina specimens were randomly intercepted close to the end of the lumber, and only one specimen was produced from one piece of lumber.

To adjust the moisture content (MC) of the lamina specimens to 12%, all specimens were saved in a climate box set to a temperature of 20 °C ± 2 °C and with a relative humidity of 65 ± 5% for more than two weeks before compressive strength testing. The density of the lamina specimens was calculated based on the weight, length, width, and thickness. A universal test machine was used to evaluate the compressive strength parallel to the grain of the lamina specimens with reference to GB/T 28993-2012 [24] and ASTM D198 [25]. During testing, the loading speed of the machine was set to 3 mm/min, and the maximum compressive load $P_{max}$ was recorded. The compressive strength of the lamina was then calculated using Formula (1), and the strength was accurate to 0.01 MPa.

f_c = P_max/(d·b)

(1)

In Formula (2), m is the mass of the sample (g); l is the length of the sample (mm); $b$ is the width of the sample (mm); $d$ is the thickness of the sample (mm); $f_c$ is compressive strength parallel to the grain of the lamina (MPa); and $P_{max}$ is the maximum load capacity of the sample (N).

2.2. CLT Sample Preparation and Testing

The remaining portion of the lumber after it was sawn to produce lamina specimens was used randomly to produce CLT specimens measuring 63 mm × 89 mm × 150 mm (30 specimens) and 63 mm × 178 mm × 150 mm (32 specimens). To produce CLT specimens, polyurethane (PUR) structural adhesive PURBOND HBS 309 (Henkel, Germany) with a solid content of 50% was used. The PUR adhesive was applied on only one surface of the lamina by using the laminating machine, PUR was chosen as it has the advantages, such as light color, without formaldehyde, great bonding performance, good flexibility and low temperature for curing. To ensure the bonding strength, the quality of the adhesive applied on each square meter’s bonding area of CLT was about 220 g, and the hydraulic pressing machine was used to maintain the CLT under a pressure level of 1.2 MPa for 2 h. After indoor curing for 30 days, the CLT was cut into small samples with the design dimensions.

The CLT specimens were stored in a climate box with a temperature of 20 °C ± 2 °C and relative humidity of 65 ± 5% for more than 4 weeks for their MC to be close to 12%. Similar to lamina specimen testing, the in-plane compressive strength in the main direction of the CLT and its density were tested in accordance with the relevant requirements of ANSI/APA PRG 320 [26]. A universal test machine was used to test the compressive strength of CLT shown as Figure 1, the upper steel plate that could apply the load on the CLT specimen was fixed with the load head of the testing machine, the spherical hinge base steel plate was fixed with the bottom beam of the machine, a steel plate under the CLT specimen was fixed with the spherical hinge base. In the test progress, the move speed of the load head of the test machine was about 3 mm/min, the test was stopped after the maximum load was determined. In the end, density and compressive strength of the CLT were tested and calculated.

After the maximum load is reached of the CLT samples, there were three main forms of the damage for the CLT under compressive load as shown in Figure 2, such as compression failure of the lamina in major direction and delamination near the bonding line shown as (A) in Figure 2, compression failure of the lamina in major direction and delamination along the annual rings of the lamina in minor direction shown as (B) in Figure 2, compression failure and delamination of the lamina in major direction, compression failure of the lamina in major direction and delamination of the lamina in minor direction shown as (C) in Figure 2.

2.3. Probability Distribution and Kolmogorov–Smirnov Test

The normal distribution, log-normal distribution, and Weibull distribution are the most widely used models for investigating and fitting the probability distribution of the physical and mechanical properties of engineering wood and wood composite materials [27,28]. The normal distribution is the most commonly used model in statistics; however, the properties of wood as a natural material can be affected by growth conditions, grain direction, crack, position in the tree, and so on, resulting in the variation and non-symmetrical distribution of the wood strength. To examine the distribution of the test results, three distribution models were used to fit the distribution of the density and strength of lamina. The parameters for the distribution model were determined using the programming language R version 3.6.3. The parameters were then substituted into the formula in

Table 1. Density and MOE statistics of the two-dimensional larch lumber types.

Normal	Log-Normal	2-Parameters-Weibull
$$\frac{1}{2}\left[1+erf\left(\frac{x-\mu }{\sigma \sqrt{2}}\right)\right]$$	$$\frac{1}{2}\left[1+erf\left(\frac{\ln x-\mu }{\sigma \sqrt{2}}\right)\right]$$	$$1-e^{-{(x/\lambda )}^k}$$

Notation: $x$ is the test data of lamina; μ and σ are the mean and standard deviation under normal and log-normal distributions, respectively; λ and k are the scale and shape parameters of the Weibull distribution respectively.

to calculate the cumulative distribution probability $F\left(x_i,\theta \right)$. The maximum difference value ($D_n$) between the assumed distribution model and the measured data was calculated using Formula (2).

The Kolmogorov–Smirnov (K–S) test method [29] and the method of least squares [30] are used to compare their goodness-of-fit. In the K–S test, if the value of $D_n$ calculated using Formula (2) is smaller than the critical value with a significance level of 0.05 (α = 0.05) and sample number n, the hypothetical distribution can be accepted; otherwise, the distribution model is rejected [31,32]. The sum of the squared errors ($\phi$) between the hypothetical distribution and measured data is calculated using Formula (3). The smaller the value of $\phi$, the better the hypothetical distribution. The best distribution model is ultimately selected to fit the test results of the lamina.

$$D_n=max\left|F\left(x_i,\theta \right)-y_i\right|$$

(2)

$$\phi ={\displaystyle \sum }_i^N{[F\left(x_i,\theta \right)-y_i]}^2$$

(3)

In Formulas (2) and (3), $D_n$ is the maximum difference of the cumulative probability distribution between the assumed distribution model and the measured data; $F\left(x_i,\theta \right)$ is the cumulative probability distribution value calculated using the assumed distribution model when density or strength is $x_i$; $\phi$ is the sum of the squared errors between the assumed distribution model and the measured data; $y_i$ is the cumulative probability distribution value of the measured data; $\theta$ is the parameter of the assumed distribution model.

3. Derivation Method

3.1. Derivation of Formula for Calculating the Average Compressive Strength of CLT

The resistance capacity of CLT under compressive load can be calculated by determining the sum of the resistance of the whole lamina in different layers, expressed as Formula (4) [14]. As shown in Formula (6), the compressive strength of CLT can be predicted and calculated by dividing the resistance capacity (P) by the cross-sectional area. Wood strength largely varies, rendering the precise prediction of a lamina considerably difficult. However, the wood or lumber of the same grade has stable average density and strength. Thus, the strength of CLT can be more accurately calculated using the average strength of the lamina instead of the strength of one lamina. After the average strength of CLT is determined, the design value or characteristic value of CLT is easily calculated using the parametric method.

$$P=F_{CLT}{A}_{CLT}={{\displaystyle \sum }}^{}{F}_i{A}_i$$

(4)

$$F_{CLT}=\frac{P}{A_{CLT}}$$

(5)

In Formulas (4) and (5), $P$ is the resistance capacity of CLT under compressive load; $F_{CLT}$ is the compressive strength of CLT; $A_{CLT}$ is the cross-sectional area of CLT; $F_i$ is the compressive strength of the ith lamina; and $A_i$ is the cross-sectional area of the ith lamina.

Taking the three-layer CLT as an example, the average compressive strength of CLT can be calculated by deriving Formulas (4) and (5).

To proceed with the derivation, several assumptions were made:

• Assuming that no gap exists between the lamina, the effect of the gap on the cross-sectional area of the CLT need not be considered.
• Variations in the width and thickness of the lamina are considerably smaller than the variation in strength; the small differences in the cross-sectional areas of the lamina hardly affect the calculation result. Assuming that the cross-section of the lamina is equal to A, then the cross-sectional area of CLT can be expressed as Formula (6), as follows:

$$A_{CLT}=i_{Max}\times A$$

(6)

• Assuming that the resistance of CLT contributed by the lamina in cross layers is equal to K times of the resistance of the lamina in the major direction with the same cross-section, Formula (7) is obtained:

$$F_{\perp }{A}_i=K\times F_{\parallel }\times A_i$$

(7)

The CLT resistance capacity in the main direction under compressive loading is given by Formula (8), divided by the cross-sectional area A to derive Formula (9), as A_i is equal to A in this study.

$$F_{CLT}·3·A={{\displaystyle \sum }}^{}{F}_{i}A=F_{1}A+F_{2}A+F_{3}A$$

(8)

$$F_{CLT}=\frac{F_1+F_2+F_3}{3}$$

(9)

The average compressive strength of t pieces of CLT can be calculated using Formula (10), where i_max = t.

$$\frac{{{\displaystyle \sum }}^{}{F}_{CLTi}}{t}=\frac{{{\displaystyle \sum }}^{}{F}_{1i}+{{\displaystyle \sum }}^{}{F}_{2i}+{{\displaystyle \sum }}^{}{F}_{3i}}{3t}$$

(10)

If the number of CLT is sufficiently large, the compressive strength parallel to the grain of the lamina in different layers is equal to each other as $\overline{f_c}$ as shown in Formula (11). Thus, the Formula (10) can be written as Formula (12).

$$\frac{{{\displaystyle \sum }}^{}{F}_{1i}}{t}=\frac{{{\displaystyle \sum }}^{}{F}_{3i}}{t}=\frac{{{\displaystyle \sum }}^{}{F}_{2i}}{t\times K}=\overline{f_c}$$

(11)

$$\frac{{{\displaystyle \sum }}^{}{F}_{CLTi}}{t}=\frac{2+K}{3}\overline{f_c}$$

(12)

Both $\frac{{{\displaystyle \sum }}^{}{F}_{CLTi}}{t}$ and $\overline{F_{CLT}}$ represent the average compressive strength of CLT. Therefore, the average compressive strength of CLT can be expressed as Formula (13).

$$\overline{F_{CLT}}=\frac{2+K}{3}\overline{f_c}$$

(13)

By extending Formula (13), the average compressive strength of CLT with i layers of lamina in the major direction and j layers of the lamina stacked crosswise is derived, expressed as Formula (14).

$$\overline{F_{CLT}}=\frac{i+jK}{i+j}\overline{f_c}$$

(14)

3.2. Predictive Modeling of the Compressive Strength of Lamina

3.2.1. The Linear Correlation between the Density and Compressive Strength of Lamina

As mentioned in the introduction, the compressive strength parallel to the grain is linearly correlated with density [18]. If the linear correlation prediction formula f = a × ρ + b and density of the lamina are known, then the compressive strength of the lamina (f) can be calculated. To determine the prediction model and error between the test and prediction values, the programming language R version of 3.6.3 was used to build and test the linear correlation prediction model. The proposed linear regression coefficient parameter R² was used to compare the fitting effect with other prediction models. The p-value would be used to determine whether the linear regression was significant, the estimated slope parameter and intercept value would be substituted into the linear regression equation to calculate the error between the prediction value and test results.

3.2.2. The Linear Correlation between the Density and Compressive Strength of Lamina

The large variation of wood significantly influences the accuracy of predicting compressive strength. Thus, the average compressive strength of the lamina is more important than the compressive strength of one lamina to calculate the compressive strength and design value of CLT because the former is considerably more stable than the latter. This prediction model can reduce the effect of wood variation.

The MCS method is used to predict the probability of different outcomes when the intervention of random variables is present [21]. The approach can be used to obtain final approximate numerical calculations by sampling randomly from a given model or data. In this study, MCS was used to calculate the average density and compressive strength of some lamina sampled randomly from the test data. Subsequently, a model is constructed to predict the average compressive strength of the lamina from the average density of the lamina. The MCS procedure was as follows [33]:

(1)

Determine the density and compressive strength of the lamina. All lamina specimens with indexes are added, and all lamina with test results are listed on a table or saved on a database.

(2)

Randomly sample 10 lamina specimens without replacement from the measured data.

(3)

Calculate the average compressive strength and average density of the 10 lamina specimens.

(4)

Repeat procedures (2) and (3) 10,000 times, and save all average values.

(5)

Generate a scatter plot of the average density and compressive strength, with the density and compressive strength represented by the X and Y axes, respectively.

(6)

Build a model to predict the average compressive strength of the lamina by using the average density of lamina. Determine the parameters of the linear regression model and the formula written as Formula (15).

$$\overline{f}=a\overline{ \rho }+b$$

(15)

3.2.3. Average Compressive Strength of Lamina Sorted by Density

The greater the density of the lamina, the higher the compressive strength parallel to the grain. Apart from the MCS method, the lamina test results for several groups may also be sorted according to the order of their density value to determine the linear correlation between the average compressive strength and average density of the lamina. To illustrate, the lamina may be sorted by density, listed as ρ₁, ρ₂, … ρ_n, with the corresponding compressive strengths of f₁, f₂, … f_n. In this study, the lamina was sorted into 10 groups, the average densities and the compressive strengths of each group were calculated and recorded as $\overline{{\rho }_1}$, $\overline{{\rho }_2}$, … $\overline{{\rho }_{10}}$ and $\overline{f_1}$, $\overline{f_2}$, … $\overline{f_{10}}$, respectively. The linear correlation prediction model was then built.

4. Results and Discussion

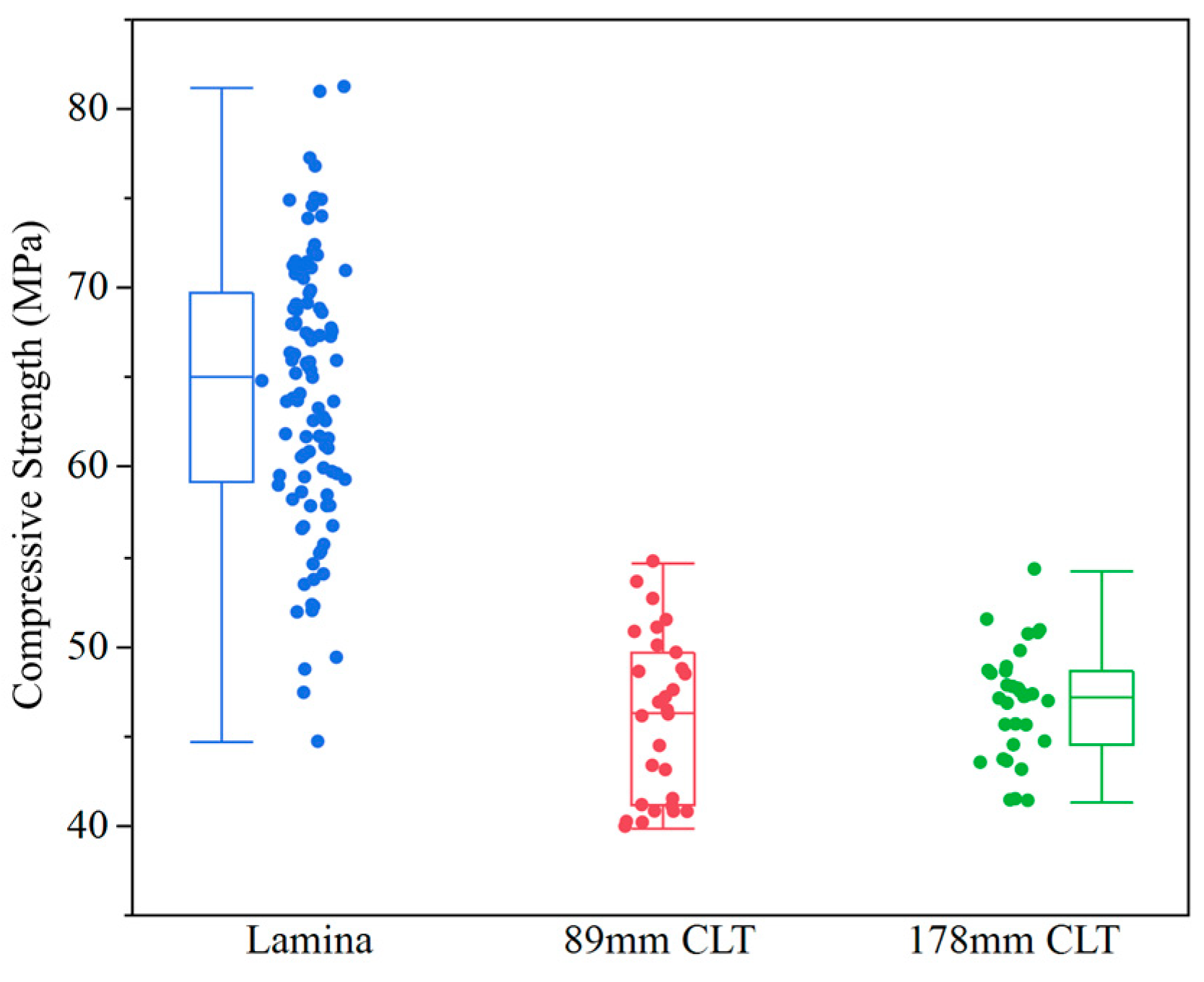
4.1. Experimental Results

The densities and compressive strengths of the lamina and CLT samples were determined using basic statistical calculations, and the results are presented in Figure 3 and Figure 4 and

Table 2. The statistical tests for the density and compressive strength of the lamina and CLT samples with two different widths.

Statistics	Lamina		89 mm CLT		178 mm CLT
	f (MPa)	ρ (g/cm3)	FCLT (MPa)	ρ (g/cm3)	FCLT (MPa)	ρ (g/cm3)
N	102	102	30	30	32	32
Mean value	64.20a	0.62A	46.15b	0.62A	46.84b	0.62A
Standard deviation	7.45	0.05	4.43	0.04	3.09	0.02
Coefficient of variation (%)	11.61	8.77	9.59	6.84	6.61	3.85
Minimum value	44.65	0.50	39.91	0.54	41.35	0.58
Maximum value	81.20	0.75	54.71	0.70	54.27	0.67
5th percentile value	51.88	0.53	40.03	0.55	41.37	0.58
25th percentile value	59.19	0.58	41.35	0.59	44.51	0.60
50th percentile value	65.08	0.63	46.29	0.62	47.18	0.62
75th percentile value	69.71	0.66	49.71	0.66	48.60	0.64
95th percentile value	74.95	0.71	54.08	0.69	52.45	0.67

Notation: ^a, ^b and ^A, ^B represent the ANOVA test results for compressive strength and density, respectively. The same letter indicates a nonsignificant difference (0.05), and different letters indicate a significant difference (0.05). For example, 64.20^a and 46.15^b indicate that the difference in compressive strength between the lamina and the 89 mm wide CLT is significant at the 0.05 significance level.

. The experimental test results were plotted as solid points with different colors, and the statistical results are shown as a boxplot. Five lines in the boxplot were generated from the five-number summary. The measured data between the lamina and CLT samples with widths measuring 89 and 178 mm, respectively, were compared using ANOVA. The ANOVA test results are listed in Table 2 and The CV difference in compressive strength between lamina and CLT can also verify the existence of the effect of homogenization [34,35,36], rendering the compressive strength of CLT more stable and causing the wider CLT to have a small variation in compressive strength. Wood defects such as cracks, knots, and inclined grains influence the compressive strength of lumber, leading to a great variation in the strength of lumber [37,38,39]. The lumber samples are then put randomly during the manufacture of CLT, their defects are distributed in different positions, and the cross-section of CLT exceeds that of the lamina. Consequently, the effect of defects on the compressive strength of CLT is reduced. The CV of the compressive strength of the lamina is similar to the test results obtained in the study by Gong YC [40], who determined that the CV of compressive strength in larch lumber was about 11.4%, and the CV of compressive strength in CLT with a cross-section of 180 mm × 75 mm was about 8.0%.

The compressive strength and CV of the 89 mm CLT and 178 mm CLT were compared; their average compressive strengths were close, but the CV of the compressive strength in the 178 mm CLT was 31.07% smaller than that in the 89 mm CLT. Therefore, the width exerted no significant effect on the average compressive strength of the CLT; however, it influenced the CV of compressive strength in CLT, which influenced the design value calculated using the parametric method. The average compressive strengths of the CLT samples with different widths were similar; thus, the average compressive strengths of the CLT components could be determined by evaluating the average compressive strength of the CLT samples with small widths.

A comparison of the density values revealed that the average density of the lamina and CLT samples was about equal to 0.62 g/cm³_, and no significant difference was observed between the lamina and CLT samples. Thus, the average density of CLT can be derived from the average density of the lamina. However, the coefficient of variation (CV) of the density of the lamina and CLT samples varied. The CV values of the lamina, CLT with a width of 89 mm, and CLT with a width of 178 mm were about 8.77%, 6.84%, and 3.85%, respectively. The difference between CV values can prove that homogenization exerts an effect, endowing conferring causing a smaller CV of the density on the CLT than on the lamina and a smaller CV of the density on the wider CLT.

Comparing the CV of the density and compressive strength, the latter is larger than the former. The CVs of the compressive strengths of the lamina, the CLT with a width of 89 mm, and the CLT with a width of 178 mm were about 32.38–71.69% larger than the CVs of density. This difference indicates that the wood defects exert a greater effect on the strength than the density of wood; for instance, the oblique texture of wood does not affect the density of wood, but it significantly decreases the compressive strength of wood.

Both the compressive strength and CV of the lamina are greater than those of the CLT samples with two different widths. The average compressive strengths of the lamina specimens, 89 mm CLT, and 178 mm CLT were about 64.20, 46.15, and 46.84 MPa, and their CV values were about 11.61%, 9.59%, and 6.61%, respectively. The average compressive strengths of the CLT measuring 89 mm×63 mm and the CLT measuring 178 mm×63 mm were about 71.88% and 72.96% of the average compressive strength of the lamina. The ANOVA for the compressive strength test indicates a significant difference between the compressive strengths of the lamina and the CLT; however, no significant difference in compressive strength was found between the CLTs with two different widths, as determined from the p-value (0.4761) in

Table 3. ANOVA test results for the compressive strength of CLT.

Source	DF	Sum of Squares	Mean Square	F Ratio	Prob > F (p Value)
CLT Wide	1	7.41138	7.4114	0.5142	0.4761
Error	60	864.88347	14.4147
Total	61	872.29486

. The CV difference in compressive strength between lamina and CLT can also verify the existence of the effect of homogenization [35,36], rendering the compressive strength of CLT more stable and causing the wider CLT to have a small variation in compressive strength. Wood defects such as cracks, knots, and inclined grains influence the compressive strength of lumber, leading to a great variation in the strength of lumber [37,38,39]. The lumber samples are then put randomly during the manufacture of CLT, their defects are distributed in different positions, and the cross-section of CLT exceeds that of the lamina. Consequently, the effect of defects on the compressive strength of CLT is reduced. The CV of the compressive strength of the lamina is similar to the test results obtained in the study by Gong YC [40], who determined that the CV of compressive strength in larch lumber was about 11.4%, and the CV of compressive strength in CLT with a cross-section of 180 mm × 75 mm was about 8.0%.

As shown in Table 3, the P value is larger than the significance level of 0.05. The reason the compressive strength of the CLT sample is smaller than that of the lamina is that the lamina exhibits resistance in cross-layers; meanwhile, the compressive strength perpendicular to the grain of the lamina is limited to about 10% of the compressive strength parallel to the grain [34]. Moreover, an edgewise gap may exist between the lamina in cross layers. Thus, some researchers assume that the resistance capacity of the lamina in cross layers is zero when calculating the compressive strength of CLT [14,15].

The CV difference in compressive strength between lamina and CLT can also verify the existence of the effect of homogenization [35,36], rendering the compressive strength of CLT more stable and causing the wider CLT to have a small variation in compressive strength. Wood defects such as cracks, knots, and inclined grains influence the compressive strength of lumber, leading to a great variation in the strength of lumber [37,38,39]. The lumber samples are put randomly during the manufacture of CLT, their defects are distributed in different positions, and the cross-section of CLT exceeds that of the lamina. Consequently, the effect of defects on the compressive strength of CLT is reduced. The CV of the compressive strength of the lamina is similar to the test results obtained in the study by Gong YC [40], who determined that the CV of compressive strength in larch lumber was about 11.4%, and the CV of compressive strength in CLT with a cross-section of 180 mm × 75 mm was about 8.0%.

The compressive strength and CV of the 89 mm CLT and 178 mm CLT were compared; their average compressive strengths were close in value, but the CV of the compressive strength in the 178 mm CLT was 31.07% smaller than that in the 89 mm CLT. Therefore, the width exerted no significant effect on the average compressive strength of the CLT; however, it influenced the CV of compressive strength of CLT, which influenced the design value calculated using the parametric method. The average compressive strengths of the CLT samples with different widths were similar; thus, the average compressive strengths of the CLT components could be determined by evaluating the average compressive strength of the CLT samples with small widths.

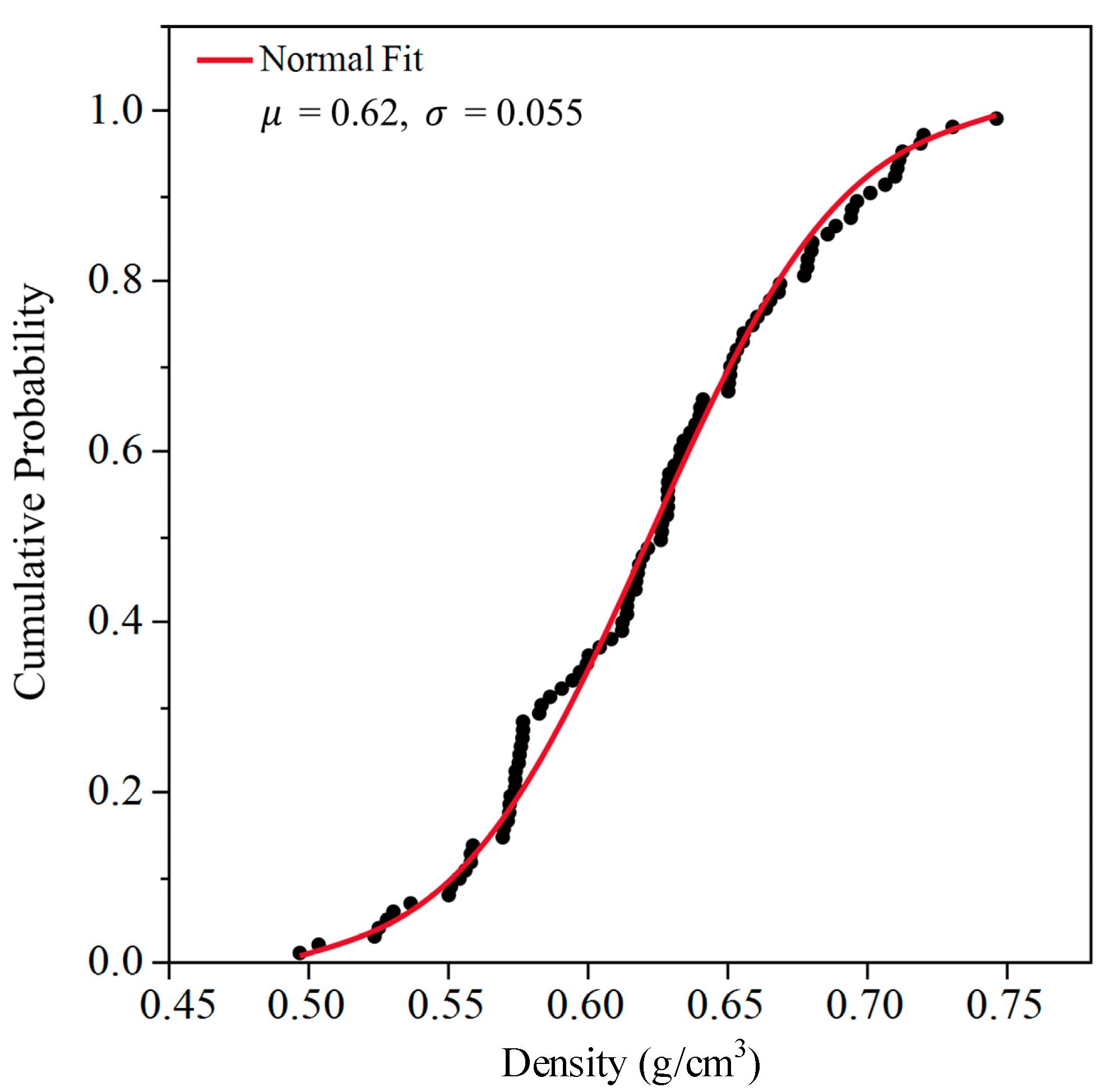
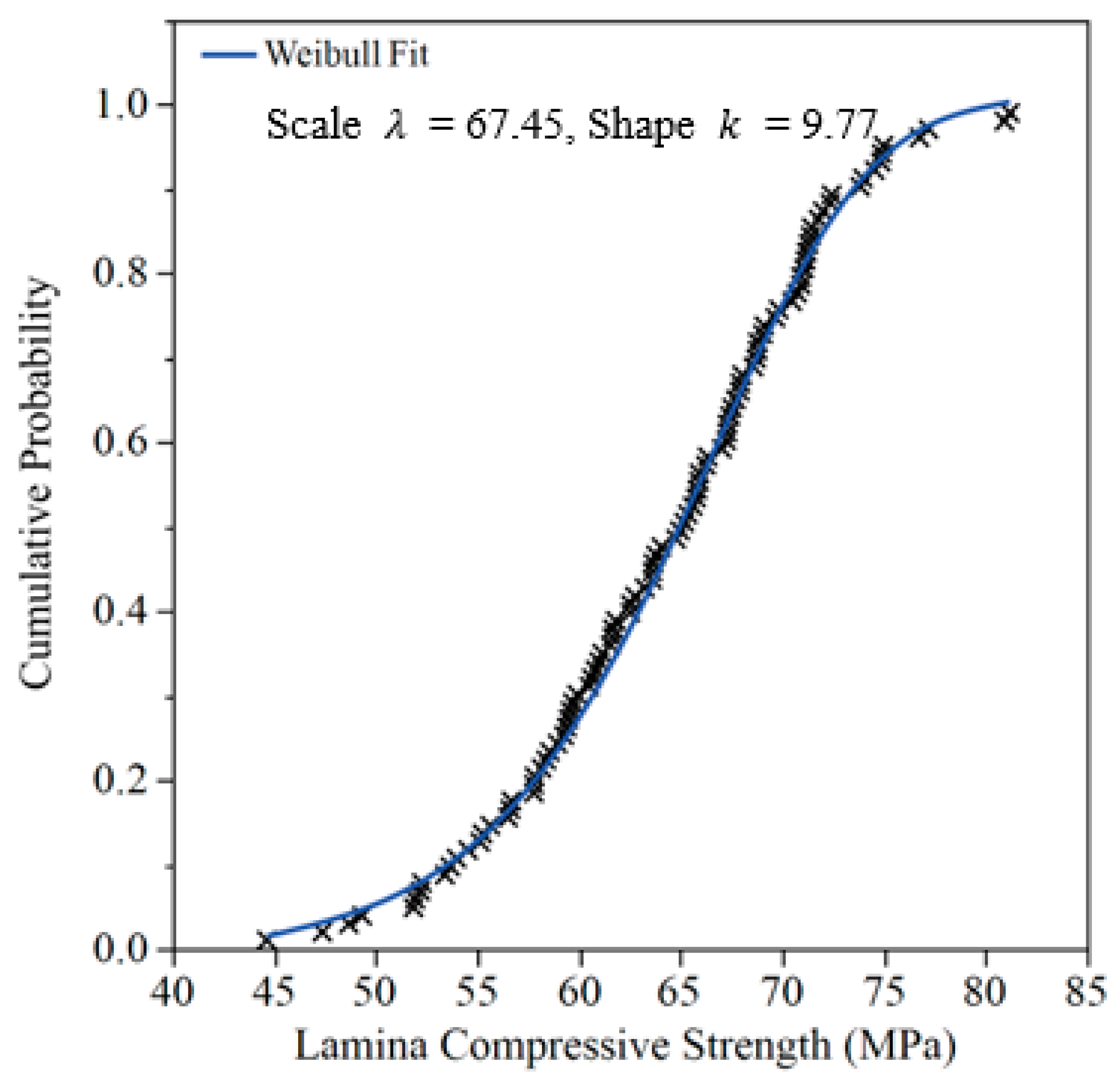
4.2. Probabilistic Distribution of the Density and Compressive Strength of Lamina

The parameters of the hypothetical distribution model and K–S test results are presented in

Table 4. K–S test result and probabilistic distribution of the lamina density.

Assumed Distribution		Parameter	${\mathit{D}}_{\mathit{n}}$	$\mathbf{Critical} \mathbf{Value} {\mathit{D}}_{\mathit{n},0.05}$	Whether to Accept the Assumed Model	$\mathit{\phi }$
Normal distribution	Location $\left(\mu \right)$	0.62	0.0790	0.0877	Yes	0.0612
	Dispersion $\left(\sigma \right)$	0.05
Log-normal distribution	Scale $\left(\mu \right)$	−0.48	0.0753	0.0877	Yes	0.0692
	Shape $\left(\sigma \right)$	0.088
Weibull distribution	Scale $\left(\lambda \right)$	0.65	0.0709	0.0879	Yes	0.1326
	Shape $\left(k\right)$	12.43

and

Table 5. K–S Test Result and Probabilistic Distribution of the Compressive Strength of the Lamina.

Assumed Distribution		Parameter	${\mathit{D}}_{\mathit{n}}$	$\mathbf{Critical} \mathbf{Value} {\mathit{D}}_{\mathit{n},0.05}$	Whether to Accept the Assumed Model	$\mathit{\phi }$
Normal distribution	Location $\left(\mu \right)$	64.20	0.0571	0.0877	Yes	0.0557
	Dispersion $\left(\sigma \right)$	7.45
Log-normal distribution	Scale $\left(\mu \right)$)	4.16	0.1001	0.0877	No	0.2054
	Shape $\left(\sigma \right)$	0.12
Weibull distribution	Scale $\left(\lambda \right)$	67.45	0.0412	0.0879	Yes	0.0249
	Shape $\left(k\right)$	9.77

and Figure 5 and Figure 6. In this study, the number of lamina was 102, and the significance level was 0.05; thus, the critical value ($D_{n,\alpha }$) for normal and log-normal distributions was 0.0877, as determined using the formula $D_{n,\alpha }$=$D_{102,0.05}=0.886/\sqrt{102}$= 0.0877; meanwhile, the critical value ($D_{n,\alpha }$) for the Weibull distribution was 0.0879, which was calculated using $0.888/\sqrt{102}$ = 0.0879. With regard to the density of the lamina, the maximum errors ($D_n$) fitted using the normal, log-normal, and Weibull distributions were 0.0790, 0.0753, and 0.0709, respectively, all of which were smaller than the critical value. The values indicate that the three distribution models could pass the K–S test and be used to fit the density distribution of the lamina. Among the three distributions models, the normal distribution model was the best for fitting the density of the lamina, considering that it had the smallest sum of squared errors $\phi$ among the distribution models. Thus, the density of the lamina in this study should be fitted using the normal distribution, with a location ($\mu$) value of 0.62 g/cm³ and a dispersion ($\sigma$) value of 0.05 (Figure 5).

With regard to the compressive strength of the lamina, the maximum errors ($D_n$) of the cumulative distribution fitted by using the normal, log-normal, and Weibull distribution were 0.0571, 0.1001, and 0.0412; except for the log-normal, the $D_n$ value fitted by using the normal and Weibull distributions were smaller than the critical value $D_{n,\alpha }$ with 0.0877 and 0.0879. These observations showed that the normal and Weibull distributions could pass the K–S test and were used to fit the compressive strength of the lamina. The sum error of the square values $\phi$ of the Weibull distribution was smaller than that of the normal distribution—0.0557 and 0.0249. Thus, the compressive strength of the lamina should be fitted using the Weibull distribution with the scale ($\lambda$) value of 67.45 MPa and shape ($k$) parameter of 9.77, as shown in Figure 6. After comparing the best distribution model of the density and compressive strength of lamina, the distribution of the density was found to be symmetrical; however, it was non-symmetric to the distribution of the compressive strength of the lamina, which could be attributed to the influence of the variation in wood.

4.3. Relationship between the Compressive Strength and Density of Lamina

To predict the compressive strength of the lamina, four models—marked according to their density as models A, B, C, and D—were developed in this study. Model A showed a linear correlation between the compressive strength and density of lamina. Models B and C exhibited the linear correlation between the average compressive strength and average density of the lamina, built using MCS. The intercept of the linear regression formula of Model B was zero, whereas that of Model C was not zero. Model D showed the linear correlation between the average compressive strength and average density of the lamina sorted by density. All these models were similar to the equation y = ax + b and could be used to predict the compressive strength of the lamina by using its density.

4.3.1. Linear Correlation of the Measured Data

The higher the density of the wood, the greater the compressive strength parallel to the grain [18]. The compressive strength and density of wood are linearly correlated; thus, their relationship can be expressed as a linear regression formula (Figure 7), where the red line is the regression line, the point in cross-form type denotes the measured data, and the gray ellipse is the confidence ellipse of the measured data with a confidence level of 0.95. The compressive strength of the lamina is linearly correlated with the density of the lamina, which can be predicted using the linear regression equation f = 93.97 × ρ + 5.685 marked as model A with a correlation coefficient (R²) of about 0.473. This equation can be used to predict the compressive strength of the lamina; regardless, the accuracy of the prediction is not very good because the linear model of the lamina has a smaller R² than that of clear wood specimens with a correlation coefficient (R²) of 0.895 [41]. Moreover, after substituting the density of the lamina into this equation, the average error between the calculated compressive strength and measured data is about 4.23 MPa, which is less than the standard deviation of the calculated compressive strength of the lamina and is about 6.59% of the average compressive strength of the lamina.

4.3.2. Linear Correlation of the Mean of the Measured Data, Calculated by Monte Carlo Simulation

Owing to the variability of wood, a relatively large error occurs when the compressive strength of the lamina is predicted by using the density of a single sample, and the linear correlation coefficient of the prediction model is not considerably large. In addition, the average value is very important to calculate the design value used in timber engineering, and calculating the average strength can reduce the effect of wood variability. Therefore, MCS is used to analyze the relationship between the average density of the lamina and average compressive strength. The result is presented in Figure 8.

Figure 8 presents a scatter plot of the average compressive strength and average density with a number of 10,000 calculated by MCS. The red line denotes the linear regression fitting equation of Model B, whose intercept is zero and the prediction formula is $\overline{f}$ = 103.10 ×$\overline{ \rho }$ (R² = 0.999). The green dashed line is the linear regression fitting equation of Model C, whose intercept is not zero as reported in a previous study [41] and prediction formula is $\overline{f}$ = 94.23 × $\overline{\rho }$ +5.517 (R² = 0.466). After substituting the average density calculated by MCS, the prediction errors of Models B and C are about 1.36 and 1.37 MPa, respectively, which are about 2.12% and 2.13% of the average compressive strength of the lamina. Model B provides a better prediction accuracy than Model C because it has a greater correlation coefficient and a smaller prediction error than Model B. Thus, the average compressive strength of the lamina can be calculated after substituting the average density of lamina into the formula $\overline{f}$ = 103.10 ×$\overline{\rho }$ (R² = 0.999).

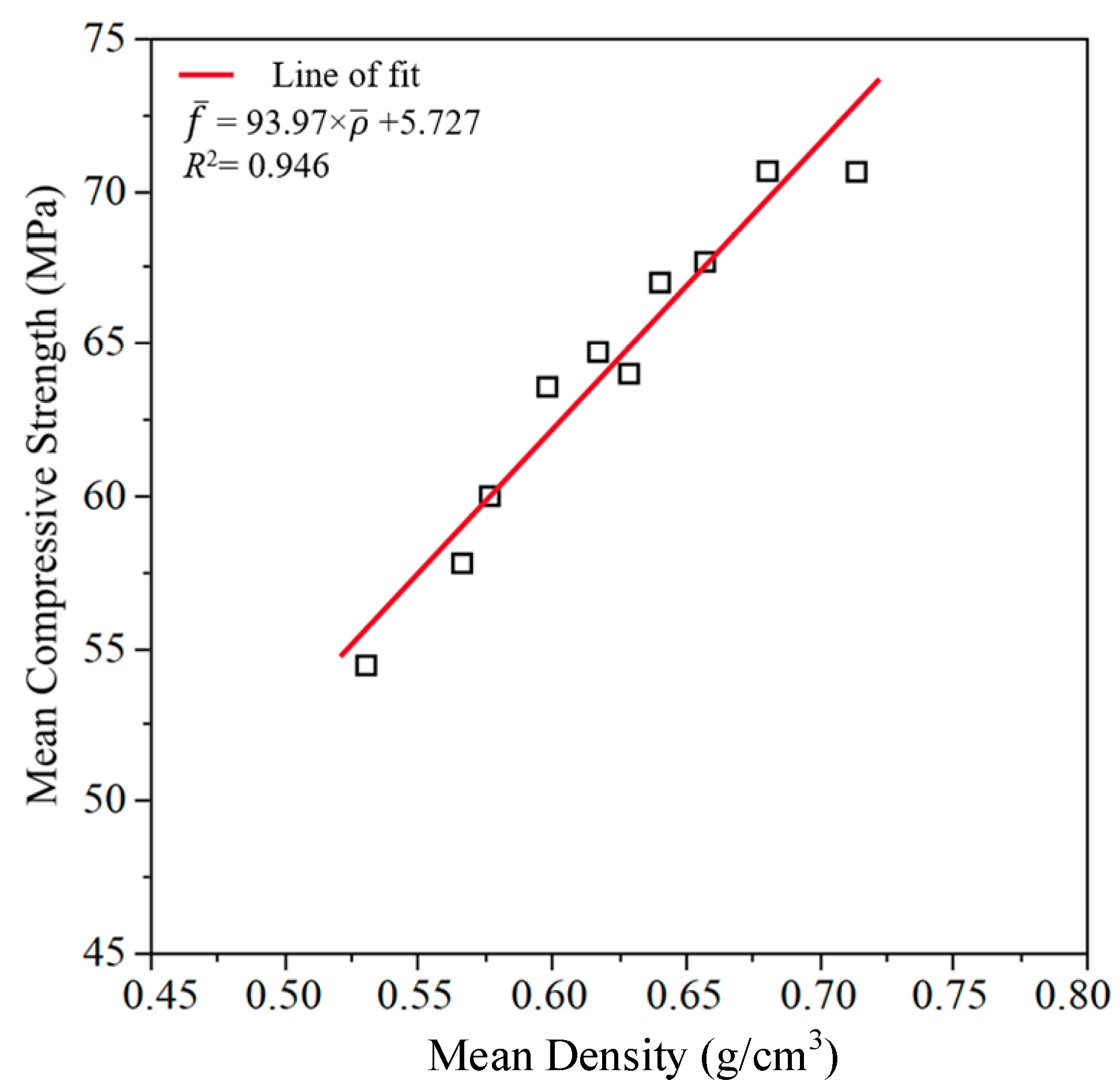
4.3.3. Linear Correlation of the Mean of the Measured Data Grouped by Density

In addition to MCS, grouping the lamina by their density can also be used to construct a prediction model of average compressive strength, based on the average density of the lamina marked as Model D, because the grouping processing can also reduce the effect of wood variation and improve the accuracy of prediction. To present this model, all lamina are sorted into 10 groups by their density. The average compressive strength and average density of the lamina in the 10 groups are calculated to build the linear regression equation between the average compressive strength and average density. The results are shown in Figure 9.

Figure 9 shows that the average compressive strength and average density of the lamina exhibit a good linear correlation. The linear regression equation is $\overline{f}$ = 93.97 ×$\overline{\rho }$ + 5.727 (R² = 0.946) with an average prediction error of 1.03 MPa, which is about 1.60% of the average compressive strength of the lamina. This prediction model, constructed by grouping the lamina by density, has good prediction accuracy and can provide theoretical support for calculating the compressive strength of the lamina with different grades by linear interpolation.

4.3.4. Comparison of the Four Prediction Models

The prediction equation and prediction error of the four prediction models are listed in

Table 6. Prediction error of the four prediction models.

Method	Prediction Model of Lamina			Prediction Equation	Prediction Error (MPa)	Model
	a	b	R2
Regression line of test result	93.97	5.69	0.473	$f$$=93.97 \times \rho$ + 5.69	4.23	A
Monte Carlo simulation	103.10	0	0.999	$\overline{f}$$=103.10 \times \overline{\rho }$	1.36	B
Monte Carlo simulation	94.23	5.52	0.466	$\overline{f}$$=94.23 \times \overline{\rho }$ + 5.52	1.37	C
Sorting by density	93.97	5.27	0.946	$\overline{f}$$=93.97 \times \overline{\rho }$ + 5.27	1.03	D

. Among the models, Model B built by MCS has the greatest squared correlation coefficient (R² = 0.999) and second-smallest prediction error (1.36 MPa), and Model D has the second-greatest squared correlation coefficient (R² = 0.946) and smallest prediction error (1.03 MPa). The average compressive strength of the lamina calculated by MCS can simulate the realistic distribution of the lamina, and the compressive strength of the lamina should be zero when the density is zero. Thus, Model B is recommended for predicting the average compressive strength of the lamina.

4.4. Relationship between the Compressive Strength and Density of Lamina

4.4.1. Determination of the K Value

The experimental test of this study shows the following results: average compressive strength of the lamina, about 64.20 MPa; average compressive strength of the 89 mm CLT, 46.15 MPa; and average compressive strength of the 178 mm CLT, 46.86 MPa. According to the derivation formula $\overline{F_{CLT}}=\left(2+K\right)\overline{f_c}/3$, K can be calculated using $K=3\overline{F_{CLT}}/\overline{f_c}-2$. Thus, K should be 0.16, calculated as (3 × 46.15)/64.20 − 2, or 0.19, calculated as (3 × 46.84)/64.20 − 2 To be conservative, K is determined as 0.16, which means that the resistance capacity of CLT contributed by the cross layer is about 0.16 times the resistance capacity of the lamina parallel to the grain. Substituting the K value into Formula (13) can determine the average compressive strength of CLT by using the average compressive strength of the lamina. The new formula, expressed as Formula (16) is given by

$$\overline{F_{CLT}}=\frac{2+K}{3}\overline{f_c}=\frac{2+0.16}{3}\overline{f_c}=0.72\overline{f_c}$$

(16)

The previous study on clear wood samples reported that the compressive strengths of larch in the radial and tangential directions were about 7.7% and 11.3%, respectively, of the compressive strength of larch in the longitudinal direction. Both values were smaller than the K value determined in the current study. This finding proves that in addition to the compressive strength perpendicular to the grain of the cross-layer lamina, the cross layers exert an enhancing effect on the lamina in major directions, improving the resistance capacity of CLT, similar to the reinforcing effect reported by R. Brandner [5]. Therefore, the resistance provided by the cross layers cannot be ignored in the calculation of the strength of CLT by using the compressive strength of the lamina. This finding also verifies the test result obtained by Jung-Kwon Oh [14] that the average compressive strength of CLT was about 80.76% of the average compressive strength of the lamina.

4.4.2. Prediction of the Average Compressive Strength of CLT by Using the Average Density of the Lamina

The average compressive strength of CLT can be determined from Formula (16) by using the average compressive strength of the lamina, and the average compressive strength of the lamina can be calculated according to the prediction models—Models A, B, C, and D—by using the average density of the lamina. In this study, the average density of CLT was equal to the average density of the lamina. Therefore, the average compressive strength of CLT can be calculated using the average density of the lamina and CLT and the prediction equation for the lamina listed in

Table 7. Equations used to calculate the average compressive strength of CLT.

Method	Prediction Equation of Lamina $\overline{\mathit{f}}$$=\mathit{a}\times \overline{\mathit{\rho }}+\mathit{b}$			Prediction Equation for CLT	Model
	a	b	R2
Regression line of test result	93.97	5.69	0.473	$\overline{F}$$=67.66 \times \overline{\rho }$ + 4.10	A
Monte Carlo simulation	103.10	0	0.999	$\overline{F}$$=74.23 \times \overline{\rho }$	B
Monte Carlo simulation	94.23	5.52	0.466	$\overline{F}$$=67.85 \times \overline{\rho }$ + 3.97	C
Sort by density	93.97	5.27	0.946	$\overline{F}$$=67.66 \times \overline{\rho }$ + 3.79	D

.

To compare the prediction accuracy, the test results for the 89 mm CLT and 178 mm were sorted by their density and divided into four groups (

Table 8. Average compressive strength of CLT, calculated using the four models.

CLT Width	Average Density (g/cm3)	Average Compressive Strength (MPa)	Predicted Compressive Strength of CLT (MPa)				Prediction Error (MPa)
			A	B	C	D	A	B	C	D
89 mm	0.58 ± 0.02	43.16 ± 2.96	43.66	43.41	43.65	43.69	0.50	0.25	0.48	0.53
89 mm	0.65 ± 0.03	48.77 ± 3.83	48.33	48.54	48.33	48.36	0.43	0.23	0.43	0.40
178 mm	0.60 ± 0.01	45.89 ± 2.35	44.49	44.32	44.48	44.52	1.39	1.56	1.40	1.36
178 mm	0.64 ± 0.02	47.69 ± 3.48	47.12	47.20	47.11	47.15	0.57	0.48	0.57	0.54

). The average density of CLT in each group was substituted into the prediction model, and the prediction average compressive strength and prediction error were calculated. The mean of the measured compressive strength of CLT, the mean minus the standard deviation, the mean plus standard deviation, and the predicted value of CLT in each group are presented in Figure 10. The predicted average compressive strength in each of the three groups was close to the tested average compressive strength of CLT. All prediction errors were smaller than the standard deviation of each group. With regard to Model B, three of four prediction errors were smaller than the prediction errors for the other prediction models. The four prediction errors for Model B were about 0.25, 0.23, 1.56, and 0.48 MPa, respectively, which were about 0.58%, 0.48%, 3.40%, and 1.01% of the average compressive strength in each group. Therefore, Model B, represented by equation $\overline{F}$ = 74.23 ×$\overline{\rho }$, is preferred for predicting the average compressive strength of CLT by using the average density of CLT, which is built by MCS, which can simulate the random distribution of the lamina when fabricating CLT from lamina and exhibits good prediction accuracy.

5. Conclusions

In this study, the average density and compressive strength of lamina and CLT made by planted larch were evaluated. The mechanical theory of composites was applied to construct a model for predicting the average compressive strength of CLT by using average density of CLT. Based on test results and discussions, the major findings are thus presented:

• The average compressive strength and density of the lamina in this study are approximately about 64.20 MPa and 0.62 g/cm³, respectively. Three distribution models—the normal, log-normal, and Weibull distribution models—can be used to fit the probability distribution of density test results for the lamina. Moreover, the symmetric normal distribution model ($\mu$ =0.62 g/cm³, $\mathsf{\sigma }$= 0.05) shows the best goodness-of-fit of density; both normal and Weibull distribution models can be used to fit the probability distribution of the compressive strength of lamina. The asymmetric Weibull distribution model ($\lambda$ = 67.45 MPa, $k$ = 9.77) shows the best goodness-of-fit of compressive strength.
• Compared with the lamina, CLT has a smaller variation in compressive strength and density because of homogenization effect of CLT; the width of CLT exerts no significant effect on the average compressive strength and density of CLT but affects the variations of the compressive strength and density of CLT. This observation indicates that the wider CLT has a smaller variation, and such a wider width further improves the design value of the compressive strength.
• The average compressive strength of CLT is approximately 72% of the average compressive strength of the lamina, they are about 46.15 MPa and 64.20 MPa, respectively. This result proves that the lamina in cross layers further improves the compressive strength of CLT and should not be ignored in calculating progress. The average compressive strength of CLT with three layers can be calculated according to the formula $\overline{F_{CLT}}=\frac{2+K}{3}$ $\overline{f_c}$(K = 0.16 in this study) by using the average compressive strength of the lamina, and the compressive strength of CLT with i layers in the major direction and j layers in the minor direction can be determined using the formula $\overline{F_{CLT}}=\frac{i+jK}{i+j}$ $\overline{f_c}$ (the K value depends on the CLT layers and layup, and it is bigger than zero).
• The compressive strength is linearly correlated with and density of the lamina. The linear correlation between the average compressive strength and average density of the lamina expressed as equation $\overline{f}$ = 103.10 ×$\overline{\rho }$ (R² = 0.999). Built by Monte Carlo simulation, the equation can be used to predict the average compressive strength of the lamina for the following reasons: This model has a great correlation coefficient, good prediction accuracy, and an average prediction error pf about 2.1% of the average compressive strength.
• The average compressive strength of CLT with three layers can be calculated according to the equation $\overline{F}$ = 74.23 ×$\overline{\rho }$ by using the average density of the CLT or lamina. To some extent, the formula $\overline{F_{CLT}}=a\times \frac{i+jK}{i+j}\overline{\rho }$ can be used to predict the average compressive strength of CLT with i layers in the major direction and j layers in the minor direction, while the K and a value depends on the CLT layers and wood species).