An Approach to Estimate Individual Tree Ages Based on Time Series Diameter Data—A Test Case for Three Subtropical Tree Species in China
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Diameter Data
2.3. Methods
2.3.1. Base Growth Equations
2.3.2. Constraint Growth Equations
2.3.3. First-Order Difference Method
2.3.4. Diameter Increment Equation with Parameter A-Classification
2.3.5. Quality of Fit and Verification
3. Results
3.1. Selection of Base Growth Equation Based on Individual Tree Diameter Data
3.1.1. Fitting Results from Base Growth Equation
3.1.2. Autocorrelation Test and Treatment
3.2. Increment Equation with Parameter Classification Based on Panel data
3.2.1. Fitting Evaluation
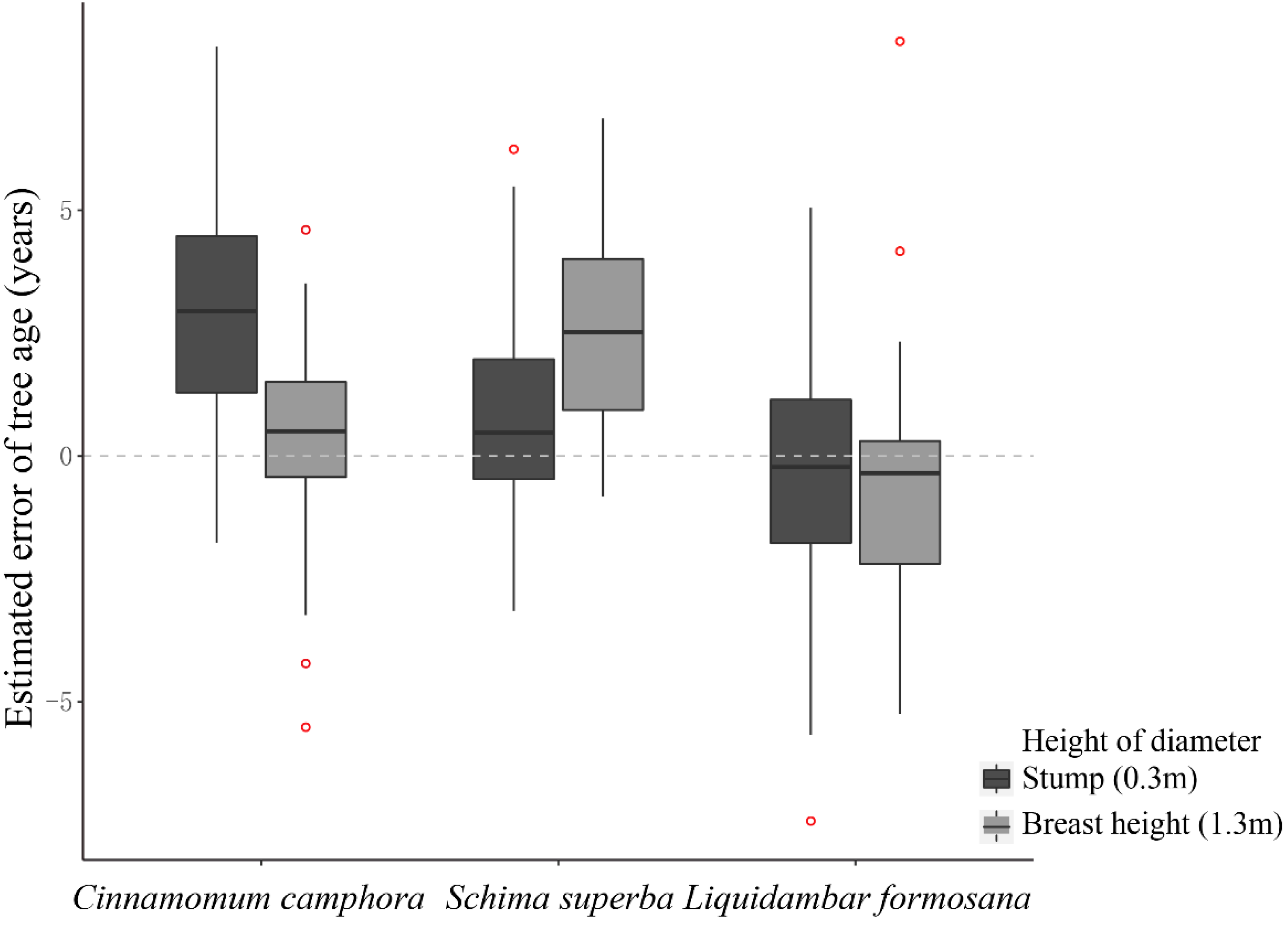
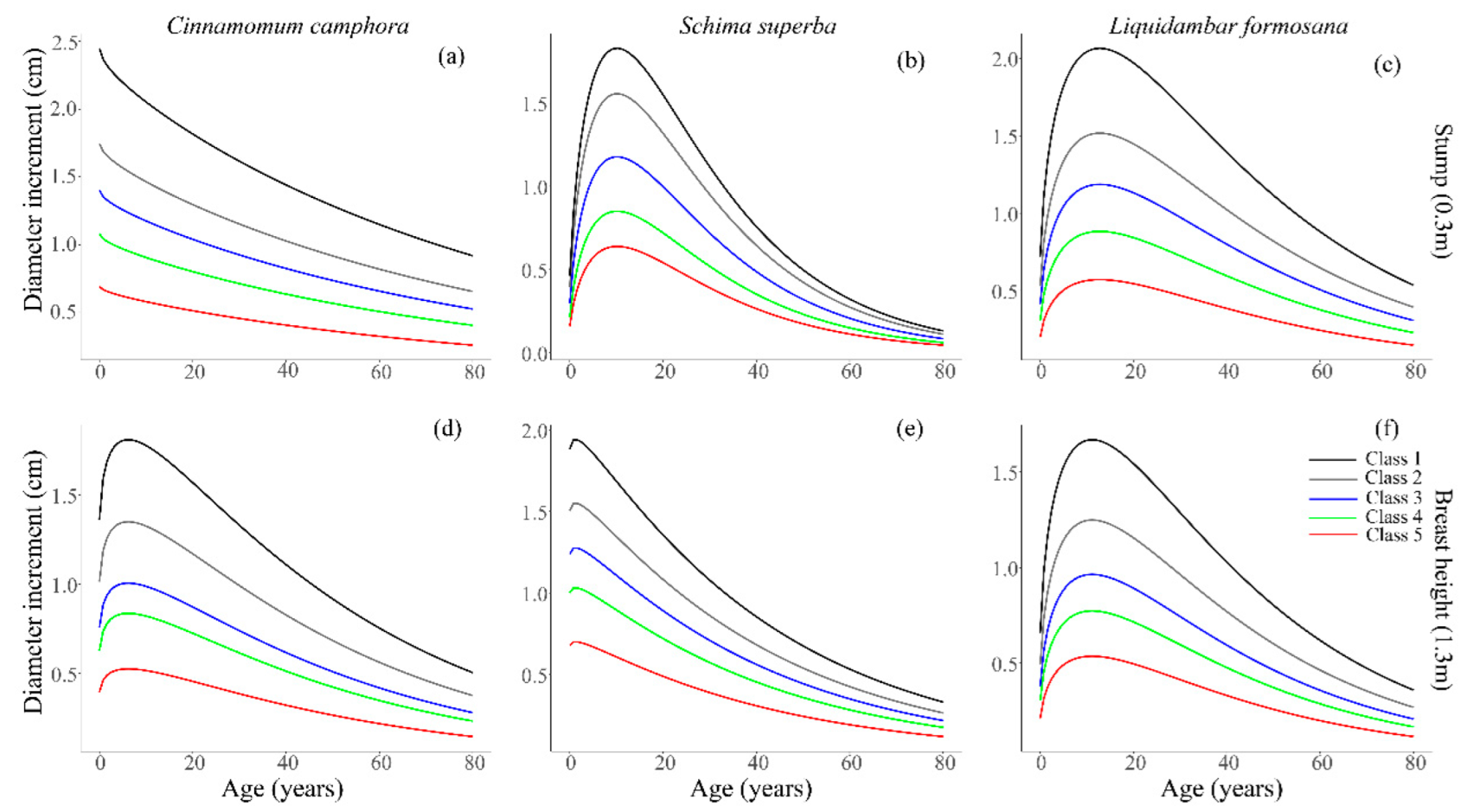
3.2.2. Comparison of Fitting Diameter Panel Data at Different Heights
4. Discussion
4.1. Estimation and Applicability
4.2. Equation Structure Analysis
4.3. Autocorrelation and Processing
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Crecente-Campo, F.; Dieguez-Aranda, U.; Rodriguez-Soalleiro, R. Resource communication. Individual-tree growth model for radiata pine plantations in northwestern Spain. For. Syst. 2012, 21, 538–542. [Google Scholar] [CrossRef]
- Garet, J.; Raulier, F.; Pothier, D.; Cumming, S.G. Forest age class structures as indicators of sustainability in boreal forest: Are we measuring them correctly? Ecol. Indic. 2012, 23, 202–210. [Google Scholar] [CrossRef]
- Silva, L.B.; Teixeira, A.; Alves, M.; Elias, R.B.; Silva, L. Tree age determination in the widespread woody plant invader Pittosporum undulatum. For. Ecol. Manag. 2017, 400, 457–467. [Google Scholar] [CrossRef]
- Hu, M.; Lehtonen, A.; Minunno, F.; Mäkelä, A. Age effect on tree structure and biomass allocation in Scots pine (Pinus sylvestris L.) and Norway spruce (Picea abies [L.] Karst.). Ann. For. Sci. 2020, 77, 90. [Google Scholar] [CrossRef]
- Hipler, S.M.; Spiecker, H.; Wu, S.R. Dynamic Top Height Growth Models for Eight Native Tree Species in a Cool-Temperate Region in Northeast China. Forests 2021, 12, 965. [Google Scholar] [CrossRef]
- Reyes-Palomeque, G.; Dupuy, J.M.; Portillo-Quintero, C.A.; Andrade, J.L.; Tun-Dzul, F.J.; Hernández-Stefanoni, J.L. Mapping forest age and characterizing vegetation structure and species composition in tropical dry forests. Ecol. Indic. 2021, 120, 106955. [Google Scholar] [CrossRef]
- Wong, C.M.; Lertzman, K.P. Errors in estimating tree age: Implications for studies of stand dynamics. Can. J. For. Res. 2001, 31, 1262–1271. [Google Scholar] [CrossRef]
- Nath, C.D.; Boura, A.; De Franceschi, D.; Pélissier, R. Assessing the utility of direct and indirect methods for estimating tropical tree age in the Western Ghats, India. Trees-Struct. Funct. 2012, 26, 1017–1029. [Google Scholar] [CrossRef]
- Fontes, L.; Tome, M.; Coelho, M.B.; Wright, H.; Luis, J.S.; Savill, P. Modelling dominant height growth of Douglas-fir (Pseudotsuga menziesii (Mirb.) Franco) in Portugal. Forestry 2003, 76, 509–523. [Google Scholar] [CrossRef] [Green Version]
- Forrester, D.I.; Tachauer, I.H.H.; Annighoefer, P.; Barbeito, I.; Pretzsch, H.; Ruiz-Peinado, R.; Stark, H.; Vacchiano, G.; Zlatanov, T.; Chakraborty, T.; et al. Generalized biomass and leaf area allometric equations for European tree species incorporating stand structure, tree age and climate. For. Ecol. Manag. 2017, 396, 160–175. [Google Scholar] [CrossRef]
- Lei, X.D.; Fu, L.Y.; Li, H.; Li, Y.T.; Tang, S.Z. Methodology and Applications of Site Quality Assessment Based on Potential Mean Annual Increment. Sci. Silvae Sin. 2018, 54, 116–126. (In Chinese) [Google Scholar] [CrossRef]
- Zhang, H.R.; Lei, X.D.; Zhang, C.Y.; Zhao, X.H.; Hu, X.F. Research on theory and technology of forest quality evaluation and precision improvement. J. Beijing For. Univ. 2019, 41, 1–18. (In Chinese) [Google Scholar] [CrossRef]
- Duerr, W.A.; Gevorkiantz, S.R. Growth prediction and site determination in uneven-aged timber stands. J. Agric. Res. 1938, 56, 81–98. [Google Scholar]
- Ek, A.R. A comparison of some estimators in forest sampling. For. Sci. 1971, 17, 2–13. [Google Scholar]
- Carmean, W.H.; Lenthall, D.J. Height-growth and site-index curves for jack pine in north central ontario. Can. J. For. Res.-Rev. Can. Rech. For. 1989, 19, 215–224. [Google Scholar] [CrossRef]
- Cieszewski, C.J.; Zasada, M.; Borders, B.E.; Lowe, R.C.; Zawadzki, J.; Clutter, M.L.; Daniels, R.F. Spatially explicit sustainability analysis of long-term fiber supply in Georgia, USA. For. Ecol. Manag. 2004, 187, 345–359. [Google Scholar] [CrossRef]
- Stokes, M.A.; Smiley, T.L. An Introduction to Tree-Ring Dating; University of Chicago Press: Chicago, IL, USA, 1968. [Google Scholar]
- Norton, D.A.; Palmer, J.G.; Ogden, J. Dendroecological studies in New Zealand 1. An evaluation of tree age estimates based on increment cores. N. Z. J. Bot. 1987, 25, 373–383. [Google Scholar] [CrossRef]
- Agren, J.; Zackrisson, O. Age and size structure of Pinus sylvestris populations on mires in central and northern Sweden. J. Ecol. 1990, 78, 1049–1062. [Google Scholar] [CrossRef]
- Lusk, C.; Ogden, J. Age structure and dynamics of a podocarp broadleaf forest in Tongariro National Park, New Zealand. J. Ecol. 1992, 80, 379–393. [Google Scholar] [CrossRef]
- Szeicz, J.M.; Macdonald, G.M. Recent white spruce dynamics at the subarctic alpine treeline of north-western Canada. J. Ecol. 1995, 83, 873–885. [Google Scholar] [CrossRef]
- Rozas, V. Tree age estimates in Fagus sylvatica and Quercus robur: Testing previous and improved methods. Plant Ecol. 2003, 167, 193–212. [Google Scholar] [CrossRef]
- Oh, J.-A.; Seo, J.-W.; Byung-Ro, K. Verifying the Possibility of Investigating Tree Ages Using Resistograph. J. Korean Wood Sci. Technol. 2019, 47, 90–100. [Google Scholar] [CrossRef]
- Wang, S.Y.; Chiu, C.M.; Lin, C.J. Application of the drilling resistance method for annual ring characteristics: Evaluation of Taiwania (Taiwania cryptomeribides) trees grown with different thinning and pruning treatments. J. Wood Sci. 2003, 49, 116–124. [Google Scholar] [CrossRef]
- Orozco-Aguilar, L.; Nitschke, C.R.; Livesley, S.J.; Brack, C.; Johnstone, D. Testing the accuracy of resistance drilling to assess tree growth rate and the relationship to past climatic conditions. Urban For. Urban Green. 2018, 36, 1–12. [Google Scholar] [CrossRef]
- Pan, H.; Lu, J.; Guo, X.Z.; Tang, S.Z.; Gao, R.D.; Xu, J.J. Tree age estimation algorithm based on spectrum analysis by Resistograph. For. Res. 2021, 34, 19–25. (In Chinese) [Google Scholar] [CrossRef]
- Rinn, F.; Schweingruber, F.H.; Schar, E. RESISTOGRAPH and X-ray density charts of wood comparative evaluation of drill resistance profiles and X-ray density charts of different wood species. Holzforschung 1996, 50, 303–311. [Google Scholar] [CrossRef]
- Jahan, M.S.; Mun, S.P. Effect of tree age on the cellulose structure of Nalita wood (Trema orientalis). Wood Sci. Technol. 2005, 39, 367–373. [Google Scholar] [CrossRef]
- Poussart, P.M.; Myneni, S.C.B.; Lanzirotti, A. Tropical dendrochemistry: A novel approach to estimate age and growth from ringless trees. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef] [Green Version]
- Wu, W.N.; Wan, T. Progress of dating methods of tree age. J. Green Sci. Technol. 2013, 7, 152–155. (In Chinese) [Google Scholar]
- Baker, P.J. Tree age estimation for the tropics: A test from the southern appalachians. Ecol. Appl. 2003, 13, 1718–1732. [Google Scholar] [CrossRef]
- Kalliovirta, J.; Tokola, T. Functions for estimating stem diameter and tree age using tree height, crown width and existing stand database information. Silva Fenn. 2005, 39, 227–248. [Google Scholar] [CrossRef] [Green Version]
- Hu, Y.Y.; Kang, X.G.; Zhao, J.H. Variable relationship between tree age and diameter at breast height for natural forests in Changbai Mountains. J. Northeast. For. Univ. 2009, 37, 38–42. (In Chinese) [Google Scholar]
- Koirala, A.; Montes, C.R.; Bullock, B.P.; Wagle, B.H. Developing taper equations for planted teak (Tectona grandis L.f.) trees of central lowland Nepal. Trees For. People 2021, 5, 100103. [Google Scholar] [CrossRef]
- Wang, M.; Borders, B.E.; Zhao, D. An empirical comparison of two subject-specific approaches to dominant heights modeling: The dummy variable method and the mixed model method. For. Ecol. Manag. 2008, 255, 2659–2669. [Google Scholar] [CrossRef]
- Sharma, R.P.; Zdeněk, V.; Stanislav, V.; Václav, J.; Miloš, K. Modelling individual tree diameter growth for Norway spruce in the Czech Republic using a generalized algebraic difference approach. J. For. Sci. 2017, 63, 227–238. [Google Scholar] [CrossRef] [Green Version]
- Davidian, M.; Giltinan, D.M. Nonlinear models for repeated measurement data: An overview and update. J. Agric. Biol. Environ. Stat. 2003, 8, 387–419. [Google Scholar] [CrossRef]
- Li, R.; Weiskittel, A.R. Comparison of model forms for estimating stem taper and volume in the primary conifer species of the North American Acadian Region. Ann. For. Sci. 2010, 67, 302. [Google Scholar] [CrossRef] [Green Version]
- Clark, J.S. Coastal forest tree populations in a changing environment, southeastern Long-Island, New-York. Ecol. Monogr. 1986, 56, 259–277. [Google Scholar] [CrossRef]
- Xue, C.Q.; Xu, Q.H.; Lin, L.P.; He, X.; Luo, Y.; Zhao, H.; Cao, L.; Lei, Y.C. Biomass models with breast height diameter and age for main nativetree species in Guangdong Province. Sci. Silvae Sin. 2019, 55, 97–108. (In Chinese) [Google Scholar] [CrossRef]
- Bai, Z.L. Econometric Analysis of Panel Data; Nankai University Press: Tianjin, China, 2008. (In Chinese) [Google Scholar]
- Chen, Q. Advanced Econometrics and Stata Application; Higher Education Press: Beijing, China, 2010. (In Chinese) [Google Scholar]
- Wooldridge, J.M. Introductory Econometrics: A Modern Approach, 2nd ed.; Thomson Learning: Stamford, CT, USA, 2003. [Google Scholar]
- Dien, N.T.; Hirai, Y.; Koshiba, J.; Sakai, S.-I. Factors affecting multiple persistent organic pollutant concentrations in the air above Japan: A panel data analysis. Chemosphere 2021, 277, 130356. [Google Scholar] [CrossRef]
- Zeide, B. Analysis of growth equations. For. Sci. 1993, 39, 594–616. [Google Scholar] [CrossRef]
- Tsoularis, A.; Wallace, J. Analysis of logistic growth models. Math. Biosci. 2002, 179, 21–55. [Google Scholar] [CrossRef] [Green Version]
- Burkhart, H.E.; Tomé, M. Modeling Forest Trees and Stands; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Meng, X.Y. Forestry Mensuration, 3rd ed.; China Forestry Publishing House: Beijing, China, 2006. (In Chinese) [Google Scholar]
- Niu, Y.L.; Dong, L.H.; Li, F.R. Site index model for Larix olgensis plantation based on generalized algebraic difference approach derivation. J. Beijing For. Univ. 2020, 42, 9–18. (In Chinese) [Google Scholar] [CrossRef]
- Bailey, R.L.; Clutter, J.L. Base-age invariant polymorphic site curves. For. Sci. 1974, 20, 155–159. [Google Scholar]
- Cieszewski, C.; Bailey, R.L. Generalized algebraic difference approach: Theory based derivation of dynamic site equations with polymorphism and variable asymptotes. For. Sci. 2000, 46, 116–126. [Google Scholar]
- He, X.Q.; Liu, W.Q. Applied Regression Analysis; China Remin University Press: Beijing, China, 2015. (In Chinese) [Google Scholar]
- Suits, D.B. Use of Dummy Variables in Regression Equations. J. Am. Stat. Assoc. 1957, 52, 548–551. [Google Scholar] [CrossRef]
- Hartigan, J.A.; Wong, M.A. A K-Means Clustering Algorithm. Appl. Stat. 1979, 28, 100–108. [Google Scholar] [CrossRef]
- Jain, A.K. Data clustering: 50 years beyond K-means. Pattern Recognit. Lett. 2010, 31, 651–666. [Google Scholar] [CrossRef]
- White, K.J. The Durbin-Watson Test for Autocorrelation in Nonlinear Models. Rev. Econ. Stat. 1992, 74, 370–373. [Google Scholar] [CrossRef]
- Niklasson, M. A comparison of three age determination methods for suppressed Norway spruce: Implications for age structure analysis. For. Ecol. Manag. 2002, 161, 279–288. [Google Scholar] [CrossRef]
- Cieszewski, C.J.; Strub, M. Generalized algebraic difference approach derivation of dynamic site equations with polymorphism and variable asymptotes from exponential and logarithmic functions. For. Sci. 2008, 54, 303–315. [Google Scholar]
- Yang, Y.; Huang, S.; Trincado, G.; Meng, S.X. Nonlinear mixed-effects modeling of variable-exponent taper equations for lodgepole pine in Alberta, Canada. Eur. J. For. Res. 2009, 128, 415–429. [Google Scholar] [CrossRef]
- Gallant, A.R.; Goebel, J.J. Nonlinear Regression with Autocorrelated Errors. J. Am. Stat. Assoc. 1976, 71, 961–967. [Google Scholar] [CrossRef]
- King, M.L. The alternative Durbin-Watson test: An assessment of Durbin and Watson’s choice of test statistic. J. Econom. 1981, 17, 51–66. [Google Scholar] [CrossRef]

| Tree Species | Sample Size | Tree Age/Year | Diameter Inside Bark/cm | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Mean | Std | Min | Max | Mean | Std | Min | Max | ||
| Stump height (0.3 m) | |||||||||
| Cinnamomum camphora | 40 | 27.80 | 9.77 | 11 | 58 | 23.71 | 9.79 | 11.49 | 45.95 |
| Schima superba | 40 | 25.13 | 8.29 | 13 | 45 | 22.97 | 9.40 | 8.17 | 49.75 |
| Liquidambar formosana | 40 | 27.05 | 13.04 | 11 | 82 | 23.69 | 8.99 | 10.59 | 42.10 |
| Breast height (1.3 m) | |||||||||
| Cinnamomum camphora | 40 | 25.55 | 9.06 | 9 | 51 | 20.71 | 8.00 | 9.94 | 36.50 |
| Schima superba | 40 | 23.38 | 8.21 | 11 | 45 | 20.67 | 8.61 | 7.18 | 44.94 |
| Liquidambar formosana | 40 | 24.48 | 13.03 | 8 | 81 | 21.29 | 8.02 | 10.06 | 38.62 |
| Tree Numbers | d(t + 1) | d(t) | d0 | Δd | Time Intervals |
|---|---|---|---|---|---|
| 102 | 5.80 | 5.46 | 5.46 | 0.35 | 0 |
| 102 | 6.82 | 5.80 | 5.46 | 1.01 | 1 |
| … | |||||
| 102 | 19.66 | 18.84 | 5.46 | 0.81 | 11 |
| 103 | 6.81 | 5.60 | 5.60 | 1.21 | 0 |
| 103 | 8.48 | 6.81 | 5.60 | 1.67 | 1 |
| … | |||||
| 103 | 27.75 | 26.68 | 5.60 | 1.07 | 12 |
| … | |||||
| 177 | 7.01 | 5.49 | 5.49 | 1.52 | 0 |
| 177 | 7.70 | 7.01 | 5.49 | 0.70 | 1 |
| … | |||||
| 177 | 36.50 | 35.04 | 5.49 | 1.46 | 25 |
| Author or Designation | Base Equation | Constraint Equation | Difference Constraint Equation | Constraint |
|---|---|---|---|---|
| Lundqvist–Korf | ||||
| Richards | ||||
| Monomolecular | ||||
| Logistic |
| Tree Species | Model | Sample Size | Parameters | Convergence Failure | ||
|---|---|---|---|---|---|---|
| a | b | c | ||||
| Stump height (0.3 m) | ||||||
| Cinnamomum camphora | Korf | 40 | 84.4(20.5~309.1) | 28.5(5.8~202) | −0.97(−2.6~−0.33) | 19 |
| Richards | 40 | 37.3 (16.7~101.1) | 0.089(0.01~0.37) | 2.8(1.03~14.2) | 12 | |
| Monomolecular | 40 | 62.1(26.5~113.8) | 0.022(0.005~0.074) | — | 27 | |
| Logistics | 40 | 30.8(15.5~60.1) | 13.5(6.0~28.7) | 0.15(0.07~0.26) | 10 | |
| Schima superba | Korf | 40 | 87.9(10.4~584.4) | 204.0(4.9~2995.230) | −1.1(−3.2~−0.38) | 15 |
| Richards | 40 | 41.8(9.1~106.6) | 0.094(0.02~0.30) | 3.4(1.3~15.9) | 5 | |
| Monomolecular | 40 | 124.5(17.5~390.2) | 0.018(0.002~0.056) | — | 27 | |
| Logistics | 40 | 27.9(12.3~62.6) | 19.0(8.0~57.1) | 0.21(0.084~0.39) | 14 | |
| Liquidambar formosana | Korf | 40 | 142.9(28.7~420.6) | 12.0(6.4~30.2) | −0.69(−1.1~−0.37) | 19 |
| Richards | 40 | 42.3 (16.8~73.6) | 0.07(0.016~0.204) | 2.1(0.66~4.04) | 12 | |
| Monomolecular | 40 | 109.9(18.3~269.5) | 0.017(0.004~0.069) | — | 25 | |
| Logistics | 40 | 30.6 (14.5~54.1) | 13.9(5.5~37.6) | 0.16(0.037~0.31) | 13 | |
| Breast height (1.3 m) | ||||||
| Cinnamomum camphora | Korf | 40 | 70.3 (18.0~205.1) | 15.6(3.7~39.6) | −0.93(−1.7~−0.38) | 23 |
| Richards | 40 | 45.8 (13.3~184.3) | 0.08(0.006~0.34) | 2.2(0.91~5.2) | 12 | |
| Monomolecular | 40 | 62.3(17.3~188.7) | 0.026(0.005~0.098) | — | 22 | |
| Logistics | 40 | 22.8(11.9~38.8) | 11.7(4.4~39.7) | 0.19(0.077~0.53) | 7 | |
| Schima superba | Korf | 40 | 103.5(9.2~338.3) | 23.9(6.1~223.1) | −0.8(−2.6~−0.38) | 11 |
| Richards | 40 | 39.7(8.1~88.1) | 0.089(0.016~0.29) | 2.3(1.2~5.7) | 3 | |
| Monomolecular | 40 | 64.9(10.5~212.2) | 0.03(0.005~0.084) | — | 26 | |
| Logistics | 40 | 24.8(7.8~47.3) | 14.6(6.5~47.5) | 0.21(0.09~0.37) | 1 | |
| Liquidambar formosana | Korf | 40 | 76.6(14.3~299.2) | 12.5(4.7~68.5) | −0.79(−2.0~−0.30) | 22 |
| Richards | 40 | 46.2(12.2~131.0) | 0.075(0.012~0.23) | 1.9(1.1~5.9) | 8 | |
| Monomolecular | 40 | 69.2(15.2~182.6) | 0.024(0.005~0.072) | — | 24 | |
| Logistics | 40 | 26.0(11.6~49.5) | 12.6(5.2~41.3) | 0.20(0.042~0.42) | 1 | |
| Tree Species | Samples | Min | 1st Quantile. | Medium | 3rd Quantile. | Max | Mean | Convergence Failure |
|---|---|---|---|---|---|---|---|---|
| Cinnamomum camphora | 40 | 0.1398 | 0.4325 | 0.6711 | 1.0382 | 2.6075 | 0.8611 | 12 |
| Schima superba | 40 | 0.2464 | 0.5403 | 0.8319 | 1.3459 | 2.4225 | 1.0913 | 3 |
| Liquidambar formosana | 40 | 0.2873 | 0.5856 | 0.7896 | 1.6657 | 2.8405 | 1.0980 | 8 |
| Tree Species | Height | R2adj | SEE | MPE/% | Parameter Estimations | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| a.c1 | a.c2 | a.c3 | a.c4 | a.c5 | b | c | |||||
| Cinnamomum camphora | Stump | 0.63 | 0.33 | 2.47 | 57.81 (4.28) | 90.28 (4.36) | 117.10 (4.32) | 145.92 (4.31) | 204.55 (4.30) | 0.011 (2.88) | 0.98 (10.85) |
| Breast height | 0.65 | 0.27 | 2.4 | 33.99 (7.33) | 54.07 (7.69) | 65.02 (7.42) | 87.21 (7.45) | 116.91 (7.37) | 0.021 (4.54) | 1.15 (13.15) | |
| Schima superba | Stump | 0.59 | 0.29 | 2.09 | 25.29 (14.06) | 33.65 (17.31) | 46.58 (19.87) | 61.58 (20.20) | 72.39 18.34 | 0.046 (9.72) | 1.63 (1.63) |
| Breast height | 0.61 | 0.26 | 2.11 | 33.28 (9.01) | 49.03 (9.51) | 60.65 (9.69) | 73.67 (9.79) | 92.22 (9.42) | 0.024 (5.28) | 1.04 (15.12) | |
| Liquidambar formosana | Stump | 0.64 | 0.28 | 2.12 | 35.44 (12.48) | 54.79 (13.15) | 73.63 (12.76) | 94.17 (12.69) | 128.22 (12.37) | 0.027 (7.83) | 1.43 (13.45) |
| Breast height | 0.7 | 0.23 | 1.9 | 30.5 (14.21) | 44.00 (14.20) | 54.87 (15.44) | 71.09 (14.86) | 95.00 (14.71) | 0.029 (8.88) | 1.40 (14.78) | |
| Tree Species | Height | ME | MAE | RMSE | Error | |||
|---|---|---|---|---|---|---|---|---|
| Min | Mean | Max | Std. | |||||
| Cinnamomum camphora | Stump | 3.05 | 3.24 | 3.89 | −1.76 | 3.05 | 8.33 | 2.45 |
| Breast height | 0.47 | 1.55 | 2.04 | −5.51 | 0.47 | 4.60 | 2.01 | |
| Schima superba | Stump | 0.84 | 1.8 | 2.42 | −3.15 | 0.84 | 6.24 | 2.29 |
| Breast height | 2.46 | 2.59 | 3.15 | −0.82 | 2.46 | 6.86 | 2 | |
| Liquidambar formosana | Stump | −0.35 | 1.93 | 2.59 | −7.42 | −0.35 | 5.05 | 2.59 |
| Breast height | −0.56 | 1.76 | 2.47 | −5.24 | −0.56 | 8.43 | 2.44 | |
| Tree Species | Height | ME | MAE | RMSE | Error | |||
|---|---|---|---|---|---|---|---|---|
| Min | Mean | Max | Std. | |||||
| Cinnamomum camphora | Stump | 3.35 | 3.49 | 4.27 | −0.96 | 3.35 | 9.07 | 2.65 |
| Breast height | 1.30 | 1.99 | 2.45 | −5.00 | 1.30 | 5.18 | 2.07 | |
| Schima superba | Stump | 1.66 | 2.11 | 2.83 | −1.70 | 1.66 | 7.39 | 2.29 |
| Breast height | 2.48 | 2.98 | 3.36 | −3.01 | 2.48 | 7.95 | 2.27 | |
| Liquidambar formosana | Stump | −6.95 | 7.02 | 9.11 | −23.80 | −6.95 | 1.33 | 5.89 |
| Breast height | −1.64 | 2.66 | 3.80 | −10.98 | −1.64 | 6.65 | 3.42 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Li, H.; Zhang, X.; Lei, Y.; Huang, J.; Liu, X. An Approach to Estimate Individual Tree Ages Based on Time Series Diameter Data—A Test Case for Three Subtropical Tree Species in China. Forests 2022, 13, 614. https://doi.org/10.3390/f13040614
Zhang Y, Li H, Zhang X, Lei Y, Huang J, Liu X. An Approach to Estimate Individual Tree Ages Based on Time Series Diameter Data—A Test Case for Three Subtropical Tree Species in China. Forests. 2022; 13(4):614. https://doi.org/10.3390/f13040614
Chicago/Turabian StyleZhang, Yiru, Haikui Li, Xiaohong Zhang, Yuancai Lei, Jinjin Huang, and Xiaotong Liu. 2022. "An Approach to Estimate Individual Tree Ages Based on Time Series Diameter Data—A Test Case for Three Subtropical Tree Species in China" Forests 13, no. 4: 614. https://doi.org/10.3390/f13040614
APA StyleZhang, Y., Li, H., Zhang, X., Lei, Y., Huang, J., & Liu, X. (2022). An Approach to Estimate Individual Tree Ages Based on Time Series Diameter Data—A Test Case for Three Subtropical Tree Species in China. Forests, 13(4), 614. https://doi.org/10.3390/f13040614





