Optimization of Wood Particleboard Drilling Operating Parameters by Means of the Artificial Neural Network Modeling Technique and Response Surface Methodology
Abstract
:1. Introduction
2. Materials and Methods
2.1. Data Colectting
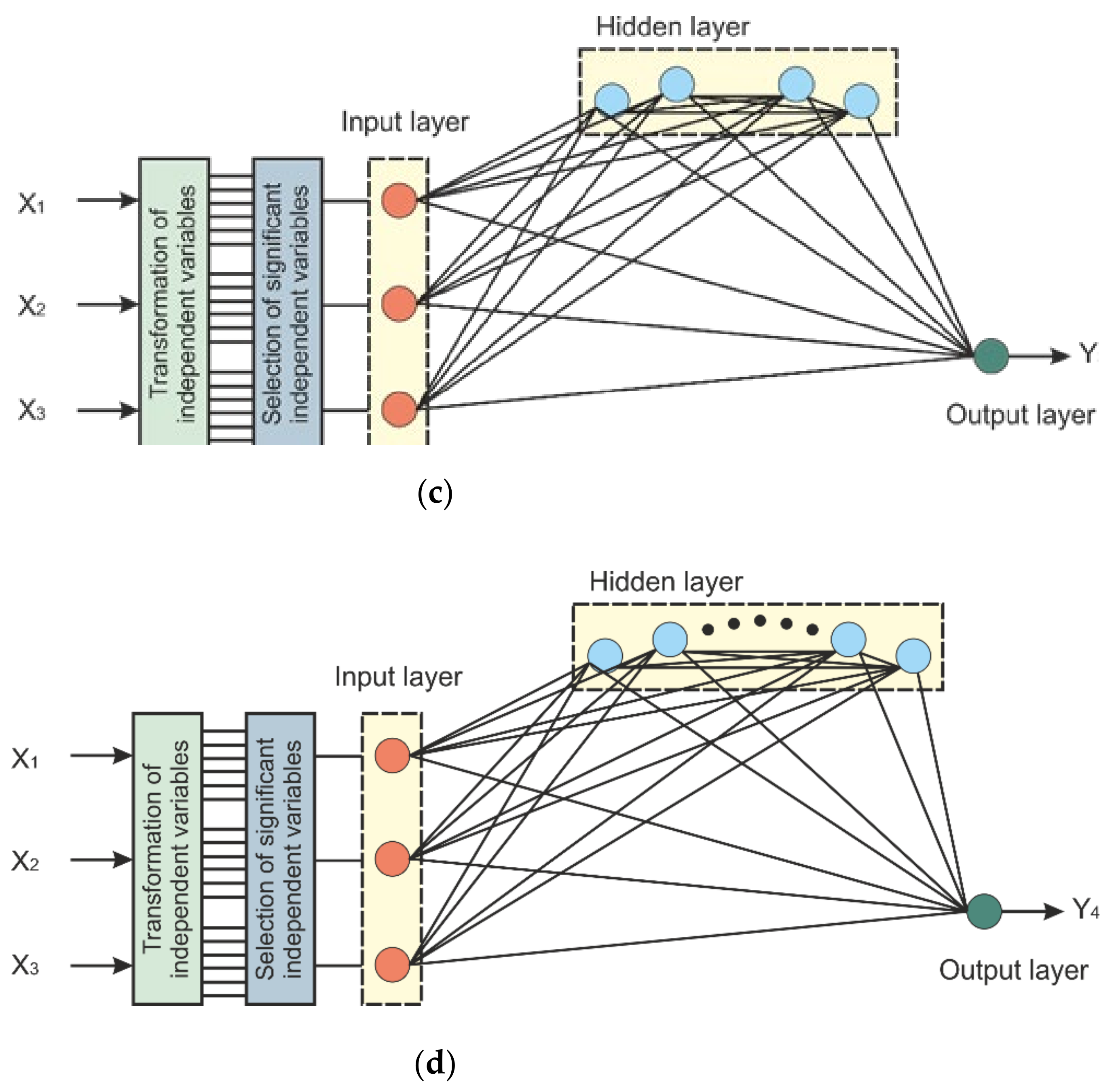
2.2. ANN Model Development
3. Results and Discussion
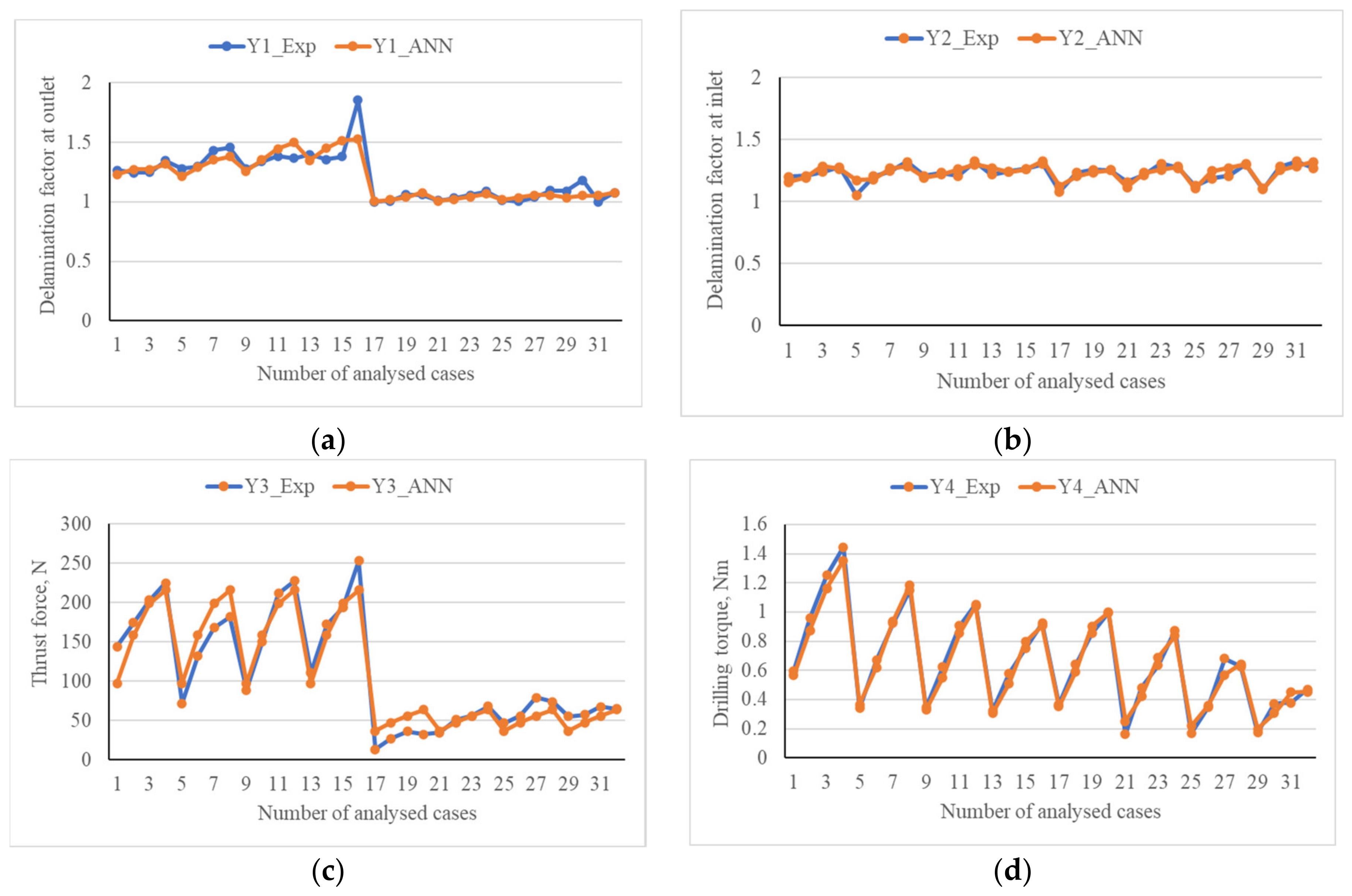
3.1. ANN Models
3.2. RSM Results
3.2.1. Delamination Factor at the Outlet (Y1)
3.2.2. Delamination Factor at the Inlet (Y2)
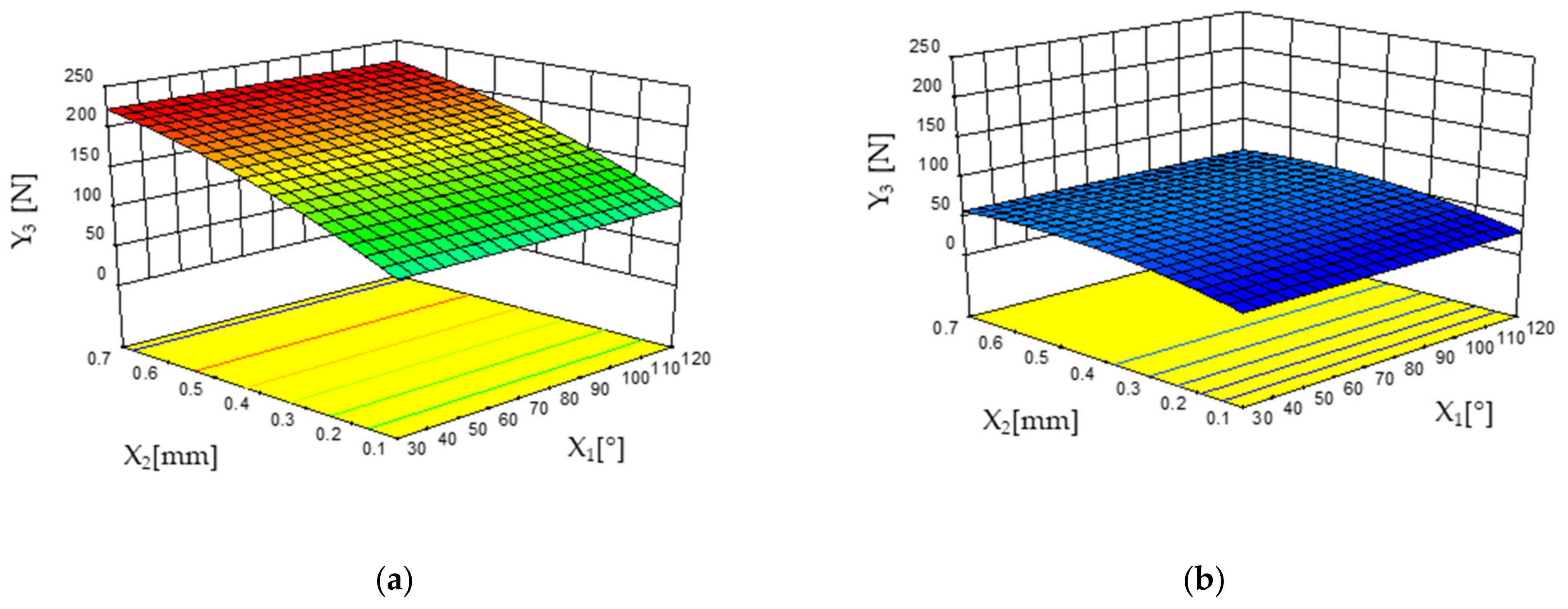
3.2.3. Thrust Force (Y3)
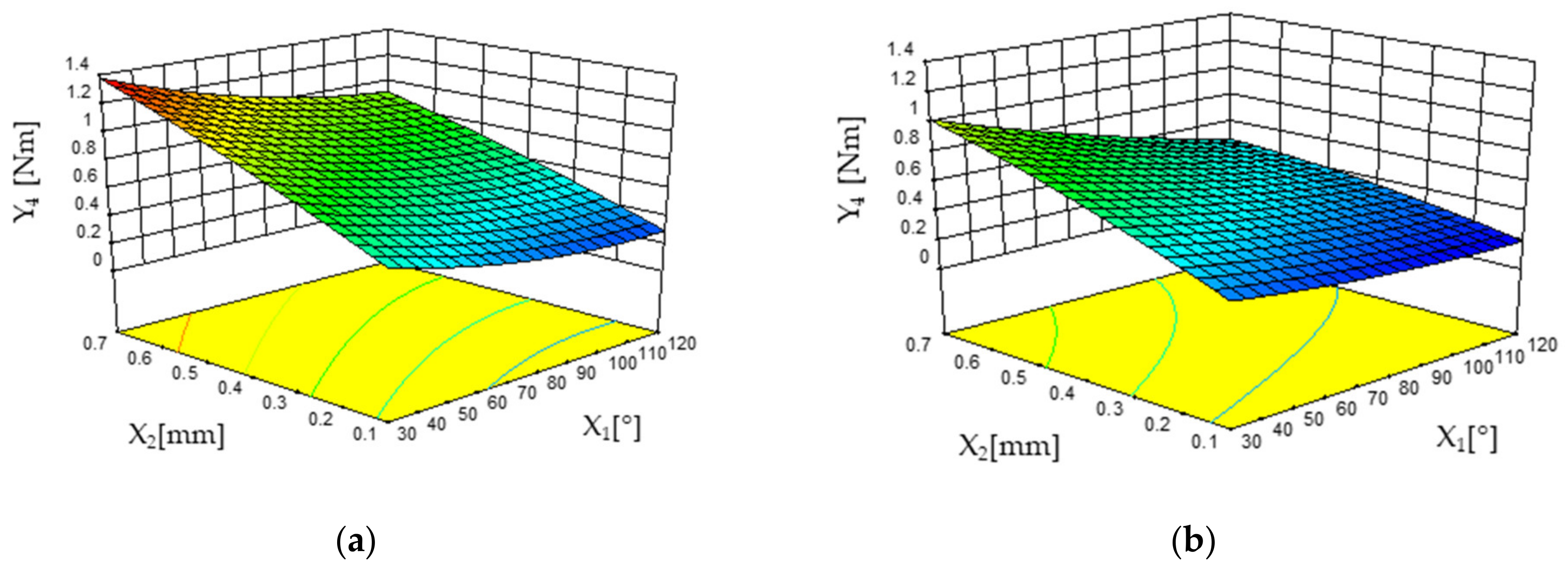
3.2.4. Drilling Torque (Y4)
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hetzel, F. About the Workability of Chipboard and Plywood—Drilling and Punching. Ph.D. Thesis, Technische Hochschule Dresden, Dresden, Germany, 1928. (In German). [Google Scholar]
- Radu, A. Contributions to the Establishment of the Optimal Parameters of Wood Drills. Ph.D. Thesis, Polytechnic Institute of Brasov, Brasov, Romania, 1967. (In Romanian). [Google Scholar]
- Valarmathi, T.N.; Palanikumar, K.; Latha, B. Measurement and analysis of thrust force in drilling of particle board (PB) composite panels. Measurement 2013, 46, 1220–1230. [Google Scholar] [CrossRef]
- Lilly, M.J.; Prakash, S.; Vijayalakshmi, P.; Putti, V.S.T. Multi response optimization of drilling parameters during drilling of particle board using Grey Relational Analysis. Appl. Mech. Mater. 2013, 592–594, 530–533. [Google Scholar] [CrossRef]
- Ispas, M.; Gurău, L.; Răcăşan, S. Study regarding the variation of the thrust force, drilling torque and surface delamination with the feed per tooth and drill tip angle at drilling pre-laminated particleboard. Pro Ligno 2014, 10, 40–52. [Google Scholar]
- Ispas, M.; Gurău, L.; Răcăşan, S. The influence of the tool point angle and feed rate on the delamination at drilling of pre-laminated particleboard. Pro Ligno 2015, 11, 494–500. [Google Scholar]
- Ispas, M.; Răcăşan, S. The influence of the tool point angle and feed rate on the dynamic parameters at drilling coated particleboard. Pro Ligno 2015, 11, 457–463. [Google Scholar]
- Podziewski, P.; Szymanowski, K.; Gorski, J.; Czarniak, P. Relative Machinability of Wood-Based Boards in the Case of Drilling—Experimental Study. Bioresources 2018, 13, 1761–1772. [Google Scholar] [CrossRef] [Green Version]
- Madhan Kumar, A.; Jayakumar, K. Drilling studies on particle board composite using HSS twist drill and spade drill. IOP Conf. Ser. Mater. Sci. Eng. 2018, 402, 012029. [Google Scholar] [CrossRef] [Green Version]
- Górski, J. The review of new scientific developments in drilling in wood-based panels with particular emphasis on the latest research trends in drill condition monitoring. Forests 2022, 13, 242. [Google Scholar] [CrossRef]
- Gürgen, A.; Çakmak, A.; Yıldız, S.; Malkoçoğlu, A. Optimization of CNC operating parameters to minimize surface roughness of Pinus sylvestris using integrated artificial neural network and genetic algorithm. Maderas-Cienc. Tecnol. 2022, 24, 1–12. Available online: http://revistas.ubiobio.cl/index.php/MCT/article/view/5163 (accessed on 5 May 2022). [CrossRef]
- Özşahin, Ş.; Singer, H. Prediction of noise emission in the machining of wood materials by means of an artificial neural network. N. Z. J. For. Sci. 2022, 52, 1–11. [Google Scholar] [CrossRef]
- Rahimi, S.; Avramidis, S. Predicting moisture content in kiln dried timbers using machine learning. Eur. J. Wood Prod. 2022, 80, 681–692. [Google Scholar] [CrossRef]
- Chai, H.; Chen, X.; Cai, Y.; Zhao, J. Artificial neural network modeling for predicting wood moisture content in high frequency vacuum drying process. Forests 2019, 10, 16. [Google Scholar] [CrossRef] [Green Version]
- Bedelean, B. Application of artificial neural networks and Monte Carlo method for predicting the reliability of RF phytosanitary treatment of wood. Eur. J. Wood Prod. 2018, 76, 1113–1120. [Google Scholar] [CrossRef]
- Avramidis, S.; Iliadis, L. Predicting wood thermal conductivity using artificial neural networks. Wood Fiber Sci. 2005, 37, 682–690. [Google Scholar]
- De Melo, D.J.; Guedes, T.O.; da Silva, J.R.M.; de Paiva, A.P. Robust optimization of energy consumption during mechanical processing of wood. Eur. J. Wood Prod. 2019, 77, 1211–1220. [Google Scholar] [CrossRef]
- Georgescu, S.; Varodi, A.M.; Răcășan, S.; Bedelean, B. Effect of the dowel length, dowel diameter, and adhesive consumption on bending moment capacity of heat-treated wood dowel joints. BioResources 2019, 14, 6619–6632. [Google Scholar] [CrossRef]
- Sova, D.; Bedelean, B.; Venetia, S. Application of response surface methodology to optimization of wood drying conditions in a pilot-scale kiln. Balt. For. 2016, 22, 348–356. [Google Scholar]
- Tiryaki, S.; Özşahin, Ş.; Aydin, A. Employing artificial neural networks for minimizing surface roughness and power consumption in abrasive machining of wood. Eur. J. Wood Prod. 2017, 75, 347–358. [Google Scholar] [CrossRef]
- Anderson, M.J.; Whitcomb, P.J. RSM Simplified: Optimizing Processes Using Response Surface Methods for Design of Experiments; CRC Press: Boca Raton, FL, USA; Taylor & Francis Group: Abingdon, UK, 2005. [Google Scholar]
- Ariaee, S.; Tutunchi, A.; Kianvash, A.; Entezami, A.A. Modeling and optimization of mechanical behavior of bonded composite–steel single lap joints by response surface methodology. Int. J. Adhes. Adhes. 2014, 54, 30–39. [Google Scholar] [CrossRef]
- Watanabe, K.; Korai, H.; Matsushita, Y.; Hayashi, T. Predicting internal bond strength of particleboard under outdoor exposure based on climate data: Comparison of multiple linear regression and artificial neural network. J. Wood Sci. 2015, 61, 151–158. [Google Scholar] [CrossRef]
- Tiryaki, S.; Aydin, A. An artificial neural network model for predicting compression strength of heat-treated woods and comparison with a multiple linear regression model. Constr. Build. Mater. 2014, 62, 102–108. [Google Scholar] [CrossRef]
- Fu, Z.; Avramidis, S.; Zhao, J.; Cai, Y. Artificial neural network modeling for predicting elastic strain of white birch disks during drying. Eur. J. Wood Prod. 2017, 75, 949–955. [Google Scholar] [CrossRef]
- Mansfield, S.D.; Iliadis, L.; Avramidis, S. Neural network prediction of bending strength and stiffness in western hemlock (Tsuga heterophylla Raf.). Holzforschung 2007, 61, 707–716. [Google Scholar] [CrossRef]



| Factor | Values | |||
|---|---|---|---|---|
| Drill point angle (X1), ° | 30 | 60 | 90 | 120 |
| Tooth bite (X2), mm | 0.1 | 0.3 | 0.5 | 0.7 |
| Drill type (X3) | Flat | Helical | ||
| Numeric Factor | Level | ||||
|---|---|---|---|---|---|
| −α * | −1 | 0 | +1 | +α * | |
| Drill tip angle (X1), ° | 30 | 30 | 75 | 120 | 120 |
| Tooth bite (X2), mm | 0.1 | 0.1 | 0.4 | 0.7 | 0.7 |
| Categoric factor | Level 1 | Level 2 | |||
| Drill type (X3) | Flat | Helical | |||
| Run | Factors | Responses | |||||
|---|---|---|---|---|---|---|---|
| Drill Tip Angle (X1), ° | Tooth Bite (X2), mm | Drill Type (X3) | Y1 | Y2 | Y3 | Y4 | |
| 1 | 30 | 0.4 | Flat | 1.28 | 182.98 | 1.03 | 1.25 |
| 2 | 30 | 0.1 | Helical | 1.01 | 37.13 | 0.35 | 1.12 |
| 3 | 75 | 0.4 | Helical | 1.04 | 52.16 | 0.51 | 1.26 |
| 4 | 75 | 0.1 | Flat | 1.23 | 97.44 | 0.34 | 1.18 |
| 5 | 120 | 0.4 | Helical | 1.05 | 52.16 | 0.39 | 1.27 |
| 6 | 120 | 0.1 | Flat | 1.35 | 97.44 | 0.31 | 1.27 |
| 7 | 75 | 0.4 | Helical | 1.04 | 52.16 | 0.51 | 1.26 |
| 8 | 75 | 0.4 | Flat | 1.36 | 182.98 | 0.73 | 1.22 |
| 9 | 30 | 0.1 | Flat | 1.23 | 97.44 | 0.57 | 1.16 |
| 10 | 75 | 0.4 | Flat | 1.36 | 182.98 | 0.73 | 1.22 |
| 11 | 30 | 0.7 | Flat | 1.32 | 215.99 | 1.35 | 1.26 |
| 12 | 75 | 0.4 | Flat | 1.36 | 182.98 | 0.73 | 1.22 |
| 13 | 75 | 0.1 | Helical | 1.01 | 37.13 | 0.23 | 1.11 |
| 14 | 75 | 0.7 | Flat | 1.46 | 215.99 | 1.11 | 1.29 |
| 15 | 30 | 0.7 | Helical | 1.08 | 64.01 | 1.00 | 1.25 |
| 16 | 120 | 0.4 | Flat | 1.49 | 182.98 | 0.65 | 1.22 |
| 17 | 75 | 0.4 | Helical | 1.04 | 52.16 | 0.51 | 1.26 |
| 18 | 120 | 0.1 | Helical | 1.04 | 37.13 | 0.20 | 1.11 |
| 19 | 75 | 0.4 | Helical | 1.04 | 52.16 | 0.51 | 1.26 |
| 20 | 75 | 0.7 | Helical | 1.06 | 64.01 | 0.75 | 1.29 |
| 21 | 120 | 0.7 | Helical | 1.08 | 64.01 | 0.45 | 1.32 |
| 22 | 75 | 0.4 | Flat | 1.36 | 182.98 | 0.73 | 1.22 |
| 23 | 75 | 0.4 | Flat | 1.36 | 182.98 | 0.73 | 1.22 |
| 24 | 75 | 0.4 | Helical | 1.04 | 52.16 | 0.51 | 1.26 |
| 25 | 120 | 0.7 | Flat | 1.53 | 215.99 | 0.90 | 1.33 |
| 26 | 30 | 0.4 | Helical | 1.03 | 52.16 | 0.75 | 1.22 |
| Model Output | Number of Neurons in the Layers of ANN Models | Coefficient of Correlation (R) | Coefficient of Determination (R2) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Input | Hidden | Outlet | Training | Testing | Validation | Training | Testing | Validation | |
| Delamination factor at the outlet (Y1) | 3 | 6 | 1 | 0.88 | 0.88 | 0.90 | 0.77 | 0.77 | 0.82 |
| Delamination factor at the inlet (Y2) | 3 | 13 | 1 | 0.76 | 0.72 | 0.67 | 0.57 | 0.51 | 0.44 |
| Thrust force (Y3) | 3 | 4 | 1 | 0.94 | 0.95 | 0.96 | 0.88 | 0.90 | 0.92 |
| Drilling torque (Y4) | 3 | 9 | 1 | 0.97 | 0.97 | 0.98 | 0.94 | 0.94 | 0.97 |
| “Source” | “Sum of Squares” | “df” | “Mean Square” | “F-Value” | “p-Value Prob > F” | Observation |
|---|---|---|---|---|---|---|
| Model | 0.73 | 3 | 0.24 | 145 | <0.0001 | Significant |
| Drill tip angle (X1) | 0.030 | 1 | 0.030 | 17.65 | 0.0004 | |
| Tooth bite (X2) | 0.037 | 1 | 0.037 | 21.67 | 0.0001 | |
| Drill type (X3) | 0.67 | 1 | 0.67 | 395.68 | <0.0001 | |
| Predicted R2 | 0.92 | |||||
| “Source” | “Sum of Squares” | “df” | “Mean Square” | “F-Value” | “p-Value Prob > F” | Observation |
|---|---|---|---|---|---|---|
| Model | 0.059 | 3 | 0.020 | 17.66 | <0.0001 | Significant |
| Drill tip angle (X1) | 0.004 | 1 | 0.004 | 4.03 | 0.05 | Not significant |
| Tooth bite (X2) | 0.054 | 1 | 0.054 | 48.57 | <0.0001 | Significant |
| Drill type (X3) | 0.0004 | 1 | 0.0004 | 0.39 | 0.5365 | Not significant |
| Predicted R2 | 0.54 | |||||
| “Source” | “Sum of Squares” | “df” | “Mean Square” | “F-Value” | “p-Value Prob > F” | Observation |
|---|---|---|---|---|---|---|
| Model | 116,130 | 8 | 14,516.30 | 251.06 | <0.0001 | Significant |
| Drill tip angle (X1) | 1.455 × 10−11 | 1 | 1.455 × 10−11 | 2.51 × 10−13 | 1 | Not Significant |
| Tooth bite (X2) | 15,862.56 | 1 | 15,862.56 | 274.35 | <0.0001 | Significant |
| Drill type (X3) | 92,711.70 | 1 | 92,711.70 | 1603 | <0.0001 | Significant |
| X1X2 | 0 | 1 | 0 | 0 | 1 | Not Significant |
| X1X3 | 0 | 1 | 0 | 0 | 1 | Not Significant |
| X2X3 | 6303.16 | 1 | 6303.16 | 109.01 | <0.0001 | Significant |
| X12 | 0 | 1 | 0 | 0 | 1 | Not Significant |
| X22 | 1071.18 | 1 | 1071.18 | 18.53 | 0.0005 | Significant |
| Predicted R2 | 0.97 | |||||
| “Source” | “Sum of Squares” | “df” | “Mean Square” | “F-Value” | “p-Value Prob > F” | Observation |
|---|---|---|---|---|---|---|
| Model | 1.96 | 11 | 0.18 | 335 | <0.0001 | Significant |
| Drill tip angle (X1) | 0.38 | 1 | 0.38 | 715 | <0.0001 | Significant |
| Tooth bite (X2) | 1.06 | 1 | 1.06 | 1992 | <0.0001 | Significant |
| Drill type (X3) | 0.14 | 1 | 0.14 | 269 | <0.0001 | Significant |
| X1X2 | 0.042 | 1 | 0.042 | 78 | <0.0001 | Significant |
| X1X3 | 0.0001 | 1 | 0.0001 | 0.19 | 0.6681 | Not significant |
| X2X3 | 0.044 | 1 | 0.044 | 83.03 | <0.0001 | Significant |
| X12 | 0.020 | 1 | 0.020 | 37.59 | <0.0001 | Significant |
| X22 | 0.006 | 1 | 0.00652 | 12.25 | 0.0035 | Significant |
| X1X2X3 | 0.005 | 1 | 0.00537 | 10.09 | 0.0067 | Significant |
| 0.003 | 1 | 0.0032 | 6.01 | 0.0279 | Significant | |
| 0.0001 | 1 | 0.00015 | 0.28 | 0.602 | Not significant | |
| Predicted R2 | 0.96 | |||||
| Factor/Response | Goal | Lower Limit | Upper Limit | Importance |
|---|---|---|---|---|
| Drill tip angle (X1) | In range | 30 | 120 | 3 |
| Tooth bite (X2) | In range | 0.1 | 0.7 | 3 |
| Drill type (X3) | In range | Flat | Helical | 3 |
| Delamination factor at the inlet (Y1) | Minimize | 1.00 | 1.52 | 3 |
| Delamination factor at the outlet (Y2) | Minimize | 1.10 | 1.32 | 3 |
| Thrust force (Y3) | Minimize | 37.13 | 215.99 | 3 |
| Drilling torque (Y4) | Minimize | 0.19 | 1.35 | 3 |
| Solution No. | X1 | X2 | X3 | Delamination Factor at the Outlet | Delamination Factor at the Inlet | Trust Force (N) | Drilling Torque (Nm) | D | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Y1 | ER1 | Y2 | ER2 | Y3 | ER3 | Y4 | ER4 | |||||||||
| 1 | 90.75 | 0.1 | Helical | 1.00 | 1.01 a | 0.9 | 1.16 | 1.11 a | 4.5 | 30 | 50 a | 40 | 0.21 | 0.19 a | 11 | 0.92 |
| 2 | 57.18 | 0.1 | Helical | 0.96 | 1.00 b | 4.0 | 1.15 | 1.14 b | 0.8 | 30 | 38 b | 21 | 0.27 | 0.21 b | 29 | 0.92 |
| 3 | 32.36 | 0.1 | Flat | 1.26 | 1.25 c | 0.8 | 1.15 | 1.18 c | 2.5 | 104 | 134 c | 23 | 0.55 | 0.59 c | 7 | 0.64 |
| 4 | 60.77 | 0.1 | Flat | 1.29 | 1.24 b | 4.0 | 1.16 | 1.10 b | 5.5 | 104 | 68 b | 35 | 0.40 | 0.36 b | 11 | 0.64 |
| 5 | 90.75 | 0.1 | Flat | 1.32 | 1.27 a | 3.9 | 1.17 | 1.23 a | 4.8 | 104 | 93 a | 12 | 0.31 | 0.33 a | 6 | 0.62 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bedelean, B.; Ispas, M.; Răcășan, S.; Baba, M.N. Optimization of Wood Particleboard Drilling Operating Parameters by Means of the Artificial Neural Network Modeling Technique and Response Surface Methodology. Forests 2022, 13, 1045. https://doi.org/10.3390/f13071045
Bedelean B, Ispas M, Răcășan S, Baba MN. Optimization of Wood Particleboard Drilling Operating Parameters by Means of the Artificial Neural Network Modeling Technique and Response Surface Methodology. Forests. 2022; 13(7):1045. https://doi.org/10.3390/f13071045
Chicago/Turabian StyleBedelean, Bogdan, Mihai Ispas, Sergiu Răcășan, and Marius Nicolae Baba. 2022. "Optimization of Wood Particleboard Drilling Operating Parameters by Means of the Artificial Neural Network Modeling Technique and Response Surface Methodology" Forests 13, no. 7: 1045. https://doi.org/10.3390/f13071045
APA StyleBedelean, B., Ispas, M., Răcășan, S., & Baba, M. N. (2022). Optimization of Wood Particleboard Drilling Operating Parameters by Means of the Artificial Neural Network Modeling Technique and Response Surface Methodology. Forests, 13(7), 1045. https://doi.org/10.3390/f13071045







